Light Trapping above the Light Cone in One-Dimensional Arrays of Dielectric Spheres
Abstract
:1. Introduction
- (i)
- (ii)
- (iii)
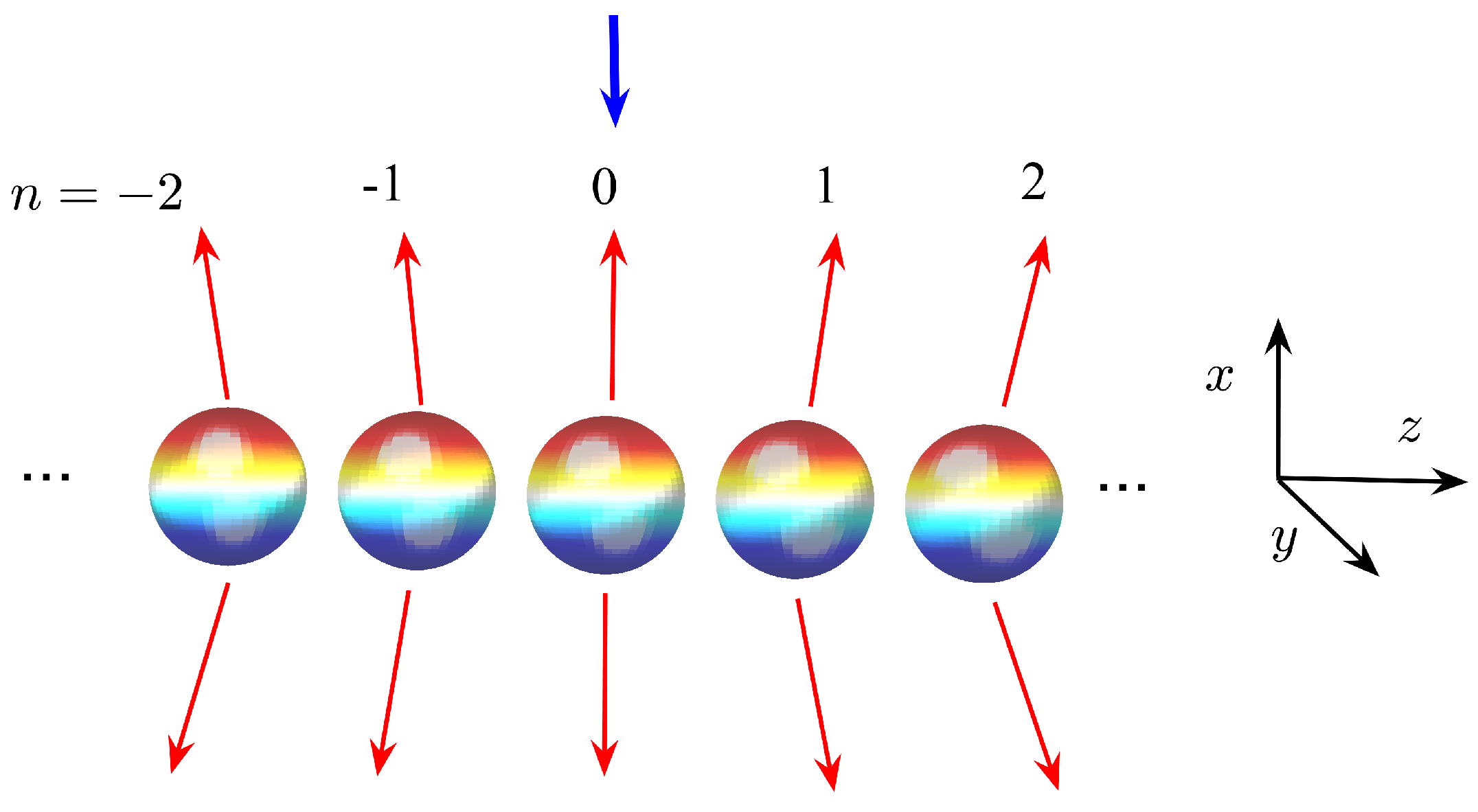
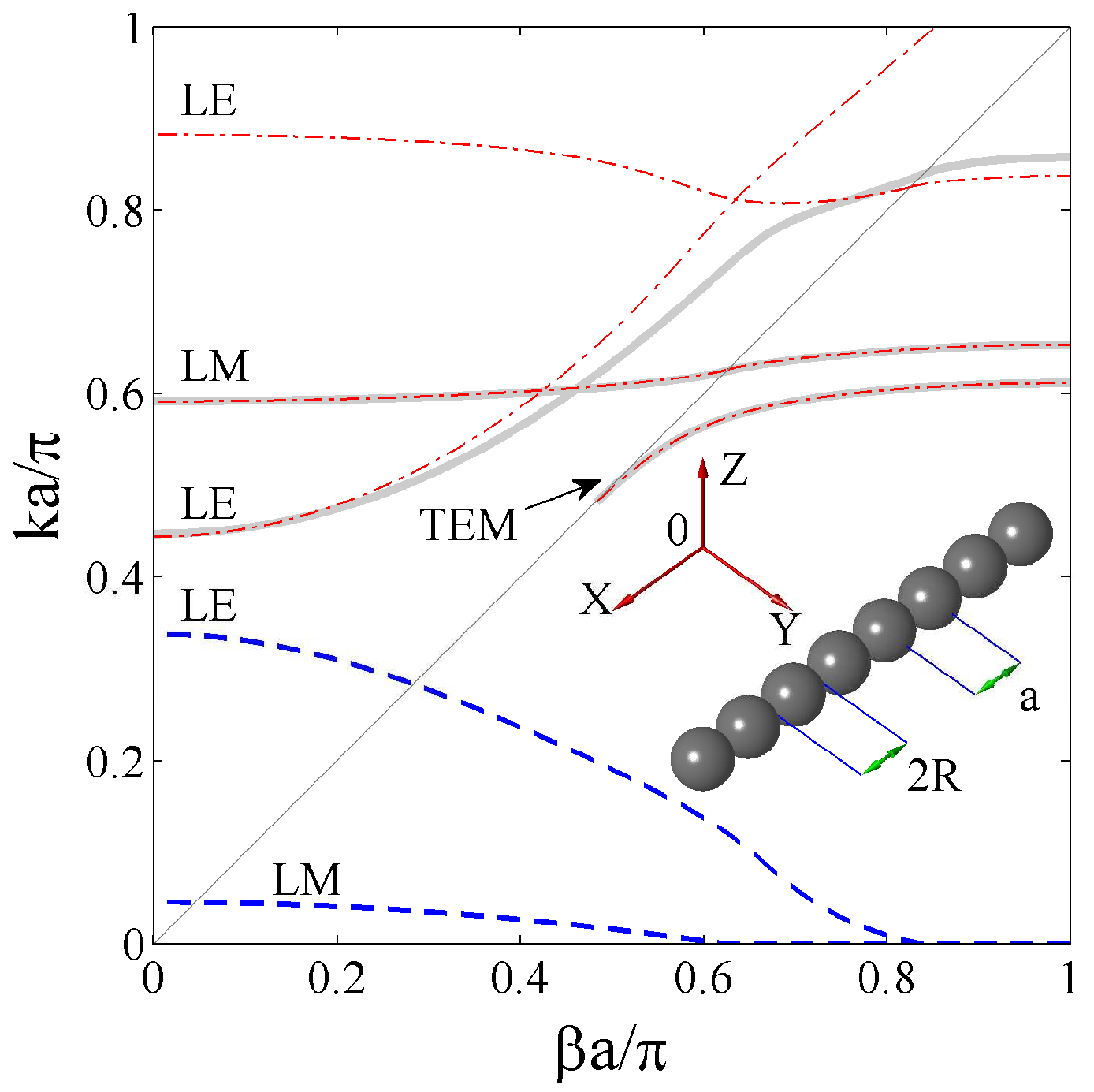
2. Basic Equations for EM Wave Scattering by a Linear Array of Spheres
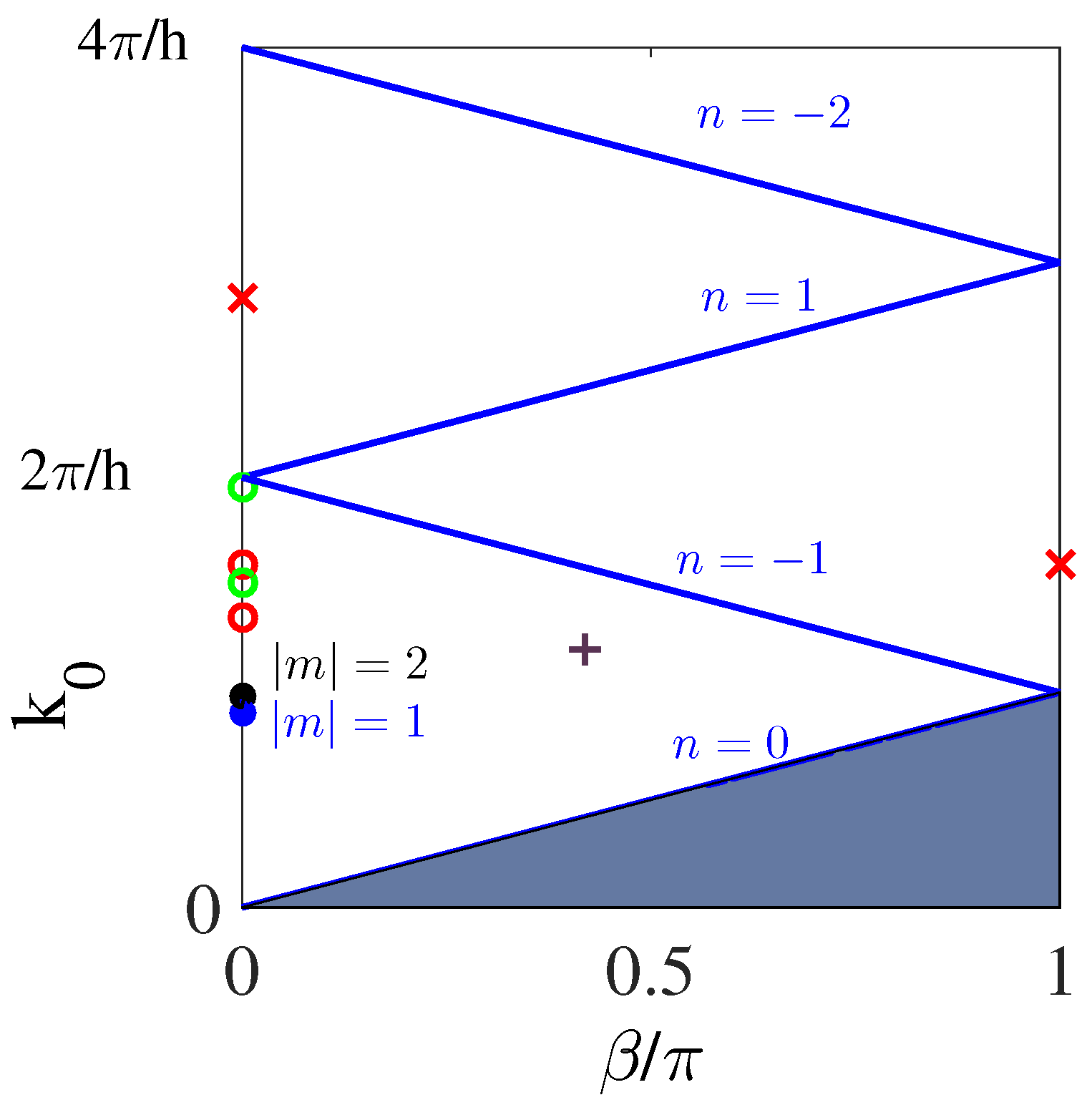
3. The Diffraction Continua of Vector Cylindrical Modes
4. Classification of BSCs in the Array of Spheres
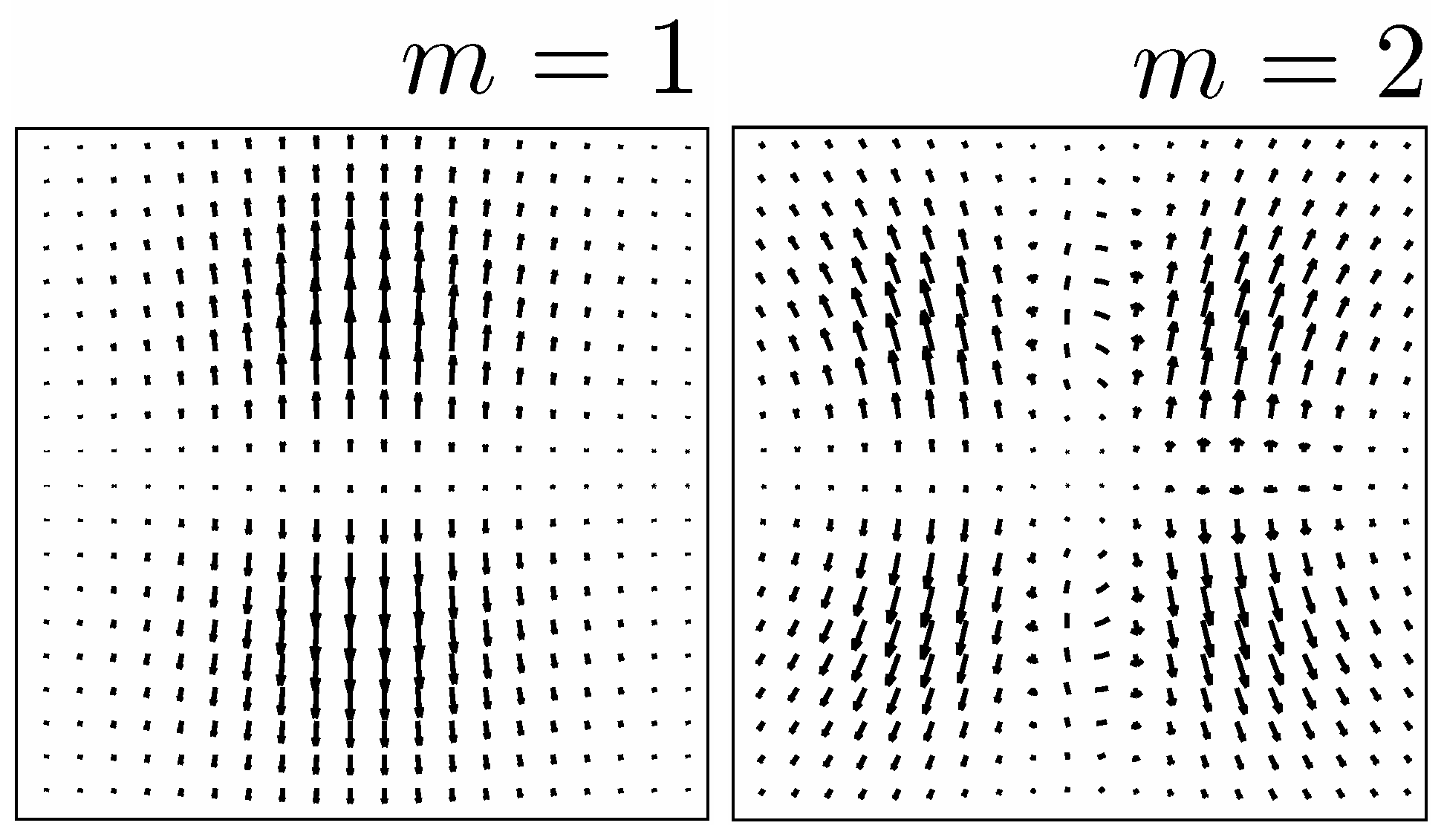
5. Symmetry Protected BSCs
5.1. Degenerate BSCs with
5.2. Robust Bloch BSCs with
6. Light Guiding above the Light Line
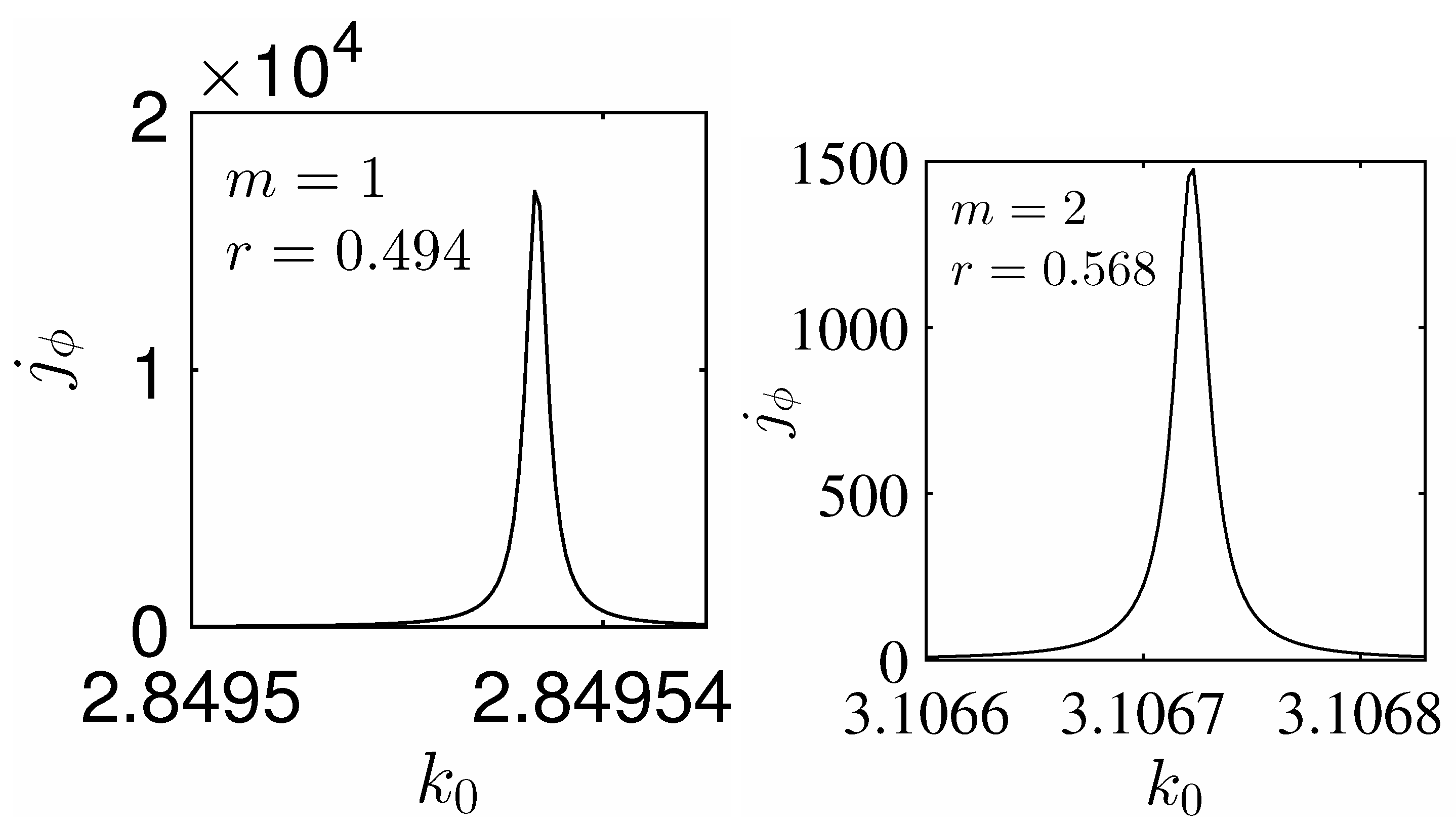
7. Emergence of the BSC in Scattering
7.1. Symmetry Protected BSCs
7.2. Scattering of Plane Waves in the Vicinity of the Quasi-BSCs with OAM
8. Scattering of Plane Waves in the Vicinity of the Bloch BSC
9. Transfer of SAM into OAM of the BSC with
10. Propagating Bloch BSCs with Orbital Angular Momentum
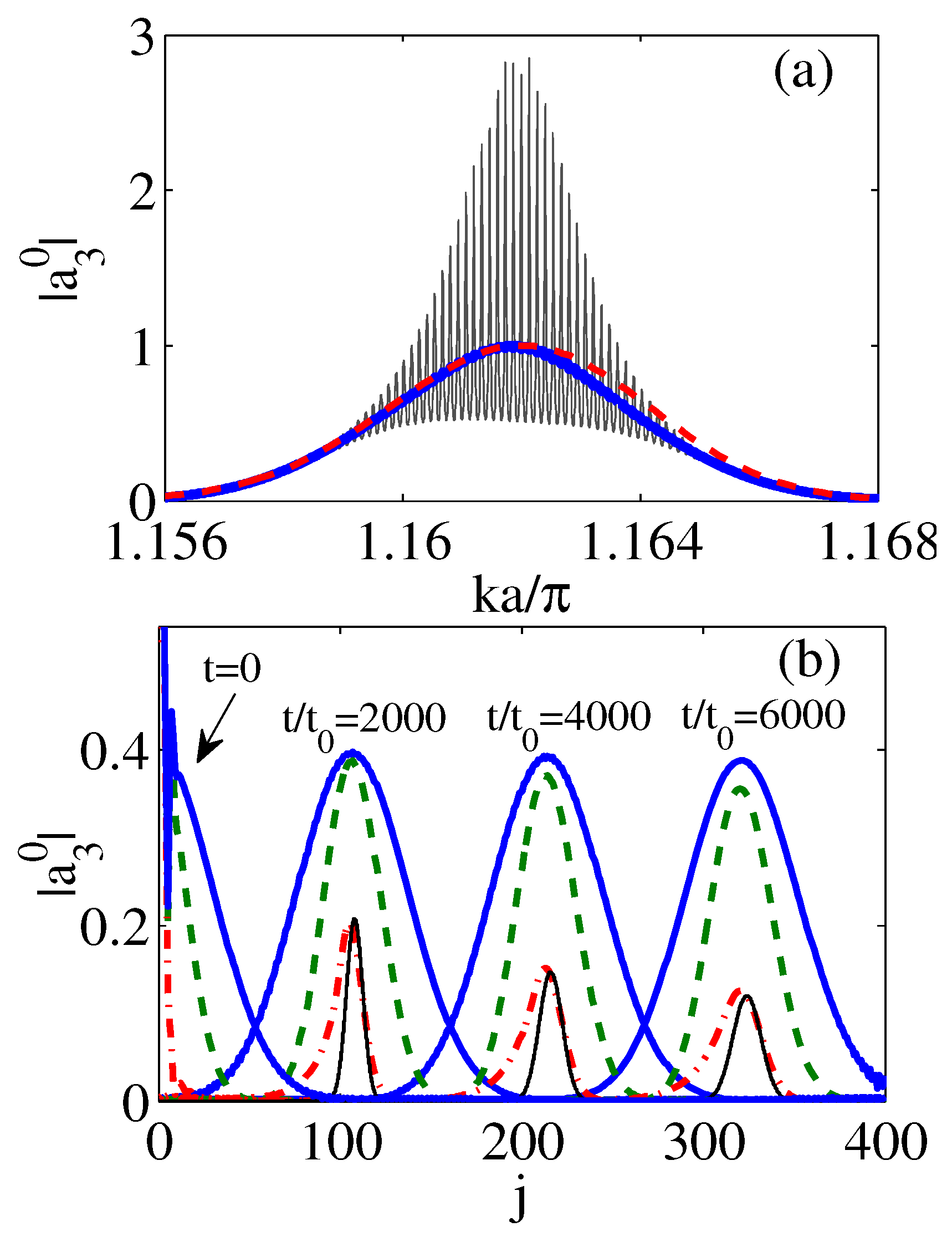
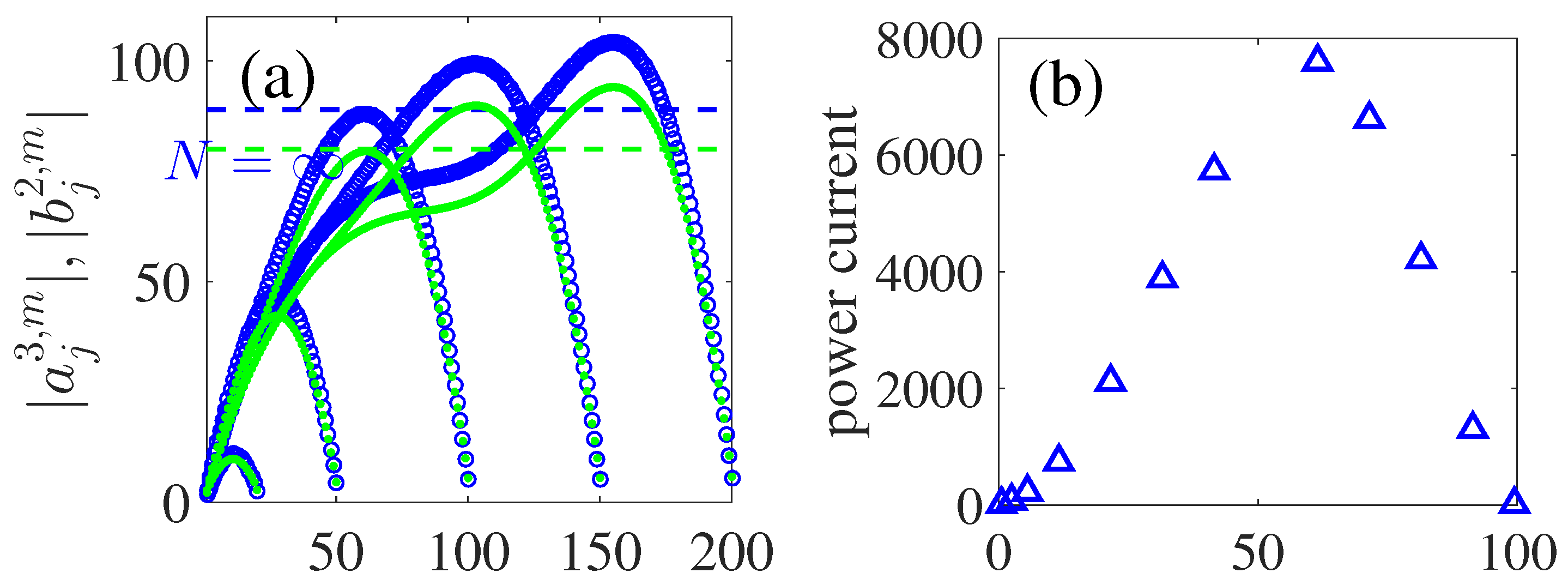
11. Array with the Finite Number of Dielectric Spheres
12. Summary and Discussion
- (1)
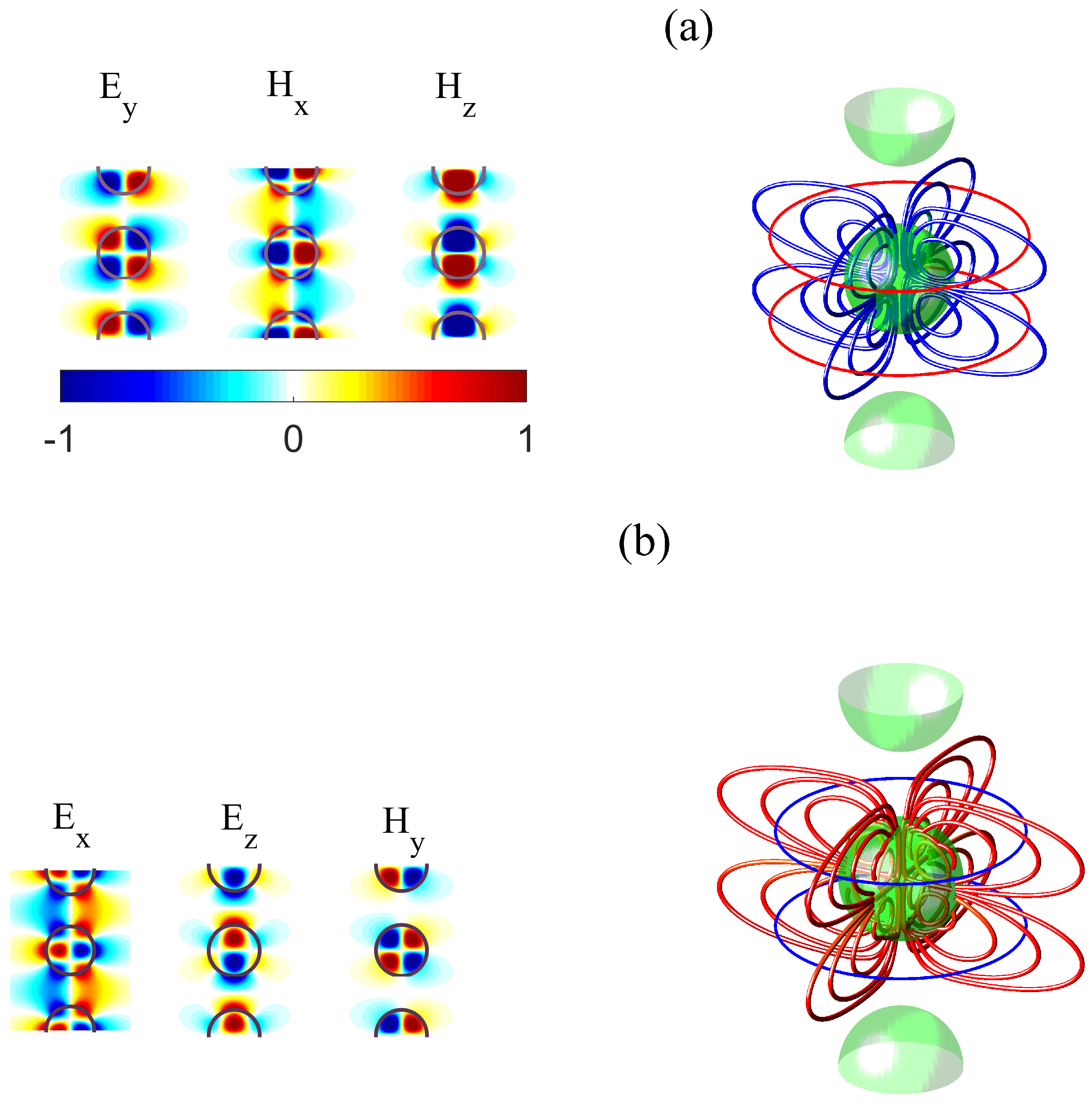
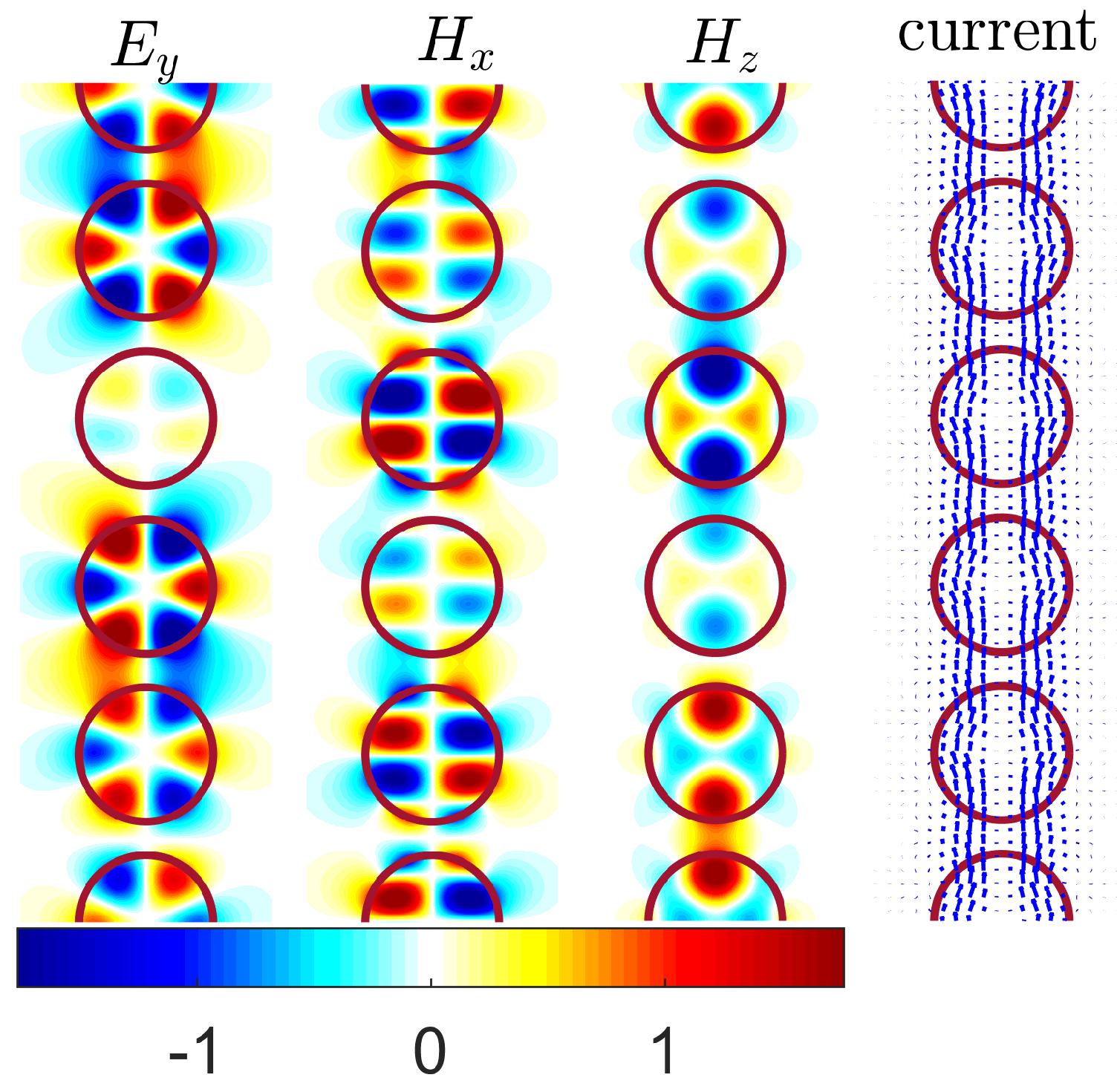
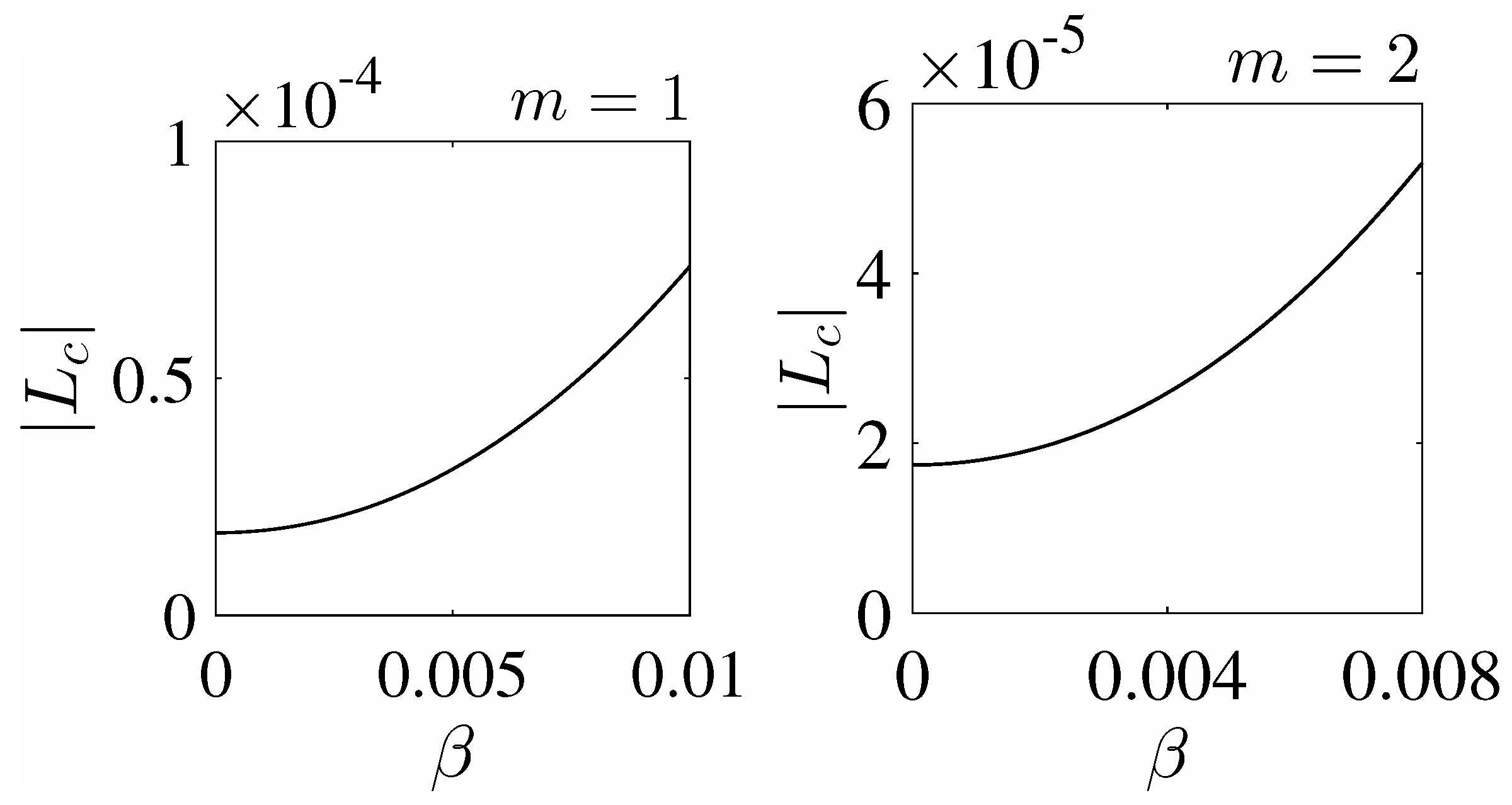
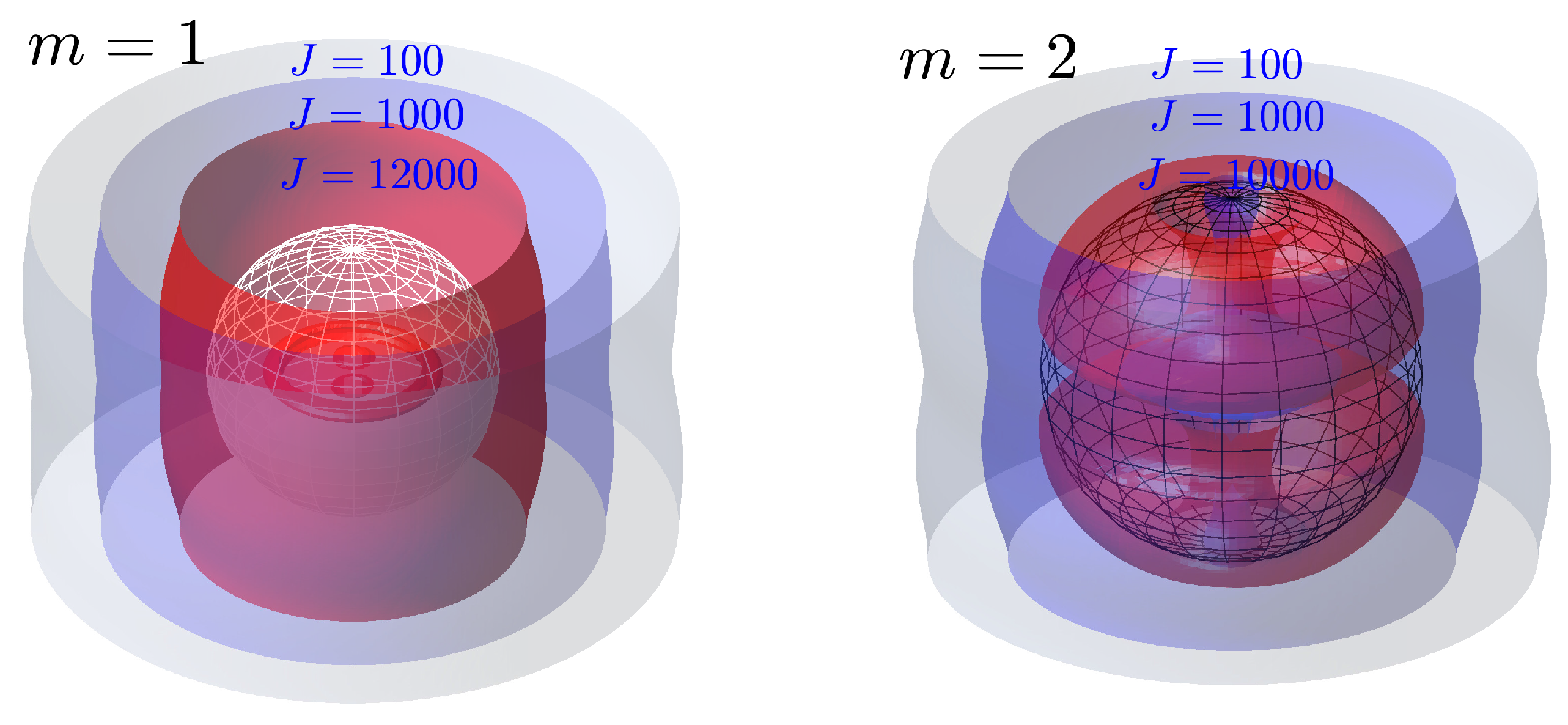
- The symmetry protected BSCs constitute the vast majority of BSCs which are symmetrically mismatched with the first diffraction continuum of both polarizations. The EM field configurations of such BSCs presented in Figure 2 show hybridizations of a few orbital numbers which specify the BSCs as multipoles of high order. Therefore the BSC solutions can not be obtained by the use of the dipole approximation [20,21]. The most remarkable property from experimental viewpoint is the robustness of the BSCs relative to choice of the material parameters of the dielectric spheres. We present in Figure 3 an example of the BSC which is symmetry protected relative to the TM diffraction continuum but a zero coupling to the TE continuum obtained through variation of the sphere radius.
- (2)
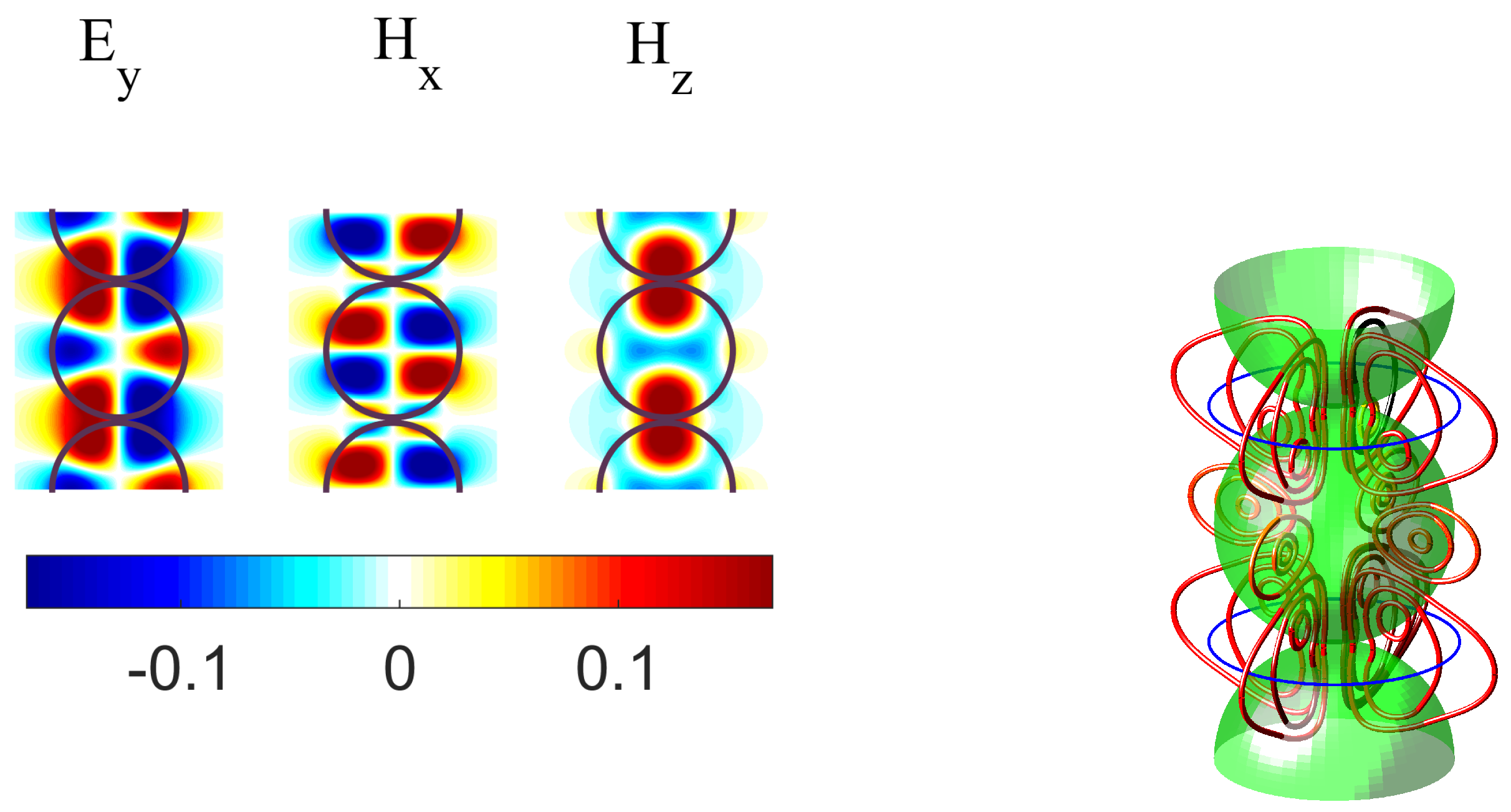
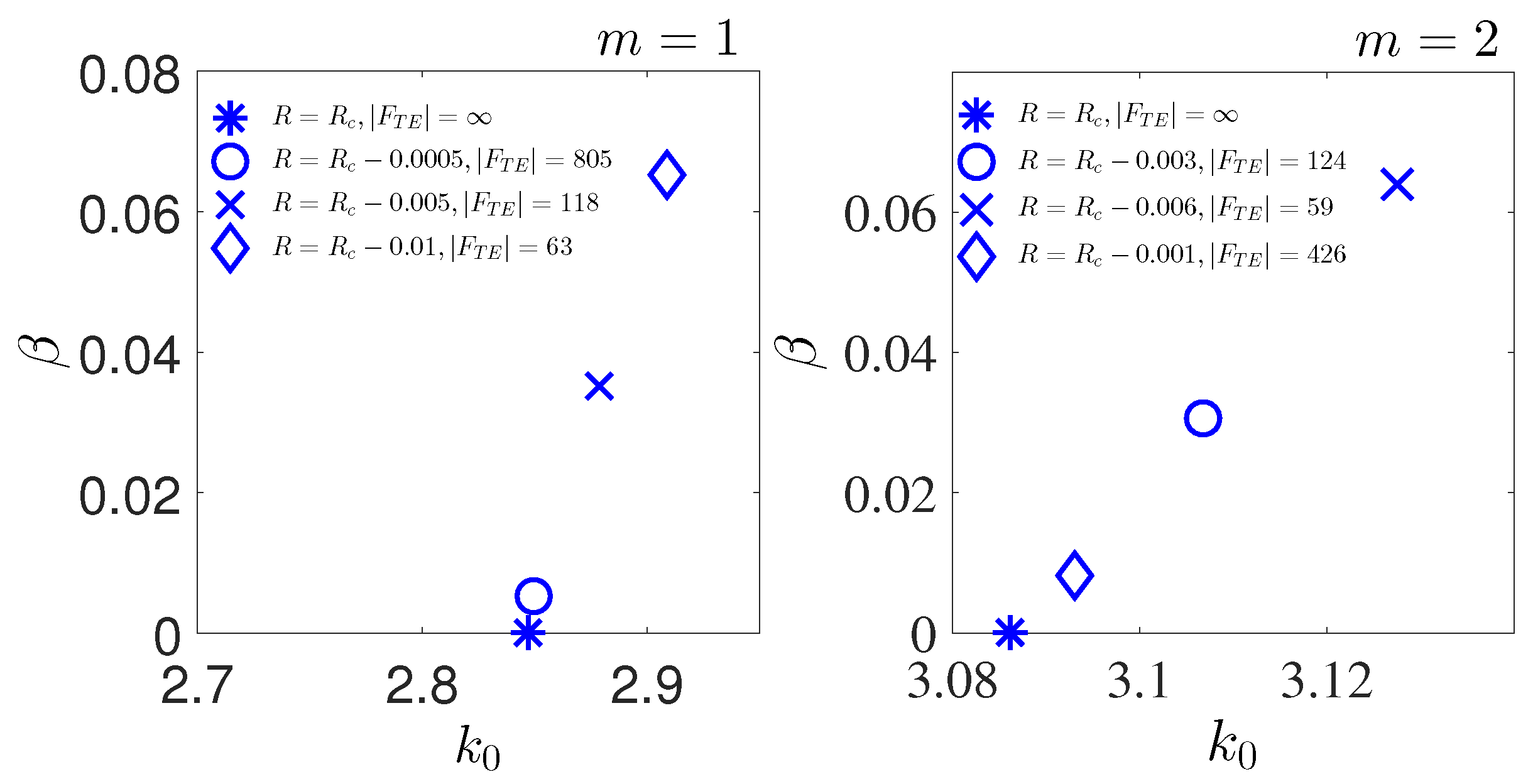
- We demonstrated that the BSC can be accessed not only by variation of the material parameters but also by variation of Bloch wave vector β along the array axis. Patterns of the Bloch BSCs are presented in Figure 3.
- (3)
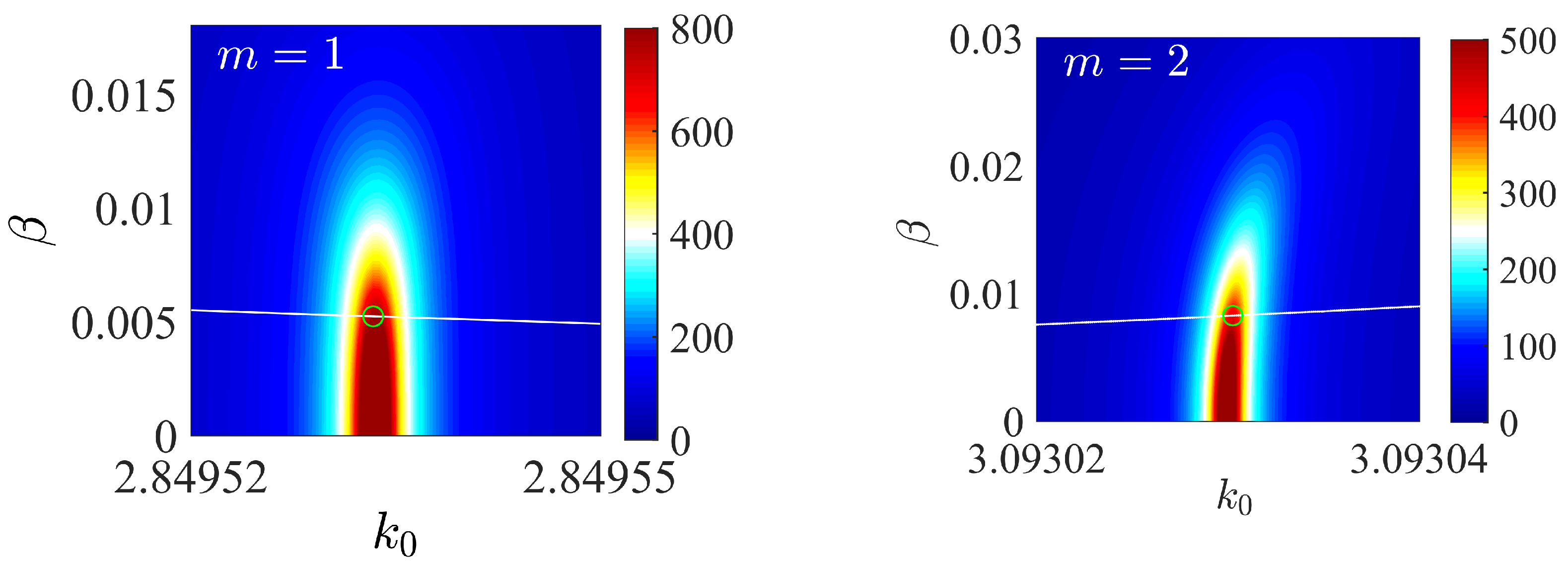
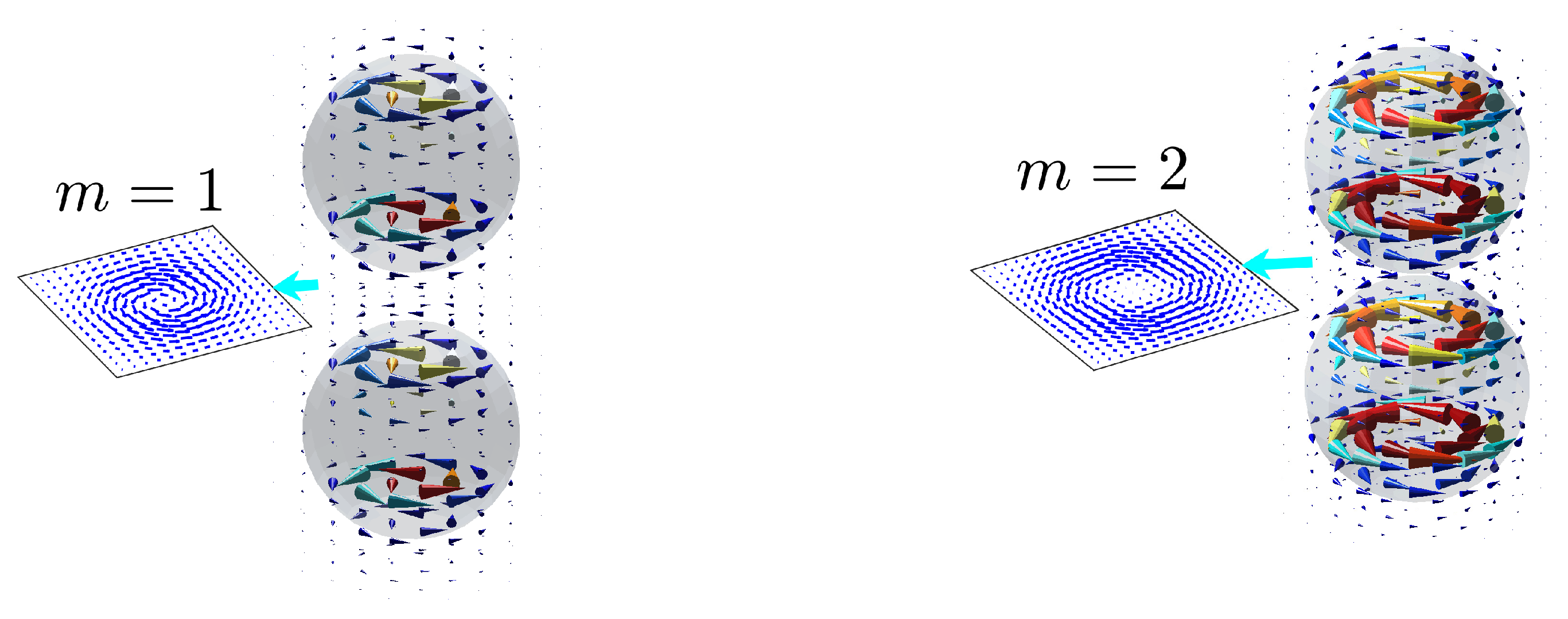
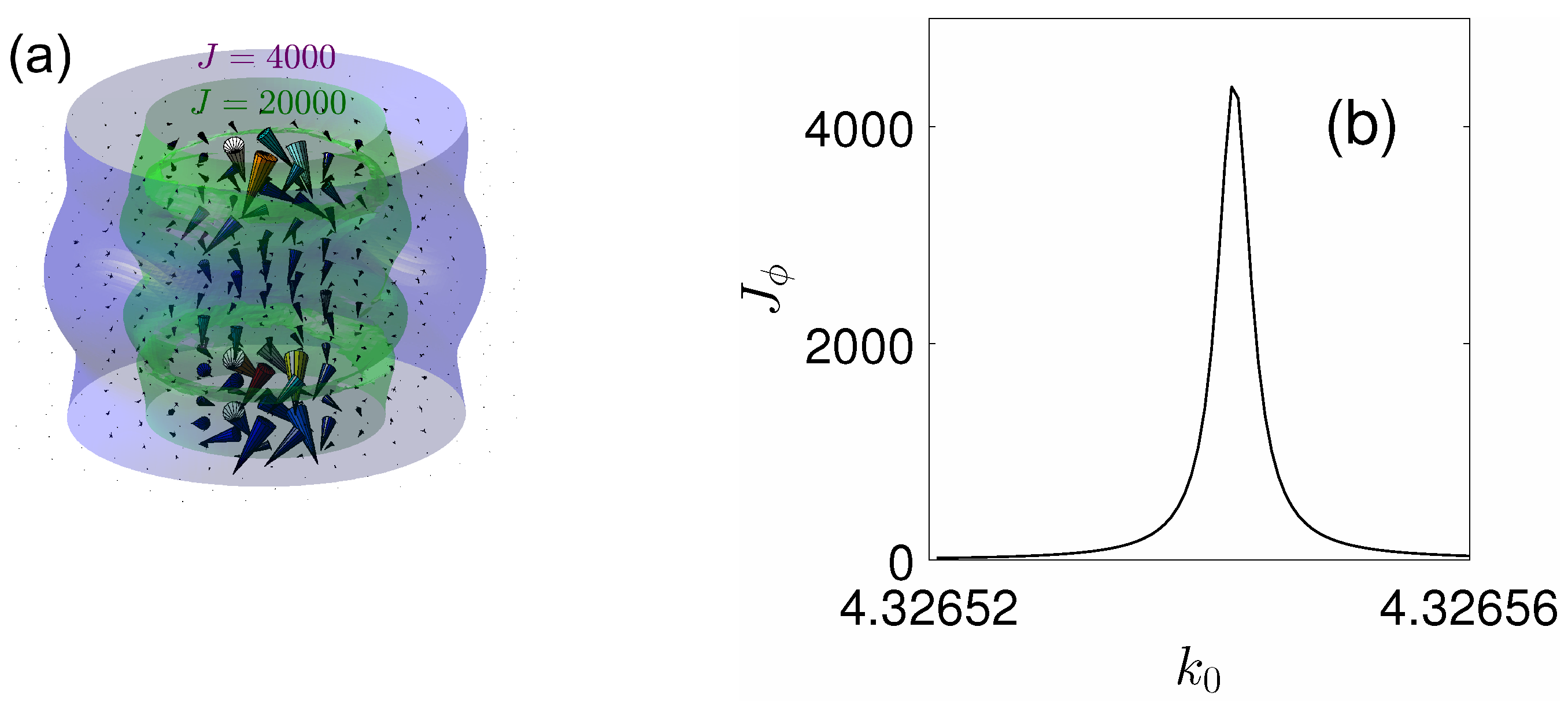
- By tuning of the radius of the spheres we found BSCs in the next sectors of continua with . These BSCs shown in Figure 4 are remarkable by that they carry the OAM with spinning Poynting vectors.
- (4)
Acknowledgments
Conflicts of Interest
Appendix A
References
- Stratton, J.A. Electromagnetic Theory; McGraw-Hill Book Company, Inc.: NewYork, NY, USA, 1941. [Google Scholar]
- Ohtaka, K. Energy band of photons and low-energy photon diffraction. Phys. Rev. B 1979, 19, 5057–5067. [Google Scholar] [CrossRef]
- Ohtaka, K. Scattering theory of low-energy photon diffraction. J. Phys. C Solid State Phys. 1980, 13, 667–680. [Google Scholar] [CrossRef]
- Miyazaki, H.; Ohtaka, K. Near-field images of a monolayer of periodically arrayed dielectric spheres. Phys. Rev. B 1998, 58, 6920–6937. [Google Scholar] [CrossRef]
- Modinos, A. Scattering of electromagnetic waves by a plane of spheres-formalism. Phys. A Stat. Mech. Its Appl. 1987, 141, 575–588. [Google Scholar] [CrossRef]
- Bruning, J.; Lo, Y. Multiple scattering of EM waves by spheres part I—Multipole expansion and ray-optical solutions. IEEE Trans. Antennas Propag. 1971, 19, 378–390. [Google Scholar] [CrossRef]
- García de Abajo, F.J. Colloquium: Light scattering by particle and hole arrays. Rev. Mod. Phys. 2007, 79, 1267–1290. [Google Scholar] [CrossRef]
- Wang, K.X.; Yu, Z.; Sandhu, S.; Liu, V.; Fan, S. Condition for perfect antireflection by optical resonance at material interface. Optica 2014, 1, 388. [Google Scholar] [CrossRef]
- Fuller, K.A.; Kattawar, G.W. Consummate solution to the problem of classical electromagnetic scattering by an ensemble of spheres I: Linear chains. Opt. Lett. 1988, 13, 90–92. [Google Scholar] [CrossRef] [PubMed]
- Hamid, A.K.; Ciric, I.; Hamid, M. Iterative solution of the scattering by an arbitrary configuration of conducting or dielectric spheres. IEE Proc. H Microw. Antennas Propag. 1991, 138, 565. [Google Scholar] [CrossRef]
- Xu, Y.L. Electromagnetic scattering by an aggregate of spheres. Appl. Opt. 1995, 34, 4573–4588. [Google Scholar] [CrossRef] [PubMed]
- Mackowski, D.W. Calculation of total cross sections of multiple-sphere clusters. J. Opt. Soc. Am. A 1994, 11, 2851–2861. [Google Scholar] [CrossRef]
- Quirantes, A.; Arroyo, F.; Quirantes-Ros, J. Multiple light scattering by spherical particle systems and its dependence on concentration: A T-matrix study. J. Colloid Interface Sci. 2001, 240, 7882. [Google Scholar] [CrossRef] [PubMed]
- Luan, P.G.; Chang, K.D. Transmission characteristics of finite periodic dielectric waveguides. Opt. Express 2006, 14, 3263–3272. [Google Scholar] [CrossRef] [PubMed]
- Zhao, R.; Zhai, T.; Wang, Z.; Liu, D. Guided resonances in periodic dielectric waveguides. J. Lightwave Technol. 2009, 27, 4544–4547. [Google Scholar] [CrossRef]
- Du, J.; Liu, S.; Lin, Z.; Zi, J.; Chui, S.T. Guiding electromagnetic energy below the diffraction limit with dielectric particle arrays. Phys. Rev. A 2009, 79, 205436. [Google Scholar] [CrossRef]
- Burin, A.L.; Cao, H.; Schatz, G.C.; Ratner, M.A. High-quality optical modes in low-dimensional arrays of nanoparticles: Application to random lasers. J. Opt. Soc. Am. B 2004, 21, 121–131. [Google Scholar] [CrossRef]
- Gozman, M.; Polishchuk, I.; Burin, A. Light propagation in linear arrays of spherical particles. Phys. Lett. A 2008, 372, 5250–5253. [Google Scholar] [CrossRef]
- Blaustein, G.S.; Gozman, M.I.; Samoylova, O.; Polishchuk, I.Y.; Burin, A.L. Guiding optical modes in chains of dielectric particles. Opt. Express 2007, 15, 17380–17391. [Google Scholar] [CrossRef] [PubMed]
- Draine, B.T.; Flatau, P.J. Discrete-dipole approximation for periodic targets: Theory and tests. J. Opt. Soc. Am. A 2008, 25, 2693–2703. [Google Scholar] [CrossRef]
- Savelev, R.S.; Slobozhanyuk, A.P.; Miroshnichenko, A.E.; Kivshar, Y.S.; Belov, P.A. Subwavelength waveguides composed of dielectric nanoparticles. Phys. Rev. B 2014, 89, 035435. [Google Scholar] [CrossRef]
- Savelev, R.S.; Filonov, D.S.; Petrov, M.I.; Krasnok, A.E.; Belov, P.A.; Kivshar, Y.S. Resonant transmission of light in chains of high-index dielectric particles. Phys. Rev. B 2015, 92, 155415. [Google Scholar] [CrossRef]
- Li, S.V.; Baranov, D.G.; Krasnok, A.E.; Belov, P.A. All-dielectric nanoantennas for unidirectional excitation of electromagnetic guided modes. Appl. Phys. Lett. 2015, 107, 171101. [Google Scholar] [CrossRef]
- Linton, C.; Zalipaev, V.; Thompson, I. Electromagnetic guided waves on linear arrays of spheres. Wave Motion 2013, 50, 29–40. [Google Scholar] [CrossRef] [Green Version]
- Bonnet-Bendhia, A.S.; Starling, F. Guided waves by electromagnetic gratings and non-uniqueness examples for the diffraction problem. Math. Methods Appl. Sci. 1994, 17, 305–338. [Google Scholar] [CrossRef]
- Porter, R.; Evans, D.V. Rayleigh-Bloch surface waves along periodic gratings and their connection with trapped modes in waveguides. J. Fluid Mech. 1999, 386, 233–258. [Google Scholar] [CrossRef]
- Evans, D.V.; Porter, R. Trapping and near-trapping by arrays of cylinders in waves. J. Eng. Math. 1999, 35, 149179. [Google Scholar] [CrossRef]
- Cohen, O.; Freedman, B.; Fleischer, J.W.; Segev, M.; Christodoulides, D.N. Grating-mediated waveguiding. Phys. Rev. Lett. 2004, 93, 103902. [Google Scholar] [CrossRef] [PubMed]
- Porter, R.; Evans, D. Embedded Rayleigh-Bloch surface waves along periodic rectangular arrays. Wave Motion 2005, 43, 29–50. [Google Scholar] [CrossRef]
- Venakides, S.; Shipman, S.P. Resonance and bound states in photonic crystal slabs. SIAM J. Appl. Math. 2003, 64, 322–342. [Google Scholar] [CrossRef]
- Shipman, S.P.; Venakides, S. Resonant transmission near nonrobust periodic slab modes. Phys. Rev. E 2005, 71, 026611. [Google Scholar] [CrossRef] [PubMed]
- Marinica, D.C.; Borisov, A.G.; Shabanov, S.V. Bound states in the continuum in photonics. Phys. Rev. Lett. 2008, 100, 183902. [Google Scholar] [CrossRef] [PubMed]
- Ndangali, R.F.; Shabanov, S.V. Electromagnetic bound states in the radiation continuum for periodic double arrays of subwavelength dielectric cylinders. J. Math. Phys. 2010, 51, 102901. [Google Scholar] [CrossRef]
- Hsueh, W.; Chen, C.; Chang, C. Bound states in the continuum in quasiperiodic systems. Phys. Lett. A 2010, 374, 4804–4807. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Lee, J.; Chua, S.L.; Johnson, S.G.; Joannopoulos, J.D.; Soljačić, M. Observation of trapped light within the radiation continuum. Nature 2013, 499, 188–191. [Google Scholar]
- Weimann, S.; Xu, Y.; Keil, R.; Miroshnichenko, A.E.; Tünnermann, A.; Nolte, S.; Sukhorukov, A.A.; Szameit, A.; Kivshar, Y.S. Compact Surface Fano States Embedded in the Continuum of Waveguide Arrays. Phys. Rev. Lett. 2013, 111, 240403. [Google Scholar] [CrossRef] [PubMed]
- Bulgakov, E.N.; Sadreev, A.F. Bloch bound states in the radiation continuum in a periodic array of dielectric rods. Phys. Rev. A 2014, 90, 053801. [Google Scholar] [CrossRef]
- Hu, Z.; Lu, Y.Y. Standing waves on two-dimensional periodic dielectric waveguides. J. Opt. 2015, 17, 065601. [Google Scholar] [CrossRef]
- Bykov, D.A.; Doskolovich, L.L. ω − kx Fano line shape in photonic crystal slabs. Phys. Rev. A 2015, 92, 013845. [Google Scholar] [CrossRef]
- Song, M.; Yu, H.; Wang, C.; Yao, N.; Pu, M.; Luo, J.; Zhang, Z.; Luo, X. Sharp Fano resonance induced by a single layer of nanorods with perturbed periodicity. Opt. Express 2015, 23, 2895–2903. [Google Scholar] [CrossRef] [PubMed]
- Zou, C.L.; Cui, J.M.; Sun, F.W.; Xiong, X.; Zou, X.B.; Han, Z.F.; Guo, G.C. Guiding light through optical bound states in the continuum for ultrahigh-Qmicroresonators. Laser Photonics Rev. 2014, 9, 114–119. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, H.; Ni, L.; Hu, W.; Peng, C. Analytical Perspective of Interfering Resonances in High-Index-Contrast Periodic Photonic Structures. IEEE J. Quantum Electron. 2016, 52, 6100109. [Google Scholar] [CrossRef]
- Li, L.; Yin, H. Bound States in the Continuum in double layer structures. Sci. Rep. 2016, 6, 26988. [Google Scholar] [CrossRef] [PubMed]
- Hsu, C.W.; Zhen, B.; Chua, S.L.; Johnson, S.G.; Joannopoulos, J.D.; Soljačić, M. Bloch surface eigenstates within the radiation continuum. Light Sci. Appl. 2013, 2, e84. [Google Scholar] [CrossRef]
- Zhen, B.; Hsu, C.W.; Lu, L.; Stone, A.D.; Soljačić, M. Topological Nature of Optical Bound States in the Continuum. Phys. Rev. Lett. 2014, 113, 257401. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Peng, C.; Liang, Y.; Li, Z.; Noda, S. Analytical Perspective for Bound States in the Continuum in Photonic Crystal Slabs. Phys. Rev. Lett. 2014, 113, 037401. [Google Scholar] [CrossRef] [PubMed]
- Colquitt, D.J.; Craster, R.V.; Antonakakis, T.; Guenneau, S. Rayleigh-Bloch waves along elastic diffraction gratings. Proc. R. Soc. A Math. Phys. Eng. Sci. 2014, 471, 20140465. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Hsu, C.W.; Zhen, B.; Lin, X.; Joannopoulos, J.D.; Soljačić, M.; Chen, H. Formation Mechanism of Guided Resonances and Bound States in the Continuum in Photonic Crystal Slabs. arXiv, 2016; arXiv:1603.02815. [Google Scholar]
- Hung, Y.J.; Lin, I.S. Visualization of Bloch surface waves and directional propagation effects on one-dimensional photonic crystal substrate. Opt. Express 2016, 24, 16003–16009. [Google Scholar] [CrossRef] [PubMed]
- Blanchard, C.; Hugonin, J.P.; Sauvan, C. Fano resonances in photonic crystal slabs near optical bound states in the continuum. Phys. Rev. B 2016, 94, 155303. [Google Scholar] [CrossRef]
- Wang, Y.; Song, J.; Dong, L.; Lu, M. Optical bound states in slotted high-contrast gratings. J. Opt. Soc. Am. B 2016, 33, 2472–2479. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, X. Ultrasensitive optical absorption in graphene based on bound states in the continuum. Sci. Rep. 2015, 5, 8266. [Google Scholar] [CrossRef] [PubMed]
- Padgett, M.; Courtial, J.; Allen, L. Light’s Orbital Angular Momentum. Phys. Today 2004, 57, 2004. [Google Scholar] [CrossRef]
- Allen, L.; Padgett, M. The Poynting vector in Laguerre-Gaussian beams and the interpretation of their angular momentum density. Opt. Commun. 2000, 184, 67–71. [Google Scholar] [CrossRef]
- Yao, A.M.; Padgett, M.J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photon. 2011, 3, 161. [Google Scholar] [CrossRef]
- Bulgakov, E.N.; Sadreev, A.F. Light trapping above the light cone in a one-dimensional array of dielectric spheres. Phys. Rev. A 2015, 92, 023816. [Google Scholar] [CrossRef]
- Bulgakov, E.; Maksimov, D.N. Light guiding above the light line in arrays of dielectric nanospheres. Opt. Lett. 2016, 41, 3888–3891. [Google Scholar] [CrossRef] [PubMed]
- Bulgakov, E.N.; Sadreev, A.F. Transfer of spin angular momentum of an incident wave into orbital angular momentum of the bound states in the continuum in an array of dielectric spheres. Phys. Rev. A 2016, 94, 033856. [Google Scholar] [CrossRef]
- Bulgakov, E.N.; Sadreev, A.F. Propagating Bloch waves with orbital angular momentum above the light cone in the array of dielectric spheres. J. Opt. Soc. Am. A 2017. submitted. [Google Scholar]
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef]
- Bykov, D.A.; Doskolovich, L.L. Numerical methods for calculating poles of the scattering matrix with applications in grating theory. J. Lightwave Technol. 2013, 31, 793–801. [Google Scholar] [CrossRef]
- Yuan, L.J.; Lu, Y.Y. Propagating Bloch modes above the light line on a periodic array of cylinders. J. Phys. B 2016. [Google Scholar] [CrossRef]
- Merchiers, O.; Moreno, F.; González, F.; Saiz, J.M. Light scattering by an ensemble of interacting dipolar particles with both electric and magnetic polarizabilities. Phys. Rev. A 2007, 76, 043834. [Google Scholar] [CrossRef]
- Evlyukhin, A.B.; Reinhardt, C.; Seidel, A.; Luk’yanchuk, B.S.; Chichkov, B.N. Optical response features of Si-nanoparticle arrays. Phys. Rev. B 2010, 82, 045404. [Google Scholar] [CrossRef]
- Wheeler, M.S.; Aitchison, J.S.; Mojahedi, M. Coupled magnetic dipole resonances in sub-wavelength dielectric particle clusters. J. Opt. Soc. Am. B 2010, 27, 1083–1091. [Google Scholar] [CrossRef]
- Shore, R.A.; Yaghjian, A.D. Traveling Electromagnetic Waves on Linear Periodic Arrays of Small Lossless Penetrable Spheres; Technical Report, DTIC Document; Defense Technical Information Center: Fort Belvoir, VA, USA, 2004. [Google Scholar]
- Shore, R.A.; Yaghjian, A.D. Travelling electromagnetic waves on linear periodic arrays of lossless spheres. Electron. Lett. 2005, 41, 578–580. [Google Scholar] [CrossRef]
- Shore, R.A.; Yaghjian, A.D. Complex waves on periodic arrays of lossy and lossless permeable spheres: 1. Theory. Radio Sci. 2012, 47, RS2014. [Google Scholar] [CrossRef]
- Deych, L.; Roslyak, A. Long-living collective optical excitations in a linear chain of microspheres. Phys. Status Solidi C 2005, 2, 3908–3911. [Google Scholar] [CrossRef]
- Deych, L.I.; Roslyak, O. Photonic band mixing in linear chains of optically coupled microspheres. Phys. Rev. E 2006, 73, 036606. [Google Scholar] [CrossRef] [PubMed]
- Monticone, F.; Alù, A. Embedded Photonic Eigenvalues in 3D Nanostructures. Phys. Rev. Lett. 2014, 112, 213903. [Google Scholar] [CrossRef]
- Tikhodeev, S.G.; Yablonskii, A.L.; Muljarov, E.A.; Gippius, N.A.; Ishihara, T. Quasiguided modes and optical properties of photonic crystal slabs. Phys. Rev. B 2002, 66, 045102. [Google Scholar] [CrossRef]
- Shore, R.A.; Yaghjian, A.D. Complex waves on periodic arrays of lossy and lossless permeable spheres: 2. Numerical results. Radio Sci. 2012, 47, RS2015. [Google Scholar] [CrossRef]
- Carrasco, S.; Saleh, B.E.A.; Teich, M.C.; Fourkas, J.T. Second- and third-harmonic generation with vector Gaussian beams. J. Opt. Soc. Am. B 2006, 23, 2134–2141. [Google Scholar] [CrossRef]
- Vuye, G.; Fisson, S.; Nguyen Van, V.; Wang, Y.; Rivory, J.; Abelès, F. Temperature dependence of the dielectric function of silicon using in situ spectroscopic ellipsometry. Thin Solid Films 1993, 233, 166–170. [Google Scholar] [CrossRef]
- Bulgakov, E.N.; Rotter, I.; Sadreev, A.F. Comment on Bound-state eigenenergy outside and inside the continuum for unstable multilevel systems. Phys. Rev. A 2007, 75, 067401. [Google Scholar] [CrossRef]
- Bulgakov, E.N.; Pichugin, K.N.; Sadreev, A.F.; Rotter, I. Bound states in the continuum in open Aharonov-Bohm rings. JETP Lett. 2006, 84, 430–435. [Google Scholar] [CrossRef]
- Sadreev, A.F.; Bulgakov, E.N.; Rotter, I. Bound states in the continuum in open quantum billiards with a variable shape. Phys. Rev. B 2006, 73, 235342. [Google Scholar] [CrossRef]
- Yoon, J.W.; Song, S.H.; Magnusson, R. Critical field enhancement of asymptotic optical bound states in the continuum. Sci. Rep. 2015, 5, 18301. [Google Scholar] [CrossRef] [PubMed]
- Sadreev, A.F.; Rotter, I. S-matrix theory for transmission through billiards in tight-binding approach. J. Phys. A Math. Gen. 2003, 36, 11433. [Google Scholar] [CrossRef]
- Bulgakov, E.N.; Sadreev, A.F. Robust bound state in the continuum in a nonlinear microcavity embedded in a photonic crystal waveguide. Opt. Lett. 2014, 39, 5212–5215. [Google Scholar] [CrossRef] [PubMed]
- Ochiai, T.; Sakoda, K. Dispersion relation and optical transmittance of a hexagonal photonic crystal slab. Phys. Rev. B 2001, 63, 125107. [Google Scholar] [CrossRef]
- Fernández-Domínguez, A.I.; Maier, S.A.; Pendry, J.B. Collection and Concentration of Light by Touching Spheres: A Transformation Optics Approach. Phys. Rev. Lett. 2010, 105, 266807. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef] [PubMed]
- Čelechovský, R.; Bouchal, Z. Optical implementation of the vortex information channel. New J. Phys. 2007, 9, 328. [Google Scholar] [CrossRef]
- Gorodetski, Y.; Drezet, A.; Genet, C.; Ebbesen, T.W. Generating Far-Field Orbital Angular Momenta from Near-Field Optical Chirality. Phys. Rev. Lett. 2013, 110, 203906. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Zhang, H.; Wang, Y.; Han, S.; Yang, H.; Xu, X.; Wang, Z.; Petrov, V.; Wang, J. Optical orbital angular momentum conservation during the transfer process from plasmonic vortex lens to light. Sci. Rep. 2013, 3, 3191. [Google Scholar] [CrossRef] [PubMed]
- Berezin, M.; Kamenetskii, E.; Shavit, R. Magnetoelectric-field microwave antennas: Far-field orbital angular momenta from chiral-topology near fields. arXiv, 2015; arXiv:1512.01393. [Google Scholar]
- Žukauskas, A.; Malinauskas, M.; Brasselet, E. Monolithic generators of pseudo-nondiffracting optical vortex beams at the microscale. Appl. Phys. Lett. 2013, 103, 181122. [Google Scholar] [CrossRef]
- Dall, R.; Fraser, M.D.; Desyatnikov, A.S.; Li, G.; Brodbeck, S.; Kamp, M.; Schneider, C.; Höfling, S.; Ostrovskaya, E.A. Creation of Orbital Angular Momentum States with Chiral Polaritonic Lenses. Phys. Rev. Lett. 2014, 113, 200404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, N.; Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 2014, 13, 139–150. [Google Scholar] [CrossRef] [PubMed]
- Schäferling, M.; Yin, X.; Giessen, H. Formation of chiral fields in a symmetric environment. Opt. Express 2012, 20, 26326–26336. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Fortunño, F.J.; Barber-Sanz, I.; Puerto, D.; Griol, A.; Martínez, A. Resolving Light Handedness with an on-Chip Silicon Microdisk. ACS Photonics 2014, 1, 762–767. [Google Scholar] [CrossRef]
- Petersen, J.; Volz, J.; Rauschenbeutel, A. Chiral nanophotonic waveguide interface based on spin-orbit interaction of light. Science 2014, 346, 67–71. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Fortunño, F.J.; Marino, G.; Ginzburg, P.; O’Connor, D.; Martinez, A.; Wurtz, G.A.; Zayats, A.V. Near-Field Interference for the Unidirectional Excitation of Electromagnetic Guided Modes. Science 2013, 340, 328–330. [Google Scholar] [CrossRef] [PubMed]
- Bulgakov, E.N.; Sadreev, A.F. Giant optical vortex in photonic crystal waveguide with nonlinear optical cavity. Phys. Rev. B 2012, 85, 165305. [Google Scholar] [CrossRef]
- Kim, C.S.; Satanin, A.M.; Joe, Y.S.; Cosby, R.M. Resonant tunneling in a quantum waveguide: Effect of a finite-size attractive impurity. Phys. Rev. B 1999, 60, 10962–10970. [Google Scholar] [CrossRef]
- Linton, C.; McIver, P. Embedded trapped modes in water waves and acoustics. Wave Motion 2007, 45, 16–29. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamic; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Hu, J.; Menyuk, C.R. Understanding leaky modes: Slab waveguide revisited. Adv. Opt. Photon. 2009, 1, 58–106. [Google Scholar] [CrossRef]
- Silveirinha, M.G. Trapping light in open plasmonic nanostructures. Phys. Rev. A 2014, 89, 023813. [Google Scholar] [CrossRef]
- Alù, A.; Silveirinha, M.G.; Salandrino, A.; Engheta, N. Epsilon-near-zero metamaterials and electromagnetic sources: Tailoring the radiation phase pattern. Phys. Rev. B 2007, 75, 155410. [Google Scholar] [CrossRef]
- Hrebikova, I.; Jelinek, L.; Silveirinha, M.G. Embedded energy state in an open semiconductor heterostructure. Phys. Rev. B 2015, 92, 155303. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Y.; Liu, W.; Yang, J.; Ma, Y.; Lu, H.; Sun, Y.; Jiang, H.; Chen, H. Controllable lasing behavior enabled by compound dielectric waveguide grating structures. Opt. Express 2016, 24, 19458–19466. [Google Scholar] [CrossRef] [PubMed]
- Kodigala, A.; Lepetit, T.; Gu, Q.; Bahari, B.; Fainman, Y.; Kante, B. Bound State in the Continuum Nanophotonic Laser. Conf. Lasers Electro-Opt. 2016, 1–2. [Google Scholar]





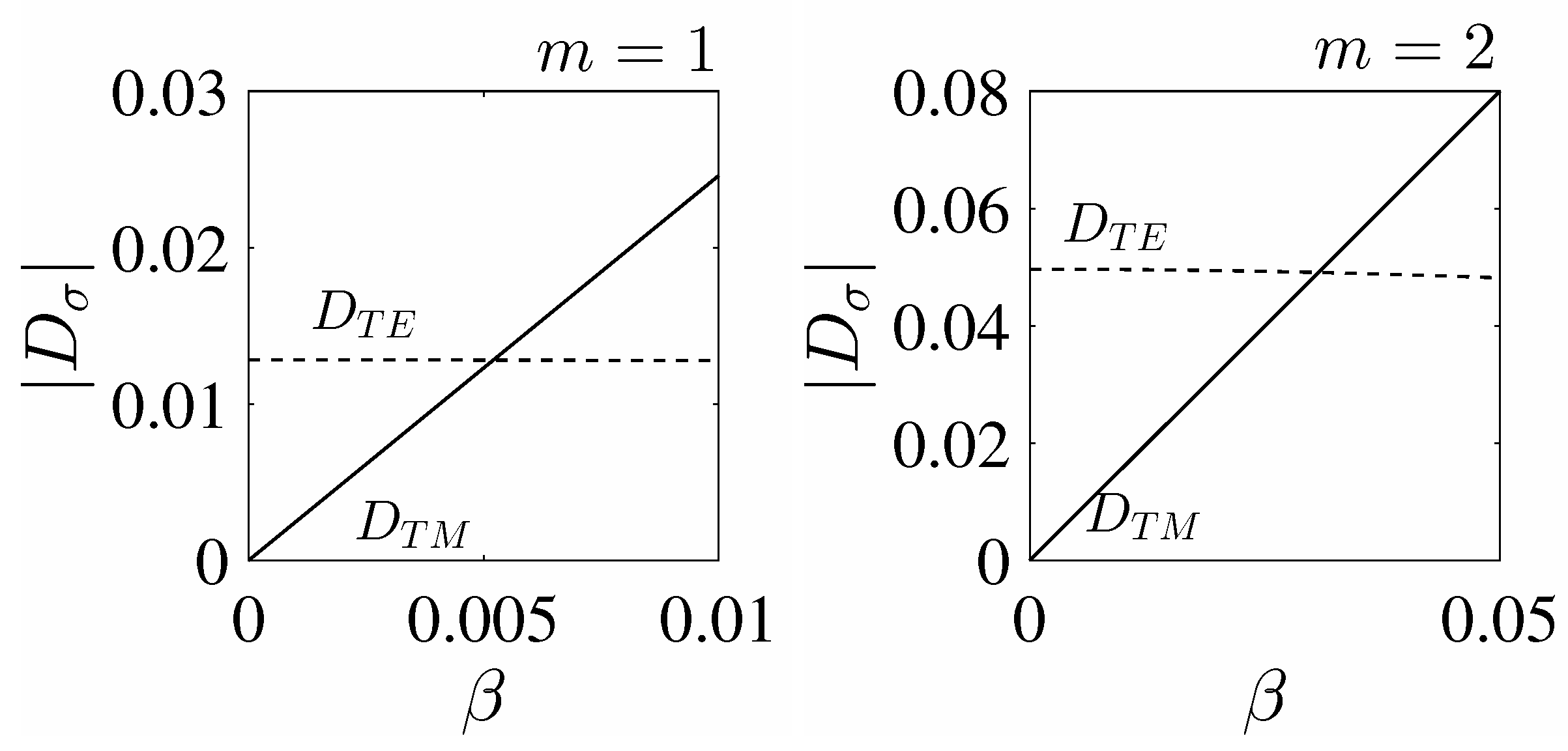





| m | β | Type I of BSC | Type II of BSC |
|---|---|---|---|
| 0 | |||
| 0 | |||
| 0 | 0 | ||
| 0 | 0 |
| Type I | Type II |
|---|---|
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bulgakov, E.N.; Sadreev, A.F.; Maksimov, D.N. Light Trapping above the Light Cone in One-Dimensional Arrays of Dielectric Spheres. Appl. Sci. 2017, 7, 147. https://doi.org/10.3390/app7020147
Bulgakov EN, Sadreev AF, Maksimov DN. Light Trapping above the Light Cone in One-Dimensional Arrays of Dielectric Spheres. Applied Sciences. 2017; 7(2):147. https://doi.org/10.3390/app7020147
Chicago/Turabian StyleBulgakov, Evgeny N., Almas F. Sadreev, and Dmitrii N. Maksimov. 2017. "Light Trapping above the Light Cone in One-Dimensional Arrays of Dielectric Spheres" Applied Sciences 7, no. 2: 147. https://doi.org/10.3390/app7020147




