L1 Adaptive Control for a Vertical Rotor Orientation System
Abstract
:1. Introduction
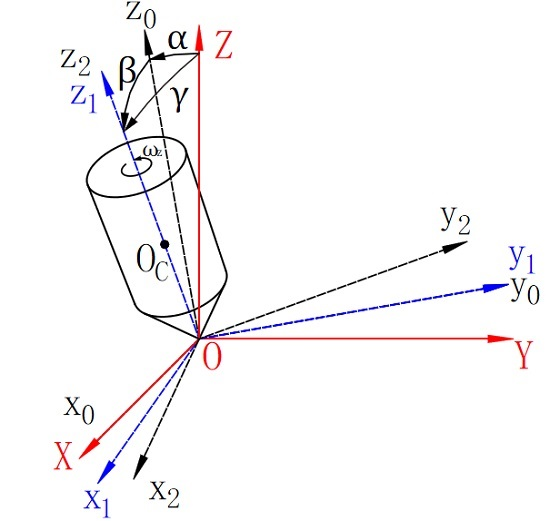
2. Problem Statement
3. Adaptive Control Design of the Rotor Orientation System
3.1. Semi-Global Linearization of the System
3.2. State Predictor
3.3. Adaptive Control Algorithm
4. Adaptive Control System Analysis
4.1. Boundedness of State Error and Parameter Error
4.2. Boundedness of State Variables
4.3. Performance of the Adaptive System
5. Simulation Results for the Adaptive Control System
5.1. Simulation of the Adaptive Controller
5.2. Simulation of the Rotor Orientation System
6. Experimental Results for the Rotor Orientation System
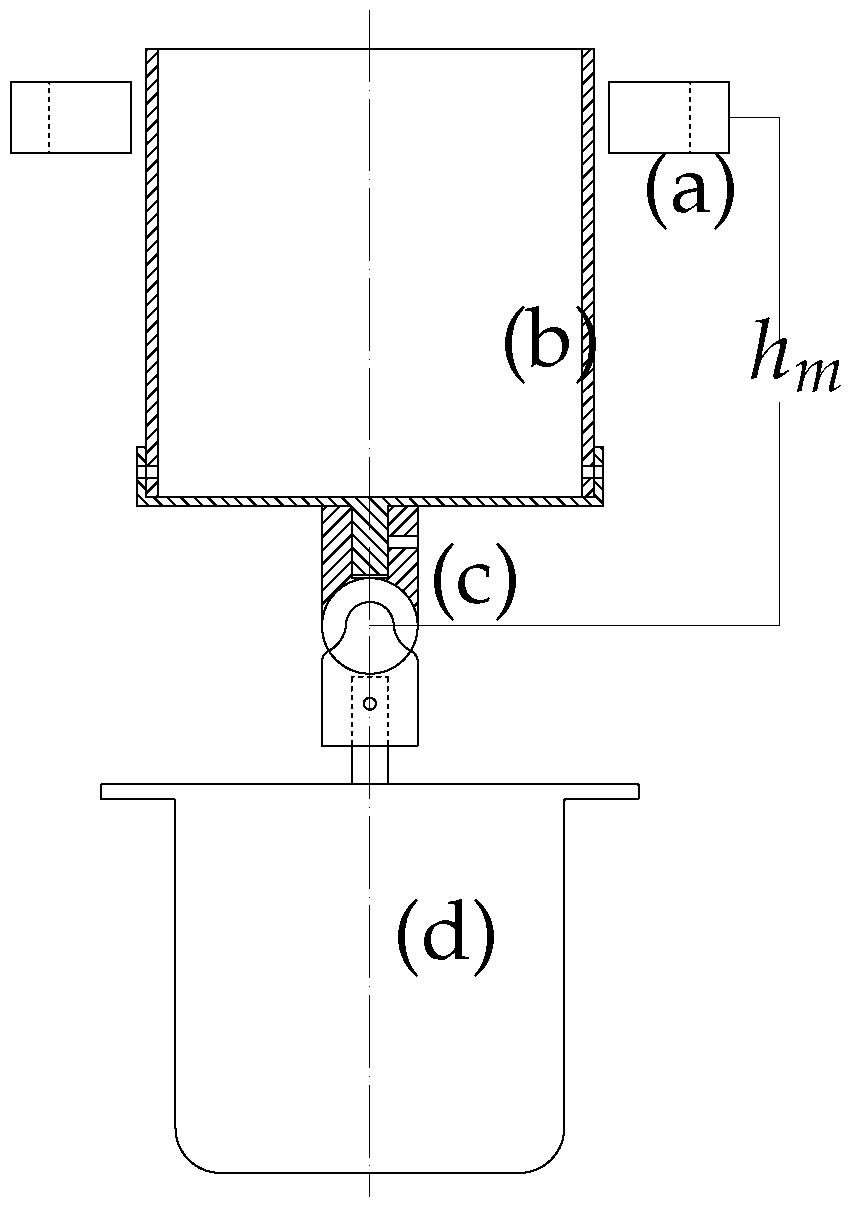
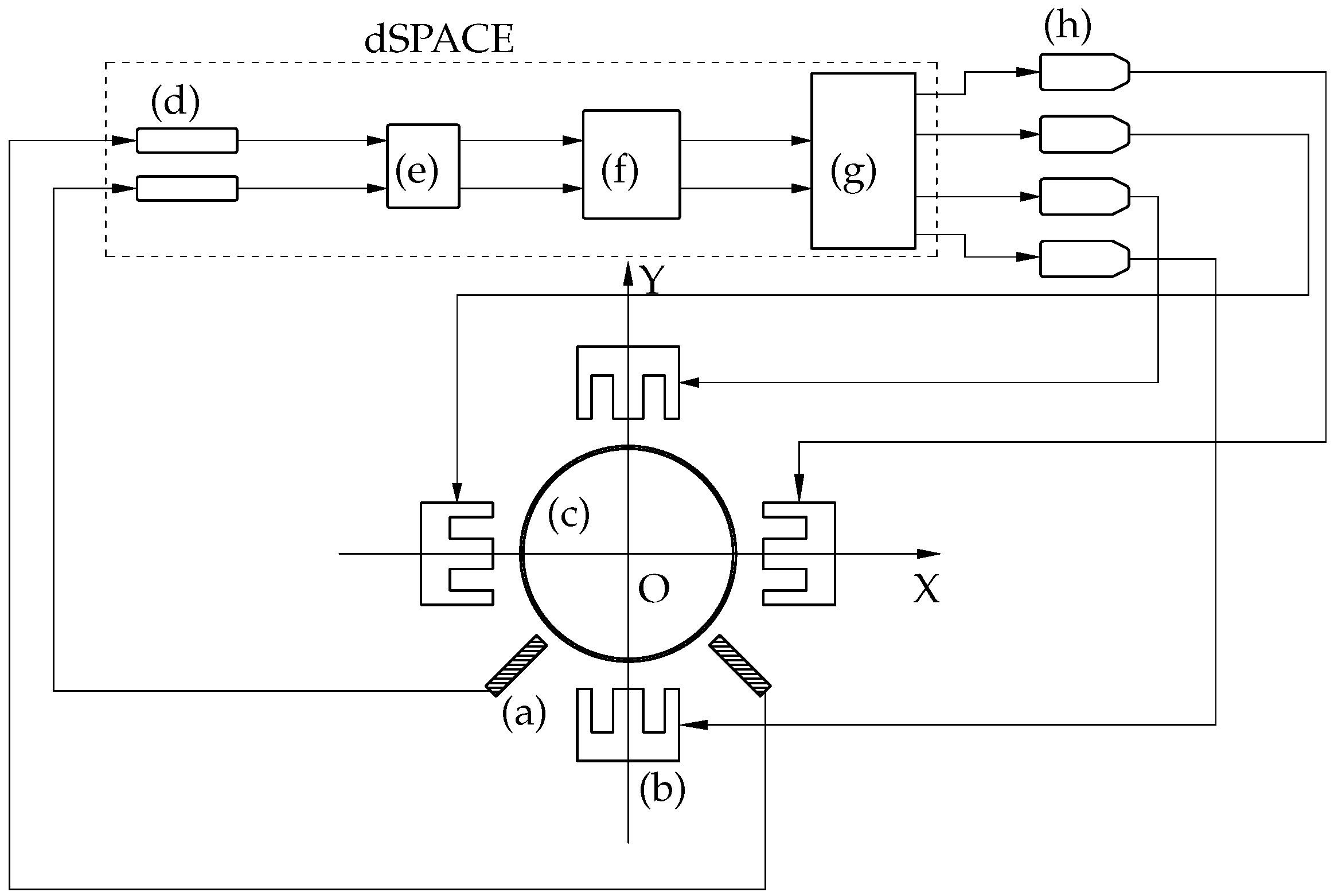
6.1. Experimental Devices
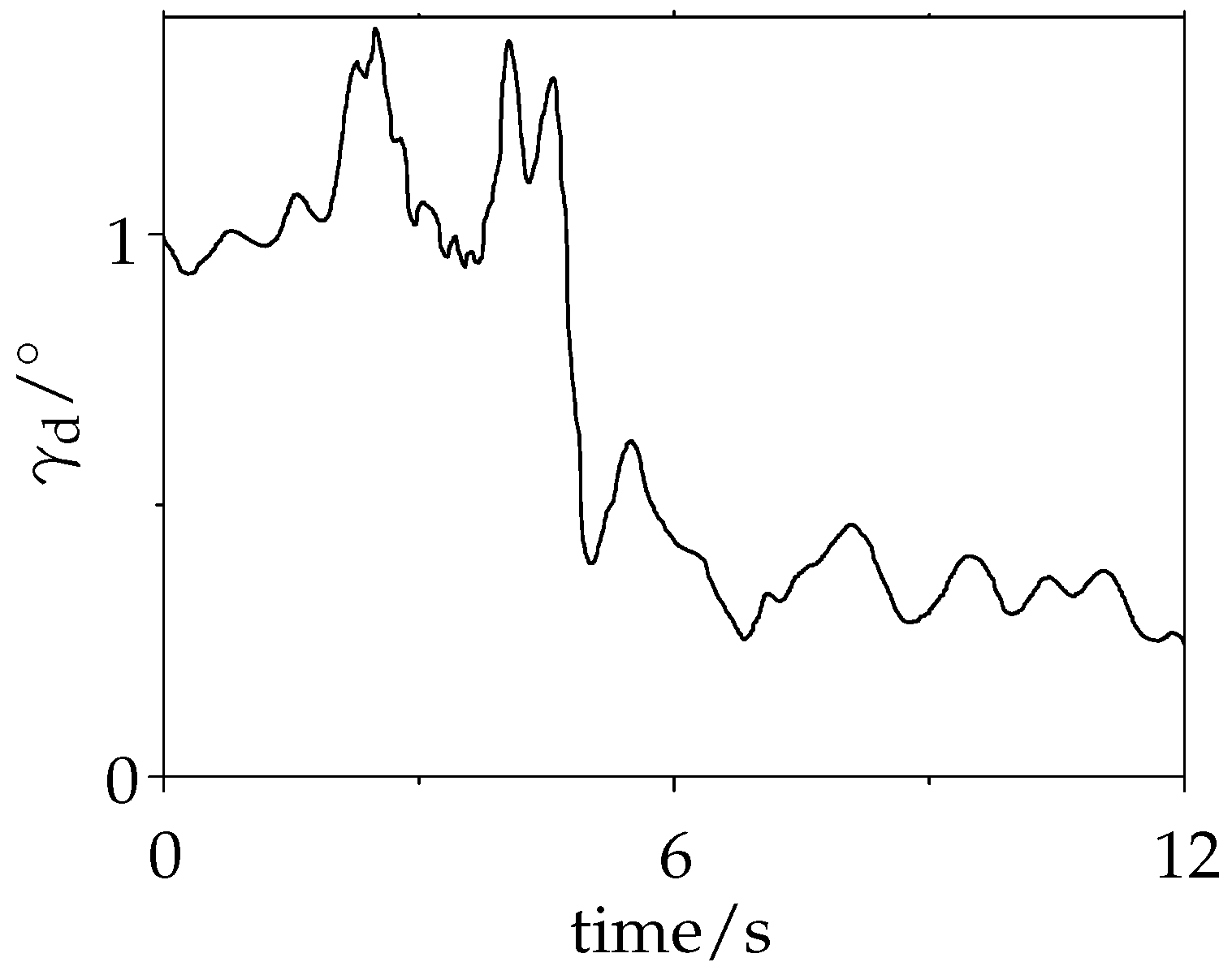
6.2. Experimental Process
- 1.
- Measurement of the rotor drift angle.
- 2.
- Calculation of the electromagnetic force.
- 3.
- Calculation of the current in every electromagnet.
6.3. Experimental Results
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bae, S.; Lee, J.; Kang, Y.; Kang, J.; Yun, J. Dynamic analysis of an automatic washing machine with a hydraulic balancer. J. Sound Vib. 2002, 257, 3–18. [Google Scholar] [CrossRef]
- Chen, H.W.; Zhang, Q.J. Stability analyses of a vertical axis automatic washing machine with a hydraulic balancer. Mech. Mach. Theory 2011, 46, 910–926. [Google Scholar] [CrossRef]
- Chen, H.W.; Zhang, Q.J.; Fan, S.Y. Study on steady-state response of a vertical axis automatic washing machine with a hydraulic balancer using a new approach and a method for getting a smaller deflection angle. J. Sound Vib. 2011, 330, 2017–2030. [Google Scholar] [CrossRef]
- Smith, R.D.; Weldon, W.F. Nonlinear control of a rigid rotor magnetic bearing system: Modeling and simulation with full state feedback. IEEE Trans. Magn. 1995, 31, 973–980. [Google Scholar] [CrossRef]
- Ahrens, M.; KuCera, L.; Larsonneur, R. Performance of a Magnetically Suspended Flywheel Energy Storage Device. IEEE Trans. Control Syst. Technol. 1996, 4, 494–502. [Google Scholar] [CrossRef]
- Lum, K.Y.; Coppola, V.; Bernstein, D. Adaptive autocentering control for an active magnetic bearing supporting a rotor with unknown mass imbalance. IEEE Trans. Control Syst. Technol. 1996, 4, 587–597. [Google Scholar]
- Gibson, N.S.; Choi, H.; Buckner, G.D. H control of active magnetic bearings using artificial neural network identification of uncertainty. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, Washington, DC, USA, 5–8 October 2003; Volume 2, pp. 1449–1456.
- Sivrioglu, S. Adaptive backstepping for switching control active magnetic bearing system with vibrating base. Control Theory Appl. IET 2007, 1, 1054–1059. [Google Scholar] [CrossRef]
- Mushi, S.E.; Lin, Z.; Allaire, P.E. Design, construction, and modeling of a flexible rotor active magnetic bearing test rig. IEEE/ASME Trans. Mechatron. 2012, 17, 1170–1182. [Google Scholar] [CrossRef]
- Tsai, N.; Kuo, C.; Lee, R. Regulation on radial position deviation for vertical AMB systems. Mech. Syst. Signal Process. 2007, 21, 2777–2793. [Google Scholar] [CrossRef]
- Shi, M.; Wang, D.; Zhang, J. Nonlinear dynamic analysis of a vertical rotor-bearing system. J. Mech. Sci. Technol. 2013, 27, 9–19. [Google Scholar] [CrossRef]
- Hovakimyan, N.; Cao, C. L1 Adaptive Control Theory: Guaranteed Robustness with Fast Adaptation; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010; Volume 21. [Google Scholar]
- Sun, H.; Li, Z.; Hovakimyan, N.; Başsar, T.; Downton, G. L1 Adaptive Control for Directional Drilling Systems. IFAC Proc. Vol. 2012, 45, 72–77. [Google Scholar] [CrossRef]
- Nguyen, K.D.; Dankowicz, H. Adaptive control of underactuated robots with unmodeled dynamics. Robot. Auton. Syst. 2014, 64, 84–99. [Google Scholar] [CrossRef]
- Tao, C.W.; Taur, J.S.; Chang, Y.H.; Chang, C.W. A novel fuzzy-sliding and fuzzy-integral-sliding controller for the twin-rotor multi-input–multi-output system. IEEE Trans. Fuzzy Syst. 2010, 18, 893–905. [Google Scholar] [CrossRef]
- Allouani, F.; Boukhetala, D.; Boudjema, F. Particle swarm optimization based fuzzy sliding mode controller for the twin rotor MIMO system. In Proceedings of the 2012 16th IEEE Mediterranean Electrotechnical Conference, Hammamet, Tunisia, 25–28 March 2012; pp. 1063–1066.
- Nejjari, F.; Rotondo, D.; Puig, V.; Innocenti, M. Quasi-LPV modelling and non-linear identification of a twin rotor system. In Proceedings of the 2012 20th Mediterranean Conference on Control & Automation (MED), Barcelona, Spain, 3–6 July 2012; pp. 229–234.
- Rădac, M.B.; Precup, R.E.; Petriu, E.M.; Preitl, S. Iterative data-driven tuning of controllers for nonlinear systems with constraints. IEEE Trans. Ind. Electron. 2014, 61, 6360–6368. [Google Scholar] [CrossRef]



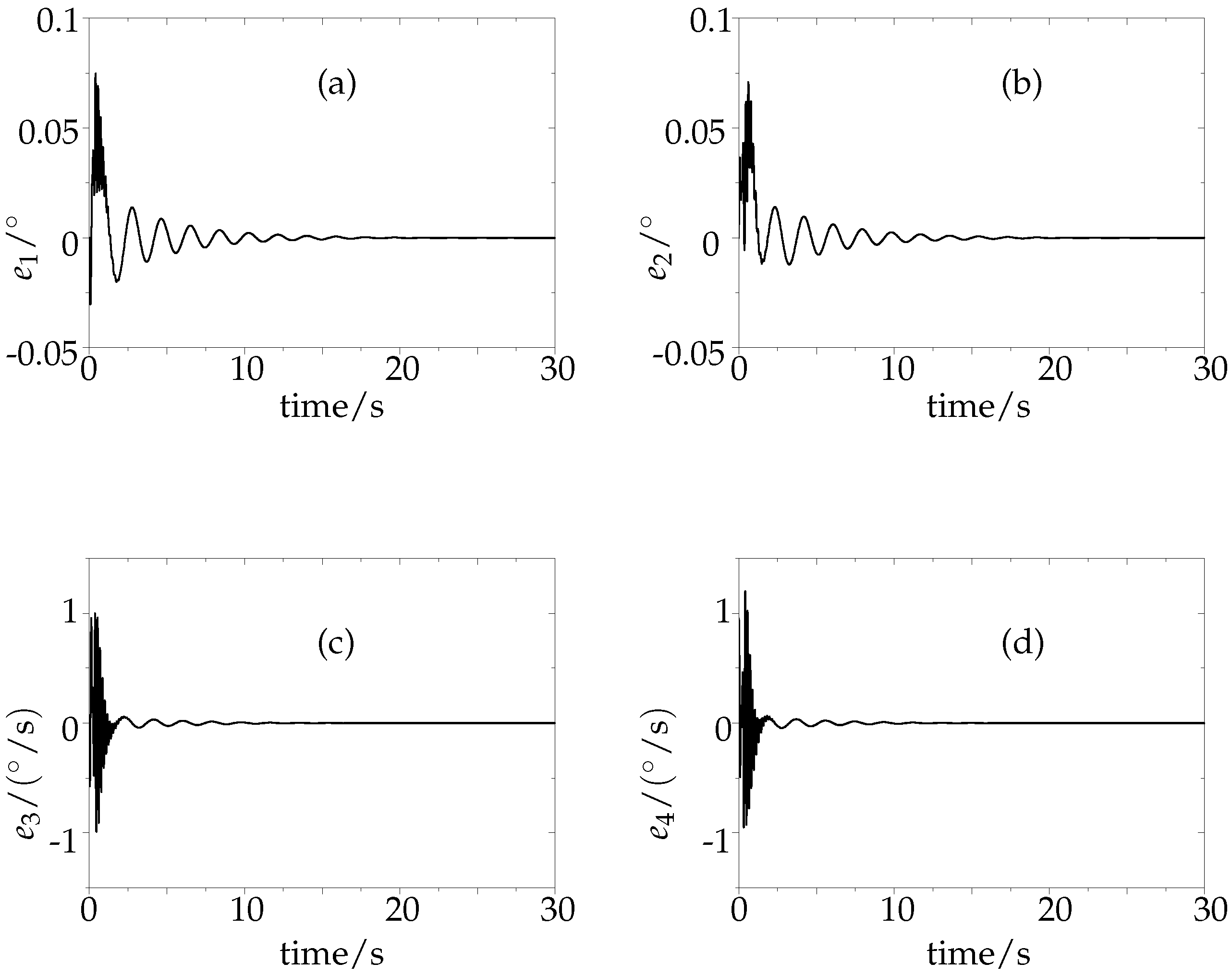
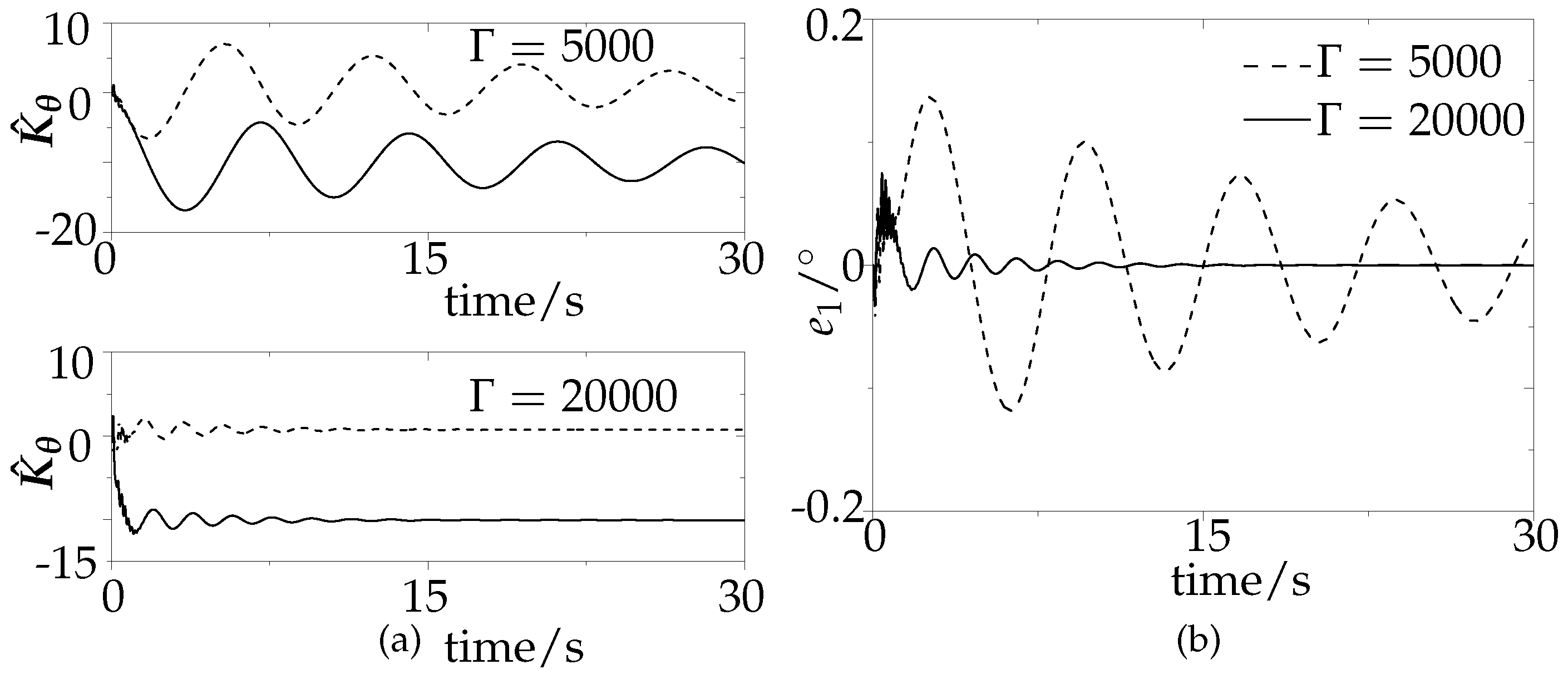

| Parameter | Value | Unit |
|---|---|---|
| Material | Iron | – |
| Outer diameter | 150 | mm |
| Inner diameter | 142 | mm |
| Height | 150 | mm |
| Mass | 1.737 | kg |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Fan, Y.; Di, J.; Ji, M. L1 Adaptive Control for a Vertical Rotor Orientation System. Appl. Sci. 2016, 6, 242. https://doi.org/10.3390/app6090242
Liu S, Fan Y, Di J, Ji M. L1 Adaptive Control for a Vertical Rotor Orientation System. Applied Sciences. 2016; 6(9):242. https://doi.org/10.3390/app6090242
Chicago/Turabian StyleLiu, Sijia, Yu Fan, Jun Di, and Mingming Ji. 2016. "L1 Adaptive Control for a Vertical Rotor Orientation System" Applied Sciences 6, no. 9: 242. https://doi.org/10.3390/app6090242