Dynamical Systems for Audio Synthesis: Embracing Nonlinearities and Delay-Free Loops †
Abstract
:1. Introduction
2. Methods
3. Results
3.1. Basic Example: Simple Harmonic Motion
3.2. Reciprocal Sync
3.3. Reciprocal Frequency Modulation
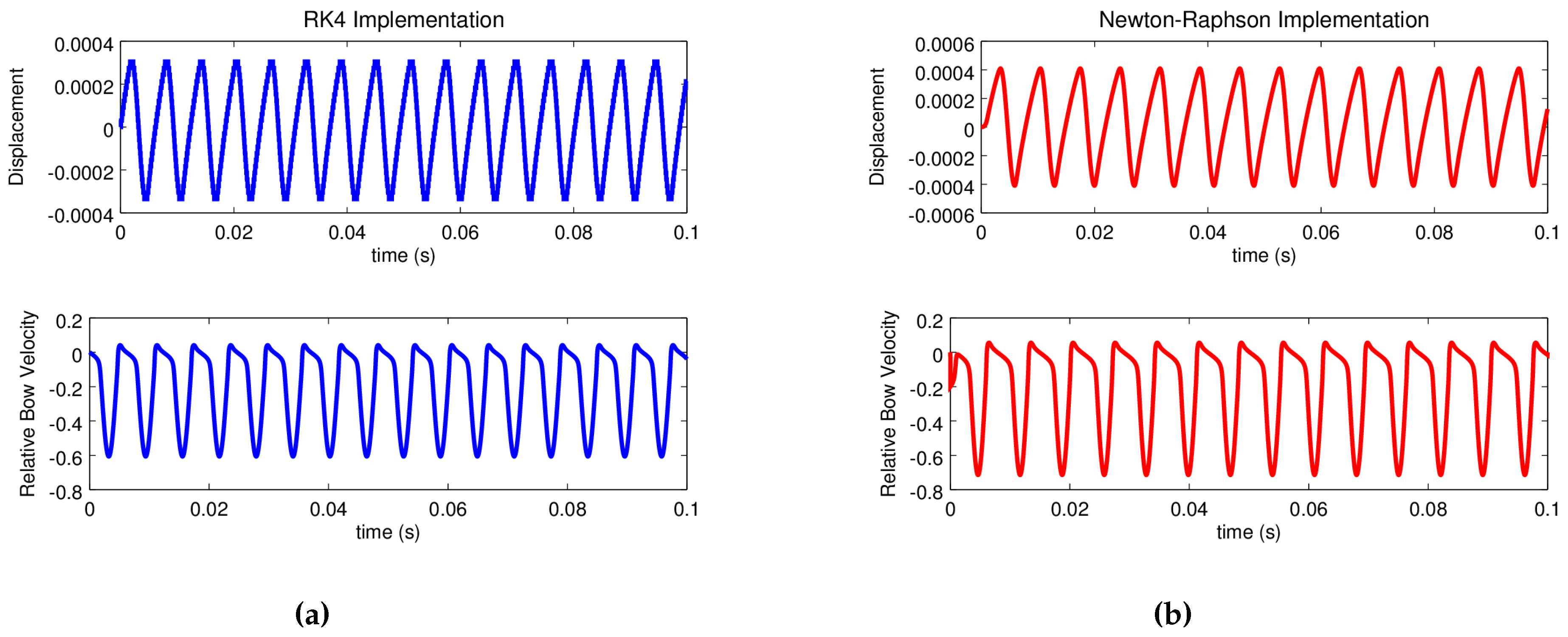
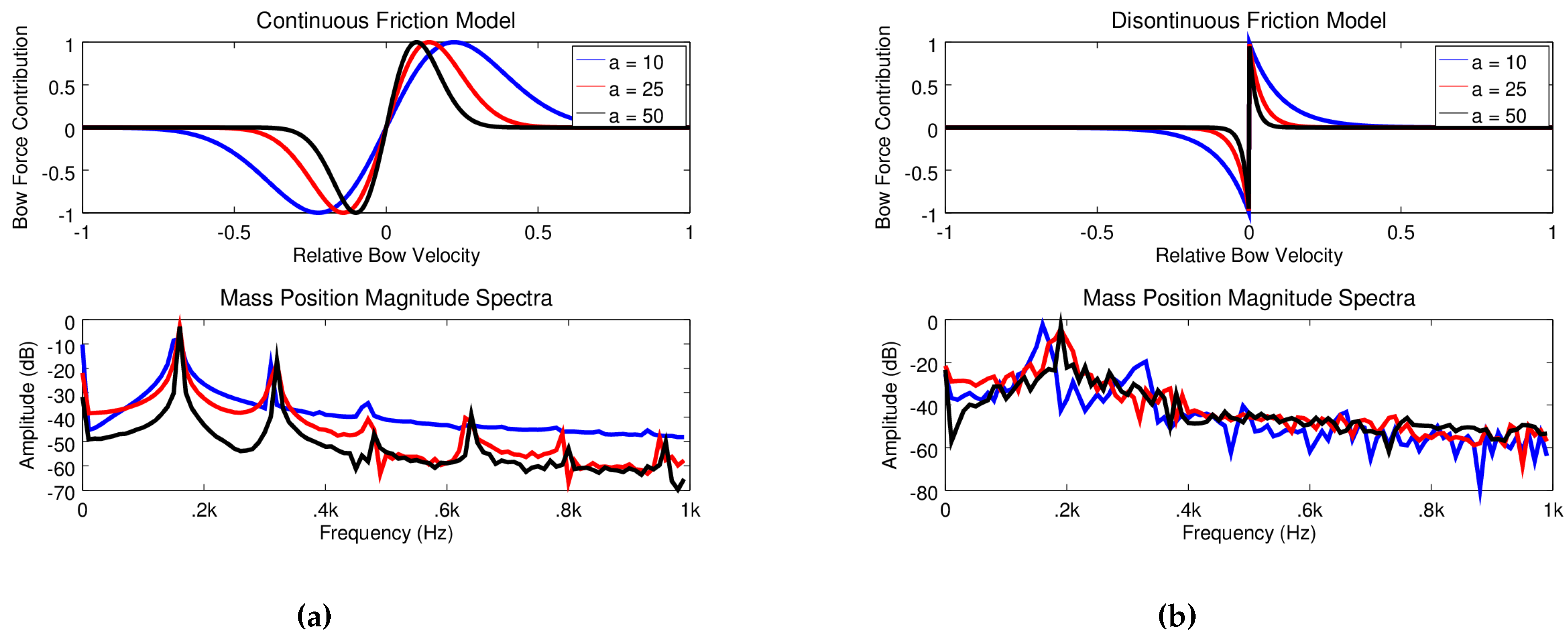
3.4. A Bowed Oscillator
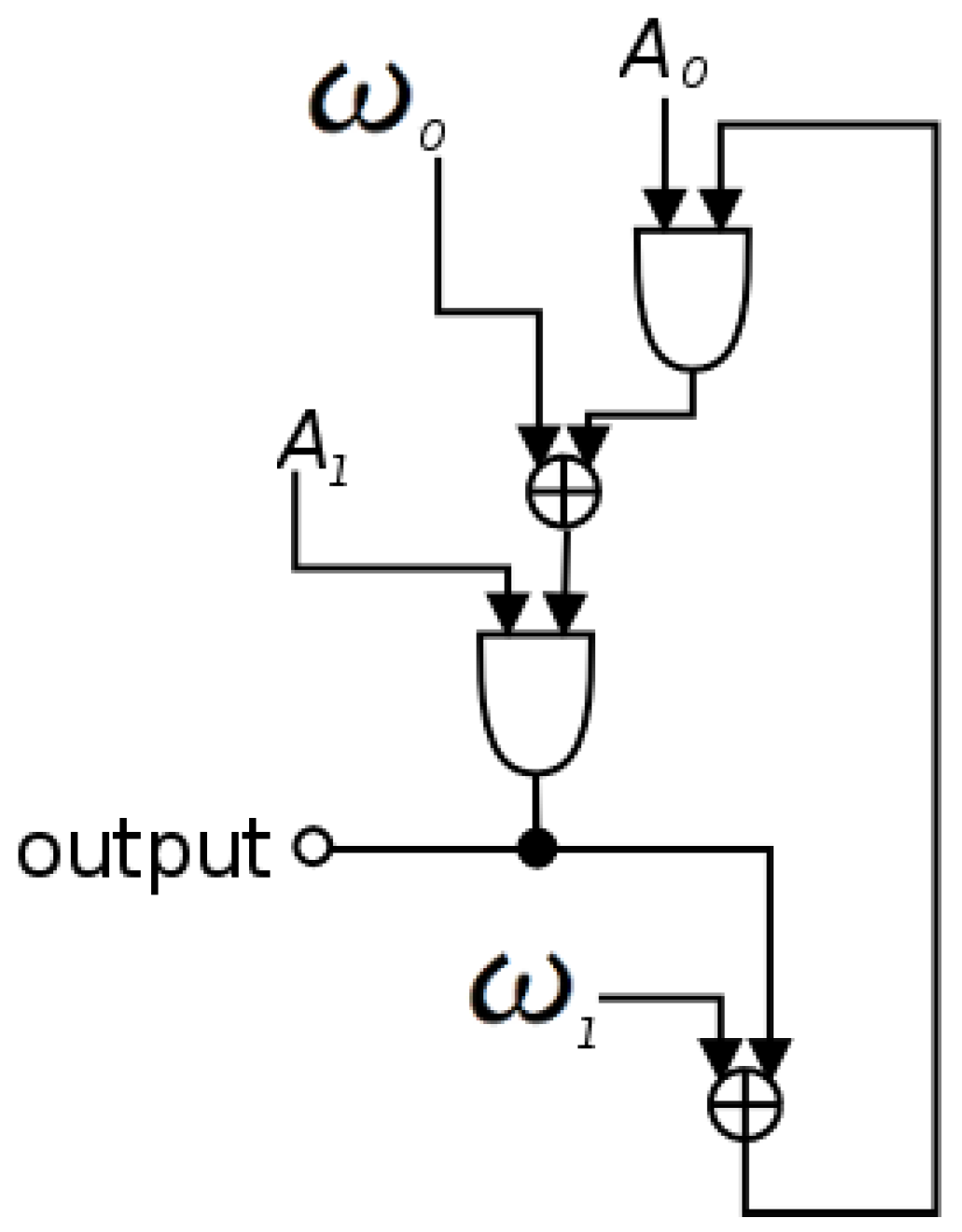
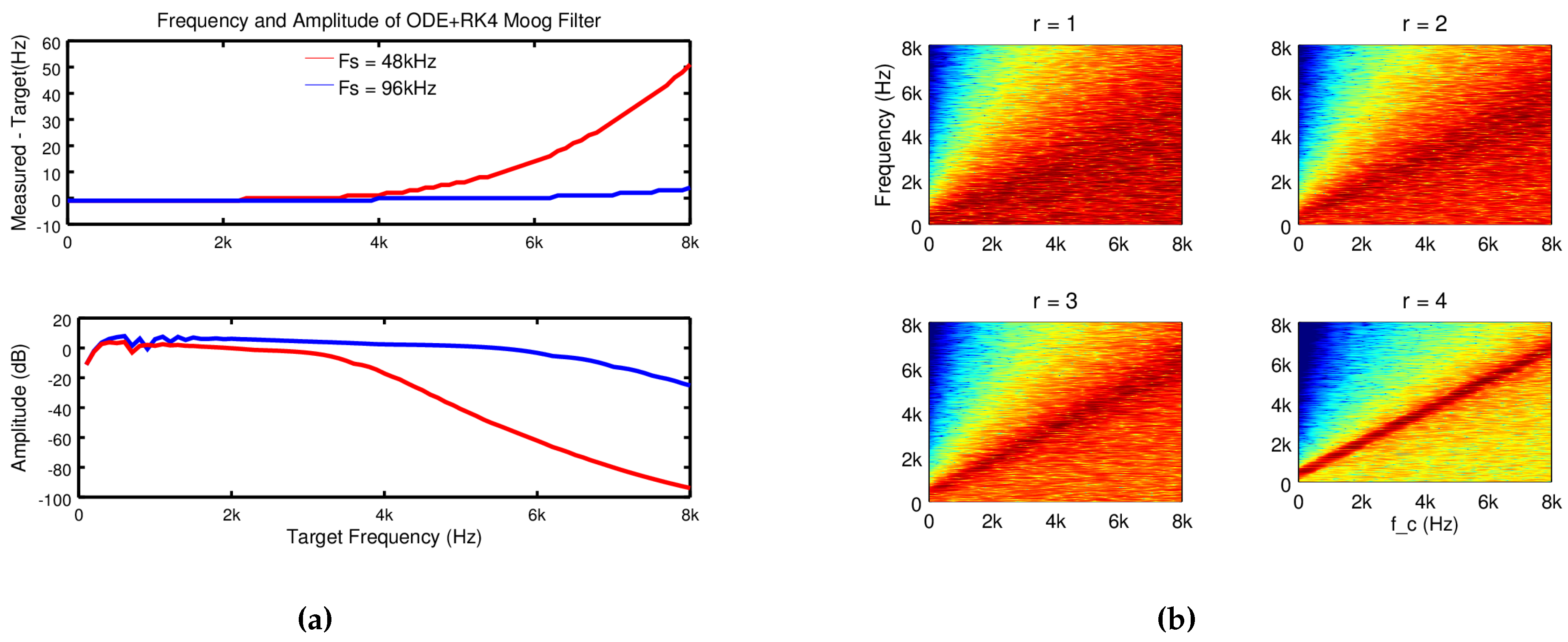
3.5. The Moog Ladder Filter
4. Discussion
5. Conclusions
Conflicts of Interest
References
- Stilson, T.; Smith, J. Analyzing the Moog VCF with considerations for digital implementation. In Proceedings of the 1996 International Computer Music Conference, Hong Kong, China, 19–24 August 1996; pp. 398–401.
- Nagel, L.W.; Pederson, D.O. SPICE: Simulation Program with Integrated Circuit Emphasis; No. UCB/ERL M382; Electronics Research Laboratory, College of Engineering, University of California: Berkeley, CA, USA, 12 April 1973. [Google Scholar]
- Fettweis, A. Digital filters related to classical structures. AEU Arch. Elektron. Ubertragungstechnik 1971, 25, 78–89. [Google Scholar]
- Pakarinen, J.; Tikander, M.; Karjalainen, M. Wave digital modeling of the output chain of a vacuum-tube amplifier. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Como, Italy, 1–4 September 2009; pp. 1–4.
- Pakarinen, J.; Karjalainen, M. Enhanced wave digital triode model for real-time tube amplifier emulation. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 738–746. [Google Scholar] [CrossRef]
- Välimäki, V.; Bilbao, S.; Smith, J.O.; Abel, J.S.; Pakarinen, J.; Berners, D. Virtual Analog Effects. In DAFX: Digital Audio Effects, 2nd ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Van Duyne, S.A.; Pierce, J.R.; Smith, J.O. Traveling wave implementation of a lossless mode-coupling filter and the wave digital hammer. In Proceedings of the International Computer Music Conference, Aarhus, Denmark, 12–17 September 1994; pp. 411–418.
- Bensa, J.; Bilbao, S.; Martinet, K.R.; Smith, J. A power normalized non-linear lossy piano hammer. In Proceedings of the Stokholm Muisc Acoustics Conference, Stokholm, Sweden, 2–9 August 2003; pp. 365–368.
- Van Walstijn, M.; Campbell, M. Discrete-time modeling of woodwind instrument bores using wave variables. J. Acoust. Soc. Am. 2003, 113, 575–585. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Borin, G.; de Poli, G.; Rocchesso, D. Elimination of delay-free loops in discrete-time models of nonlinear acoustic systems. IEEE Trans. Speech Audio Process. 2000, 8, 597–605. [Google Scholar] [CrossRef]
- Werner, K.; Nangia, V.; Smith, J., III; Abel, J. Resolving wave digital filters with multiple/multiport nonlinearities. In Proceedings of the Digital Audio Effects (DAFx), Trondheim, Norway, 30 November–3 December 2015.
- Werner, K.; Smith, J., III; Abel, J. Wave digital filter adaptors for arbitrary topologies and multiport linear elements. In Proceedings of the Digital Audio Effects (DAFx), Trondheim, Norway, 30 November–3 December 2015.
- Yeh, D.T.; Abel, J.S.; Smith, J.O., III. Automated physical modeling of nonlinear audio circuits for real-time audio effects—Part I: theoretical development. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 728–737. [Google Scholar] [CrossRef]
- Yeh, D.T. Automated physical modeling of nonlinear audio circuits for real-time audio effects—Part II: BJT and vacuum tube examples. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 1207–1216. [Google Scholar] [CrossRef]
- Dempwolf, K.; Holters, M.; Zölzer, U. Discretization of parametric analog circuits for real-time simulations. In Proceedings of the 13th International Conference on Digital Audio Effects, Graz, Austria, 4–6 September 2010.
- Yeh, D.T.M. Digital Implementation of Musical Distortion Circuits by Analysis and Simulation. Ph.D. Thesis, Stanford University, Stanford, CA, USA, June 2009. [Google Scholar]
- Puckette, M. Pure Data: Another integrated computer music environment. In Proceedings of the Second Intercollege Computer Music Concerts, Tachikawa, Japan, 7 May 1997; pp. 37–41.
- Medine, D. Unsampled Digitial Synthesis: Computing the Output of Implicit and Non-Linear Systems. In Proceedings of the International Computer Music Conference, Denton, TX, USA, 25 September–1 October 2015; pp. 90–93.
- Yeh, D.T.; Abel, J.; Smith, J.O. Simulation of the diode limiter in guitar distortion circuits by numerical solution of ordinary differential equations. In Proceedings of the 10th International Conference on Digital Audio Effects, Bordeaux, France, 10–15 September 2007; pp. 197–204.
- Macak, J.; Schimmel, J. Nonlinear circuit simulation using time-variant filter. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Como, Italy, 1–4 September 2009.
- Bilbao, S. Numerical Sound Synthesis: Finite Difference Schemes and Simulation in Musical Acoustics; Wiley Online Library: Hoboken, NJ, USA, 2009. [Google Scholar]
- Mathews, M.; Smith, J.O. Methods for synthesizing very high Q parametrically well behaved two pole filters. In Proceedings of the Stockholm Musical Acoustics Conference (SMAC), Stockholm, Sweden, 6–9 August 2003.
- Puckette, M. The Theory and Technique of Electronic Music; World Scientific: Singapore, 2007. [Google Scholar]
- Chowning, J.M. The synthesis of complex audio spectra by means of frequency modulation. J. Audio Eng. Soc. 1973, 21, 526–534. [Google Scholar]
- Chowning, J.M. Method of synthesizing a musical sound. US Patent 4,018,121, April 1977. [Google Scholar]
- Tomisawa, N. Tone production method for an electronic musical instrument. US Patent 4,249,447, February 1981. [Google Scholar]
- McIntyre, M.; Woodhouse, J. On the fundamentals of bowed-string dynamics. Acta Acust. United Acust. 1979, 43, 93–108. [Google Scholar]
- Cremer, L.; Allen, J.S. The Physics of the Violin; MIT Press: Cambridge, MA, USA, 1984. [Google Scholar]
- Serafin, S. The Sound of Friction: Real-time Models, Playability and Musical Applications. Ph.D. Thesis, Stanford University, Stanford, CA, USA, June 2004. [Google Scholar]
- Moog, R.A. A voltage-controlled low-pass high-pass filter for audio signal processing. In Proceedings of the 17th Audio Engineering Society Convention, New York, NY, USA, 11–15 October 1965.
- D’Angelo, S.; Valimaki, V. An improved virtual analog model of the Moog ladder filter. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 729–733.
- Huovilainen, A. Nonlinear digital implementation of the Moog ladder filter. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Naples, Italy, 5–8 October 2004; pp. 61–64.
- Daly, P. A Comparison of Virtual Analogue Moog VCF Models. Master’s Thesis, University of Edinburgh, Edinburgh, UK, August 2012. [Google Scholar]
- Hélie, T. On the use of Volterra series for real-time simulations of weakly nonlinear analog audio devices: Application to the Moog ladder filter. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Montreal, QC, Canada, 18–20 September 2006; pp. 7–12.
- Hélie, T. Volterra series and state transformation for real-time simulations of audio circuits including saturations: Application to the Moog ladder filter. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 747–759. [Google Scholar] [CrossRef]
- D’Angelo, S.; Valimaki, V. Generalized Moog ladder filter: Part II–Explicit nonlinear model through a novel delay-free loop implementation method. IEEE/ACM Trans. Audio Speech. Lang. Process. 2014, 22, 1873–1883. [Google Scholar] [CrossRef]
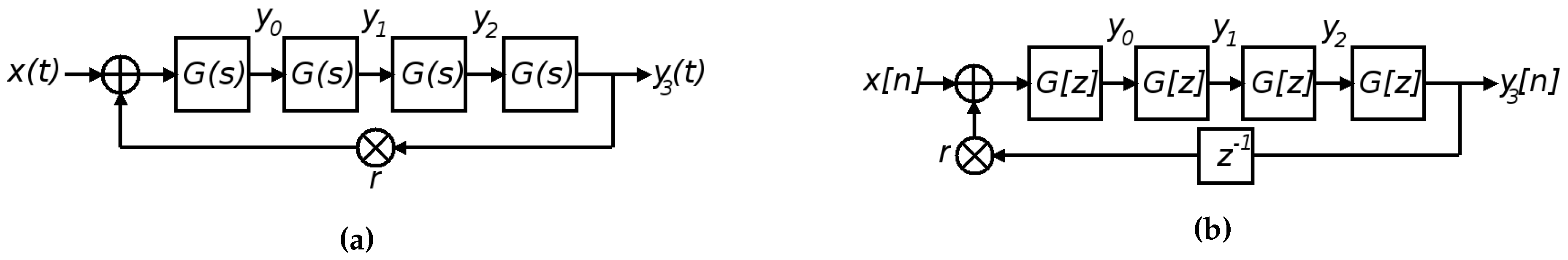




© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medine, D. Dynamical Systems for Audio Synthesis: Embracing Nonlinearities and Delay-Free Loops. Appl. Sci. 2016, 6, 134. https://doi.org/10.3390/app6050134
Medine D. Dynamical Systems for Audio Synthesis: Embracing Nonlinearities and Delay-Free Loops. Applied Sciences. 2016; 6(5):134. https://doi.org/10.3390/app6050134
Chicago/Turabian StyleMedine, David. 2016. "Dynamical Systems for Audio Synthesis: Embracing Nonlinearities and Delay-Free Loops" Applied Sciences 6, no. 5: 134. https://doi.org/10.3390/app6050134




