Magnetohydrodynamic Flow and Heat Transfer of Nanofluids in Stretchable Convergent/Divergent Channels
Abstract
:1. Introduction
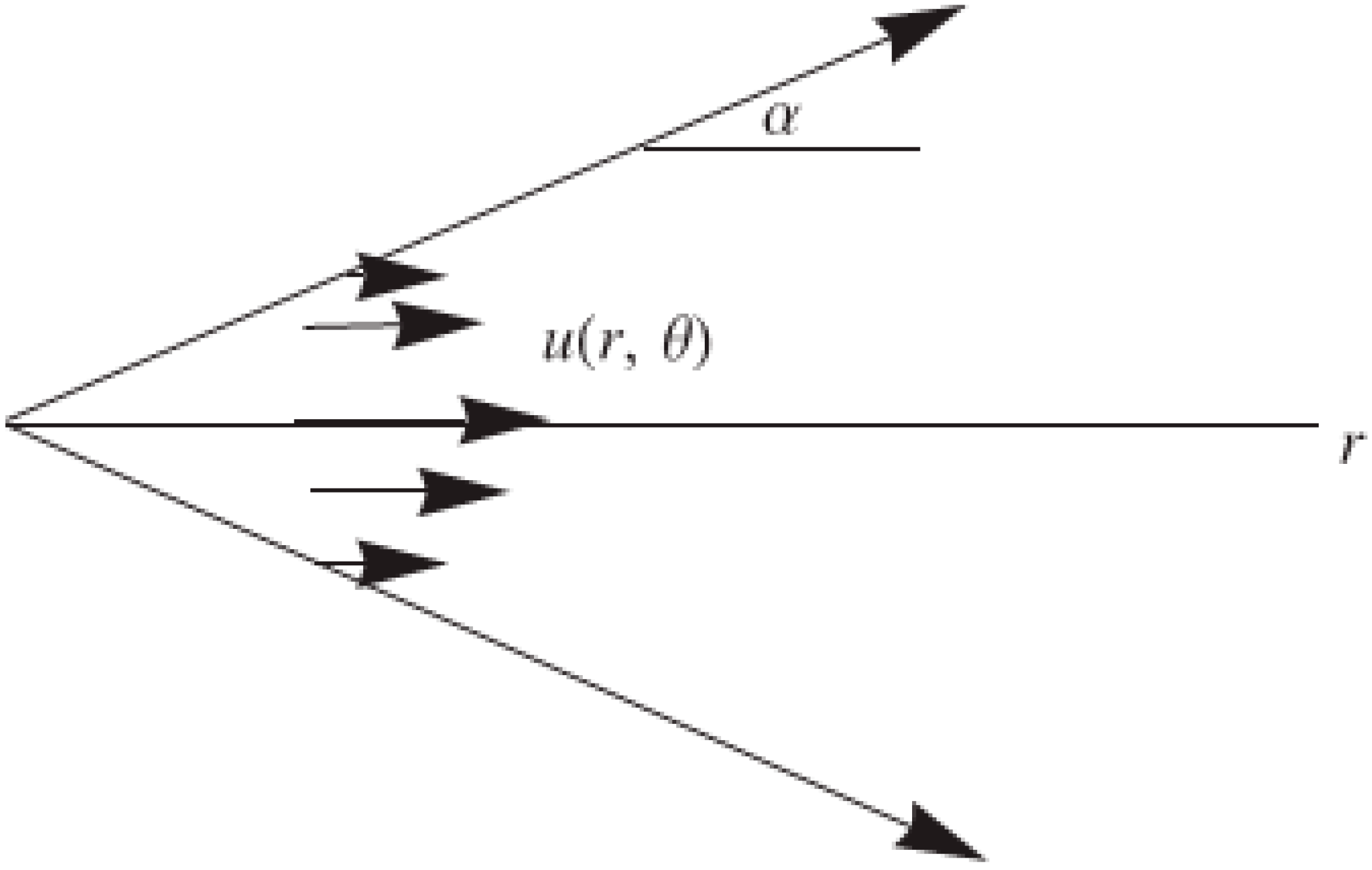
2. Governing Equations
3. Solution Procedure
4. Results and Discussion
| Electrical Conductivity | ||||
|---|---|---|---|---|
| Pure Water | 997.1 | 4179 | 0.613 | 0.05 |
| Copper (Cu) | 8933 | 385 | 401 | 5.96 × 107 |
| Silver | 10,500 | 235 | 429 | 6.3 × 107 |
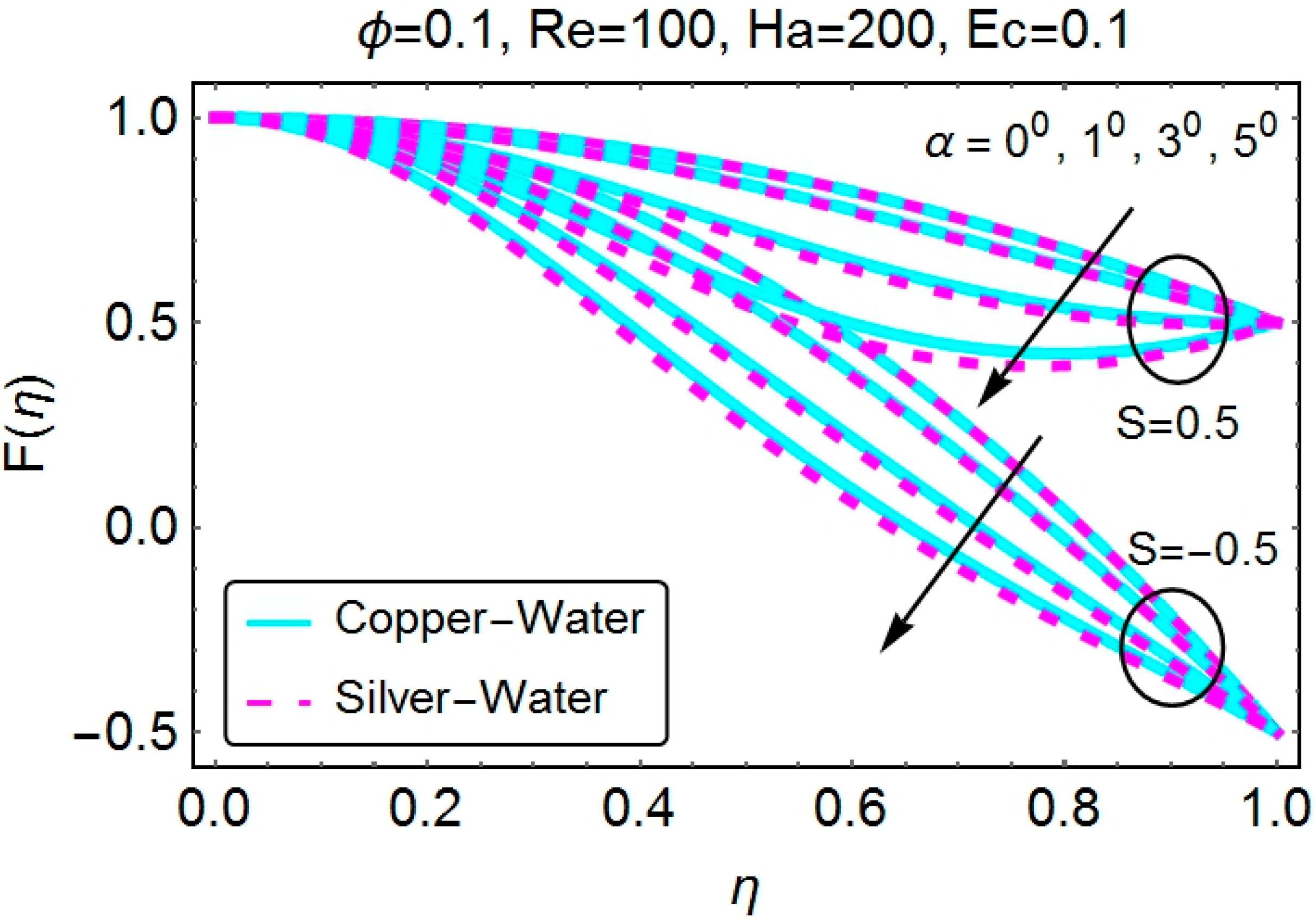
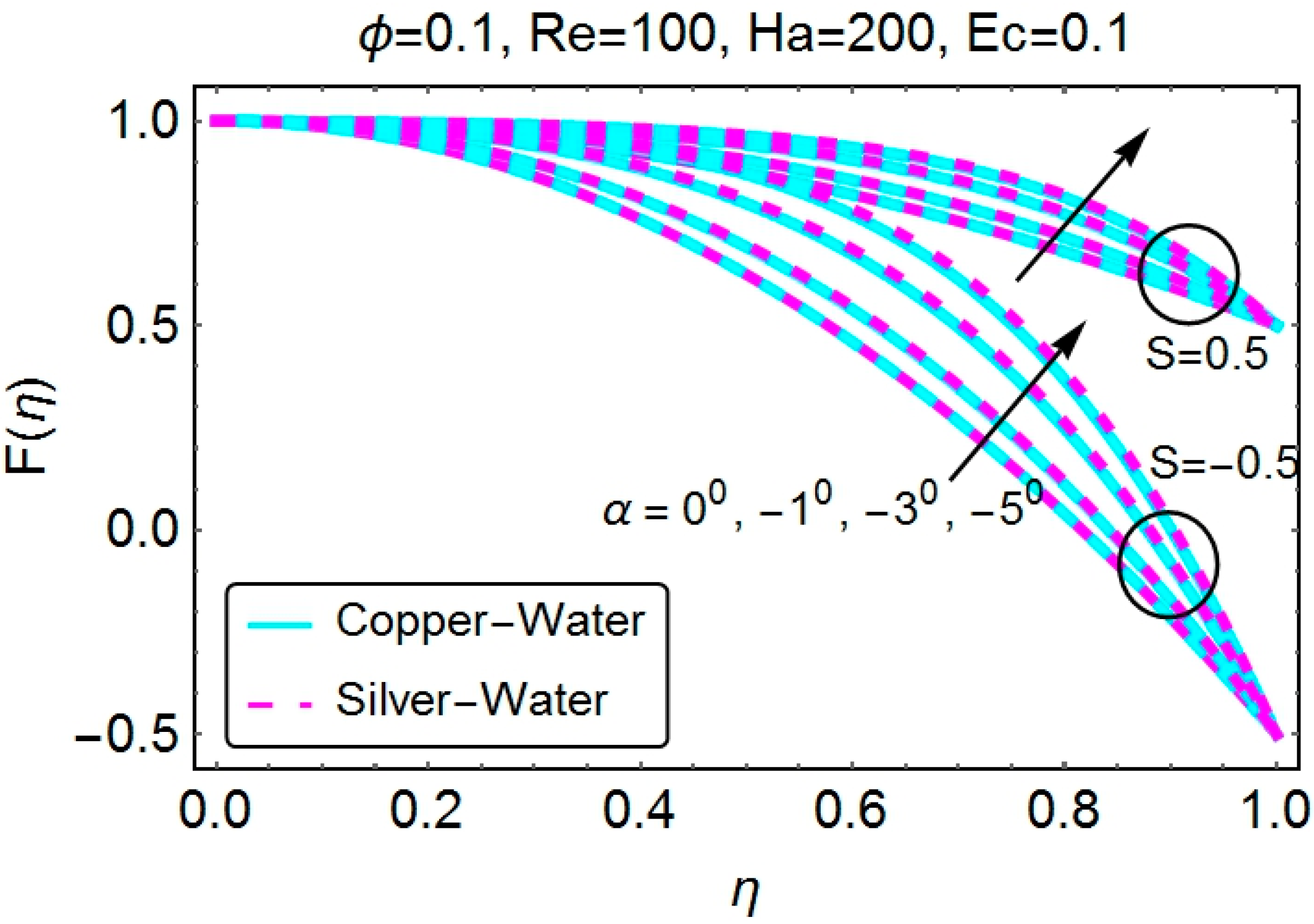
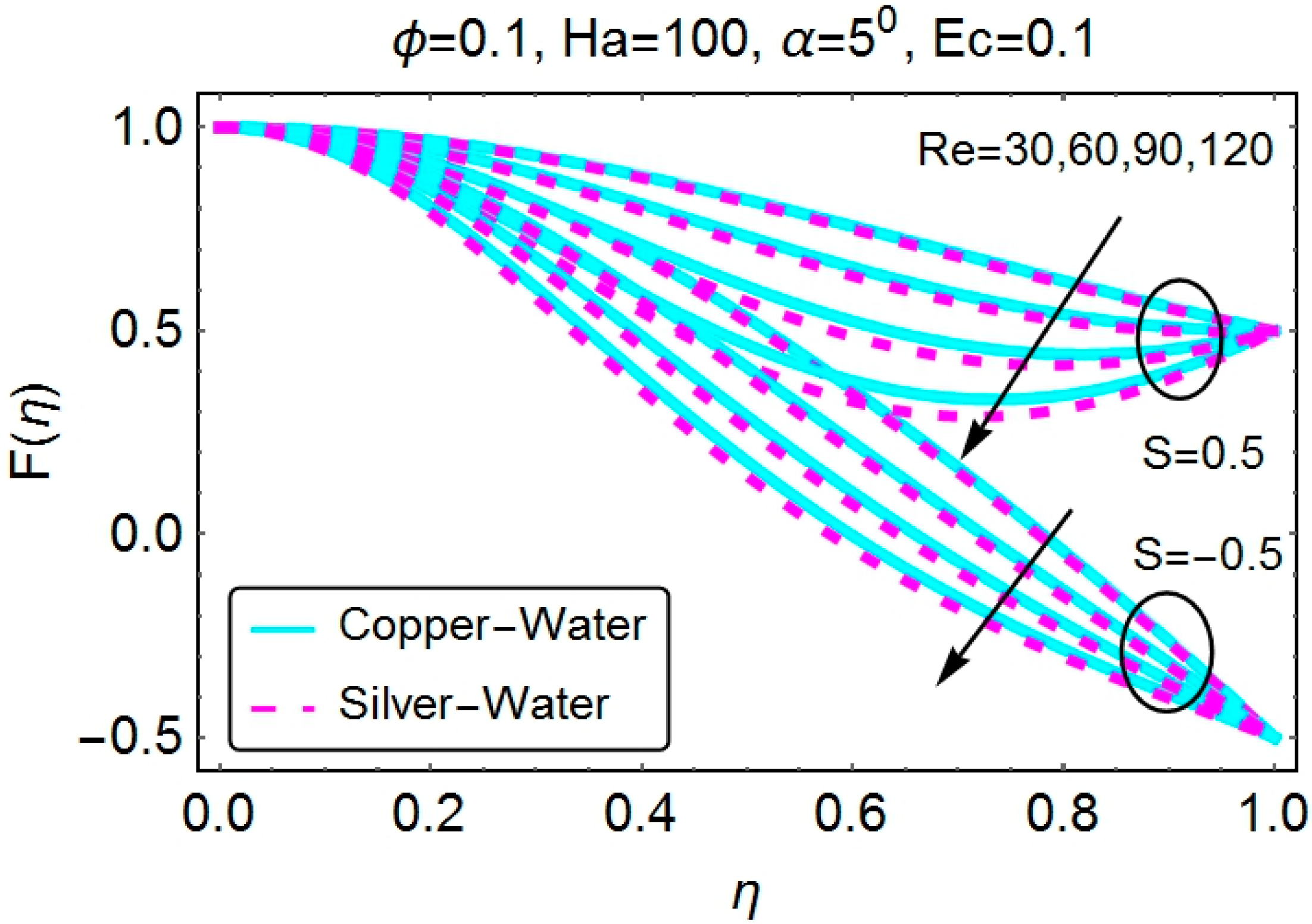
4.1. Velocity Profile



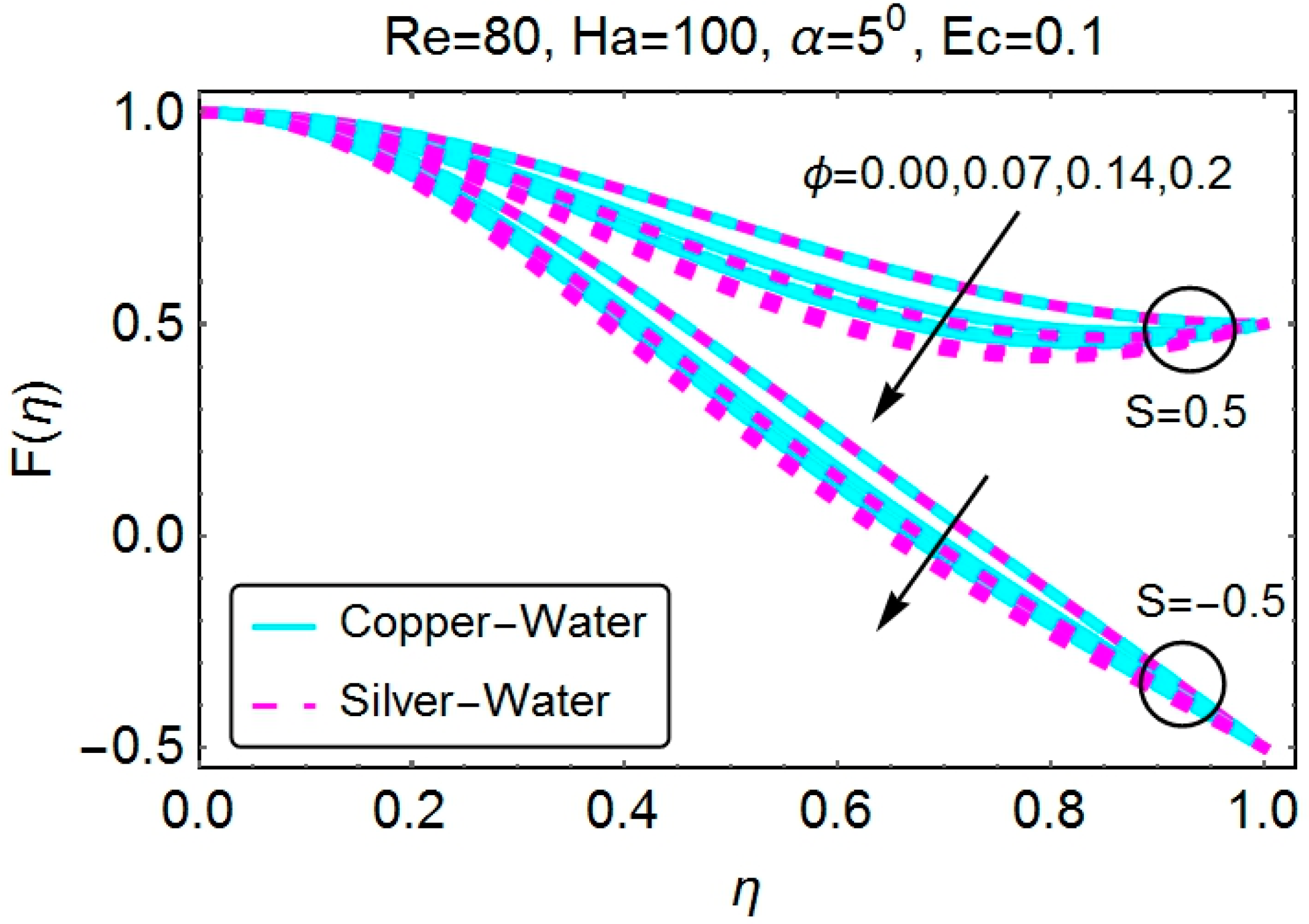
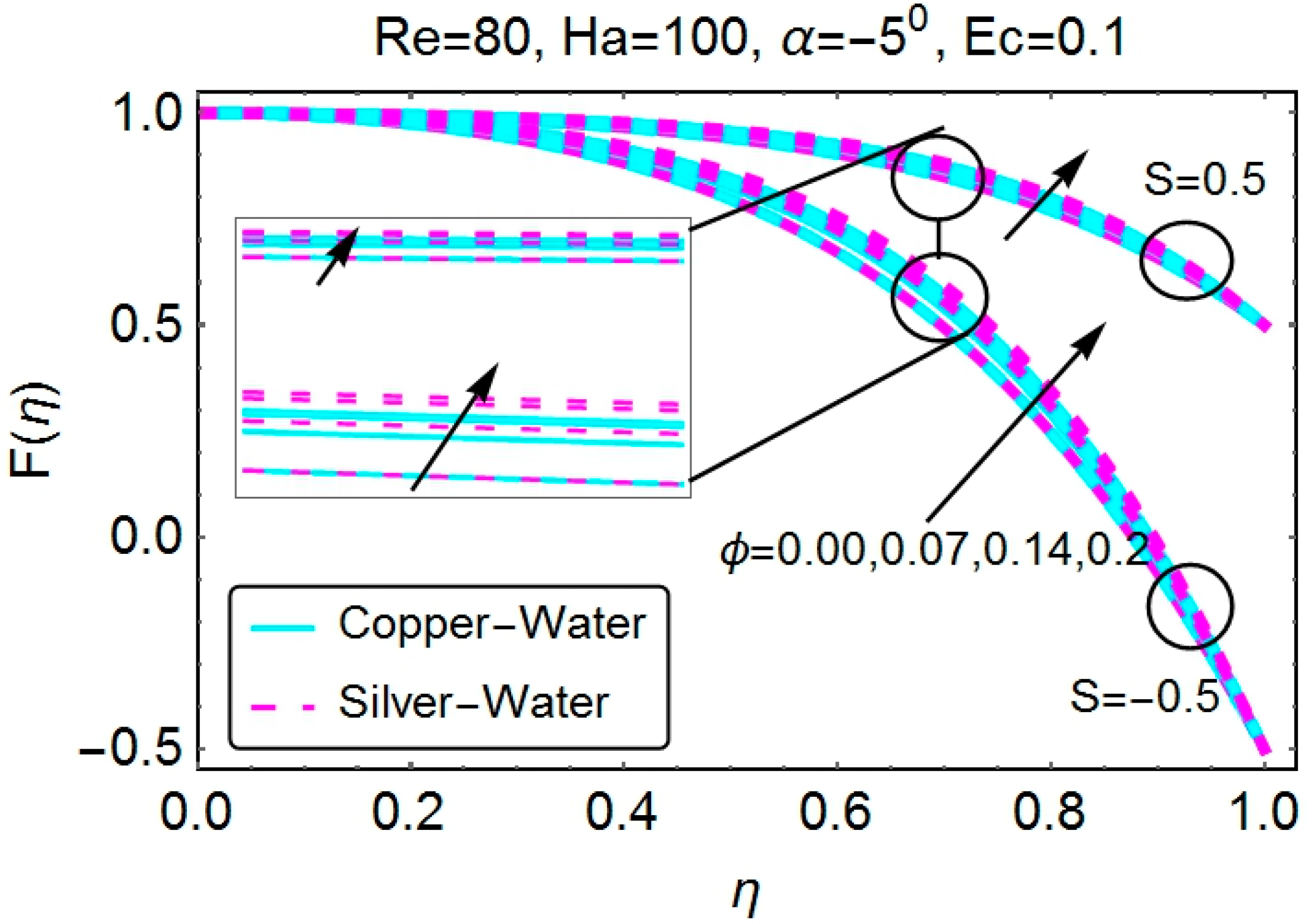
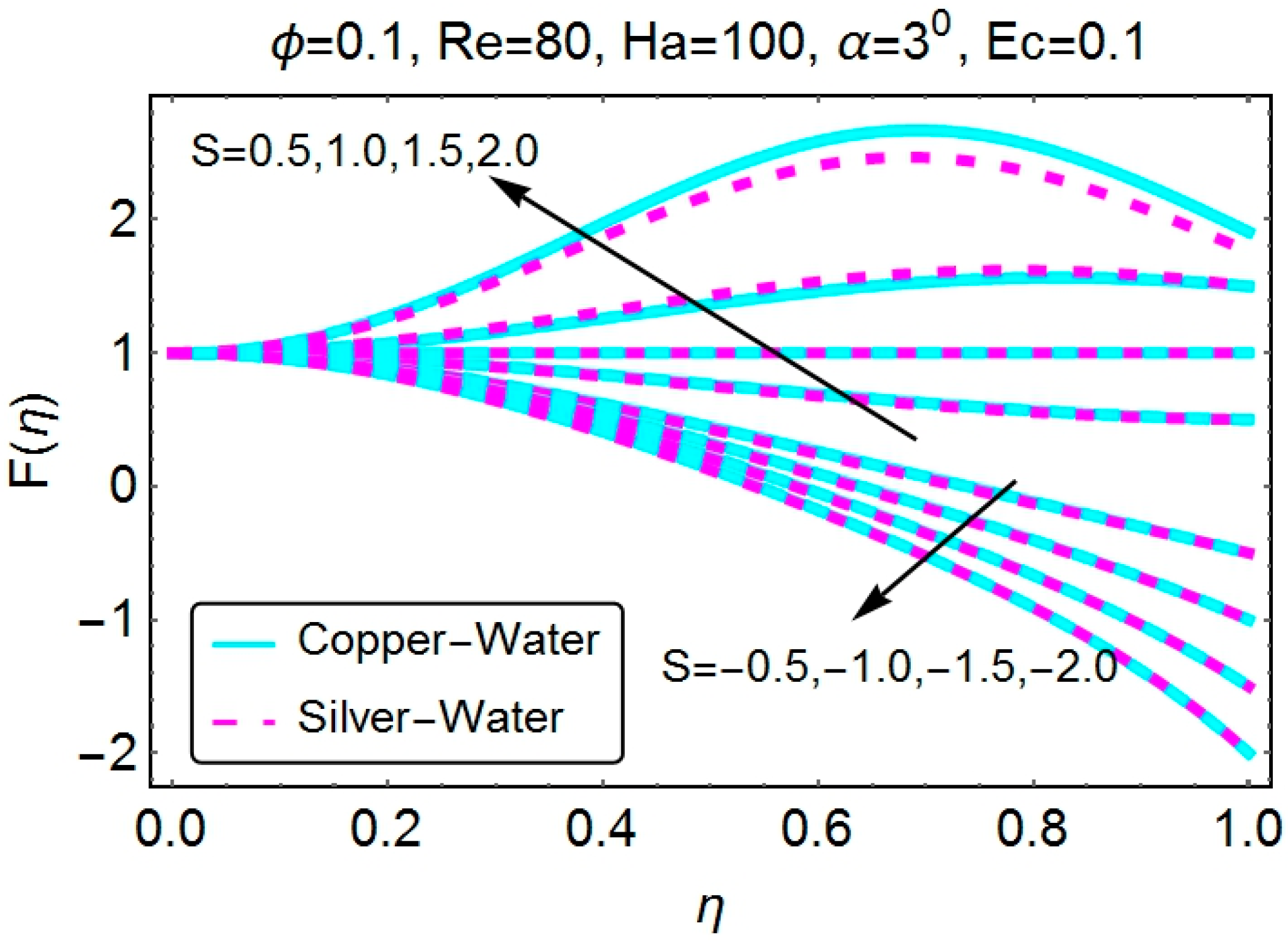

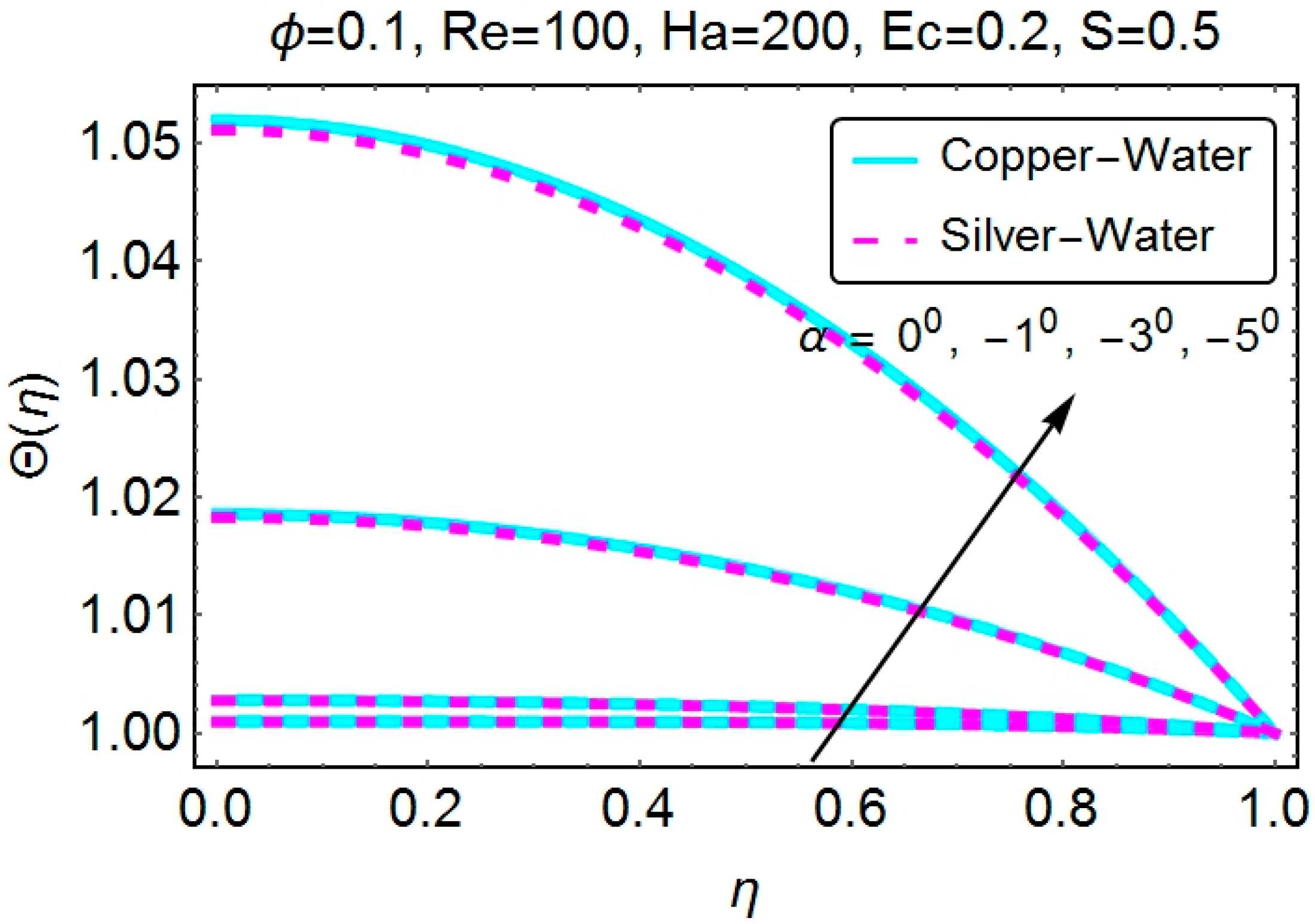
4.2. Temperature Profile


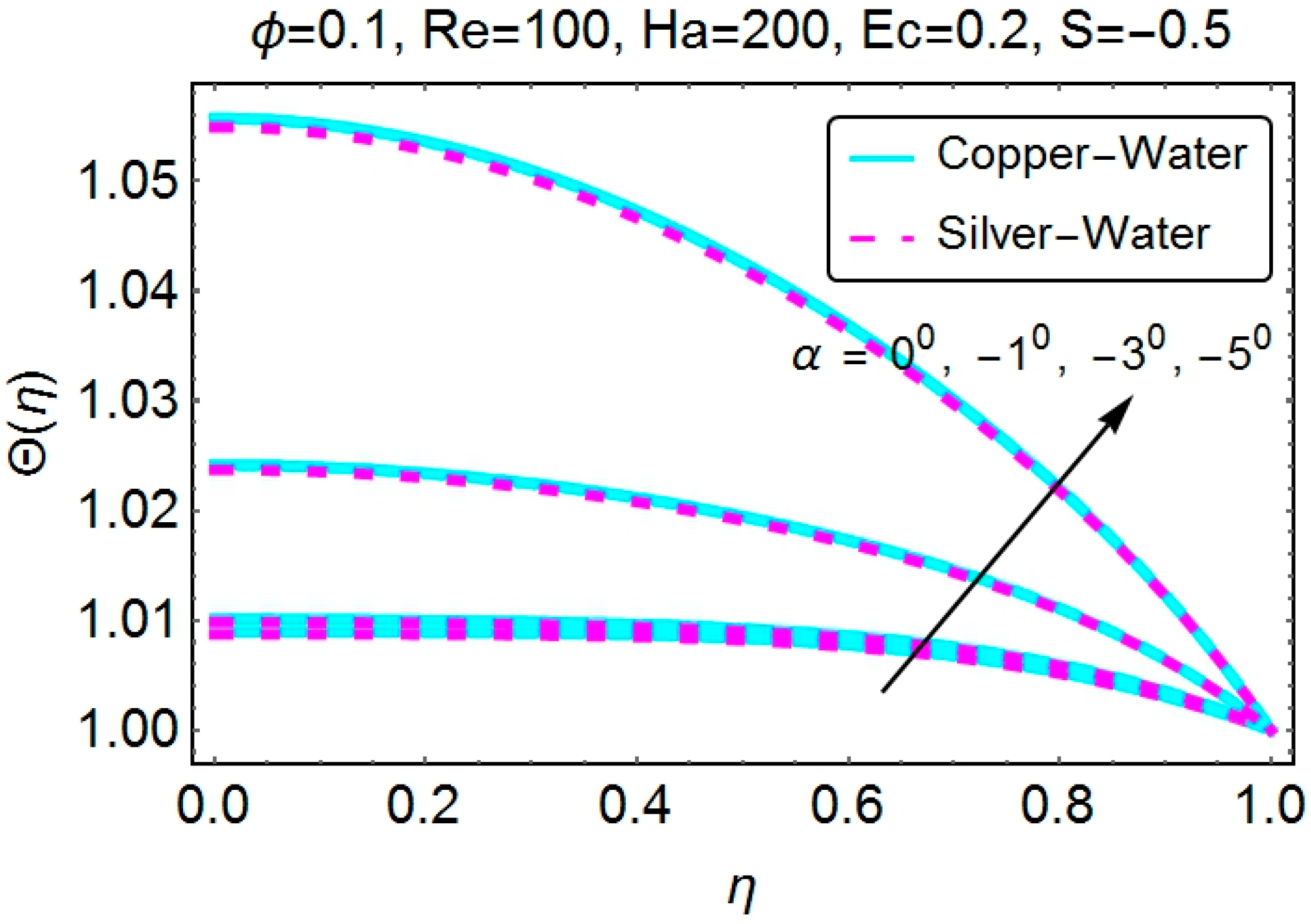
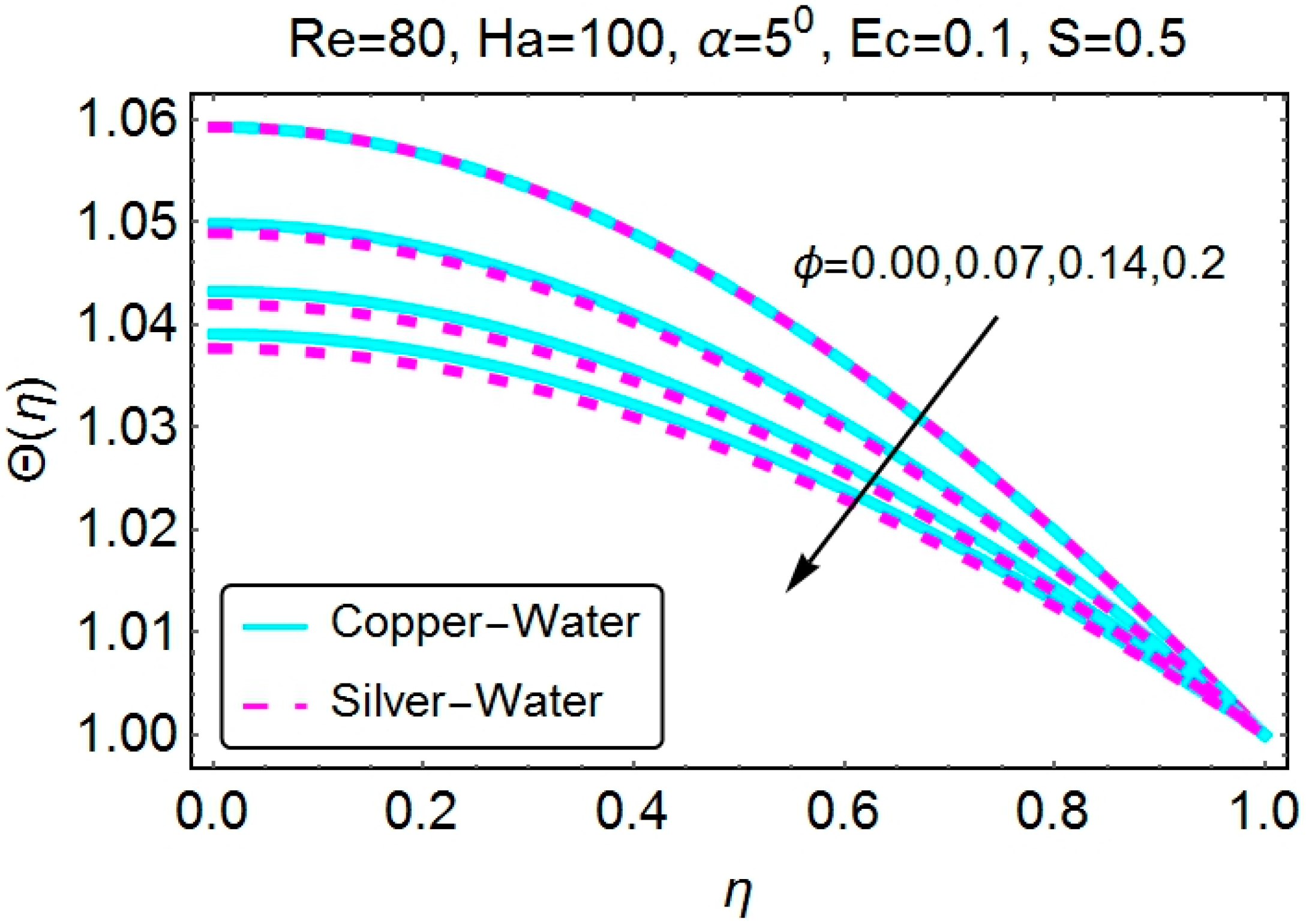
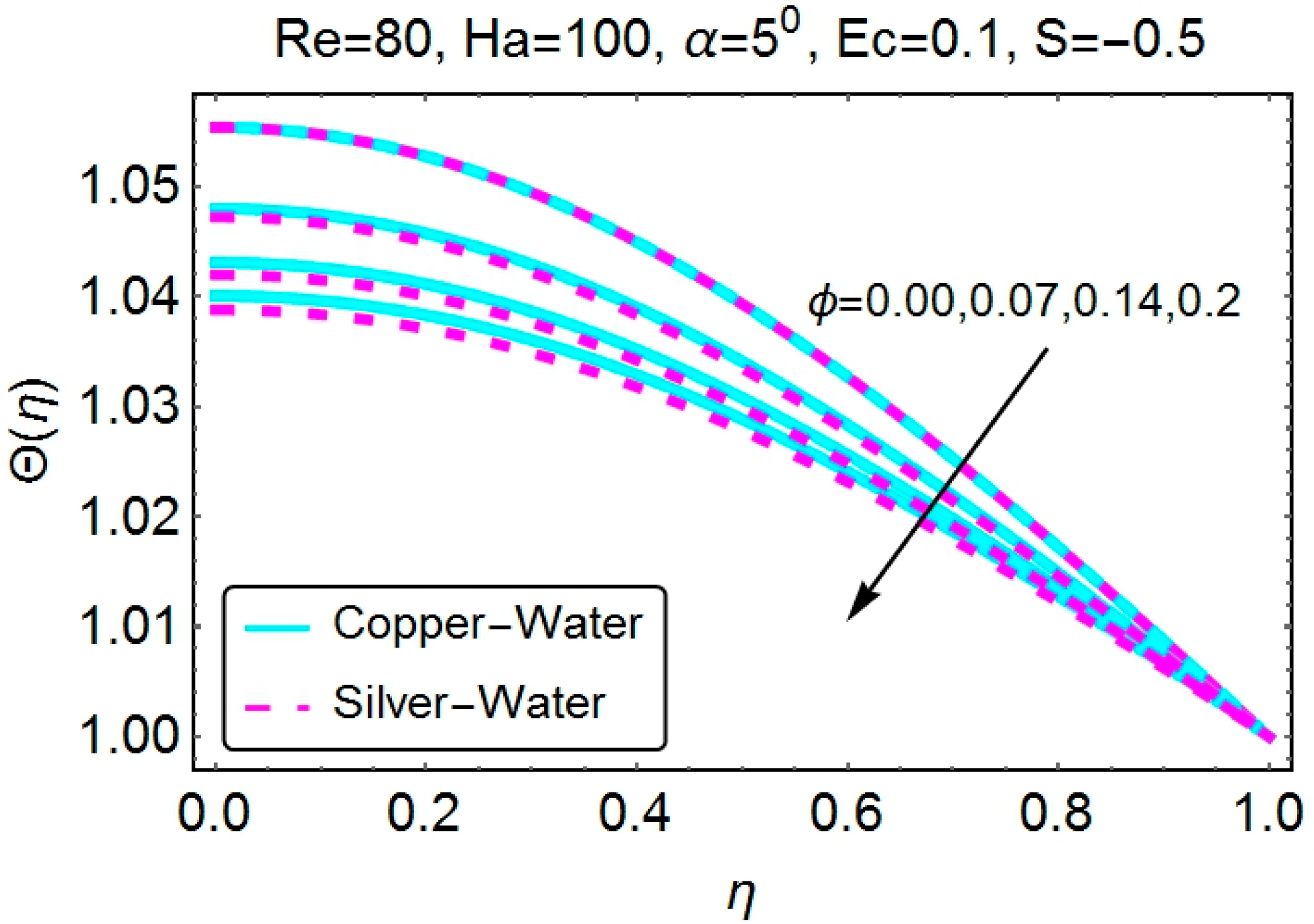


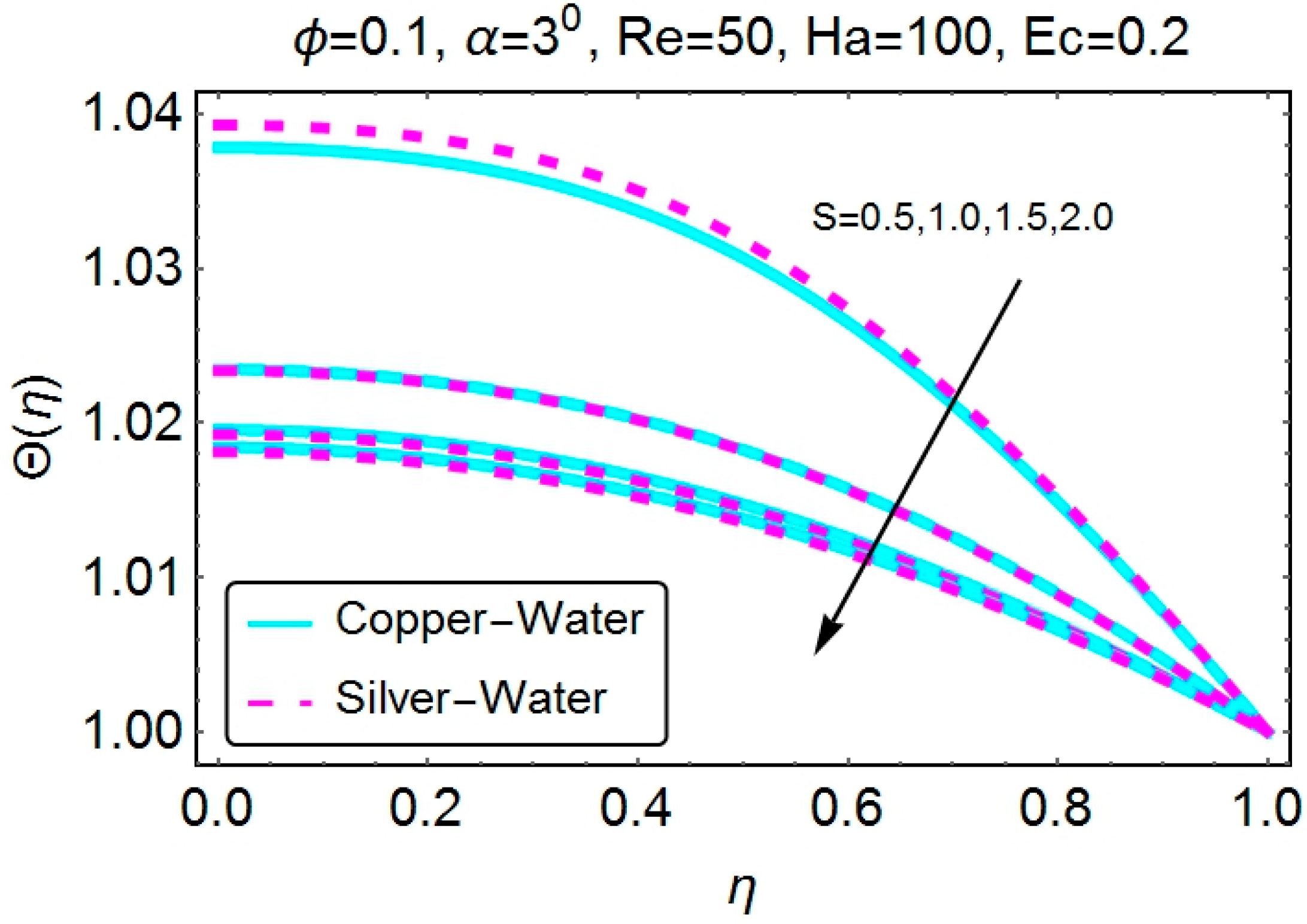

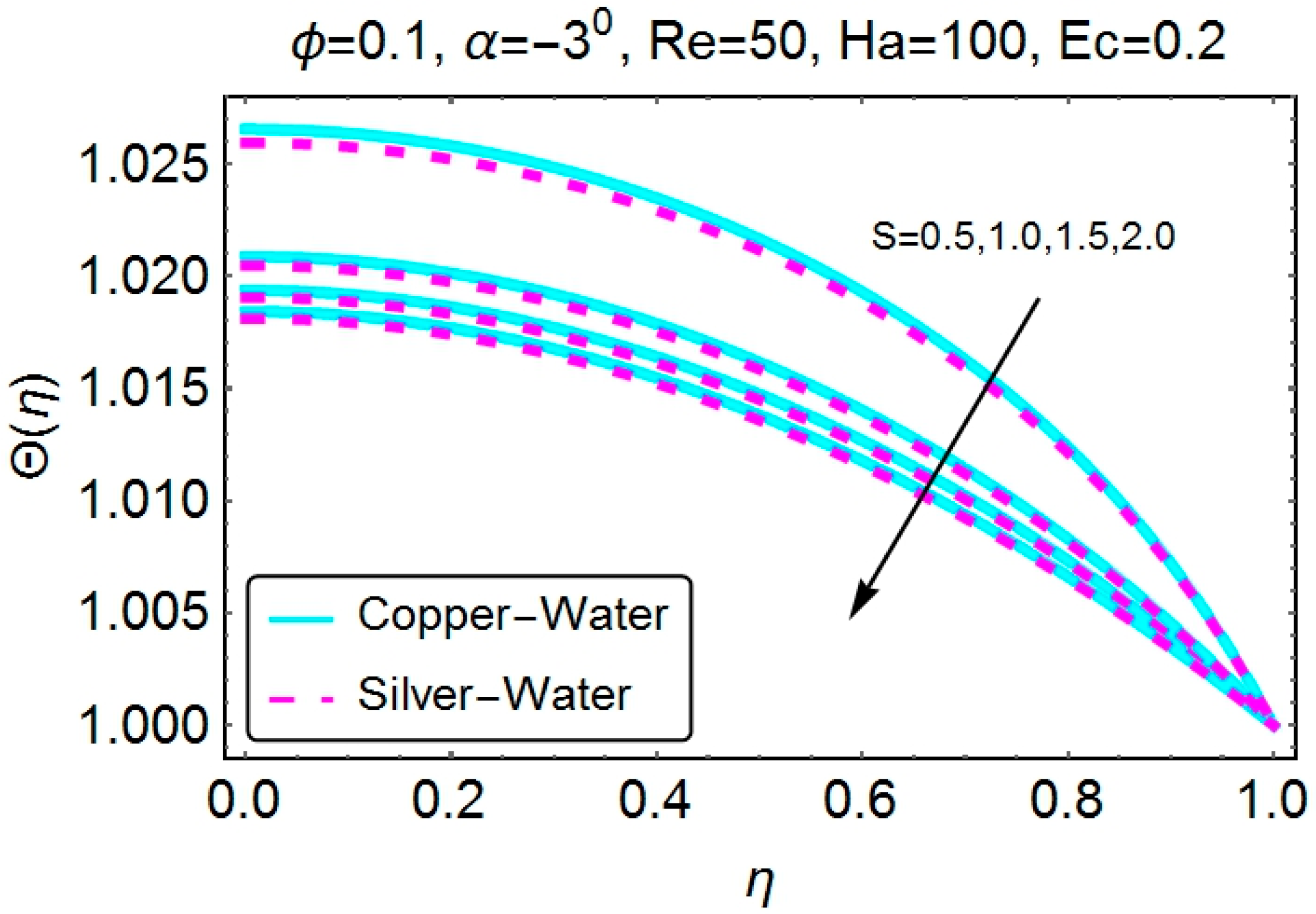


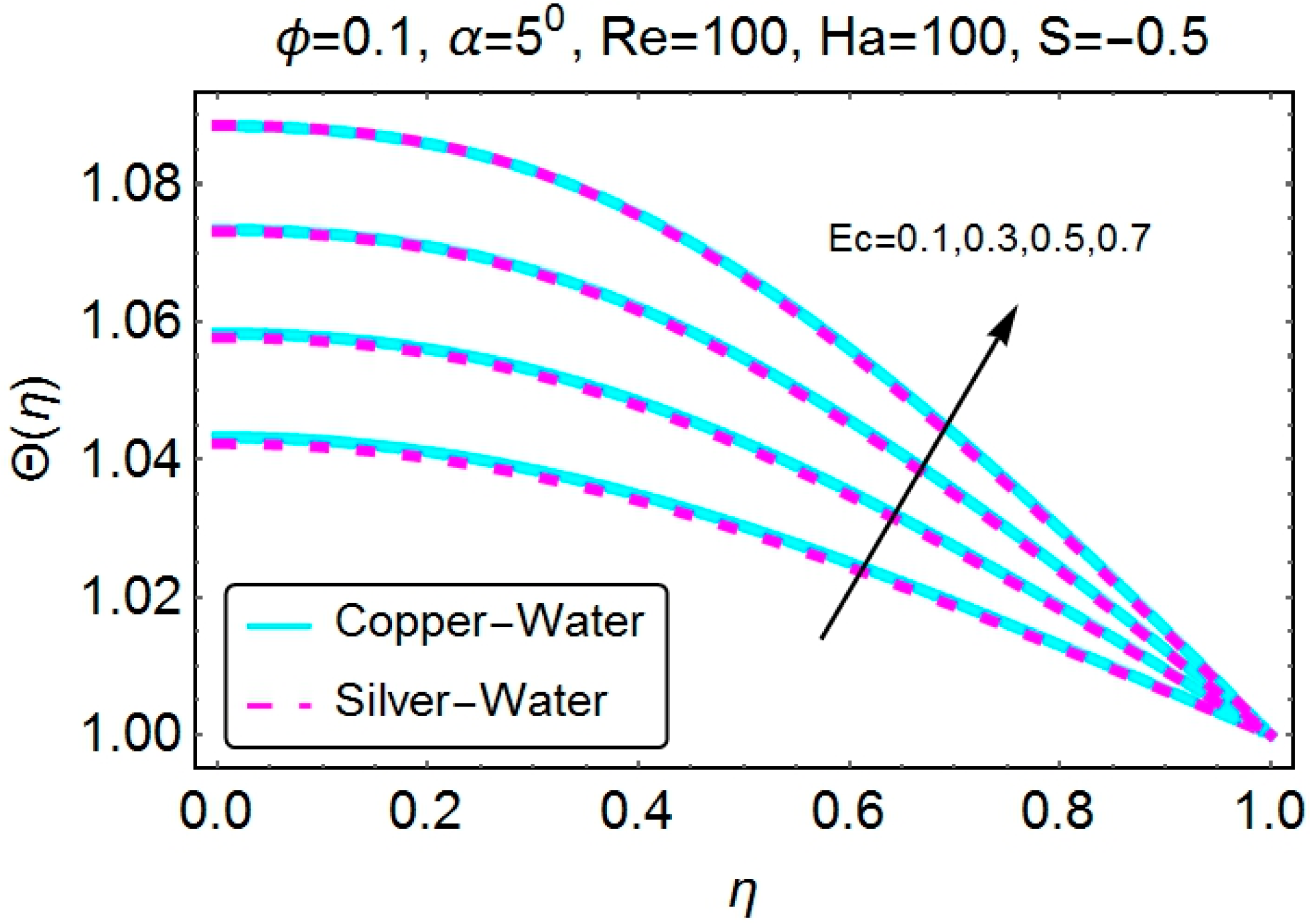
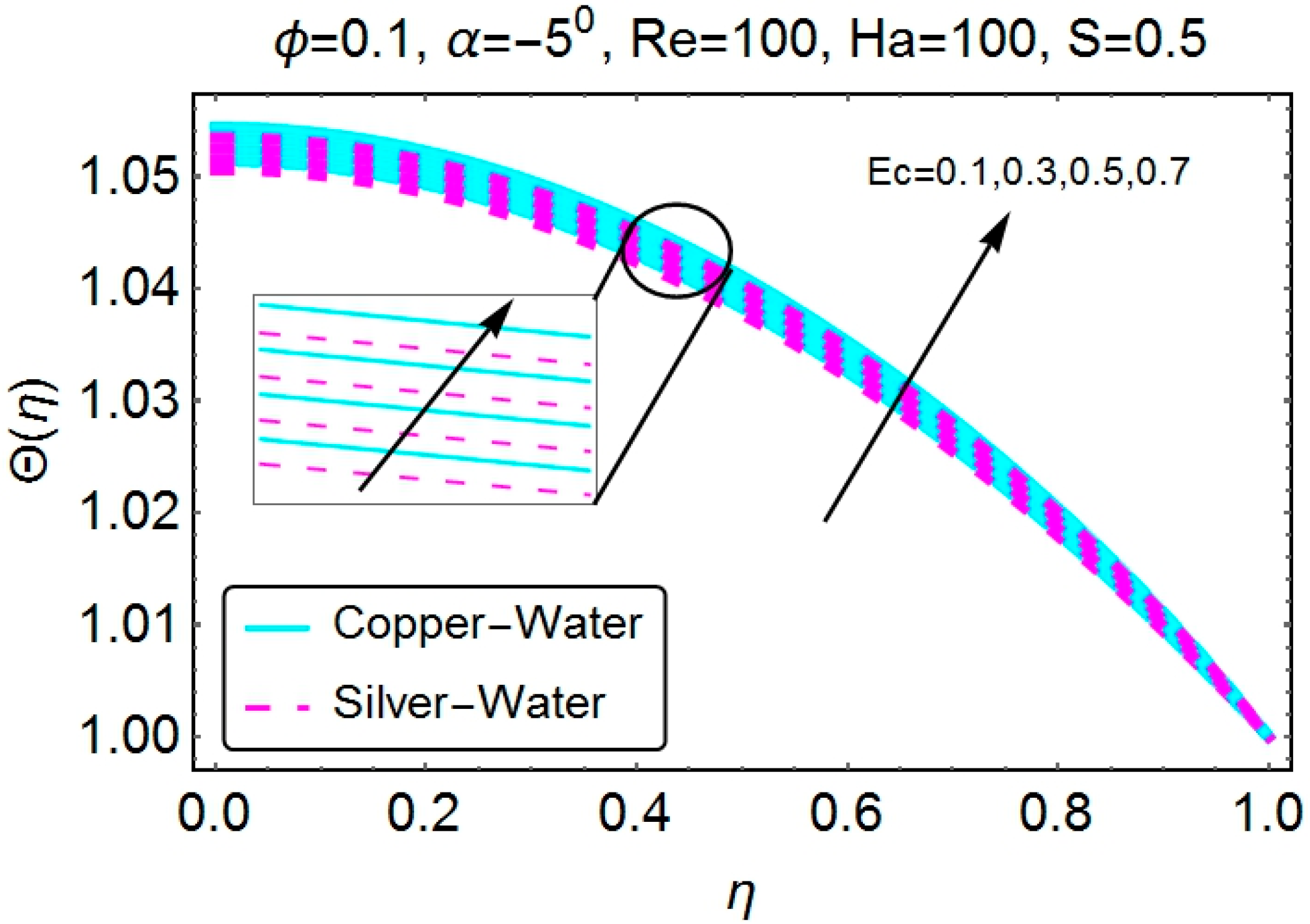

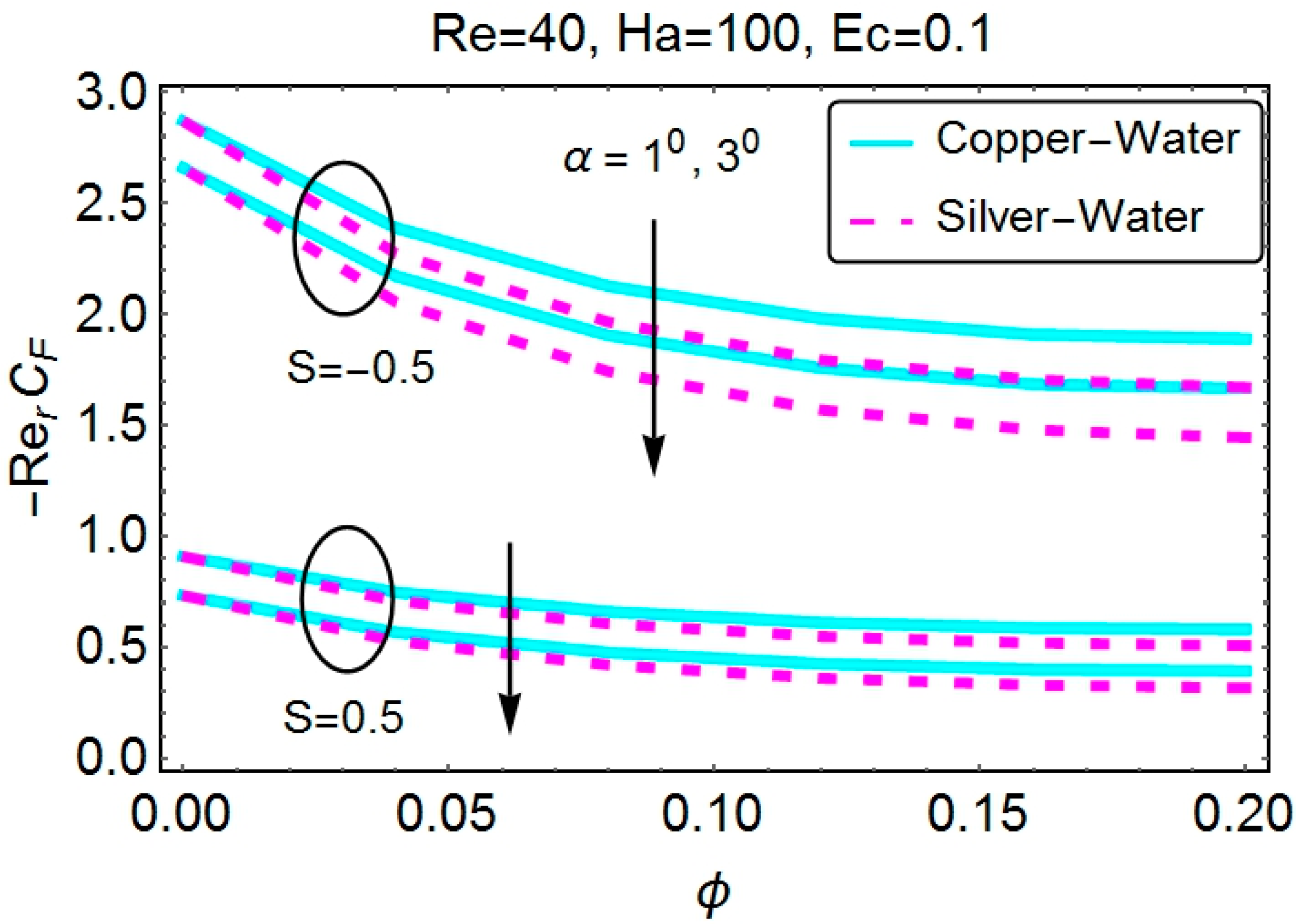
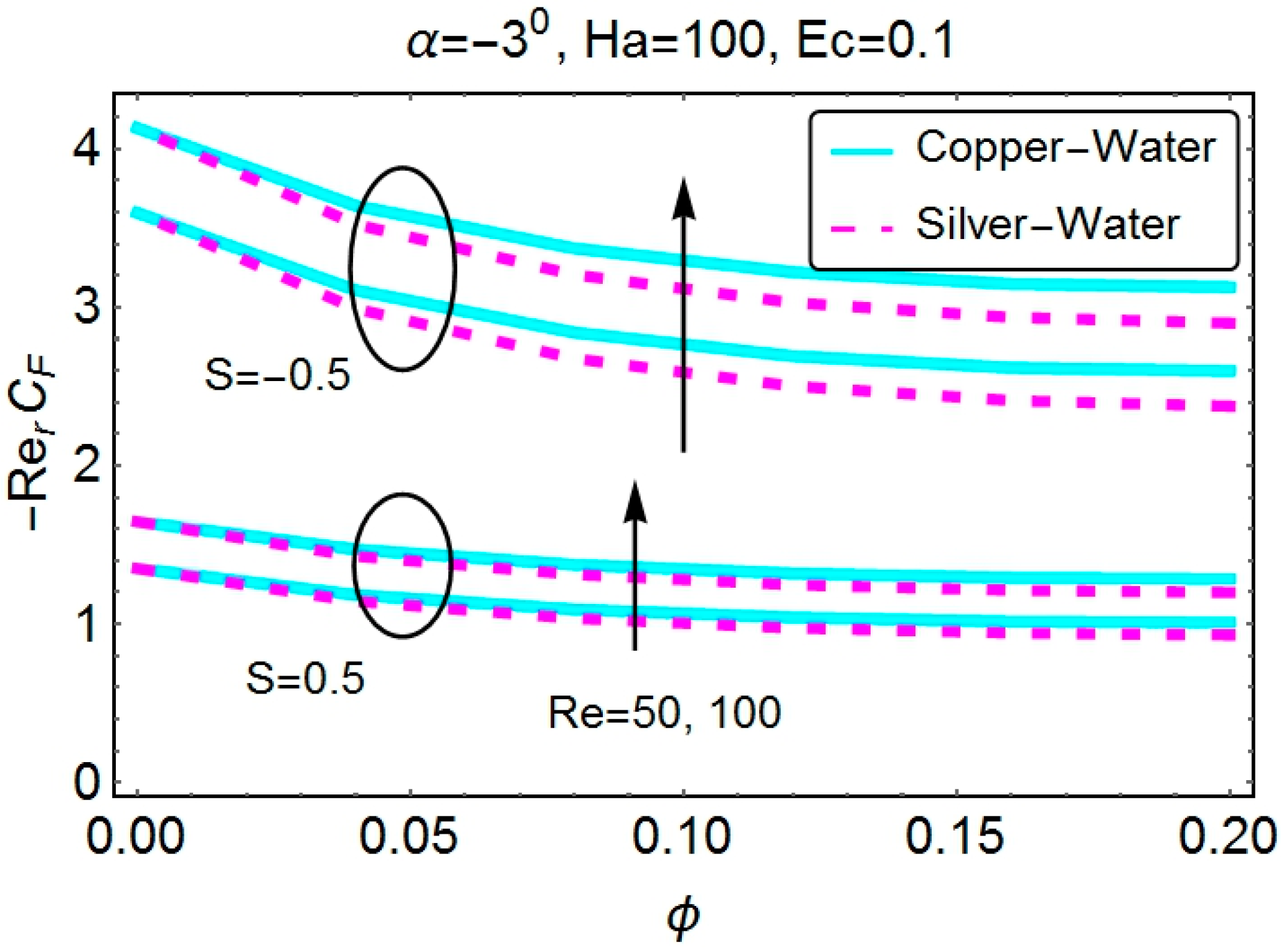
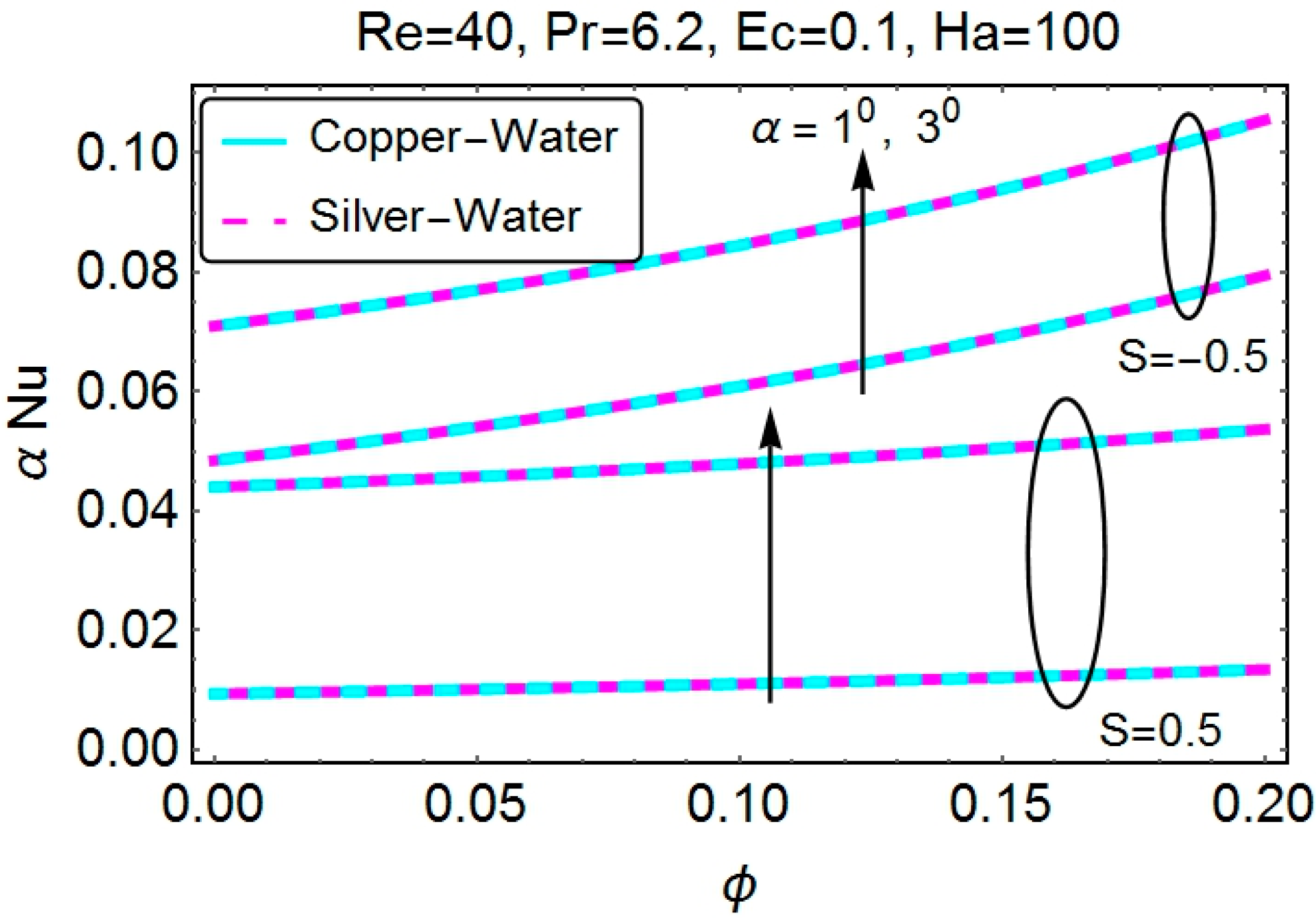
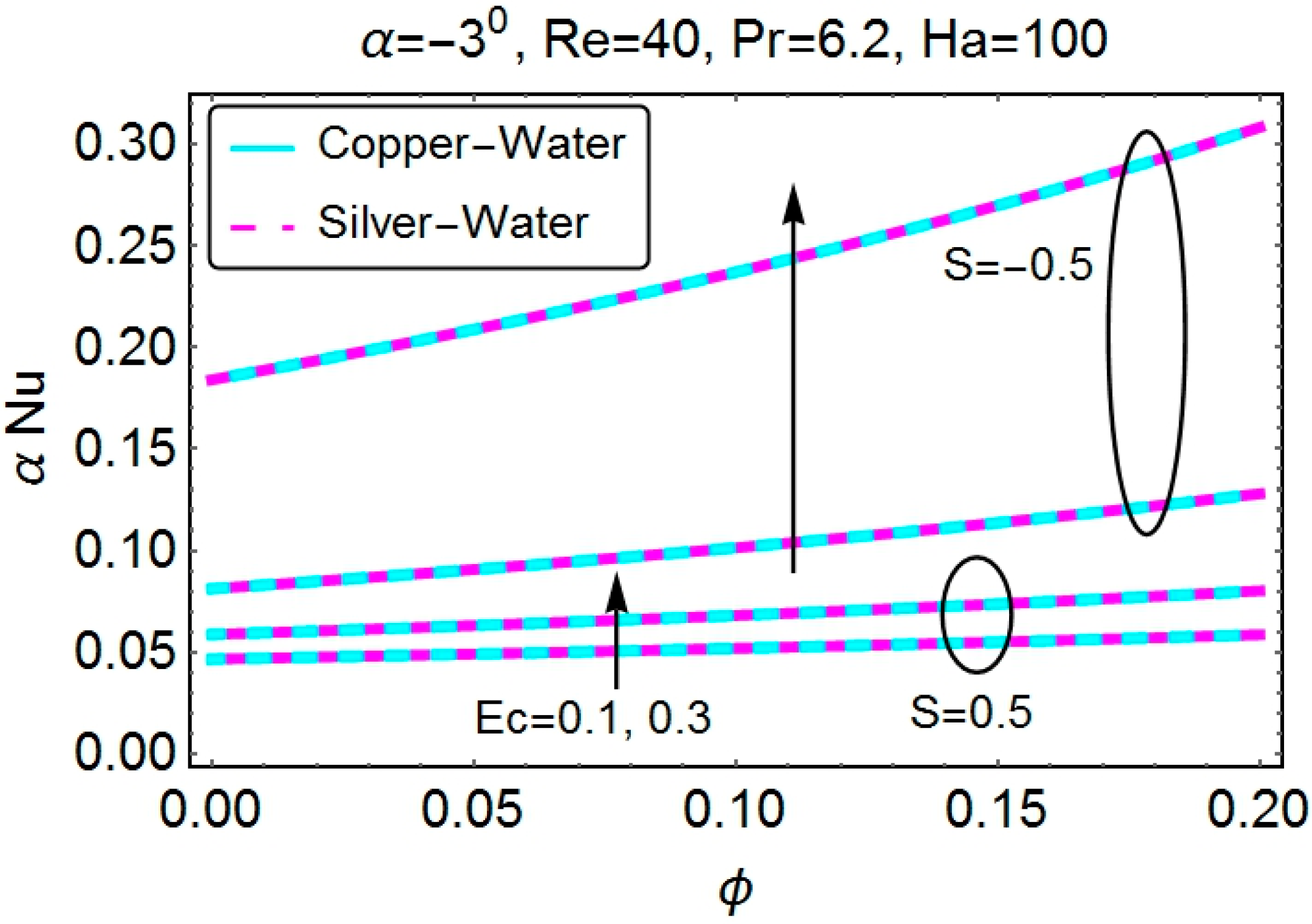
4.3. Skin Friction Coefficient and the Nusselt Number




| S | S | ||||||
|---|---|---|---|---|---|---|---|
| ↓ | VIM | RKF | Turkyilmazoglu [38] | ↓ | VIM | RKF | Turkyilmazoglu [38] |
| −1 | −3.508103 | −3.508103 | −3.508103 | −2 | −5.130922 | −5.130922 | −5.130922 |
| −1/2 | −2.173044 | −2.173044 | −2.173044 | −1 | −4.652159 | −4.652159 | −4.652159 |
| 0 | 0.000000 | 0.000000 | 0.000000 | 0 | −2.833951 | −2.833951 | −2.833951 |
| 1/2 | −0.361846 | −0.361846 | −0.361846 | 1 | 0.000000 | 0.000000 | 0.000000 |
| 1 | 0.000000 | 0.000000 | 0.000000 | 2 | 3.669711 | 3.669711 | 3.669711 |
| S | S | ||||||
|---|---|---|---|---|---|---|---|
| ↓ | VIM | RKF | Turkyilmazoglu [38] | ↓ | VIM | RKF | Turkyilmazoglu [38] |
| −1 | 0.034775 | 0.034775 | 0.034775 | −2 | 0.031576 | 0.031576 | 0.031576 |
| −1/2 | 0.0372685 | 0.0372685 | 0.0372685 | −1 | 0.037322 | 0.037322 | 0.037322 |
| 0 | 0.039982 | 0.039982 | 0.039982 | 0 | 0.042151 | 0.042151 | 0.042151 |
| 1/2 | 0.042986 | 0.042986 | 0.042986 | 1 | 0.046401 | 0.046401 | 0.046401 |
| 1 | 0.046401 | 0.046401 | 0.046401 | 2 | 0.050242 | 0.050242 | 0.050242 |
5. Conclusions
- Angle opening and the Reynolds number have opposite effects on the velocity profile for convergent and divergent channels.
- Stretching walls may result in backflow regimes for divergent channels, because this moves the particles near the wall away. An increase in the angle opening and Reynolds number may result in backflow and, thus, separation. This result might cause instabilities in the flow.
- The Hartmann number gives a solution to the backflow regions. An increase in the Hartmann number removes the backflow for stretching divergent channels. This effect can be useful in several physical phenomena.
- The nanoparticle volume fraction reduces the velocity of the fluid for both copper and silver nanoparticles in the case of a divergent channel. For a convergent channel, the increase in the volume fraction increases the velocity.
- Stretching of the divergent channel increases the flow near the walls of the channel. Additionally, shrinking reduces the velocity of the fluid near the walls of the channel. Identical behavior is seen for the case of a convergent channel.
- The almost identical behavior of the temperature profile for increasing channel opening is observed for both convergent and divergent channels, both for stretching and shrinking channels.
- Temperature is seen to be decreasing for increasing values of the nanoparticle volume fraction. Both stretching and shrinking channels have an almost identical behavior.
- Stretching of the walls results in lower temperature values for both convergent and divergent channels. Increasing values of temperature near the walls of the channel are observed for the shrinking case.
- The Eckert number increases the temperature of the fluid for all of the cases.
- The nanoparticle volume fraction reduces the skin friction coefficient for all of the cases. Stretching channels have lower skin friction values than shrinking channels.
- The opposite behavior of the skin friction coefficient for increasing Re is observed for convergent and divergent channels.
- The rate of heat transfer at the wall increases with a higher nanoparticle volume fraction and Eckert number. These two parameters have the same behavior for all of the cases.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jeffery, G.B. The two-dimensional steady motion of a viscous fluid. Philos. Mag. 1915, 6, 455–465. [Google Scholar] [CrossRef]
- Hamel, G. Spiralförmige Bewgungen ZäherFlüssigkeiten. Jahresber. Deutsch. Math. Verein. 1916, 25, 34–60. [Google Scholar]
- Asadullah, M.; Khan, U.; Ahmed, N.; Manzoor, R.; Mohyud-Din, S.T. MHD Flow of a Jeffery Fluid in Converging and Diverging Channels. Int. J. Mod. Math. Sci. 2013, 6, 92–106. [Google Scholar]
- Motsa, S.S.; Sibanda, P.; Marewo, G.T. On a new analytical method for flow between two inclined walls. Numer. Algorithms 2012, 61, 499–514. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Phys. 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S.; Haq, R.U.; Khan, Z.H. Radiation effects on MHD stagnation point flow of nano fluid towards a stretching surface with convective boundary condition. Chin. J. Aeronaut. 2013, 26, 1389–1397. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U. Effect of Thermal Radiation for Megnetohydrodynamic Boundary Layer Flow of a Nanofluid Past a Stretching Sheet with Convective Boundary Conditions. J. Comput. Theor. Nanosci. 2013, 11, 32–40. [Google Scholar] [CrossRef]
- Magyari, E.; Keller, B. Exact solutions for self-similarboundary-layerflows induced by permeable stretching walls. Eur. J. Mech. B Fluids 2000, 19, 109–122. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticle. In Proceedings of ASME International Mechanical Engineering Congress & Exposition, San Francisco, CA, USA, 12–17 November 1995.
- Choi, S.U.S.; Zhang, Z.G.; Yu, W.; Lockwood, F.E.; Grulke, E.A. Anomalously thermal conductivity enhancement in nanotube suspensions. Appl. Phys. Lett. 2001, 79, 2252–2254. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. ASME J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Xue, Q. Model for thermal conductivity of carbon nanotube-based composites. Phys. B Condens. Matter 2005, 368, 302–307. [Google Scholar] [CrossRef]
- Hamilton, R.L.; Crosser, O.K. Thermal conductivity of heterogeneous two component systems. Ind. Eng. Chem. Fundam. 1962, 1, 187–191. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism, 3rd ed.; Clarendon: Oxford, UK, 1904. [Google Scholar]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Akbar, N.S. MHD three-dimensional boundary layer flow of casson nanofluid past a linearly stretching sheet with convective boundary condition. Nanotechnol. IEEE Trans. 2014, 13, 109–115. [Google Scholar] [CrossRef]
- Noor, N.F.M.; Haq, R.U.; Nadeem, S. Mixed convection stagnation flow of a micropolarnanofluid along a vertically stretching surface with slip effects. Meccanica 2015. [Google Scholar] [CrossRef]
- Khan, U.; Ahmed, N.; Khan, S.I.U.; Mohyud-Din, S.T. Thermo-diffusion and MHD effects on stagnation point flow towards a stretching sheet in a nanofluid. Propuls. Power Res. 2014, 3, 151–158. [Google Scholar] [CrossRef]
- Khan, U.; Ahmed, N.; Mohyud-Din, S.T. Heat transfer effects on carbon nanotubes suspended nanofluid flow in a channel with non-parallel walls under the effect of velocity slip boundary condition: A numerical study. Neural Comput. Appl. 2015. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T.; Zaidi, Z.A.; Khan, U.; Ahmed, N. On heat and mass transfer analysis for the flow of a nanofluid between rotating parallel plates. Aerosp. Sci. Technol. 2015, 46, 514–522. [Google Scholar] [CrossRef]
- Khalid, A.; Khan, I.; Shafie, S. Exact solutions for free convection flow of nanofluids with ramped wall temperature. Eur. Phys. J. Plus 2015, 130. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Hatami, M.; Ganji, D.D. Nanofluid flow and heat transfer in a rotating system in the presence of a magnetic field. J. Mol. Liq. 2014, 190, 112–120. [Google Scholar] [CrossRef]
- Sheikholislami, M.; Ellahi, R. Electrohydrodynamic nanofluid hydrothermal treatment in an enclosure with sinusoidal upper wall. Appl. Sci. 2015, 5, 294–306. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ellahi, R. Three dimensional mesoscopic simulation of magnetic field effect on natural convection of nanofluid. Int. J. Heat Mass Transf. 2015, 89, 799–808. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Study on magnetohydrodynamic nanofluid by means of single and multi-walled carbon nanotubes suspended in a salt water solution. IEEE Trans. Nanotechnol. 2015, 14, 726–734. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ellahi, R. Simulation of ferrofluid flow for magnetic drug targeting using Lattice Boltzmann method. J. Z. Naturforsch. A 2015, 70, 115–124. [Google Scholar]
- Akbar, N.S.; Raza, M.; Ellahi, R. Influence of induced magnetic field and heat flux with the suspension of carbon nanotubes for the peristaltic flow in a permeable channel. J. Magn. Magn. Mater. 2015, 381, 405–415. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Shape effects of nanosize particles in Cu-H2O nanofluid on entropy generation. Int. J. Heat Mass Transf. 2015, 81, 449–456. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D.; Javed, M.Y.; Ellahi, R. Effect of thermal radiation on nanofluid flow and heat transfer using two phase model. J. Magn. Magn. Mater. 2015, 374, 36–43. [Google Scholar] [CrossRef]
- Rashidi, S.; Dehghan, M.; Ellahi, R.; Riaz, M.; Jamal-Abad, M.T. Study of stream wise transverse magnetic fluid flow with heat transfer around a porous obstacle. J. Magn. Magn. Mater. 2015, 378, 128–137. [Google Scholar] [CrossRef]
- Ellahi, R. The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: Analytical solutions. Appl. Math. Model. 2013, 37, 1451–1457. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Hatami, M.; Ganji, D.D. Nanofluid flow and heat transfer in a rotating system in the presence of a magnetic field. J. Mol. Liq. 2014, 190, 112–120. [Google Scholar] [CrossRef]
- Ellahi, R.; Bhatti, M.M.; Khan, A.A. Influence of wall compliances on unsteady peristaltic transport of a nanofluid in a vertical rectangular duct. Wulfenia 2015, 22, 248–265. [Google Scholar]
- Nawaz, M.; Zeeshan, A.; Ellahi, R.; Abbasbandy, S.; Rashidi, S. Joules heating effects on stagnation point flow over a stretching cylinder by means of genetic algorithm and Nelder-Mead method. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 665–684. [Google Scholar] [CrossRef]
- Khan, W.A.; Khan, Z.H.; Rahi, M. Fluid flow and heat transfer of carbon nanotubes along a flat plate with Navier slip boundary. Appl. Nanosci. 2014. [Google Scholar] [CrossRef]
- Noor, M.A.; Mohyud-Din, S.T. Variational iteration technique for solving higher order boundary value problems. Appl. Math. Comput. 2007, 189, 1929–1942. [Google Scholar] [CrossRef]
- Abdou, M.A.; Soliman, A.A. New applications of Variational iteration method. Phys. D Nonlinear Phenom. 2005, 211, 1–8. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Extending the traditional Jeffery Hamel flow tostretchable convergent/divergent channels. Comput. Fluids 2014, 100, 196–203. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohyud-Din, S.T.; Khan, U.; Ahmed, N.; Hassan, S.M. Magnetohydrodynamic Flow and Heat Transfer of Nanofluids in Stretchable Convergent/Divergent Channels. Appl. Sci. 2015, 5, 1639-1664. https://doi.org/10.3390/app5041639
Mohyud-Din ST, Khan U, Ahmed N, Hassan SM. Magnetohydrodynamic Flow and Heat Transfer of Nanofluids in Stretchable Convergent/Divergent Channels. Applied Sciences. 2015; 5(4):1639-1664. https://doi.org/10.3390/app5041639
Chicago/Turabian StyleMohyud-Din, Syed Tauseef, Umar Khan, Naveed Ahmed, and Saleh M. Hassan. 2015. "Magnetohydrodynamic Flow and Heat Transfer of Nanofluids in Stretchable Convergent/Divergent Channels" Applied Sciences 5, no. 4: 1639-1664. https://doi.org/10.3390/app5041639






