Ion Acceleration by Short Chirped Laser Pulses
Abstract
:1. Introduction
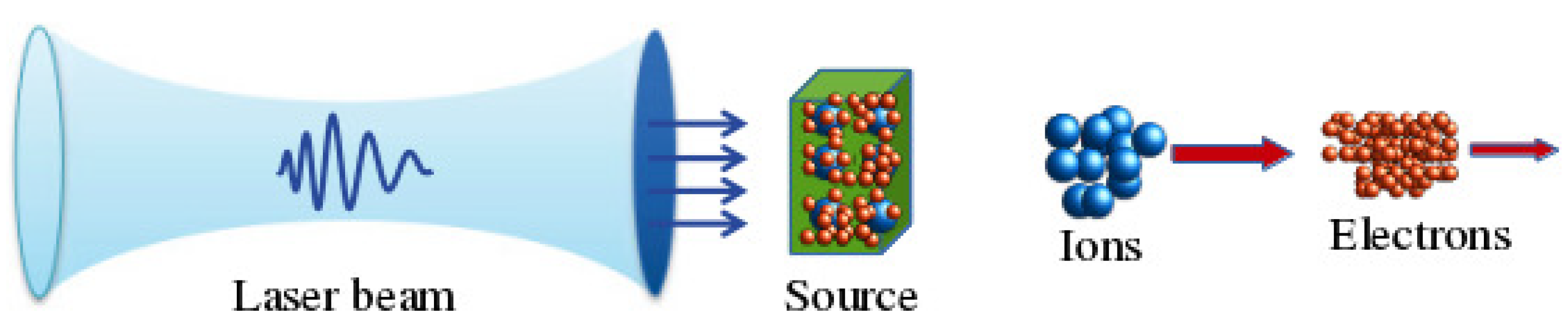
2. Laser Acceleration Simulations
2.1. Description of Few-Cycle Chirped Focused Laser Pulses
2.2. Particle Dynamics
3. Results and Discussion
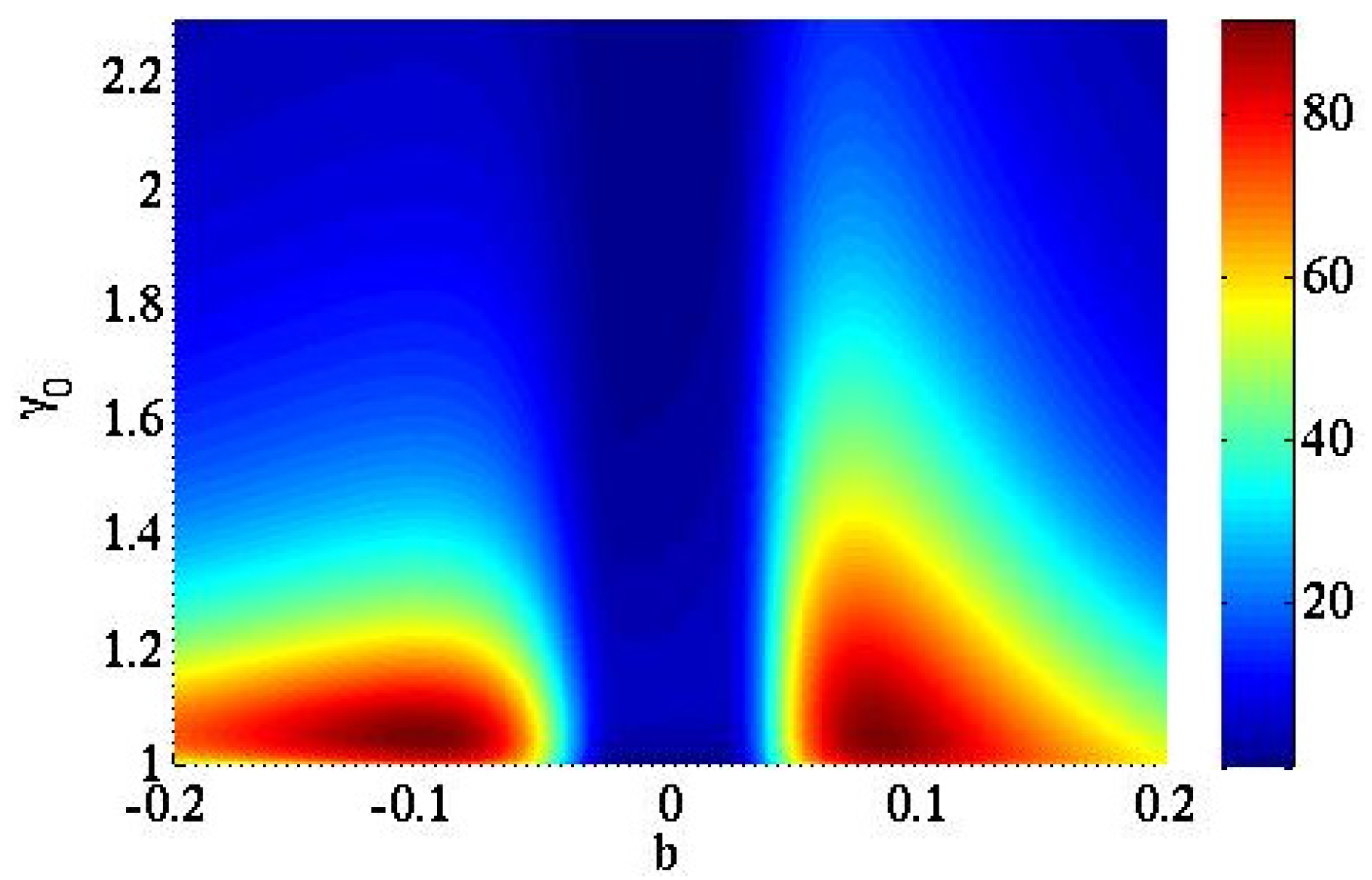
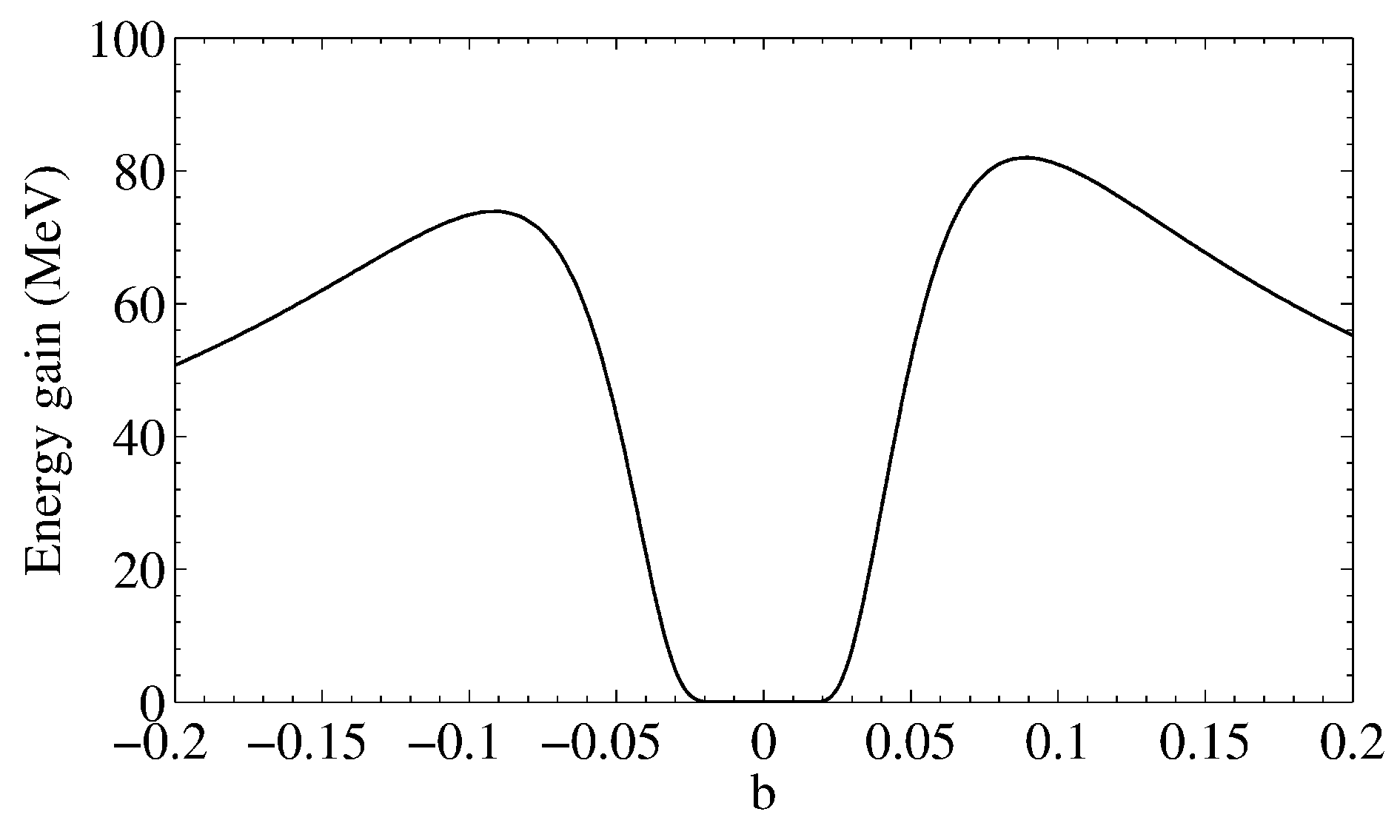
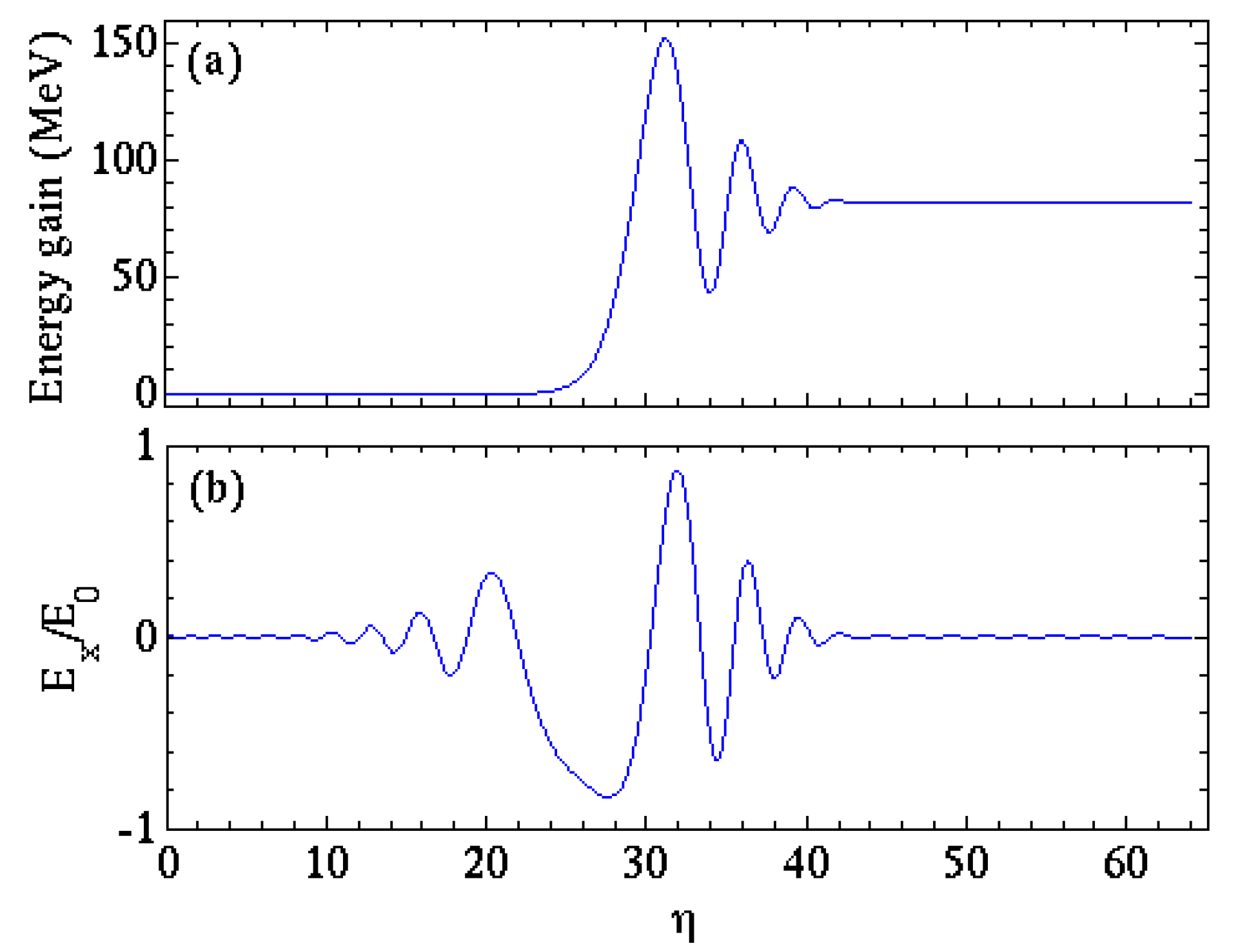
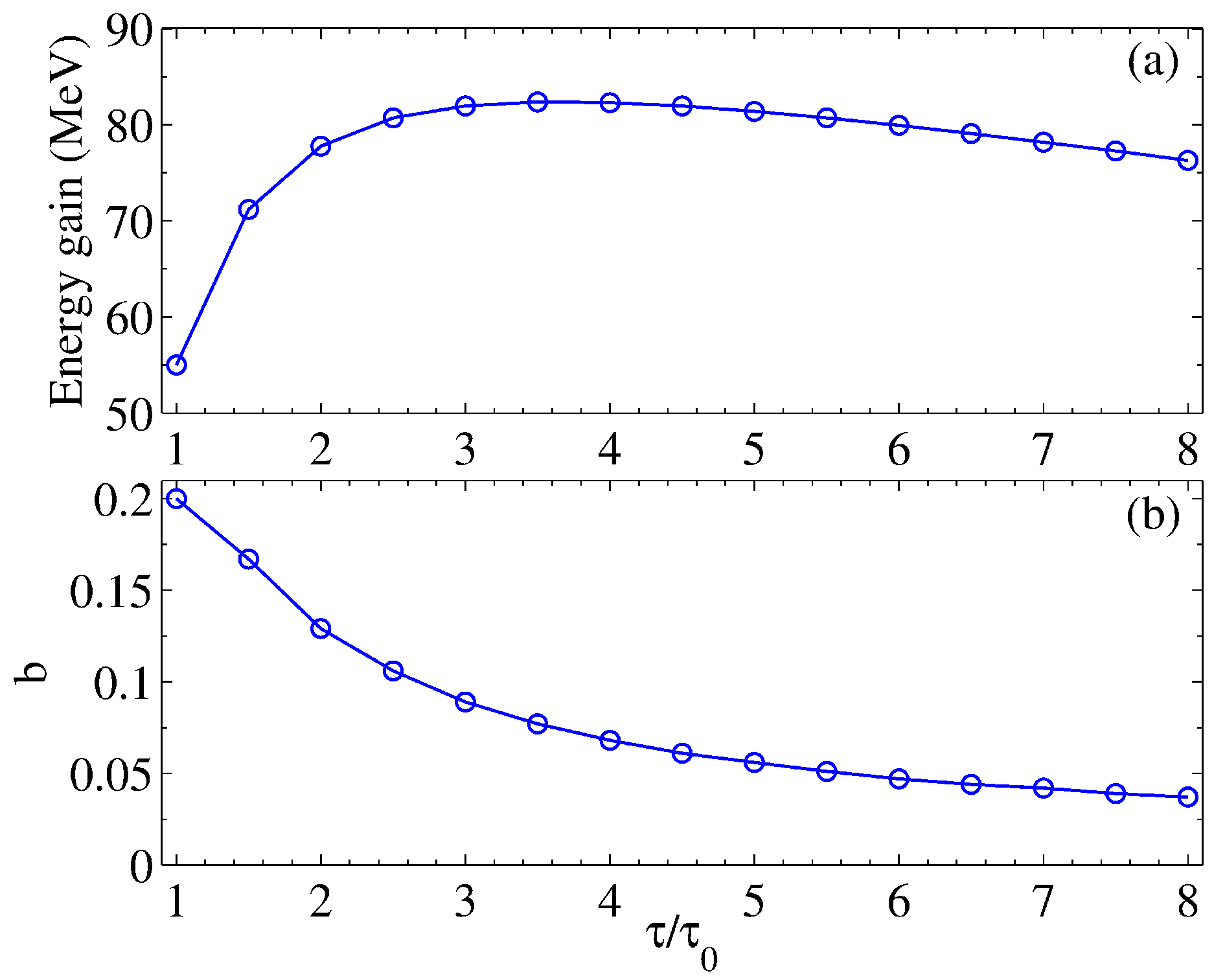
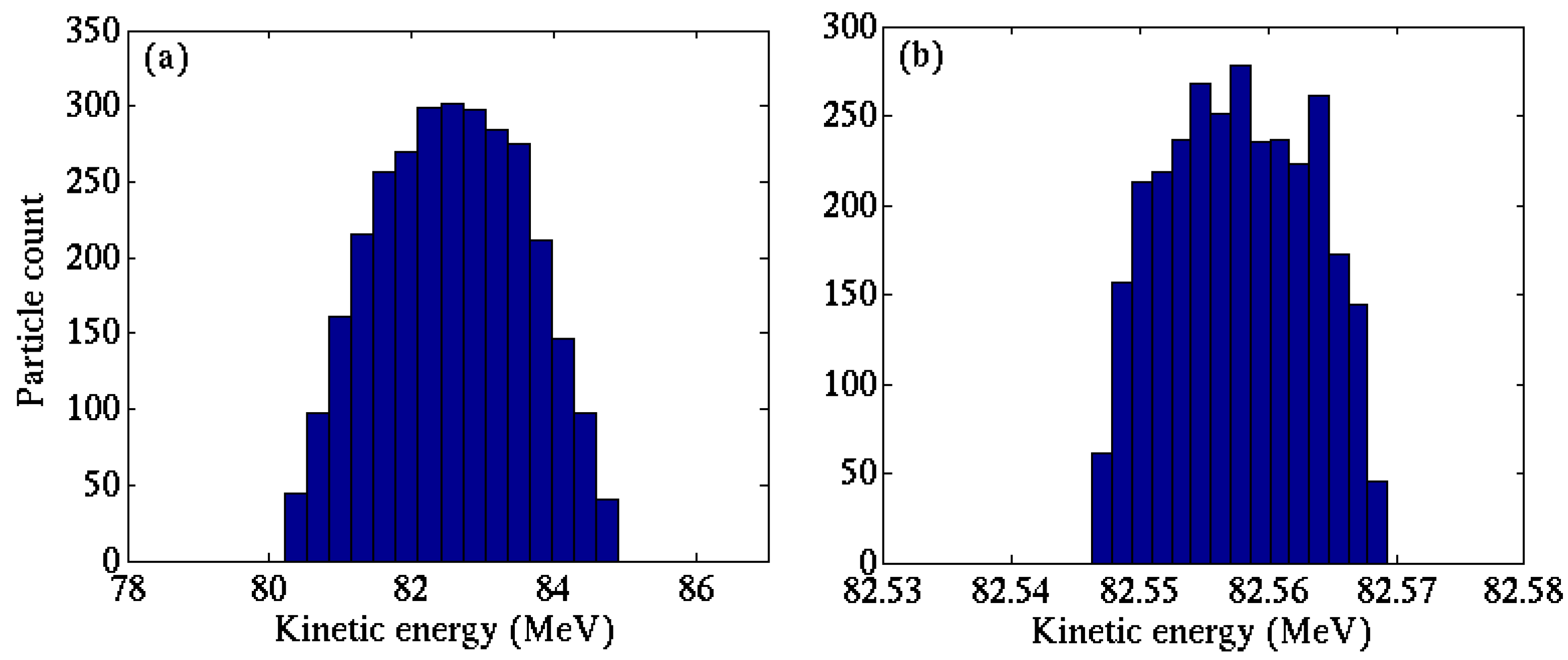

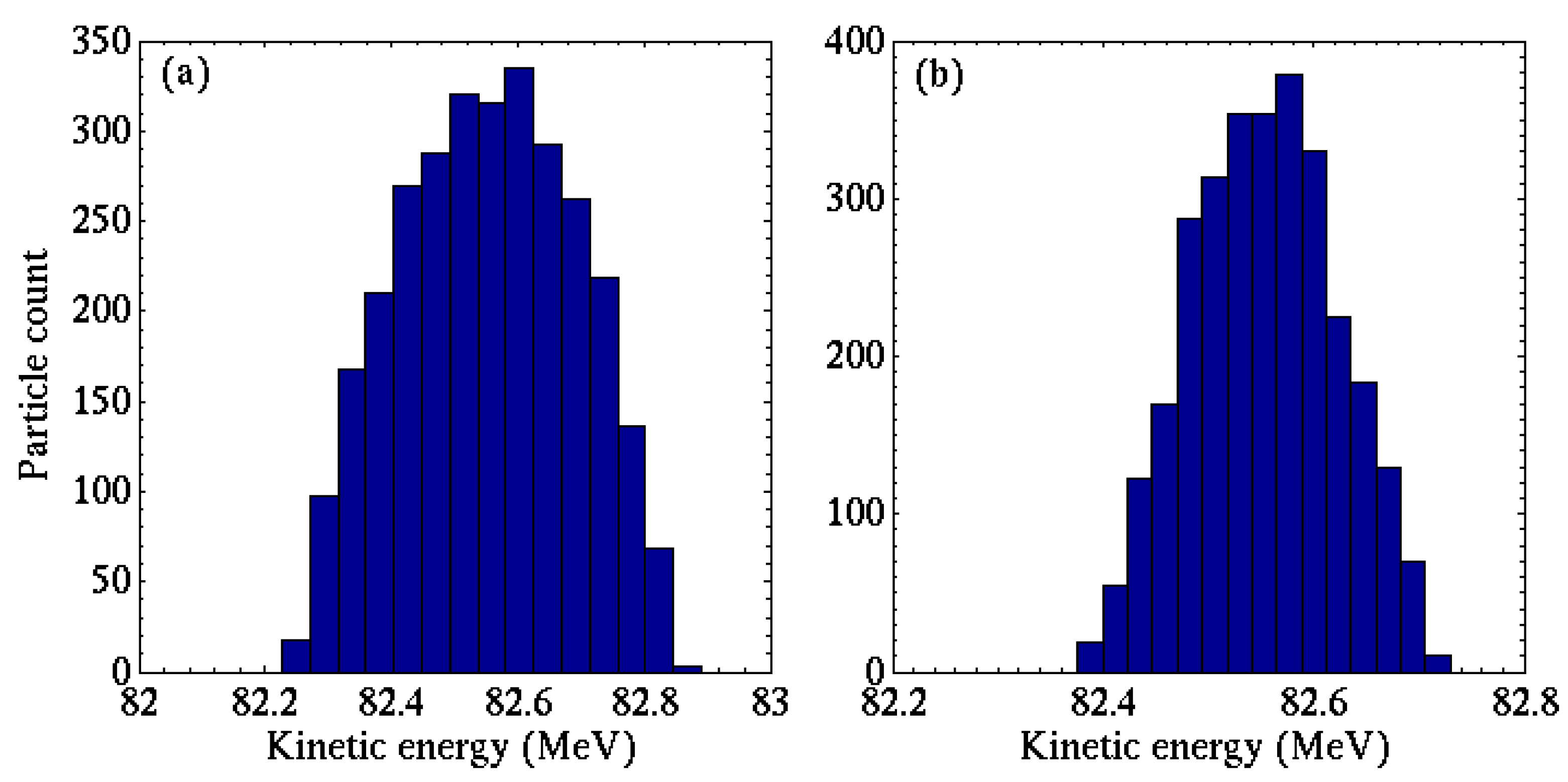

4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Schwoerer, H.; Pfotenhauer, S.; Jäckel, O.; Amthor, K.U.; Liesfeld, B.; Ziegler, W.; Sauerbrey, R.; Ledingham, K.W.D.; Esirkepov, T. Laser-plasma acceleration of quasi-monoenergetic protons from microstructured targets. Nature 2006, 439, 445–448. [Google Scholar] [CrossRef] [PubMed]
- Hegelich, B.M.; Albright, B.J.; Cobble, J.; Flippo, K.; Letzring, S.; Paffett, M.; Ruhl, H.; Schreiber, J.; Schulze, R.K.; Fernández, J.C. Laser acceleration of quasi-monoenergetic MeV ion beams. Nature 2006, 439, 441–444. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, J.; Antici, P.; d’Humières, E.; Lefebvre, E.; Borghesi, M.; Brambrink, E.; Cecchetti, C.A.; Kaluza, M.; Malka, V.; Manclossi, M.; et al. Laser-driven proton scaling laws and new paths towards energy increase. Nat. Phys. 2006, 2, 48–54. [Google Scholar] [CrossRef]
- Esirkepov, T.; Yamagiwa, M.; Tajima, T. Laser ion-acceleration scaling laws seen in multiparametric particle-in-cell simulations. Phys. Rev. Lett. 2006, 96, 105001. [Google Scholar] [CrossRef] [PubMed]
- Robson, L.; Simpson, P.T.; Clarke, R.J.; Ledingham, K.W.D.; Lindau, F.; Lundh, O.; McCanny, T.; Mora, P.; Neely, D.; Wahlström, C.G.; et al. Scaling of proton acceleration driven by petawatt-laser-plasma interactions. Nat. Phys. 2007, 3, 58–62. [Google Scholar] [CrossRef]
- Maksimchuk, A.; Gu, S.; Flippo, K.; Umstadter, D.; Bychenkov, V.Y. Forward ion ccceleration in thin films driven by a high-intensity laser. Phys. Rev. Lett. 2000, 84, 4108–4111. [Google Scholar] [CrossRef] [PubMed]
- Snavely, R.A.; Key, M.H.; Hatchett, S.P.; Cowan, T.E.; Roth, M.; Phillips, T.W.; Stoyer, M.A.; Henry, E.A.; Sangster, T.C.; Singh, M.S.; et al. Intense high-energy proton beams from petawatt-laser irradiation of solids. Phys. Rev. Lett. 2000, 85, 2945–2948. [Google Scholar] [CrossRef]
- Karsch, S.; Düsterer, S.; Schwoerer, H.; Ewald, F.; Habs, D.; Hegelich, M.; Pretzler, G.; Pukhov, A.; Witte, K.; Sauerbrey, R. High-intensity laser induced ion acceleration from heavy-water droplets. Phys. Rev. Lett. 2003, 91, 015001. [Google Scholar] [CrossRef] [PubMed]
- Romagnani, L.; Fuchs, J.; Borghesi, M.; Antici, P.; Audebert, P.; Ceccherini, F.; Cowan, T.; Grismayer, T.; Kar, S.; Macchi, A.; et al. Dynamics of electric fields driving the laser acceleration of multi-MeV protons. Phys. Rev. Lett. 2005, 95, 195001. [Google Scholar] [CrossRef] [PubMed]
- Cowan, T.E.; Fuchs, J.; Ruhl, H.; Sentokua, Y.; Kempa, A.; Audebertb, P.; Roth, M.; Stephens, R.; Barton, I.; Blazevic, A.; et al. Ultra-low emittance, high current proton beams produced with a laser-virtual cathode sheath accelerator. Nuclear Instrum. Methods Phys. Res. 2005, 544, 277–284. [Google Scholar] [CrossRef]
- Albright, B.J.; Yin, L.; Hegelich, B.M.; Bowers, K.J.; Kwan, T.J.T.; Fernández, J.C. Theory of laser acceleration of light-ion beams from interaction of ultrahigh-intensity lasers with layered targets. Phys. Rev. Lett. 2006, 97, 115002. [Google Scholar] [CrossRef] [PubMed]
- Tajima, T.; Dawson, J.M. Laser electron accelerator. Phys. Rev. Lett. 1979, 43, 267–270. [Google Scholar] [CrossRef]
- Badziak, J. Laser-driven generation of fast particles. Opto-Electron. Rev. 2007, 15, 1–12. [Google Scholar] [CrossRef]
- Salamin, Y.I.; Harman, Z.; Keitel, C.H. Direct high-power laser acceleration of ions for medical applications. Phys. Rev. Lett. 2008, 100, 155004. [Google Scholar] [CrossRef] [PubMed]
- Galow, B.J.; Harman, Z.; Keitel, C.H. Intense high-quality medical proton beams via laser fields. Opt. Express 2010, 18, 25950–25957. [Google Scholar] [CrossRef] [PubMed]
- Salamin, Y.I.; Hu, S.X.; Hatsagortsyan, K.Z.; Keitel, C.H. Relativistic high-power laser-matter interactions. Phys. Rep. 2006, 427, 41–155. [Google Scholar] [CrossRef]
- Di Piazza, A.; Müller, C.; Hatsagortsyan, K.Z.; Keitel, C.H. Extremely high-intensity laser interactions with fundamental quantum systems. Rev. Mod. Phys. 2012, 84, 1177–1228. [Google Scholar] [CrossRef]
- Peralta, E.A.; Soong, K.; England, R.J.; Colby, E.R.; Wu, Z.; Montazeri, B.; McGuinness, C.; McNeur, J.; Leedle, K.J.; Walz, D.; et al. Demonstration of electron acceleration in a laser-driven dielectric microstructure. Nature 2013, 503, 91–94. [Google Scholar] [CrossRef] [PubMed]
- Haberberger, D.; Tochitsky, S.; Fiuza, F.; Gong, C.; Fonseca, R. Collisionless shocks in laser-produced plasma generate monoenergetic high-energy proton beams. Nat. Phys. 2012, 8, 95–99. [Google Scholar]
- Hooker, S.M. Developments in laser-driven plasma accelerators. Nat. Photonics 2013, 7, 775–782. [Google Scholar] [CrossRef]
- Zigler, A.; Eisenman, S.; Botton, M.; Nahum, E.; Schleifer, E.; Baspaly, A.; Pomerantz, I.; Abicht, F.; Branzel, J.; Priebe, G.; et al. Enhanced proton acceleration by an ultrashort laser interaction with structured dynamic plasma targets. Phys. Rev. Lett. 2013, 110, 215004. [Google Scholar] [CrossRef] [PubMed]
- Harman, Z.; Salamin, Y.I.; Galow, B.J.; Keitel, C.H. Optimizing direct intense-field laser acceleration of ions. Phys. Rev. A 2011, 84, 053814. [Google Scholar] [CrossRef]
- Combs, S.E.; Nikoghosyan, A.; Jäkel, O.; Karger, C.P.; Haberer, T.; Münter, M.W.; Huber, P.E.; Debus, J.; Schulz-Ertner, D. Carbon ion radiotherapy for pediatric patients and young adults treated for tumors of the skull base. Cancer 2009, 115, 1348–1355. [Google Scholar] [CrossRef] [PubMed]
- Jäkel, O.; Krämer, M.; Karger, C.P.; Debus, J. Treatment planning for heavy ion radiotherapy: Clinical implementation and application. Phys. Med. Biol. 2001, 46, 1101–1116. [Google Scholar] [CrossRef] [PubMed]
- Yock, T.I.; Tarbell, N.J. Technology Insight: Proton beam radiotherapy for treatment in pediatric brain tumors. Nat. Clin. Pract. Oncol. 2004, 1, 97–103. [Google Scholar] [PubMed]
- Levin, M.P.; Kooy, H.; Loeffler, J.S.; DeLaney, T.F. Proton beam therapy. Br. J. Cancer 2005, 93, 849–854. [Google Scholar] [CrossRef] [PubMed]
- Coen, J.J.; Zietman, A.L. Proton radiation for localized prostate cancer. Nat. Rev. Urol. 2009, 6, 324–330. [Google Scholar] [CrossRef] [PubMed]
- Fokas, E.; Kraft, G.; An, H.; Engenhart-Cabillic, R. Ion beam radiobiology and cancer: Time to update ourselves. Biochim. Biophy. Acta (BBA) 2009, 1796, 216–229. [Google Scholar]
- Galow, B.; Salamin, Y.I.; Liseykina, T.; Harman, Z.; Keitel, C.H. Dense monoenergetic proton beams from chirped laser-plasma interaction. Phys. Rev. Lett. 2011, 107, 185002. [Google Scholar] [CrossRef] [PubMed]
- Singh, K.P. Electron acceleration by a chirped short intense laser pulse in vacuum. Appl. Phys. Lett. 2005, 87, 254102. [Google Scholar] [CrossRef]
- Sohbatzadeh, F.; Mirzanejhad, S.; Ghasemi, M. Electron acceleration by a chirped Gaussian pulse. Phys. Plasmas 2006, 13, 123108. [Google Scholar] [CrossRef]
- Sohbatzadeh, F.; Mirzanejhad, S.; Aku, H. Synchronization scheme in electron vacuum acceleration by a chirped Gaussian pulse. Phys. Plasmas 2009, 16, 023106. [Google Scholar]
- Li, J.X.; Salamin, Y.I.; Hatsagortsyan, K.Z.; Keitel, C.H. Fields of an ultrashort tightly-focused laser pulse. Opt. Lett. 2014. submitted. [Google Scholar]
- Li, J.X.; Hatsagortsyan, K.Z.; Keitel, C.H. Robust signatures of quantum radiation reaction in focused ultrashort laser pulses. Phys. Rev. Lett. 2014, 113, 044801. [Google Scholar] [CrossRef] [PubMed]
- Esarey, E.; Sprangle, P.; Pilloff, M.; Krall, J. Theory and group velocity of ultrashort, tightly focused laser pulses. J. Opt. Soc. Am. B 1995, 12, 1695–1703. [Google Scholar] [CrossRef]
- Lin, Q.; Zheng, J.; Becker, W. Subcycle pulsed focused vector beams. Phys. Rev. Lett. 2006, 97, 253902. [Google Scholar] [CrossRef] [PubMed]
- Salamin, Y.I.; Keitel, C.H. Electron acceleration by a tightly focused laser beam. Phys. Rev. Lett. 2002, 88, 095005. [Google Scholar] [CrossRef] [PubMed]
- Goulielmakis, E.; Koehler, S.; Reiter, B.; Schultze, M.; Verhoef, A.J.; Serebryannikov, E.E.; Zheltikov, A.M.; Krausz, F. Ultrabroadband, coherent light source based on self-channeling of few-cycle pulses in helium. Opt. Lett. 2008, 33, 1407–1409. [Google Scholar] [CrossRef] [PubMed]
- Wirth, A.; Hassan, M.T.; Grguraš, I.; Gagnon, J.; Moulet, A.; Luu, T.T.; Pabst, S.; Santra, R.; Alahmed, Z.A.; Azzeer, A.M.; et al. Synthesized light transients. Science 2011, 334, 195–200. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.-X.; Galow, B.; Keitel, C.H.; Harman, Z. Ion Acceleration by Short Chirped Laser Pulses. Appl. Sci. 2015, 5, 36-47. https://doi.org/10.3390/app5010036
Li J-X, Galow B, Keitel CH, Harman Z. Ion Acceleration by Short Chirped Laser Pulses. Applied Sciences. 2015; 5(1):36-47. https://doi.org/10.3390/app5010036
Chicago/Turabian StyleLi, Jian-Xing, Benjamin Galow, Christoph H. Keitel, and Zoltán Harman. 2015. "Ion Acceleration by Short Chirped Laser Pulses" Applied Sciences 5, no. 1: 36-47. https://doi.org/10.3390/app5010036




