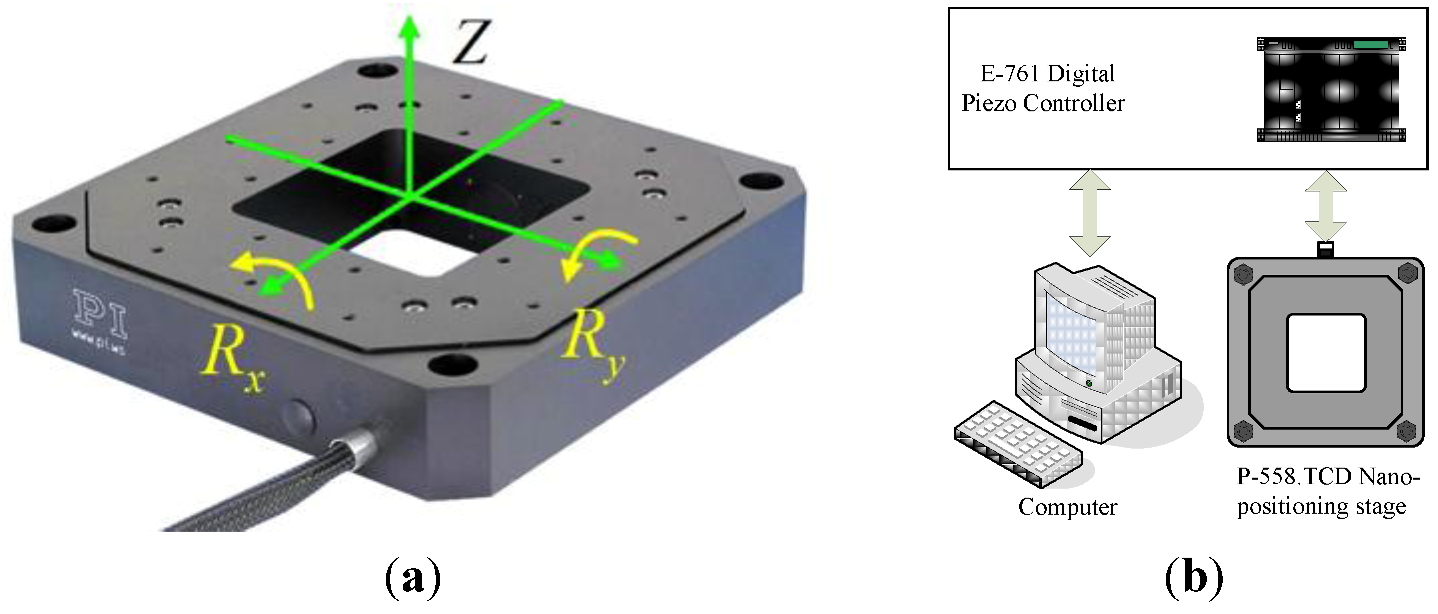
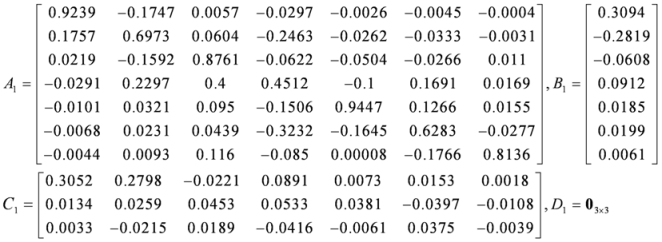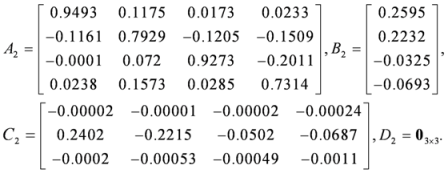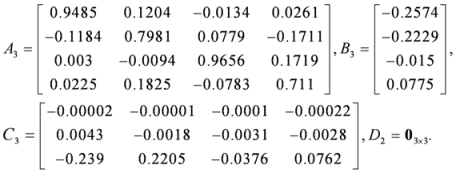To verify the effectiveness of the state space model and the proposed identification method, experiments were implemented on a commercially-available 3-DOF piezo-actuator-driven stage (P-558.TCD, Physik Instrumente), as shown in
Figure 1a. Driven by four piezoelectric actuators, the P558.TCD can generate linear displacements in the vertical direction Z and rotation around two orthogonal horizontal axes
Rx and
Ry.
Table 1 shows the motion range and resolution in each DOF.
Figure 1.
Experimental settings on the piezo-actuator-driven stage: (a) picture and (b) schematic.
For displacement measurements, three capacitive sensors built in the stage are employed. All displacements were measured with a sampling interval of 2 ms in the present study. Both the actuators and the sensors in the stage were connected to a host computer via a digital controller (E-761, Physik Instrumente) and controlled through Labview, as shown in
Figure 1b. As instructed by its manual, the piezo controller can drive the actuator with a maximum operating frequency of 10-20 Hz if an input voltage in the range of 30–50 V is applied. During operation, the motion of the four piezoelectric elements must be coordinated to reduce the internal forces generated due to the over actuation, which may cause reduced stiffness and even break or damage the piezo-actuator-driven stage. This is realized by a user program interface provided by the manufacturer, which is used to generate the voltage input of each piezoelectric actuator from the user defined reference signal.
3.1. Linearity of the 3-DOF Piezo-Actuator-Driven Stage
To examine the linearity of the 3-DOF piezo-actuator-driven stage, a case study was conducted prior to the system identification. In particular, a 1 Hz 1 μm sinusoidal reference signal with 1 μm offset, a 2 Hz 200 μm sinusoidal reference signal with 2 s time delay and a 100 μm step reference signal with 3 s time delay were provided to the Z,
Rx and
Ry channel, respectively, and the corresponding outputs were measured. Then, the stage displacement output, as these three signals were applied simultaneously, was measured. The criterion used for the linearity examination is that if the output with three input signals equals or approximately equals the sum of the outputs when the signals is applied individually, the 3-DOF piezo-actuator-driven stage is linear or can be approximately considered to be linear.
Figure 2 shows the comparison between the two outputs mentioned above. It can be seen that they overlapped with each other, indicating that the stage can be approximately considered to be a linear system. Differences between the measured output when the three inputs were provided to the different channels simultaneously and the sum of the outputs when the three inputs were provided separately exist. For example, in the
Rx direction, the maximum difference is approximately 3 μm, which is only 1.5% of the amplitude of the reference signal. This difference might be due to the nonlinearities of the 3-DOF piezo-actuator-driven stage, which is ignored in the model development presented in this paper.
Figure 2.
Linearity of the 3-DOF piezo-actuator-driven stage: (a–c) comparison between the measured output when the three inputs were provided to the different channels simultaneously and the sum of the outputs when the three inputs were provided separately; (d–f) difference between these two outputs.
Figure 2.
Linearity of the 3-DOF piezo-actuator-driven stage: (a–c) comparison between the measured output when the three inputs were provided to the different channels simultaneously and the sum of the outputs when the three inputs were provided separately; (d–f) difference between these two outputs.
3.2. System Identification of the 3-DOF Piezo-Actuator-Driven Stage
Figure 3 shows the flow chart of system identification. Since different signals applied in system identification may lead to the difference in the model identified, the effects of applying the random signal and the chirp signal in the parameter estimation were investigated in the signal selection in this study. The two signals were compared, and the one with less model prediction error was employed as the input for order selection, in which state space models with different orders were identified and compared. The one with less model prediction error was employed as the model for the piezo-actuator-driven stage.
Figure 3.
Flow chart of black box system identification.
Figure 3.
Flow chart of black box system identification.
For signal selection, a 20 μm reference chirp signal with 20 μm offset and frequency ranging from 1 to 100 Hz was provided to channel 1 (reference Z channel), and the corresponding output in each channel was measured. Based on the empirical knowledge of our previous study on piezoelectric actuators, the order of the state space model was originally set to be three, and
![Actuators 02 00001 i078]()
in Equation (17) was set to be a zero matrix. Since the covariance of the parameters is unknown,
P0 is set to be a diagonal matrix with big covariance designated in the diagonal elements. By applying online estimation with the identified Hankel matrix, the system matrices of the state space model (Equation (19),
I = 1) were obtained.
The estimation error varied, depending on the values of parameter
p in Equation (2).
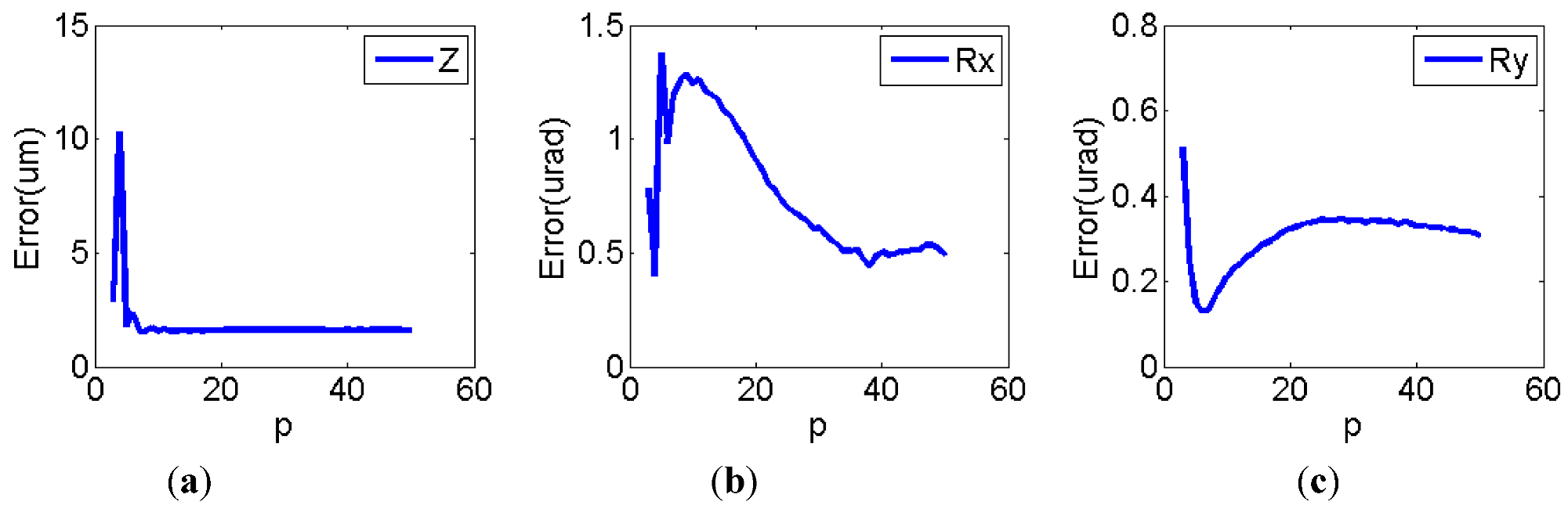
Figure 4 (a–c) shows the estimated error
versus the
p-value. It can be seen that if
p = 8, the estimation errors in all three output directions approached or reached their individual minimum values. Therefore, it is reasonable to set
p = 8, as the chirp signal is provided to channel 1.
Figure 4.
Estimation error changes with p-value when reference input was applied in channel (a) Z direction; (b) Rx direction; (c) Ry direction.
Figure 4.
Estimation error changes with p-value when reference input was applied in channel (a) Z direction; (b) Rx direction; (c) Ry direction.
For other two channels, a 200 μrad reference chirp signal with frequency ranging from 1 to 100 Hz was applied. By employing the aforementioned procedure,
p was set to 25 and 27 for channel 2 and 3 respectively.
Table 2 shows the prediction error in each direction, as a 1 Hz sinusoidal reference input was applied to the three channels, respectively. The prediction errors are calculated in terms of the 2-norm of the error vector (defined as the difference between the measurement and the model prediction). It is seen that the diagonal prediction error is 0.1944 μm, 4.864 μrad and 4.3387 μrad in the Z,
Rx and
Ry direction, respectively, which is 0.49%, 2.43% and 2.16% of the desired movement in the individual direction.
Table 2.
Model prediction error if chirp inputs were applied.
Table 2.
Model prediction error if chirp inputs were applied.
| Direction | Z (μm) | Rx (μrad) | Ry (ΜRAD) |
|---|
| 1 Hz 20 μm sinusoidal inputs with 20 μm offset in channel 1 | 0.1944 | 0.4030 | 0.2008 |
| 1 Hz 200 μrad sinusoidal inputs in channel 2 | 0.0192 | 4.8640 | 0.0760 |
| 1 Hz 200 μrad sinusoidal inputs in channel 3 | 0.0263 | 0.2060 | 4.3387 |
Similar to the use of the chirp signal, 40 μm and 200 μrad reference random signals were also applied to each channel, respectively. The order of each sub-model was chosen to be three, and
p was set to nine, 14 and 13 for the three channels, respectively. The same 1 Hz sinusoidal inputs were provided to difference channels, and the output was measured and compared with the model prediction.
Table 3 illustrates the model prediction error. In contrast to the chirp signal, it can be concluded that the model prediction errors is much bigger when random signals are used in the model identification. For example, when a 1 Hz 200 μrad sinusoidal reference input was provided to channel 2, the model prediction error in the
Rx direction reached 57.362 μrad by using the random inputs, which is over 10-times larger than that derived by using the chirp signal. As a result, a chirp signal was employed as the reference input for model identification below.
Table 3.
Model prediction error if random inputs were applied.
Table 3.
Model prediction error if random inputs were applied.
| Direction | Z (μm) | Rx (μrad) | Ry (ΜRAD) |
|---|
| 1 Hz 20 μm sinusoidal inputs with 20 μm offset in channel 1 | 0.8670 | 0.8946 | 0.2061 |
| 1 Hz 200 μrad sinusoidal inputs in channel 2 | 0.0542 | 57.362 | 0.1020 |
| 1 Hz 200 μrad sinusoidal inputs in channel 3 | 0.0624 | 1.0143 | 45.9597 |
To determine the order of the state space model, the parameter identification, as described previously, was repeated with varying values of
n (Equation (1)) in each channel.
Table 4,
Table 5,
Table 6 show the estimation errors in each channel.
Parameter p was chosen to have different values for varying orders based on the method mentioned above. It can be concluded that if the chirp signal was used in channel 1, the estimation error in the Z direction reached its minimum value of 1.4906 μm with the order of the sub-model being six or seven. For the Ry direction, the optimal choice was to set n = 7. Therefore, the sub-model for channel 1 was considered to be a seventh order state space system. The system matrices were determined as given in Equation (23). Using a similar procedure, the orders of the sub-model for the other two channels were both chosen to be four, and the system matrices were determined, as shown in Equations (24) and (25).
Table 4.
Estimation error from the chirp inputs in channel 1.
Table 4.
Estimation error from the chirp inputs in channel 1.
| Order | p | Estimation error |
|---|
| Z (μm) | Rx (ΜRAD) | Ry (ΜRAD) |
|---|
| 2 | 11 | 1.5635 | 1.1174 | 0.1614 |
| 3 | 8 | 1.5368 | 1.2597 | 0.1631 |
| 4 | 11 | 1.4936 | 0.8100 | 0.3496 |
| 5 | 14 | 1.4914 | 0.1876 | 0.1607 |
| 6 | 31 | 1.4906 | 0.1184 | 0.1238 |
| 7 | 38 | 1.4906 | 0.1192 | 0.0908 |
| 8 | 38 | 1.4907 | 0.1180 | 0.1099 |
| 9 | 38 | 1.4907 | 0.1202 | 0.1031 |
| 10 | 30 | 1.4912 | 0.1195 | 0.1251 |
| 11 | 30 | 1.4913 | 0.1186 | 0.1236 |
| 12 | 28 | 1.4912 | 0.1266 | 0.1180 |
Table 5.
Estimation error from the chirp inputs in channel 2.
Table 5.
Estimation error from the chirp inputs in channel 2.
| Order | p | Estimation error |
|---|
| Z (μm) | Rx (μrad) | Ry (μrad) |
|---|
| 2 | 47 | 0.0118 | 18.0440 | 0.0565 |
| 3 | 25 | 0.0106 | 17.8752 | 0.0474 |
| 4 | 42 | 0.0107 | 17.7877 | 0.0476 |
| 5 | 47 | 0.0128 | 17.7751 | 0.0483 |
| 6 | 42 | 0.0129 | 17.8071 | 0.0477 |
| 7 | 42 | 0.0125 | 17.8073 | 0.0480 |
| 8 | 47 | 0.0133 | 17.8073 | 0.0477 |
| 9 | 42 | 0.0118 | 17.8179 | 0.0484 |
| 10 | 39 | 0.0103 | 17.8363 | 0.0479 |
| 11 | 42 | 0.0120 | 17.8154 | 0.0475 |
| 12 | 42 | 0.0119 | 17.8166 | 0.0481 |
Table 6.
Estimation error from the chirp inputs in channel 3.
Table 6.
Estimation error from the chirp inputs in channel 3.
| Order | p | Estimation error |
|---|
| Z (μm) | Rx (μrad) | Ry (μrad) |
|---|
| 2 | 41 | 0.0124 | 1.0996 | 16.9180 |
| 3 | 27 | 0.0108 | 1.0995 | 16.7524 |
| 4 | 39 | 0.0111 | 1.0994 | 16.5991 |
| 5 | 41 | 0.0144 | 1.1006 | 16.5917 |
| 6 | 39 | 0.0109 | 1.0993 | 16.6212 |
| 7 | 39 | 0.0111 | 1.0996 | 16.6183 |
| 8 | 39 | 0.0112 | 1.0996 | 16.6183 |
| 9 | 39 | 0.0112 | 1.0996 | 16.6177 |
| 10 | 39 | 0.0111 | 1.0996 | 16.6188 |
| 11 | 39 | 0.0111 | 1.0993 | 16.6184 |
| 12 | 39 | 0.0111 | 1.0994 | 16.1686 |
3.3. Model Verification
To illustrate the effectiveness of the MAP online estimation method, 1, 5 and 10 Hz sinusoidal reference inputs were provided to different channels, respectively. For comparison, the estimation method introduced in [
25] was implemented as well. The parameter
p was defined as 21, four and seven, respectively, for the three input channels.
Table 7,
Table 8 show the prediction error in each direction based on the different identification methods. The prediction errors were calculated in terms of the 2-norm of the error vector, illustrating that the prediction error increases with the frequency.
Table 7.
Estimation error by applying the online estimation method.
Table 7.
Estimation error by applying the online estimation method.
| Input | Channel | Z (μm) | Rx (μrad) | Ry (ΜRAD) |
|---|
| 1 Hz 10 μm | 1 | 0.1468 | 0.1584 | 0.0642 |
| 1 Hz 200 μrad | 2 | 0.0176 | 1.0305 | 0.0742 |
| 1 Hz 200 μrad | 3 | 0.0196 | 0.2574 | 9.9402 |
| 5 Hz 10 μm | 1 | 0.3666 | 0.3743 | 0.0956 |
| 5 Hz 200 μrad | 2 | 0.0538 | 2.3801 | 0.2044 |
| 5 Hz 200 μrad | 3 | 0.0510 | 0.2128 | 3.1906 |
| 10 Hz 10 μm | 1 | 0.5296 | 0.2699 | 0.0576 |
| 10 Hz 200 μrad | 2 | 0.0530 | 6.3244 | 0.3327 |
| 10 Hz 200 μrad | 3 | 0.0517 | 1.1101 | 5.6707 |
In contrast to the identification method introduced in [
25], the use of
posteriori parameter information in MAP online estimation leads to better estimations on the Hankel matrix. For example, the estimation errors for the 5 Hz, 10 μm sinusoidal inputs to channel 1 were 0.3666 μm, 0.3843 μrad and 0.0956 in the Z,
Rx and
Ry directions, respectively. These results are 7.3%, 40.6% and 24%, respectively, of those derived using the identification method introduced in [
25].
Table 8.
Estimation error by applying the identification method introduced in [
25].
Table 8.
Estimation error by applying the identification method introduced in [25].
| Input | Channel | Z (μm) | Rx (μrad) | Ry (ΜRAD) |
|---|
| 1 Hz 10 μm | 1 | 1.1124 | 0.9433 | 0.3675 |
| 1 Hz 200 μrad | 2 | 0.0180 | 2.2639 | 0.3403 |
| 1 Hz 200 μrad | 3 | 0.0374 | 0.3065 | 5.3670 |
| 5 Hz 10 μm | 1 | 5.0639 | 0.9224 | 0.3974 |
| 5 Hz 200 μrad | 2 | 0.0541 | 4.5928 | 0.3567 |
| 5 Hz 200 μrad | 3 | 0.0608 | 0.6449 | 11.349 |
| 10 Hz 10 μm | 1 | 6.2860 | 0.9419 | 0.4139 |
| 10 Hz 200 μrad | 2 | 0.0525 | 17.785 | 0.2683 |
| 10 Hz 200 μrad | 3 | 0.0543 | 1.0064 | 13.497 |
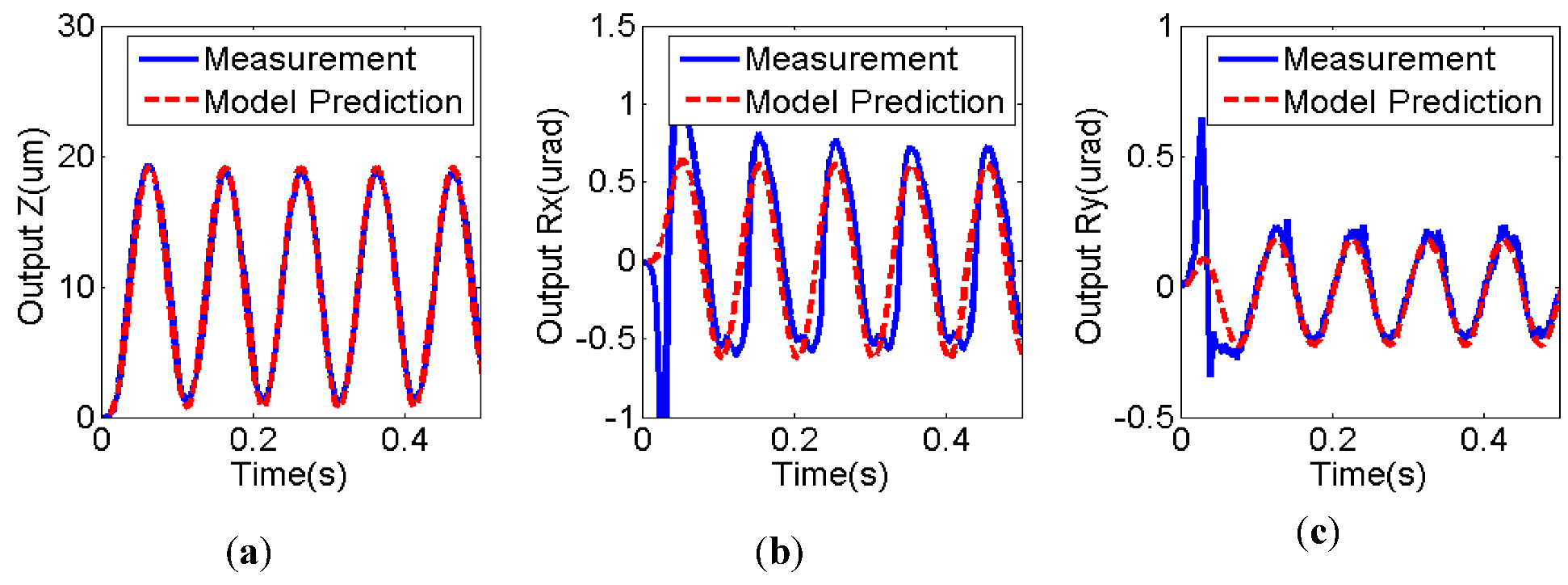
Figure 5 shows the output in each direction as a result of a 10 μm 10 Hz sinusoidal reference input with 10 μm offset in the Z direction compared with the model prediction. It can be clearly seen that the identified state space model is able to describe the coupling effect between each axle.
Figure 5.
Comparison of experimental results and model prediction under 10 μm 10 Hz sinusoidal input in channel 1: (a) Z direction; (b) Rx direction; (c) Ry direction.
Figure 5.
Comparison of experimental results and model prediction under 10 μm 10 Hz sinusoidal input in channel 1: (a) Z direction; (b) Rx direction; (c) Ry direction.
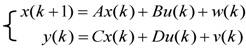
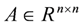 ,
, 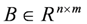 ,
, 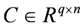 and
and 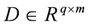 are system matrices,
are system matrices, 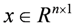 is the state,
is the state, 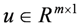 is the input,
is the input, 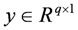 is the output,
is the output, 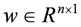 and
and 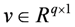 represent the ignored nonlinearity and uncertainties of the piezo-actuator-driven stage and m and q are the number of inputs and outputs, respectively. By iteration, one has:
represent the ignored nonlinearity and uncertainties of the piezo-actuator-driven stage and m and q are the number of inputs and outputs, respectively. By iteration, one has:
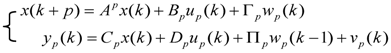
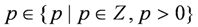 , where up and yp are defined as column vectors of the input and output data going p steps towards the future,
, where up and yp are defined as column vectors of the input and output data going p steps towards the future,


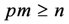 , there exists an interaction matrix M such that:
, there exists an interaction matrix M such that:
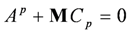
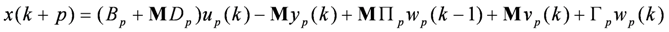
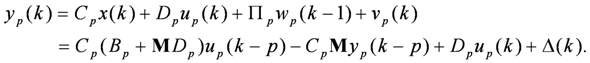
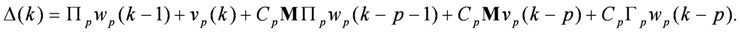
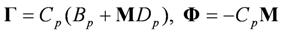
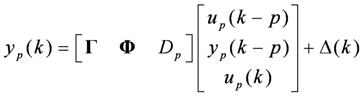
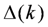 represents the combined model noises and can be regarded as the model estimation error.
represents the combined model noises and can be regarded as the model estimation error. 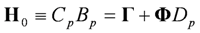
 can be calculated by using Equation (5) such that:
can be calculated by using Equation (5) such that:
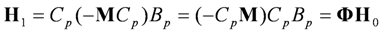
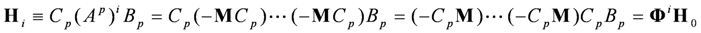
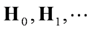 as building blocks, a Hankel matrix of any size can be constructed. For example:
as building blocks, a Hankel matrix of any size can be constructed. For example:
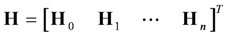
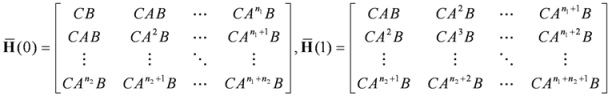
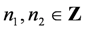 . Comparing Equation (14) with Equations (4), (12) and (13);
. Comparing Equation (14) with Equations (4), (12) and (13); 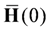 and
and 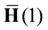 can then be extracted from H by rearrangement of its elements. The state space matrices are reconstructed from the Hankel matrix by employing the following Lemma 1.
can then be extracted from H by rearrangement of its elements. The state space matrices are reconstructed from the Hankel matrix by employing the following Lemma 1.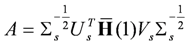
 , C is the first q rows of
, C is the first q rows of 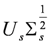 and
and 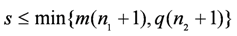 . The matrix Us and Vs are made up of s left and right singular vectors of
. The matrix Us and Vs are made up of s left and right singular vectors of 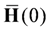 , and the diagonal matrix,
, and the diagonal matrix, 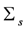 , is made up of s corresponding singular values of
, is made up of s corresponding singular values of 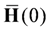 [24].
[24].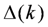 :
:
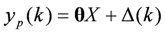
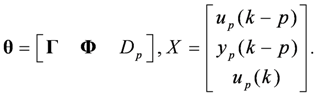
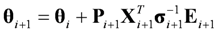
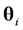 is the value of identified parameters based on the first i groups of data, Pi is the covariance of identified parameters from the first i groups of data,
is the value of identified parameters based on the first i groups of data, Pi is the covariance of identified parameters from the first i groups of data, 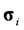 is the variance matrix of measurement errors and Ei is the estimation error of the i-th group of data. Integration of the prior information regarding the parameters and the information regarding the measurement errors can have the beneficial effect of reducing variances of parameter estimators. As a result, the parameter identification could be improved.
is the variance matrix of measurement errors and Ei is the estimation error of the i-th group of data. Integration of the prior information regarding the parameters and the information regarding the measurement errors can have the beneficial effect of reducing variances of parameter estimators. As a result, the parameter identification could be improved.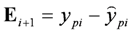
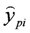 is the estimation output of the piezo-actuator-driven stage calculated through i-1 iterations.
is the estimation output of the piezo-actuator-driven stage calculated through i-1 iterations. , the three-dimensional output
, the three-dimensional output  , can be obtained from the identified one-input-three-output model by applying the method mentioned above:
, can be obtained from the identified one-input-three-output model by applying the method mentioned above:
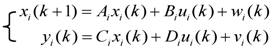
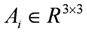 ,
, 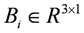 ,
, 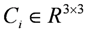 and
and 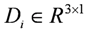 are system matrices of the one-input-three-output system.
are system matrices of the one-input-three-output system. 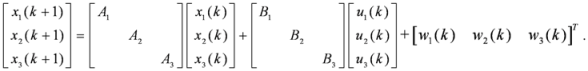
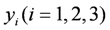 , such that:
, such that:

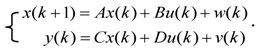
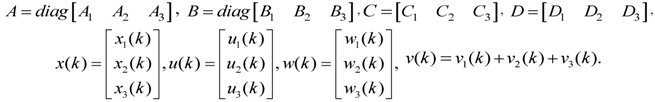


 in Equation (17) was set to be a zero matrix. Since the covariance of the parameters is unknown, P0 is set to be a diagonal matrix with big covariance designated in the diagonal elements. By applying online estimation with the identified Hankel matrix, the system matrices of the state space model (Equation (19), I = 1) were obtained.
in Equation (17) was set to be a zero matrix. Since the covariance of the parameters is unknown, P0 is set to be a diagonal matrix with big covariance designated in the diagonal elements. By applying online estimation with the identified Hankel matrix, the system matrices of the state space model (Equation (19), I = 1) were obtained.