Introduction of an Innovative Cladding Panel System for Multi-Story Buildings
Abstract
:1. Introduction
2. EDCS Design and Mathematical Modeling
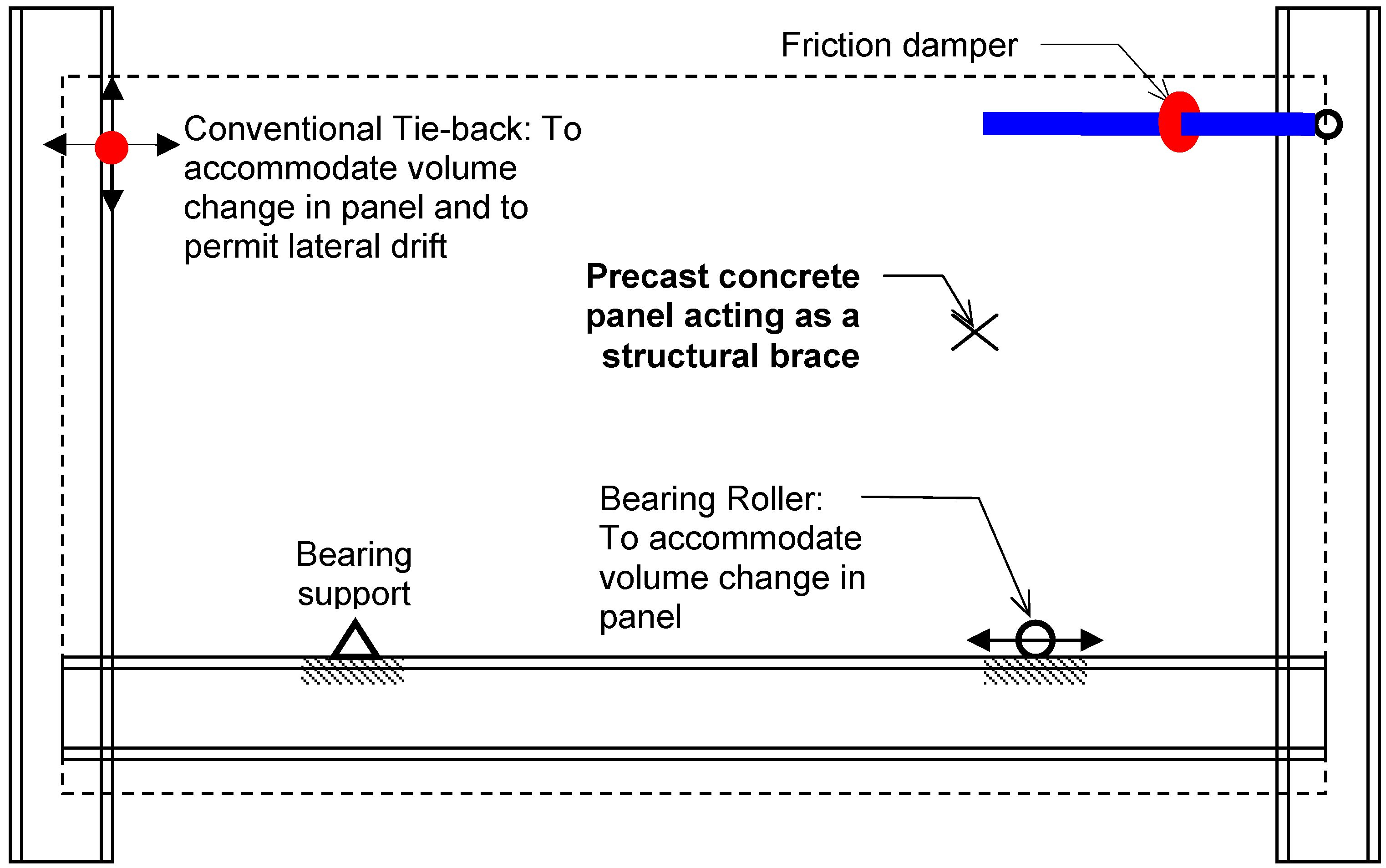
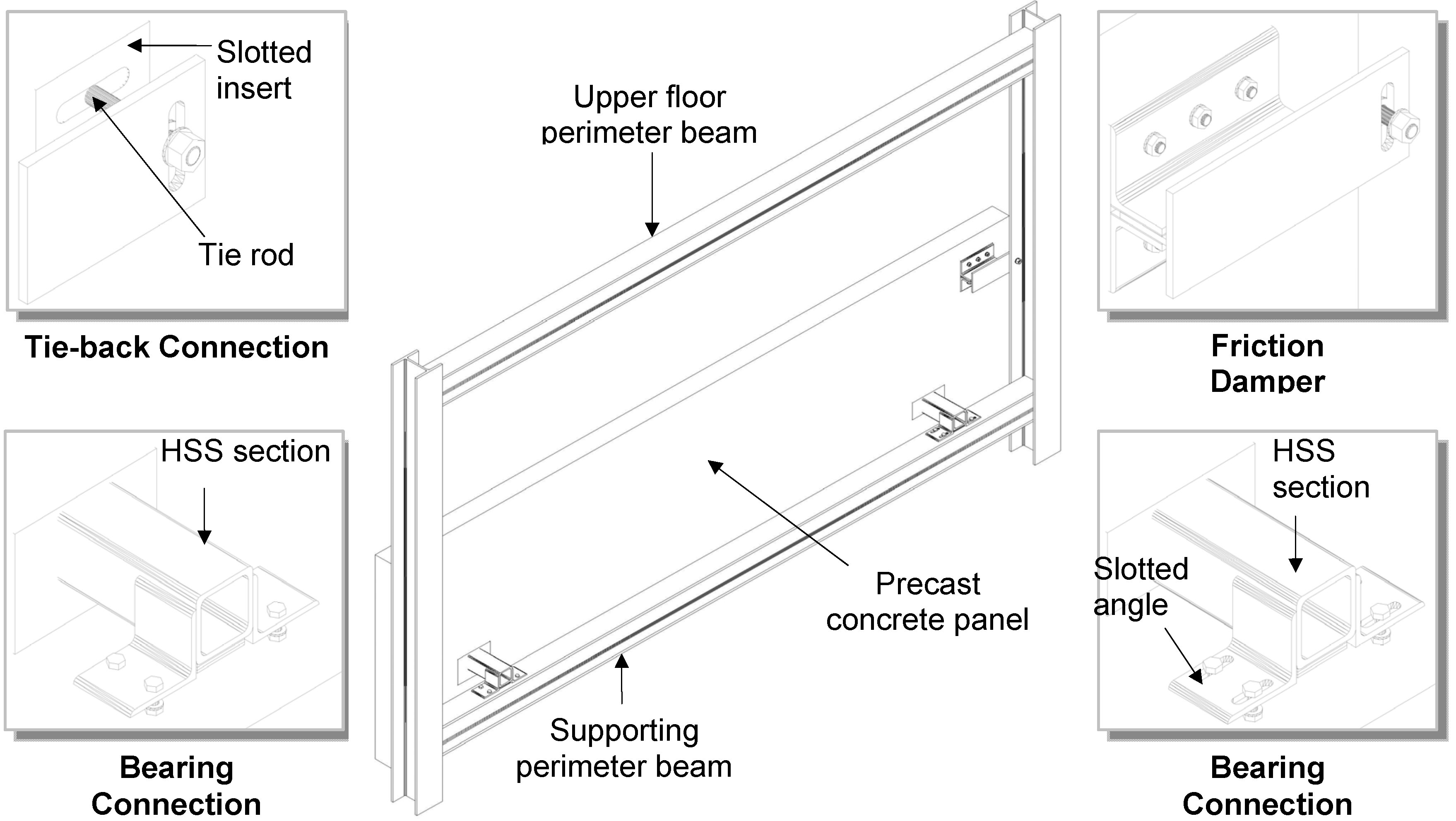
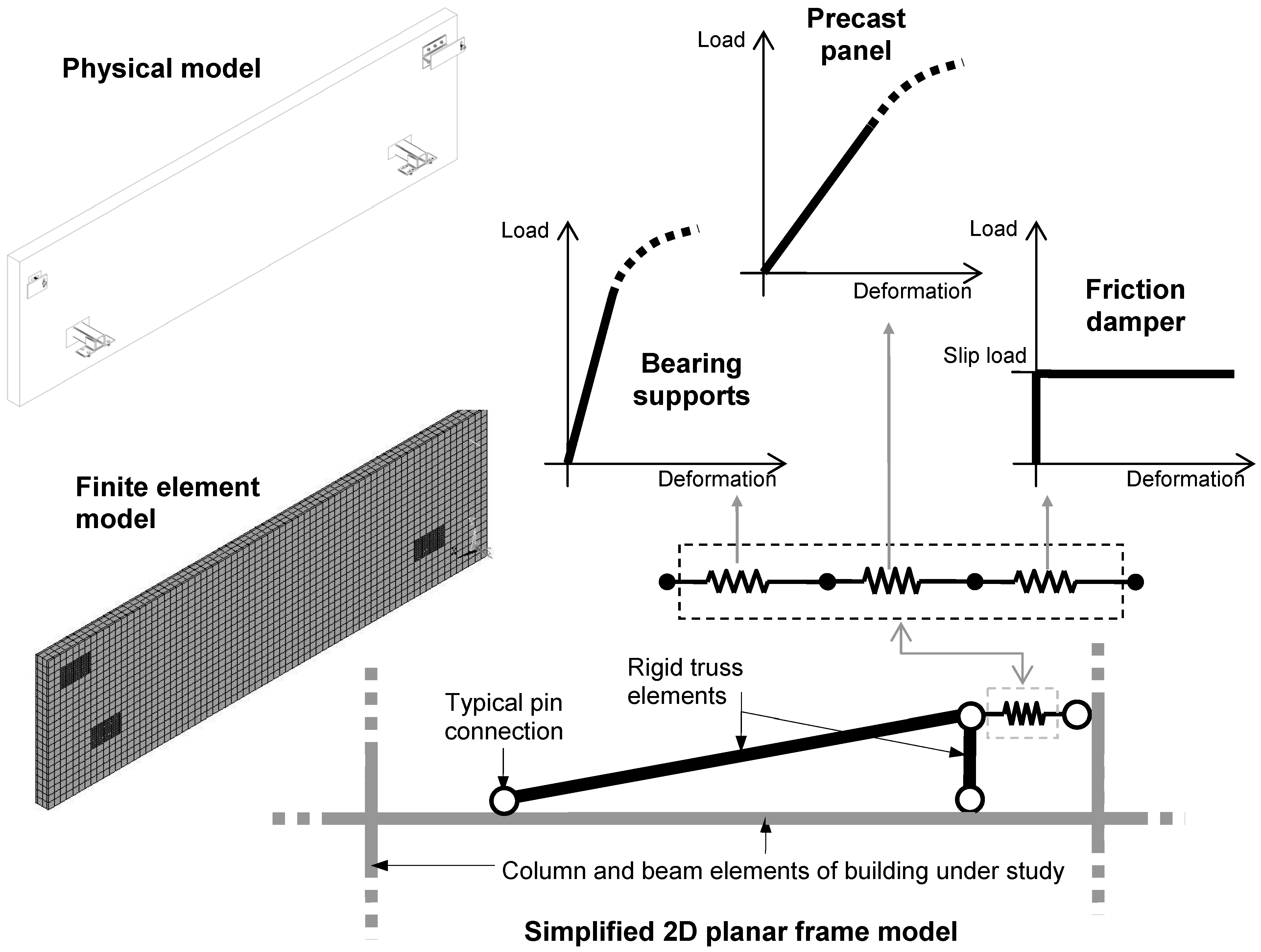
3. Performance of EDCS in Reference Structures
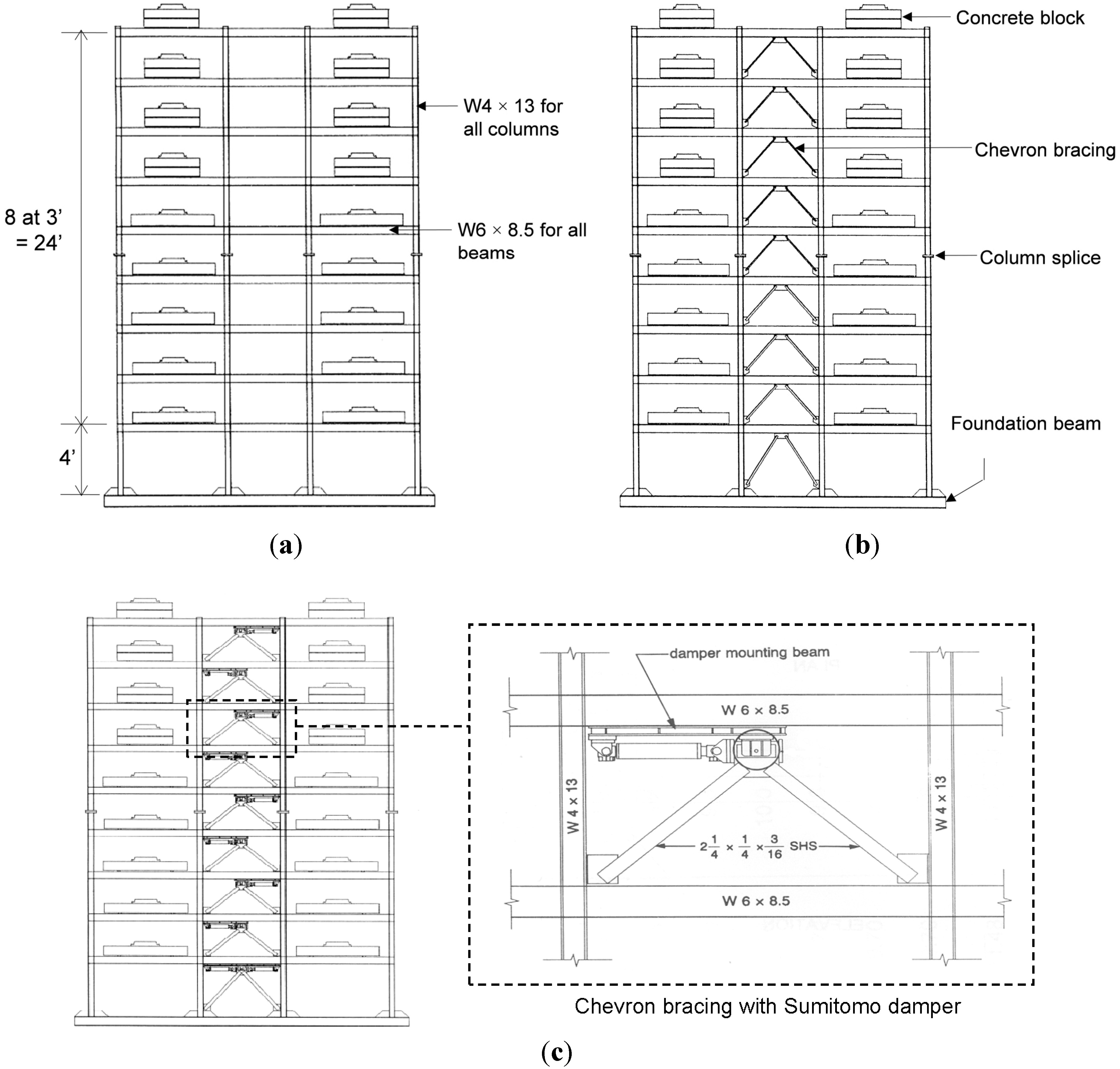
3.1. Modeling of Reference Frames
3.2. Performance of EDCS in OMF and FD Models

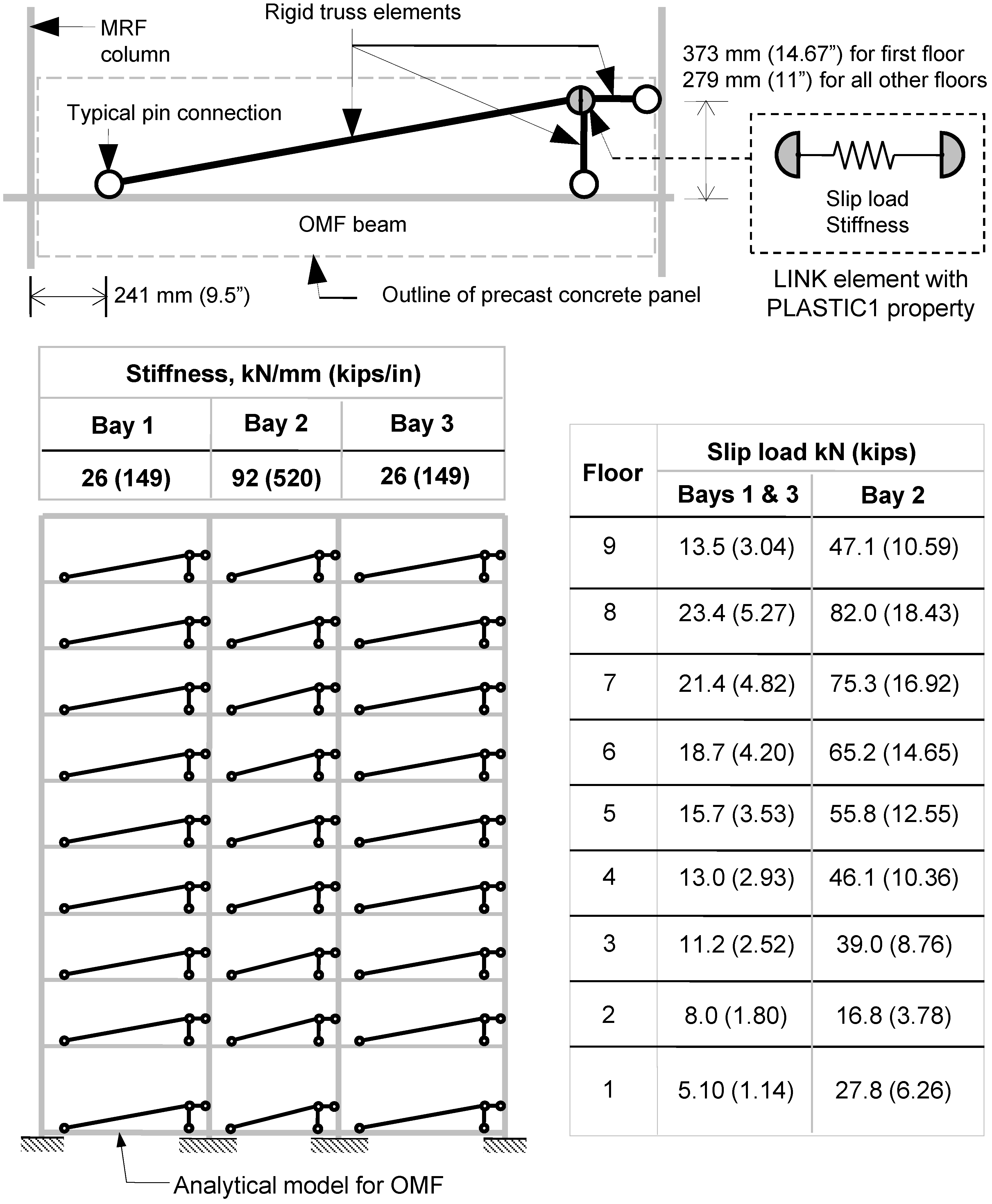
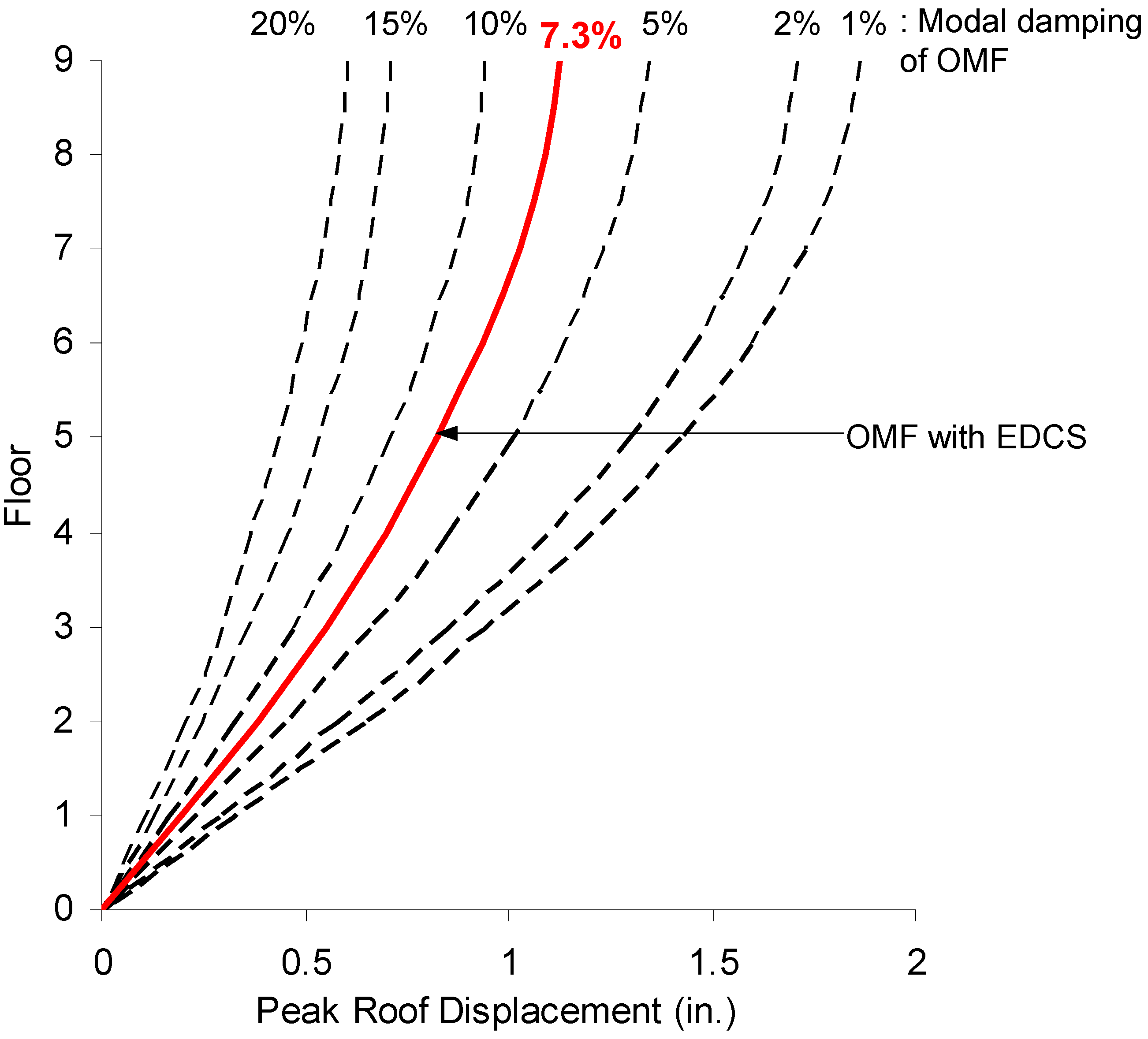
4. Building Case Study
4.1. Building Description
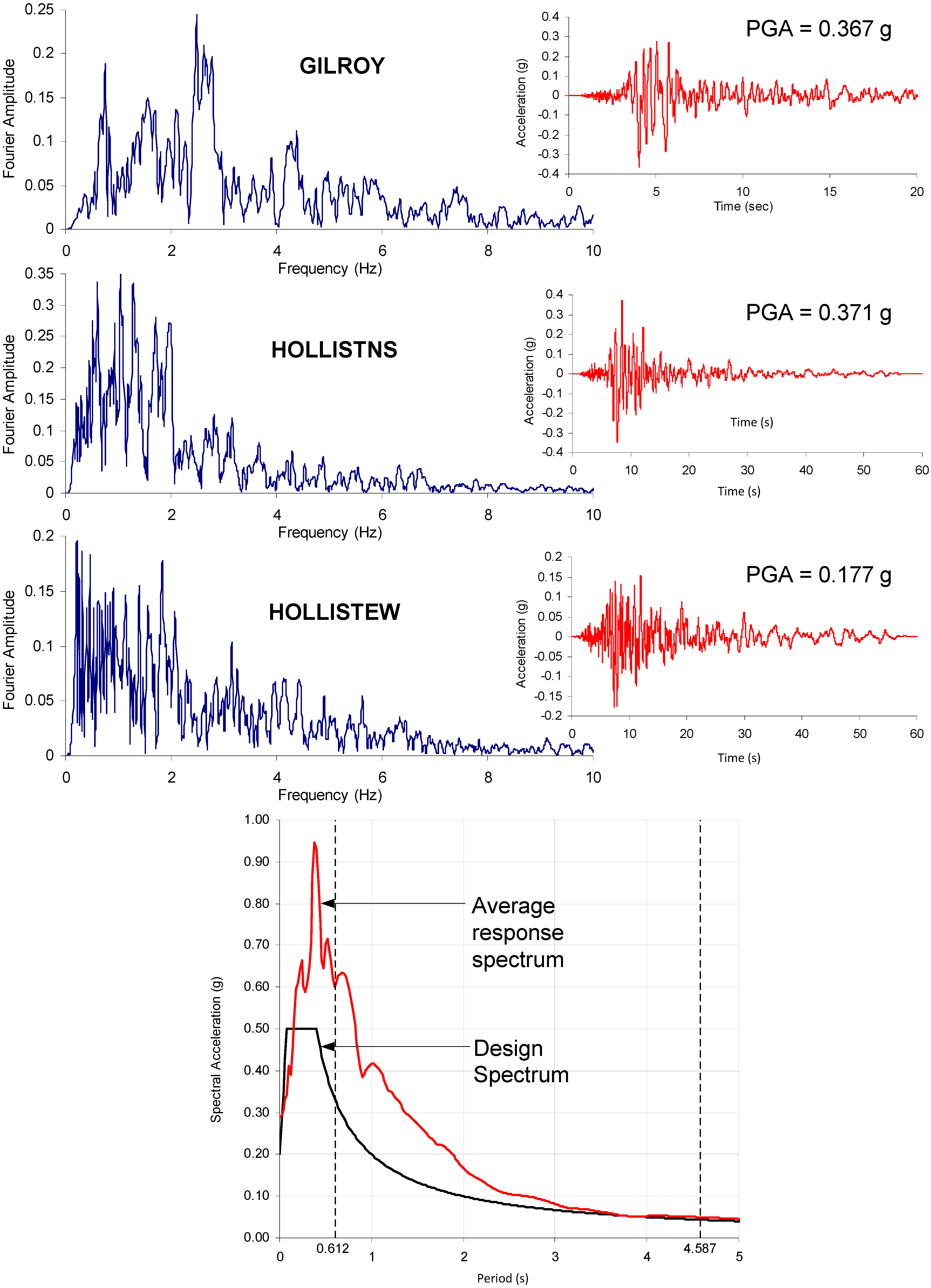
4.2. Design Approach
| Parameter | Symbol | Value |
|---|---|---|
| Seismic importance factor | I | 1.0 |
| Design short period (0.2 s) ground acceleration | SDS | 0.50 g |
| Design long period (1.0 s) ground acceleration | SD1 | 0.20 g |
| Calculated fundamental period | T | 3.09 s |
| Response modification factor (for linear procedures only) | R | 3.5 |
| Reliability/redundancy factor | ρ | 1.0 |
| System overstrength factor | Ωο | 3.0 |
| Drift amplification factor (for BMF) | CD | 3.0 |
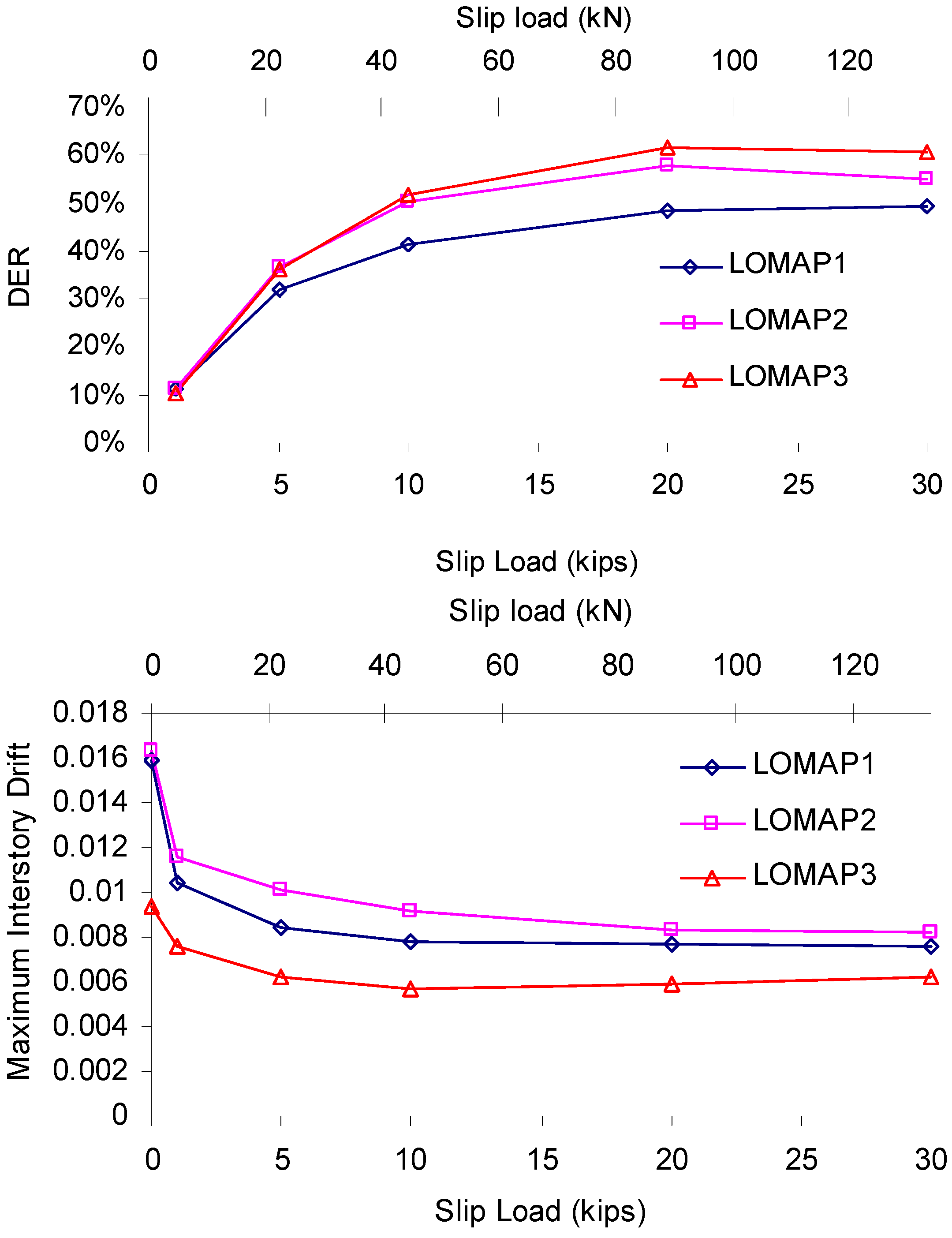
4.3. Design Analysis of MFEDCS
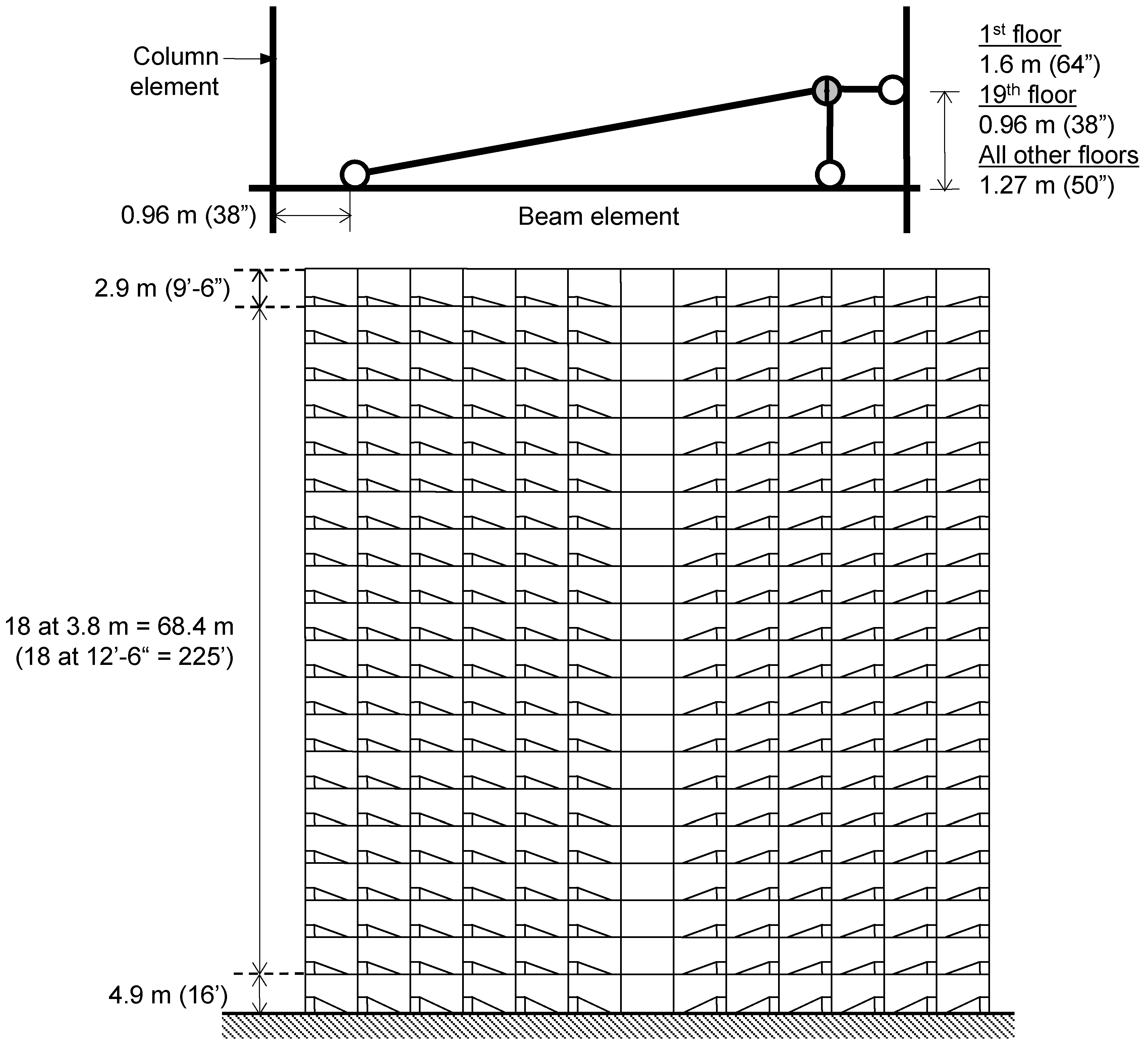

5. Architectural and Constructional Aspects of EDCS
5.1. Protection against Environmental Effects
5.2. Externally Applied Insulation Materials
5.3. Creep Effects and Relaxation of Bolts
5.4. Use of Other Materials
6. Summary and Conclusions
- (1)
- Based on the results of the nonlinear time-history analyses performed on the nine-story one-quarter scale test structure and the 20-story full-scale moment frame building, one can conclude that the new EDCS is able to significantly reduce interstory drift and member forces through the combined action of added stiffness and energy dissipation. This was achieved through careful selection of the slip load level and distribution. Therefore, the selection of slip load is a key design parameter for EDCS.
- (2)
- The loading condition and stresses developed in the framing members of building with EDCS are expected to be different from conventional moment frame members as a result of the interaction with the EDCS. In particular, columns on which the EDCS is attached are subjected to concentrated load (i.e., slip load) along its height (at about one-third height). The study revealed that this should not pose an issue because the maximum slip load is typically controlled by the capacities of the supporting framing elements.
- (3)
- The study on the 20-story building demonstrated that by incorporating the EDCS into a moment resisting frame, it is possible to achieve a reduction in building response comparable to that of a code-specified ordinary moment frame (i.e., response modification factor of 3.5). However, the EDCS design in the example shown does not demand any form of ductility or redundancy from the structural frame itself.
- (4)
- The design approach adopted for the building incorporating the EDCS is conservative in the sense that the moment frame remains essentially elastic throughout the design earthquake event. This means that the moment frame with EDCS could survive a higher than expected earthquake. Furthermore, the EDCS could be retrofitted into existing ordinary moment frame that was not originally designed for higher levels of ground motions.
- (5)
- A less conservative approach could be used whereby both the framing members and the EDCS are specifically designed to contribute to the inelastic demand leading to significantly higher reduction in building response because of reduced force demand as a result of inelasticity and ductility. Although this approach could lead to considerable reduction in the size of the structural members and cost saving, it has its challenges. It would be necessary to model accurately both the inelastic behavior of both framing elements and EDCS. However, the inelastic behavior (e.g., location and numbers of plastic hinges) of the ductile moment frame may change as a result of attaching the EDCS. Furthermore, it may not be easy to separate the contribution of each system in reducing the building response. More importantly, the failure of any one of the systems may lead to possible collapse. It is therefore concluded that for a more conservative design, the moment frame should be designed to remain elastic with all inelastic demand provided by the EDCS (i.e., as a DCS).
Author Contributions
Conflicts of Interest
References
- Wada, A.; Connor, J.J.; Kawai, H.; Iwata, M.; Watanabe, A. Damage tolerant structures. In Proceedings of 5th US-Japan Workshop on the Improvement of Building Structural Design and Construction Practices, San Diego, CA, USA, 1992; pp. 1–12.
- Structural Engineers Association of California Seismology Committee. Recommended Lateral Force Requirements and Commentary, 7th ed.; Structural Engineers Association of California: Sacramento, CA, USA, 1999. [Google Scholar]
- Maneetes, H. Development of a Seismic Dissipating Mechanism for Precast Concrete Cladding Panels. Ph.D. Thesis, The Pennsylvania State University, University Park, PA, USA, May 2007. [Google Scholar]
- Arnold, C. Seismic Safety of the Building Envelope. 2009. Whole Building Design Guide, National Institute of Building Sciences. Available online: http://www.wbdg.org/resources/env_seismicsafety.php (accessed on 21 June 2014).
- Maneetes, H.; Memari, A.M. Finite element modelling and analysis of reinforced concrete cladding panels. Electron. J. Struct. Eng. 2009, 9, 62–72. [Google Scholar]
- Liu, Y.; Hutchinson, T.C. Nonlinear Modeling for Precast Concrete Cladding Subsystems for High Seismicity Regions. 2011. REU Site University of California at San Diego. Available online: http://nees.org/site/media/pdf/reu2011finalpapers/liu_nees_reu_finalpaper.pdf (accessed on 21 June 2014).
- Aiken, I.D.; Kelly, J.M. Earthquake Simulator Testing and Analytical Studies of Two Energy-Absorbing Systems for Multistory Structures; No. UCB/EERC-90/03; Earthquake Engineering Research Center, College of Engineering, University of California: Berkeley, CA, USA, 1990. [Google Scholar]
- Computers and Structures Inc. ETABS Analysis Reference Manual Version 8; Computers and Structures Inc.: Berkeley, CA, USA, 2002. [Google Scholar]
- Wen, Y.-K. Method for random vibration of hysteretic systems. J. Eng. Mech. Div. 1976, 102, 249–263. [Google Scholar]
- American Society of Civil Engineers. Minimum Design Loads for Buildings and Other Structures, ASCE 7-05; American Society of Civil Engineers: New York, NY, USA, 2005. [Google Scholar]
- Goodno, B.J.; Craig, J.I. Ductile Cladding Connection Systems for Seismic Design; No. NIST GCR 98-758; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1998. [Google Scholar]
- International Code Council, Inc. International Building Code; International Code Council, Inc.: Washington, DC, USA, 2006. [Google Scholar]
- American Institute of Steel Construction. AISC Load and Resistance Factor Design Specification for Structural Steel Buildings; American Institute of Steel Construction: Chicago, IL, USA, 2002. [Google Scholar]
- Pall, A.S.; Vezina, S.; Proulx, P.; Pall, R. Friction-dampers for seismic control of Canadian space agency headquarters. Earthq. Spectra 1993, 9, 547–557. [Google Scholar]
- Filiatrault, A.; Cherry, S. Performance evaluation of friction damped braced frame under simulated earthquake loads. Earthq. Spectra 1987, 3, 57–78. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Maneetes, H.; Memari, A.M. Introduction of an Innovative Cladding Panel System for Multi-Story Buildings. Buildings 2014, 4, 418-436. https://doi.org/10.3390/buildings4030418
Maneetes H, Memari AM. Introduction of an Innovative Cladding Panel System for Multi-Story Buildings. Buildings. 2014; 4(3):418-436. https://doi.org/10.3390/buildings4030418
Chicago/Turabian StyleManeetes, Hathairat, and Ali M. Memari. 2014. "Introduction of an Innovative Cladding Panel System for Multi-Story Buildings" Buildings 4, no. 3: 418-436. https://doi.org/10.3390/buildings4030418





