An Incremental Physically-Based Model of P91 Steel Flow Behaviour for the Numerical Analysis of Hot-Working Processes

Abstract

This paper is aimed at modelling the flow behaviour of P91 steel at high temperature and a wide range of strain rates for constant and also variable strain-rate deformation conditions, such as those in real hot-working processes. For this purpose, an incremental physically-based model is proposed for the P91 steel flow behavior. This formulation considers the effects of dynamic recovery (DRV) and dynamic recrystallization (DRX) on the mechanical properties of the material, using only the flow stress, strain rate and temperature as state variables and not the accumulated strain. Therefore, it reproduces accurately the flow stress, work hardening and work softening not only under constant, but also under transient deformation conditions. To accomplish this study, the material is characterised experimentally by means of uniaxial compression tests, conducted at a temperature range of 900–1270 °C and at strain rates in the range of 0.005–10 s⁻¹. Finally, the proposed model is implemented in commercial finite element (FE) software to provide evidence of the performance of the proposed formulation. The experimental compression tests are simulated using the novel model and the well-known Hansel–Spittel formulation. In conclusion, the incremental physically-based model shows accurate results when work softening is present, especially under variable strain-rate deformation conditions. Hence, the present formulation is appropriate for the simulation of the hot-working processes typically conducted at industrial scale.

1. Introduction

The P91 steel grade is a widely used material in power-plant header applications, such as heavy-section boiler components, heat exchangers, piping and tubing, etc. The interest in this ferritic–martensitic steel arises mainly due to its high creep strength and toughness at elevated temperatures, enhanced oxidation and corrosion resistance, low thermal expansion coefficient and low cost as compared to other high-temperature alloys [1]. Due to its outstanding characteristics, this material has been extensively investigated in the past few years. The research has mainly focused on the thermomechanical processing of the microstructure under high temperature, which determines the high-temperature creep and fatigue performance in both thermal and nuclear power-generation applications [1,2,3,4,5,6,7,8,9].

One of the aspects which has been investigated to a much lesser extent is that concerning the formulation of the constitutive description of this material during deformation under hot-working conditions. Such relationships are of fundamental importance in numerical behaviour and the optimisation of industrial hot-working operations employed in the manufacturing of high-temperature components by means, for example, of the Mannesmann process for the production of seamless tubes. In such a process, the material is pre-heated in the temperature range of 1200–1280 °C and, due to deformational heating, it can achieve up to approximately 1300 °C. In addition, according to the literature and the preliminary finite element (FE) simulations conducted by the authors, the applied strain could vary in the range of 5 to 10 and the strain rate in the span of 40–50 s⁻¹ [10]. Thus, it can be clearly observed that the manufacturing of such components is conducted under severe transient deformation conditions and, therefore, the prediction of flow stress, work-hardening and work-softening rates has to be carried out on the basis of valid state parameters.

Concerning the analysis of the constitutive description of the P91 steel under hot-working conditions, Samantaray and co-workers [11] have conducted an investigation in order to compare the capability of the Johnson–Cook (JC), modified Zerilli–Armstrong (ZA), and strain-compensated Arrhenius-type (SCAT) constitutive models for representing the elevated temperature flow behaviour of a modified 9Cr-1Mo steel, by means of hot compression tests. These authors concluded that both the ZA and SCAT models were able to provide a good description of the experimental data, although the SCAT model seemed to be more accurate due to the higher number of material constants involved in the formulation.

In subsequent investigations on the same alloy, Samantaray and co-workers [12], described the effects of temperature and strain rate on deformation behaviour by assuming that the Zener–Hollomon parameter and the different constants involved in the hyperbolic sine relationship were a function of the applied strain through simple parametric relationships. According to their results, the apparent activation energy for hot deformation of this material could vary between 369 kJ∙mol⁻¹ and 391 kJ∙mol⁻¹ in the course of plastic deformation. Krishnan et al. [13], despite using similar parametric relationships for a temperature range of 1173–1373 K, presented an apparent activation energy value slightly higher, also dependent on the plastic deformation which could fluctuate between 395 kJ∙mol⁻¹ and 465 kJ∙mol⁻¹.

Samantaray et al. [14] conducted a further analysis analysis of the hot workability of the P91 alloy when the material is deformed in the temperature range of 1123–1373 K at strain rates in the span of 0.001–10 s⁻¹. According to their results, based on the so-called dynamic materials model approach, the apparent activation energy for hot deformation in the optimum domain is of approximately 400 kJ∙mol⁻¹.

Further research on the constitutive formulation of the P91 alloy under hot-working conditions led Samantaray and co-workers [15] to the development of a strain-dependent rate equation for the evaluation of processing conditions on the hot-deformation behaviour of this alloy. More recent work conducted by the same research group [16] involved the analysis of the flow-stress data of the P91 steel on the basis of the Dorn power-law equation and by introducing the concept of resisting stress to dislocation motion. In this analysis, the authors also evaluated the different parameters involved in the rate equation employed for the computation of the stress, at different applied strains.

In a recent investigation, Li and Ma [17] developed the constitutive formulation of a 30Cr-2Ni-4Mo-V steel grade. The constitutive description was based on the integrated expression of the Estrin–Mecking work-hardening law and its modified form, which takes into account flow softening due to dynamic recrystallization (DRX). In the latter, the volume fraction recrystallized dynamically, and ($X_v$) is computed as a function of the strain applied. The effect of deformation temperature and strain rate were introduced in the analysis by means of the hyperbolic sine relationship, by assuming that the pre-exponential constant varies with deformation temperature.

The above account clearly shows that, although important contributions have been made toward describing in a precise manner the flow stress of the P91 steel and other steel grades employed in high-temperature applications, most of the proposed formulations are based on the use of different relationships, whose parameters are expressed as a function of the strain applied to the material, or in which the flow stress is given in the form of integrated equations, also as a function of strain. In spite of the fact that these formulations could provide a satisfactory description of the flow stress when the material is deformed under constant conditions of temperature and strain rate, their applicability for modelling industrial deformation processes, which occur under severe transient deformation conditions, would be limited.

Therefore, the present investigation has been conducted in order to formulate, for the first time, a more general constitutive description, able to predict accurately the flow stress and work-hardening and work-softening rates of the P91 steel either under constant and transient deformation conditions. In such a formulation, the flow stress of this steel grade is independent of the strain applied to the material, which is not a valid state parameter. On the contrary, it is computed recursively, from its previous value and as a function of the current values of deformation temperature and strain rate during each strain interval in the course of plastic deformation, from the corresponding expression of the work-hardening rate of the material. The different constants involved in the analysis are determined in a systematic and rational manner from the experimental values of the flow-stress and deformation conditions. The formulation is then validated by means of hot-compression tests conducted under both constant and transient loading conditions, involving a wide range of temperature and strain rate. The formulation is subsequently implemented in the commercial FE computer code FORGE^® (NxT 2.1, Transvalor S.A., Mougins, France) in order to model the deformation behaviour of the material under hot axisymmetric compression conditions.

2. Constitutive Model Description

The constitutive model proposed for the description of the flow-stress curves of the P91 steel deformed under hot-working conditions is presented in the following section. A methodology similar to that used for other materials which exhibit DRX is followed [18,19,20,21].

2.1. Basis of the Model

The basis is the original model advanced by Jonas et al. [22]. In this model, the description of the work hardening (WH) and dynamic recovery (DRV) is given by the evolution of the dislocation density with the plastic strain applied to the material $\epsilon$, derived by Estrin and Mecking [23]:

$$\frac{\mathrm{d}\rho }{\mathrm{d}\epsilon }=h-r\rho .$$

(1)

In the above equation, $\rho$ stands for the dislocation density, $h$ is the athermal dislocation storage rate and $r$ the dynamic recovery rate. The flow stress $\sigma$ is assumed to be dependent on the dislocation density of the material according to:

$$\sigma =\alpha \mu b{\rho }^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},$$

(2)

where $b$ represents the Burgers vector, $\mu$ the shear modulus, and $\alpha \cong 1$ [23,24]. This makes the constitutive model dependent on a single state parameter. In addition, a direct proportionality relation is established between the flow stress $\sigma$ and the dislocation density $\rho$, from which the flow stress along the work-hardening and DRV transient, ${\sigma }_{\mathrm{DRV}}$ is given by

$${\sigma }_{\mathrm{DRV}}={\left[{\sigma }_{\mathrm{S}}{}^2-({\sigma }_{\mathrm{S}}{}^2-{\sigma }_0{}^2)\exp (-r\epsilon )\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}.$$

(3)

Here, ${\sigma }_{\mathrm{S}}$ and ${\sigma }_0$ represent the saturation and yield stress, respectively, being directly dependent on the peak stress ${\sigma }_{\mathrm{P}}$ by means of a simple relation. The dynamic recovery rate $r$ is also dependent on the peak stress, but is obtained from the slope of the line that relates $\sigma \mathrm{d}\sigma /\mathrm{d}\epsilon$ versus ${\sigma }^2$. Equation (3) is valid as long as the strain applied to the material does not overcome the critical strain for the onset of DRX, ${\epsilon }_{\mathrm{c}}$. Once it happens, the softening induced by DRX has to be subtracted from Equation (3), leading to:

$$\sigma ={\sigma }_{\mathrm{DRV}}-({\sigma }_{\mathrm{S}}-{\sigma }_{\mathrm{SS}})X_v.$$

(4)

The DRX microstructural softening mechanism subtracts from the DRV equation the difference between the values of saturation stress ${\sigma }_{\mathrm{S}}$ and steady-state stress ${\sigma }_{\mathrm{SS}}$, which is also expressed as a fraction of peak stress ${\sigma }_{\mathrm{P}}$ by the authors. Similarly, it is used to describe the critical stress for the onset of DRX ${\sigma }_{\mathrm{c}}$ and, thus, it can be assumed that ${\sigma }_{\mathrm{c}}\cong {\sigma }_{\mathrm{SS}}$. $X_v$ stands for the volume fraction recrystallized dynamically, which defines the kinetics of the recrystallization phenomenon by the Avrami relation according to:

$$X_v=1-\exp \left(-0.693{\left(\frac{t}{t_{50}}\right)}^{n_{\mathrm{Av}}}\right),$$

(5)

where $t$ is the accumulated time in which recrystallization is developed, $n_{\mathrm{Av}}$ is the Avrami exponent, and $t_{50}$ is the time required for attaining a recrystallized fraction of a 50% and is given by:

$$t_{50}=A{Z}^{-q}{d}_0{}^v\exp \left(\frac{Q_{\mathrm{DRX}}}{\mathrm{R}T}\right).$$

(6)

In the above equation, $A$, $q$ and $v$ are material constants, $Q_{\mathrm{DRX}}$ is the activation energy for DRX, $d_0$ the initial austenitic grain size, $\mathrm{R}$ is the universal gas constant, $T$ the temperature, and $Z$ represents the Zener–Hollomon parameter given by:

$$Z=\dot{\epsilon }\exp \left(\frac{Q}{\mathrm{R}T}\right).$$

(7)

Finally, the Zener–Hollomon parameter is present in the hyperbolic sine relation that allows the determination of the peak stress ${\sigma }_{\mathrm{P}}$, as a function of strain rate and temperature by means of the hyperbolic sine relation [25], also known as the Sellars-Tegart-Garofalo (STG) model:

$$Z=\dot{\epsilon }\exp \left(\frac{Q}{\mathrm{R}T}\right)=B{[\sinh (\alpha {\sigma }_{\mathrm{P}})]}^m,$$

(8)

where $B$, $\alpha$ and $m$ are material parameters. The presented set of Equations (3)–(8) defines the basis of the original model advanced by Jonas et al. [22], which is able to define accurately the flow-stress evolution during constant conditions of deformation in terms of strain rate and temperature.

However, as it was pointed out in the previous section, a flow-stress formulation cannot be dependent on the strain applied to the material or use the strain as a state parameter if it is intended to be valid for constant and transient deformation conditions. Therefore, in order to extent the aforementioned original model to transient deformation conditions, two alternative formulations are possible. On the one hand, a differential formulation can be used. This is the method more extensively used for the definition of flow-stress formulations for different steels [20,26,27], as it allows the updating of strain rate and temperature after each strain increment. On the other hand, on the base of the differential formulation, a novel incremental constitutive formulation has been proposed by Puchi-Cabrera et al. [21] showing similar results. This incremental formulation presents the advantage of being easier to be implemented in a commercial FE solver and is more efficient in terms of calculation time, as it does not require the use of an integration scheme such as fourth order Runge–Kutta like the respective differential formulation does.

2.2. Incremental Constitutive Formulation

The incremental constitutive formulation proposed by Puchi-Cabrera et al. [21] presents an alternative formulation for the transient ${\sigma }_{\mathrm{DRV}}$ described in Equation (3), given by:

$${\sigma }_{\mathrm{DRV}}^{(j)}={\left[{\left({\sigma }_{\mathrm{S}}^{(j)}\right)}^2-\left({\left({\sigma }_{\mathrm{S}}^{(j)}\right)}^2-{\left({\sigma }_{\mathrm{DRV}}^{(j-1)}\right)}^2\right)\exp \left(-\frac{2{\theta }_0\Delta {\epsilon }^{(j)}}{{\sigma }_{\mathrm{S}}^{(j)}}\right)\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},$$

(9)

with:

$${\sigma }_{\mathrm{DRV}}^{(1)}={\sigma }_{\mathrm{y}}^{(1)},$$

(10)

where ${\sigma }_{\mathrm{y}}$ is the yield stress and ${\theta }_0$ the initial work-hardening rate, which can be normalized by the temperature-dependent shear modulus of the material $\mu (T)$ and expressed as a function of $Z$ according to:

$$\frac{{\theta }_0}{\mu (T)}=k_{\theta }{Z}^{m_{\theta }},$$

(11)

being the shear modulus computed according to Kocks [28],

$$\mu (T)=88884.6-37.3T.$$

(12)

The formulation proposed in Equations (9) and (10) allows updating the strain rate and temperature values after each increment and thus computes the WH and DRV at each increment from its previous value. For this purpose, three critical stress parameters have to be calculated at each increment, namely yield stress ${\sigma }_{\mathrm{y}}$, saturation stress ${\sigma }_{\mathrm{S}}$ and steady-state stress ${\sigma }_{\mathrm{SS}}$. They can be computed by means of the STG model [25] as function of temperature and strain rate, yielding:

$${\sigma }_{\mathrm{y}}\left(\dot{\epsilon },T\right)={\sigma }_{\mathrm{a}}+{\delta }_{\mathrm{y}}{\sinh }^{-1}{\left(\frac{Z}{B_{\mathrm{y}}}\right)}^{\frac{1}{m_{\mathrm{y}}}},$$

(13)

$${\sigma }_{\mathrm{S}}\left(\dot{\epsilon },T\right)={\delta }_{\mathrm{S}}{\sinh }^{-1}{\left(\frac{Z}{B_{\mathrm{S}}}\right)}^{\frac{1}{m_s}}$$

(14)

and,

$${\sigma }_{\mathrm{SS}}\left(\dot{\epsilon },T\right)={\delta }_{\mathrm{SS}}{\sinh }^{-1}{\left(\frac{Z}{B_{\mathrm{SS}}}\right)}^{\frac{1}{m_{\mathrm{SS}}}}.$$

(15)

As pointed out earlier, $Z$ stands for the Zener–Hollomon parameter, whereas ${\sigma }_{\mathrm{a}}$ is the athermal stress and ${\delta }_{\mathrm{y}}$, $B_{\mathrm{y}}$, $m_{\mathrm{y}}$, ${\delta }_{\mathrm{S}}$, $B_{\mathrm{S}}$, $m_{\mathrm{S}}$, ${\delta }_{\mathrm{SS}}$, $B_{\mathrm{SS}}$, $m_{\mathrm{SS}}$ are material parameters determined from the experimentation.

In order to compute the DRX softening, the condition for the onset of dynamic recrystallization is similar to that of the original model (${\sigma }_{\mathrm{c}}\cong {\sigma }_{\mathrm{SS}}$). However, the parametric relationship for accounting DRX kinetics presented in Equation (6) is slightly simplified by the combination of the material parameter A and the initial austenitic grain size $d_0$ within a single grain size-dependent material parameter D, resulting in:

$$t_{50}=D{Z}^{-q}\exp \left(\frac{Q_{\mathrm{DRX}}}{\mathrm{R}T}\right).$$

(16)

The volume fraction recrystallized is then calculated in an incremental manner, substituting Equation (5) with:

$$X_v^{(j)}=1-\exp \left(-0.693{\left({\displaystyle \sum _{i=N_0}^j\frac{\Delta t^{(j)}}{t_{50}^{(j)}}}\right)}^{n_{\mathrm{Av}}}\right),$$

(17)

where,

$$\Delta t^{(j)}=\frac{\Delta {\epsilon }^{(j)}}{{\left(\dot{\epsilon }\right)}^{(j)}}.$$

(18)

In Equation (17), $N_0$ represents the increment at which DRX is initiated. As long as the DRV stress does not overcome the critical value for the onset of DRX (${\sigma }_{\mathrm{DRV}}<{\sigma }_{\mathrm{SS}}$), Equation (9) is valid for the computation of stress, as only work-hardening and dynamic recovery restoration mechanisms act. However, if the DRV stress exceeds the value for the onset of DRX (${\sigma }_{\mathrm{DRV}}\ge {\sigma }_{\mathrm{SS}}$), the stress results in:

$${\sigma }^{(j)}={\sigma }_{\mathrm{DRV}}^{(j)}-\left({\sigma }_{\mathrm{S}}^{(j)}-{\sigma }_{\mathrm{SS}}^{(j)}\right)X_v^{(j)}.$$

(19)

Equations (9)–(19) represent the incremental constitutive model employed in the description of the behaviour of the P91 steel. In the following section, all the required material parameters are determined from the experimental stress–strain curves under different conditions of strain rate and temperature.

3. Materials and Methods

The aim is the determination of the stress–strain curves as well as the force–time curves for all considered deformation conditions. Axisymmetric compression tests were performed in vacuum on Gleeble-3500 thermo-mechanical testing equipment (Dynamic Systems Inc., Poestenkill, NY, USA) by using samples of a commercial 9Cr-1Mo-V-Nb steel, which corresponds to a P91 grade. Its chemical composition according to the ASTM A335 standard is listed in

Table 1. Chemical composition of the P91 grade steel (%).

C	Mn	P	S	Si	Cr	Mo
0.08–0.12	0.3–0.6	0.02 max	0.01 max	0.2–0.5	8–9.5	0.85–1.05

.

Samples were machined directly from the as-cast billet, which allowed the manufacturing of cylindrical specimens of 10 mm diameter and 15 mm height. Prior to testing, the specimens were polished on their flat faces with the aid of SiC abrasive papers of 240 mesh, and a Ni-based lubricant stable at high temperatures was applied to reduce the frictional effect on the results. The thermal etching technique was used for the evaluation of the initial austenitic grain size [29]. The P91 steel prior-austenite grain boundaries are shown in Figure 1. An average initial austenitic grain size of 120 µm is identified using the average grain intercept technique.

The temperatures considered for the tests were 900 °C, 950 °C, 1050 °C, 1150 °C and 1270 °C, whereas the strain rates encompassed 0.005 s⁻¹, 0.01 s⁻¹, 0.1 s⁻¹, 1 s⁻¹ and 10 s⁻¹. The temperature was measured during the tests with a K-type thermocouple welded at the middle position of the sample, which allowed for measurement and correction of the deformation heating of the sample during the tests. Diffusion was minimised by the inclusion of a Ta foil placed between the sample and the device testing clamps. The control of temperature and strain rate allowed the completion of both constant and transient conditions of loading.

The heating of the samples was performed at a rate of 2 °C∙s⁻¹ and, once the objective temperature of the test was attained, they were kept at this temperature over 300 s to guarantee the homogeneity of the temperature of the sample.

Two tests were performed under each deformation condition to ensure the reproducibility of the results and four extra tests for evaluating transient loading. Finally, they were used for the characterization of the P91 steel and the numerical simulation of the compression tests, respectively.

4. Experimental Results

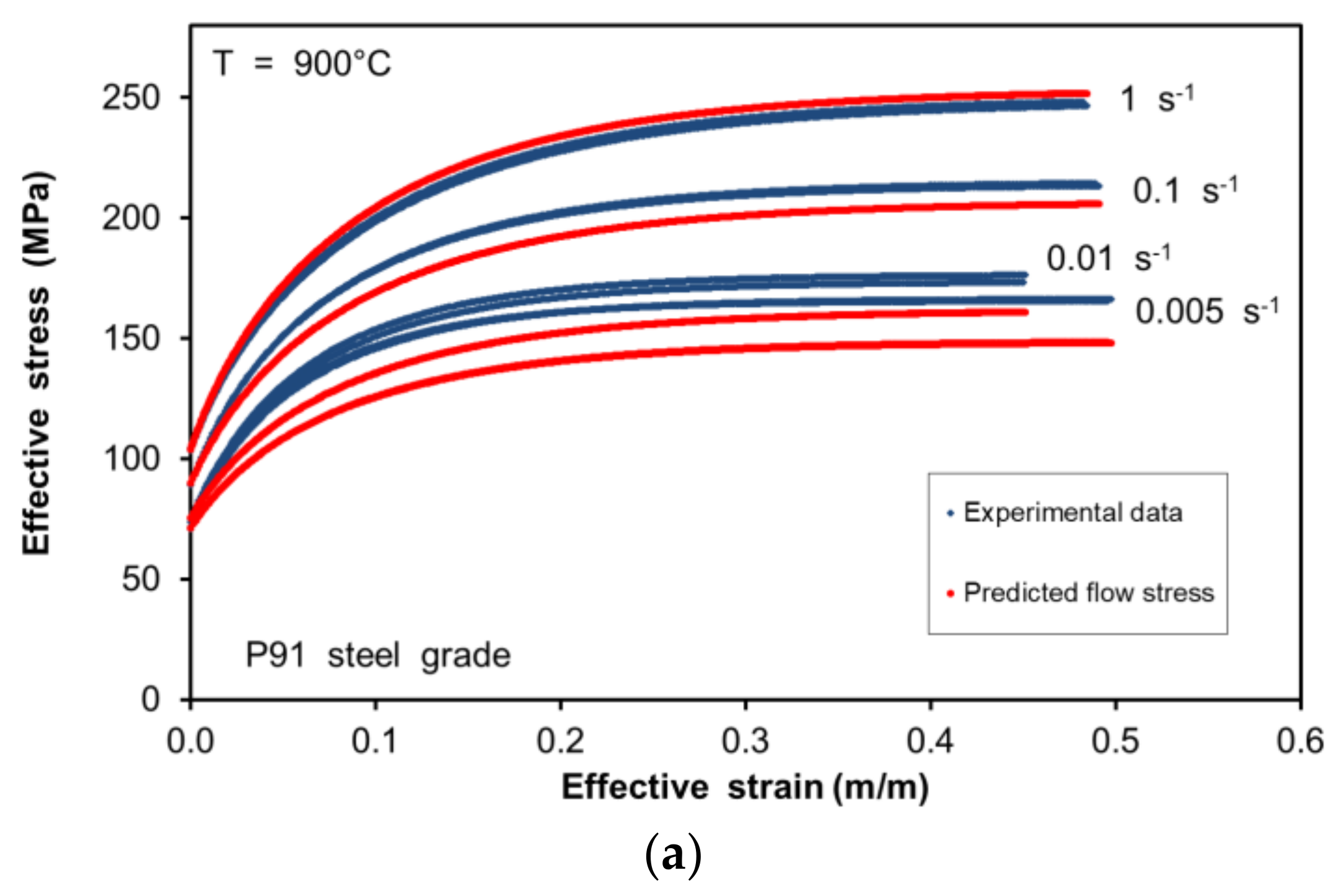
The experimental stress–strain curves obtained from the axisymmetric compression tests under the deformation conditions presented in the previous section are illustrated in Figure 2. All curves present an initial WH transient stage and, depending on the dynamic restoration mechanism prevailing afterwards, the flow stress curves tend to achieve a saturation value (DRV) or to reach a peak value followed by the work softening of the material (DRX), which exhibits a final steady state stress value.

According to the results in the indicated plots, at temperatures lower than 950 °C only DRV is present and thus all the curves reach a saturation stress value. This stress parameter is dependent on strain-rate and temperature conditions through the Zener–Hollomon parameter Z, being higher when the strain rate is increased or the temperature decreased.

However, under temperatures higher than 950 °C, both DRV and DRX dynamic restoration mechanisms are present depending on the strain rate conditions under which the deformation is conducted. This clearly indicates that the Z value is crucial for the definition of the flow-stress and microstructural changes taking place during the hot deformation of the material. Therefore, a critical Z_c value must be determined in order to associate the deformation conditions (strain rate and temperature) with the prevailing restoration mechanisms.

In the present study, from the analysis under constant deformation conditions, all the material-dependent parameters presented in the description of the constitutive model are determined.

As pointed out in the introductory section, among the material-dependent parameters the apparent activation energy for hot deformation of the material Q is of fundamental importance. In fact, it directly influences the value of Z, describing the deformation conditions and thus all the stress parameters considered in the constitutive model description. Although previous studies for the P91 steel used Q values that vary in the course of plastic deformation for an accurate description of the flow stress [13], in the present study a single value of Q is sufficient for the description of the flow stress under all evaluated deformation conditions.

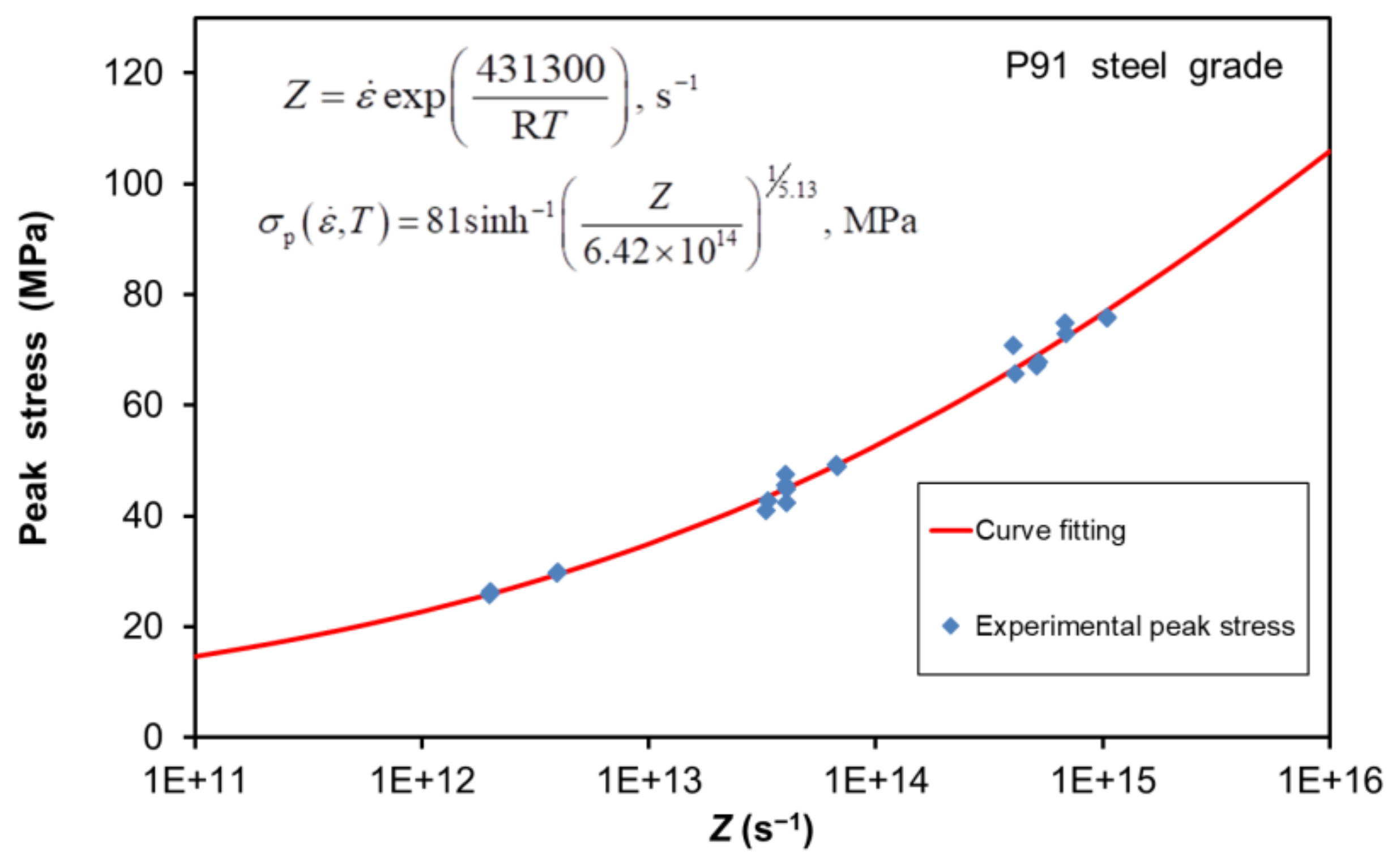
The determination of the Q value is based on the procedure reported for other materials [20,21,26,27,30] which, according to Luton and Sellars [31], allows the determination of its magnitude from the dependence of the peak stress on the temperature and strain rate. This procedure is illustrated in Figure 3, giving as a result a confident Q value of approximately 431.7 kJ∙mol⁻¹. The magnitude determined is slightly higher than the previous values reported by Samantaray et al. for the P91 steel, who observed a maximum value of 391 kJ∙mol⁻¹ [12], whereas in a later study reported an optimum magnitude of about 400 kJ∙mol⁻¹ [16]. However, this is in good agreement with the reported values of Krishnan et al. [13], which varied between 395 kJ∙mol⁻¹ and 465 kJ∙mol⁻¹.

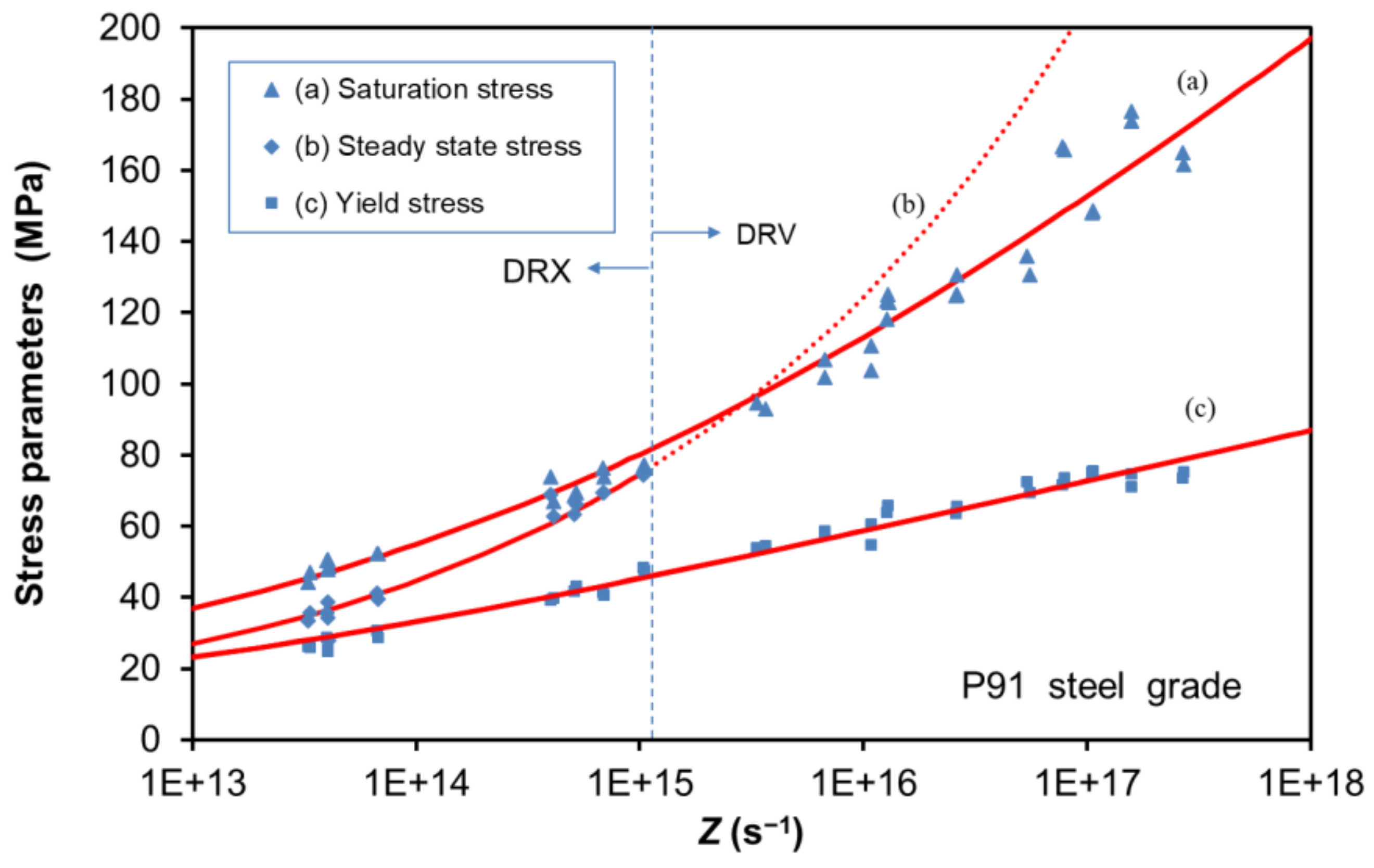
After the determination of the Q value, it is possible to identify the critical Zener–Hollomon parameter Z_c, which defines the deformation conditions under which the material undergoes DRV ($Z\ge 1.1\times {10}^{15} {\mathrm{s}}^{-1}$) or if DRX is the prevailing restoration mechanism ($Z<1.1\times {10}^{15} {\mathrm{s}}^{-1}$).

When DRV is the only dynamic restoration mechanism, the description of the flow-stress curve is described by means of Equation (9), which implies that only three parameters ought to be determined, namely ${\sigma }_{\mathrm{y}}$, ${\theta }_0$ and ${\sigma }_{\mathrm{S}}$. However, whenever DRX prevails, Equation (19) defines the flow-stress curves, which besides the above parameters, requires the determination of $t_{50}$, ${\sigma }_{\mathrm{SS}}$ and $n_{\mathrm{Av}}$.

Figure 4 illustrates the existing transition between restoration mechanisms depending on the Z value.

In addition, under the same Z basis the saturation, yield and steady-state stress values according to STG model are compared with the experimental data from the individual curves. When the Z value increases, the stress parameters exhibit a similar behaviour, but in a clear non-linear trend. However, it can be appreciated how the STG model is capable of reproducing correctly the non-linear variation of these stress parameters with respect to temperature and strain rate through the Z value, giving a good prediction under a wide range of deformation conditions. All the values of the parameters involved in the STG model for the definition of ${\sigma }_{\mathrm{y}}$, ${\sigma }_{\mathrm{S}}$ and ${\sigma }_{\mathrm{SS}}$ are reported in

Table 2. STG parameter values.

${\sigma }_{\mathrm{a}}$	${\delta }_{\mathrm{y}}$	$B_{\mathrm{y}}$	$m_{\mathrm{y}}$	${\delta }_{\mathrm{S}}$
3.7	28	3.52 × 1013	4.5	116.9
$B_{\mathrm{s}}$	$m_{\mathrm{s}}$	${\delta }_{\mathrm{SS}}$	$B_{\mathrm{ss}}$	$m_{\mathrm{ss}}$
5.2 × 1015	5.5	1260	3.34 × 1020	4.5

.

Another important aspect to be defined is the WH transient stage, which is directly related to the initial work-hardening rate ${\theta }_0$. The stress–strain curves presented in Figure 2 illustrate that depending on the deformation conditions, the slope of the curves in the initial stage varies. Therefore, ${\theta }_0$ is defined by Equation (11), being dependent on Z and the temperature-dependent shear modulus. According to its definition, the ${\theta }_0$ value tends to be higher as Z increases, which agrees with the initial slopes of the experimental measured curves.

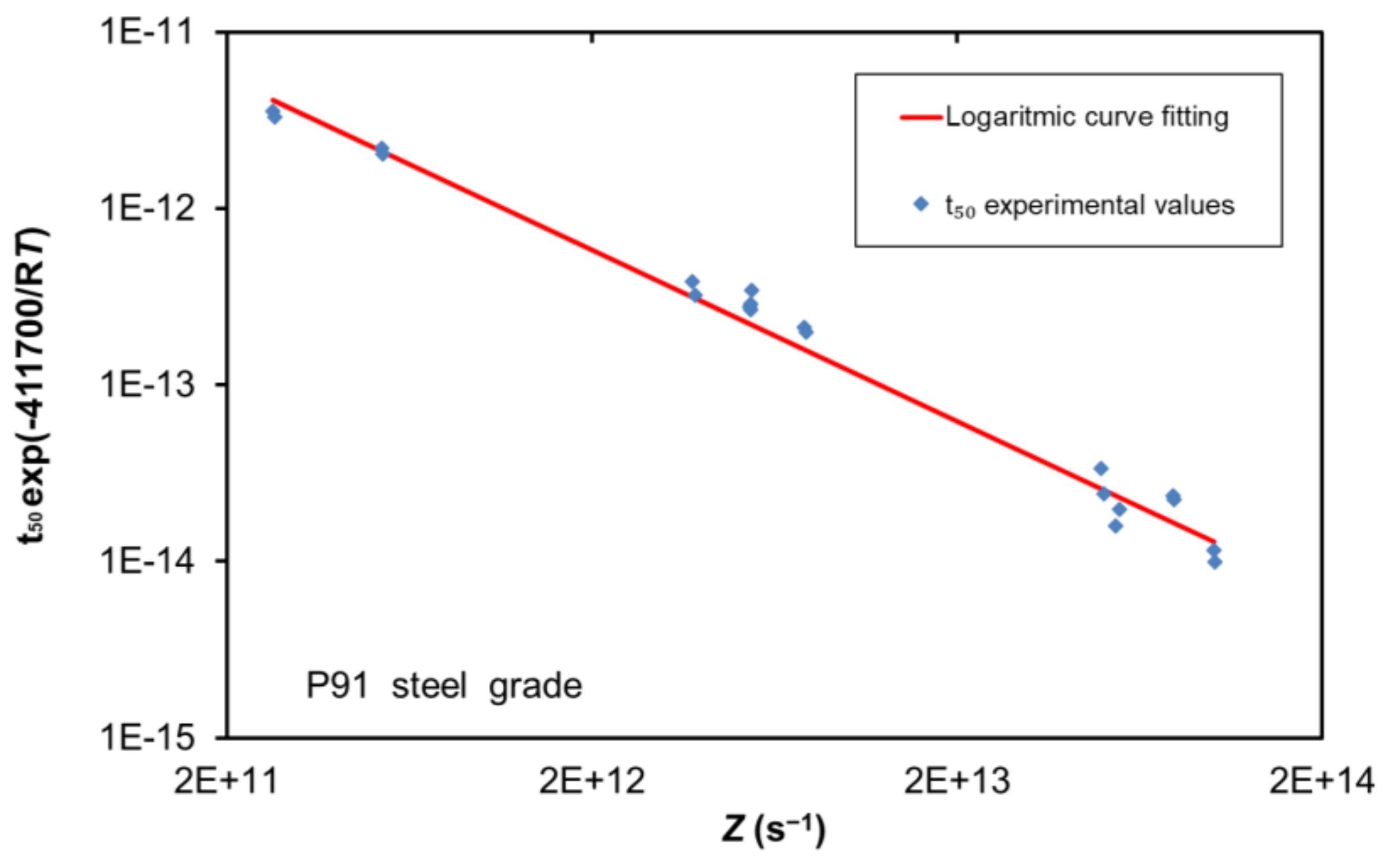
Finally, it is important to define correctly the DRX kinetics, through the determination of all the parameters involved in Equation (16), relative to the description of the time required for 50% DRX. The kinetics description is accomplished by the evaluation of all the material parameters under different deformation conditions as illustrated in Figure 5. The calculated values are shown on the plot. It is remarkable that the value for the apparent activation energy for the initiation of DRX, $Q_{\mathrm{DRX}}$, presents a value of 411.7 kJ∙mol⁻¹ slightly lower than its analogous value for hot deformation.

The recrystallized fraction $X_v$ can be evaluated subsequently by the determination of the Avrami exponent $n_{\mathrm{Av}}$, which is performed using a global least-squares optimisation procedure, yielding a final value of 2. This optimisation procedure is performed by the minimisation of the following sum of squares:

$$\psi ={\displaystyle {\sum }_{i=1}^N{\left({\sigma }_{\exp }-{\sigma }_{\mathrm{cal}}\right)}^2}.$$

(20)

In the previous expression ${\sigma }_{\exp }$ stands for the experimental stress value, ${\sigma }_{\mathrm{cal}}$ is the calculated stress value under similar deformation conditions, and N is the total number of data values considered in the characterization of the P91 steel, which in this study reached approximately 32,000.

The predicted flow-stress values are shown in combination with its corresponding experimental values in Figure 2, showing the capability of the constitutive model to describe the material behaviour under different deformation conditions.

The accuracy of the proposed model has also been evaluated. To this aim, the calculated flow-stress values are directly compared with their corresponding experimental ones in Figure 6.

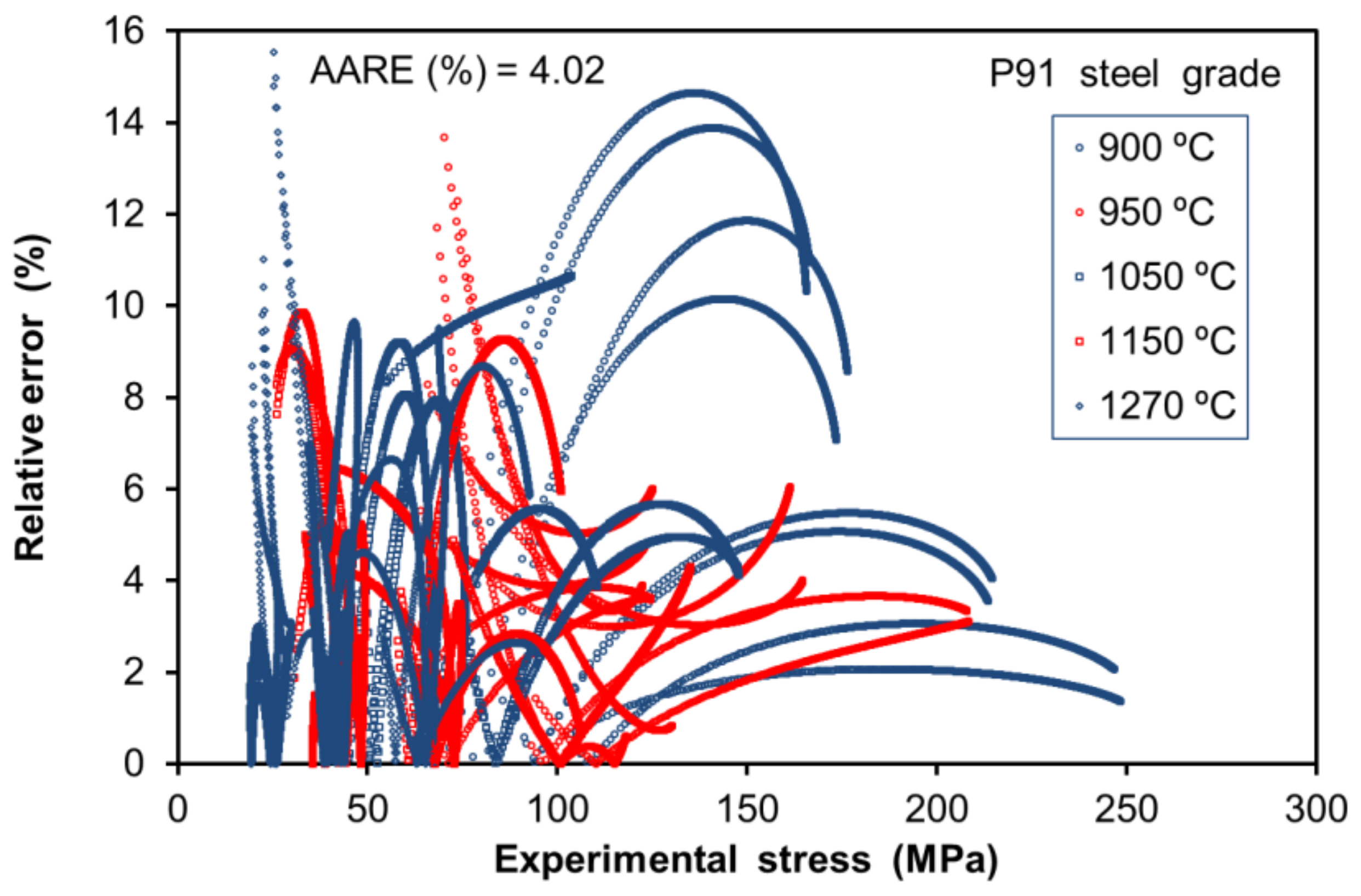
There is a good correlation between the predicted and experimental values (${\mathrm{r}}^2$ = 0.988), which, considering the high number of data points and wide range of temperatures and strain rates, illustrates the capability of the proposed constitutive model. The error of the proposed model is illustrated in Figure 7, showing the change in relative error, defined by:

$$\mathrm{RE}(\%)={\displaystyle {\sum }_{i=1}^N\frac{\left|{\sigma }_{\exp }^i-{\sigma }_{\mathrm{cal}}^i\right|}{{\sigma }_{\exp }^i}}.$$

(21)

The maximum relative error (RE) value is lower than 16% and up to 94% of the predicted stress values show a RE value lower than 10%, which indicates the reliability of the proposed constitutive formulation. In addition, the average absolute relative error (AARE) is shown in Figure 7, which is calculated as:

$$\mathrm{AARE}(\%)=\frac{1}{N}{\displaystyle {\sum }_{i=1}^N\frac{\left|{\sigma }_{\exp }^i-{\sigma }_{\mathrm{cal}}^i\right|}{{\sigma }_{\exp }^i}}\cdot 100,$$

(22)

presenting a value of approximately 4%. As a result, it can be concluded that the model certainly reproduces the flow-stress values of P91 steel under a wide range of deformation conditions.

The results of the numerical implementation of the presented formulation in the FE software FORGE^® are evaluated in the next section. Similarly, its potential under transient deformation conditions compared to other well-known constitutive formulations is assessed in the following section.

5. Numerical Application of the Constitutive Model

After the characterization of the P91 grade steel flow behaviour under the basis of an incremental physically-based formulation, this section is intended to demonstrate the possibilities of implementing and applying this model for the simulation of metal-forming processes. For this purpose, the FE model of the axisymmetric compression test is developed and, subsequently, the implementation and application of the proposed constitutive formulation presented in Section 2 is evaluated.

The characterization of the P91 grade steel has only been conducted under constant deformation conditions. However, in this section both constant and transient experimental tests are used for proving the advantages of the physically-based formulation.

5.1. Finite Element (FE) Numerical Model

The numerical model is illustrated in Figure 8. The dimensions of the sample are equivalent to those of the real test presented in Section 3. The mesh is generated with P1+ type tetrahedrons of 0.5 mm, which are isoparametric elements with an extra node placed in the centroid.

The top and bottom compression platens are assumed as rigid surfaces. In order to reproduce correctly the deformation conditions, the motion of the top platen is set from the recorded positions of the stroke during the compression tests. Such a condition ensures that the material is being deformed at a similar strain rate.

Regarding the boundary conditions at the tool–material interface, the constant shear friction model [32] is considered. The value of the friction factor is obtained from a set of experiments in which numerical and experimental sample geometries are compared. It is concluded that a value of 0.3 reproduces correctly the geometry of the compressed specimen in terms of height and maximum diameter, showing the maximum deviation of 8% under the tested conditions. This value is in agreement with the literature [33]. With respect to the thermal modelling, the process is assumed to be adiabatic and isothermal.

5.2. Simulation Results under Constant Deformation Conditions

The numerical testing of the proposed physically-based incremental constitutive model is conducted for the first time by its implementation in a commercial FE solver and the subsequent simulation of the axisymmetric compression tests. The parameter chosen for the comparison of the simulations and experimental tests is the measured axial force as a function of time.

Furthermore, to show the numerical advantages of the incremental physically-based formulation, it is compared to a different constitutive model. The Hansel–Spittel law [34] is chosen for this purpose, as it is the default constitutive formulation available in FORGE^® and its validity for simulating hot-forming processes has been proved, including axisymmetric compression tests [35]. The flow stress is described by:

$$\sigma \left(\overline{\epsilon },\dot{\overline{\epsilon }},T\right)=C \exp \left(m_{1}T\right){\overline{\epsilon }}^{m_2}{\dot{\overline{\epsilon }}}^{m_3}\exp \left(\frac{m_4}{\overline{\epsilon }}\right),$$

(23)

where $C$, $m_1$, $m_2$, $m_3$ and $m_4$ are material parameters that have to be determined. They have been obtained from the stress–strain experimental curves presented in Section 4 by the minimisation of the residual sum of squares, and their values are listed in

Table 3. Hansel–Spittel law parameter values.

$C$	$m_1$	$m_2$	$m_3$	$m_4$
12,582.63	−0.0042	0.1163	0.1116	−0.0007

. The resulting formulation presents an AARE of 16.2% and an acceptable correlation with the experimental values (${\mathrm{r}}^2$ = 0.953).

Figure 9 illustrates the results of the numerically-computed forces as compared to the experimental measured ones under constant deformation conditions. In order to enhance the graphical representation, the experimental curves show fewer points that the experimentally evaluated, being approximately 15% of the total.

The results confirm the good accuracy expected for the incremental constitutive formulation. This shows a good prediction of the force exerted during the compression tests as compared to that of the experiment with an AARE of 8%, under a wide range of constant deformation conditions. In contrast, the Hansel–Spittel law presents an AARE of 22.3% under similar conditions. This confirms that the physically-based incremental model results are clearly more precise, especially when the material experiences work softening due to DRX.

5.3. Simulation Results under Transient Loading

The industrial manufacturing of different components by hot-metalworking operations, is mostly conducted under transient deformation conditions and, therefore, the prediction of the flow stress, work-hardening and work-softening rate must be carried out based on valid state parameters. If the numerical formulations aim at reproducing the flow-stress behaviour under such transient loading conditions, the total plastic strain applied cannot be used as a state parameter.

While the Hansel–Spittel law depends directly on the total plastic strain applied, the physically-based incremental formulation depends on the strain path followed by the material. Figure 10 shows the stress–strain curves differences between both formulations under deformation conditions at a temperature of 1150 °C and a strain rate that starts at 0.01 s⁻¹ and is progressively increased up to 0.1 s⁻¹.

As expected, the Hansel–Spittel results are only consistent when initially the strain rate is constant. When the strain rate increases progressively, a small step can be appreciated in the stress prediction, which is evidence that the results are no longer consistent. However, the physically-based incremental model can cope with fluctuations in the deformation conditions if they are not extremely sharp [21].

Four experimental tests were performed under transient deformation conditions and their force–time curves were compared to the results of the simulation by employing both the physically-based and Hansel–Spittel constitutive models. The graphical representation is similar to the curves under constant conditions. Figure 11 illustrates how, as expected, the accuracy of the predicted results of the physical-based formulation are less affected by the transient loading conditions.

6. Discussion

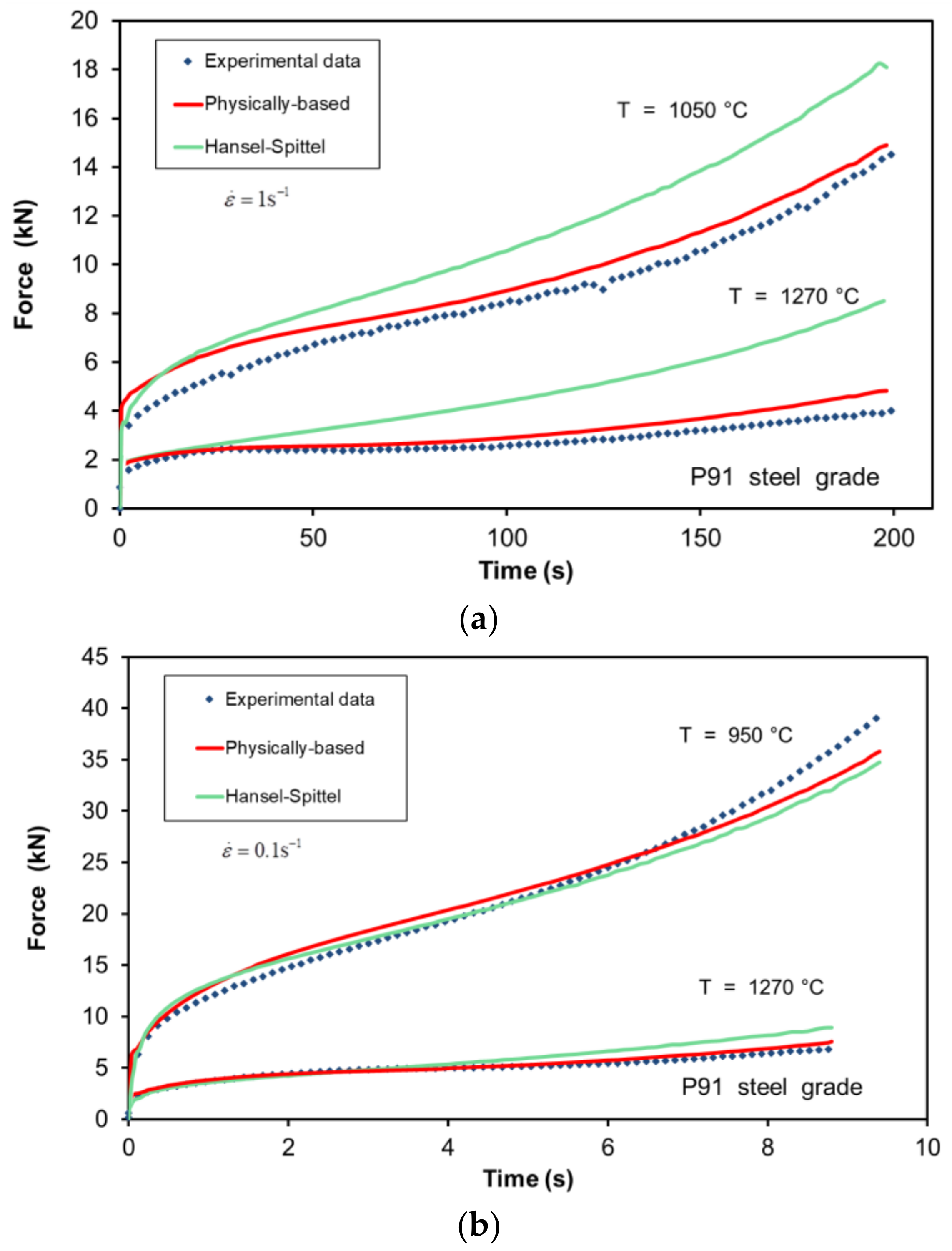
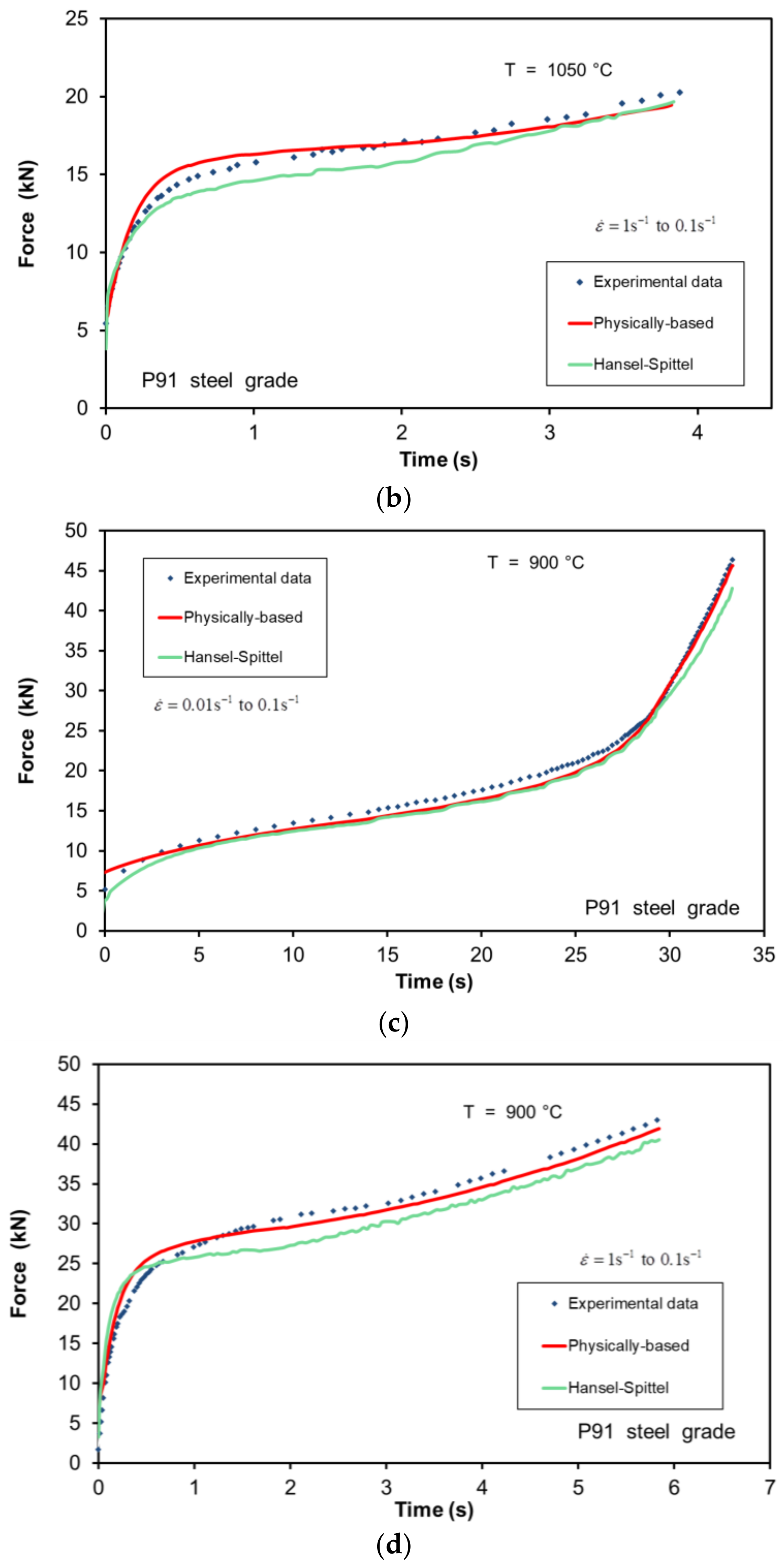
The flow-stress behaviour of the P91 steel has been characterized from a set of axisymmetric compression tests, on the basis of both a phenomenological model and a physically-based incremental model under constant deformation conditions. In addition, the applicability of the physically-based formulation has been demonstrated in FE software. Figure 9 shows the comparison between both formulations in terms of force versus time under a wide range of temperatures and strain rates. In this section, the accuracy of both formulations is discussed on the basis of their differences.

The Zener–Hollomon parameter defines the deformation conditions under which a given dynamic restoration process prevails. On the one hand, in those simulations in which the Z value is greater than 1.1 × 10¹⁵ s⁻¹, like in Figure 9a, the sample is subjected to an initial WH stage followed by DRV until the material reaches a saturation stress. This restoration mechanism prevails for temperatures lower than 950 °C and for higher temperatures if the strain rate is sufficiently high. As under these conditions there is no material softening due to DRX, both formulations can reproduce correctly the experimental force recorded during the compression tests. However, under deformation conditions in which both formulations are thought to be valid, the physically-based formulation continues to be more accurate than the Hansel–Spittel law.

On the other hand, when the Z value is less than 1.1 × 10¹⁵ s⁻¹, the prevailing restoration mechanism, besides DRV, is DRX and, therefore, the material softens. Due to its formulation, the Hansel–Spittel law is not capable of reproducing the work softening of the material. Therefore, the physically-based model gives better results under these deformation conditions. In Figure 9d, due to the high temperature (up to 1270 °C), both curves show work softening and thus the force predicted by the Hansel Spittel law shows a higher deviation with respect to the experimental one. 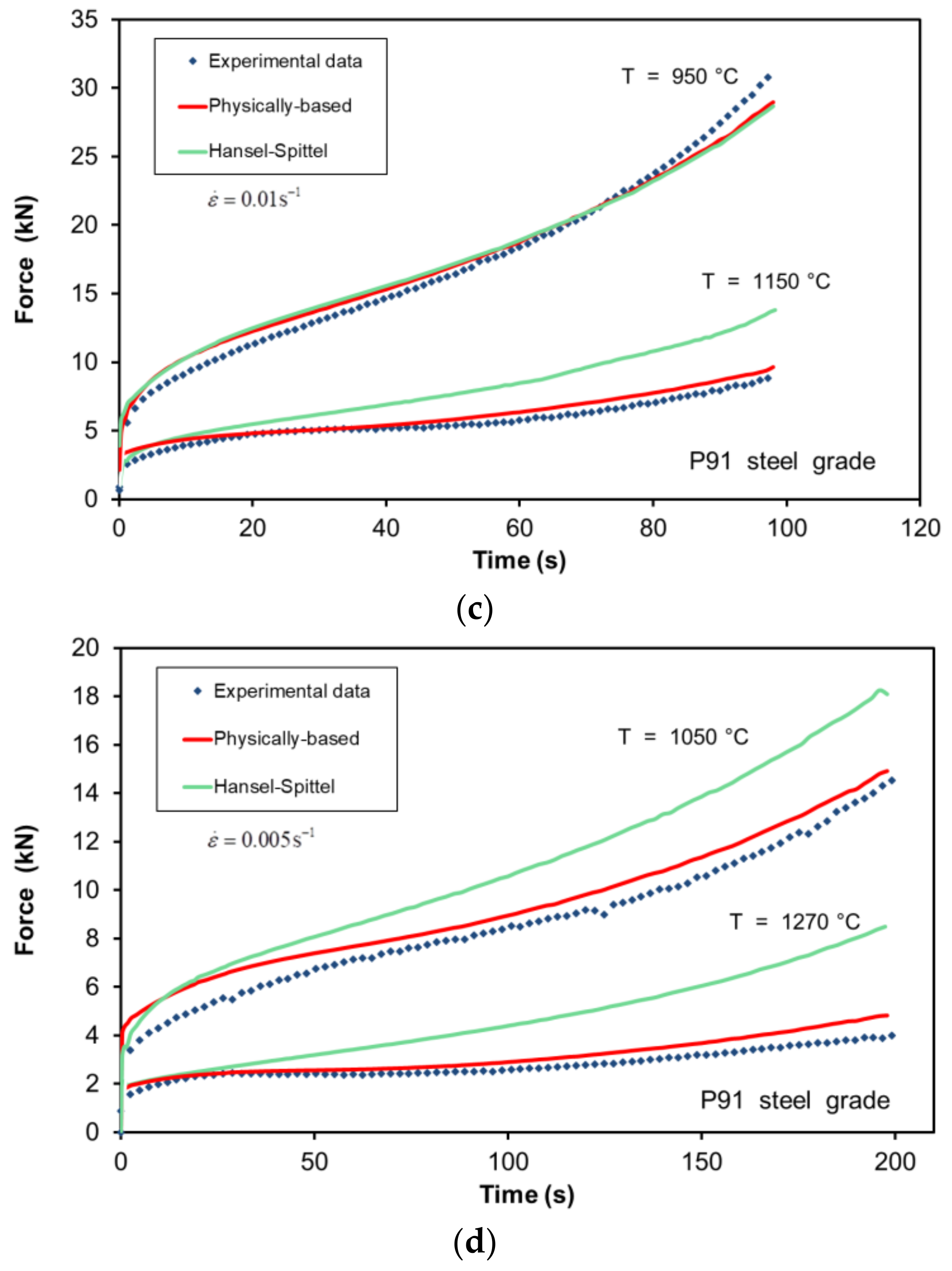Figure 9b,c illustrate two test sets in which DRV and DRX are present in each of them at a strain rate of 0.1 s⁻¹ and 0.01 s⁻¹, respectively. In both figures the experimental curve at a lower temperature represents the case in which DRV is the prevailing restoration mechanism and, as stated, the constitutive models present fewer appreciable differences. However, higher deviations are present in the curves corresponding to higher temperatures, as DRX is the main restoration mechanism and, as previously stated, the Hansel–Spittel law cannot reproduce it.

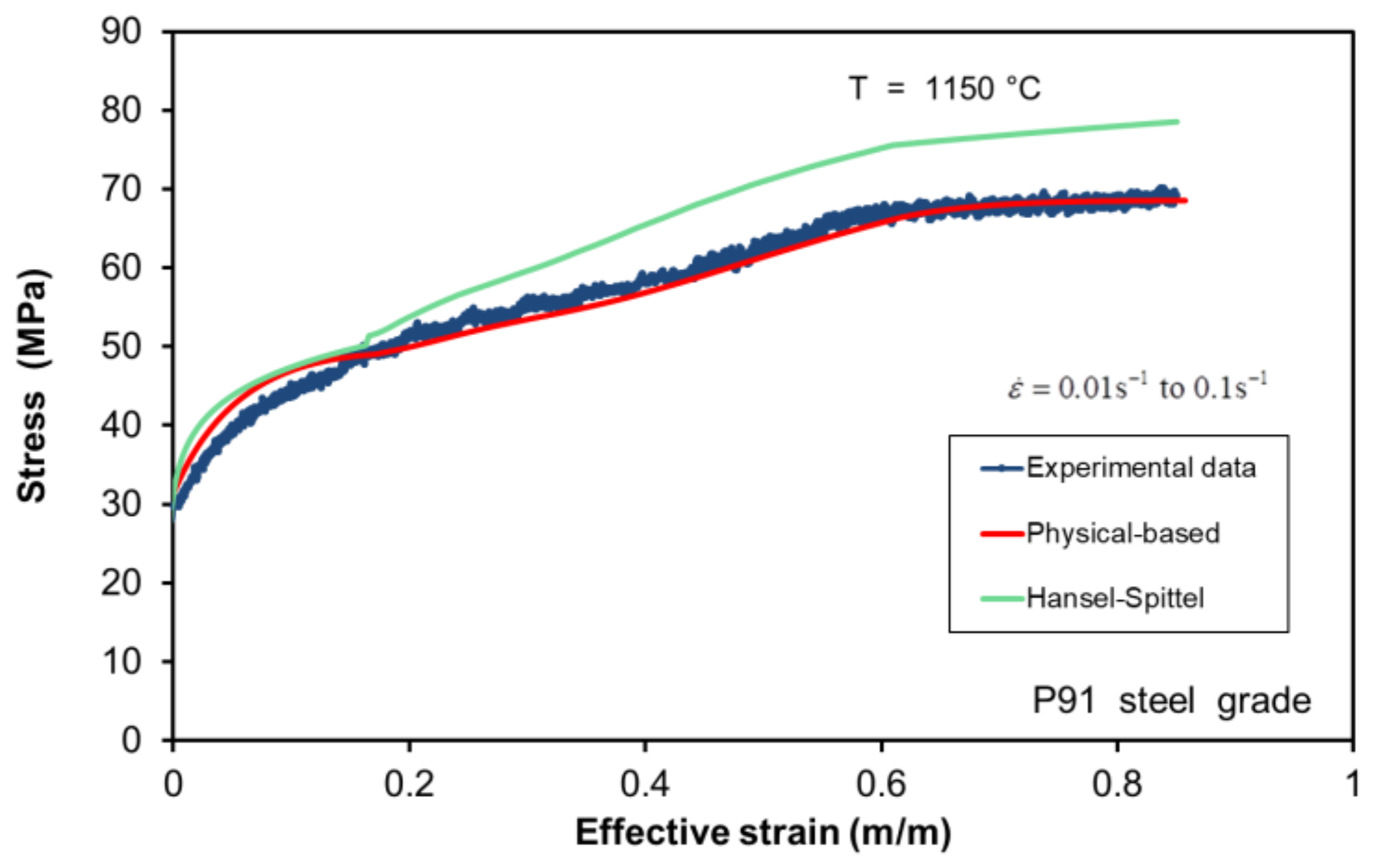
Another important aspect to be discussed is the feasibility of reproducing transient loading conditions with the considered constitutive models. Figure 10 shows an experimental stress–strain curve at a constant temperature of 1150 °C and variable strain rate. The strain rate starts at 0.01 s⁻¹, keeping it constant up to an effective strain of 0.17, then it is progressively increased together with the strain up to 0.1 s⁻¹. This test shows that the Hansel–Spittel model cannot deal with transient deformation conditions and that it only shows an acceptable result when the strain rate is constant. During the transient stage, the flow stress shows a small step when the strain rate starts to increase and an abrupt variation when the strain rate reaches 0.1 s⁻¹. However, the physically-based incremental model can cope with transient loading conditions, showing a smoother curve, which follows quite well the experimental flow-stress curve. This is confirmed by the experimental force–time curves presented in Figure 11, in which the physically-based model shows better overall results. It is remarkable in Figure 11a, as it reproduces precisely the force at the end of the test when work softening is present.

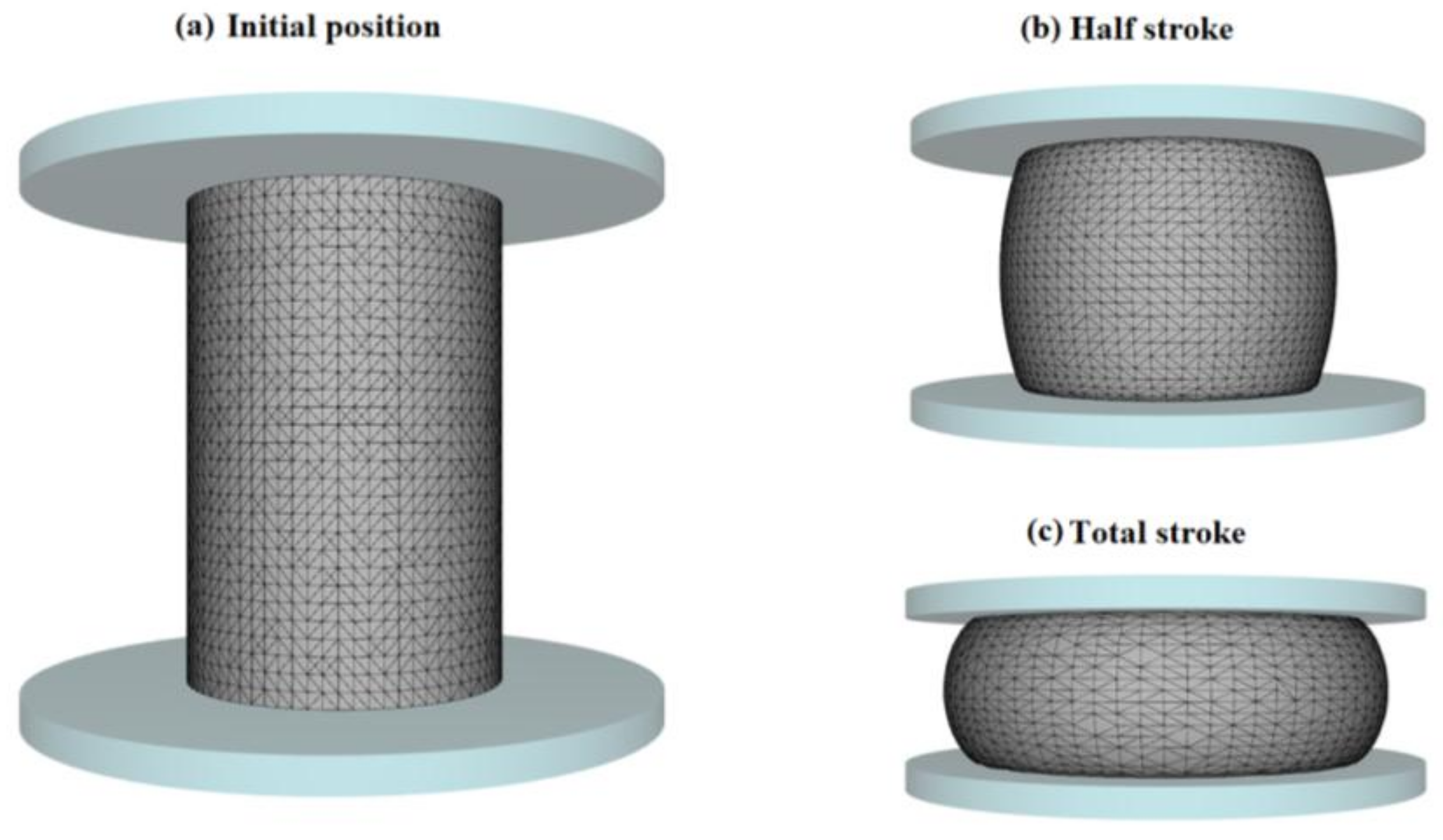
It is also important to point out that for the first time the incremental physically-based model has been implemented in FE software. The axisymmetric compression test simulation results (Figure 9 and Figure 11) indicate the accuracy of the implemented model under both constant and transient deformation conditions. Therefore, for the simulation of metal-forming processes conducted under transient deformation conditions, the use of the proposed formulation is highly recommended. Similarly, if the deformation conditions are prone to favour the work softening of the material, the importance of using a constitutive model that accounts for such phenomenon has been proved.

Finally, regarding the computation time, the physically-based model presents an average increase of approximately 35% in the axisymmetric compression test simulations as compared to the Hansel–Spittel law.

7. Conclusions

The flow behaviour of the P91 steel grade has been analysed under deformation conditions in the temperature range of 900–1270 °C and at strain rates in the range of 0.005–10 s⁻¹. A physically-based model advanced by Jonas et al. and recently described as an incremental formulation by Puchi-Cabrera et al. has been used. This model allows the description of the flow stress, initial work hardening and, unlike other constitutive formulations, reproduces correctly the work-softening rates of the material under constant or transient loading conditions.

The physically-based formulation computes the current values of deformation temperature and strain rate during each strain interval during plastic deformation. In this way, the flow stress of this steel grade is totally independent of the total plastic strain applied to the material, which is not a valid state parameter.

In order to evaluate the appropriateness of this constitutive description, it has been implemented in a commercial FE numerical code and compared to the results provided by the Hansel–Spittel law. Hence, a compression test numerical analysis has been assessed for both formulations under constant and transient deformation conditions. The parameter chosen for the comparison of the simulations and experimental tests is the evolution of the measured axial force as a function of time. The results clearly show that the physically-based incremental formulation can reproduce the experimental forces with a decrease in the AARE error from 22.3% (Hansel–Spittel law) to 8%. It is explained by the higher accuracy of the physically-based formulation when the material softens during the deformation.

Regarding the tests conducted under transient loading conditions, the physically-based formulation reproduces smoothly the stress–strain curves, whereas the Hansel–Spittel formulation experiences abrupt changes and cannot cope with these deformation conditions. It was also verified with the numerical simulation of the compression tests under transient loading, in which the physically-based formulation shows a smaller error compared to the measured experimental forces.

Finally, it is important to point out that the computation time experiences an average increase of 35% as compared to the Hansel–Spittel law.