Numerical and Experimental Investigation of the Influence of Growth Restriction on Grain Size in Binary Cu Alloys
Abstract
:1. Introduction
2. Materials and Methods
2.1. Melt Treatment Procedure
2.2. Model Description
2.2.1. Grain Initiation
2.2.2. Grain Growth
2.2.3. Calculation of Solidified Grain Size
3. Results and Discussion
3.1. Grain Size Modelling
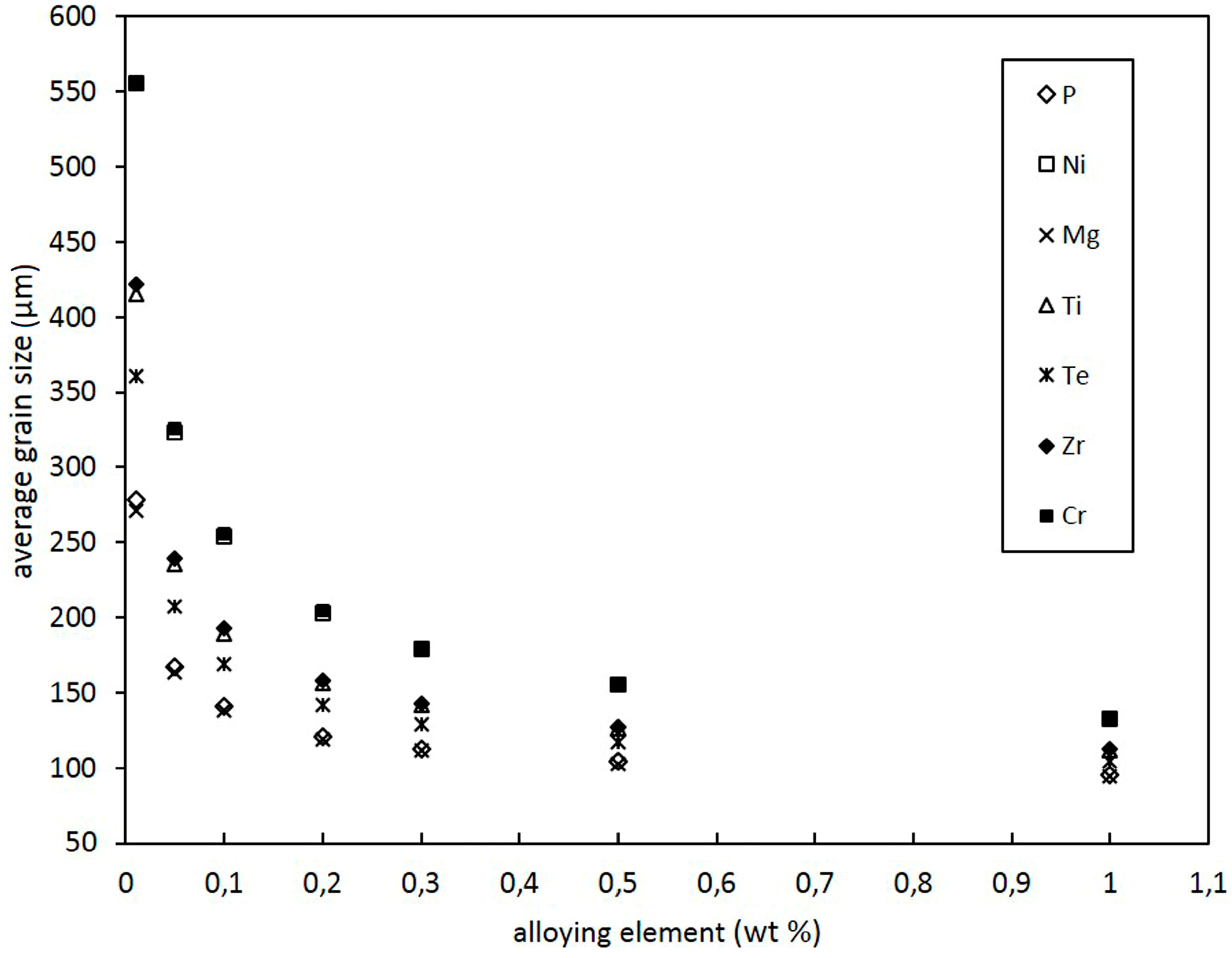
3.2. Effect of Alloying Elements and Concentration on Grain Size of Binary Cu Alloys
3.3. Transition in Grain Size in Cu Alloys
4. Conclusions
- A grain size model based on Greer’s free-growth model [3] was used in this work to predict grain size for Cu alloys depending on the growth restriction factor Q.
- Nine alloying elements with various Q-factors were investigated to determine the variation in grain size with increasing solute content under defined cooling conditions of the TP-1 grain refiner test.
- Despite a low growth restriction potency, Ni, Bi, and Te were found to decrease grain size continuously with increasing alloy concentration. The results obtained by the melting experiments are in good agreement with the results of the grain size model.
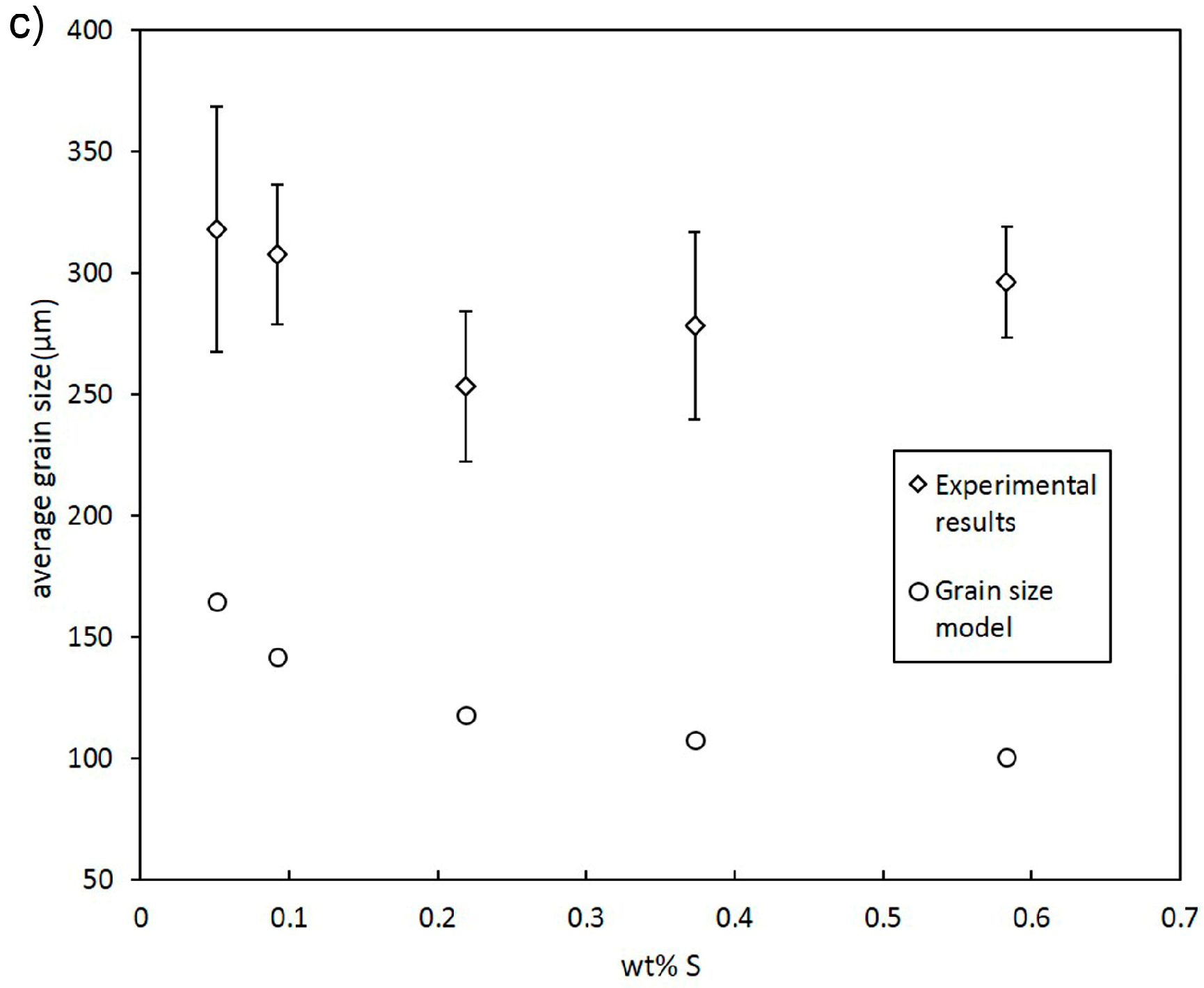
- In addition to Ni, Bi, and Te, S was found to decrease grain size efficiently.
- Contradictory results were found for Mg, P, Ti, Zr, and Cr, as grain size decreases at low alloy concentrations. However, excessive grain coarsening can be observed with increasing solute content.
- It is assumed that variations in grain size, as found for Mg, P, Ti, Zr, and Cr, result from a change in the nucleating particle density of the melt that may occur due to reactions of the added alloying elements with particles in the initial melt. Significant decreases in grain size, as found for Ti and Zr, are supposed to be due to the in situ formation of potent nucleation sites, potentially with residual O. Excessive grain coarsening with increasing solute content may occur due to the removal of nucleating particles. The model shows that the difference in the actual number of particles before and beyond the transition point must be in the range of several orders of magnitude.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Easton, M.; StJohn, D. Grain refinement of aluminum alloys: Part I. The nucleant and solute paradigms—A review of the literature. Metall. Mater. Trans. A 1999, 30, 1613–1623. [Google Scholar] [CrossRef]
- Quested, T.E.; Dinsdale, A.; Greer, A.L. Thermodynamic modelling of growth-restriction effects in aluminium alloys. Acta Mater. 2005, 53, 1323–1334. [Google Scholar] [CrossRef]
- Greer, A.L.; Bunn, A.M.; Tronche, A.; Evans, P.V.; Bristow, D.J. Modelling of inoculation of metallic melts: Application to grain refinement of aluminium by Al-Ti-B. Acta Mater. 2000, 48, 2823–2835. [Google Scholar] [CrossRef]
- Murty, B.S.; Kori, S.A.; Chakraborty, M. Grain refinement of aluminium and its alloys by heterogeneous nucleation and alloying. Int. Mater. Rev. 2002, 47, 3–29. [Google Scholar] [CrossRef]
- Quested, T.E. Understanding mechanisms of grain refinement of aluminium alloys by inoculation. Mater. Sci. Technol. 2004, 20, 1357–1369. [Google Scholar] [CrossRef]
- StJohn, D.H.; Qian, M.; Easton, M.A.; Cao, P.; Hildebrand, Z. Grain refinement of magnesium alloys. Metall. Mater. Trans. A 2005, 36, 1669–1679. [Google Scholar] [CrossRef]
- Campbell, J. Casting alloys. In Complete Casting Handbook, 1st ed.; Elsevier: Oxford, UK, 2011; pp. 255–390. [Google Scholar]
- Cibula, A. Grain-refining additions for cast copper alloys. J. Inst. Met. 1954, 82, 513–524. [Google Scholar]
- Dennison, J.P.; Tull, E.V. The refinement of cast grain-size in copper-aluminium alloys containing 7–9 per cent Aluminium. J. Inst. Met. 1957, 85, 8–10. [Google Scholar]
- Henke, R. Kornfeinung von NE-Metallgußlegierungen. Gießerei-Praxis 1965, 1, 14–20. (In German) [Google Scholar]
- Couture, A.; Edwards, J.O. Kornfeinung von Kupfer-Sandgußlegierungen und ihr Einfluß auf die Güteeigenschaften. Gießerei-Praxis 1974, 21, 425–435. (In German) [Google Scholar]
- Romankiewicz, F.; Ellerbrok, R.; Engler, S. Einfluß einer Kornfeinung mit Zirconium auf Erstarrungsmorphologie, Speisungsvermögen und Festigkeitseigenschaften von Messing CuZn30 und Siliciummessing CuZn15Si4. Gießereiforschung 1974, 39, 25–33. (In German) [Google Scholar]
- Mannheim, R.; Reif, W.; Weber, G. Untersuchung der Kornfeinung von Kupfer-Zinn-Legierungen mit Zirconium und/oder Bor und Eisen sowie ihres Einflusses auf die mechanischen Eigenschaften. Gießereiforschung 1988, 40, 1–16. (In German) [Google Scholar]
- Reif, W.; Weber, G. A New grain refiner for copper-zinc alloys containing 25–42% Zinc. Metall 1987, 41, 1131–1137. [Google Scholar]
- Romankiewicz, F.; Glazowska, I.; Rybakowski, M. Kornfeinung von Kupferlegierungen. Metall 1994, 48, 865–871. (In German) [Google Scholar]
- Sadayappan, M.; Thomson, J.P.; Elboujdaini, M.; Gu, G.P.; Sahoo, M. Grain Refinement of Permanent Mold Cast Copper Base Alloys. Final Report. Available online: https://www.osti.gov/scitech/biblio/823242/ (accessed on 8 July 2017).
- Bustos, O.C. Untersuchung zur Kornfeinung von Reinst-Kupfer durch Chemische Zusätze und Deutung der Vorgänge. Ph.D. Thesis, TU Berlin, Berlin, Germany, 1990. (In German). [Google Scholar]
- The Aluminium Association. Standard Test Procedure for Aluminium Alloy Grain Refiners: TP-1; The Aluminium Association: Washington, DC, USA, 2012. [Google Scholar]
- Balart, M.J.; Patel, J.B.; Fan, Z. Grain refinement of DHP copper by particle inoculation. Int. J. Cast Met. Res. 2015, 28, 242–247. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Z.; Ding, D.; Tang, H.; Qiu, L.; Luo, X.; Shi, G. Strengthening and toughening strategies for tin bronze alloy through fabricating in-situ nanostructured grains. Mater. Des. 2015, 66, 60–66. [Google Scholar] [CrossRef]
- Chen, K.; Chen, X.; Ding, D.; Shi, G.; Wang, Z. Heterogeneous nucleation effect of in situ iron-rich nanoparticles on grain refinement of copper alloy. Mater. Lett. 2016, 168, 188–191. [Google Scholar] [CrossRef]
- Chen, K.; Chen, X.; Ding, D.; Shi, G.; Wang, Z. Formation mechanism of in-situ nanostructured grain in cast Cu-10Sn-2Zn-1.5Fe-0.5Co (wt %) alloy. Mater. Des. 2016, 94, 338–344. [Google Scholar] [CrossRef]
- Greer, A.L. Overview: Application of heterogeneous nucleation in grain-refining of metals. J. Chem. Phys. 2016, 145, 211704. [Google Scholar] [CrossRef] [PubMed]
- Greer, A.L.; Cooper, P.S.; Meredith, M.W.; Schneider, W.; Schumacher, P.; Spittle, J.A.; Tronche, A. Grain Refinement of Aluminium Alloys by Inoculation. Adv. Eng. Mater. 2003, 5, 81–91. [Google Scholar] [CrossRef]
- Easton, M.A.; StJohn, D.H. A model of grain refinement incorporating alloy constitution and potency of heterogeneous nucleant particles. Acta Mater. 2001, 49, 1867–1878. [Google Scholar] [CrossRef]
- Moriceau, J. Discussion of the mechanisms of aluminum grain refining by titanium and boron. Rev. L’aluminium 1972, 413, 977–988. [Google Scholar]
- Shu, D.; Sun, B.; Mi, J.; Grant, P.S. A quantitative study of solute diffusion field effects on heterogeneous nucleation and the grain size of alloys. Acta Mater. 2011, 59, 2135–2144. [Google Scholar] [CrossRef]
- Northcott, L. The influence of alloying elements on the crystallization of copper: Part I. Small additions and the effect of atomic structure. J. Inst. Met. 1938, 62, 101–136. [Google Scholar]
- Tiller, W.A.; Jackson, K.A.; Rutter, J.W.; Chalmers, B. The redistribution of solute atoms during the solidification of metals. Acta Metall. 1953, 1, 428–437. [Google Scholar] [CrossRef]
- Cziegler, A.K.; Schumacher, P. Preliminary Investigation of the Grain Refinement Mechanism in Cu Alloys. In Shape Casting, Proceeding of the 6th International Symposium (TMS 2016), Nashville, TN, USA, 14–18 February 2016; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016; pp. 159–166. [Google Scholar]
- Balart, M.J.; Patel, J.B.; Gao, F.; Fan, Z. Grain refinement of deoxidized copper. Metall. Mater. Trans. A 2016, 47, 4988–5011. [Google Scholar] [CrossRef]
- Cziegler, A.K.; Schumacher, P. Investigation of the correlation between growth restriction and grain size in Cu alloys. Int. J. Cast Met. Res. 2017, 30, 251–255. [Google Scholar] [CrossRef]
- Stefanescu, D.M. Thermal analysis—Theory and applications in metalcasting. Int. J. Metalcast. 2015, 9, 7–22. [Google Scholar] [CrossRef]
- Spittle, J.A.; Sadli, S. Effect of alloy variables on grain refinement of binary aluminium alloys with Al–Ti–B. Mater. Sci. Technol. 1995, 11, 533–537. [Google Scholar] [CrossRef]
- Günther, R.; Hartig, C.; Bormann, R. Grain refinement of AZ31 by (SiC)P: Theoretical calculation and experiment. Acta Mater. 2006, 54, 5591–5597. [Google Scholar] [CrossRef]
- Kurz, W.; Fisher, D.J. Fundamentals of Solidification, 4th ed.; Trans. Tech. Publications: Uetikon-Zürich, Switzerland, 1998. [Google Scholar]
- Maxwell, I.; Hellawell, A. A simple model for grain refinement during solidification. Acta Metall. 1975, 23, 229–237. [Google Scholar] [CrossRef]
- Quested, T.E.; Greer, A.L. The effect of the size distribution of inoculant particles on as-cast grain size in aluminium alloys. Acta Mater. 2004, 52, 3859–3868. [Google Scholar] [CrossRef]
- Men, H.; Fan, Z. Effects of solute content on grain refinement in an isothermal melt. Acta Mater. 2011, 59, 2704–2712. [Google Scholar] [CrossRef]
- Ejima, T.; Kameda, M. Diffusion of iron and cobalt in liquid copper. J. Jpn. Inst. Met. 1969, 33, 96–103. [Google Scholar] [CrossRef]
- Stefanescu, D.M. Science and Engineering of Casting Solidification; Springer: Boston, MA, USA, 2002. [Google Scholar]
- Lee, Y.C.; Dahle, A.K.; StJohn, D.H. The role of solute in grain refinement of magnesium. Metall. Mater. Trans. A 2000, 31, 2895–2906. [Google Scholar] [CrossRef]
- Klösch, G. Kornfeinen von Aluminiumhältigen Magnesiumlegierungen. Ph.D. Thesis, Montanuniversitaet Leoben, Leoben, Austria, 2006. (In German). [Google Scholar]
- Cziegler, A.K. Aspects of Grain Refinement in Copper Alloys. Master’s Thesis, Montanuniversitaet Leoben, Leoben, Austria, 2015. [Google Scholar]








| Element (wt %) | |||||||
|---|---|---|---|---|---|---|---|
| Sn | Pb | Zn | Ni | P | S | Bi | Cr |
| <0.0005 | <0.0005 | 0.0332 | <0.001 | <0.001 | <0.001 | <0.002 | <0.0005 |
| Mg | Te | Ti | Zr | Si | Fe | Al | Cu |
| <0.0001 | <0.001 | <0.0004 | <0.0003 | <0.001 | <0.0005 | <0.0003 | balance |
| Alloy System (Alloy No.) | Solute Concentration (wt %) | Q (K) | Alloy System (Alloy No.) | Solute Concentration (wt %) | Q (K) |
|---|---|---|---|---|---|
| Cu-Mg (1) | 0.002 | 0.06 | Cu-Ti (6) | 0.708 | 6.16 |
| Cu-Mg (2) | 0.007 | 0.19 | Cu-Ti (7) | 1.627 | 14.15 |
| Cu-Mg (3) | 0.023 | 0.67 | Cu-Zr (1) | 0.001 | 0.01 |
| Cu-Mg (4) | 0.066 | 1.93 | Cu-Zr (2) | 0.012 | 0.10 |
| Cu-Mg (5) | 0.185 | 5.43 | Cu-Zr (3) | 0.023 | 0.19 |
| Cu-Mg (6) | 0.346 | 10.08 | Cu-Zr (4) | 0.091 | 0.76 |
| Cu-S (1) | 0.051 | 1.44 | Cu-Zr (5) | 0.182 | 1.52 |
| Cu-S (2) | 0.092 | 2.60 | Cu-Zr (6) | 0.398 | 3.33 |
| Cu-S (3) | 0.219 | 6.20 | Cu-Zr (7) | 0.814 | 6.82 |
| Cu-S (4) | 0.373 | 10.55 | Cu-Ni (1) | 0.011 | 0.04 |
| Cu-S (5) | 0.583 | 16.49 | Cu-Ni (2) | 0.06 | 0.21 |
| Cu-P (1) | 0.012 | 0.32 | Cu-Ni (3) | 0.12 | 0.42 |
| Cu-P (2) | 0.043 | 1.16 | Cu-Ni (4) | 0.241 | 0.85 |
| Cu-P (3) | 0.087 | 2.35 | Cu-Ni (5) | 0.381 | 1.34 |
| Cu-P (4) | 0.189 | 5.11 | Cu-Ni (6) | 0.564 | 1.94 |
| Cu-P (5) | 0.298 | 8.05 | Cu-Ni (7) | 0.949 | 3.35 |
| Cu-P (6) | 0.501 | 13.54 | Cu-Bi (1) | 0.009 | 0.02 |
| Cu-P (7) | 0.958 | 25.89 | Cu-Bi (2) | 0.036 | 0.13 |
| Cu-Te (1) | 0.001 | 0.01 | Cu-Bi (3) | 0.098 | 0.35 |
| Cu-Te (2) | 0.013 | 0.17 | Cu-Bi (4) | 0.176 | 0.62 |
| Cu-Te (3) | 0.062 | 0.81 | Cu-Bi (5) | 0.248 | 0.88 |
| Cu-Te (4) | 0.175 | 2.29 | Cu-Bi (6) | 0.449 | 1.58 |
| Cu-Te (5) | 0.299 | 3.91 | Cu-Bi (7) | 0.897 | 3.17 |
| Cu-Te (6) | 0.564 | 7.38 | Cu-Cr (1) | 0.001 | 0.003 |
| Cu-Te (7) | 1.225 | 16.02 | Cu-Cr (2) | 0.013 | 0.04 |
| Cu-Ti (1) | 0.001 | 0.01 | Cu-Cr (3) | 0.049 | 0.17 |
| Cu-Ti (2) | 0.014 | 0.12 | Cu-Cr (4) | 0.113 | 0.39 |
| Cu-Ti (3) | 0.058 | 0.51 | Cu-Cr (5) | 0.226 | 0.78 |
| Cu-Ti (4) | 0.197 | 1.72 | Cu-Cr (6) | 0.389 | 1.34 |
| Cu-Ti (5) | 0.375 | 3.26 | Cu-Cr (7) | 0.786 | 2.71 |
| Parameter | Symbol | Value | Ref. |
|---|---|---|---|
| Solid/liquid interfacial energy | γ | 0.177 J·m−2 | [41] |
| Entropy of fusion | ΔSv | 1.2 × 106 J·m−3·K−1 | [36] |
| Enthalpy of fusion | ΔHv | 1.62 × 109 J·m−3 | [36] |
| Heat capacity of melt | cpv | 3.96 × 106 J·m−3·K | [36] |
| Diffusivity of solute in melt | DFe | 3.88 × 10−9 m2·s−1 | [40] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cziegler, A.; Geraseva, O.; Schumacher, P. Numerical and Experimental Investigation of the Influence of Growth Restriction on Grain Size in Binary Cu Alloys. Metals 2017, 7, 383. https://doi.org/10.3390/met7090383
Cziegler A, Geraseva O, Schumacher P. Numerical and Experimental Investigation of the Influence of Growth Restriction on Grain Size in Binary Cu Alloys. Metals. 2017; 7(9):383. https://doi.org/10.3390/met7090383
Chicago/Turabian StyleCziegler, Andreas, Olga Geraseva, and Peter Schumacher. 2017. "Numerical and Experimental Investigation of the Influence of Growth Restriction on Grain Size in Binary Cu Alloys" Metals 7, no. 9: 383. https://doi.org/10.3390/met7090383





