Optimization by Using Taguchi Method of the Production of Magnesium-Matrix Carbide Reinforced Composites by Powder Metallurgy Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Preparation of Materials and Experimental Plan
- ρb = Relative density (%);
- ρ = Experimentally measured density (gr/cm3);
- ρk = Theoretical density calculated based on powder mixture ratios (gr/cm3).
- P = Bending strength (MPa);
- F = The force applied to the sample at the moment of the fracture (N);
- L = Distance between support points (mm);
- b = Sample width (mm);
- h = Sample height (mm).
2.2. Taguchi Method
- The bigger, the better;
- The smaller, the better;
- Nominal values are better.
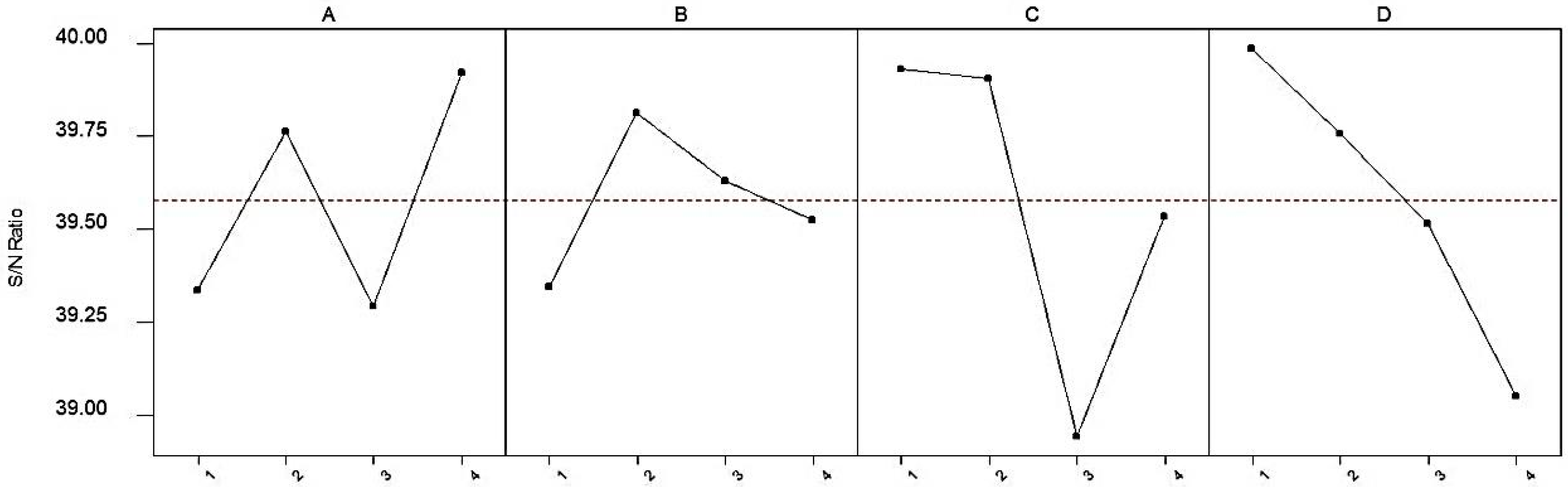
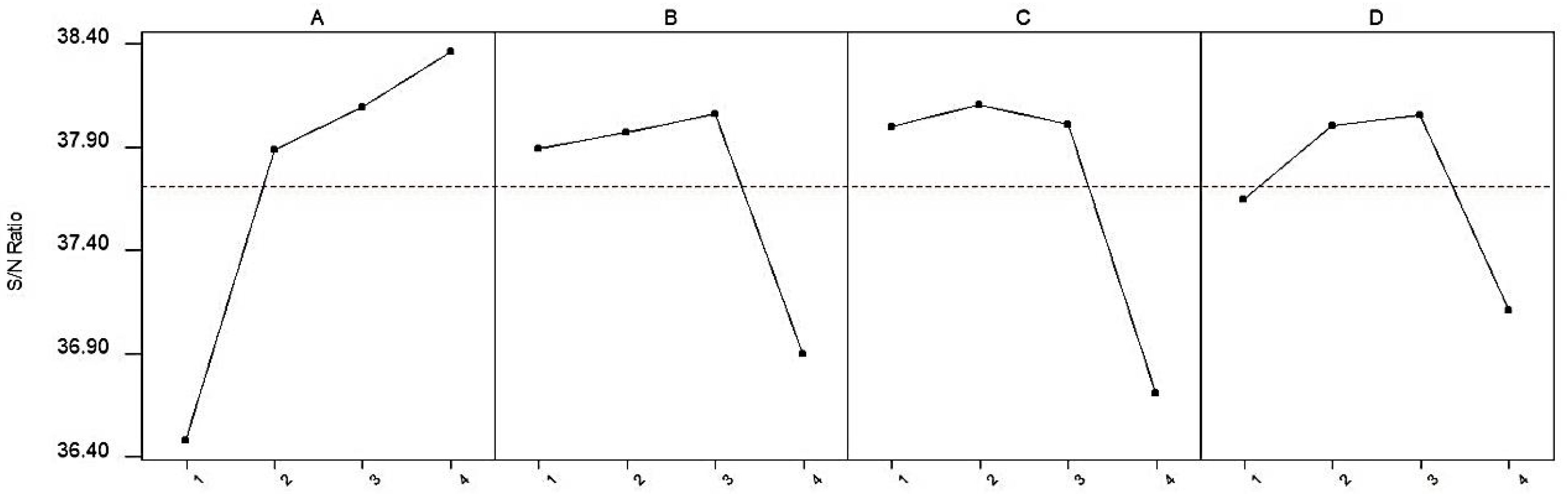
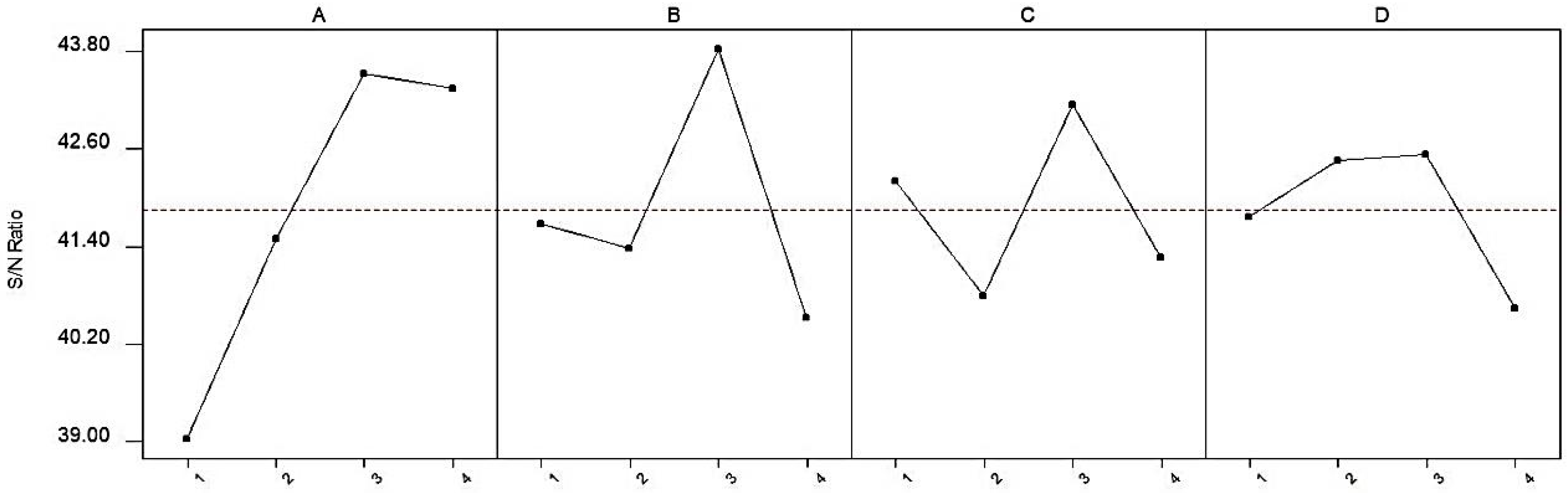
3. Results and Discussion
3.1. Statistical Analysis
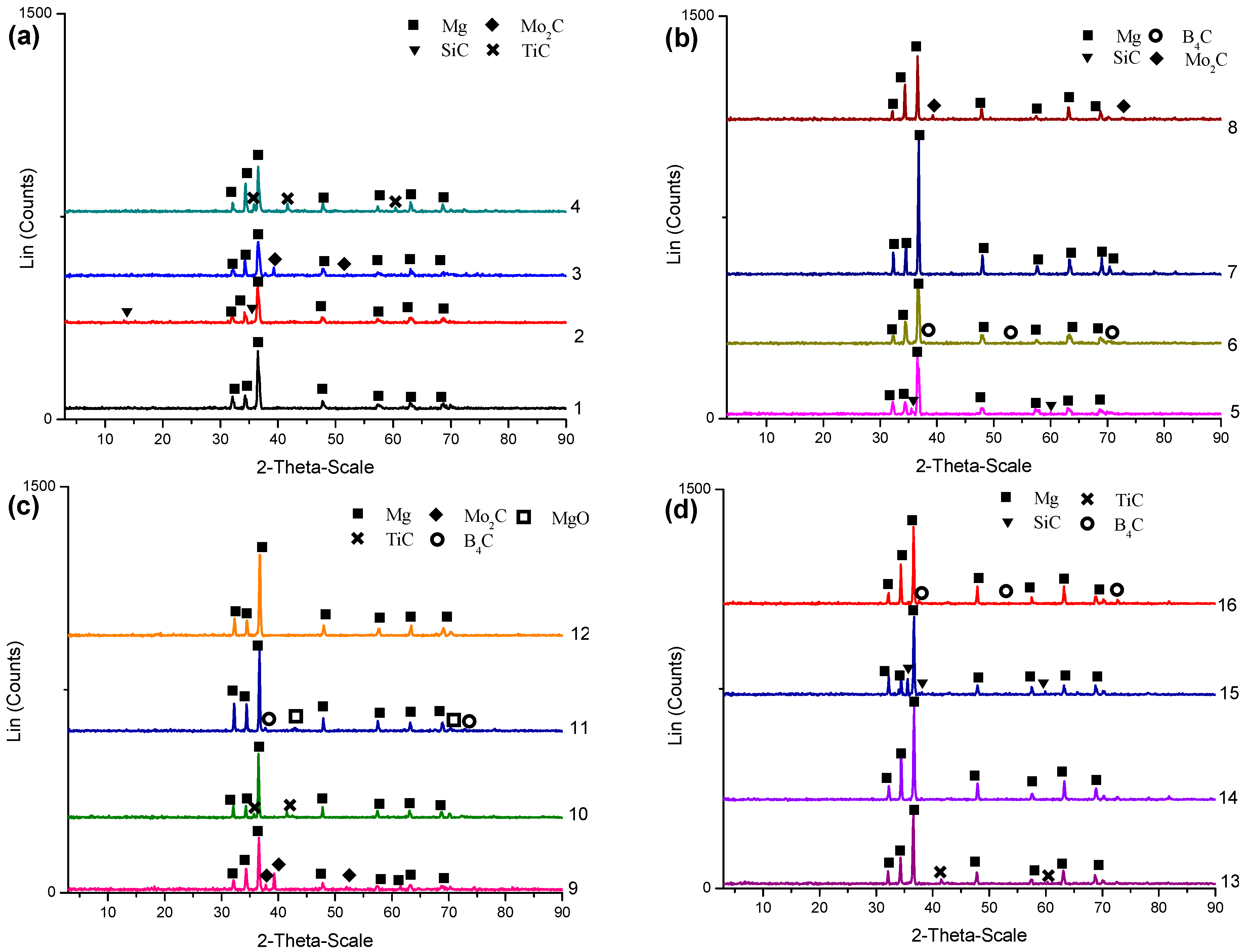
3.2. SEM-EDS and XRD Studies
4. Conclusions
- While the all parameters have an effect on relative density (%) and bending strength, the most effective parameters on hardness HB10 are the sintering time and additive type.
- Optimum conditions determined by considering all experiments were sintering temperature of 500 °C, sintering time of 5 min, additive type of B4C, and additive ratio of 2.5%. The results obtained under these conditions were 98.74 (%) for relative density, 87.16 HB10 for hardness, and 193.65 MPa for bending strength.
- Since the optimum conditions determined by the Taguchi method in the laboratory environment can also be produced in real production environments, the results of this study can be very useful for industrial scale machining.
- In the Taguchi method, only selected combinations are tested. These combinations are determined by considering studies in the literature. The parameters that affect the study are known. Experiments are carried out by determining the levels of parameters. However, experiments can be analyzed by using methods such as artificial neural networks, where all the values considered can be tested [29,30].
- SEM studies showed that distribution of the carbides in the MgAl matrix were homogeneous. In addition, the addition of carbide caused the formation of pores.
- According to XRD analysis, Mg, MgO, B4C, TiC, Mo2C, and SiC phases were observed in the composites. The reason for not seeing Al in the graphs is that it was dissolved in Mg and formed a solid solution.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ye, H.Z.; Liu, X.Y. Review of recent studies in magnesium matrix composites. J. Mater. Sci. 2004, 39, 6153–6173. [Google Scholar] [CrossRef]
- Chang, S.Y.; Sung, J.C.; Hong, S.K.; Dong, H.S. Microstructure and tensile properties of bimaterials with macro-interface between unreinforced magnesium and composite. J. Alloys Compd. 2001, 316, 275–279. [Google Scholar] [CrossRef]
- Jayalakshmi, S.; Kailas, S.V.; Seshan, S. Tensile behaviour of squeeze cast AM100 magnesium alloy and its Al2O3 fibre reinforced composites. Compos. Part A Appl. Sci. Manuf. 2002, 33, 1135–1140. [Google Scholar] [CrossRef]
- Hassan, S.F.; Gupta, M. Development of a novel magnesium/nickel composite with improved mechanical properties. J. Alloys Compd. 2002, 335, L10–L15. [Google Scholar] [CrossRef]
- Zheng, M.Y.; Wu, K.; Yao, C.K. Effect of interfacial reaction on mechanical behavior of SiCw/AZ91 magnesium matrix composites. Mater. Sci. Eng. A 2001, 318, 50–56. [Google Scholar] [CrossRef]
- Jiang, Q.C.; Wang, H.Y.; Ma, B.X.; Wang, Y.; Zhao, F. Fabrication of B4C particulate reinforced magnesium matrix composite by powder metallurgy. J. Alloys Compd. 2005, 386, 177–181. [Google Scholar] [CrossRef]
- Islak, S.; Çelik, E.; Kir, D.; Özorak, C. Characterization of hot pressed CuAl-TiC composites with different TiC grain sizes. Russ. J. Non-Ferrous Met. 2016, 57, 374–380. [Google Scholar] [CrossRef]
- Buytoz, S.; Dagdelen, F.; Islak, S.; Kok, M.; Kir, D.; Ercan, E. Effect of the TiC content on microstructure and thermal properties of Cu-TiC composites prepared by powder metallurgy. J. Therm. Anal. Calorim. 2014, 117, 1277–1283. [Google Scholar] [CrossRef]
- Casati, R.; Vedani, M. Metal matrix composites reinforced by nano-particles—A review. Metals 2014, 4, 65–83. [Google Scholar] [CrossRef]
- Chawla, N.; Chawla, K.K. Metal Matrix Composites, 1st ed.; Springer: New York, NY, USA, 2006; pp. 43–63. [Google Scholar]
- Clyne, T.W.; Withers, P.J. An Introduction to Metal Matrix Composites, 1st ed.; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Esmaily, M.; Mortazavi, N.; Svensson, J.E.; Halvarsson, M.; Wessén, M.; Johansson, L.G.; Jarfors, A.E. A new semi-solid casting technique for fabricating SiC-reinforced Mg alloys matrix composites. Compos. Part B Eng. 2016, 94, 176–189. [Google Scholar] [CrossRef]
- Sun, F.; Shi, C.; Rhee, K.Y.; Zhao, N. In situ synthesis of CNTs in Mg powder at low temperature for fabricating reinforced Mg composites. J. Alloys Compd. 2013, 551, 496–501. [Google Scholar] [CrossRef]
- Gui, M.; Li, P.; Han, J. Fabrication and characterization of cast magnesium matrix composites by vacuum stir casting process. J. Mater. Eng. Perform. 2003, 12, 128–134. [Google Scholar]
- Degischer, H.P.; Schulz, P.A.; Lacom, W. Properties of continuous fibre reinforced Al and Mg-matrix composites produced by gas pressure infiltration. Key Eng. Mater. 1996, 127, 99–110. [Google Scholar] [CrossRef]
- Tun, K.S.; Gupta, M. Improving mechanical properties of magnesium using nanoyttria reinforcement and microwave assisted powder metallurgy method. Compos. Sci. Technol. 2007, 67, 2657–2664. [Google Scholar] [CrossRef]
- Hu, H. Squeeze casting of magnesium alloys and their composites. J. Mater. Sci. 1998, 33, 1579–1589. [Google Scholar] [CrossRef]
- White, J.; Willis, T.C. The production of metal matrix composites by spray deposition. Mater. Des. 1989, 10, 121–127. [Google Scholar] [CrossRef]
- Loh, N.H.; Tor, S.B.; Khor, K.A. Production of metal matrix composite part by powder injection molding. J. Mater. Process. Technol. 2001, 108, 398–407. [Google Scholar] [CrossRef]
- Şirvancı, M. Kalite Için Deney Tasarımı, 2nd ed.; Literatür Yayınları: İstanbul, Türkiye, 2011; pp. 13–18. [Google Scholar]
- Roy, R.K. A Primer on the Taguchi Method, 1st ed.; Van Nostrand Reinhold Company: New York, NY, USA, 1990; p. 247. [Google Scholar]
- Phadke, M.S.; Kackar, R.N.; Speeney, D.D.; Grioce, M.J. Off-line quality control in integrated circuit fabrication using experimental design. Bell Syst. Tech. J. 1983, 62, 1273–1309. [Google Scholar] [CrossRef]
- Taguchi, G. System of Experimental Design; Quality Resources: New York, NY, USA, 1987; Volume 1. [Google Scholar]
- Çopur, M. An optimization study of dissolution of Zn and Cu in ZnS concentrate with HNO3 solutions. Chem. Biochem. Eng. Q. 2002, 15, 191. [Google Scholar]
- Küçük, Ö. Application of Taguchi method in the optimization of dissolution of ulexite in NH4Cl solutions. Korean J. Chem. Eng. 2006, 23, 21. [Google Scholar] [CrossRef]
- Phadke, M.S. Quality Engineering Using Robust Design; Prentice Hall: Upper Saddle River, NJ, USA, 1989; pp. 61–292. [Google Scholar]
- Islak, S.; Kir, D.; Buytoz, S. Effect of sintering temperature on electrical and microstructure properties of hot pressed Cu-TiC composites. Sci. Sinter. 2014, 46, 15–21. [Google Scholar] [CrossRef]
- Lee, D.W.; Ha, G.H.; Kim, B.K. Synthesis of Cu-Al2O3 nano composite powder. Scr. Mater. 2001, 44, 2137–2140. [Google Scholar] [CrossRef]
- Arnaiz-González, A.; Fernández-Valdivielso, A.; Bustillo, A.; Norberto López de Lacalle, N. Using artificial neural networks for the prediction of dimensional error on inclined surfaces manufactured by ball-end milling. Int. J. Adv. Manuf. Technol. 2016, 83, 847–859. [Google Scholar] [CrossRef]
- Ukar, E.; Lamikiz, A.; Martínez, S.; Tabernero, I.; López de Lacalle, L.N. Roughness prediction on laser polished surfaces. J. Mater. Process. Technol. 2012, 212, 1305–1313. [Google Scholar] [CrossRef]

| Parameters | Levels | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| A | Sintering Temperature (°C) | 400 | 450 | 500 | 550 |
| B | Sintering Time (min) | 1 | 3 | 5 | 7 |
| C | Additive Type | B4C | SiC | Mo2C | TiC |
| D | Addition Rate (% by weight) | 0 | 2.5 | 5 | 10 |
| No. | Parameters | Parameter Values | ||||||
|---|---|---|---|---|---|---|---|---|
| A | B | C | D | A | B | C | D | |
| 1 | 1 | 1 | 1 | 1 | 400 | 1 | B4C | 0 |
| 2 | 1 | 2 | 2 | 2 | 400 | 3 | SiC | 2.5 |
| 3 | 1 | 3 | 3 | 3 | 400 | 5 | Mo2C | 5 |
| 4 | 1 | 4 | 4 | 4 | 400 | 7 | TiC | 10 |
| 5 | 2 | 1 | 2 | 3 | 450 | 1 | SiC | 5 |
| 6 | 2 | 2 | 1 | 4 | 450 | 3 | B4C | 10 |
| 7 | 2 | 3 | 4 | 1 | 450 | 5 | TiC- | 0 |
| 8 | 2 | 4 | 3 | 2 | 450 | 7 | Mo2C | 2.5 |
| 9 | 3 | 1 | 3 | 4 | 500 | 1 | Mo2C | 10 |
| 10 | 3 | 2 | 4 | 3 | 500 | 3 | TiC | 5 |
| 11 | 3 | 3 | 1 | 2 | 500 | 5 | B4C | 2.5 |
| 12 | 3 | 4 | 2 | 1 | 500 | 7 | SiC | 0 |
| 13 | 4 | 1 | 4 | 2 | 550 | 1 | TiC | 2.5 |
| 14 | 4 | 2 | 3 | 1 | 550 | 3 | Mo2C | 0 |
| 15 | 4 | 3 | 2 | 4 | 550 | 5 | SiC | 10 |
| 16 | 4 | 4 | 1 | 3 | 550 | 7 | B4C | 5 |
| No. | Compound | Production Parameters | Relative Density (%) | Hardness (HB10) | Bending Strength (MPa) | |||
|---|---|---|---|---|---|---|---|---|
| MgAl | Additive Material % by Weight | Temperature (°C) | Time (min) | Pressure (MPa) | ||||
| 1 | 100 | Additive-free | 400 | 1 | 40 | 99.80 | 73.5 | 99.11 |
| 2 | 97.5 | 2.5% SiC | 400 | 3 | 98.68 | 76.5 | 83.56 | |
| 3 | 95 | 5% Mo2C | 400 | 5 | 86.14 | 77.2 | 142.61 | |
| 4 | 90 | 10% TiC | 400 | 7 | 86.82 | 45.5 | 54.16 | |
| 5 | 95 | 5% SiC | 450 | 1 | 98.39 | 78.5 | 96.74 | |
| 6 | 90 | 10% B4C | 450 | 3 | 98.14 | 80.5 | 103.17 | |
| 7 | 100 | Additive-free | 450 | 5 | 99.83 | 74.3 | 143.48 | |
| 8 | 97.5 | 2.5% Mo2C | 450 | 7 | 92.99 | 80.4 | 139.18 | |
| 9 | 90 | 10% Mo2C | 500 | 1 | 76.73 | 81.5 | 154.69 | |
| 10 | 95 | 5% TiC | 500 | 3 | 94.81 | 80.7 | 157.32 | |
| 11 | 97.5 | 2.5% B4C | 500 | 5 | 99.36 | 80.6 | 183.09 | |
| 12 | 100 | Additive-free | 500 | 7 | 99.88 | 78.5 | 114.28 | |
| 13 | 97.5 | 2.5% TiC | 550 | 1 | 98.16 | 80.5 | 146.28 | |
| 14 | 100 | Additive-free | 550 | 3 | 99.92 | 79.0 | 138.80 | |
| 15 | 90 | 10% SiC | 550 | 5 | 98.75 | 88.6 | 155.74 | |
| 16 | 95 | 5% B4C | 550 | 7 | 99.59 | 83.5 | 147.90 | |
| Parameters | Degree of Freedom | Sum of Squares | Mean Squares | F | Effectiveness | |
|---|---|---|---|---|---|---|
| A | Sintering Temperature (°C) | 3 | 249.68 | 83.23 | 41.27 | Effective |
| B | Sintering Time (min) | 3 | 91.25 | 30.42 | 15.08 | Effective |
| C | Additive Type | 3 | 551.28 | 183.76 | 91.12 | Effective |
| D | Additive Ratio (% by weight) | 3 | 414.88 | 138.29 | 68.57 | Effective |
| - | Error | 19 | 38.32 | 2.02 | - | - |
| - | Total | 31 | 1345.40 | - | - | - |
| Parameters | Degree of Freedom | Sum of Squares | Mean Squares | F | Effectiveness | |
|---|---|---|---|---|---|---|
| A | Sintering Temperature (°C) | 3 | 999.55 | 333.18 | 13.33 | Effective |
| B | Sintering Time (min) | 3 | 331.83 | 110.61 | 4.43 | Not Effective |
| C | Additive Type | 3 | 559.25 | 186.42 | 7.46 | Less Effective |
| D | Additive Ratio (% by weight) | 3 | 188.59 | 62.86 | 2.52 | Not Effective |
| - | Error | 19 | 474.80 | 24.99 | - | - |
| - | Total | 31 | 2554.04 | - | - | - |
| Parameters | Degree of Freedom | Sum of Squares | Mean Squares | F | Effectiveness | |
|---|---|---|---|---|---|---|
| A | Sintering Temperature (°C) | 3 | 16,885.9 | 5628.4 | 63.05 | Effective |
| B | Sintering Time (min) | 3 | 8492.2 | 2830.7 | 31.71 | Effective |
| C | Additive Type | 3 | 4170.2 | 1390.1 | 15.57 | Effective |
| D | Additive Ratio (% by weight) | 3 | 2428.4 | 809.5 | 9.07 | Less Effective |
| - | Error | 19 | 1696.0 | 89.3 | - | - |
| - | Total | 31 | 33,672.0 | - | - | - |
| Parameters | Case | ||
|---|---|---|---|
| Value | Level | ||
| A | Sintering Temperature (°C) | 500 | 3 |
| B | Sintering Time (min) | 5 | 3 |
| C | Additive Type | B4C | 1 |
| D | Addition Rate (% by weight) | 2.5 | 2 |
| Observed Values (Respectively, relative density, hardness, and the bending strength) | 98.74 (%), 87.16 HB10 and 193.65 MPa | ||
| Predicted Values (Respectively, relative density, hardness, and the bending strength) | 99.36 (%), 80.6 HB10 and 183.09 MPa | ||
| Confidence limits of prediction “Se” (Respectively, relative density, hardness, and the bending strength) | ±3.62, ±12.75 and ±24.09 | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Küçük, Ö.; Elfarah, T.T.K.; Islak, S.; Özorak, C. Optimization by Using Taguchi Method of the Production of Magnesium-Matrix Carbide Reinforced Composites by Powder Metallurgy Method. Metals 2017, 7, 352. https://doi.org/10.3390/met7090352
Küçük Ö, Elfarah TTK, Islak S, Özorak C. Optimization by Using Taguchi Method of the Production of Magnesium-Matrix Carbide Reinforced Composites by Powder Metallurgy Method. Metals. 2017; 7(9):352. https://doi.org/10.3390/met7090352
Chicago/Turabian StyleKüçük, Özkan, Tayeb Taher Kalefe Elfarah, Serkan Islak, and Cihan Özorak. 2017. "Optimization by Using Taguchi Method of the Production of Magnesium-Matrix Carbide Reinforced Composites by Powder Metallurgy Method" Metals 7, no. 9: 352. https://doi.org/10.3390/met7090352




