Emergence and Progression of Abnormal Grain Growth in Minimally Strained Nickel-200
Abstract
:1. Introduction
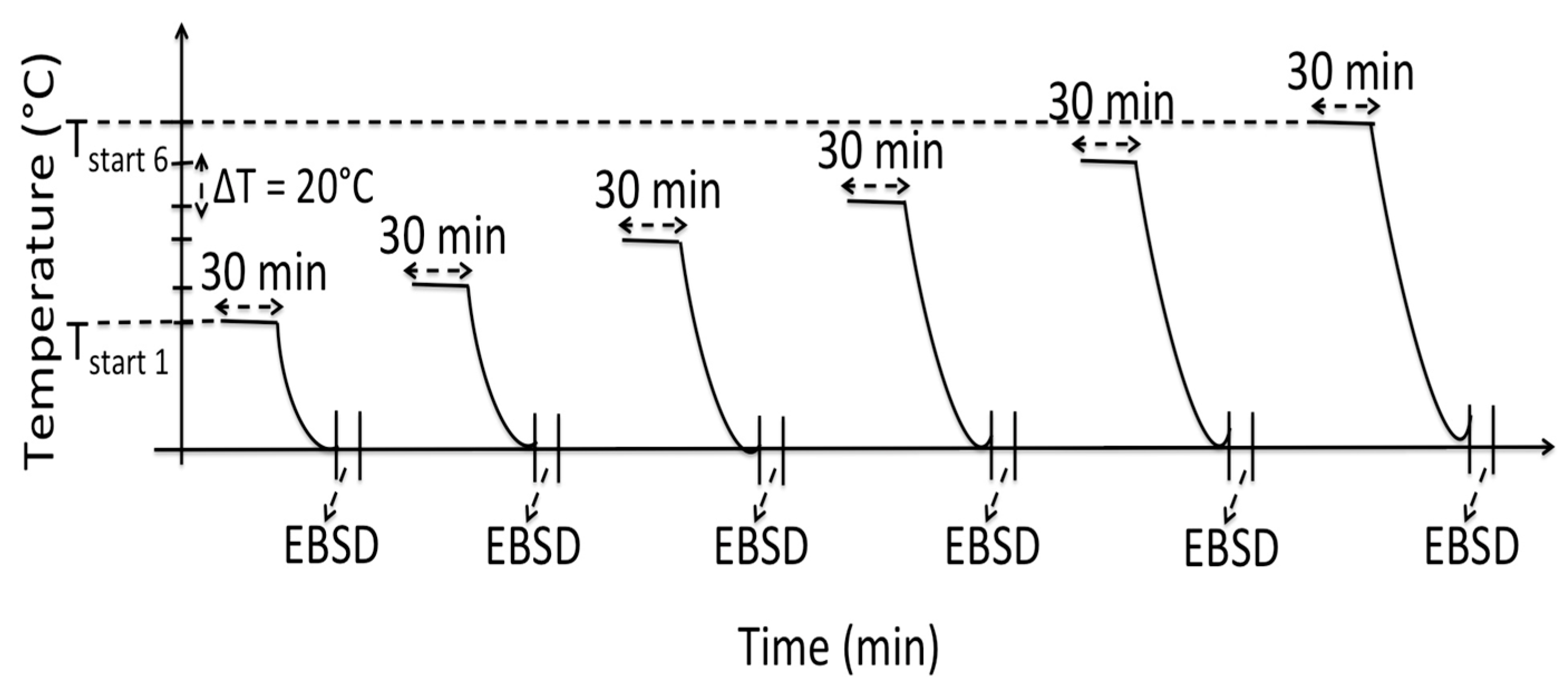
2. Materials and Methods
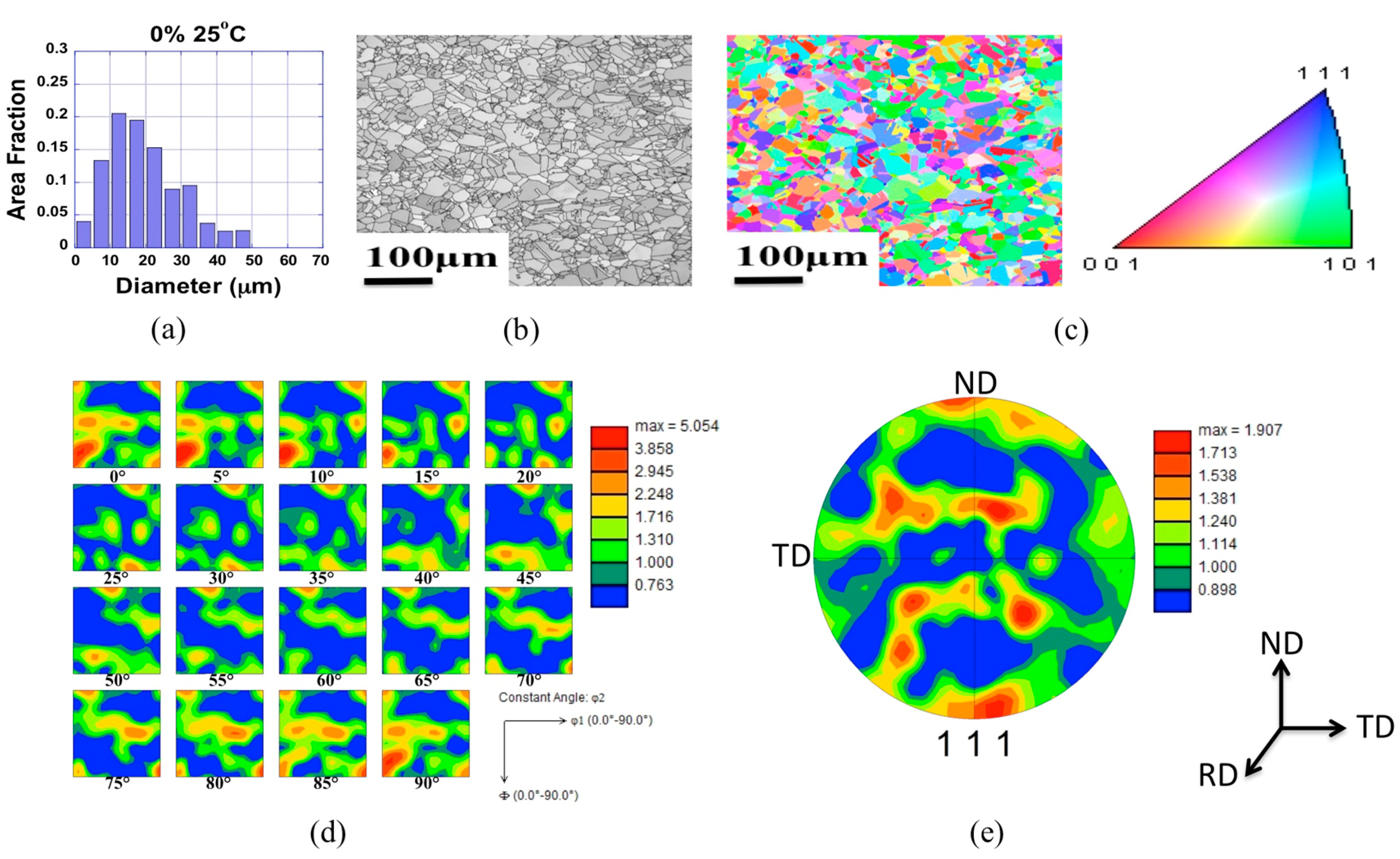
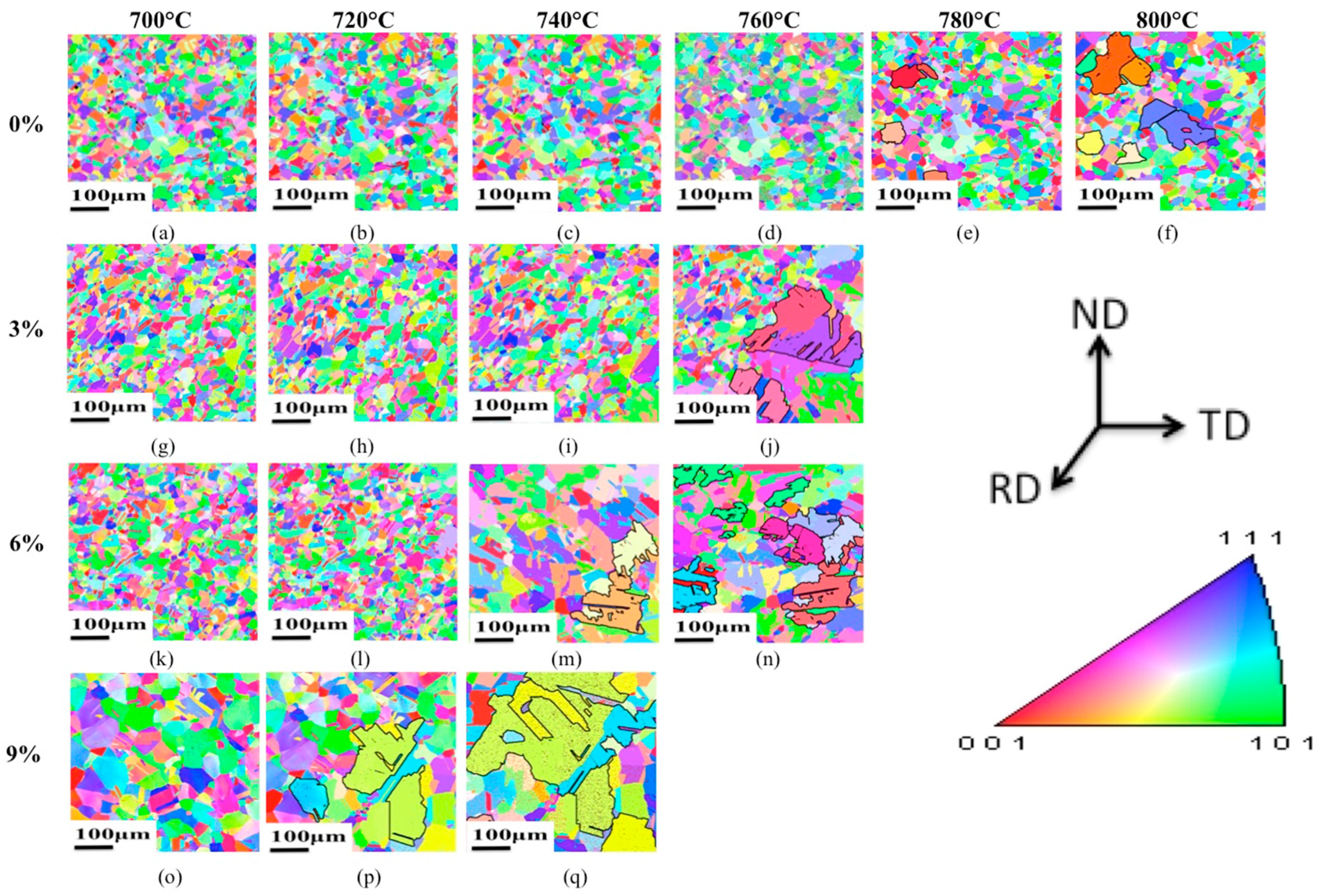
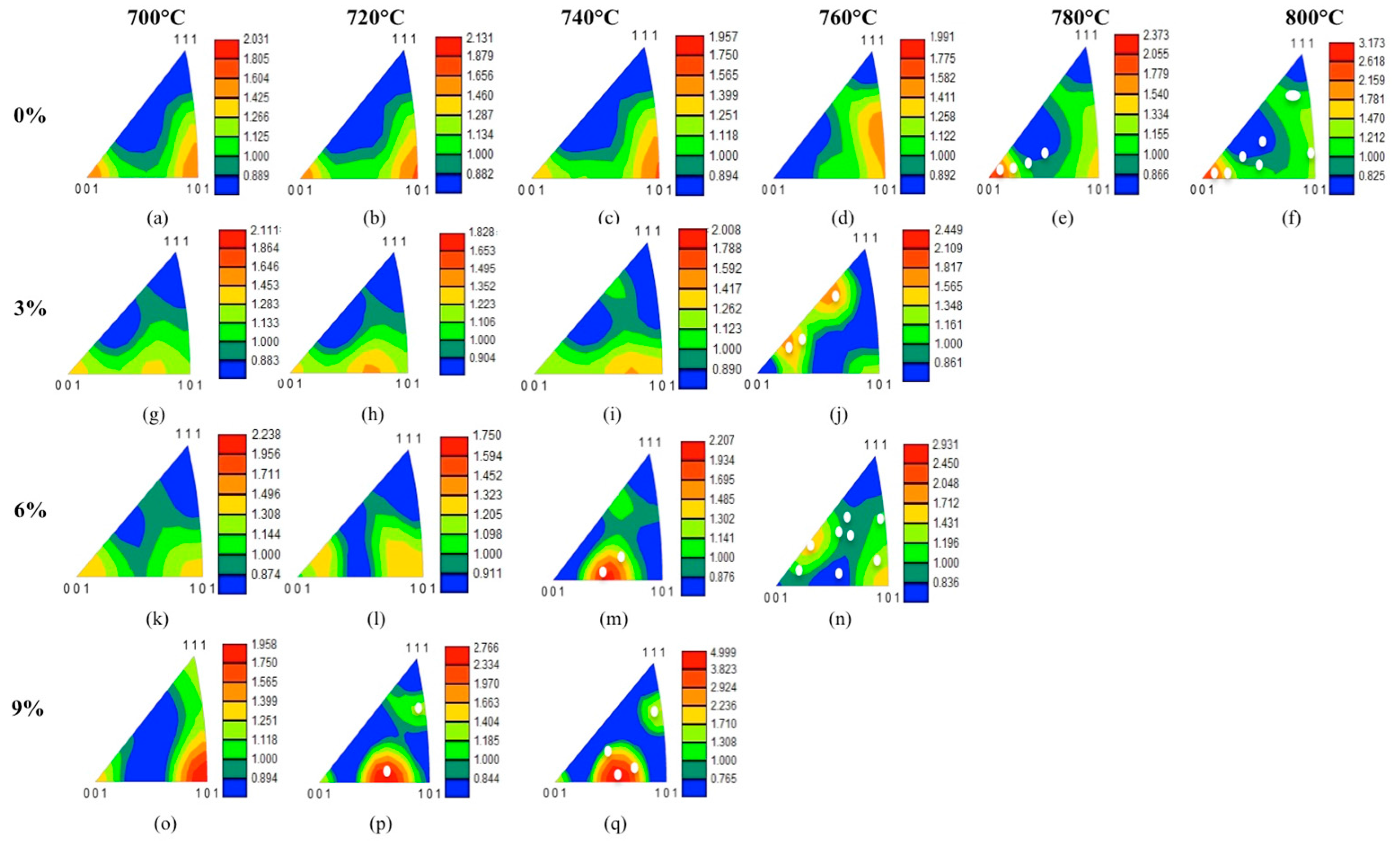
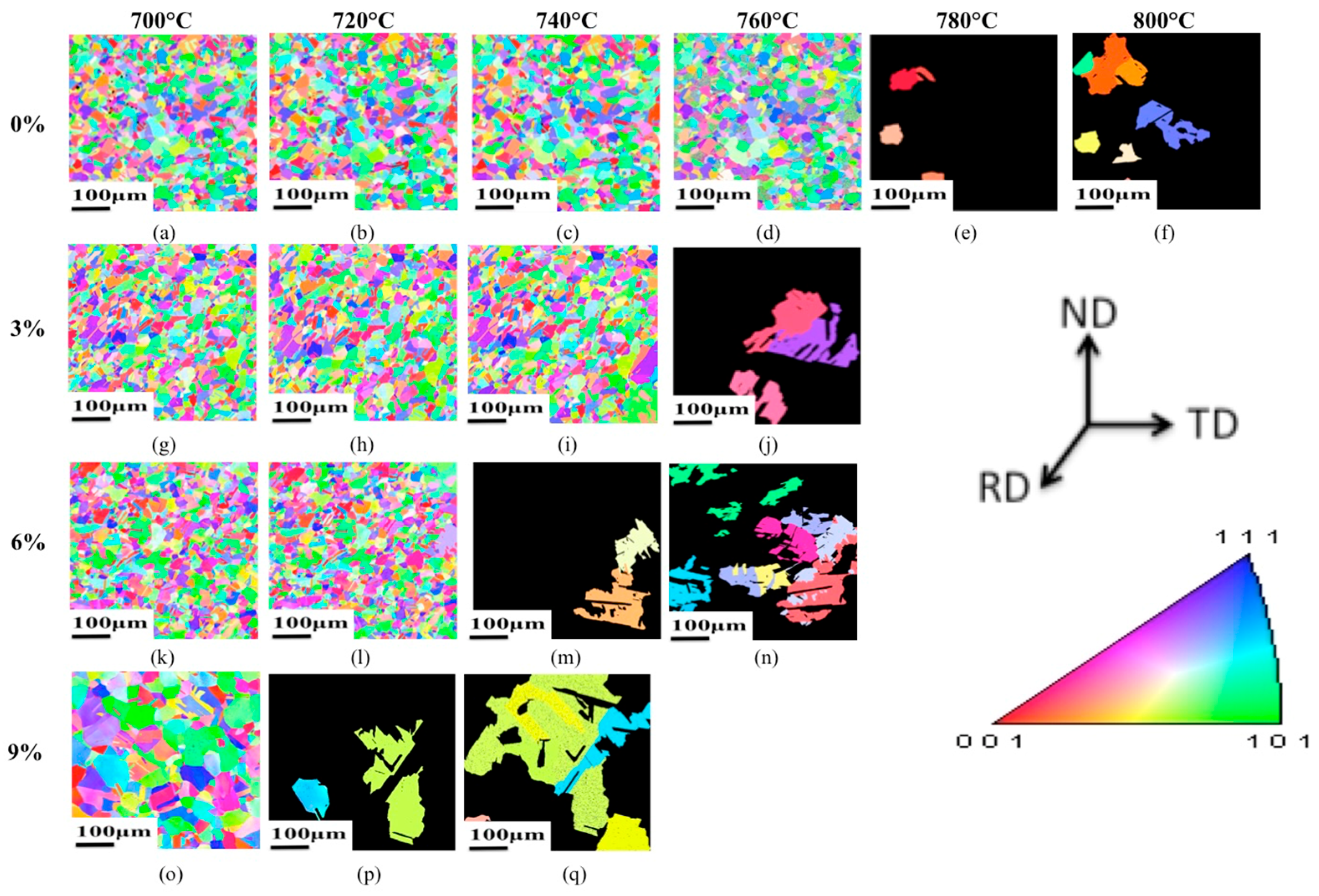
3. Results
4. Discussion
5. Conclusions
- (1)
- Emergence and progression rates for abnormally large grains in minimally strained, commercially pure Ni-200 were observed experimentally by EBSD and quantified using image segmentation based on crystallographic orientation and grain size distributions.
- (2)
- Emergence and progression growth rates were shown to scale directly with increased initial strain content and inversely with onset AGG temperature.
- (3)
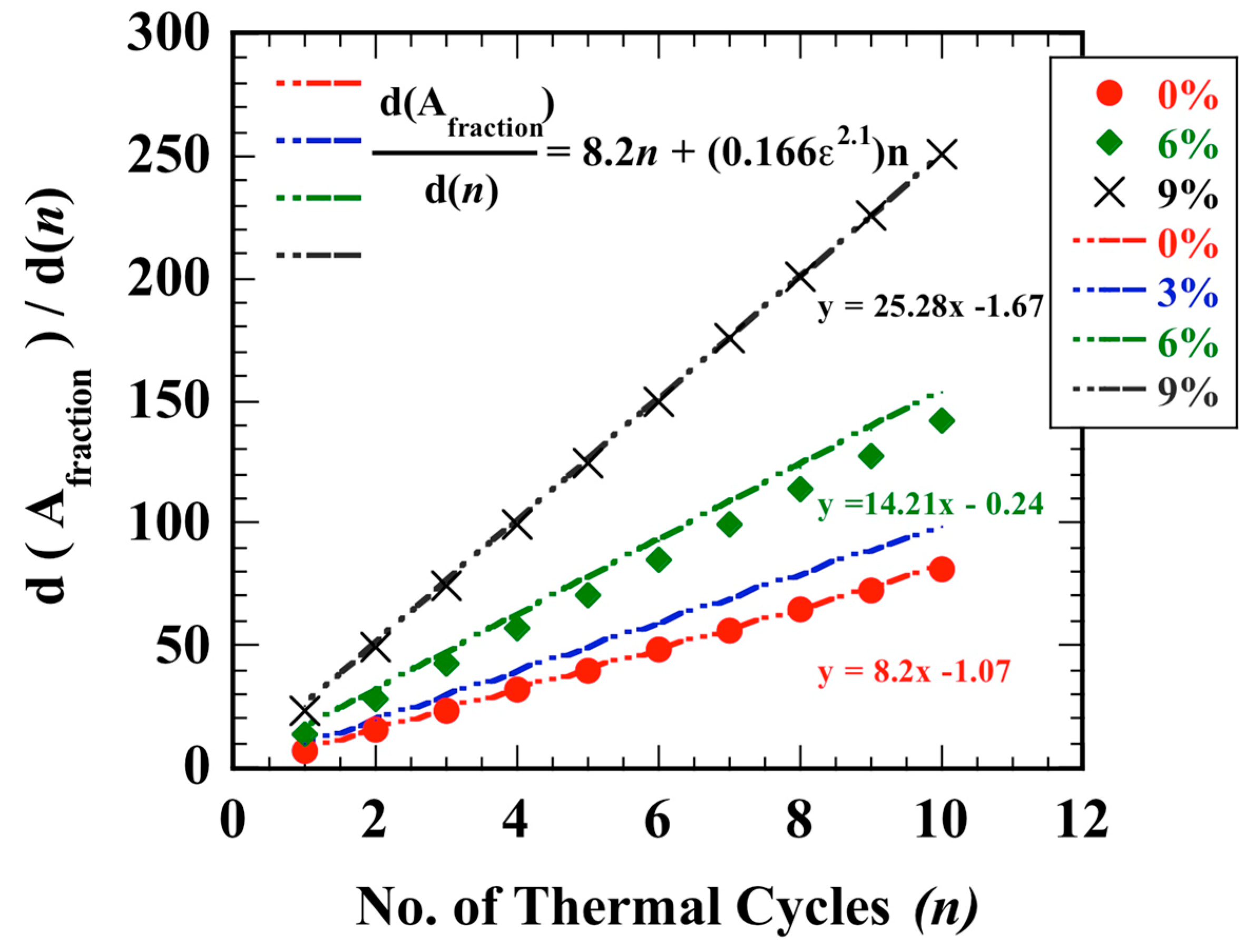
- A predictive estimate for the rate of AGG area fraction advancement, as a function of repeated thermal cycles, was determined based on the derivative of the experimental area fraction measures. This estimate has the following form:where for the experiments performed herein, C1 = 8.2, C2 = 1/6 and α = 2.1.
- (4)
- This numeric estimate indicates two notable implications:
- i.
- Area fraction advancement rates for AGG in minimally strained, commercially pure Ni-200 proceed at unique rates for a given initial strain content;
- ii.
- This advancement rate can be reasonably approximated across the low strain regime by the superposition of a nominal rate (where ε = 0) combined with the contribution of additional plastic strain (ε), modified by some prefactor value (C2), and scaled by an appropriate exponential (α).
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Madison, J.D.; Spowart, J.E.; Rowenhorst, D.J.; Aagesen, L.K.; Thorton, K.; Pollock, T.M. Fluid flow and defect formation in the three-dimensional dendritic structure of nickel-based single crystals. Metall. Mater. Trans. A 2012, 43, 369–380. [Google Scholar] [CrossRef]
- Pollock, T.M.; Tin, S. Nickel-Based Superalloys for Advanced Turbine Engines: Chemistry, Microstructure, and Properties. J. Propuls. Power 2006, 22, 361–374. [Google Scholar] [CrossRef]
- Osorio, W.R.; Goulart, P.R.; Santos, G.A.; Neto, C.M.; Garcia, A. Effect of dendritic arm spacing on mechanical properties and corrosion resistance of Al 9 Wt Pct Si and Zn 27 Wt Pct Al alloys. Metall. Mater. Trans. A 2006, 37, 2525–2538. [Google Scholar] [CrossRef]
- Gabb, T.P.; Kantzos, P.T.; Palsa, B.; Telesman, J.; Gayda, J.; Sudbrack, C.K. Fatigue Failure Modes of the Grain Size Transition Zone in a Dual Microstructure Disk; John Wiley & Sons: New York, NY, USA, 2012; pp. 63–72. [Google Scholar]
- Flageolet, B.; Yousfi, O.; Dahan, Y.; Villechaise, P.; Cormier, J. Characterization of Microstructures Containing Abnormal Grain Growth Zones in Alloy 718; John Wiley & Sons: New York, NY, USA, 2012; pp. 594–606. [Google Scholar]
- Gabb, T.P.; Kantzos, P.T.; Gayda, J.; Sudbrack, C.K.; Palsa, B. Fatigue resistance of the grain size transition zone in a dual microstructure superalloy disk. Int. J. Fatigue 2011, 33, 414–426. [Google Scholar] [CrossRef]
- Randle, V.; Coleman, M. Grain growth control in grain boundary engineered microstructures. Mater. Sci. Forum 2012, 715–716, 103–108. [Google Scholar] [CrossRef]
- Holm, E.A.; Miodownik, M.A.; Rollett, A.D. On abnormal subgrain growth and the origin of recrystallization nuclei. Acta Mater. 2003, 51, 2701–2716. [Google Scholar] [CrossRef]
- Fang, S.; Dong, Y.P.; Wang, S. The abnormal grain growth of P/M nickel-base superalloy: Strain storage and CSL boundaries. Adv. Mater. Res. 2015, 1064, 49–54. [Google Scholar] [CrossRef]
- Watson, R.; Preuss, M.; Da Fonseca, J.Q.; Witulski, T.; Terlinde, G.; Buscher, M. Characterization of Abnormal Grain Coarsening in Alloy 718. MATEC Web Conf. 2014, 14, 1–5. [Google Scholar] [CrossRef]
- Brons, J.G.; Thompson, G.B. A comparison of grain boundary evolution during grain growth in FCC metals. Acta Mater. 2013, 61, 3936–3944. [Google Scholar] [CrossRef]
- Randle, V.; Booth, M.; Owen, G. Time evolution of sigma 3 annealing twins in secondary recrystallized nickel. J. Microsc. 2005, 217, 162–166. [Google Scholar]
- Kazaryan, A.; Wang, Y.; Dregia, S.A.; Patton, B.R. Grain growth in anisotropic systems: Comparison of effects of energy and mobility. Acta Mater. 2002, 50, 2491–2502. [Google Scholar] [CrossRef]
- Upmanyu, M.; Hassold, G.N.; Kazaryan, A.; Holm, E.A.; Wang, Y.; Patton, B.; Srolovitz, D.J. Boundary mobility and energy anisotropy effects on microstructural evolution during grain growth. Int. Sci. 2002, 10, 201–216. [Google Scholar]
- Homma, H.; Hutchinson, B. Orientation dependence of secondary recrystallization in silicon-iron. Acta Mater. 2003, 51, 3795–3805. [Google Scholar] [CrossRef]
- Lin, P.; Palumbo, G.; Harase, J.; Aust, K.T. Coincident site lattice (CSL) grain boundaries and goss texture development in Fe-3% Si Alloy. Acta Mater. 1996, 44, 4677–4683. [Google Scholar] [CrossRef]
- Watanabe, T. An approach to grain boundary design for strong and ductile polycrystals. J. Glob. 1984, 11, 47–84. [Google Scholar]
- Randle, V. Twinning-related grain boundary engineering. Acta Mater. 2004, 52, 4067–4081. [Google Scholar] [CrossRef]
- Underwood, O.D.; Madison, J.D.; Martens, R.L.; Thompson, G.B.; Welsh, S.L.; Evans, J.L. An examination of abnormal grain growth in low strain nickel-200. Metallogr. Microstruct. Anal. 2016, 5, 302–312. [Google Scholar] [CrossRef]
- Randle, V.; Horton, D. Grain growth phenomena in nickel. Scr. Metall. Mater. 1994, 31, 891–895. [Google Scholar] [CrossRef]
- Hillert, M. On the theory of normal and abnormal grain growth. Acta Metall. 1965, 13, 227–238. [Google Scholar] [CrossRef]
- Holm, E.A.; Hassold, G.N.; Miodownik, M.A. On misorientation distribution evolution during anisotropic grain growth. Acta Mater. 2001, 49, 2981–2991. [Google Scholar] [CrossRef]
- Rollett, A.D.; Srolovitz, D.J.; Anderson, M.P. Simulation and theory of abnormal grain growth-anisotropic grain boundary energies and mobilities. Acta Metall. 1989, 37, 1227–1240. [Google Scholar] [CrossRef]
- Rollett, A.D.; Mulins, W.W. On the growth of abnormal grains. Scr. Mater. 1997, 36, 975–980. [Google Scholar] [CrossRef]
- Thompson, C.V.; Frost, H.J.; Spaepen, F. The relative rates of secondary and normal grain growth. Acta Metall. 1987, 35, 887–890. [Google Scholar] [CrossRef]
- Sztwiertnia, K. Recrystallization textures and the concept of oriented growth revisited. Mater. Lett. 2014, 123, 41–43. [Google Scholar] [CrossRef]
- Jensen, D.J. Growth rates and misorientation relationships between growing nuclei/grains and the surrounding deformed matrix during recrstalization. Acta Metall. Mater. 1995, 43, 4117–4129. [Google Scholar] [CrossRef]
- Akhiani, H.; Nezakat, M.; Sonboli, A.; Szpunar, J. The origin of annealing texture in a cold-rolled incoloy 800H/Ht after different strain paths. Mater. Sci. Eng. 2014, 619, 334–344. [Google Scholar] [CrossRef]
- Akhiani, H.; Nezakat, M.; Szpunar, J.A. Evolution of deformation and annealing textures in incoloy 800H/HT via different rolling paths and strains. Mater. Sci. Eng. 2014, 614, 250–263. [Google Scholar] [CrossRef]
- Wilson, A.W.; Madison, J.D.; Spanos, G. Determining phase volume fraction in steels by electron backscattered diffraction. Sci. Mater. 2001, 45, 1335–1340. [Google Scholar] [CrossRef]
- Sahay, S.S.; Malhotra, C.P.; Kolkhede, A.M. Accelerated grain growth behavior during cyclic annealing. Acta Mater. 2003, 51, 339–346. [Google Scholar] [CrossRef]
- Decker, R.F.; Rush, A.I.; Dano, A.G.; Freeman, J.W. Abnormal Grain Growth in Nickel-Base Heat-Resistant Alloys; University of North Texas: Denton, TX, USA, 1957. [Google Scholar]
- He, G.; Tan, L.; Liu, F.; Huang, L.; Huang, Z.; Jiang, L. Unraveling the formation mechanism of abnormally large grains in an advanced polycrystalline nickel base superalloy. J. Alloys Compd. 2017, 718, 405–413. [Google Scholar] [CrossRef]
- He, G.; Liu, F.; Huang, L.; Huang, Z.; Jiang, L. Controlling grain size via dynamic recrystallization in an advanced polycrystalline nickel base superalloy. J. Alloys Compd. 2017, 701, 909–919. [Google Scholar] [CrossRef]
- He, G.; Tan, L.; Liu, F.; Huang, L.; Huang, Z.; Jiang, L. Revealing the role of strain rate during multi-pass compression in an advanced polycrystalline nickel base superalloy. Mater. Charact. 2017, 128, 123–133. [Google Scholar] [CrossRef]
- Cho, Y.K.; Yoon, D.Y.; Henry, M.F. The Effects of deformation and pre-heat treatment on abnormal grain growth in RENÉ 88 superalloy. Metall. Mater. Trans. A 2001, 32, 3077–3090. [Google Scholar] [CrossRef]
- Bozzolo, N.; Agnoli, A.; Souai, N.; Bernacki, M.; Loge, R.E. Strain induced abnormal grain growth in nickel base superalloys. Mater. Sci. Forum 2013, 753, 321–324. [Google Scholar] [CrossRef]

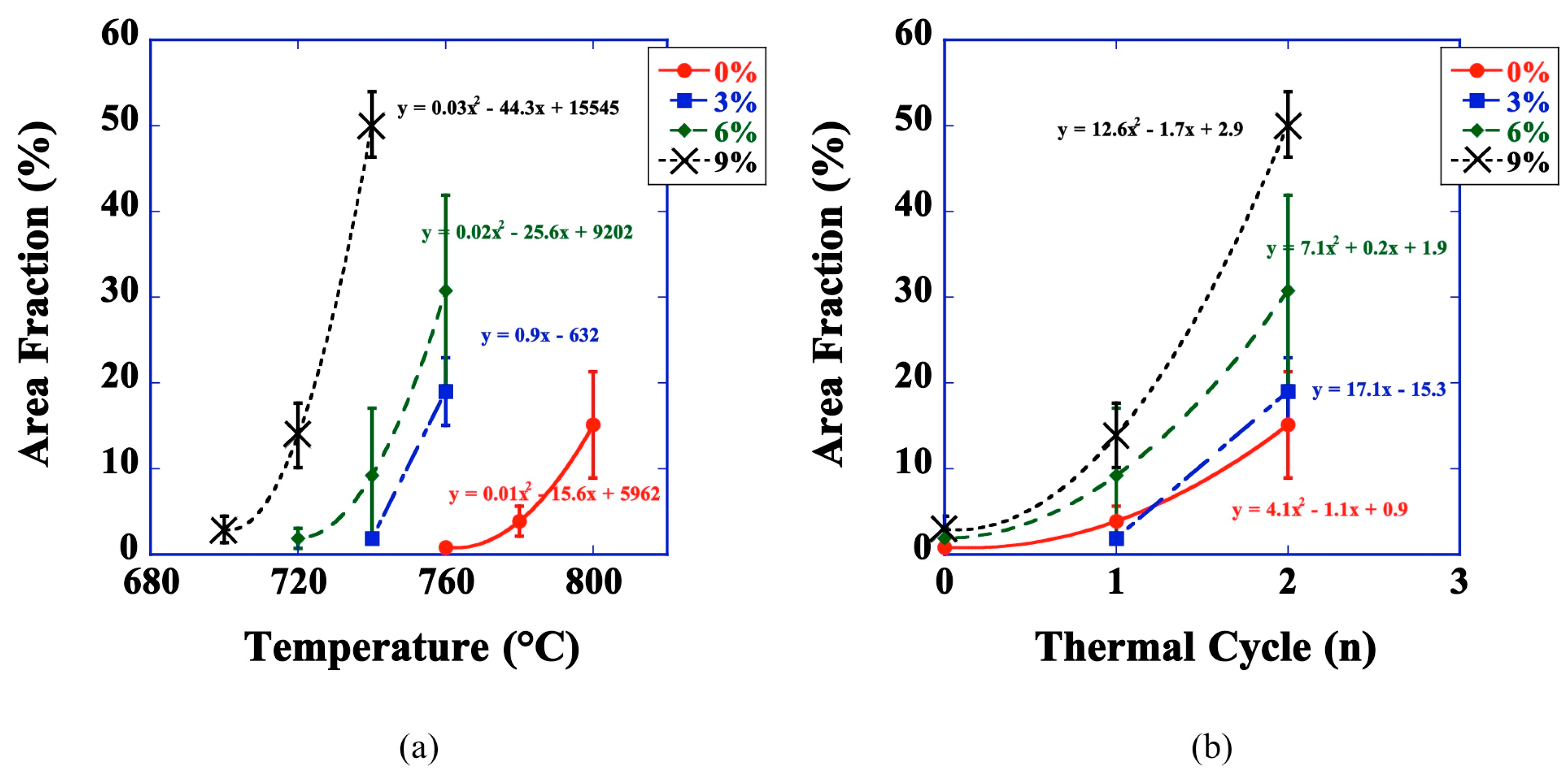
| ε (%) | Emergence | Progression | Progression/Emergence |
|---|---|---|---|
| Δ (Area Fraction n = 1–0) | Δ (Area Fraction n = 2–1) | ||
| 0 | 3.03 | 11.23 | 3.71 |
| 3 | - | 17.12 | - |
| 6 | 7.34 | 21.55 | 2.93 |
| 9 | 10.97 | 36.25 | 3.30 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Underwood, O.D.; Madison, J.D.; Thompson, G.B. Emergence and Progression of Abnormal Grain Growth in Minimally Strained Nickel-200. Metals 2017, 7, 334. https://doi.org/10.3390/met7090334
Underwood OD, Madison JD, Thompson GB. Emergence and Progression of Abnormal Grain Growth in Minimally Strained Nickel-200. Metals. 2017; 7(9):334. https://doi.org/10.3390/met7090334
Chicago/Turabian StyleUnderwood, Olivia D., Jonathan D. Madison, and Gregory B. Thompson. 2017. "Emergence and Progression of Abnormal Grain Growth in Minimally Strained Nickel-200" Metals 7, no. 9: 334. https://doi.org/10.3390/met7090334





