Understanding of the Structural Relaxation of Metallic Glasses within the Framework of the Interstitialcy Theory
Abstract
:1. Introduction
2. Background
3. Interstitialcy-Mediated Structural Relaxation and Related Relaxation of the Shear Modulus
3.1. Relaxation Kinetics
3.2. Activation Energy Spectra
4. Interrelationship between the Shear Modulus of Glass, Concentration of Frozen-In Interstitialcy Defects and Shear Modulus of the Maternal Crystal
5. Structural Relaxation-Induced Heat Effects
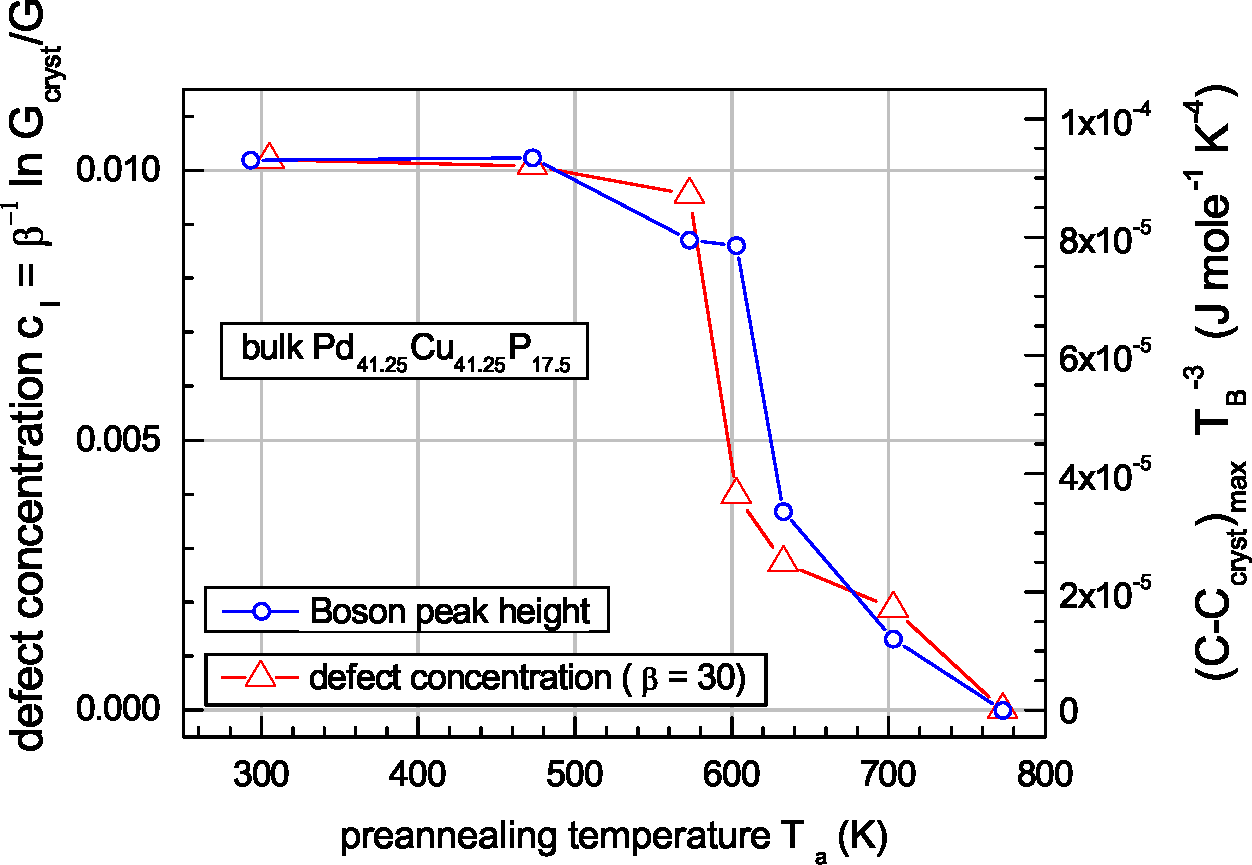
6. Interstitialcies and Low Temperature Heat Capacity
7. Interstitialcies, Free Volume and Enthalpy Release
8. Elastic Dipole Approach
9. Summary
Acknowledgments
Conflicts of Interest
References
- Taub, A.I.; Spaepen, F. Isoconfigurational flow of amorphous Pd82Si18. Scr. Metall. 1979, 13, 195–198. [Google Scholar]
- Khonik, V.A. The kinetics of irreversible structural relaxation and rheological behavior of metallic glasses under quasi-static loading. J. Non-Cryst. Sol. 2001, 296, 147–157. [Google Scholar]
- Chen, H.S. Glassy metals. Rep. Prog. Phys. 1980, 43, 353–432. [Google Scholar]
- Schuh, C.A.; Hufnagel, T.C.; Ramamurty, U. Mechanical behavior of amorphous alloys. Acta Mater. 2007, 55, 4067–4109. [Google Scholar]
- Greer, A.L. Metallic Glasses. In Physical Metallurgy; Volume I, Laughlin, D.E., Hono, K., Eds.; Elsevier: Oxford, UK, 2014; pp. 305–385. [Google Scholar]
- Doolittle, A.K. Studies in newtonian flow. II. The dependence of the viscosity of liquids on free-space. J. Appl. Phys. 1951, 22, 1471–1475. [Google Scholar]
- Turnbull, D.; Cohen, M.H. Free volume model of the amorphous phase: glass transition. J. Chem. Phys. 1961, 34, 120–125. [Google Scholar]
- Turnbull, D.; Cohen, M.H. On the free volume model of the liquid-glass transition. J. Chem. Phys. 1970, 52, 3038–3041. [Google Scholar]
- Spaepen, F. A microscopic mechanism for steady state inhomogeneous flow in metallic glasses. Acta Metall. 1977, 25, 407–415. [Google Scholar]
- Argon, A.S. Plastic deformation in metallic glasses. Acta Metall. 1979, 27, 47–58. [Google Scholar]
- Spaepen, F. Homogeneous flow of metallic glasses: A free volume perspective. Scr. Mater. 2006, 54, 363–367. [Google Scholar]
- Van den Beukel, A.; Radelaar, S. On the kinetics of structural relaxation in metallic glasses. Acta Metall. 1990, 31, 419–427. [Google Scholar]
- Van den Beukel, A.; Sietsma, J. The glass transition as a free volume related kinetic phenomenon. Acta Metall. Mater. 1990, 38, 383–389. [Google Scholar]
- Koebrugge, G.W.; Sietsma, J.; van den Beukel, A. Structural relaxation in amorphous Pd40Ni40P20. Acta Metall. Mater. 1992, 40, 753–760. [Google Scholar]
- Slipenyuk, A.; Eckert, J. Correlation between enthalpy change and free volume reduction during structural relaxation of Zr55Cu30Al10Ni5 metallic glass. Scr. Mater. 2004, 50, 39–44. [Google Scholar]
- Bobrov, O.P.; Khonik, V.A.; Lyakhov, S.A.; Csach, K.; Kitagawa, K.; Neuhäuser, H. Shear viscosity of bulk and ribbon glassy Pd40Cu30Ni10P20 well below and mear the glass transition. J. Appl. Phys. 2006, 100, 033518. [Google Scholar]
- Cheng, Y.Q.; Ma, E. Indicators of internal structural states for metallic glasses: Local order, free volume, and configurational potential energy. Appl. Phys. Lett. 2008, 93, 051910. [Google Scholar]
- Granato, A.V. Interstitialcy model for condensed matter states of face-centered-cubic metals. Phys. Rev. Lett. 1992, 68, 974–977. [Google Scholar]
- Granato, A.V. Interstitialcy theory of simple condensed matter. Eur. J. Phys. 2014, 87, 18. [Google Scholar]
- Frenkel, J. Kinetic Theory of Liquids; Oxford University Press: New York, NY, USA, 1946. [Google Scholar]
- Mei, Q.S.; Lu, K. Melting and superheating of crystalline solids: From bulk to nanocrystals. Prog. Mater. Sci. 2007, 52, 1175–1262. [Google Scholar]
- Slater, J.C. Introduction to Chemical Physics; McGraw-Hill Book Company: New York, NY, USA; Toronto, ON, Canada; London, UK, 1963. [Google Scholar]
- Granato, A.V. A comparison with empirical results of the Interstitialcy theory of condensed matter. J. Non-Cryst. Sol. 2006, 352, 4821–4825. [Google Scholar]
- Seitz, F. On the theory of diffusion in metals. Acta Cryst. 1950, 3, 355–363. [Google Scholar]
- Gibson, J.B.; Goland, A.N.; Milgram, M.; Vineyard, G.H. Dynamics of radiation damage. Phys. Rev. 1960, 120, 1229–1253. [Google Scholar]
- Erginsoy, C.; Vineyard, G.H.; Englert, A. Dynamics of radiation damage in a body-centered cubic lattice. Phys. Rev. 1964, 133, A595–A606. [Google Scholar]
- Schilling, W. Self-interstitial atoms in metals. J. Nucl. Mater. 1978, 69–70, 465–489. [Google Scholar]
- Robrock, K.H. Mechanical Relaxation of Interstitials in Irradiated Metals; Springer-Verlag: Berlin, Germany, 1990. [Google Scholar]
- Wolfer, W.G. Fundamental Properties of Defects in Metals. In Comprehensive Nuclear Materials; Konings, R.J.M., Ed.; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Konchakov, R.A.; Khonik, V.A.; Kobelev, N.P. Split Interstitials in computer models of single-crystal and amorphous copper. Phys. Sol. State (Pleiades Publishing) 2015, 57, 844–852. [Google Scholar]
- Holder, J.; Granato, A.V.; Rehn, L.E. Experimental evidence for split interstitials in copper. Phys. Rev. Lett. 1974, 32, 1054–1057. [Google Scholar]
- Holder, J.; Rehn, L.E.; Granato, A.V. Effect of self-interstitials on the elastic constants of copper. Phys. Rev. B 1974, 10, 363–375. [Google Scholar]
- Born, M. Thermodynamics of crystals and melting. J. Chem. Phys. 1939, 7, 591–603. [Google Scholar]
- Dederichs, P.H.; Lehman, C.; Schober, H.R.; Scholz, A.; Zeller, R. Lattice theory of point defects. J. Nucl. Mater. 1978, 69–70, 176–199. [Google Scholar]
- Nordlund, K.; Averback, R.S. Role of self-interstitial atoms on the high temperature properties of metals. Phys Rev. Lett. 1998, 80, 4201–4204. [Google Scholar]
- Spaepen, F. A survey of energies in materials science. Phil. Mag. 2005, 85, 2979–2987. [Google Scholar]
- De Podesta, M. Understanding the Properties of Matter, 2nd ed; Taylor & Francis: London, UK, 2001. [Google Scholar]
- Nordlund, K.; Ashkenazy, Y.; Averback, R.S.; Granato, A.V. Strings and interstitials in liquids, glasses and crystals. Europhys. Lett. 2005, 71, 625–631. [Google Scholar]
- Granato, A.V.; Joncich, D.M.; Khonik, V.A. Melting, thermal expansion, and the Lindemann rule for elemental substances. Appl. Phys. Lett. 2010, 97, 171911. [Google Scholar]
- Stillinger, F.H.; Weber, T.A. Point defects in bcc crystals: Structures, transition kinetics, and melting implications. J. Chem. Phys. 1984, 81, 5095–51034. [Google Scholar]
- Lee, G.C.S.; Li, J.C.M. Molecular-dynamics studies of crystal defects and melting. Phys. Rev. B 1989, 39, 9302–9311. [Google Scholar]
- Kanigel, A.; Adler, J.; Polturak, E. Influence of point defects on the shear elastic coefficients and on the melting temperature of copper. Int. J. Mod. Phys. C 2001, 12, 727–737. [Google Scholar]
- Zhang, H.; Khalkhali, M.; Liu, Q.; Douglas, J.F. String-like cooperative motion in homogeneous melting. J. Chem. Phys. 2013, 138, 12A538. [Google Scholar]
- Ashkenazy, Y.; Averback, R.S. Atomic mechanisms controlling crystallization behavior in metals at deep undercoolings. Europhys. Lett. 2007, 79, 26005. [Google Scholar]
- Betancourt, B.A.P.; Douglas, J.F.; Starr, F.W. String model for the dynamics of glass-forming liquids. J. Chem. Phys. 2014, 140, 204509. [Google Scholar]
- Schober, H.R. Collectivity of motion in undercooled liquids and amorphous solids. J. Non-Cryst. Sol. 2002, 307–310, 40–49. [Google Scholar]
- Donati, C.; Douglas, J.F.; Kob, W.; Plimpton, S.J.; Poole, P.H.; Glotzer, S.C. Stringlike cooperative motion in a supercooled liquid. Phys. Rev. Lett. 1998, 80, 2338–2341. [Google Scholar]
- Oligschleger, C.; Schober, H.R. Collective jumps in a soft-sphere glass. Phys. Rev. B 1999, 59, 811–821. [Google Scholar]
- Granato, A.V. The specific heat of simple liquids. J. Non-Cryst. Sol. 2002, 307–310, 376–386. [Google Scholar]
- Konchakov, R.A.; Khonik, V.A. Effect of vacancies and interstitials in the dumbbell configuration on the shear modulus and vibrational density of states of copper. Phys. Sol. State (Pleiades Publishing) 2014, 56, 1368–1373. [Google Scholar]
- Schober, H.R. Phonons 89; Hunklinger, S., Ludwig, W., Weiss, G., Eds.; World Scientific: Singapore, 1989; Volume I, p. 444. [Google Scholar]
- Okamoto, P.R.; Rehn, L.E.; Pearson, J.; Bhadra, R.; Grimsditch, M. Brillouin scattering and transmission electron microscopy studies of radiation-induced elastic softening, disordering and amorphization of metallic compounds. J. Less-Common Met. 1988, 14, 231–244. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity; Pergamon Press: Oxford, UK, 1970. [Google Scholar]
- Nemilov, S.V. The kinetics of elementary processes in the condensed state. II. Shear relaxation and the equation of state for solids. Russ. J. Phys. Chem. 1968, 42, 726–731. [Google Scholar]
- Dyre, J.C.; Olsen, N.B.; Christensen, T. Local elastic expansion model for viscous-flow activation energies of glass-forming molecular liquids. Phys. Rev. B 1996, 53, 2171–2174. [Google Scholar]
- Johnson, W.L.; Samwer, K. A universal criterion for plastic yielding of metallic glasses with a (T/Tg)2/3 temperature dependence. Phys Rev. Lett. 2005, 95, 195501. [Google Scholar]
- Nemilov, S.V. Interrelation between shear modulus and the molecular parameters of viscous flow for glass forming liquids. J. Non-Cryst. Sol. 2006, 352, 2715–2725. [Google Scholar]
- Dyre, J.C. The glass transition and elastic models of glass-forming liquids. Rev. Mod. Phys. 2006, 78, 953–972. [Google Scholar]
- Wang, W.H. The elastic properties, elastic models and elastic perspertives of metallic glasses. Prog. Mater. Sci. 2012, 57, 487–656. [Google Scholar]
- Tsao, S.S.; Spaepen, F. Structural relaxation of a metallic glass near equilibrium. Acta Metall. 1985, 33, 881–889. [Google Scholar]
- Mitrofanov, Yu.P.; Khonik, V.A.; Granato, A.V.; Joncich, D.M.; Khonik, S.V.; Khoviv, A.M. Relaxation of a metallic glass to the metastable equilibrium: Evidence for the existence of the Kauzmann pseudocritical temperature. Appl. Phys. Lett. 2012, 100, 171901. [Google Scholar]
- Khonik, V.A.; Mitrofanov, Y.P.; Makarov, A.S.; Konchakov, R.A.; Afonin, G.V.; Tsyplakov, A.N. Structural relaxation and shear softening of Pd- and Zr-based bulk metallic glasses near the glass transition. J. Alloys Comp. 2015, 628, 27–31. [Google Scholar]
- Khonik, V.A.; Mitrofanov, Y.P.; Khonik, S.V.; Saltykov, S.N. Unexpectedly large relaxation time determined by in situ high-frequency shear modulus measurements near the glass transition of bulk glassy Pd40Cu30Ni10P20. J. Non-Cryst. Sol. 2010, 356, 1191–1193. [Google Scholar]
- Gibbs, M.R.J.; Evetts, J. E.; Leake, J.A. Activation energy spectra and relaxation in amorphous materials. J. Mater. Sci. 1983, 18, 278–288. [Google Scholar]
- Wagner, H.; Bedorf, D.; Küchemann, S.; Schwabe, M.; Zhang, B.; Arnold, W.; Samwer, K. Local elastic properties of a metallic glass. Nat. Mater. 2011, 10, 439–442. [Google Scholar]
- Khonik, V.A. The kinetics of irreversible structural relaxation and homogeneous plastic flow of metallic glasses. Phys. Status Sol. (A) 2000, 177, 173–189. [Google Scholar]
- Khonik, S.V.; Granato, A.V.; Joncich, D.M.; Pompe, A.; Khonik, V.A. Evidence of distributed interstitialcy-like relaxation of the shear modulus due to structural relaxation of metallic glasses. Phys. Rev. Lett. 2008, 100, 065501. [Google Scholar]
- Bothe, K.; Neuhäuser, H. Relaxation of metallic glass structure measured by elastic modulus and internal friction. J. Non-Cryst. Sol. 1983, 56, 279–284. [Google Scholar]
- Mitrofanov, Yu.P.; Khonik, V.A.; Vasil’ev, A.N. Isothermal kinetics and relaxation recovery of high-frequency shear modulus in the course of structural relaxation of Pd40Cu30Ni10P20 bulk glass. J. Exp. Theor. Phys. 2009, 108, 830–835. [Google Scholar]
- Mitrofanov, Yu.P.; Khonik, V.A.; Granato, A.V.; Joncich, D.M.; Khonik, S.V. Relaxation of the shear modulus of a metallic glass near the glass transition. J. Appl. Phys. 2011, 109, 073518. [Google Scholar]
- Khonik, V.A.; Kitagawa, K.; Morii, H. On the determination of the crystallization activation energy of metallic glasses. J. Appl. Phys. 2000, 87, 8440–8443. [Google Scholar]
- Tsyplakov, A.N.; Mitrofanov, Yu.P.; Makarov, A.S.; Afonin, G.V.; Khonik, V.A. Determination of the activation energy spectrum of structural relaxation in metallic glasses using calorimetric and shear modulus relaxation data. J. Appl. Phys. 2014, 116, 123507. [Google Scholar]
- Makarov, A.S.; Khonik, V.A.; Mitrofanov, Yu.P.; Granato, A.V.; Joncich, D.M.; Khonik, S.V. Interrelationship between the shear modulus of a metallic glass, concentration of frozen-in defects, and shear modulus of the parental crystal. Appl. Phys. Lett. 2013, 102, 091908. [Google Scholar]
- Khonik, V.A.; Mitrofanov, Yu.P.; Lyakhov, S.A.; Khoviv, D.A.; Konchakov, R.A. Recovery of structural relaxation in aged metallic glass as determined by high-precision in situ shear modulus measurements. J. Appl. Phys. 2009, 105, 123521. [Google Scholar]
- Makarov, A.S.; Khonik, V.A.; Wilde, G.; Mitrofanov, Yu.P.; Khonik, S.V. “Defect”-induced heat flow and shear modulus relaxation in a metallic glass. Intermetallics 2014, 44, 106–109. [Google Scholar]
- Makarov, A.S.; Mitrofanov, Yu.P.; Afonin, G.V.; Khonik, V.A.; Kobelev, N.P. The dependence of the shear modulus of glass on the shear modulus of crystal and kinetics of structural relaxation for Zr46Cu46Al8 system. Phys. Sol. State (Pleiades Publishing) 2015, 57. in press. [Google Scholar]
- Kobelev, N.P.; Khonik, V.A.; Makarov, A.S.; Afonin, G.V.; Mitrofanov, Yu.P. On the nature of heat effects and shear modulus softening in metallic glasses: A generalized approach. J. Appl. Phys. 2014, 115, 033513. [Google Scholar]
- Mitrofanov, Yu.P.; Makarov, A.S.; Khonik, V.A.; Granato, A.V.; Joncich, D.M.; Khonik, S.V. On the nature of enthalpy relaxation below and above the glass transition of metallic glasses. Appl. Phys. Lett. 2012, 101, 191903. [Google Scholar]
- Makarov, A.S.; Khonik, V.A.; Mitrofanov, Yu.P.; Granato, A.V.; Joncich, D.M. Determination of the susceptibility of the shear modulus to the defect concentration in a metallic glass. J. Non-Cryst. Sol. 2013, 370, 18–20. [Google Scholar]
- Khonik, V.A.; Kobelev, N.P. Alternative understanding for the enthalpy vs. volume change upon structural relaxation of metallic glasses. J. Appl. Phys. 2014, 115, 093510. [Google Scholar]
- Phillips, W.A. Amorphous Solids: Low Temperature Properties; Springer: Berlin, Germany, 1981. [Google Scholar]
- Shintani, H.; Tanaka, H. Universal link between the boson peak and transverse phonons in glass. Nat. Mater. 2008, 7, 870–877. [Google Scholar]
- Granato, A.V. Interstitial resonance modes as a source of the boson peak in glasses and liquids. Phys. B 1996, 219–220, 270–272. [Google Scholar]
- Vasiliev, A.N.; Voloshok, T.N.; Granato, A.V.; Joncich, D.M.; Mitrofanov, Yu.P.; Khonik, V.A. Relationship between low-temperature boson heat capacity peak and high-temperature shear modulus relaxation in a metallic glass. Phys. Rev. B 2009, 80, 172102. [Google Scholar]
- Miracle, D.B.; Egami, T.; Flores, K.M.; Kelton, K.F. Structural aspects of metallic glasses. MRS Bull. 2007, 32, 629–634. [Google Scholar]
- Trexler, M.M.; Thadhani, N.N. Mechanical properties of bulk metallic glasses. Prog. Mater. Sci. 2010, 55, 759–839. [Google Scholar]
- Gordon, C.A.; Granato, A.V.; Simmons, R.O. Evidence for the self-interstitial model of liquid and amorphous states from lattice parameter measurements in krypton. J. Non-Cryst. Sol. 1996, 205–207, 216–220. [Google Scholar]
- Ehrhart, P; Jung, P.; Schultz, H.; Ullmaier, H. Properties and Interactions of Atomic Defects in Metals and Alloys. In Atomic Defects in Metals, Landolt-Börnstein New Series III; Madelung, O., Ed.; Springer: Berlin, Germany, 1991; Volume 25, pp. 88–371. [Google Scholar]
- Bünz, J.; Wilde, G. Direct measurement of the kinetics of volume and enthalpy relaxation of an Au-based metallic glass. J. Appl. Phys. 2013, 114, 223503. [Google Scholar]
- Nowick, A.S.; Berry, B.S. Anelastic Relaxation in Crystalline Solids; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Kobelev, N.P.; Khonik, V.A.; Afonin, G.V.; Kolyvanov, E.L. On the origin of the shear modulus change and heat release upon crystallization of metallic glasses. J. Non-Cryst. Sol. 2015, 411, 1–4. [Google Scholar]
- Erofeyev, V.I. Wave Processes in Solids With Microstructure; World Scientific: Singapore, 2003. [Google Scholar]
- Kobelev, N.P.; Kolyvanov, E.L.; Khonik, V.A. Higher order elastic moduli of the bulk metallic glass Zr52.5Ti5Cu17.9Ni14.6Al10. Phys. Sol. State (Pleiades Publishing) 2007, 49, 1209–1215. [Google Scholar]
- Nakamura, A.; Kamimura, Y.; Edagawa, K.; Takeuchi, S. Elastic and plastic characteristics of a model Cu-Zr amorphous alloy. Mater. Sci. Eng. 2014, A614, 16–26. [Google Scholar]
- Tsyplakov, A.N.; Mitrofanov, Yu.P.; Khonik, V.A.; Kobelev, N.P.; Kaloyan, A.A. Relationship between the heat flow and relaxation of the shear modulus in bulk PdCuP metallic glass. J. Alloys Comp. 2015, 618, 449–454. [Google Scholar]
- Lambson, E.F.; Lambson, W.A.; Macdonald, J.E.; Gibbs, M.R.J.; Saunders, G.A.; Turnbull, D. Elastic behavior and vibrational anharmonicity of a bulk Pd40Ni40P20 metallic glass. Phys. Rev. B 1986, 33, 2380–2385. [Google Scholar]
- Wang, R.J.; Wang, W.H.; Li, F.Y.; Wang, L.M.; Zhang, Y.; Wen, P.; Wang, J.F. The Grüneisen parameter for bulk amorphous materials. J. Phys.: Condens. Matter 2003, 15, 603–608. [Google Scholar]
- Novikov, V.N.; Sokolov, A.P. Poisson ratio and the fragility of glass-forming liquids. Nature 2004, 431, 961–963. [Google Scholar]
- Tarumi, R.; Hirao, M.; Ichitsubo, T.; Matsubara, E.; Saida, J.; Kato, H. Low-temperature acoustic properties and quasiharmonic analysis for Cu-based bulk metallic glasses. Phys. Rev. B 2007, 76, 104206. [Google Scholar]
- Safarik, D.J.; Schwarz, R.B. Evidence for highly anharmonic low-frequency vibrational modes in bulk amorphous Pd40Cu40P20. Phys. Rev. B 2009, 80, 094109. [Google Scholar]
- Chen, L.Y.; Li, B.Z.; Wang, X.D.; Jiang, F.; Ren, Y.; Liaw, P.K.; Jiang, J.Z. Atomic-scale mechanisms of tension–compression asymmetry in a metallic glass. Acta Mater. 2013, 61, 1843–1850. [Google Scholar]
- Wang, H.; Li, M. Symmetry breaking and other nonlinear elastic responses of metallic glasses subject to uniaxial loading. J. Appl. Phys. 2013, 113, 213515. [Google Scholar]
- Wang, H.; Li, M. Estimate of the maximum strength of metallic glasses from finite deformation theory. Phys. Rev. Lett. 2013, 111, 065507. [Google Scholar]
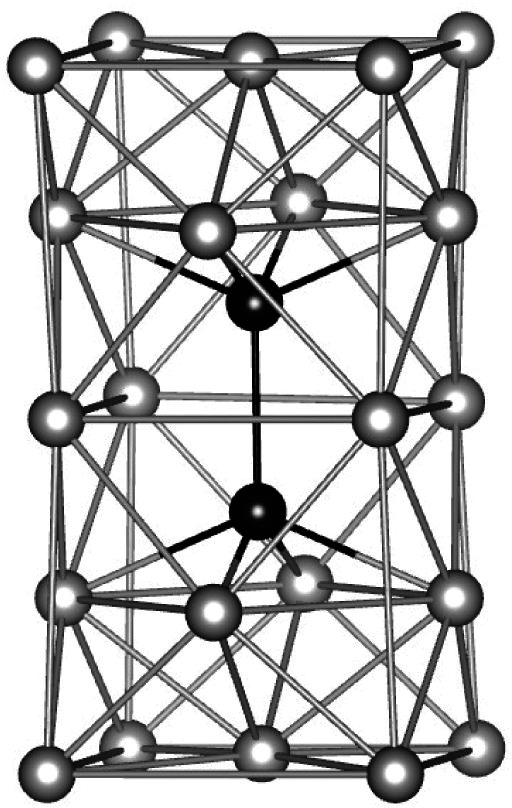
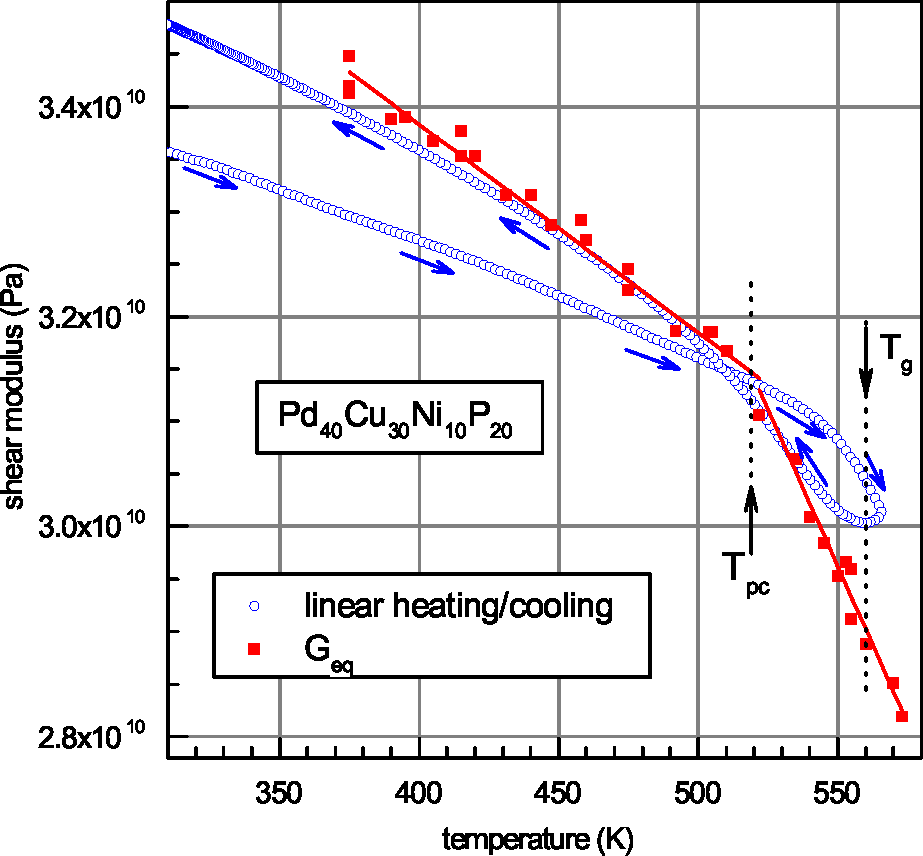

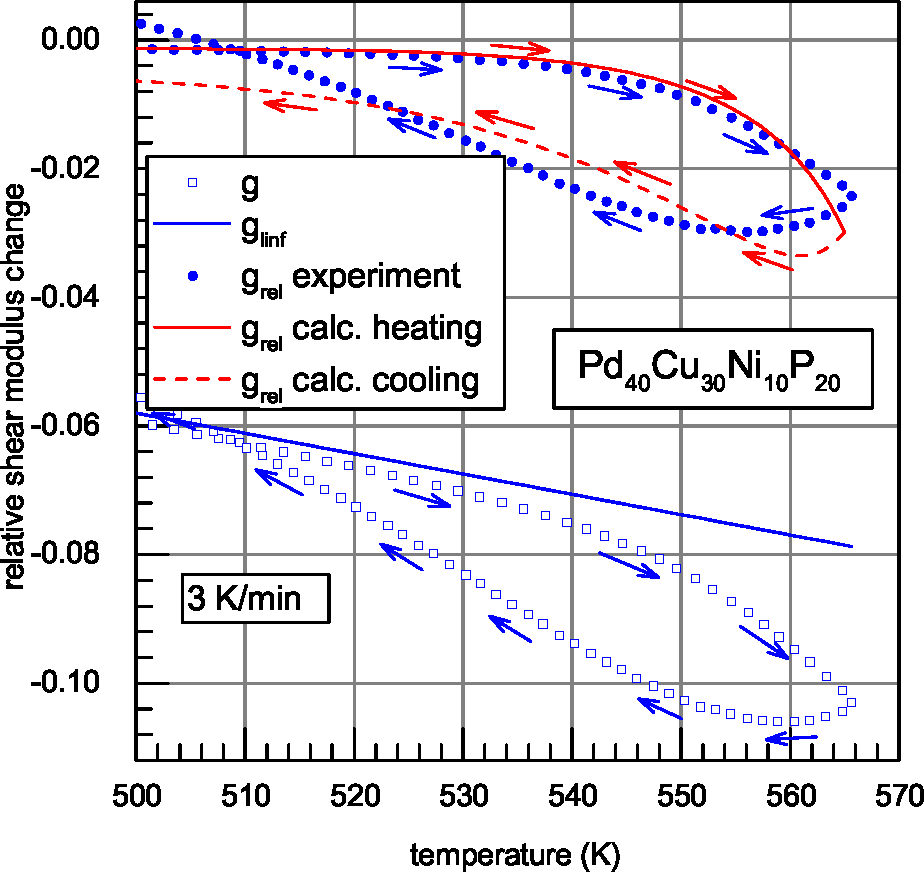
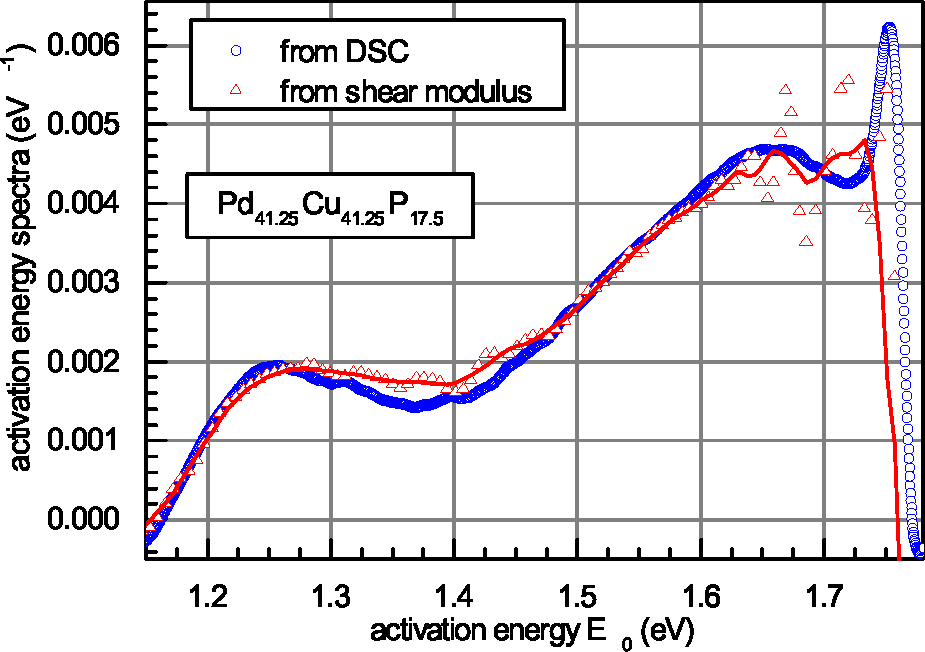
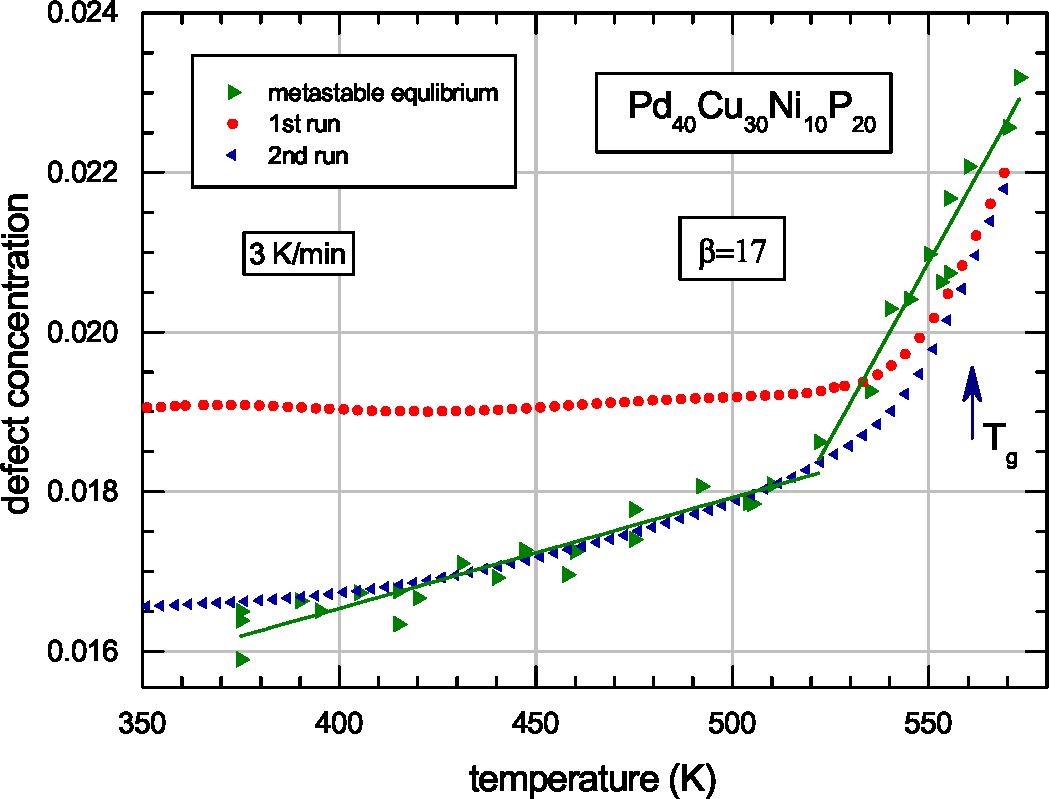
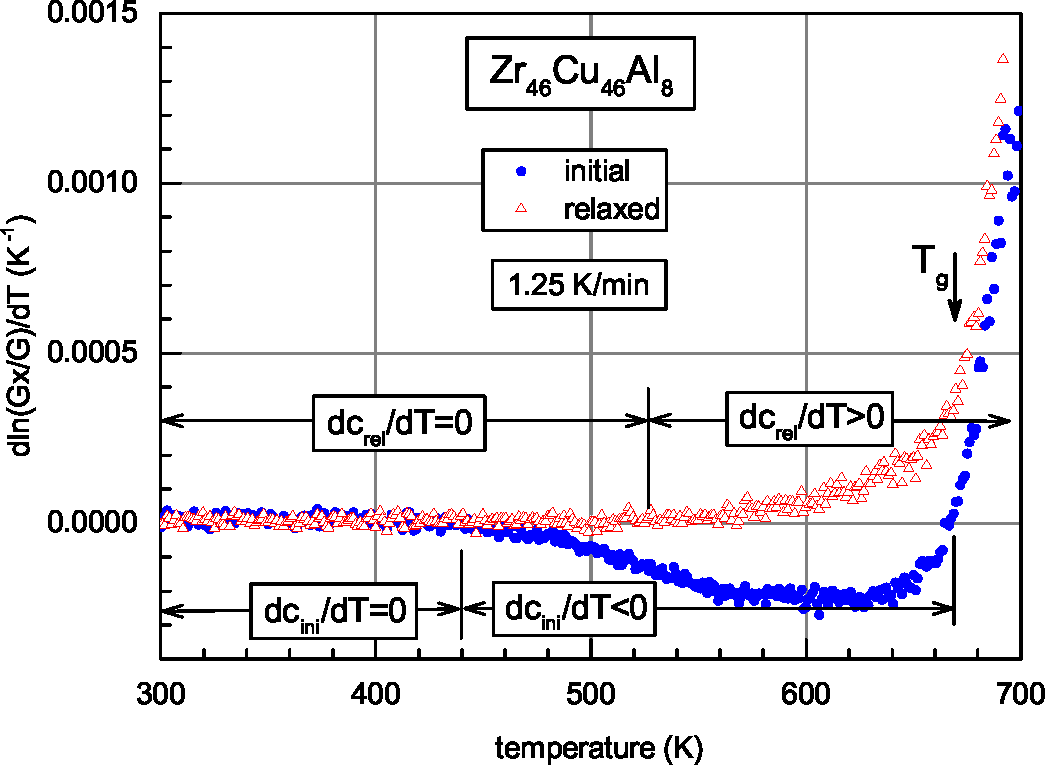
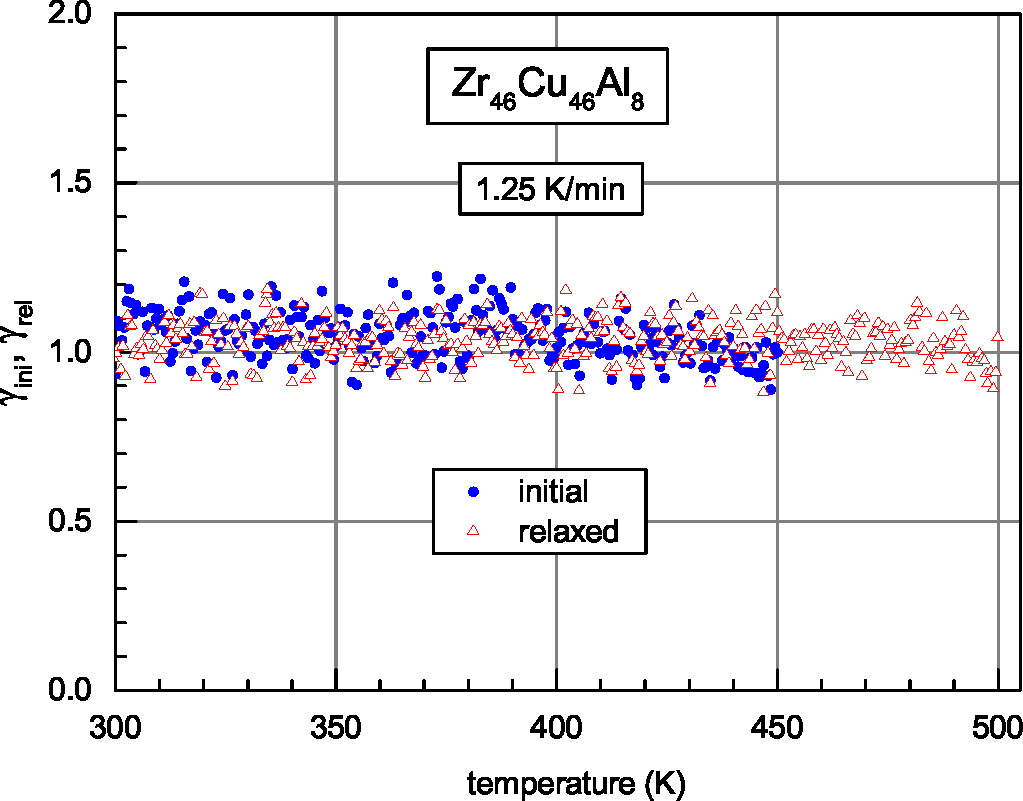
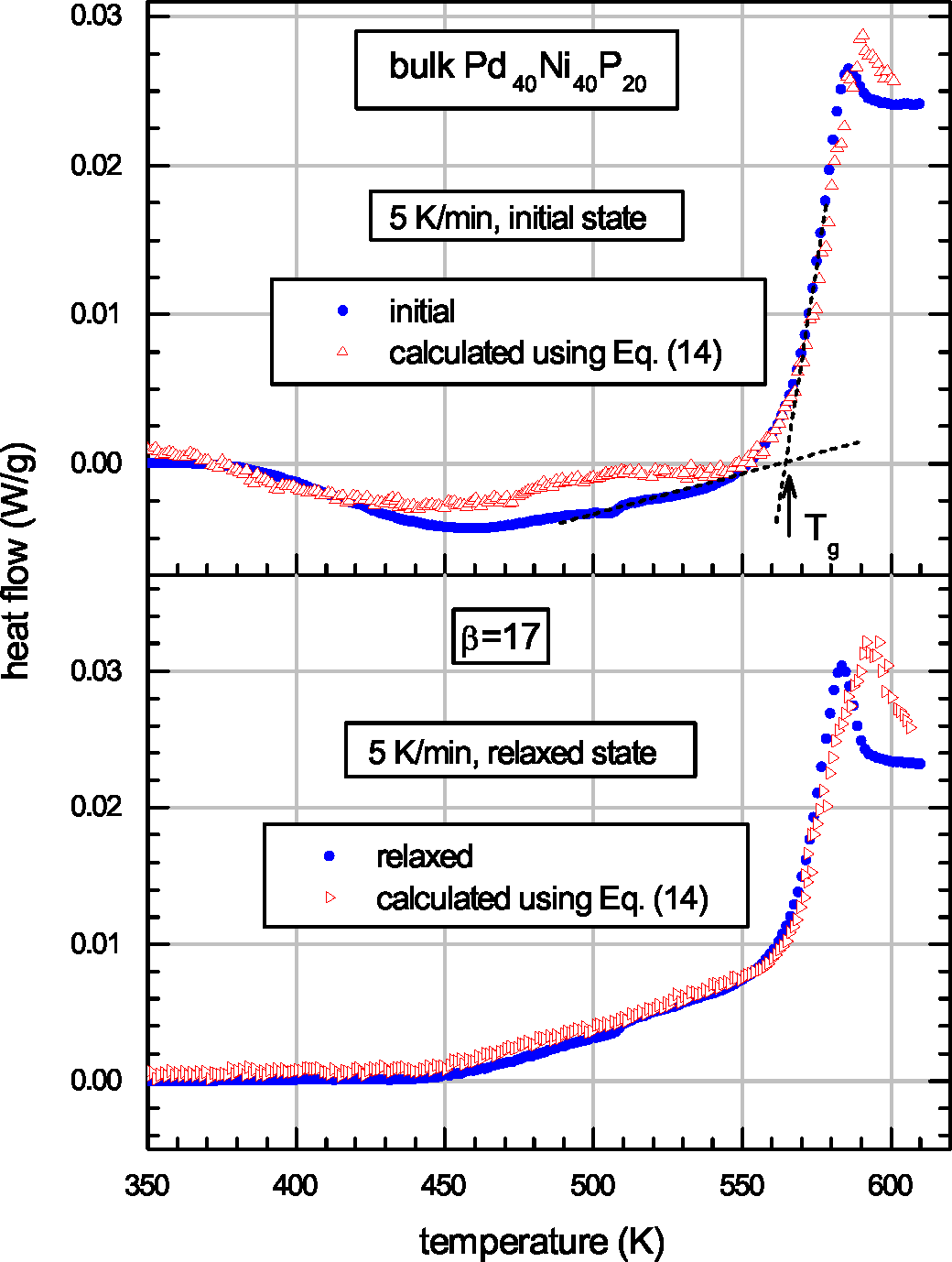
| Glass | Δcg | Δcw | Qμ | Nμ | Qd | GRT | Ω | H | |
|---|---|---|---|---|---|---|---|---|---|
| PdCuP | 0.00161 | 0.00165 | 0.00163 | 432 | 9.8 | 2.75 | 32.7 | 1.33 | 2.72 |
| PdNiP | 0.00332 | 0.00314 | 0.00323 | 931 | 19.5 | 2.98 | 38.6 | 1.28 | 3.09 |
| ZrCuAl | 0.00206 | 0.00220 | 0.00213 | 786 | 12.8 | 3.84 | 34.3 | 1.73 | 3.71 |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khonik, V.A. Understanding of the Structural Relaxation of Metallic Glasses within the Framework of the Interstitialcy Theory. Metals 2015, 5, 504-529. https://doi.org/10.3390/met5020504
Khonik VA. Understanding of the Structural Relaxation of Metallic Glasses within the Framework of the Interstitialcy Theory. Metals. 2015; 5(2):504-529. https://doi.org/10.3390/met5020504
Chicago/Turabian StyleKhonik, Vitaly A. 2015. "Understanding of the Structural Relaxation of Metallic Glasses within the Framework of the Interstitialcy Theory" Metals 5, no. 2: 504-529. https://doi.org/10.3390/met5020504





