Contaminant Particle Motion in Lubricating Grease Flow: A Computational Fluid Dynamics Approach
Abstract
:1. Introduction
2. Method
2.1. Particle Migration Model by Baart et al. [11]
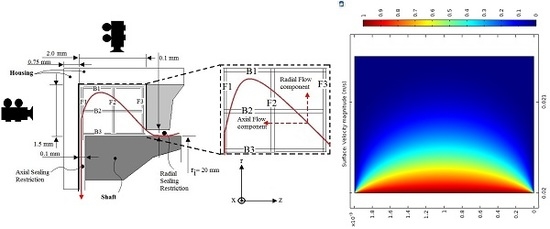
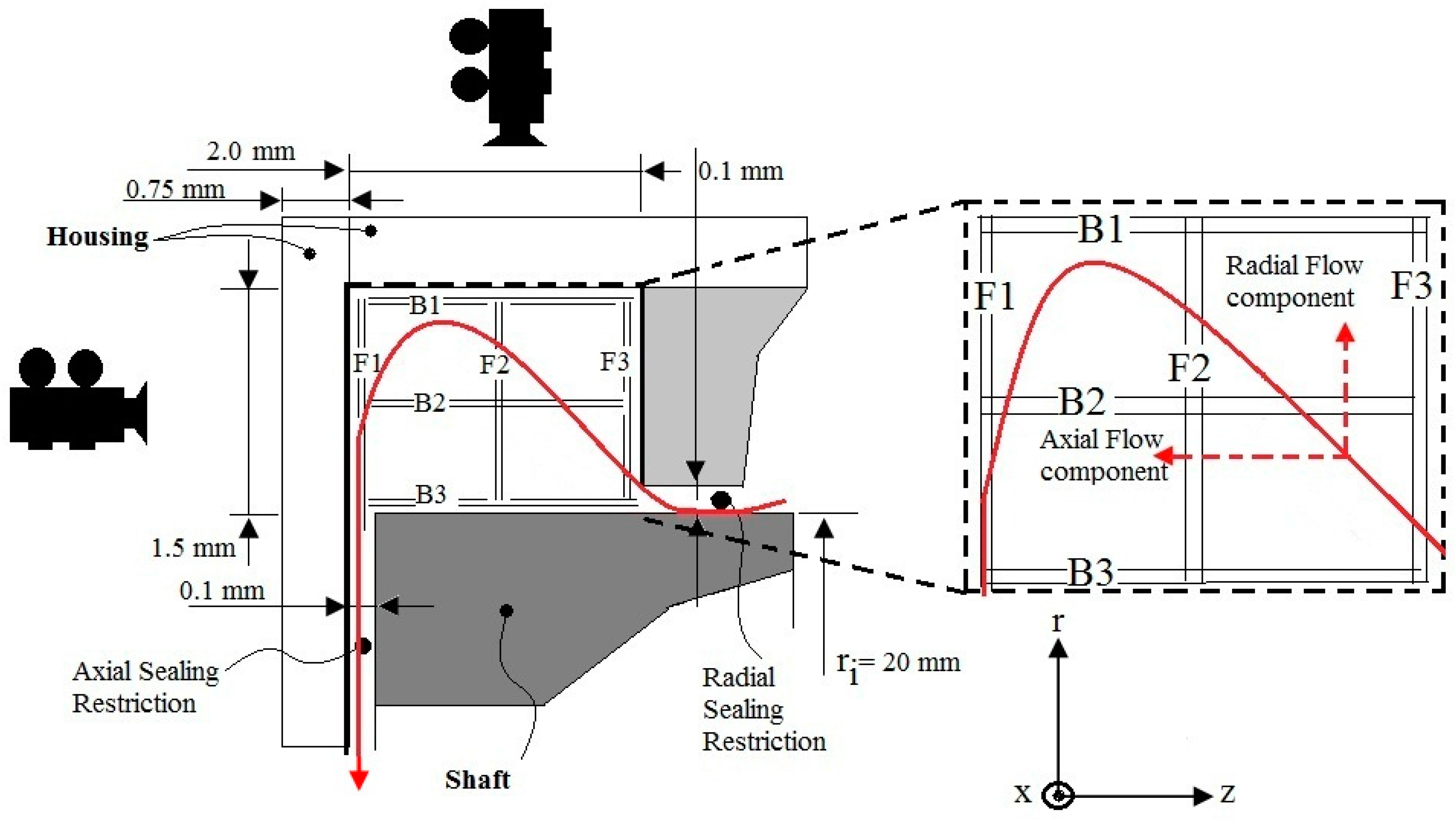
2.2. Numerical Modeling of Particle Position in the Grease Pocket
Flow and Migration Model
3. Results and Discussion
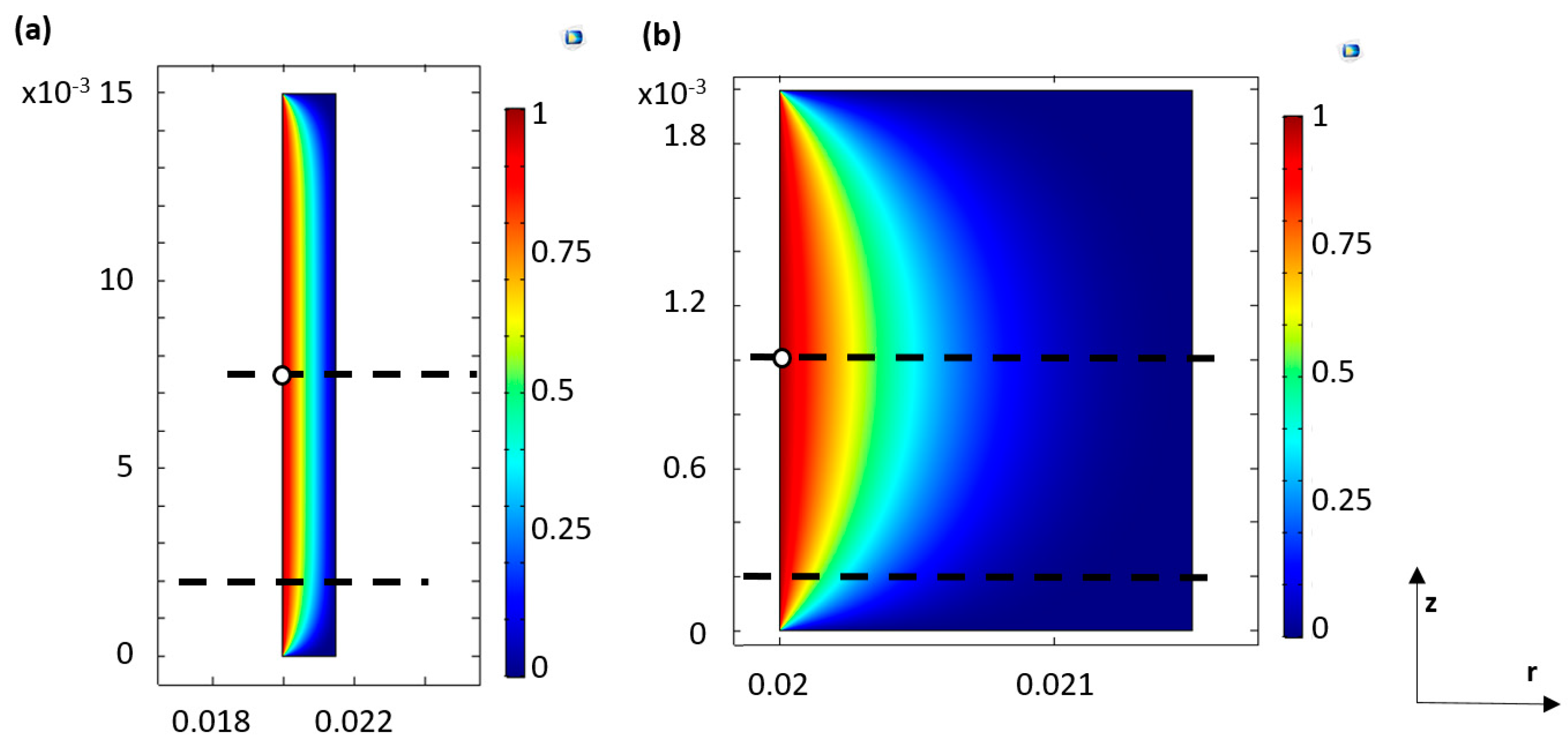
3.1. Velocity Field and Velocity Profiles in the Wide and Narrow Grease Pocket
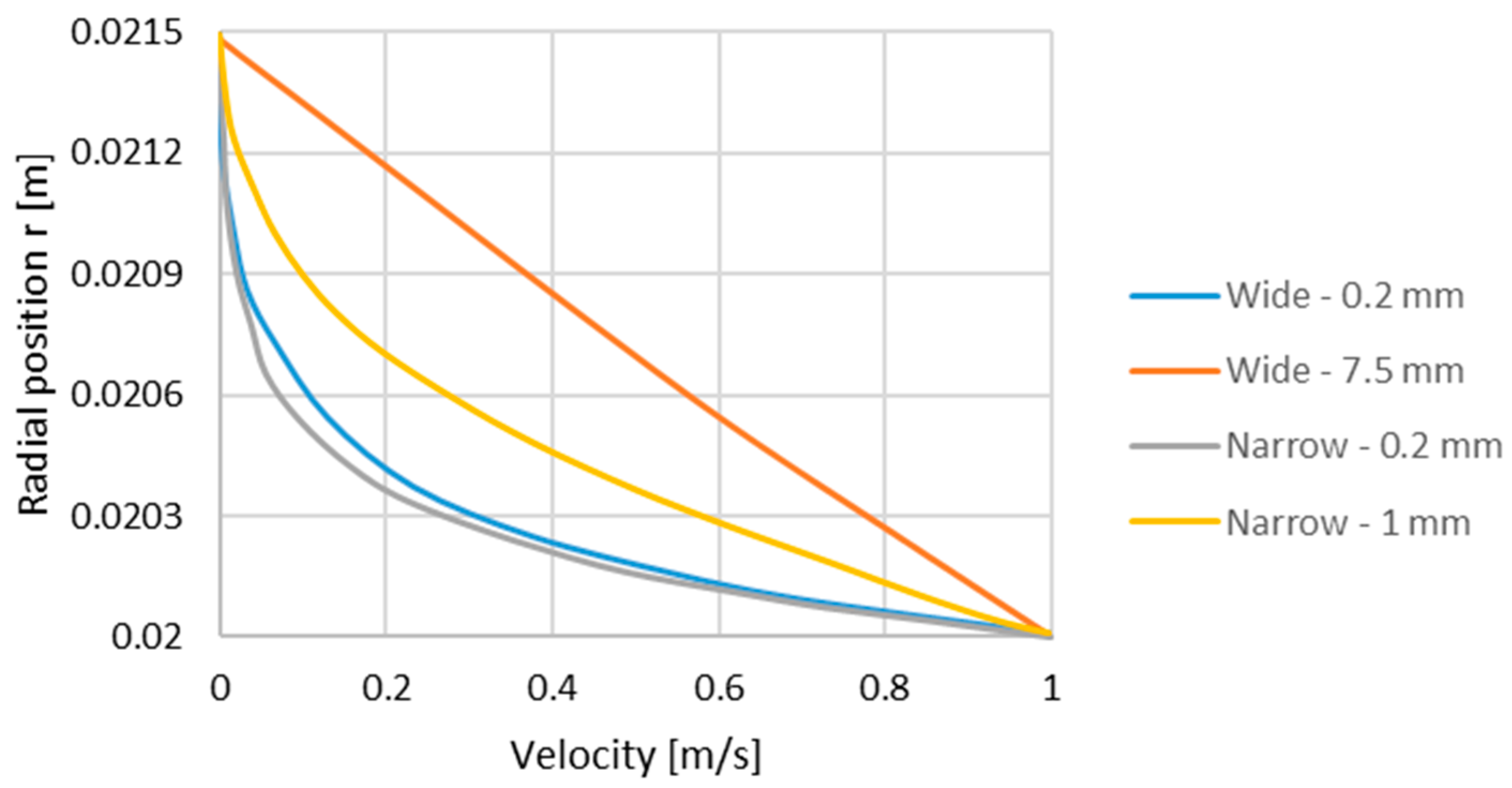
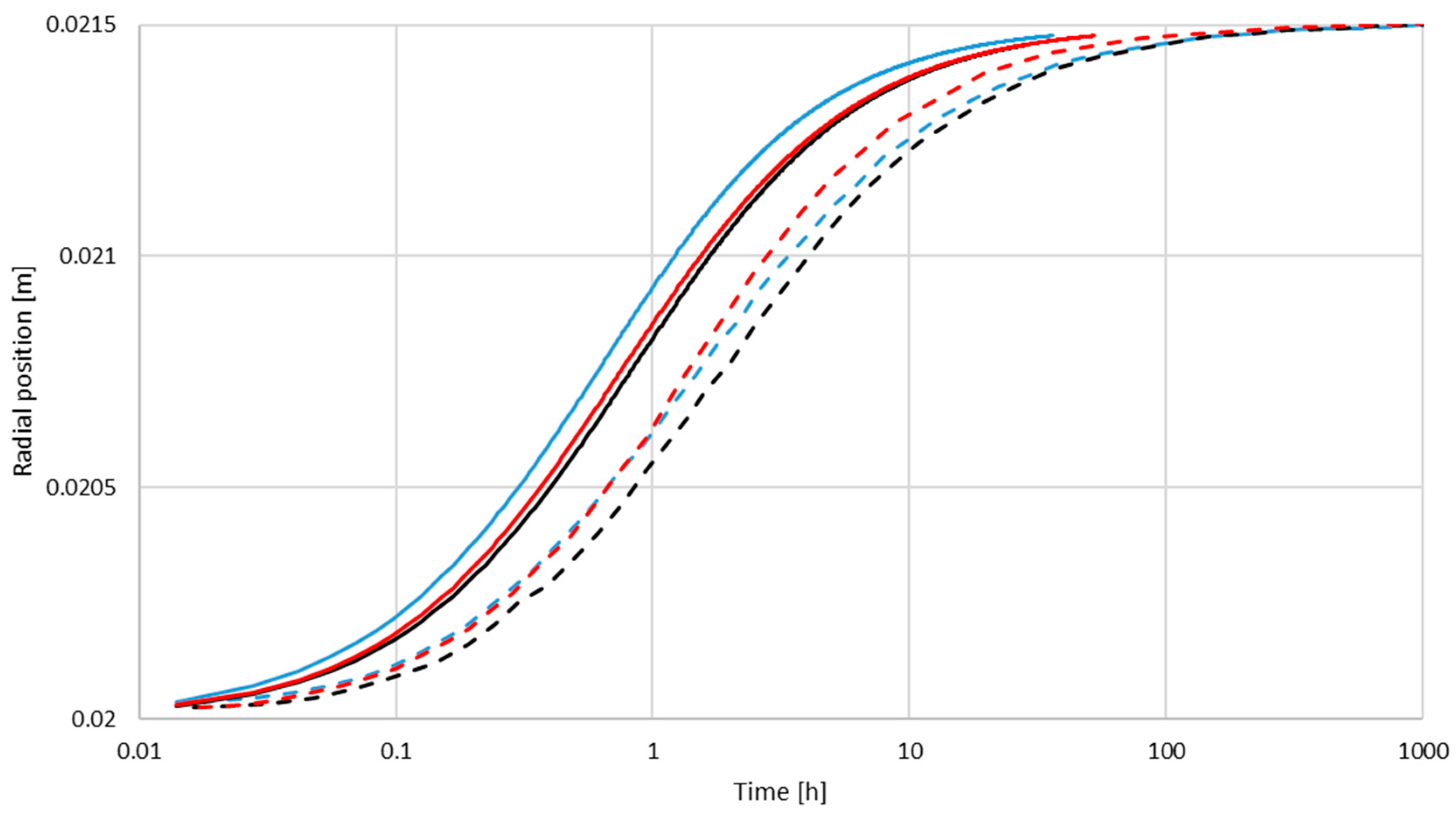
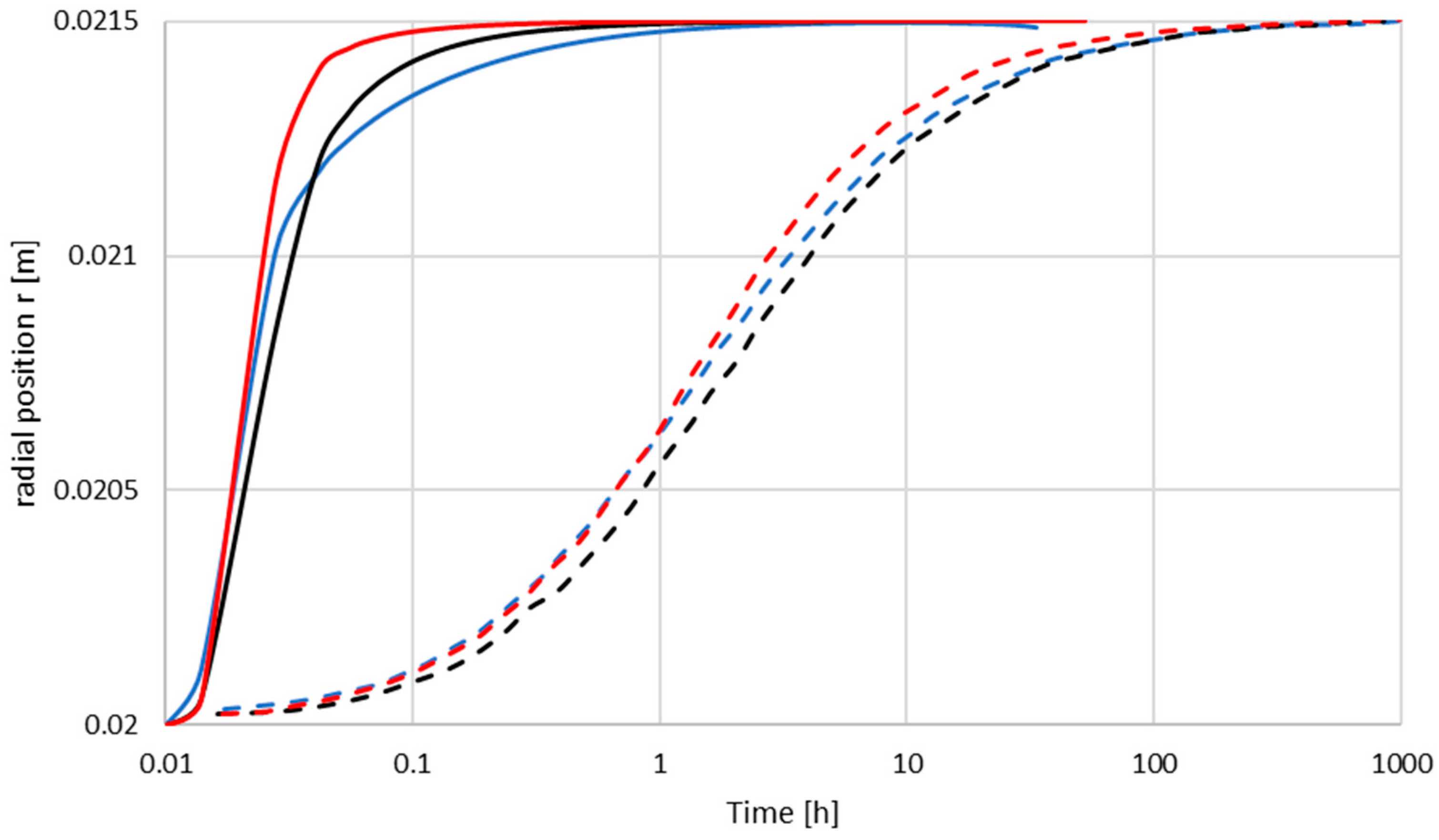
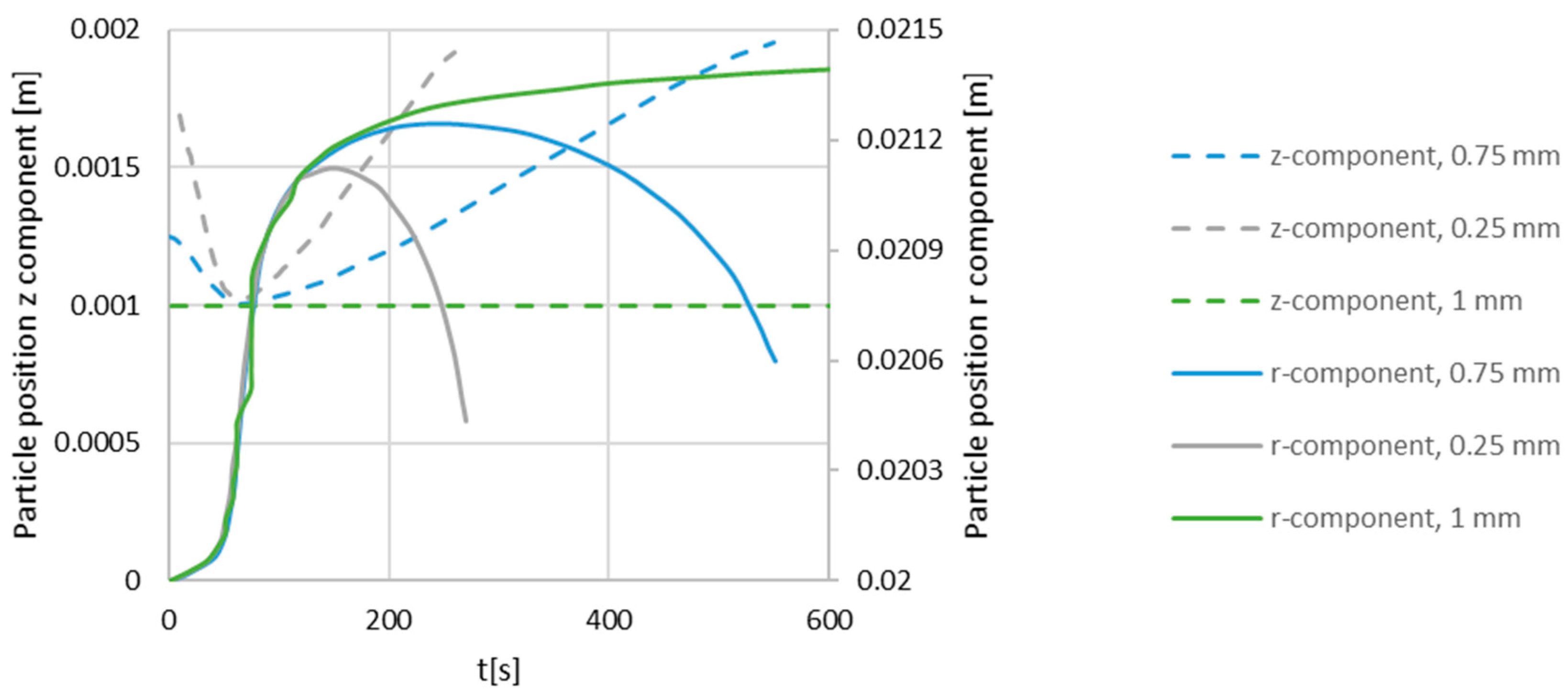
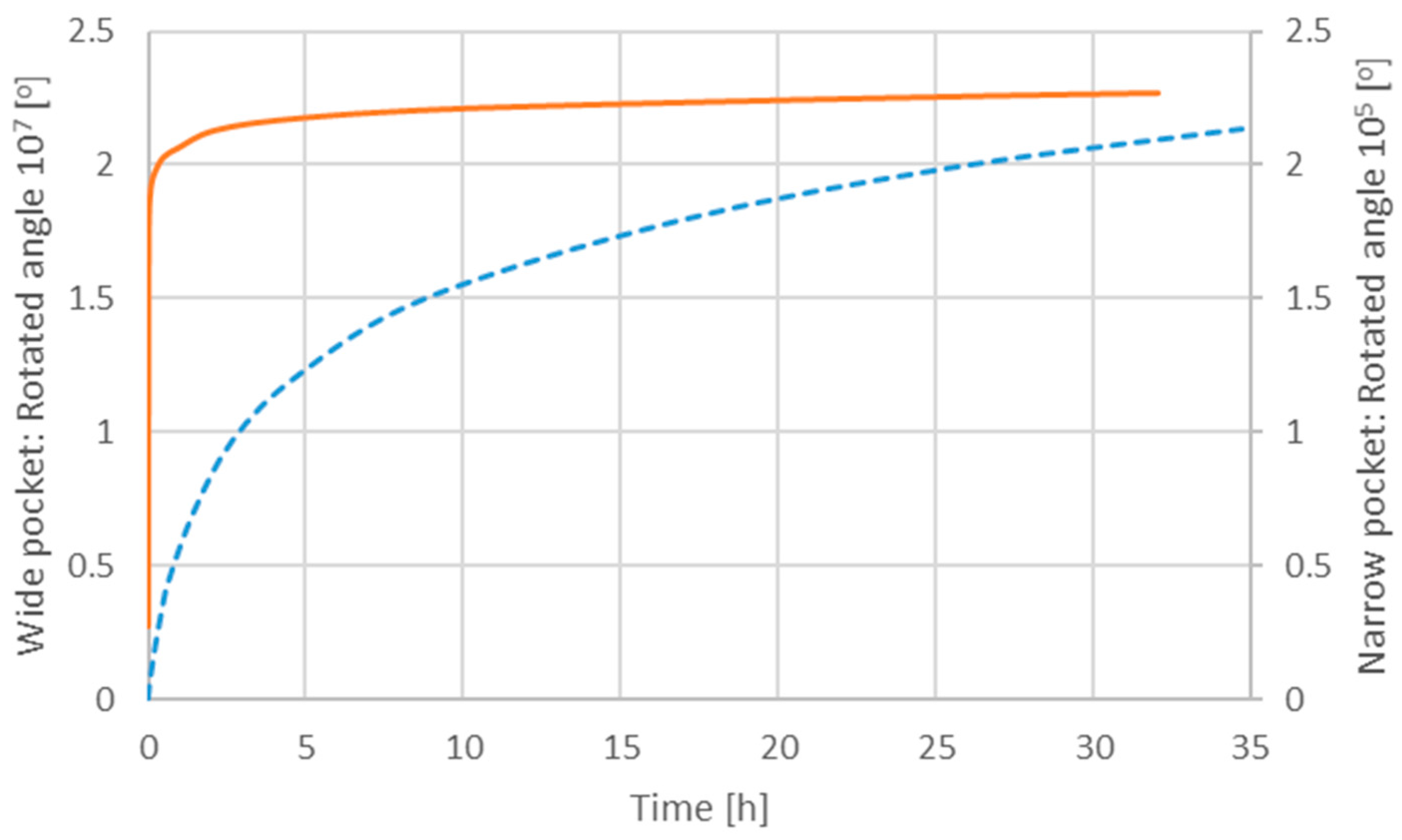
3.2. Particle Migration in the Wide Grease Pocket
3.3. Particle Migration in the Narrow Grease Pocket
4. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lugt, P.M. Grease Lubrication in Rolling Bearings; Wiley: Hoboken, NJ, USA, 2013; ISBN 978-1-118-35391-2. [Google Scholar]
- Torbacke, M.; Rudolphi, A.K.; Kassfeldt, E. Lubricants Properties and Performance; Luleå Tekniska Universitet: Luleå, Sweden, 2012; ISBN 978-91-7439-410-8. [Google Scholar]
- Rizvi, S.Q.A. A Comprehensive Review of Lubricant Chemestry, Technology, Selection and Design; ASTM International: Conshohocken, PA, USA, 2009; ISBN 978-0-8031-7000-1. [Google Scholar]
- Westerberg, L.G.; Lundström, T.S.; Höglund, E.; Lugt, P.M. Investigation of Grease Flow in a Rectangular Channel Including Wall Slip Effects Using Microparticle Image. Tribol. Trans. 2010, 53, 600–609. [Google Scholar] [CrossRef]
- Li, J.X.; Höglund, E.; Westerberg, L.G.; Green, T.M.; Lundström, T.S.; Lugt, P.M.; Baart, P. μpIV measurement of grease velocity profiles in channels with two different types of flow restrictions. Tribol. Int. 2012, 54, 94–99. [Google Scholar] [CrossRef]
- Tallian, T.E. Failure Atlas for Hertz Contact Machine Elements, 2nd ed.; ASME Press: New York, NY, USA, 1999; ISBN 0-7918-0084-9. [Google Scholar]
- Farré-Lladós, J.; Westerberg, L.G.; Casals-Terré, J. New method for lubricating wind turbine pitch gears using embedded micro-nozzles. J. Mech. Sci. Technol. 2017, 31, 797–806. [Google Scholar] [CrossRef]
- Strubel, V.; Simoens, S.; Vergne, P.; Fillot, N.; Ville, F.; El Hajem, M.; Devaux, N.; Mondelin, A.; Maheo, Y. Fluorescence Tracking and µ-PIV of Individual Particles and Lubricant Flow in and around Lubricated Point Contacts. Tribol. Lett. 2017, 65, 75. [Google Scholar] [CrossRef]
- Tropea, C.; Yarin, A.L.; Foss, J.F. Handbook of Experimental Fluid Mechanics; Springer: Berlin, Germany, 2007; ISBN 978-3-540-25141-5. [Google Scholar]
- Franken, M.J.Z.; Chennaoui, M.; Wang, J. Mapping of Grease Migration in High-Speed Bearings Using a Technique Based on Fluorescence Spectroscopy. Tribol. Trans. 2017, 60, 789–793. [Google Scholar] [CrossRef]
- Baart, P.; Green, T.M.; Li, J.X.; Lundström, T.S.; Westerberg, L.G.; Höglund, E.; Lugt, P.M. The Influence of Speed, Grease Type, and Temperature on Radial Contaminant Particle Migration in a Double Restriction Seal. Tribol. Trans. 2011, 54, 867–877. [Google Scholar] [CrossRef]
- Green, T.M.; Baart, P.; Westerberg, L.G.; Lundström, T.S.; Höglund, E.; Lugt, P.M.; Li, J.X. A New Method to Visualize Grease Flow in a Double Restriction Seal Using Microparticle Image Velocimetry. Tribol. Trans. 2011, 54, 784–792. [Google Scholar] [CrossRef]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Westerberg, L.G.; Sarkar, C.; Farre, J.; Lundstrom, T.S. Lubricating Grease Flow in a Double Restriction Seal Geometry: A Computational Fluid Dynamics Approach. Tribol. Lett. 2017, 65, 1–17. [Google Scholar] [CrossRef]
- Raffel, M.; Willert, C.E.; Wereley, S.; Kompenhans, J. Particle Image Velocimetry, 2nd ed.; Springer: Berlin, Germany, 2007. [Google Scholar]
- Karnis, A.; Mason, S.G. Particle Motions in Sheared Suspensions. XIX. Viscoelastic Media. J. Rheol. 1966, 10, 571–592. [Google Scholar] [CrossRef]
- Moin, P. Fundamentals of Engineering Numerical Analysis; Cambridge University Press: Cambridge, UK, 2010; ISBN 9780511781438. [Google Scholar]
| a (µm) | ρp (kg/m3) | (m/s) | Temperature Test (°C) |
|---|---|---|---|
| 7 | 2100 | 1 | 25 |
| NLGI 1 grade | τyield (Pa) | K (Pa.s) | n | ƞbo (Pa.s) | ρg (kg/m3) | α (m−1) |
|---|---|---|---|---|---|---|
| 00 | 15 | 12 | 0.63 | 0.89 | 890 | −1000 |
| 1 | 260 | 61 | 0.42 | 0.49 | 910 | −2000 |
| 2 | 500 | 8.2 | 0.63 | 0.25 | 930 | −3000 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Westerberg, L.-G.; Farré-Lladós, J.; Sarkar, C.; Casals-Terré, J. Contaminant Particle Motion in Lubricating Grease Flow: A Computational Fluid Dynamics Approach. Lubricants 2018, 6, 10. https://doi.org/10.3390/lubricants6010010
Westerberg L-G, Farré-Lladós J, Sarkar C, Casals-Terré J. Contaminant Particle Motion in Lubricating Grease Flow: A Computational Fluid Dynamics Approach. Lubricants. 2018; 6(1):10. https://doi.org/10.3390/lubricants6010010
Chicago/Turabian StyleWesterberg, Lars-Göran, Josep Farré-Lladós, Chiranjit Sarkar, and Jasmina Casals-Terré. 2018. "Contaminant Particle Motion in Lubricating Grease Flow: A Computational Fluid Dynamics Approach" Lubricants 6, no. 1: 10. https://doi.org/10.3390/lubricants6010010