Padé Approximant and Minimax Rational Approximation in Standard Cosmology

Abstract

The luminosity distance in the standard cosmology as given by ΛCDM and, consequently, the distance modulus for supernovae can be defined by the Padé approximant. A comparison with a known analytical solution shows that the Padé approximant for the luminosity distance has an error of $4\%$ at redshift $=10$. A similar procedure for the Taylor expansion of the luminosity distance gives an error of $4\%$ at redshift $=0.7$; this means that for the luminosity distance, the Padé approximation is superior to the Taylor series. The availability of an analytical expression for the distance modulus allows applying the Levenberg–Marquardt method to derive the fundamental parameters from the available compilations for supernovae. A new luminosity function for galaxies derived from the truncated gamma probability density function models the observed luminosity function for galaxies when the observed range in absolute magnitude is modeled by the Padé approximant. A comparison of ΛCDM with other cosmologies is done adopting a statistical point of view.

1. Introduction

In order to obtain astronomical observables, such as the distance modulus and the absolute magnitude for supernovae (SN) of Type Ia in the standard cosmological approach, as given by the ΛCDM model, we need the evaluation of the luminosity distance, which is derived from the comoving distance. At the moment of writing, there is no analytical expression for the integral of the comoving distance in ΛCDM, and a numerical integration should be implemented. An analytical expression for the integral of the comoving distance in ΛCDM can be obtained by adopting the technique of the Padé approximant; see [1,2,3]. Once an approximate solution is obtained for the luminosity distance, we can evaluate the distance modulus and the absolute magnitude for SNs. Furthermore, the minimax rational approximation can provide a compact formula for the two above astronomical observables as functions of the redshift. From an observational point of view, the progressive increase in the number of supernova (SN) of Type Ia for which the distance modulus is available, 34 SNein the sample, which produced evidence for the accelerating universe (see [4]), 580 SNe in the Union 2.1 compilation (see [5]) and 740 SNe in the joint light-curve analysis (JLA) (see [6]), allows analyzing both the ΛCDM and other cosmologies from a statistical point of view. The statistical approach to cosmology is not new and has been recently adopted by [7,8]. In order to cover the previous arguments, Section 2 introduces the Padé approximant and determines the basic integral of the ΛCDM, which allows deriving the approximate luminosity distance. The approximate magnitude here derived is applied to parametrize a new luminosity function for galaxies at high redshift; see Section 3. The distance modulus in different cosmologies is reviewed, and the main statistical parameters connected with the distance modulus are derived; see Section 4.

2. The Standard Cosmology

This section introduces the Hubble distance, the dark energy density, the curvature, the matter density and the comoving distance (which is presented as the integral of the inverse of the Hubble function). In the absence of a general analytical formula for the comoving distance, we introduce the Padé approximation. As a consequence, we deduce an approximate solution for the transverse comoving distance, the luminosity distance and the distance modulus. The shift that the Padé approximation introduces in the relationship for the poles is discussed. The calibration of the Padé approximation for the distance modulus on two astronomical catalogs allows deducing the minimax polynomial approximation for the observed distance modulus for SNs of Type Ia.

2.1. The Padé Approximant

We use the same symbols as in [9], where the Hubble distance $D_{\mathrm{H}}$ is defined as:

$$D_{\mathrm{H}}\equiv {\displaystyle \frac{c}{H_0}}$$

(1)

We then introduce the first parameter: ${\Omega }_{\mathrm{M}}$

$${\Omega }_{\mathrm{M}}={\displaystyle \frac{8\pi G{\rho }_0}{3H_0^2}}$$

(2)

where G is the Newtonian gravitational constant and ${\rho }_0$ is the mass density at the present time. The second parameter is ${\Omega }_{\Lambda }$:

$${\Omega }_{\Lambda }\equiv {\displaystyle \frac{\Lambda c^2}{3H_0^2}}$$

(3)

where Λ is the cosmological constant; see [10]. The two previous parameters are connected with the curvature ${\Omega }_K$ by:

$${\Omega }_{\mathrm{M}}+{\Omega }_{\Lambda }+{\Omega }_K=1$$

(4)

The comoving distance, $D_{\mathrm{C}}$, is:

$$D_{\mathrm{C}}=D_{\mathrm{H}}{\int }_0^z{\displaystyle \frac{d{z}^{\prime }}{E(z^{\prime })}}$$

(5)

where $E(z)$ is the `Hubble function’:

$$E(z)=\sqrt{{\Omega }_{\mathrm{M}}{(1+z)}^3+{\Omega }_K{(1+z)}^2+{\Omega }_{\Lambda }}$$

(6)

The above integral does not have an analytical formula, except for the case of ${\Omega }_{\Lambda }=0$, but the Padé approximant (see Appendix B) gives an approximate evaluation, and the indefinite integral is (B3), where the coefficients $a_j$ and $b_j$ can be found in Appendix A. The approximate definite integral for (5) is therefore:

$$D_{\mathrm{C},2,2}=F_{2,2}(z;a_0,a_1,a_2,b_0,b_1,b_2)-F_{2,2}(0;a_0,a_1,a_2,b_0,b_1,b_2)$$

(7)

The transverse comoving distance $D_{\mathrm{M}}$ is:

$$D_{\mathrm{M}}=\left\{\begin{array}{cc}{D}_{\mathrm{H}}{\displaystyle \frac{1}{\sqrt{{\Omega }_K}}}sinh\left[\sqrt{{\Omega }_K}{D}_{\mathrm{C}}/D_{\mathrm{H}}\right]\hfill & \mathrm{for}{\Omega }_K>0\hfill \\ D_{\mathrm{C}}\hfill & \mathrm{for}{\Omega }_K=0\hfill \\ D_{\mathrm{H}}{\displaystyle \frac{1}{\sqrt{|{\Omega }_K|}}}sin\left[\sqrt{|{\Omega }_K|}{D}_{\mathrm{C}}/D_{\mathrm{H}}\right]\hfill & \mathrm{for}{\Omega }_K<0\hfill \end{array}\right.$$

(8)

and the approximate transverse comoving distance $D_{\mathrm{M},2,2}$ computed with the Padé approximant is:

$$D_{\mathrm{M},2,2}=\left\{\begin{array}{cc}{D}_{\mathrm{H}}{\displaystyle \frac{1}{\sqrt{{\Omega }_K}}}sinh\left[\sqrt{{\Omega }_K}{D}_{\mathrm{C},2,2}/D_{\mathrm{H}}\right]\hfill & \mathrm{for}{\Omega }_K>0\hfill \\ D_{\mathrm{C},2,2}\hfill & \mathrm{for}{\Omega }_K=0\hfill \\ D_{\mathrm{H}}{\displaystyle \frac{1}{\sqrt{|{\Omega }_K|}}}sin\left[\sqrt{|{\Omega }_K|}{D}_{\mathrm{C},2,2}/D_{\mathrm{H}}\right]\hfill & \mathrm{for}{\Omega }_K<0\hfill \end{array}\right.$$

(9)

An analytic expression for $D_{\mathrm{M}}$ can be obtained when: ${\Omega }_{\Lambda }=0$:

$$D_{\mathrm{M}}=D_{\mathrm{H}}{\displaystyle \frac{2[2-{\Omega }_{\mathrm{M}}(1-z)-(2-{\Omega }_{\mathrm{M}})\sqrt{1+{\Omega }_{\mathrm{M}}z}]}{{\Omega }_{\mathrm{M}}^2(1+z)}}\mathrm{for}{\Omega }_{\Lambda }=0$$

(10)

This expression is useful for calibrating the numerical codes, which evaluate $D_{\mathrm{M}}$ when ${\Omega }_{\Lambda }\ne 0$.

The luminosity distance is:

$$D_{\mathrm{L}}=(1+z)D_{\mathrm{M}}$$

(11)

which in the case of ${\Omega }_{\Lambda }=0$ becomes:

$$D_{\mathrm{L}}=2{\displaystyle \frac{c\left(2-{\Omega }_M\left(1-z\right)-\left(2-{\Omega }_M\right)\sqrt{z{\Omega }_M+1}\right)}{H_0{{\Omega }_M}^2}}$$

(12)

and the distance modulus when ${\Omega }_{\Lambda }=0$ is:

$$m-M=25+5{\displaystyle \frac{1}{ln\left(10\right)}}ln(2{\displaystyle \frac{c\left(2-{\Omega }_M\left(1-z\right)-\left(2-{\Omega }_M\right)\sqrt{z{\Omega }_M+1}\right)}{H_0{{\Omega }_M}^2}})$$

(13)

The Padé approximant luminosity distance when ${\Omega }_{\Lambda }\ne 0$ is:

$$D_{\mathrm{L},2,2}=(1+z)D_{\mathrm{M},2,2}$$

(14)

and the Padé approximant distance modulus, ${(m-M)}_{2,2}$, in its compact version, is:

$${(m-M)}_{2,2}=25+5{log}_{10}(D_{\mathrm{L},2,2})$$

(15)

and, as a consequence, the Padé approximant absolute magnitude, $M_{2,2}$, is:

$$M_{2,2}=m-25-5{log}_{10}(D_{\mathrm{L},2,2})$$

(16)

The expanded version of the Padé approximant distance modulus is:

$${(m-M)}_{2,2}=25+5{\displaystyle \frac{1}{ln\left(10\right)}}ln\left({\displaystyle \frac{c\left(1+z\right)}{H_0\sqrt{{\Omega }_K}}}sinh\left(1/2{\displaystyle \frac{\sqrt{{\Omega }_K}A}{{b_2}^2\sqrt{4b_0{b}_2-{b_1}^2}}}\right)\right)$$

(17)

with:

$$\begin{array}{cc}\hfill A=& ln\left(z^2{b}_2+z{b}_1+b_0\right)a_1{b}_2\sqrt{4b_0{b}_2-{b_1}^2}-ln\left(z^2{b}_2+z{b}_1+b_0\right)a_2{b}_1\sqrt{4b_0{b}_2-{b_1}^2}\hfill \\ & -ln\left(b_0\right)a_1{b}_2\sqrt{4b_0{b}_2-{b_1}^2}+ln\left(b_0\right)a_2{b}_1\sqrt{4b_0{b}_2-{b_1}^2}+2a_{2}z{b}_2\sqrt{4b_0{b}_2-{b_1}^2}\hfill \\ & +4arctan\left({\displaystyle \frac{2z{b}_2+b_1}{\sqrt{4b_0{b}_2-{b_1}^2}}}\right)a_0{b_2}^2-2arctan\left({\displaystyle \frac{2z{b}_2+b_1}{\sqrt{4b_0{b}_2-{b_1}^2}}}\right)b_1{a}_1{b}_2\hfill \\ & -4arctan\left({\displaystyle \frac{2z{b}_2+b_1}{\sqrt{4b_0{b}_2-{b_1}^2}}}\right)a_2{b}_0{b}_2+2arctan\left({\displaystyle \frac{2z{b}_2+b_1}{\sqrt{4b_0{b}_2-{b_1}^2}}}\right){b_1}^2{a}_2\hfill \\ & -4arctan\left({\displaystyle \frac{b_1}{\sqrt{4b_0{b}_2-{b_1}^2}}}\right)a_0{b_2}^2+2arctan\left({\displaystyle \frac{b_1}{\sqrt{4b_0{b}_2-{b_1}^2}}}\right)b_1{a}_1{b}_2\hfill \\ & +4arctan\left({\displaystyle \frac{b_1}{\sqrt{4b_0{b}_2-{b_1}^2}}}\right)a_2{b}_0{b}_2-2arctan\left({\displaystyle \frac{b_1}{\sqrt{4b_0{b}_2-{b_1}^2}}}\right){b_1}^2{a}_2\hfill \end{array}$$

The above procedure can also be applied when the argument of the integral (5) is expanded about z = 0 in a Taylor series of order six. The resulting luminosity distance, $D_{\mathrm{L},6}$, is:

$$D_{\mathrm{L},6}=-{\displaystyle \frac{c\left(1+z\right)}{\sqrt{{\Omega }_K}{H}_0}}sinh\left({\displaystyle \frac{\sqrt{{\Omega }_K}z{\mathit{C}}_{\mathit{T}}}{7680}}\right)$$

(18)

where:

$$\begin{array}{ccc}\hfill C_T=& & 315{{\Omega }_M}^5{z}^5+350{{\Omega }_M}^4{z}^5-420{{\Omega }_M}^4{z}^4+400{{\Omega }_M}^3{z}^5-480{{\Omega }_M}^3{z}^4+480{{\Omega }_M}^2{z}^5\hfill \\ & & +600{{\Omega }_M}^3{z}^3-576{{\Omega }_M}^2{z}^4+640z^5{\Omega }_M+720{{\Omega }_M}^2{z}^3-768z^4{\Omega }_M+1280z^5-960{{\Omega }_M}^2{z}^2\hfill \\ & & +960z^3{\Omega }_M-1536z^4-1280z^2{\Omega }_M+1920z^3+1920z{\Omega }_M-2560z^2+3840z-7680\hfill \end{array}$$

(19)

The goodness of the approximation is evaluated through the percentage error, δ, which is:

$$\delta ={\displaystyle \frac{|D_{\mathrm{L}}(z)-D_{\mathrm{L},\mathrm{app}}(z)|}{D_{\mathrm{L}}(z)}}\times 100$$

(20)

where $D_{\mathrm{L}}(z)$ is the exact luminosity distance when ${\Omega }_{\Lambda }=0$ (see Equation (11)) and $D_{\mathrm{L},\mathrm{app}}(z)$ is the Taylor or Padé approximate luminosity distance; see also Formula (2.12) in [1].

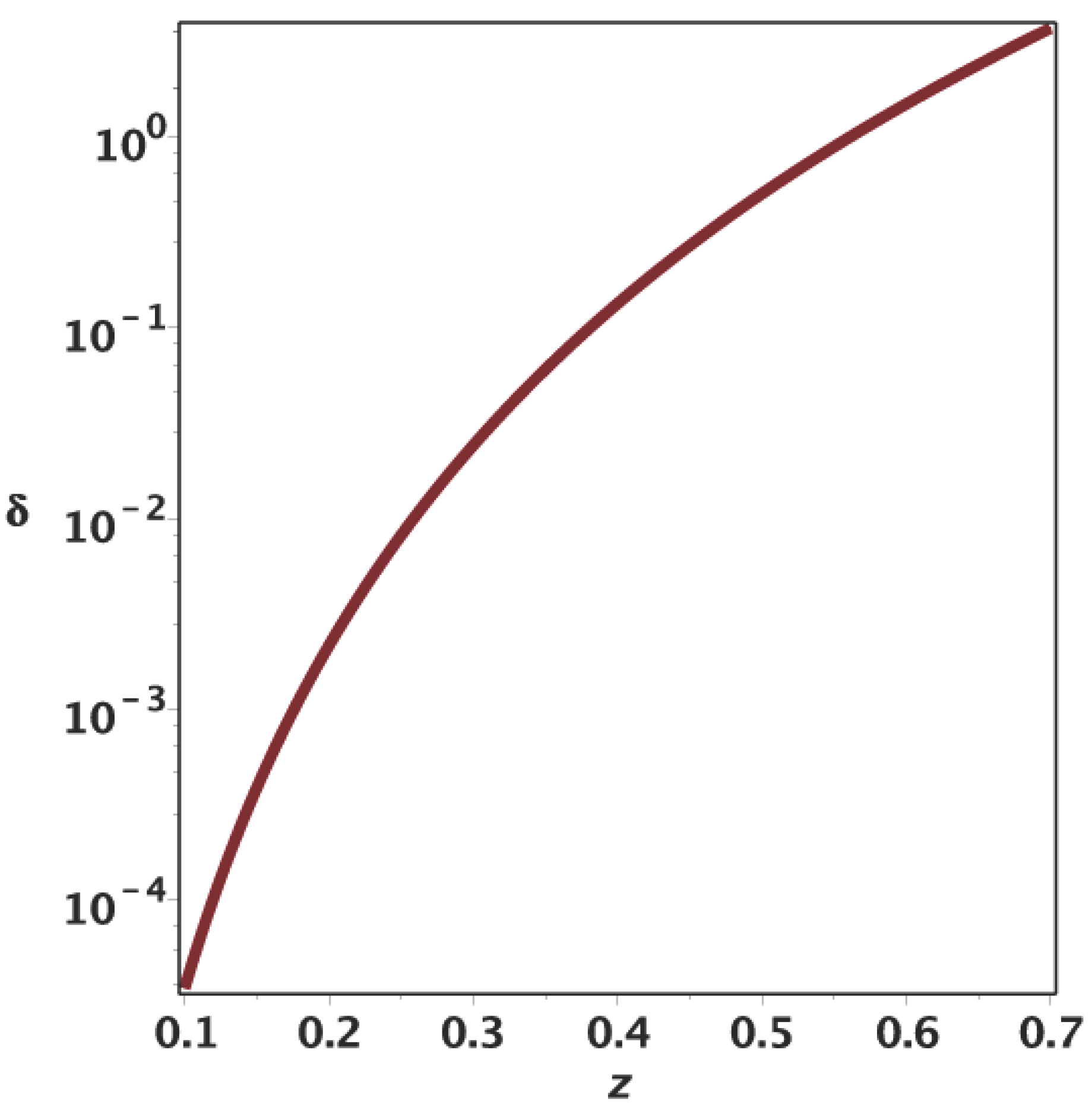
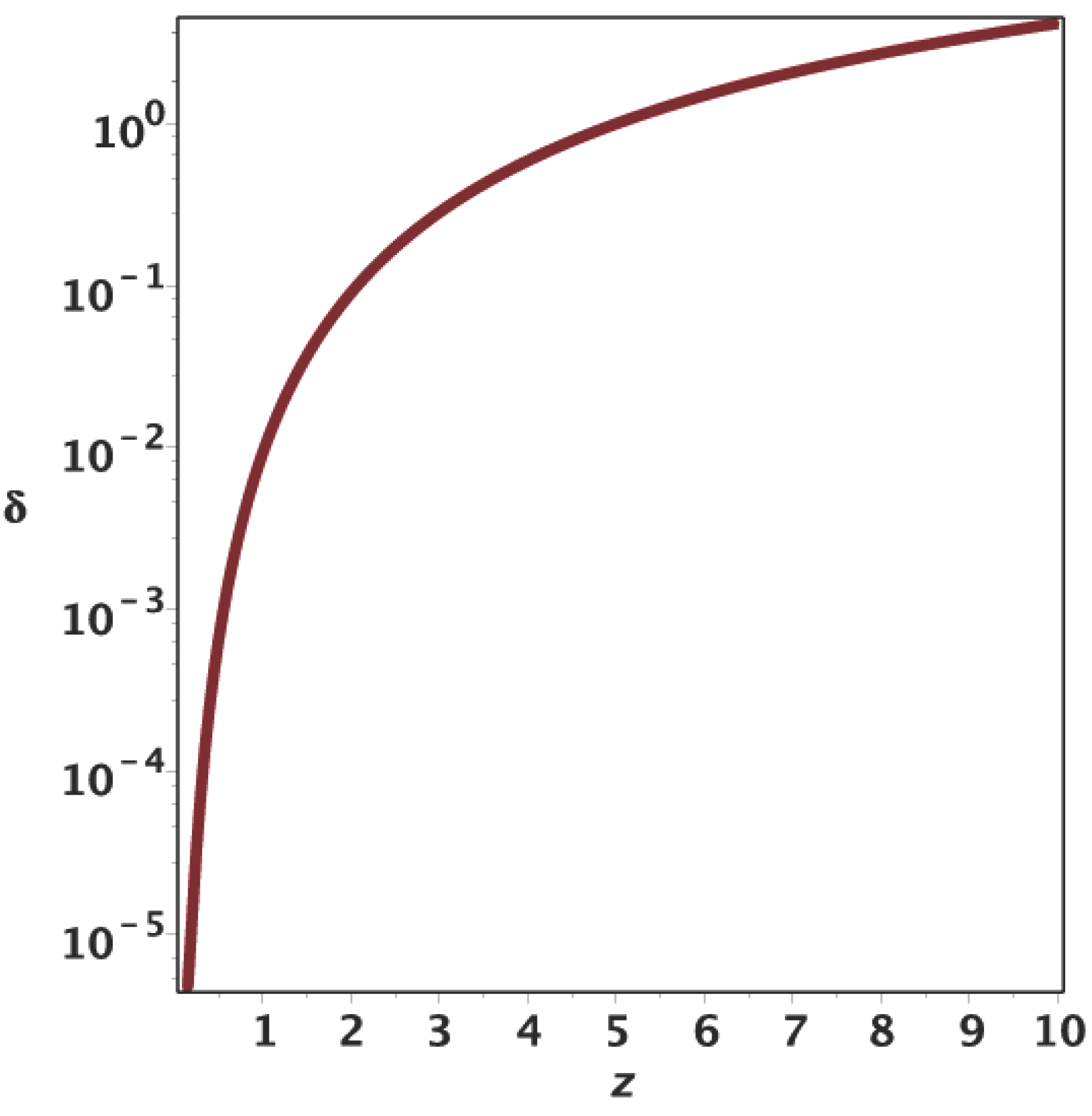
Figure 1 and Figure 2 report the percentage error as a function of the redshift z for the Taylor and Padé approximations, respectively. The Padé approximation is superior to the truncated Taylor expansion, because $\delta \approx 4$ is reached at $z=10$ for the Padé approximant and at $z=0.7$ for the Taylor expansion.

2.2. The Presence of Poles

The integrand of (5) contains poles or singularities for a given set of parameters; see Figure 3.

The equation which models the poles is:

$$E(z)=0$$

(21)

The exact solution of the above equation $z({\Omega }_{\Lambda };{\Omega }_K=0.11)$ is shown in Figure 4, together with the Padé approximated solution $z_{2,2}({\Omega }_{\Lambda };{\Omega }_K=0.11)$. Is therefore possible to conclude that the Padé approximation shifts the locations of the poles by $\Delta z$; this shift expressed as a percentage error is $\delta \approx 17\%$ in the considered interval ${\Omega }_{\Lambda }=[1.15,1.85]$.

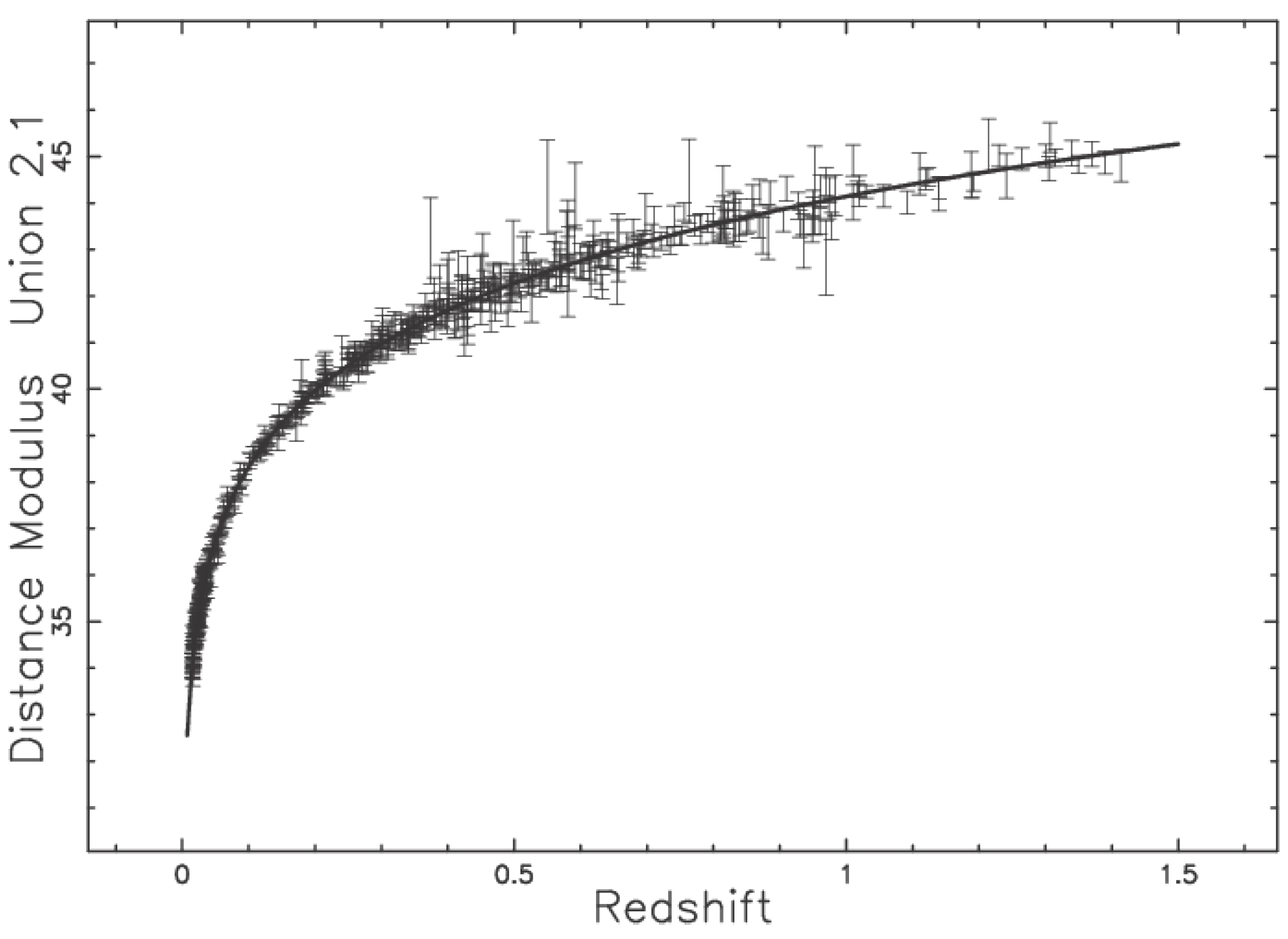
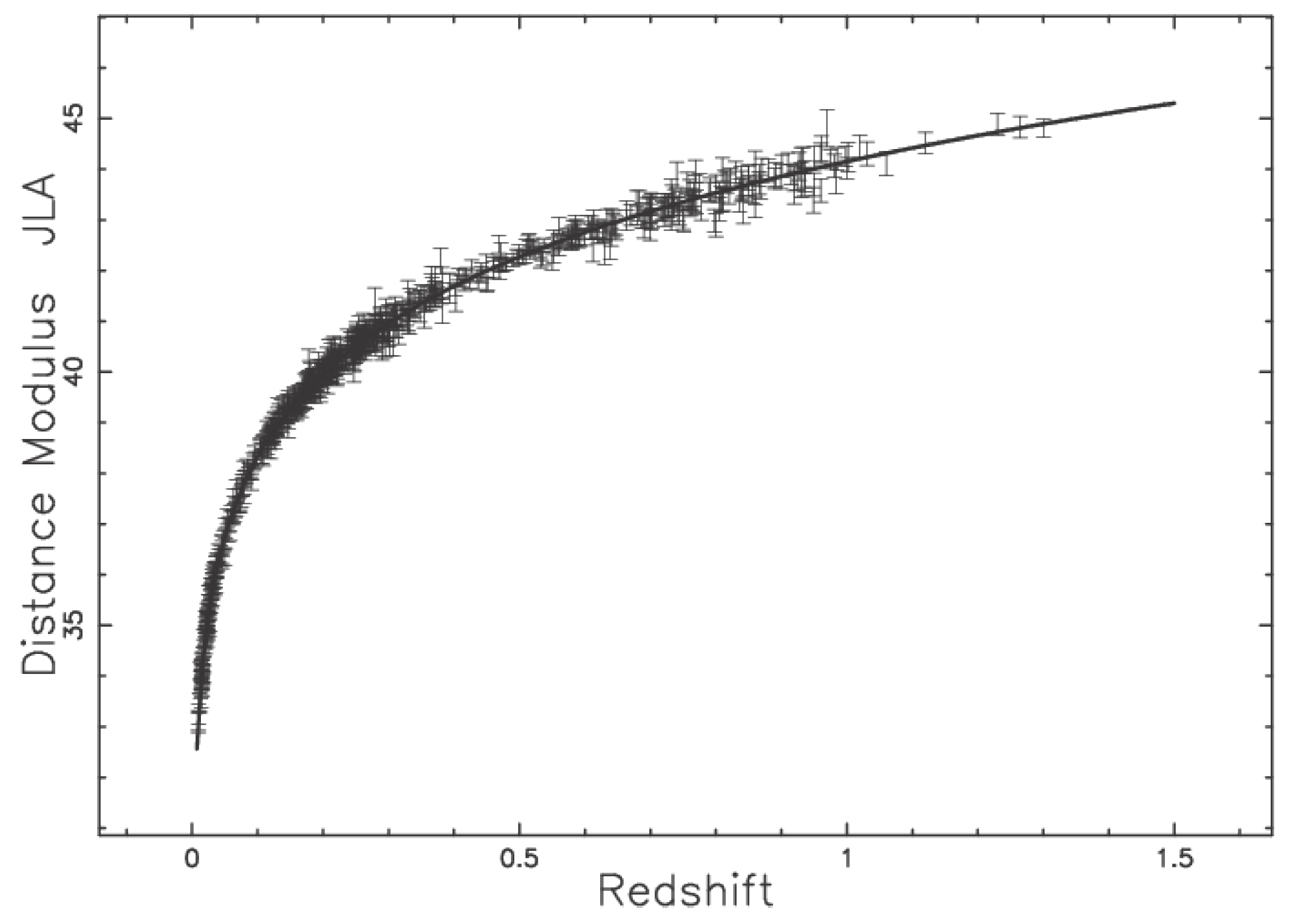
2.3. An Astrophysical Application

We now have a Padé approximant expression for the distance modulus as a function of of $H_0$, ${\Omega }_{\mathrm{M}}$ and ${\Omega }_{\Lambda }$. We now perform an astronomical test on the 580 SNe in the Union 2.1 compilation (see [5]) and on the 740 SNe in the joint light-curve analysis (JLA). The JLA compilation is available at the Strasbourg Astronomical Data Center (CDS) and consists of SNe (Type I-a) for which we have a heliocentric redshift, z, apparent magnitude $m_{\mathrm{B}}^{\star }$ in the B band, error in $m_{\mathrm{B}}^{\star }$, ${\sigma }_{m_{\mathrm{B}}^{\star }}$, parameter $X1$, error in $X1$, ${\sigma }_{X1}$, parameter C, error in the parameter C, ${\sigma }_C$ and ${log}_{10}(M_{stellar})$. The observed distance modulus is defined by Equation (4) in [6]:

$$m-M=-C\beta +\mathit{X}1\alpha -M_b+m_{\mathrm{B}}^{\star }$$

(22)

The adopted parameters are $\alpha =0.141$, $\beta =3.101$ and:

$$M_b=\left\{\begin{array}{cc}-19.05\hfill & \text{if}{M}_{stellar}<{10}^{10}{M}_{\odot }\hfill \\ -19.12\hfill & \text{if}{M}_{stellar}\ge {10}^{10}{M}_{\odot }\hfill \end{array}\right.$$

(23)

see Line 1 in Table 10 of [6]. The uncertainty in the observed distance modulus, ${\sigma }_{m-M}$, is found by implementing the error propagation equation (often called the law of errors of Gauss) when the covariant terms are neglected; see Equation (3.14) in [11],

$${\sigma }_{m-M}=\sqrt{{\alpha }^2{{\sigma }_{\mathit{X}1}}^2+{\beta }^2{{\sigma }_C}^2+{{\sigma }_{{\mathit{m}}_B^{\star }}}^2}$$

(24)

The three astronomical parameters in question, $H_0$, ${\Omega }_{\mathrm{M}}$ and ${\Omega }_{\Lambda }$, can be derived trough the Levenberg–Marquardt method (subroutine MRQMINin [12]) once an analytical expression for the derivatives of the distance modulus with respect to the unknown parameters is provided. As a practical example, the derivative of the distance modulus, ${(m-M)}_{2,2}$, with respect to $H_0$ is:

$${\displaystyle \frac{d{(m-M)}_{2,2}}{d{H}_0}}=-5{\displaystyle \frac{1}{H_{0}ln\left(10\right)}}$$

(25)

This numerical procedure minimizes the merit function ${\chi }^2$ evaluated as:

$${\chi }^2=\sum _{i=1}^N[{\displaystyle \frac{{(m-M)}_i-(m-M){(z_i)}_{th}}{{\sigma }_i}}{]}^2$$

(26)

where $N=480$, ${(m-M)}_i$ is the observed distance modulus evaluated at $z_i$, ${\sigma }_i$ is the error in the observed distance modulus evaluated at $z_i$ and $(m-M){(z_i)}_{th}$ is the theoretical distance modulus evaluated at $z_i$; see Formula (15.5.5) in [12]. A reduced merit function ${\chi }_{red}^2$ is evaluated by:

$${\chi }_{red}^2={\chi }^2/NF$$

(27)

where $NF=n-k$ is the number of degrees of freedom, n is the number of SNe and k is the number of parameters. Another useful statistical parameter is the associated Q-value, which has to be understood as the maximum probability of obtaining a better fitting; see Formula (15.2.12) in [12]:

$$Q=1-GAMMQ({\displaystyle \frac{N-k}{2}},{\displaystyle \frac{{\chi }^2}{2}})$$

(28)

where GAMMQ is a subroutine for the incomplete gamma function. The Akaike information criterion (AIC) (see [13]) is defined by:

$$AIC=2k-2ln(L)$$

(29)

where L is the likelihood function. We assume a Gaussian distribution for the errors, and the likelihood function can be derived from the ${\chi }^2$ statistic $L\propto exp(-{\displaystyle \frac{{\chi }^2}{2}})$, where ${\chi }^2$ has been computed by Equation (26); see [14,15]. Now, the AIC becomes:

$$AIC=2k+{\chi }^2$$

(30)

Table 1. Numerical values of ${\chi }^2$, ${\chi }_{red}^2$, Q, and the AIC of the Hubble diagram for two compilations; k stands for the number of parameters. SN, supernoval; JLA, joint light-curve analysis.

Compilation	SNs	k	Parameters	$\mathit{\chi }\mathbf{2}$	${\mathit{\chi }}_{\mathit{r}\mathit{e}\mathit{d}}^{\mathbf{2}}$	Q	AIC
Union 2.1	577	3	$H_0$ = 69.81; ${\Omega }_{\mathrm{M}}=0.239$; ${\Omega }_{\Lambda }=0.651$	562.699	0.975	0.657	568.699
JLA	740	3	$H_0$ = 69.398; ${\Omega }_{\mathrm{M}}=0.181$; ${\Omega }_{\Lambda }=0.538$	625.733	0.849	0.998	631.733

reports the three astronomical parameters for the two catalogs of SNs, and Figure 5 and Figure 6 display the best fits.

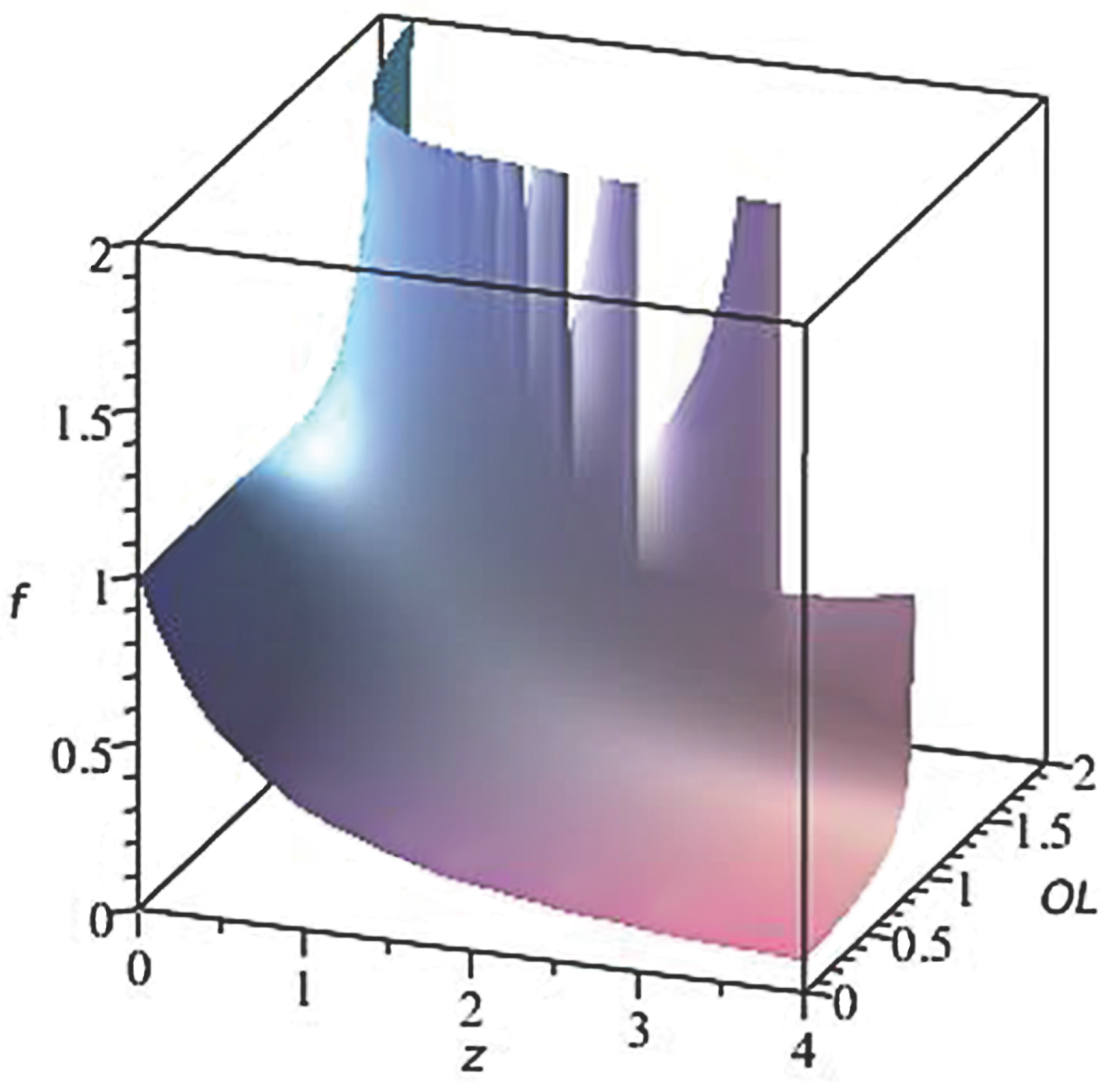
In order to see how $\chi 2$ varies around the minimum found by the Levenberg–Marquardt method, Figure 7 presents a 2D color map for the values of $\chi 2$ when $H_0$ and ${\Omega }_{\mathrm{M}}$ are allowed to vary around the numerical values, which fix the minimum.

The Padé approximant distance modulus has a simple expression when the minimax rational approximation is used, as an example $p=3,q=2$; see Appendix C for the meaning of p and q. In the case of the Union 2.1 compilation, the approximation of Formula (17) with the parameters of Table 1 over the range in $z\in [0,4]$ gives the following minimax equation:

$${(m-M)}_{3,2}={\displaystyle \frac{0.359725+5.612031z+5.627811z^2+0.054794z^3}{0.010587+0.137541z+0.115904z^2}}Union2.1compilation$$

(31)

the maximum error being 0.0024. The maximum error of the polynomial approximation as a function of p and q is shown in

Table 2. The maximum error in the minimax rational approximation for the distance modulus in the case of the Union 2.1 compilation.

p	q	Maximum Error
1	1	0.2872
2	2	0.0197
3	2	0.0024
3	3	0.0006

.

In the case of the JLA compilation, the minimax equation is:

$${(m-M)}_{3,2}={\displaystyle \frac{0.442988+6.355991z+5.40531z^2+0.044133z^3}{0.012985+0.154698z+0.109749z^2}}JLAcompilation$$

(32)

the maximum error being 0.003.

The maximum difference between the two minimax formulas, which approximate the distance modulus, Equations (31) and (32), is at $z=4$ and is 0.0584 mag. In the case of the luminosity distance as given by the Padé approximation (see Equation (14)), the minimax approximation gives:

$$\begin{array}{cc}{D}_{\mathrm{L},3,2}={\displaystyle \frac{-7.7618-1788.535z-3203.0635z^2-65.8463z^3}{-0.438-0.3348z+0.02039z^2}}Mpc\hfill & \hfill Union2.1\end{array}$$

(33a)

$$\begin{array}{cc}{D}_{\mathrm{L},3,2}={\displaystyle \frac{-1.1674-2413.8956z-2831.4248z^2-100.2959z^3}{-0.562-0.2367z+0.007746z^2}}Mpc\hfill & \hfill JLA\end{array}$$

(33b)

3. Application at High Redshift

This section introduces a new luminosity function (LF) for galaxies, which has a lower and an upper bound. The presence of a lower bound for the luminosity of galaxies allows one to model the evolution of the LF as a function of the redshift.

3.1. The Schechter Luminosity Function

The Schechter LF, after [16], is the standard LF for galaxies:

$$\Phi ({\displaystyle \frac{L}{L^{*}}})dL=({\displaystyle \frac{{\Phi }^{*}}{L^{*}}}){({\displaystyle \frac{L}{L^{*}}})}^{\alpha }exp\left(-{\displaystyle \frac{L}{L^{*}}}\right)dL$$

(34)

Here, α sets the shape, $L^{*}$ is the characteristic luminosity and ${\Phi }^{*}$ is the normalization. The distribution in absolute magnitude is:

$$\Phi (M)dM=0.921{\Phi }^{*}{10}^{0.4(\alpha +1)(M^{*}-M)}exp(-{10}^{0.4(M^{*}-M)})dM$$

(35)

where $M^{*}$ is the characteristic magnitude.

3.2. The Gamma Luminosity Function

The gamma LF is:

$$f(L;{\Psi }^{*},L^{*},c)={\Psi }^{*}{\displaystyle \frac{{\left({\displaystyle \frac{L}{L^{*}}}\right)}^{c-1}{\mathrm{e}}^{-{\displaystyle \frac{L}{L^{*}}}}}{L^{*}\Gamma \left(c\right)}}$$

(36)

where ${\Psi }^{*}$ is the total number of galaxies per unit Mpc${}^3$,

$$\Gamma (z)={\int }_0^{\infty }{e}^{-t}{t}^{z-1}dt$$

(37)

is the gamma function, $L^{*}>0$ is the scale and $c>0$ is the shape; see Formula (17.23) in [17]. Its expected value is:

$$E({\Psi }^{*},L^{*},c)={\Psi }^{*}{L}^{*}c$$

(38)

The change of parameter $(c-1)=\alpha$ allows obtaining the same scaling as for the Schechter LF (34).

3.3. The Truncated Gamma Luminosity Function

We assume that the luminosity L takes values in the interval $[L_l,L_u]$ where the indices l and u mean lower and upper; the truncated gamma LF is:

$$f(L;{\Psi }^{*},L^{*},c,L_l,L_u)={\Psi }^{*}k{({\displaystyle \frac{L}{{\mathit{L}}^{*}}})}^{c-1}{\mathrm{e}}^{-{\displaystyle \frac{L}{{\mathit{L}}^{*}}}}$$

(39)

where ${\Psi }^{*}$ is the total number of galaxies per unit Mpc${}^3$, and the constant k is:

$$k={\displaystyle \frac{c}{{\mathit{L}}^{*}\left({\left({\displaystyle \frac{L_u}{{\mathit{L}}^{*}}}\right)}^c{\mathrm{e}}^{-{\displaystyle \frac{L_u}{{\mathit{L}}^{*}}}}-\Gamma \left(1+c,{\displaystyle \frac{L_u}{{\mathit{L}}^{*}}}\right)+\Gamma \left(1+c,{\displaystyle \frac{L_l}{{\mathit{L}}^{*}}}\right)-{\left({\displaystyle \frac{L_l}{{\mathit{L}}^{*}}}\right)}^c{\mathrm{e}}^{-{\displaystyle \frac{L_l}{{\mathit{L}}^{*}}}}\right)}}$$

(40)

where:

$$\Gamma (a,z)={\int }_z^{\infty }{t}^{a-1}{e}^{-t}dt$$

(41)

is the upper incomplete gamma function; see [18,19]. Its expected value is:

$$E({\Psi }^{*},L^{*},c,L_l,L_u)={\Psi }^{*}{\displaystyle \frac{-c\left(\Gamma \left(1+c,{\displaystyle \frac{L_u}{{\mathit{L}}^{*}}}\right)-\Gamma \left(1+c,{\displaystyle \frac{L_l}{{\mathit{L}}^{*}}}\right)\right){\mathit{L}}^{*}}{{\left({\displaystyle \frac{L_u}{{\mathit{L}}^{*}}}\right)}^c{\mathrm{e}}^{-{\displaystyle \frac{L_u}{{\mathit{L}}^{*}}}}-\Gamma \left(1+c,{\displaystyle \frac{L_u}{{\mathit{L}}^{*}}}\right)+\Gamma \left(1+c,{\displaystyle \frac{L_l}{{\mathit{L}}^{*}}}\right)-{\left({\displaystyle \frac{L_l}{{\mathit{L}}^{*}}}\right)}^c{\mathrm{e}}^{-{\displaystyle \frac{L_l}{{\mathit{L}}^{*}}}}}}$$

(42)

More details on the truncated gamma PDF can be found in [20,21]. The four luminosities $L,L_l,L^{*}$ and $L_u$ are connected to the absolute magnitude M, $M_l$, $M_u$ and $M^{*}$ through the following relationship:

$${\displaystyle \frac{L}{L_{\odot }}}={10}^{0.4(M_{\odot }-M)},{\displaystyle \frac{L_l}{L_{\odot }}}={10}^{0.4(M_{\odot }-M_u)},{\displaystyle \frac{L^{*}}{L_{\odot }}}={10}^{0.4(M_{\odot }-M^{*})},{\displaystyle \frac{L_u}{L_{\odot }}}={10}^{0.4(M_{\odot }-M_l)}$$

(43)

where the indices u and l are inverted in the transformation from luminosity to absolute magnitude, and $M_{\odot }$ is the absolute magnitude of the Sun in the considered band. The gamma truncated LF in magnitude is:

$$\Psi (M)dM={\displaystyle \frac{0.4c{\left({10}^{0.4{\mathit{M}}^{*}-0.4M}\right)}^c{\mathrm{e}}^{-{10}^{0.4{\mathit{M}}^{*}-0.4M}}{\Psi }^{*}\left(ln\left(2\right)+ln\left(5\right)\right)}{D}}$$

(44)

where

$$\begin{array}{c}\hfill D={\mathrm{e}}^{-{10}^{-0.4M_l+0.4{\mathit{M}}^{*}}}{\left({10}^{-0.4M_l+0.4{\mathit{M}}^{*}}\right)}^c-{\mathrm{e}}^{-{10}^{0.4{\mathit{M}}^{*}-0.4M_u}}{\left({10}^{0.4{\mathit{M}}^{*}-0.4M_u}\right)}^c\\ \hfill -\Gamma \left(1+c,{10}^{-0.4M_l+0.4{\mathit{M}}^{*}}\right)+\Gamma \left(1+c,{10}^{0.4{\mathit{M}}^{*}-0.4M_u}\right)\end{array}$$

(45)

The first test on the reliability of the truncated gamma LF was performed on the data of the Sloan Digital Sky Survey (SDSS) (see [22]) in the band $z^{*}$. The number of variables can be reduced to two once $M_u$ and $M_l$ are identified with the maximum and minimum absolute magnitude of the considered sample. The LFs considered here are displayed in Figure 8. A second test is represented by the behavior of the LF at high z. We expect a progressive decrease of the low luminosity galaxies (high magnitude) when z is increasing. A formula that models the previous statement can be obtained by Equation (16), which models the absolute magnitude, M, as a function of the redshift, inserting as the apparent magnitude, m, the limiting magnitude of the considered catalog. We now outline how to build an observed LF for a galaxy in a consistent way; the selected catalog is zCOSMOS, which is made up of 9697 galaxies up to $z=$4; see [23]. The observed LF for zCOSMOS can be built by employing the following algorithm.

(1)

The minimax approximation for the luminosity distance in the case of the JLA compilation parameters (see Equation (33b)) allows fixing the distance, in the following r, once z is given.

(2)

A value for the redshift is fixed, z, as well as the thickness of the layer, $\Delta z$.

(3)

All of the galaxies comprised between z and $\Delta z$ are selected.

(4)

The absolute magnitude is computed from Equation (16).

(5)

The distribution in magnitude is organized in frequencies versus absolute magnitude.

(6)

The frequencies are divided by the volume, which is $V=\Omega \pi r^2\Delta r$, where r is the considered radius, $\Delta r$ is the thickness of the radius and Ω is the solid angle of ZCOSMOS.

(7)

The error in the observed LF is obtained as the square root of the frequencies divided by the volume.

Figure 9, Figure 10 and Figure 11 present the LF of zCOOSMOS, as well as the fit with the truncated beta LF at $z=0.2$, $z=0.4$ and $z=0.6$, respectively.

4. Different Cosmologies

Here, we analyze the distance modulus for SNe in other cosmologies in the framework of general relativity (GR), an expanding flat universe, special relativity (SR) and a Euclidean static universe.

4.1. Simple GR Cosmology

In the framework of GR, the received flux, f, is:

$$f={\displaystyle \frac{L}{4\pi d_L^2}}$$

(46)

where $d_L$ is the luminosity distance, which depends on the cosmological model adopted; see Equation (7.21) in [24] or Equation (5.235) in [25].

The distance modulus in the simple GR cosmology is:

$$m-M=43.17-{\displaystyle \frac{1}{ln\left(10\right)}}ln\left({\displaystyle \frac{{\mathit{H}}_0}{70}}\right)+5{\displaystyle \frac{ln\left(z\right)}{ln\left(10\right)}}+1.086\left(1-{\mathit{q}}_0\right)z$$

(47)

see Equation (7.52) in [24]. The number of free parameters in the simple GR cosmology is two: $H_0$ and $q_0$.

4.2. Flat Expanding Universe

This model is based on the standard definition of luminosity in the flat expanding universe. The luminosity distance, $r_L^{\prime }$, is:

$$r_L^{\prime }={\displaystyle \frac{c}{H_0}}z$$

(48)

and the distance modulus is:

$$m-M=-5{log}_{10}+5{log}_{10}{r}_L^{\prime }+2.5log(1+z)$$

(49)

see Formulae (13) and (14) in [26]. The number of free parameters in the flat expanding model. is one: $H_0$.

4.3. Einstein–De Sitter Universe in SR

In the Einstein–De Sitter model, which is developed in SR, the luminosity distance, after [27,28], is:

$$d_L=2{\displaystyle \frac{c\left(1+z-\sqrt{z+1}\right)}{H_0}}$$

(50)

and the distance modulus for the Einstein–De Sitter model is:

$$m-M=25+5{\displaystyle \frac{1}{ln\left(10\right)}}ln\left(2{\displaystyle \frac{c\left(1+z-\sqrt{z+1}\right)}{H_0}}\right)$$

(51)

The number of free parameters in the Einstein–De Sitter model is one: $H_0$.

4.4. Milne Universe in SR

In the Milne model, which is developed in the framework of SR, the luminosity distance, after [29,30,31], is:

$$d_L={\displaystyle \frac{c\left(z+{\displaystyle \frac{1}{2}}{z}^2\right)}{H_0}}$$

(52)

and the distance modulus for the Milne model is:

$$m-M=25+5{\displaystyle \frac{1}{ln\left(10\right)}}ln\left({\displaystyle \frac{c\left(z+{\displaystyle \frac{1}{2}}{z}^2\right)}{H_0}}\right)$$

(53)

The number of free parameters in the Milne model is one: $H_0$.

4.5. Plasma Cosmology

In a Euclidean static framework, among many possible absorption mechanisms, we selected a photo-absorption process between the photon and the electron in the IGM. This relativistic process produces a nonlinear dependence between redshift and distance:

$$z=\left(exp(H_{0}d)-1\right)$$

(54)

see Equation (4) in [32]. The previous equation is identical to our Equation (59). The Hubble constant in this first plasma model is:

$$H_0=1.2649{10}^8<n_e>\text{km}{\mathrm{s}}^{-1}{\text{Mpc}}^{-1}$$

(55)

where <$n_e$> is expressed in cgsunits. The second mechanism is a plasma effect, which produces the following relationship:

$$d={\displaystyle \frac{c}{H_0}}ln(1+z)$$

(56)

see Equation (50) in [33]. Furthermore, this second mechanism produces the same nonlinear d-z dependence as our Equation (59). In the presence of plasma absorption, the observed flux is:

$$f={\displaystyle \frac{L·exp\left(-bd-H_{0}d-2H_{0}d\right)}{4\pi d^2}}$$

(57)

where the factor $exp\left(-bd\right)$ is due to Galactic and host galactic extinctions, $-H_{0}d$ is reduction to the plasma in the IGM and $-2H_{0}d$ is the reduction due to Compton scattering; see the formula before Equation (51) in [33]. The resulting distance modulus in the plasma mechanism is:

$$m-M=5{\displaystyle \frac{ln\left(ln\left(z+1\right)\right)}{ln\left(10\right)}}+{\displaystyle \frac{15}{2}}{\displaystyle \frac{ln\left(z+1\right)}{ln\left(10\right)}}+5{\displaystyle \frac{1}{ln\left(10\right)}}ln\left({\displaystyle \frac{c}{H_0}}\right)+25+1.086b$$

(58)

see Equation (7) in [34]. The number of free parameters in the plasma cosmology is one: $H_0$ when $b=0$.

4.6. Modified Tired Light

In a Euclidean static framework, the modified tired light (MTL) has been introduced in Section 2.2 in [35]. The distance in MTL is:

$$d={\displaystyle \frac{c}{H_0}}ln(1+z)$$

(59)

The distance modulus in the modified tired light (MTL) is:

$$m-M={\displaystyle \frac{5}{2}}{\displaystyle \frac{\beta ln\left(z+1\right)}{ln\left(10\right)}}+5{\displaystyle \frac{1}{ln\left(10\right)}}ln\left({\displaystyle \frac{ln\left(z+1\right)c}{H_0}}\right)+25$$

(60)

Here, β is a parameter comprised between one and three, which allows one to match theory with observations. The number of free parameters in MTL is two: $H_0$ and β.

4.7. Results for Different Cosmologies

The statistical parameters for the different cosmologies here analyzed can be found in

Table 5. Numerical values of ${\chi }^2$, ${\chi }_{red}^2$, Q and the AIC of the Hubble diagram for the Union 2.1 compilation; k stands for the number of parameters; $H_0$ is expressed in $\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$.

Cosmology	Equation	k	Parameters	$\mathit{\chi }\mathbf{2}$	${\mathit{\chi }}_{\mathit{r}\mathit{e}\mathit{d}}^{\mathbf{2}}$	Q	AIC
simple (GR)	(47)	2	$H_0=73.79\pm 0.024$, $q_0$ = −0.1	689.34	1.194	8.6 ${10}^{-4}$	793.34
flat expanding model	(49)	1	$H_0=66.84\pm 0.22$	653	1.12	0.017	655
Einstein–De Sitter (SR)	(51)	1	$H_0=63.17\pm 0.2$	1171.39	2.02	2 ${10}^{-42}$	1173.39
Milne (SR)	(53)	1	$H_0=67.53\pm 0.22$	603.37	1.04	0.23	605.37
plasma (Euclidean)	(58)	1	$H_0=74.2\pm 0.24$	895.53	1.546	5.2 ${10}^{-16}$	897.5
MTL (Euclidean)	(60)	2	β = 2.37, $H_0=69.32\pm 0.34$	567.96	0.982	0.609	571.9

in the case of the Union 2.1 compilation and in

Table 6. Numerical values of ${\chi }^2$, ${\chi }_{red}^2$, Q and the AIC of the Hubble diagram for the JLA compilation; k stands for the number of parameters; $H_0$ is expressed in $\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$.

Cosmology	Equation	k	Parameters	$\mathit{\chi }\mathbf{2}$	${\mathit{\chi }}_{\mathit{r}\mathit{e}\mathit{d}}^{\mathbf{2}}$	Q	AIC
simple (GR)	(47)	2	$H_0=73.79\pm 0.023$, $q_0$ = −0.14	749.14	1.016	0.369	755.14
flat expanding model	(49)	1	$H_0=66.49\pm 0.18$	717.3	0.97	0.709	719.3
Einstein–De Sitter (SR)	(51)	1	$H_0=62.57\pm 0.17$	1307.75	1.76	3.27 ${10}^{-34}$	1309.75
Milne (SR)	(53)	1	$H_0=67.19\pm 0.18$	656.11	0.887	0.986	658.11
plasma (Euclidean)	(58)	1	$H_0=74.45\pm 0.2$	1017.79	1.377	3.59 ${10}^{-11}$	1019.79
MTL (Euclidean)	(60)	2	β = 2.36, $H_0=69.096\pm 0.32$	626.27	0.848	0.998	630.27

for the JLA compilation.

5. Conclusions

5.1. Padé approximant

It is generally thought that in the case of the luminosity distance, the Padé approximant is more accurate than the Taylor expansion. As an example, at $z=1.5$, which is the maximum value of the redshift here considered, the percentage error of the luminosity distance is $\delta =0.036\%$ in the case of the Padé approximation. In the case of of the Taylor expansion, $\delta =0.036\%$ for the luminosity distance is reached $z=0.322$, which means a more limited range of convergence than for the Padé approximation. Once a precise approximation for the luminosity distance was obtained (see Equation (11)), we derived an approximate expression for the distance modulus (see Equation (17)) and the absolute magnitude (see Equation (16)).

5.2. Astrophysical Applications

The availability of the observed distance modulus for a great number of SNs of Type Ia allows deducing $H_0$, ${\Omega }_{\mathrm{M}}$ and ${\Omega }_{\Lambda }$ for two catalogs; see Table 1. In order to derive the above parameters, the Levenberg–Marquardt method was implemented, and therefore, the first derivative of the distance modulus (see Equation (17)) with respect to three parameters is provided. The value of $H_0$ is a matter of research rather than a well-defined constant. As an example, a recent evaluation with a sample of Cepheids gives $H_0=73.8\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$; see [36]. Once the above value is considered the `true’ value, we have found, adopting the Padé approximant, $H_0=69.81\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$, which means a percentage error $\delta =5.4\%$, for the Union 2.1 compilation, and $H_0=69.398\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$, which means a percentage error $\delta =5.9\%$, for the JLA compilation; see Table 1.

5.3. Evolutionary Effects

The evolution of the LF for galaxies as a function of the redshift is here modeled by an upper and lower truncated gamma PDF. This choice allows modeling the lower bound in luminosity (the higher bound in absolute magnitude) according to the evolution of the absolute magnitude; see Equation (16). According to the LF here considered (see Equation (44)), the evolution with z of the LF is simply connected to the evolution of the higher bound in absolute magnitude; see Figure 9, Figure 10 and Figure 11. Is not necessary to modify the shape parameters of the LF, which are c and $M^{*}$, but only to calculate the normalization ${\Psi }^{*}$ at different values of the redshift.

5.4. Statistical Tests for Union 2.1

In the case of the Union 2.1 compilation, the best results for ${\chi }_{red}^2$ are obtained by the ΛCDM cosmology (GR), ${\chi }_{red}^2=0.975$, against ${\chi }_{red}^2=0.982$ of the MTL cosmology (Euclidean), but the situation is inverted when the AIC is considered: the AIC is 571.9 for the MTL cosmology and 568.7 for the ΛCDM cosmology (GR); see Table 1 and Table 5.

The simple model (GR), the Einstein–De Sitter model (SR), the Milne model (SR) and the plasma model (Euclidean) are rejected because the reduced merit function ${\chi }_{red}^2$ is smaller than one; see Table 5. The best performing one-parameter model is that of Milne, ${\chi }_{red}^2=1.04$, followed by the flat expanding model, ${\chi }_{red}^2=1.12$; see Table 5.

5.5. Statistical Tests for JLA

In the case of the JLA compilation, the best results for ${\chi }_{red}^2$ are obtained by the MTL cosmology (Euclidean), ${\chi }_{red}^2=0.848$, against ${\chi }_{red}^2=0.849$ for the ΛCDM cosmology (GR); see Table 1 and Table 6. The simple model (GR), the Einstein–De Sitter model (SR) and the plasma model (Euclidean) are rejected because the reduced merit function ${\chi }_{red}^2$ is smaller than one; see Table 6. In the case of the JLA, the test on the Milne model is positive because ${\chi }_{red}^2$ is smaller than one. The best performing one-parameter model is that of Milne, ${\chi }_{red}^2=0.887$, followed by the flat expanding model, ${\chi }_{red}^2=0.97$; see Table 6.

5.6. Different Approaches

Table 7. Arguments treated in papers on Padé approximants and here.

Problem	Aviles 2014	Wei 2014	Adachi 2012	Here
luminosity distance	Y	Y	Y	Y
distance modulus	Y	Y	Y	Y
empty beam	N	N	Y	N
distance modulus minimax	N	N	N	Y
poles	N	N	N	Y
LF=f(z)	N	N	N	Y

reports six items connected to the use of the Padé approximant in Cosmology: the letters Y/N indicate if the item is treated or not, and the columns identifies the paper in question; LF means the luminosity function for galaxies.