Topological Signals of Singularities in Ricci Flow
Abstract
:1. Introduction
2. Preliminaries and Background
2.1. Persistent Homology
2.2. Ricci Flow
- 1.
- Type-I singularity at a maximal time if
- 2.
- Type-IIa singularity at a maximal time if:
- 3.
- Type-IIb singularity at a maximal time if:
- 4.
- Type-III singularity at a maximal time if:
3. Methodology
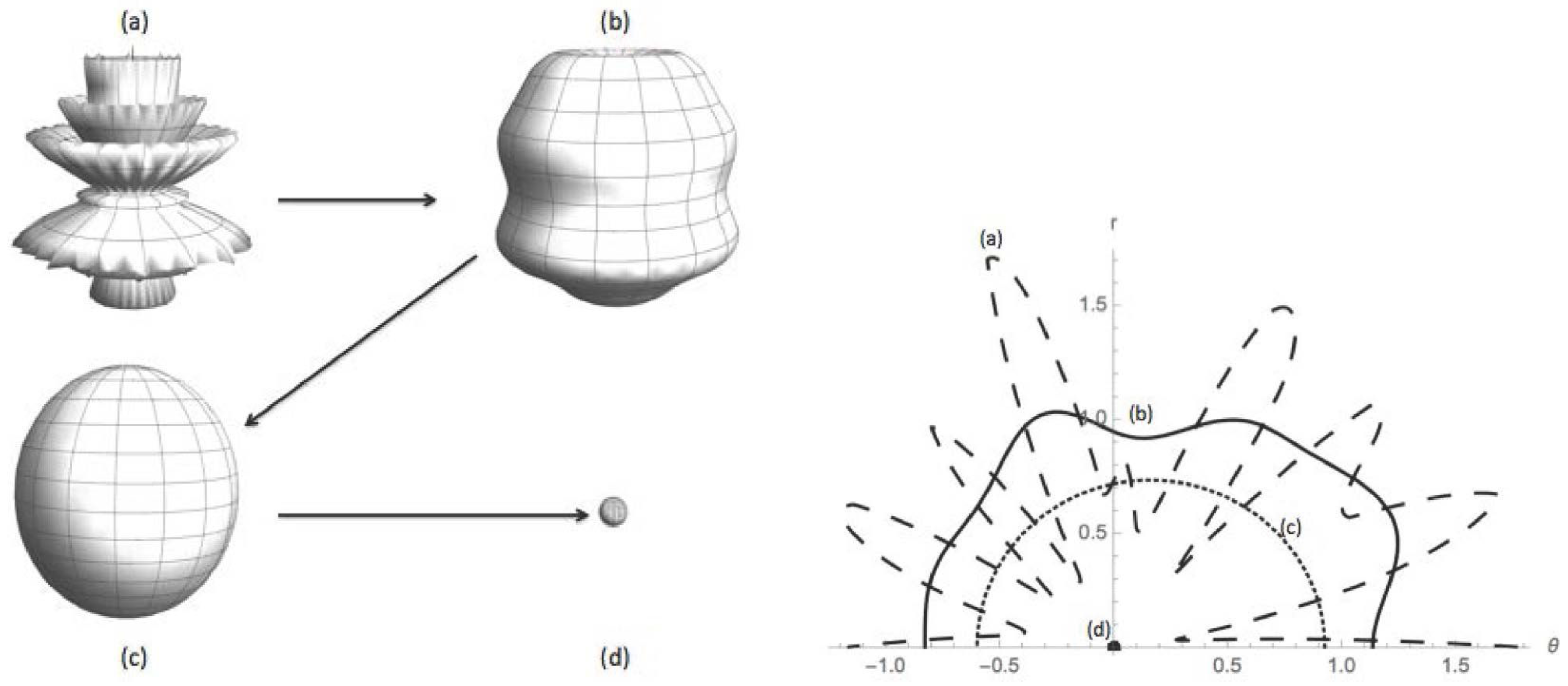
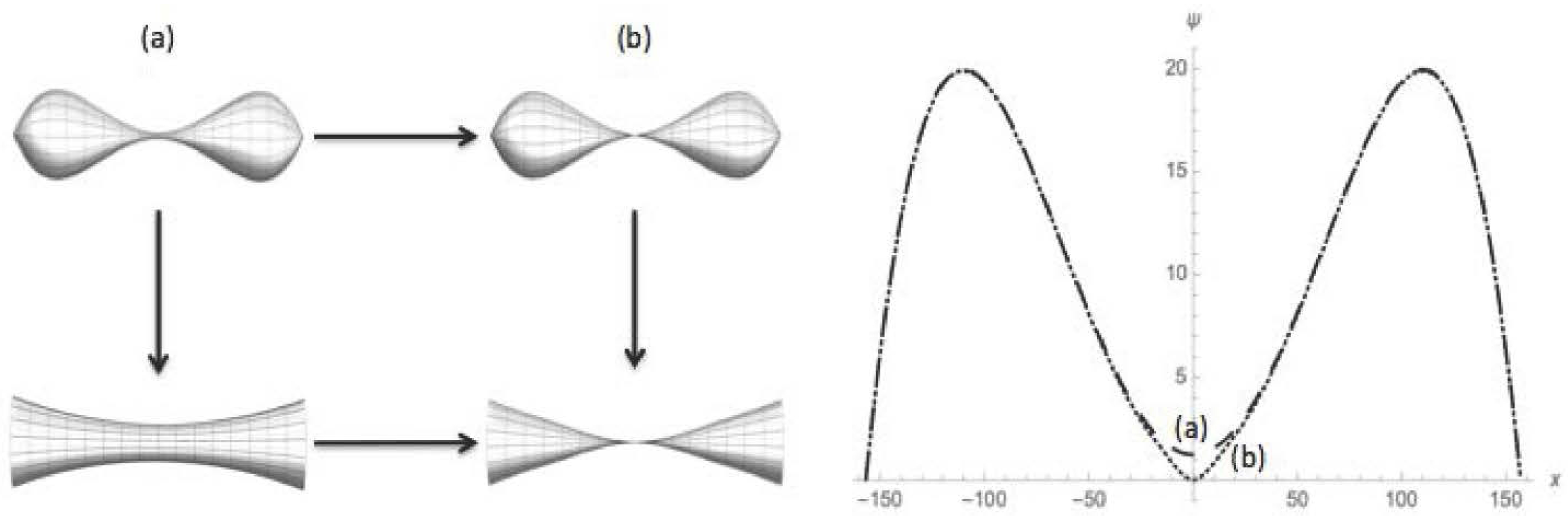
3.1. Models
- 1.
- The sectional curvature L of planes tangent to each sphere is positive.
- 2.
- The Ricci curvature (where K is the sectional curvature of a plane orthogonal to ) is positive on each polar cap.
- 3.
- The scalar curvature is positive everywhere.
- 4.
- The metric has at least one neck and is “sufficiently pinched” in the sense that the value of the radial function ψ at the smallest neck is sufficiently small relative to its value at either adjacent bump.
- 5.
- The metric is reflection symmetric, and the smallest neck is at .
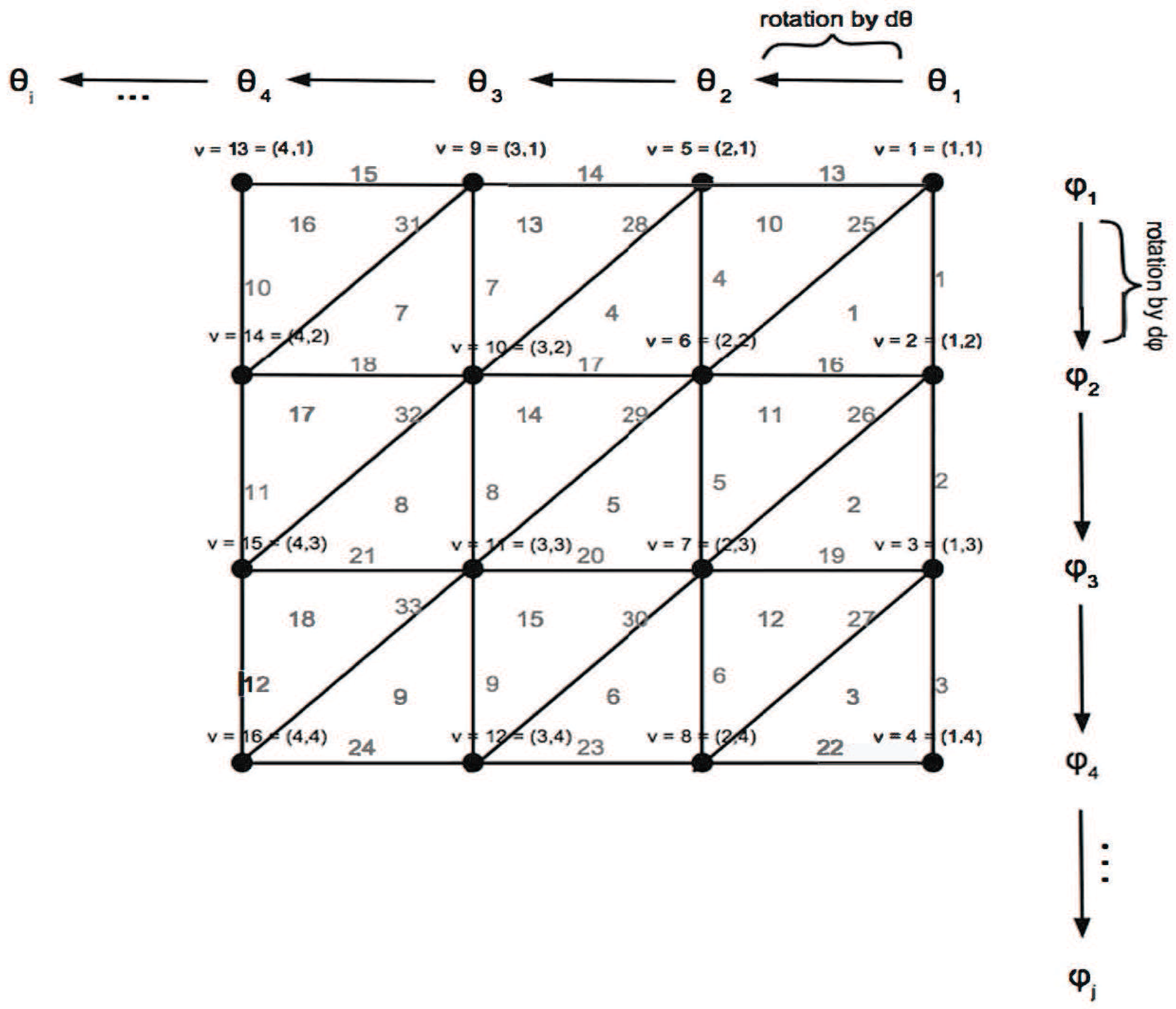
3.2. Persistence Computations
- and there is some d-dimensional co-face with , or
- and , or
- and there is some d-dimensional face with .
- for each , compute curvature values assigned to all vertices,
- construct the upper star filtration along these values,
- produce the corresponding PDs in dimensions 0 and 1,
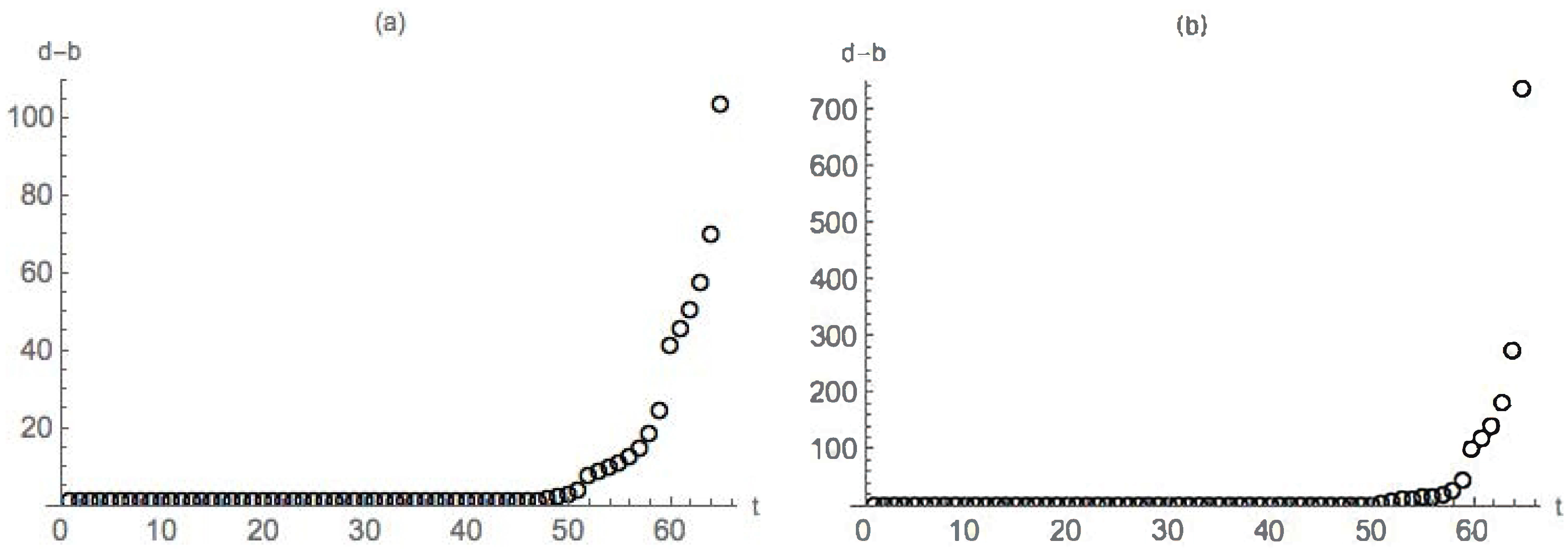
- instead of birth-death pairs , restrict attention to the differences , called persistence intervals or lifespans.
3.3. Data Generation and Preparation Algorithm
4. Results
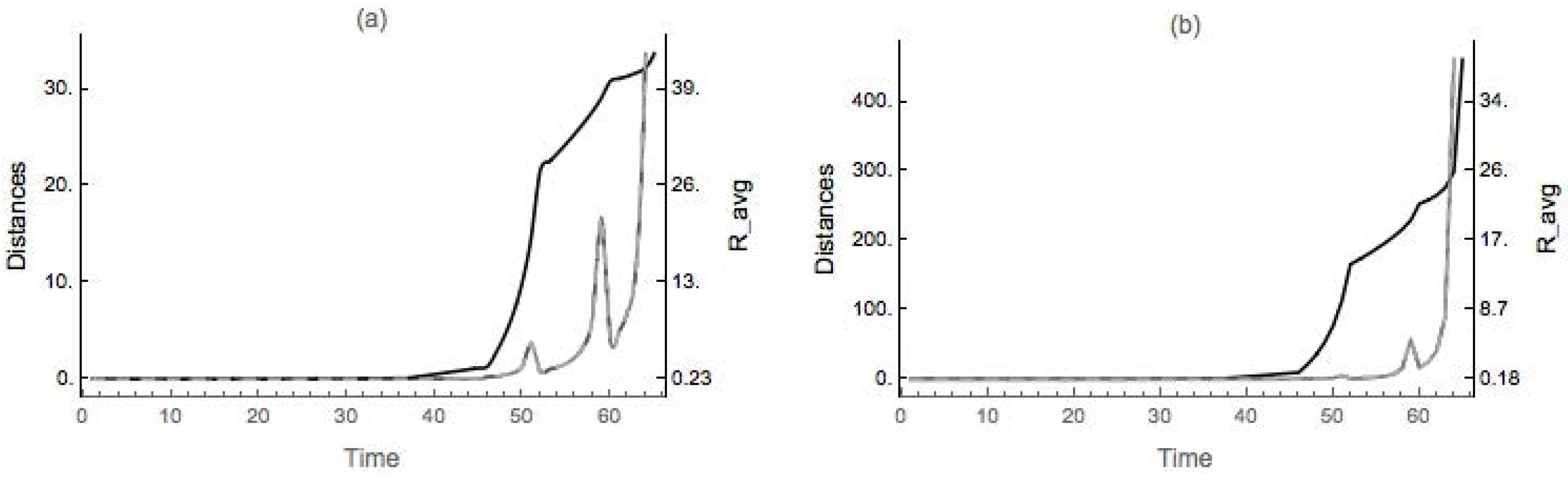
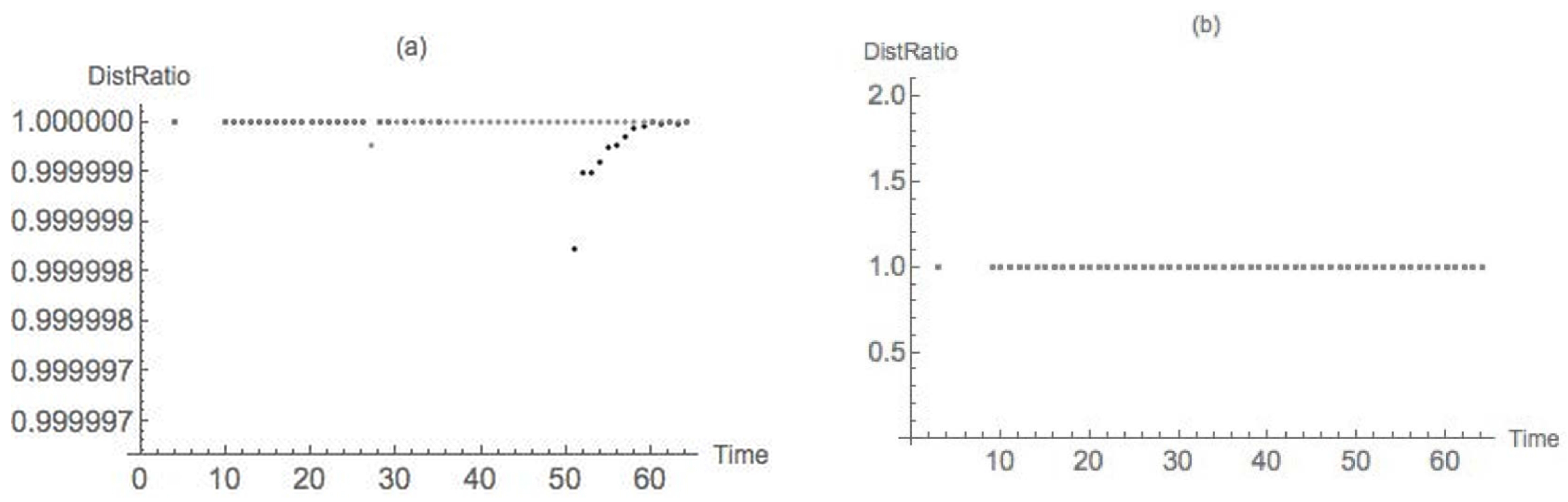
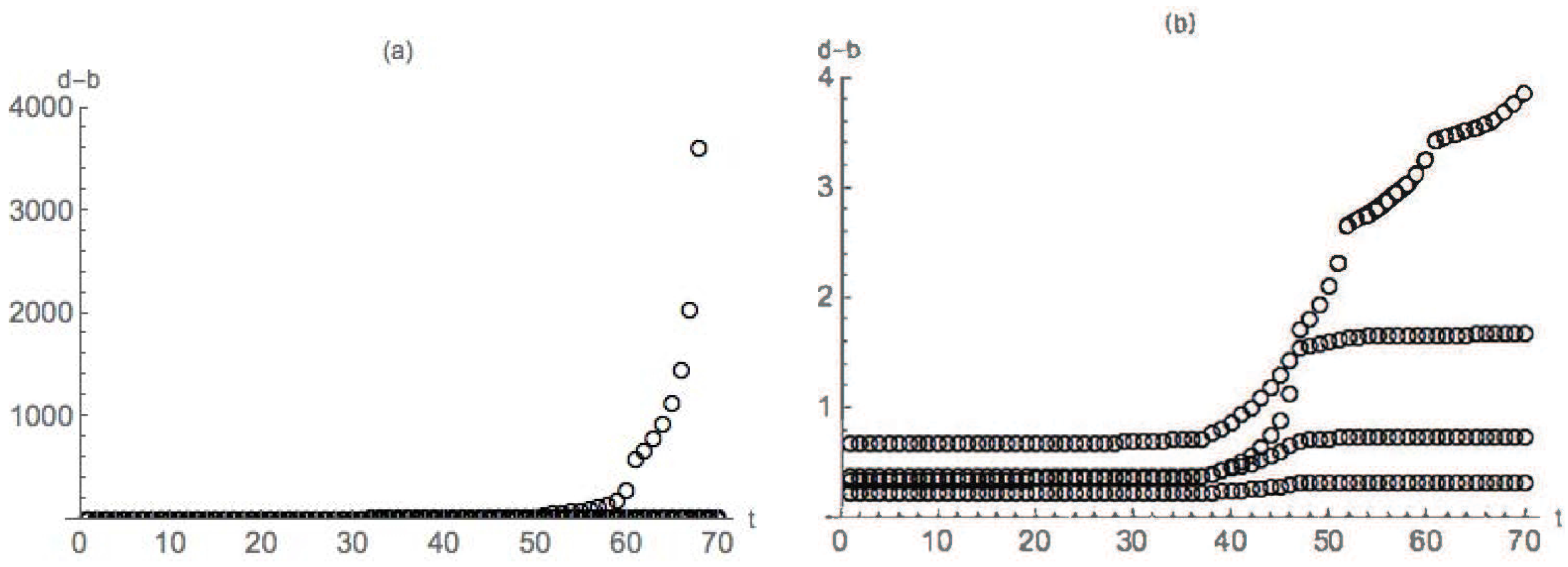
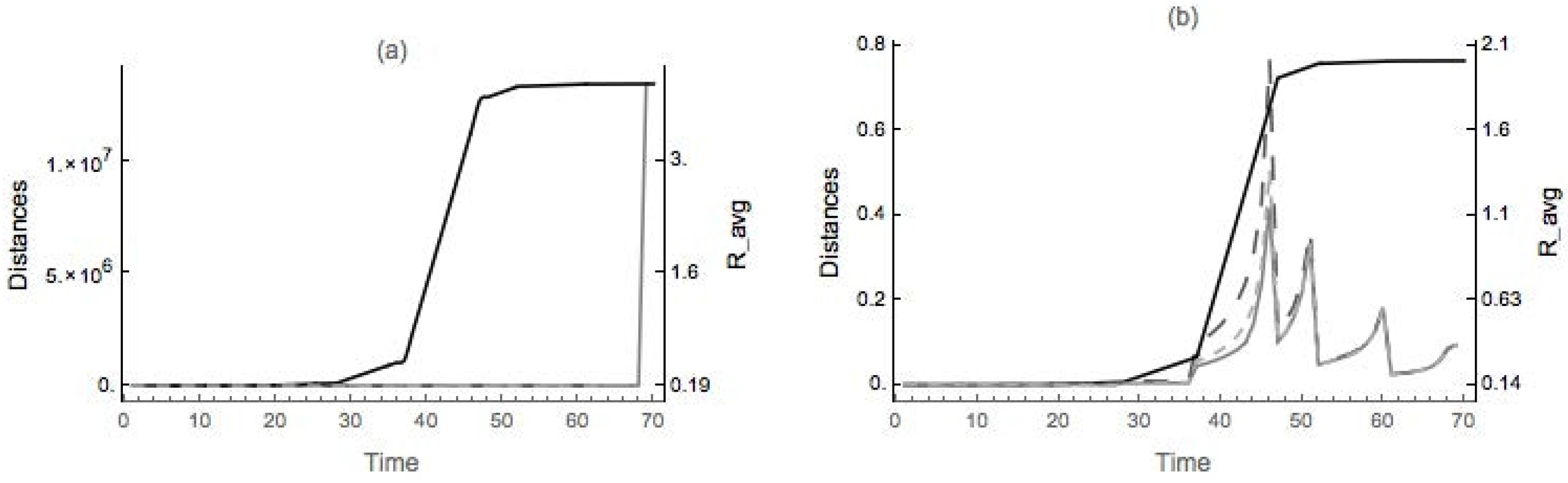
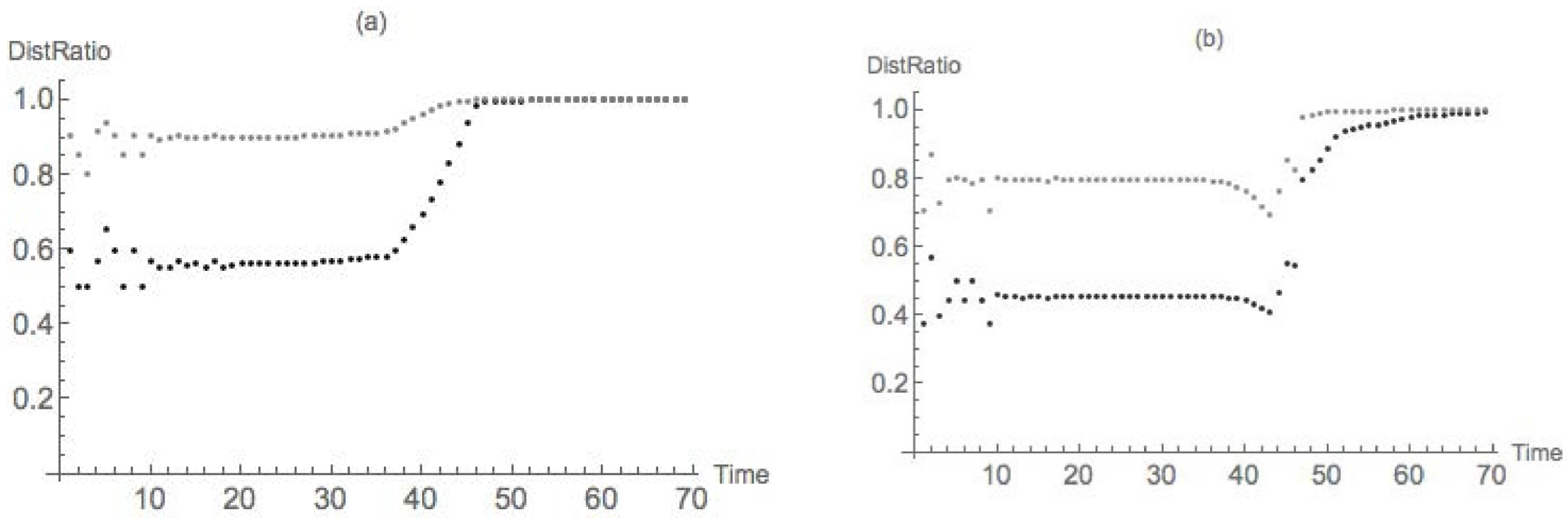
4.1. Dimpled Sphere
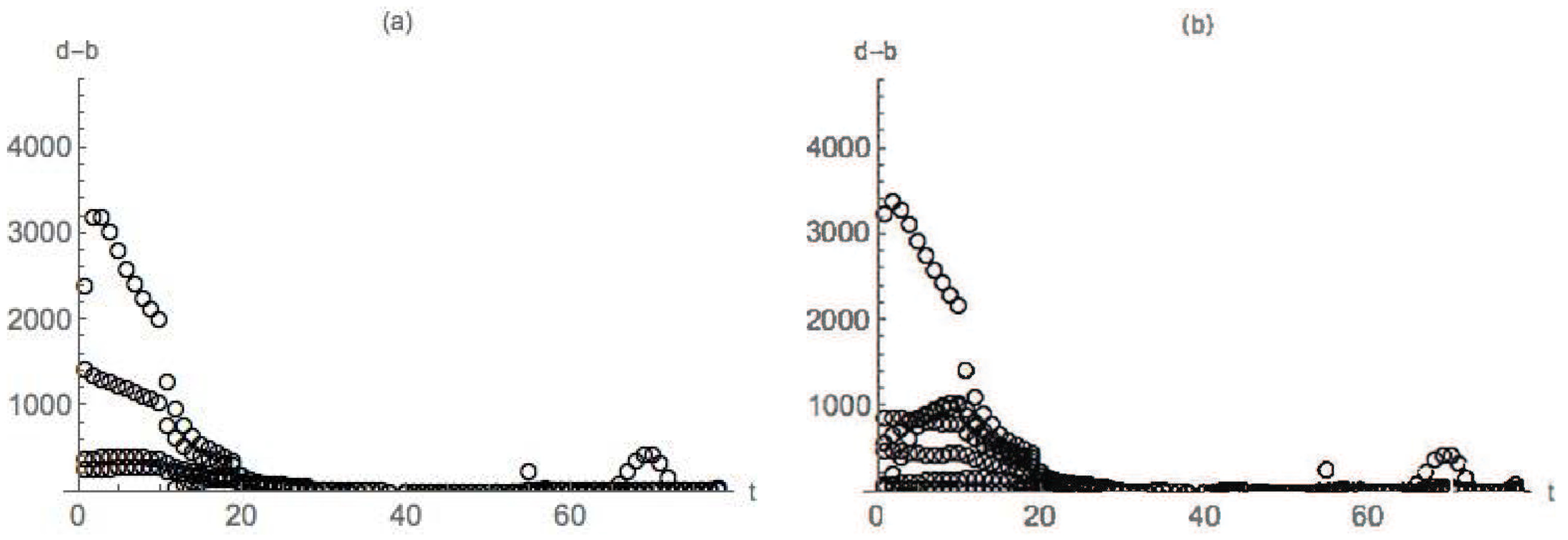
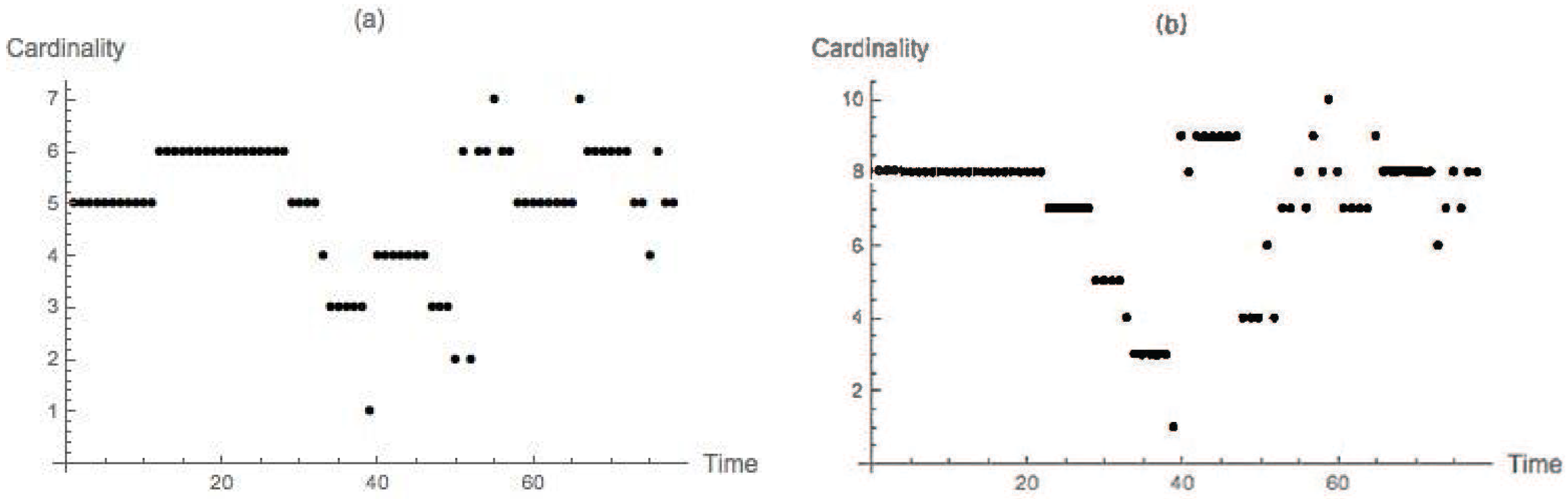
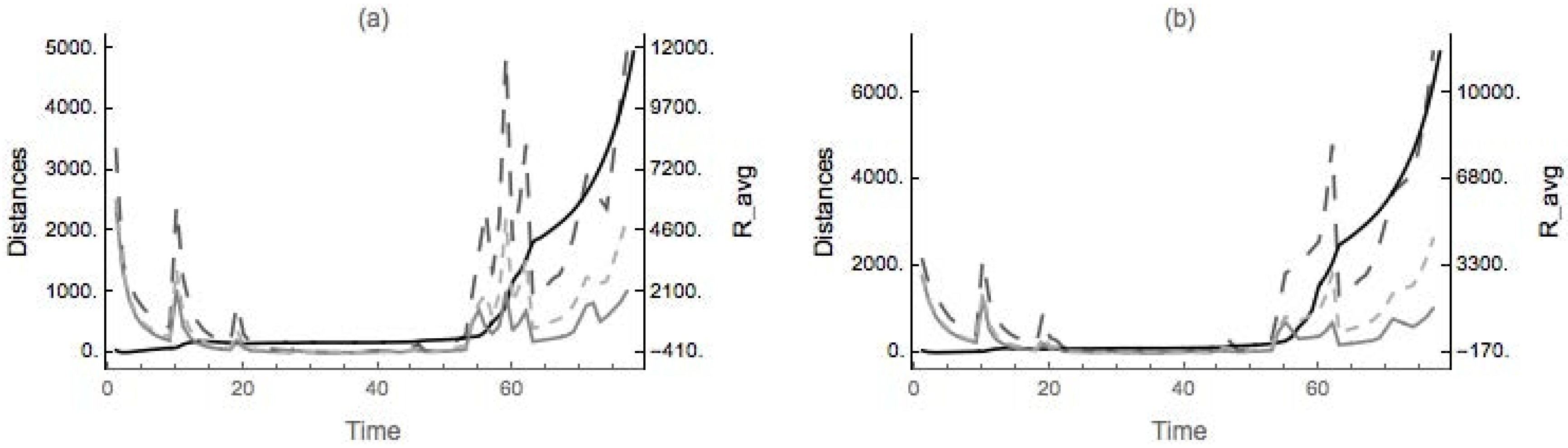
4.2. Nondegenerate Neckpinch
4.2.1. Symmetric Dumbbell
4.2.2. Dimpled Dumbbell
5. Conclusions and Future Directions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| PH | Persistent Homology |
| RF | Ricci Flow |
| TDA | Topological Data Analysis |
| PDE | Partial Differential Equations |
| RG | Renormalization Group |
| PD | Persistence Diagram |
References
- Hamilton, R.S. Three manifolds with positive Ricci curvature. J. Differ. Geom. 1982, 17, 255–306. [Google Scholar] [CrossRef]
- Chow, B.; Knopf, D. The Ricci Flow: An Introduction. In Mathematical Surveys and Monographs; American Mathematical Society: Providence, RI, USA, 2004; Volume 110. [Google Scholar]
- Thurston, W. Three-Dimensional Geometry and Topology; Princeton Mathematical Series 35; Levy, S., Ed.; Princeton University Press: Princeton, NJ, USA, 1997; Volume 1. [Google Scholar]
- Angenent, S.; Isenberg, J.; Knopf, D. Formal matched asymptotics for degenerate Ricci flow neckpinches. Nonlinearity 2011, 24, 2265–2280. [Google Scholar] [CrossRef]
- Angenent, S.; Isenberg, J.; Knopf, D. Degenerate neckpinches in Ricci flow. J. Reine Angew. Math. Crelle 2015, 709, 81–118. [Google Scholar] [CrossRef]
- Angenent, S.; Knopf, D. An example of neckpinching for Ricci flow on Sn+1. Math. Res. Lett. 2004, 11, 493–518. [Google Scholar] [CrossRef]
- Gu, H.-L.; Zhu, X.-P. The Existence of Type II Singularities for the Ricci Flow on Sn+1. arXiv, 2007; arXiv:0707.0033. [Google Scholar]
- Perelman, G. The entropy formula for the Ricci flow and its geometric applications. arXiv, 2003; arXiv:math.DG/0211159. [Google Scholar]
- Perelman, G. Ricci flow with surgery on three manifolds. arXiv, 2003; arXiv:math.DG/0303109. [Google Scholar]
- Carfora, M. Renormalization group and the Ricci flow. Milan J. Math. 2010, 78, 319–353. [Google Scholar] [CrossRef]
- Carfora, M. Ricci flow conjugated initial data sets for Einstein equations. Adv. Theor. Math. Phys. 2011, 15, 1411–1484. [Google Scholar] [CrossRef]
- Carfora, M. The Wasserstein geometry of non-linear sigma models and the Hamilton-Perelman Ricci flow. Rev. Math. Phys. 2017, 29, 1–71. [Google Scholar] [CrossRef]
- Raamsdonk, M.V. Building up spacetime with quantum entanglemen. arXiv, 2010; arXiv:1005.3035. [Google Scholar]
- Woolgar, E. Some applications of Ricci flow in physics. Can. J. Phys. 2008, 86, 645. [Google Scholar] [CrossRef]
- Yu, X.; Yin, X.; Han, W.; Gao, J.; Gu, X. Scalable routing in 3D high genus sensor networks using graph embedding. In Proceedings of the INFOCOM 2012, Orlando, FL, USA, 25–30 March 2012; pp. 2681–2685. [Google Scholar]
- Wang, Y.; Shi, J.; Yin, X.; Gu, X.; Chan, T.F.; Yau, S.-T.; Toga, A.W.; Thompson, P.M. Brain surface conformal parameterization with the Ricci flow. IEEE Trans. Med. Imaging 2012, 31, 251–264. [Google Scholar] [PubMed]
- Miller, W.A.; McDonald, J.R.; Alsing, P.M.; Gu, D.; Yau, S.-T. Simplicial Ricci flow. Commun. Math. Phys. 2014, 239, 579–608. [Google Scholar] [CrossRef]
- Carlsson, G. Topology and Data. Bull. Am. Math. Soc. 2009, 46, 255–308. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Harer, J. Computational Topology; American Mathematical Society: Providence, RI, USA, 2009. [Google Scholar]
- Kaczynski, T.; Mischaikow, K.; Mrozek, M. Computational Homology; Applied Mathematical Sciences 157; Springer: New York, NY, USA, 2004. [Google Scholar]
- Nanda, V.; Sazdanovic, R. Simplicial Models and Topological Inference in Biological Systems. In Discrete and Topological Models in Molecular Biology; Jonoska, N., Saito, M., Eds.; Springer: Heidelberg, Germany, 2014. [Google Scholar]
- Goullet, A.; Kramár, M.; Kondic, L.; Mischaikow, K. Evolution of Force Networks in Dense Particulate Media. Phys. Rev. E 2014, 90, 052203. [Google Scholar]
- Bhattachayra, S.; Ghrist, R.; Kumar, V. Persistent homology in ℤ2 coefficients for robot path planning in uncertain environments. IEEE Trans. Robot. 2015, 31, 578–590. [Google Scholar] [CrossRef]
- De Silva, V.; Ghrist, R. Coverage in sensor networks via persistent homology. Algebraic Geom. Topol. 2007, 7, 339–358. [Google Scholar] [CrossRef]
- Bendich, P.; Chin, S.P.; Clark, J.; Desena, J.; Harer, J.; Munch, E.; Newman, A.; Porter, D.; Rouse, D.; Watkins, A.; et al. Topological and Statistical Behavior Classifiers for Tracking Applications. arXiv, 2014; arXiv:1406.0214. [Google Scholar]
- Weygaert, R.V.D.; Vegter, G.; Edelsbrunner, H.; Jones, B.J.T.; Pranav, P.; Park, C.; Hellwing, W.A.; Eldering, B.; Kruithof, N.; Patrick Bos, E.G.; et al. Alpha, Betti, and the Megaparsec Universe: On the Topology of the Cosmic Web. In Transactions on Computational Science XIV; Springer: Berlin, Germany, 2011; pp. 60–101. [Google Scholar]
- Garfinkle, D.; Isenberg, J. Numerical Studies of the Behavior of Ricci Flow. Contemp. Math. 2005, 367, 103. [Google Scholar]
- Garfinkle, D.; Isenberg, J. The Modelling of Degenerate Neck Pinch Singularities in Ricci Flow by Bryant Solitons. arXiv, 2009; arXiv:0709.0514. [Google Scholar]
- Ghrist, R. Barcodes: The persistent topology of data. Bull. Am. Math. Soc. 2008, 45, 61–75. [Google Scholar] [CrossRef]
- Miller, W.A.; Alsing, P.M.; Corne, M.; Ray, S. Equivalence of simplicial Ricci flow and Hamilton’s Ricci flow for 3D neckpinch geometries. arXiv, 2014; arXiv:1404.4055. [Google Scholar]
- Zomorodian, A.; Carlsson, G. Computing persistent homology. Discret. Comput. Geom. 2005, 33, 249–274. [Google Scholar] [CrossRef]
- Chazal, F.; de Silva, V.; Glisse, M.; Oupoint, S. The structure and stability of persistence modules. arXiv, 2012; arXiv:1207.3674. [Google Scholar]
- Bishop, R.L.; Goldberg, S.I. Tensor Analysis on Manifolds; Dover Publications Inc.: New York, NY, USA, 1980. [Google Scholar]
- Nakahara, M. Geometry, Topology, and Physics; Institute of Physics Publishing: Philadelphia, PA, USA, 2003. [Google Scholar]
- Cao, H.-D.; Chow, B.; Chu, S.-C.; Yau, S.-T. (Eds.) Collected Papers on Ricci Flow; Series in Geometry and Topology 37; International Press: Somerville, MA, USA, 2003. [Google Scholar]
- Hamilton, R.S. The Formation of Singularities in the Ricci Flow; Surveys in Differential Geometry II; International Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Chow, B.; Chu, S.-C.; Glickenstein, D.; Guenther, C.; Isenberg, J.; Ivey, T.; Knopf, D.; Lu, P.; Luo, F.; Ni, L. The Ricci Flow: Techniques and Applications, Part 1: Geometric Aspects; Mathematical Surveys and Monographs 135; American Mathematical Society: Providence, RI, USA, 2007. [Google Scholar]
- Robins, V.; Wood, P.J.; Sheppard, A.P. Theory and algorithms for constructing discrete Morse complexes from grayscale digital images. IEEE Trans. Pattern Anal. Mach. Learn. 2011, 33, 1646–1658. [Google Scholar] [CrossRef] [PubMed]
- Nanda, V. Perseus: The Persistent Homology Software. Available online: http://people.maths.ox.ac.uk/nanda/perseus/index.html (accessed on 28 July 2017).
- Edelsbrunner, H.; Harer, J. Persistent Homology: A Survey; Surveys on Discrete and Computational Geometry; American Mathematical Society: Providence, RI, USA, 2008. [Google Scholar]
- Anand, K.; Bianconi, G. Entropy measures for networks: Toward an information theory of complex topologies. Phys. Rev. E 2009, 80, 045102. [Google Scholar] [CrossRef] [PubMed]
- Coffman, V.; Kundu, J.; Wootters, W.K. Distributed Entanglement. Phys. Rev. A 2000, 61, 052306. [Google Scholar] [CrossRef]
- Walck, S.N.; Glasbrenner, J.K.; Lochman, M.H.; Hilbert, S.A. Topology of the three-qubit space of entanglement types. Phys. Rev. A 2005, 72, 052324. [Google Scholar] [CrossRef]
- Haegeman, J.; Mariën, M.; Osborne, T.J.; Verstraete, F. Geometry of matrix product states: Metric, parallel transport, and curvature. J. Math. Phys. 2014, 55, 021902. [Google Scholar] [CrossRef] [Green Version]
- Saucan, E.; Jost, J. Network Topology vs. Geometry: From Persistent Homology to Curvature. In Proceedings of the NIPS 2016 Workshop on Learning in High Dimensions with Structure, Barcelona, Spain, 05–10 December 2016; Available online: http://www.cs.utexas.edu/~rofuyu/lhds-nips16/papers/11.pdf (accessed on 24 July 2017).


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsing, P.M.; Blair, H.A.; Corne, M.; Jones, G.; Miller, W.A.; Mischaikow, K.; Nanda, V. Topological Signals of Singularities in Ricci Flow. Axioms 2017, 6, 24. https://doi.org/10.3390/axioms6030024
Alsing PM, Blair HA, Corne M, Jones G, Miller WA, Mischaikow K, Nanda V. Topological Signals of Singularities in Ricci Flow. Axioms. 2017; 6(3):24. https://doi.org/10.3390/axioms6030024
Chicago/Turabian StyleAlsing, Paul M., Howard A. Blair, Matthew Corne, Gordon Jones, Warner A. Miller, Konstantin Mischaikow, and Vidit Nanda. 2017. "Topological Signals of Singularities in Ricci Flow" Axioms 6, no. 3: 24. https://doi.org/10.3390/axioms6030024




