1. Introduction
The differential equations (DE) are of paramount importance both in pure mathematics and in physics since they describe a very broad range of physical processes. Rapid development of computer methods and machine calculations in the 21st century facilitated equation solving. A good description of the major numerical methods is given, for example, in [
1,
2,
3,
4,
5,
6]. Here they allow numerical modelling of complicated physical processes [
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19], including multidimensional heat transfer in rectangles and cylinders [
20,
21,
22,
23]. However, proper understanding of the solutions and of the obtained results can be best done when they are obtained in analytical form. Analytical studies generally are more suitable for the analysis of the undergoing physical processes rather than numerical models, the latter giving precise description of the performance of the devices and of the specific studied cases. Analytical solutions are highly appreciated, but only a few types of DE allow explicit, if any, exact analytical solutions. Recently some fractional ordinary DE and partial differential equations (PDE) were analyzed and analytically solved in [
24,
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37]. They benefit from the use of special functions [
38,
39,
40]. The mathematical instruments, used to solve DE, generally range from a variety of integral transforms [
41,
42] to expansion in a series of generalized orthogonal polynomials [
43] with many variables and indices [
44,
45,
46], which arise naturally in studies of physical problems, such as the radiation and dynamics of beams of charges [
47,
48,
49,
50,
51,
52,
53,
54], heat and mass transfer [
55,
56,
57,
58,
59], etc. Moreover, exponential operators and matrices are currently used also for description of such nature fundamentals as neutrino and quarks in theoretical [
60,
61,
62,
63,
64,
65] and in experimental [
66,
67,
68] frameworks. The method of inverse differential and exponential operators has multiple applications for treating the above mentioned problems and related processes; some examples of DE solution by the inverse derivative method with regard to the heat equation, the diffusion equation, and their extensions, involving the Laguerre derivative, were given in [
46,
69,
70,
71,
72,
73]. Orthogonal polynomials can be defined in forms through operational relations [
74], although we will also use their series presentations.
In what follows we treat the problem of heat conduction by the operational method in the framework of classical thermodynamics. We obtain, compare, and explore exact solutions for relevant DE in the framework of heat conduction models for Fourier [
75], Cattaneo [
76], and Guyer-Krumhansl [
77] heat laws.
2. Fourier Heat Equation and Its Operational Solution
Fourier’s law of heat propagation imposes a linear relation between the temperature gradient and the heat flux. This is one of the most popular laws in continuum physics and it is in excellent agreement with everyday life and with more than 90% experiments. Recently the Fourier heat equation with a linear term
was studied operationally as a special case of the Schrödinger equation in imaginary time [
70,
73]. The solution of such DE with the initial condition
is given by the Gauss transform:
where
,
,
. The heat diffusion operator
was thoroughly explored by Srivastava in [
78]. The exponential differential operator
(3) reduces to the exponential differential operator
upon the application of the following integral presentation [
41]:
where
in our case. Thus, the above formula reads as follows:
The action of the operator of translation
for
produces a shift
The solution (2) consists of the action of the evolution operator on the initial condition
, which is transformed by
and
. Interestingly, for the Airy initial condition
the operational method readily yields the fading oscillating solution without any spread [
71], while the solution for the Gauss initial function demonstrates the spread of the packet.
In direct analogy with (1) the following two dimensional DE
with the initial condition
has the solution, which reads:
and it includes the phase
. The solution consists of the two-dimensional Gauss transform due to the action of the heat diffusion operators (3)
, and of the consequent shift along both coordinates, executed by the translation operators
,
.
In the context of the operational method the orthogonal polynomials are useful and their operational definitions are necessary. Indeed, the action of the heat diffusion operator on the monomial
yields
according to the operational definition of the Hermite polynomials of two variables
[
74]
and we obtain the solution of DE (1)
, where
as follows:
It is easy to demonstrate that for the initial condition
the following operational rule applies:
so that we obtain
,
. The consequent action of the translation operator
yields the shift along the
x argument and results in
where
.
Now we can easily solve the following extended heat equation:
which can be considered as the generalization of Equation (1) upon the substitution of the derivative
. To address Equation (13) we note that if
is the solution of Equation
with the initial function
, then
is the solution of the equation
with the initial function
. Distinguishing the perfect square of the operator
, we come to the solution of Equation (13) in the following form:
where
satisfies Equation (1) for
with the initial condition
. Let us set
without substantial loss of generality and choose the monomial
initial condition for (13). Then
is the initial condition for the Equation
. Its solution is given by (12) upon the substitution of
and we end up with the following solution of the extended heat Equation (13)
where
is the additional phase. This solution reduces to (10) in the proper limiting case.
3. Propagation of a Heat Surge with Fourier Heat Diffusion Type Equation
In heat conduction experiments the relaxation of the instant point-like heat surge is the standard technique, approved for thermal diffusivity measurements [
79]. In practical terms it is executed with the flash method—the standard engineering procedure for measuring thermal diffusivity with intense and ultra-short laser heat pulses. The latter can be modelled by the initial
δ-function space distribution. Let us consider this example now:
. With the help of Equation (5) we immediately obtain the action of the
operator on
δ-function as follows:
In two dimensions Equation (16) becomes
. Then the operators
induce the space shift and yield the particular solution (8) for the initial function
, which evolves in the Gaussian as follows:
One-dimensional solution for the initial flash condition
simply reads
, and unsurprisingly resembles the solution
[
71] for the initial Gaussian function
.
Consider the Equation (13) for
,
. This case represents the Fourier heat propagation, including heat exchange with the environment. Consider the flash initial condition
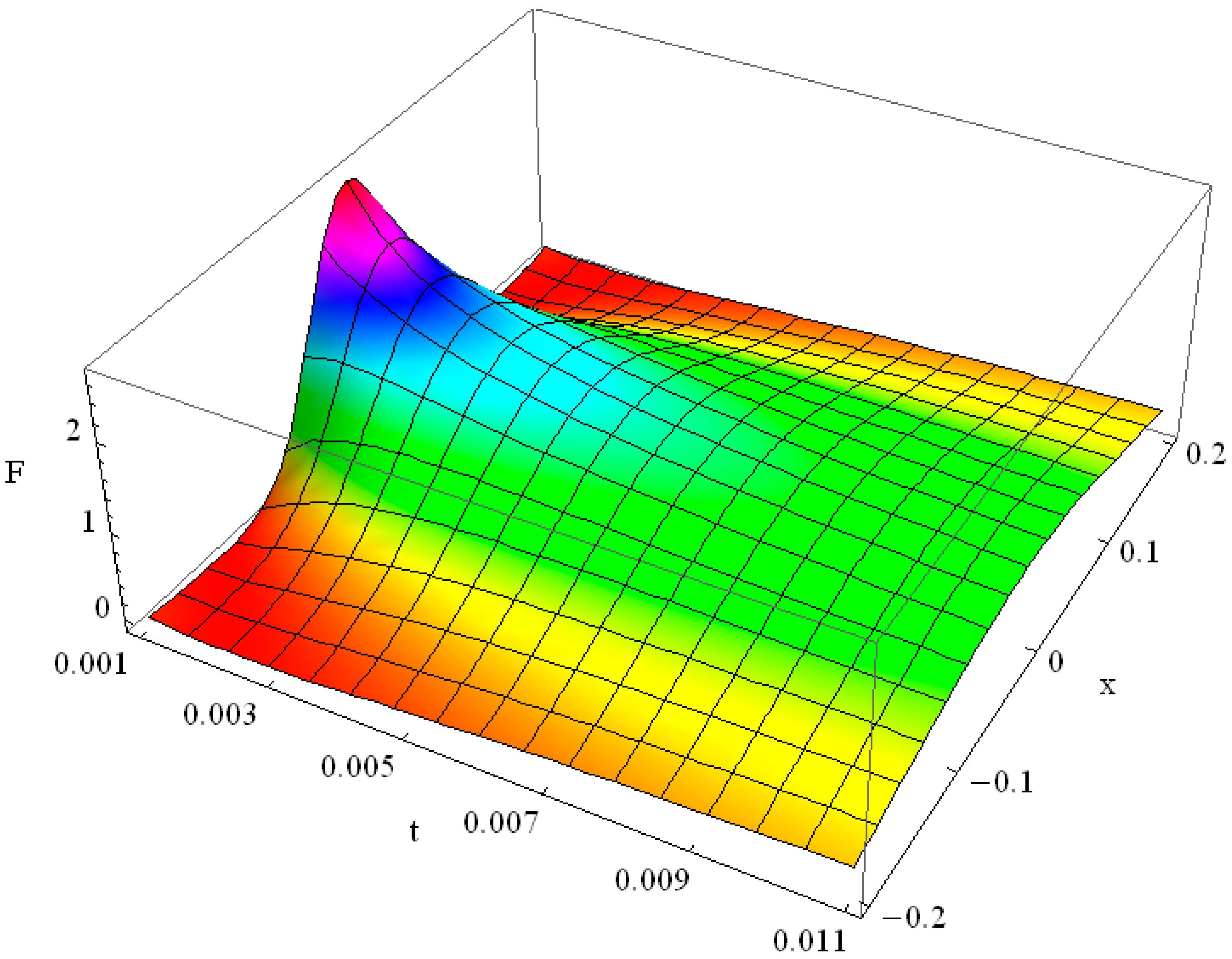
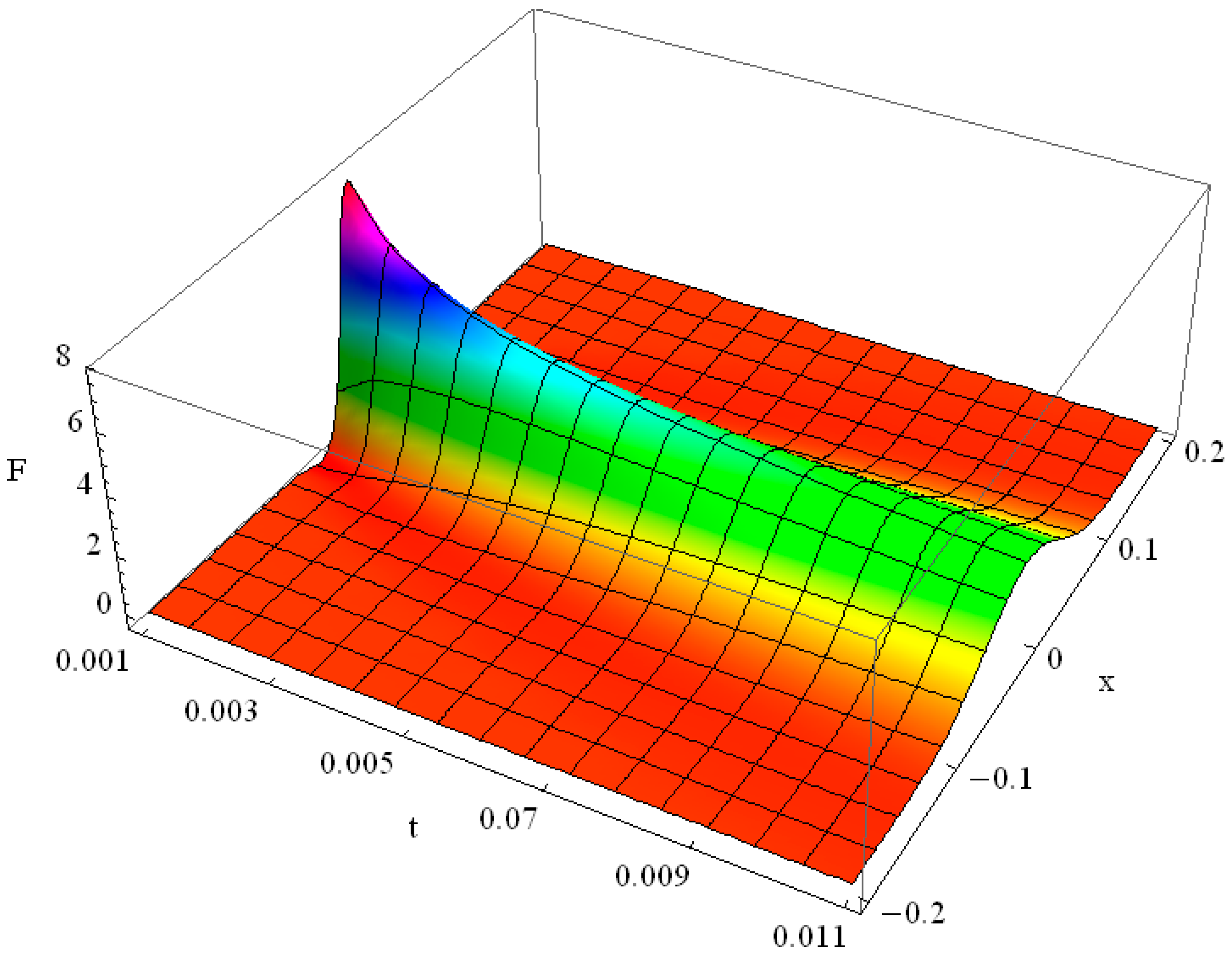
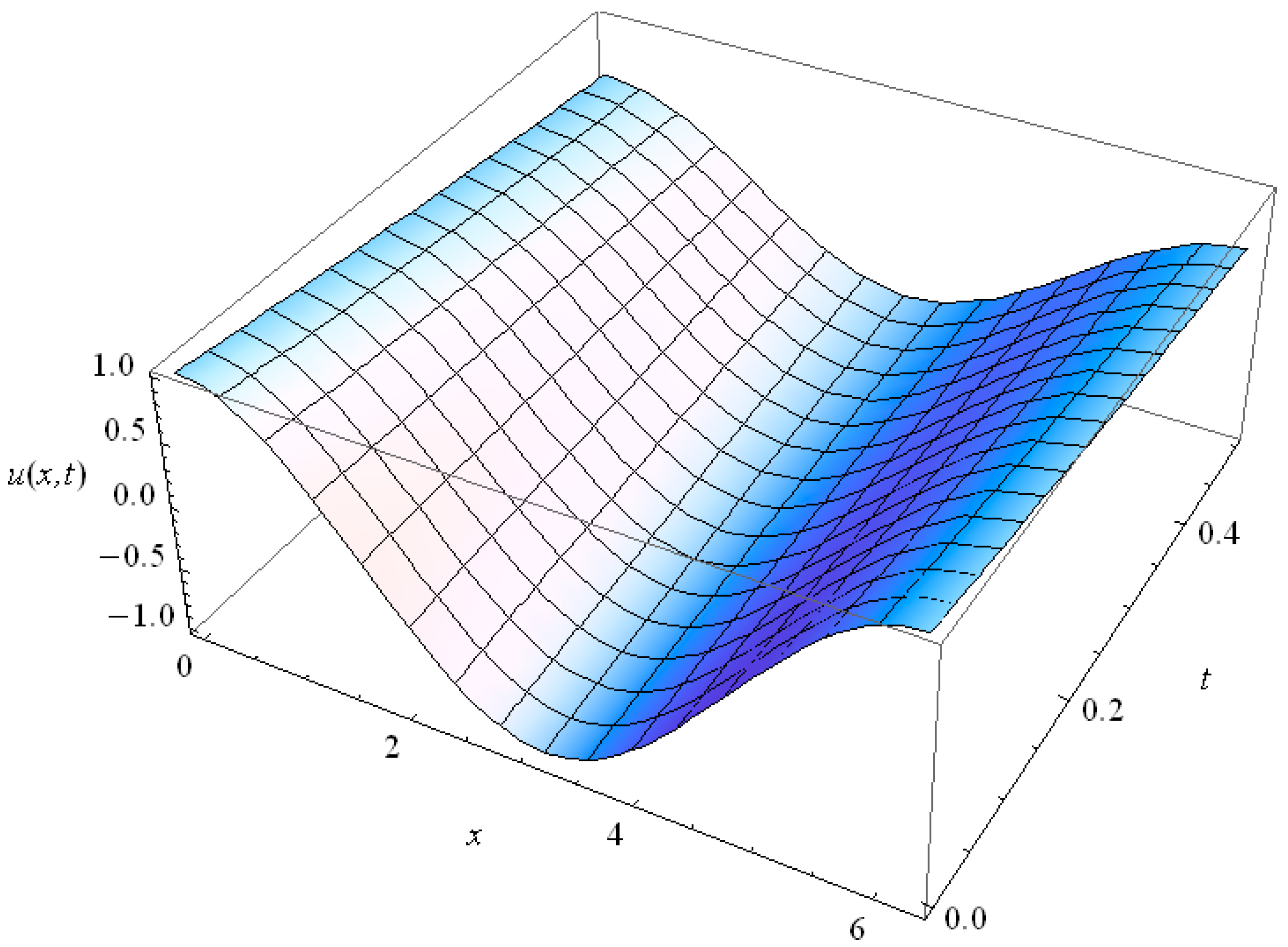
for it. The solution is shown in
Figure 1 and it evidences significant spread of the initial function already for the times
.
The plot in
Figure 1 is compiled for
α = 1,
γ = 1, which represents the Fourier heat solution with some heat exchange with the environment. At the moment
t = 0.001 we see the Gaussian as the result of the evolution of the
δ-function; at the moment
t = 0.01 this Gaussian has faded and the contribution of the heat exchange term
γ is noticeable. The relaxed solution slowly grows due to non-zero heat exchange with
.
4. Operational Solution of the Hyperbolic Heat Conduction Equation
The Fourier heat law [
75] has some shortcomings, noted by L. Onsager in 1931, who said [
80] that it “contradicts the principle of microscopic reversibility, but this contradiction is removed if we recognize that it is only an approximate description of the process of conduction, neglecting the time needed for acceleration of the heat flow”. The Fourier law does not properly describe heat conduction at low temperature <25 K in dielectric crystals and in systems with reduced dimensions. Moreover, it has some unphysical properties, such as lack of inertia. In other words, if an instant temperature perturbation is applied at a point in the solid, it will be felt everywhere instantaneously. This contradicts the phenomenon of the second sound, when the temperature perturbation propagates like a wave with damping. To overcome these problems Cattaneo [
76] proposed a time-dependent relaxational model, which yielded the following equation:
, where
DT is the heat conductivity and the relaxation time
τ in heat conduction is extremely small (
τ ≈ 10
−13 s) at room temperature. This equation models the phenomenon of the second sound, first observed in liquid helium [
81]. With the development of the second sound theoretical background [
77], it was then later detected also in solid crystals [
82,
83,
84,
85]. In the relevant tests heat flash technology [
79] was used for the sensitive measurement of the thermal diffusivity.
The application of the operational method for solution of the second order PDE was given in [
72]. The following PDE with initial conditions:
where
and
are differential operators, acting over the coordinate, dependently on the specific form of the operators
and
, describes a variety of physical processes in thermodynamics, electrodynamics etc. The particular fading with time solution of Equation (18) formally reads as follows [
72]:
The other solution of Equation (18) has a positive sign in the exponential:
, and does not satisfy the requirement
, which otherwise can be formulated as
, i.e., the solution converges at infinite time. Both of these assumptions are reasonable for physical applications. We perform the Laplace transforms [
41] in (19):
and, provided the integral converges, we obtain for Equation (18) the following vanishing at infinite time solution:
whose particular form depends on the differential operators
,
and on the initial condition
. In what follows, we consider some examples.
Let us first of all consider
and
, keeping the linear term
κ in the r.h.s. of Equation (18). Then we end with the telegraph equation, also known as a hyperbolic heat conduction equation (HHE):
Its fading at
solution reads as follows:
The action of the heat diffusion operator
can be accomplished with the help of the identity (4), resulting in
where
. Consider an example of the initial function
, which, is useful for the description of heat pulses of a variety of shapes, custom modelled by the sum
. With the help of the operational identity (11) we obtain the exact form of the solution:
We omit the bulky result of the above integration for arbitrary
, which can be computed with account for (9). In the particular case of given
n and
γ, for the example for
, we obtain
For
,
,
we have the following solution:
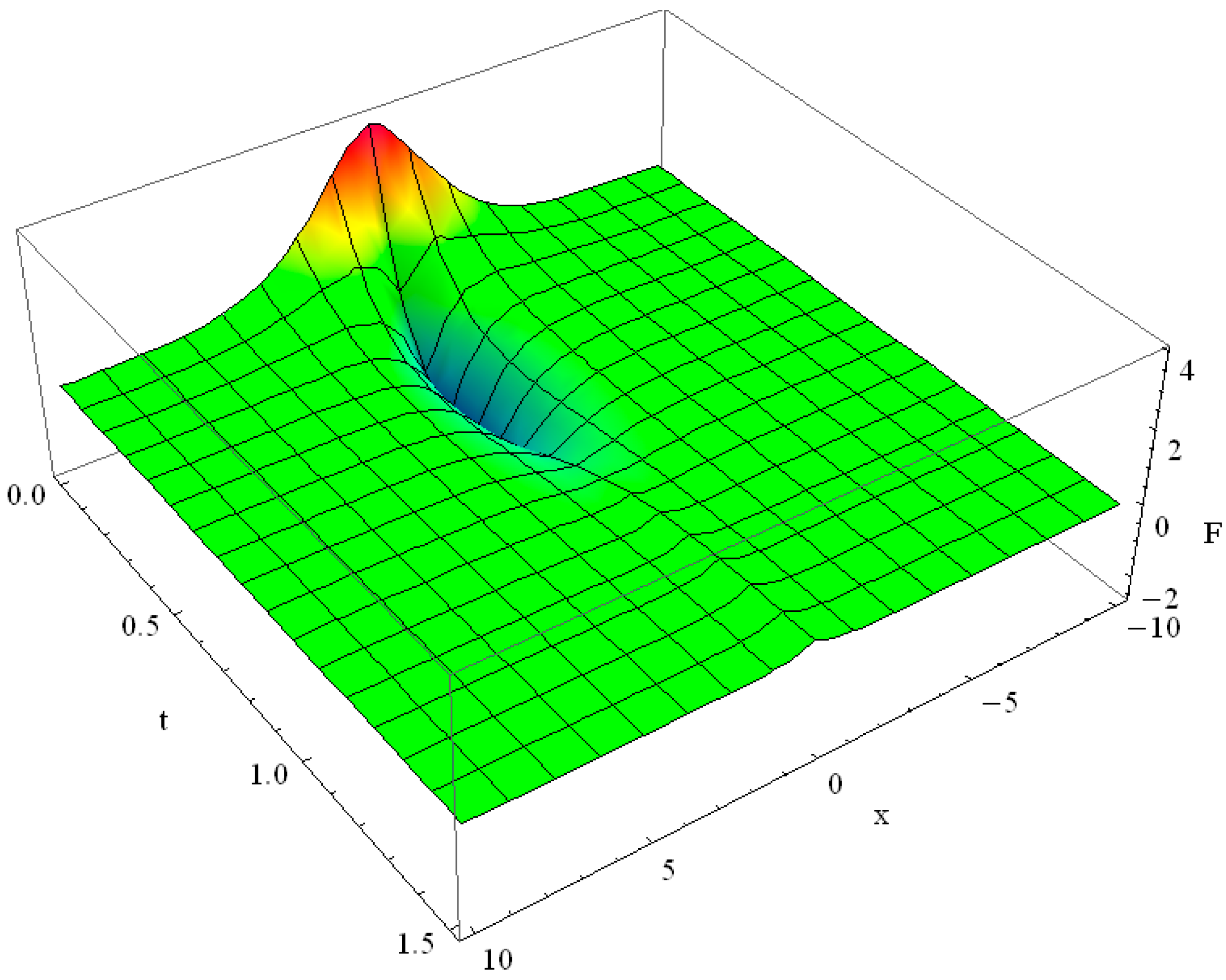
The solution for the initial function
is too bulky to be presented in its analytical form; it describes the damped wave propagation as shown in
Figure 2.
By choosing
in (22), i.e.,
,
, the influence of the second time derivative
in the Cattaneo equation is reduced, but the heat conductivity
remains unchanged, as compared with the case
. The relaxation of the solution occurs much earlier for
, than for
, as follows from the comparison of the plot in
Figure 2 with that in
Figure 3; the reason is that the diffusive heat transfer in this case prevails over the wave heat transfer.
5. Propagation of a Heat Surge with the Hyperbolic Heat Conduction Equation
We now consider the example of initial
δ-function
for Equation (22). The action of the operator
in our solution (23) can be accomplished with the help of Equation (16), where
, as follows:
. Now the integration in (23) can be completed for the times
, where the solution exists:
Physical meaning of the condition
, i.e.,
is that the time, needed for the initial
δ(
x) function to reach the point
x in space, is exactly
and before that the heat surge is just not felt in the point
x at all. The value
is the velocity of the surge propagation, finite in the Cattaneo model, contrary to the infinite signal propagation speed in the Fourier law. The solution of Equation (22) for
for the initial function
is shown in
Figure 4 for the moments of time
t = 0.01 (light blue line),
t = 0.1 (lilac line),
t = 0.3 (pink line),
t = 0.6 (blue line) and
t = 1.1 (yellow–green line). Differently from the Fourier law, the initial flash reaches the point
x at the moment
and there is still no non-trivial solution in the point
x before this moment of time. The initial
δ-function is not shown in
Figure 4 because of its infinite amplitude.
Higher values of α and ε reduce the contribution of the second order time-derivative in the Cattaneo Equation respectively to the role of other terms in (22). The damping of the solution in this case occurs sooner. We omit the proper plot for conciseness. Note that in the case of negative κ, i.e., when positive κ is in the l.h.s. of the hyperbolic Equation (22), the integral in (28) converges for , . Interestingly, despite the fact that the solution (28) was obtained for , it holds true for any . For we obtain positive values for , while for as well as for we obtain complex values for the resulting function . For we obtain . For the solution (28) diverges.
Heat propagation in three spatial dimensions in the Cattaneo model is governed by the direct three-dimensional generalization of (22) for
κ = 0:
, where
is the heat conductivity. The ratio
has the dimension of velocity and it stands for the speed of the heat wave propagation in the medium,
τ is the material parameter, describing the time, needed for the initiation of a heat flow after a temperature gradient was imposed at the boundary of the domain. Thus, it determines the time lag for the appearance or disappearance of the heat flow after the temperature gradient is imposed or removed. This relaxation time is associated in the framework of the Cattaneo model with the linkage time of phonon-phonon collision and it measures the thermal inertia of the medium through the time, needed for the heat flow to fade in or out. The role of the constant term in the HHE becomes clearer in the context of the signal propagation in long telephone lines. We will consider it in what follows. At the moment we will keep for generality the constant term in the three-dimensional telegraph equation, thus writing it as follows:
where
is the thermal diffusivity,
k is the thermal conductivity,
ρ is the mass density,
cp is the specific heat capacity,
is the relaxation time, often related to the speed of the second sound
C in media:
. The operational solution of (29) includes the action of the heat diffusion operators for each coordinate on the initial function:
The action of , where is easy to obtain: the result for each coordinate heat operator action is given by the inner integral in (24) and then the integration over can be performed if the integral converges.
For experimental measurement of the thermal conductivity the flash technique is commonly approved. For this reason we choose the initial function
, modelling an intense instant point-like volume heating. The application of the heat operators
gives
yields the following solution for HHE (29) with
:
The above integral converges for
and we obtain the following simple analytical expression, involving modified Bessel functions
K2:
Note, that the above solution also holds for . As well as in the one-dimensional case (28) for , that is for the times, inferior , when the heat wave reaches point x, we obtain positive values for the solution for negative κ, such that . For as well as for we obtain complex solution . In the limiting case of we obtain the finite limit for the solution: , but for the solution diverges.
Despite that the Cattaneo heat Equation (22) for is reversible on the time scale of the thermal relaxation time τ, and despite that it predicts a finite value for the heat wave velocity , its quantitative value disagrees with the experimental data at high frequencies and low temperatures. However, the HHE is widely used in radio engineering.
6. Propagation of a Harmonic Signal with the Telegraph Equation
In the context of signal propagation in cable lines without radiation loss the HHE (22) is perfectly usable for the description of the voltage and current 86. For this reason we choose the initial harmonic function
. The action of the operator
with account for (5) yields
,
. Integration in (24) in turn yields the following solution for the telegraph Equation (22) for
:
The harmonic solution (33) is not spreading in space, but only fading in time. Its physical meaning is clarified if we attribute the constants
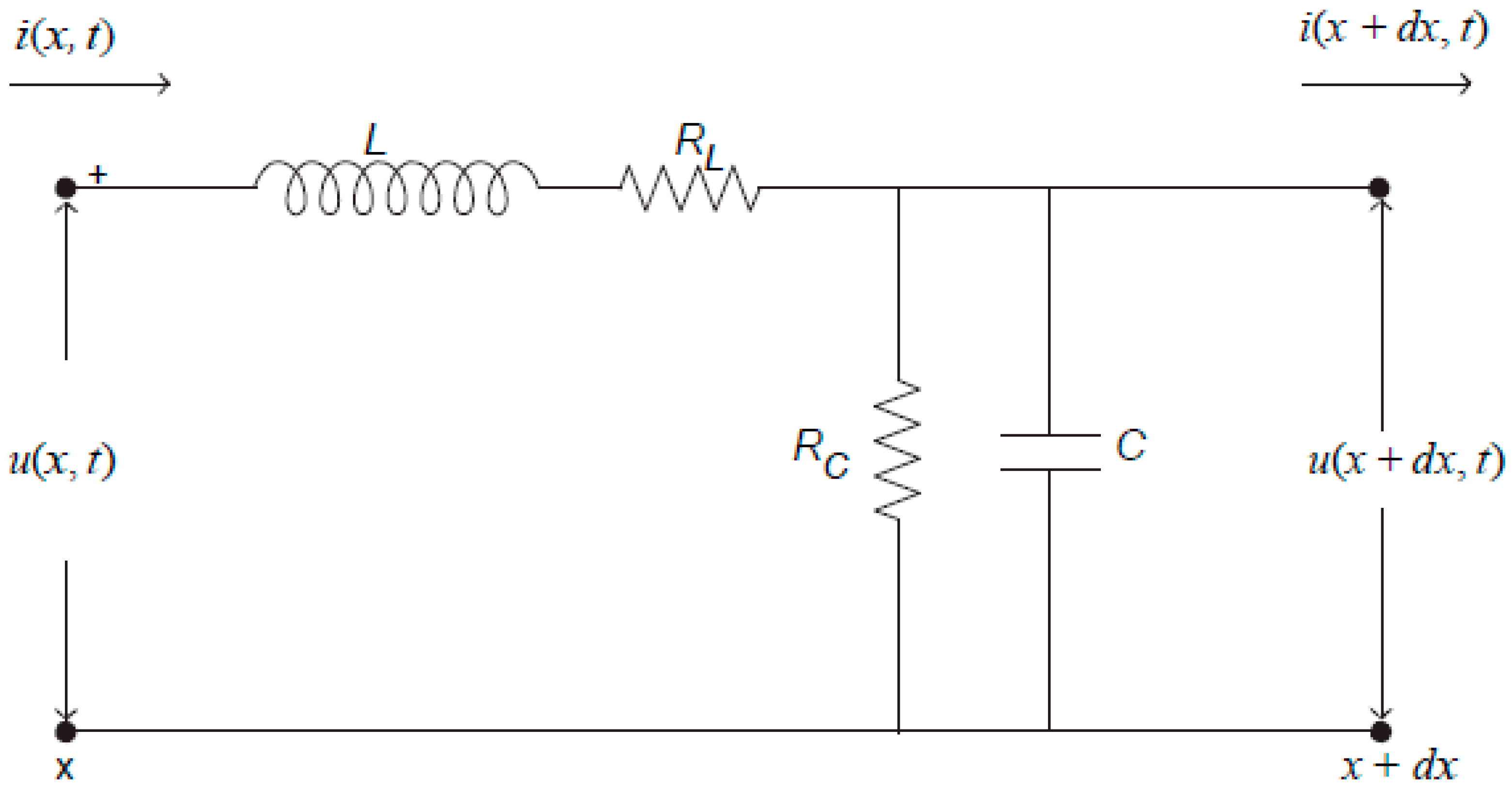
in HHE (22) the values according to the schematic diagram of the electric circuit in
Figure 5, where the electric line with finite resistance, inductivity, capacitance, and leakage is shown.
In terms of the resistance
RL, inductivity
L, capacitance
C and leakage resistance
RC the voltage
along the transmission line, shown in
Figure 5, is described by the one-dimensional telegraph equation [
86]:
In our notations , and . The solutions (28) and (32) for the initial δ-surge are valid and converge also for provided .
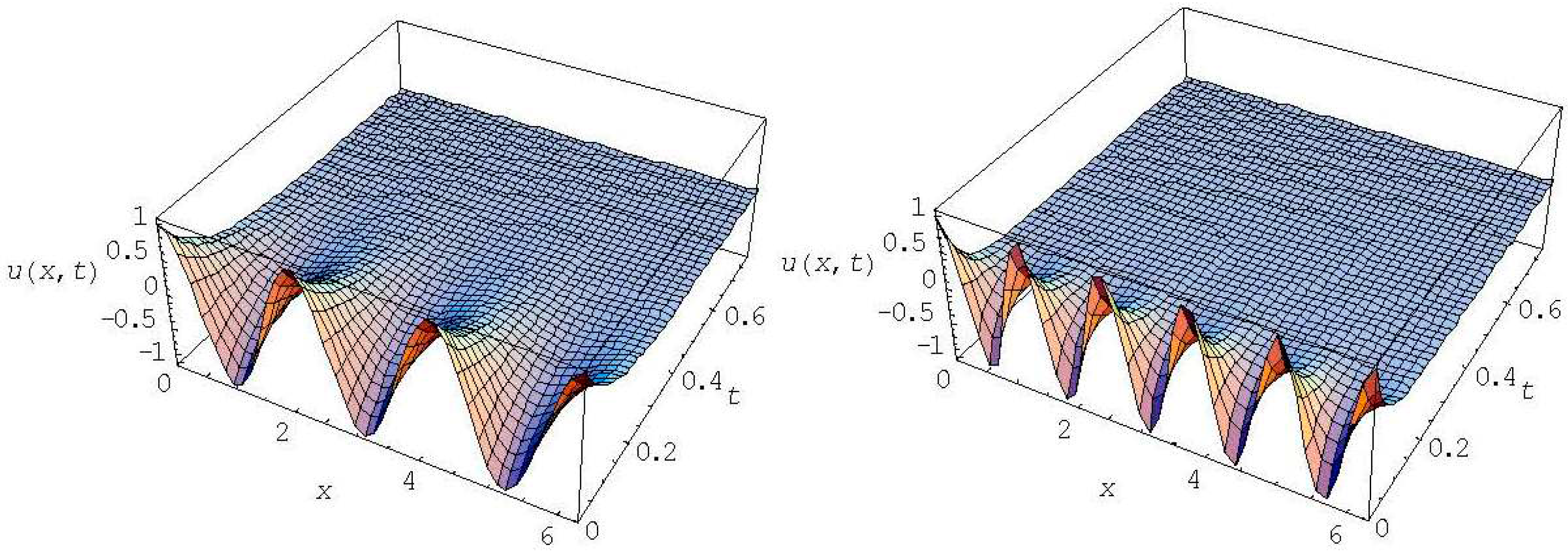
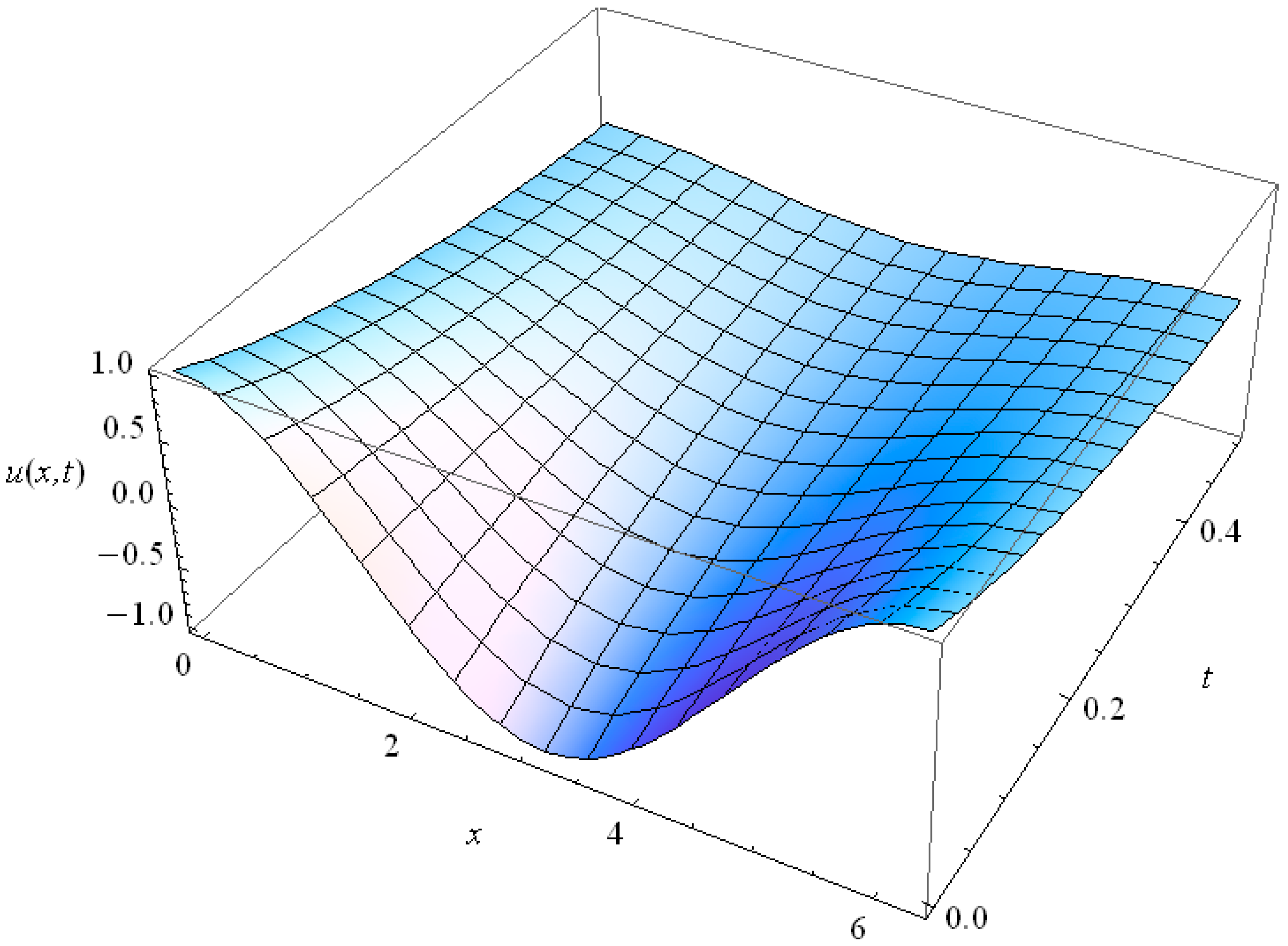
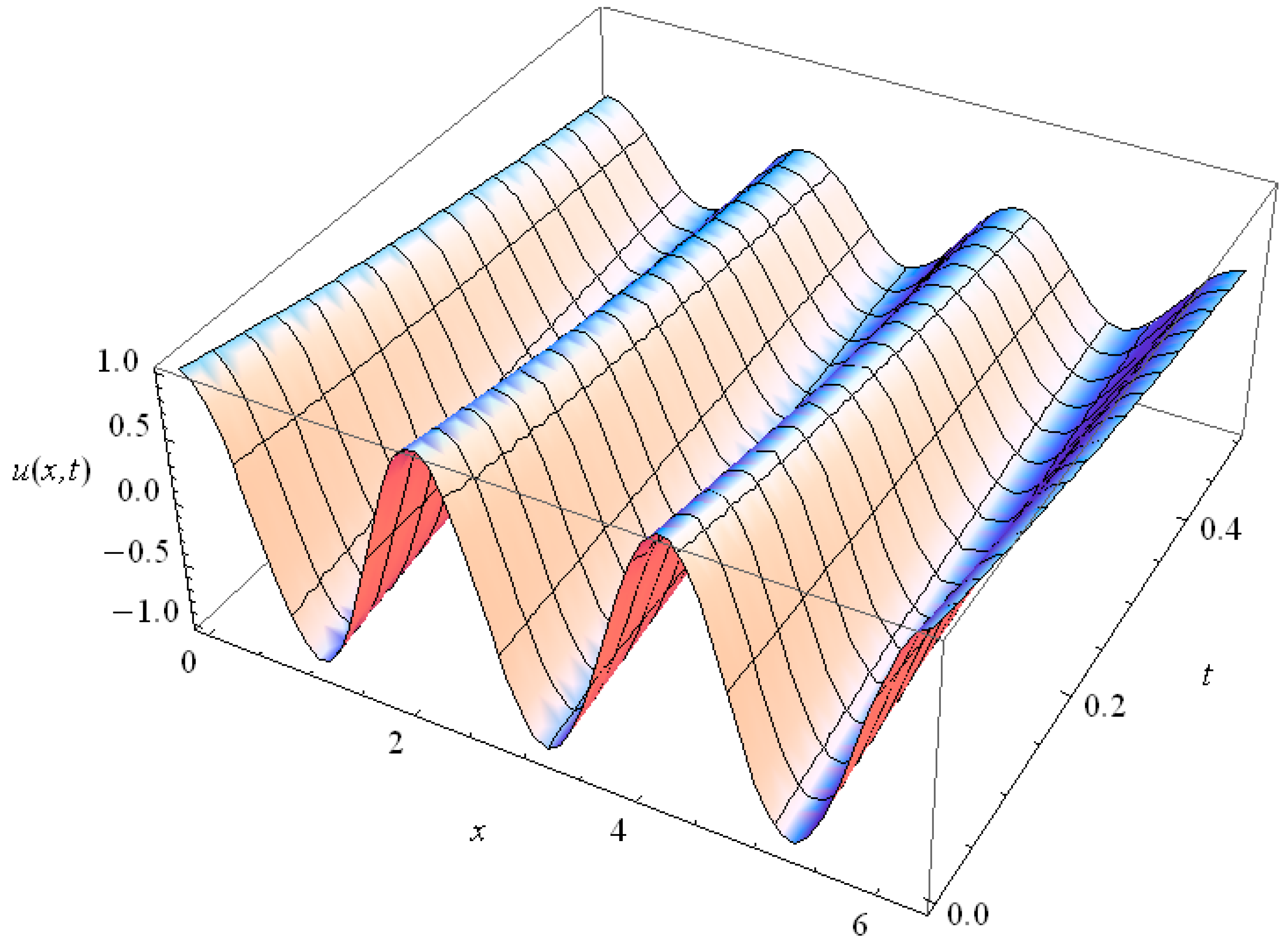
For
the periodic solution
(33) is realized; it fades without the space shift (see examples in
Figure 6). In the case of
the voltage behavior in the circuit has space shift and its time fading depends exclusively on
(see examples in
Figure 7):
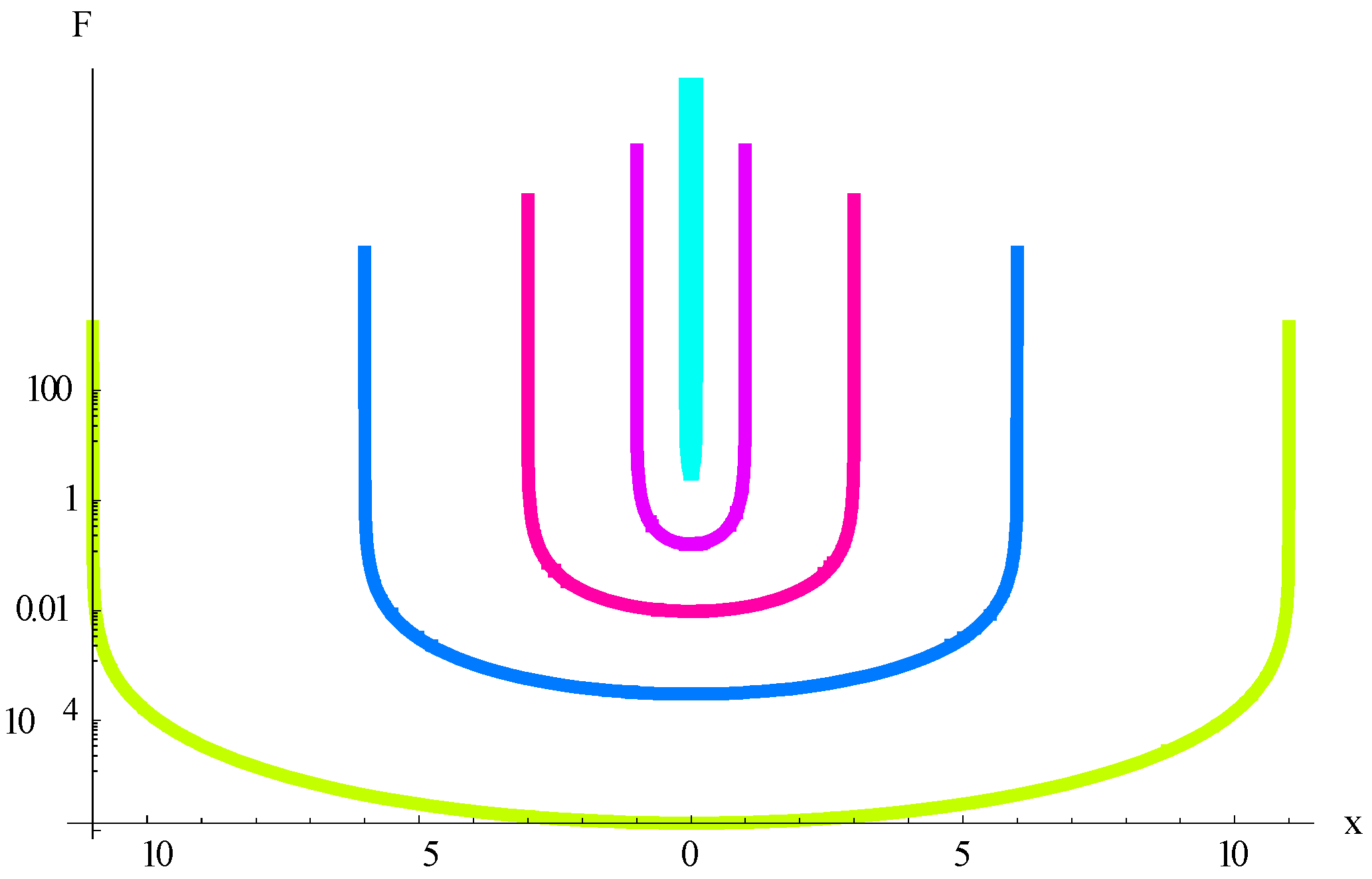
The essential difference between the plots in
Figure 6 and
Figure 7 is in the time dependent spatial phase shift, which is seen in
Figure 7 for
and is absent in
Figure 6 for
.
Thus the first three harmonics for
RC = 7,
C = L = RL = 1 develop in time without the space shift with decent fading (see examples for
n = 2, 3 in
Figure 6); for them the solution (33) is realized. The harmonics with
are governed by the solution (35), they have a time-dependent space shift (see examples for
n = 4, 5 in
Figure 7). With increase of
n the relaxation time of the harmonics also increases, but from a certain harmonic, for which the space shift appears, the relaxation time stabilizes and remains equal for all higher harmonics. In the context of heat conduction it means that the heat conduction for higher harmonics is lower than the heat conduction for low harmonics. It may also occur that, dependent on the values of the parameters in the HHE all harmonics have time-dependent space shift, i.e., the solution (35) is realized for
. This frequency dependent heat conductivity is typical for HHE and it is absent in the Fourier law.
Concluding the study of the hyperbolic heat Equation (22) we note that it can be easily modified by adding non-commuting with terms and mixed derivatives over time and coordinate. Such a modified hyperbolic equation can be solved with the help of the above developed operational technique.
7. Operational Solution of Guyer-Krumhansl Type Heat Equation and Heat Conduction in Thin Films
The Cattaneo hyperbolic equation gives a qualitatively correct description of the second sound through the heat wave propagation at finite velocity, but numerical results do not match the experiment. The predicted values for the speed of the heat wave in matter disagree with the data on ultrasonic wave propagation in dilute gases. Neither the heat pulse propagation at very low temperature is described correctly in non-metallic very pure crystals of Bi and Na F. In response to this disagreement, further generalizations of the Fourier law were developed. Among them the Guyer-Krumhansl (GK) equation [
87] is distinguished for simplicity and coherence with observed data. In addition to the heat waves the GK model takes into consideration the so-called ballistic transport, which can be observed when the mean free path of a particle significantly exceeds the dimension of the medium in which it travels. The mean free path increases at low temperatures For example, for electrons in a medium with negligible electrical resistance, their motion is altered by collisions with the walls. Ballistic conduction applies also to phonons. It is typically observed in low dimensional structures, such as very thin films, silicon nanowires, carbon nanotubes, graphene etc. (see, for example, [
88,
89,
90,
91,
92]). When the bulk phonon mean free path
l is comparable to the structure size
L, neither the Casimir phonon theory [
93] nor Fourier diffusion [
75] describe the heat transfer well, which is affected by boundary as well as internal scattering. The common rule that determines which type of transport dominates is the following: when
l <<
L, the heat diffusion prevails, but for
l >>
L, or when the temperature gradient becomes large, the ballistic transport cannot be ignored. Recently the conditions for the transition region between the ballistic heat transport and the diffusion were described in [
92]. Whether the heat transfer is ballistic or diffusive is also important for experimentalists, because the account for the ballistic phonon transport requires the knowledge of the boundary quality, while the wave and diffusive transport constants are intrinsic material properties [
94,
95,
96]. The three dimensional Guyer-Krumhansl (GK) heat law was derived from the solution of the linearized Boltzmann equation for a phonon field in dielectric crystals at low temperature. It is good for the description of phonon gases in low temperature samples and even for some heat propagation processes on the microscopic [
97] and macroscopic [
98,
99,
100,
101,
102] level at room temperature [
103,
104,
105]. The relaxation of the laser flash was shown to follow the GK law [
106], which was reconsidered in the framework of weakly non-local thermodynamics in [
107]. Due to the wide interest in the GK equation and its relatively good agreement with an array of experiments over a broad temperature range, conducted in various materials, we will consider the GK equation solution for propagation of spatial heat waves and flash pulses. To this end we will use the operational technique.
Let us choose the operators
and
in (18), which results in the following GK type equation with mixed derivative:
The one-dimensional GK equation is essentially Equation (36) with
κ = 0; we will keep
for the sake of generality. Its role is not indifferent and it will be discussed in what follows. Introducing the operators
and
, we can rewrite (36) with positive coefficients
in the following form:
Note that equations
represent Fourier law. If
and
, we have
, and, provided the Fourier Equation
is fulfilled, we have the particular case of GK equation, which is Equation (37) with
, also satisfied by this solution
. The form of the heat conduction equation Equation (36) with
arises in the study of heat propagation in a one-dimensional thin film with account for the phonon transport [
108]. From (21), where
,
, we write the solution of Equation (36) as follows:
By means of the integral presentation
(see (5)) we obtain after grouping the 2nd order derivative terms in the exponential
the particular bounded solution for the modified hyperbolic heat conduction Equation (36) with initial function
as follows:
where
,
,
. Note, that the obtained integral solution is valid also if the constant term in the r.h.s. of the Equation (36) is negative:
and
, which insures the integral convergence. Equations with negative sign of
κ have sense and they arise for ballistic heat propagation in thin films [
108].
The application of the above solution is direct: it was demonstrated that heat propagation in thin films obeys the extended form of GK Equation (36). In particular, the following equation for thin films was proposed [
108]:
where
is the ballistic component of the dimensionless energy (or quasi-temperature) and
Kn is the Knudsen number, describing the molecular and the boundary effects. Equation (40) is a GK type Equation (36) with the following coefficients:
,
,
,
.
In what follows, we will consider some examples of heat pulse propagation.
8. Propagation of a Heat Surge with the Guyer-Krumhansl Heat Equation
Consider the example of the initial flash
, corresponding to an intense and instant laser point heating at
at the moment of time
. From Equation (16) for
we obtain
. Then from (39) the analytical solution of GK type Equation (36) with
follows:
where we denote the special function
Function
reduces for some particular values of
a and
b to the hypergeometric function
, this last being the particular case of
. Moreover,
and
. The numerical calculation of the double integral (41), taken with care around the point
a = 0, corresponding to the time
, yields real values. The example of the solution (41) of the GK type Equation (36) with
for the initial flash
is shown in
Figure 8.
From the comparison of
Figure 8 with
Figure 1 we conclude that the solution of the Fourier heat Equation (1) (see
Figure 1) is more pronounced at short times, it has a higher peak, while the solution of GK Equation (36) spreads faster (see
Figure 8) when the additional terms
ε =
δ = 1 are comparable with the others order.
In the context of heat conduction in thin films we solved the respective GK equation for
and for
. The results for the ballistic dimensionless energy change after a laser pulse heating of a thin film, modelled by the GK type Equation (40), are shown in
Figure 9 for Knudsen number
Kn = 1 and in
Figure 10 for Knudsen number
Kn = 0.2. Their comparison confirms much faster heat propagation in a thin film with
Kn = 1, where the ballistic transport mechanism contributes noticeably, as compared with the film with small value of
Kn = 0.2.
9. Solution of the Guyer-Krumhansl Equation for the Exponential–Polynomial Initial Function
Interesting features of the heat conduction, governed by the Guyer-Krumhansl equation, arise from consideration of the evolution of the power–exponential initial function
. Consideration of such a function is useful not only because it allows better approximation of experimental data than the usual polynomial
and
,
γx < 0, but also as itself it represents a pulse, and practically any solitary space wave or surge is easy to approximate by its sum
. The operational method allows the exact analytical solutions for these functions to be obtained. Indeed, we make use of the operational identity (11) to obtain for
,
,
. The solution for arbitrary values of
can be obtained upon the following integration:
where
,
,
,
. The integration can be done in elementary functions if we account for the series presentation
. We omit the final result for conciseness. For example, in the simplest case of
, i.e.,
we obtain the following solution of the GK equation:
Let us now consider the initial smooth function
. By means of the above developed operational technique we obtained the following exact analytical solution of the GK equation in elementary functions:
Direct substitution of the solution satisfies the GK equation. Earlier it was demonstrated that such solutions can show bizarre behavior with local maximums and local minimums even with negative values, occurring in the middle of the domain, so that theoretically for a certain set of parameters of the GK equation the maximum principle can be violated [
58]. However, for applications, such as those in the thin films, modelled by the GK type Equation (40), there is no problem with the second law of thermodynamics violation. Indeed, the propagation of the smooth spatial heat distribution
in the range of the values of the Knudsen number between
changes no more than three percent.
The difference between these plots is not distinguishable visually and we present here just one example for
in
Figure 11. It corresponds to the values
,
. The behavior of the solution surprisingly resembles that for
α ≈
ε ≈
δ ≈ 1, which we omit for brevity, as well as that for
, for which
,
.
To contrast it, we demonstrate the behavior of the solution of GK equation (see (36),
κ = 0) for relatively small contribution of the Cattaneo’s term:
α =
ε =
δ = 10, which does not depend on the sign and on the exact value of the constant term
κ (we omit proper figures with
κ ≠ 0) for conciseness) and it has bizarre non-Fourier behavior, shown in
Figure 12.
The initial pulse rapidly decreases and assumes negative values, then it gradually approaches zero. It maintains negative values in the whole space domain, but for the vicinity of . Around the solution becomes positive: and then it relaxes to zero: .
In this case, based on the obtained exact vanishing analytical solution of the GK equation with the initial function
and
, we conclude the minimum of the solution over the time-space domain is in the middle of the domain (see
Figure 12). The local maximum of the solution may also occur in the middle of the domain (see [
58,
59]).
10. Harmonic Solution of Guyer-Krumhansl Equation and Temperature Distribution in Thin Films
The other good example of a given initial temperature distribution, is given by a harmonic function
, which is necessary to consider approximations or expansion of the initial function into the Fourier series to fit experimental data distributions. The action of the heat conduction operator yields the following bounded at infinite times solution:
Upon integration we end up with the explicit solution of the GK Equations (36) and (37) for the periodic initial function
, expressed in elementary functions as follows:
Interestingly, the solution (47) of GK type Equation (36) for the initial harmonic function
repeats the solution of telegraph Equation (33) upon the substitution
, where
, in (33). In other words, the solution (47) of Equation GK type (36) for
is also the solution of the HHE (22) with the harmonic dependent coefficient
for the first order time derivative:
Thus, for the initial harmonic function
and same values of the coefficients
in Equations (36) and (48), these share identical particular solution (47). For the initial function
, the solution of Equations (36) and (48) will be given by the series
, where
is the solution of (47). In this sense the GK type equation with the harmonic initial function can be viewed as the telegraph equation with the harmonic dependent coefficient for
:
and the GK equation for
is in fact the Cattaneo equation for
with
instead of
term. This radically changes the solution behavior. Indeed, the relaxation time for all higher harmonics
in the telegraph Equation (33) is the same; only low harmonics may fade out faster. On the contrary, the solution (47) of the GK type Equation (36) for the harmonic function
and the solution of the equivalent telegraph equation with
(48) for high harmonics show that these harmonics fade out faster than the fundamental one
(
n = 1) and the higher the harmonic number
n, the lower is its relaxation time. The examples for
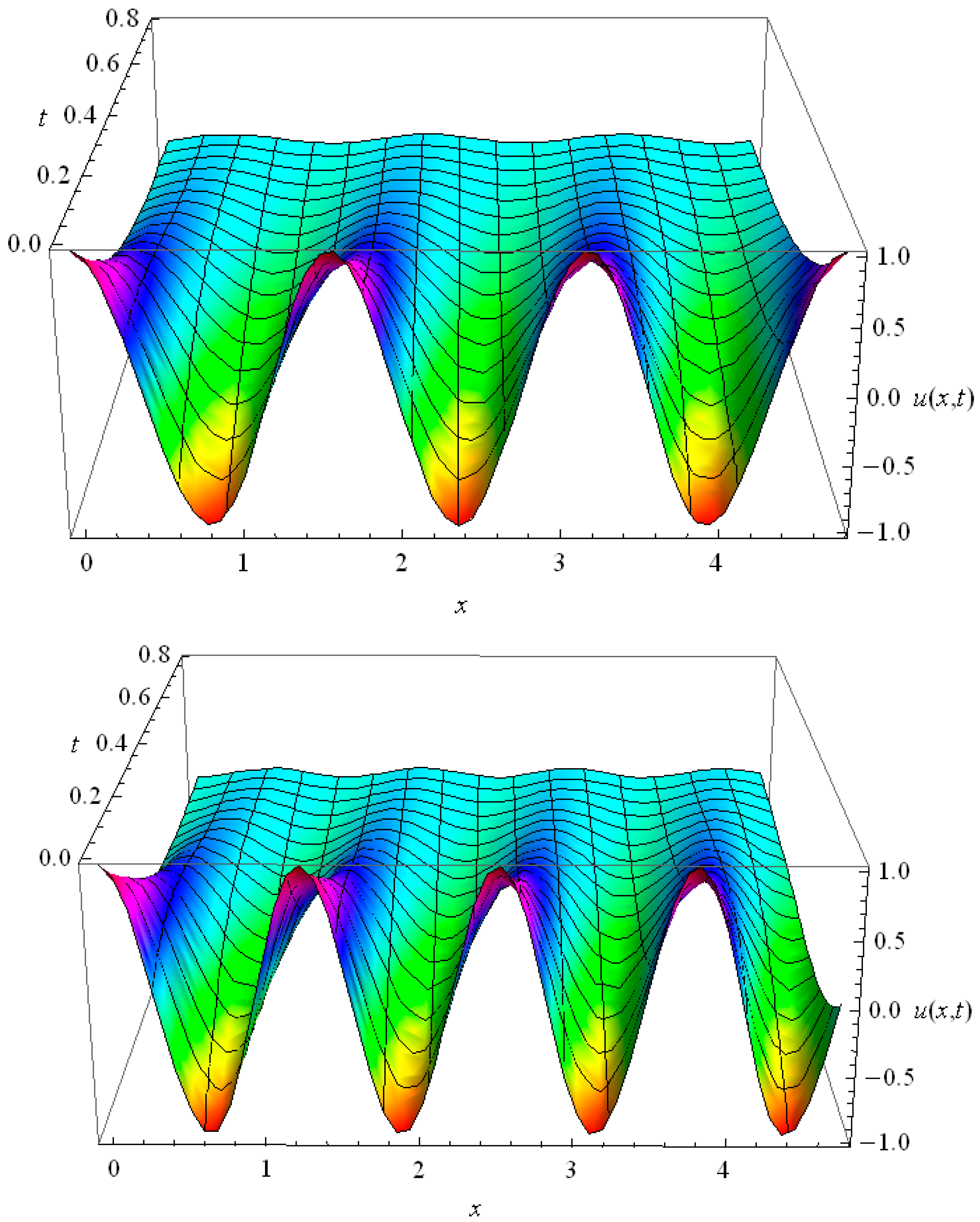
n = 3, 5 are shown in
Figure 13.
Compare
Figure 13 with the solution of the telegraph Equation (22) (see
Figure 6 and
Figure 7). High harmonics of the telegraph equation, shown in
Figure 7, fade out slower than the low harmonics, shown in
Figure 6. For the GK type equation or the HHE with
on the contrary, high harmonics fade out faster than the fundamental and the low ones, as evidenced in
Figure 13. The effective thermal conductivity in the common telegraph Equation (22) is constant for higher harmonics and in certain cases even for all
n. On the contrary, in the GK type Equation (36), which is HHE with
for
(see (48)), the thermal conductivity for the harmonic function
rises with increase of the harmonic number
n.
In the context of the heat conduction in thin films, for
Kn = 1 we plotted the bounded solutions of Equation (40), for
,
n = 1, 3, in
Figure 14 and
Figure 15 respectively. High harmonics fade out rapidly as follows from their comparison with teach other. For
Kn = 0.2 we present the solutions in
Figure 16 and
Figure 17 for
n = 1, 3 respectively. The comparison with
Figure 14,
Figure 15 shows that the solutions for
Kn = 0.2 relax much slower than those for
Kn = 1.
This means that high values of the Knudsen number provide the ballistic transport contribution to the heat conduction, and the latter increases in the GK model, in particular, for high harmonics. The proper relaxation times for the first harmonic read as follows: n=1τKn=1 ≈ 0.5 and n=1τKn=0.2 ≈ 2.5; for the third harmonic the relaxation times are n=3τKn=1 ≈ 0.2 and n=3τKn=0.2 ≈ 3. The ratios of proper relaxation times are and . The heat conduction is evidently better for Kn = 1 than for Kn = 0.2.
11. Conclusions
We obtained exact analytical solutions for heat conduction in the Fourier, Cattaneo, and Guyer-Krumhansl heat transport models. Extended forms of these equations with additional constant terms were solved by the operational method. The obtained solutions directly satisfy the considered equations. The initial functions, modelling various types of pulses and signals were considered. The power–exponential pulse and the flash heat pulse were considered, modelling the laser heat pulse experimental technique, common for thermal conductivity measurements.
The analytical solutions were compared with each other. The finite speed of the heat propagation in the Cattaneo model was demonstrated. By reducing the effect of the second time derivative in the equation for , maintaining the heat conductivity unchanged, we obtain faster fading of the solution. In this case diffusive heat conduction prevails over the wave-like propagation process. On the contrary, for the wave-like propagation of the initial function dominates. For , both heat transport mechanisms contribute; the wave propagates at a constant speed, accompanied by fading.
The exact analytical solution of HHE in three space dimensions for initial flash was obtained in terms of modified Bessel functions. The HHE was solved with the harmonic initial function . The obtained solution fades in time exponentially and does not spread. The space phase shift of the solution depends on the sign of the linear term in HHE.
The GK type heat equation with linear term was solved operationally; the solution was written in terms of integrals and special functions. The propagation of the initial heat flash was studied and demonstrated for the model of heat conduction in thin films. Small values of Knudsen number result in slower relaxation of the initial heat surge; for the ballistic heat transport contributes and the heat surge fades out much faster. An exact solution for the evolution of the exponential-monomial function in the GK equation was obtained. This allows not only the propagation of a surge with power rise, followed by the common exponential fade, to be studied but also the result for the initial function to be obtained, which can be expanded in the series or approximated by them. The example of the initial smooth heat pulse relaxation in a thin film was considered.
We found that variation of the Knudsen number values in a reasonable range practically does not influence the relaxation time of the initial smooth pulse: the values of the solution of GK type equation vary less than 3% for . Thus in thin films the conditions on the surface, expressed by the Knudsen number, are particularly important for laser heat flash, but not that important for relaxation of a wide heat spot without a sharp boundary.
For the propagation of the initial laser heat flash the relaxation time is ten times smaller for Kn = 1 than for Kn = 0.2. The relaxation time τ for the harmonic initial function for the first harmonic (n = 1) is five times shorter for Kn = 1 than for Kn = 0.2: n=1τKn=1 ≈ 0.5 and n=1τKn=0.2 ≈ 2.5; for the third harmonic the relaxation time τ is 15 times shorter for Kn = 1 than τ for Kn = 0.2: the proper relaxation times are n=3τKn=1 ≈ 0.2 and n=3τKn=0.2 ≈ 3. The ratios of proper relaxation times are and .
We obtained exact analytical solutions in terms of the orthogonal polynomials and special functions for three different models of heat conduction: Fourier, Cattaneo, and Guyer-Krumhansl. These solutions allow analytical modelling of the space–time propagation for heat flashes and pulses, which is the established experimental technique. We can also model the relaxation of any initial function, expandable in the Fourier series and in the series of the exponential-polynomial function. This series approximation is applicable practically to any pulse.
In conclusion we stress that the operational technique, used for the solution of hyperbolic heat equations, yields exact analytical solutions. They have clear physical meaning and allow easy understanding of the role of different terms in the equations. The validity of the obtained analytical solutions was checked by their substitution in the equations, the latter were satisfied. Our study not only has theoretical interest, but it also provides practical results of experimental technique and measurements. The obtained exact analytical solutions can be used as a benchmark for numerical solutions of more sophisticated forms of the studied equations.