A Class of Extended Fractional Derivative Operators and Associated Generating Relations Involving Hypergeometric Functions
Abstract
:1. Introduction, Definitions and Preliminaries
1.1. The Extended Beta, Gamma and Hypergeometric Functions
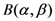 :
:
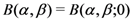
 in the Definition (1.1) are motivated by the connection of the extended Beta function
in the Definition (1.1) are motivated by the connection of the extended Beta function 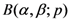 with the Macdonald (or modified Bessel) function
with the Macdonald (or modified Bessel) function  (see, for details, [8,9]).
(see, for details, [8,9]).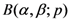 defined by (1.1), Chaudhry et al. [8] introduced the extended hypergeometric function as follows:
defined by (1.1), Chaudhry et al. [8] introduced the extended hypergeometric function as follows: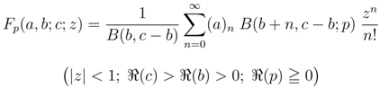
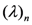 denotes the Pochhammer symbol or the shifted factorial, which is defined (for
denotes the Pochhammer symbol or the shifted factorial, which is defined (for 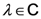 and
and 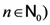 by
by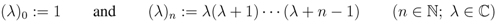
 .
. defined by (1.2), the following integral representation of the Pfaff–Kummer type was also given by Chaudhry et al. [8, p. 592, Equation (3.2)]:
defined by (1.2), the following integral representation of the Pfaff–Kummer type was also given by Chaudhry et al. [8, p. 592, Equation (3.2)]: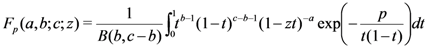
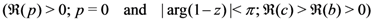
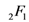 , we have
, we have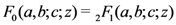
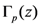 (see, for details [9]), the extended Beta function
(see, for details [9]), the extended Beta function 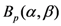 and the extended Gauss hypergeometric function
and the extended Gauss hypergeometric function 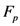 were considered more recently by Özergin et al. [7]:
were considered more recently by Özergin et al. [7]: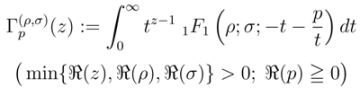
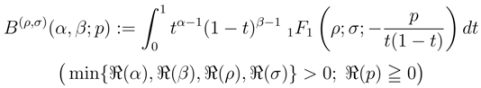
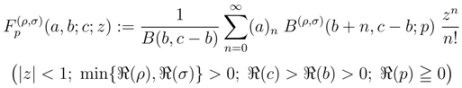
 being the (Kummer’s) confluent hypergeometric function. The following integral representation of the Pfaff–Kummer type was also given by Özergin et al. [7]:
being the (Kummer’s) confluent hypergeometric function. The following integral representation of the Pfaff–Kummer type was also given by Özergin et al. [7]: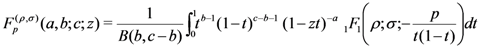
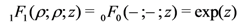
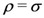 would immediately yield Equations (1.1), (1.2) and (1.4), respectively.
would immediately yield Equations (1.1), (1.2) and (1.4), respectively. and various other lower (or denominator) parameters are not zero or negative integers (that is, no zeros appear in the denominators).
and various other lower (or denominator) parameters are not zero or negative integers (that is, no zeros appear in the denominators).1.2. The Riemann–Liouville Fractional Derivative Operator and Its Generalizations
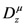 defined by (see, for example [10, p. 181] [11] and [12, p. 70 et seq.])
defined by (see, for example [10, p. 181] [11] and [12, p. 70 et seq.])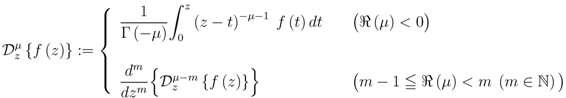
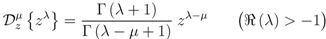
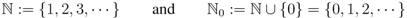
 -plane from
-plane from 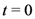 to
to  .
. of the type which is involved in (for example) the Definitions (1.1) and (1.2), Özarslan and Özergin [1] defined the correspondingly extended Riemann–Liouville fractional derivative operator
of the type which is involved in (for example) the Definitions (1.1) and (1.2), Özarslan and Özergin [1] defined the correspondingly extended Riemann–Liouville fractional derivative operator 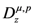 by
by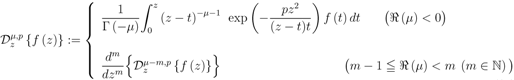
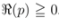 . The path of integration in the Definition (1.13), which immediately yields the definition (1.10) when
. The path of integration in the Definition (1.13), which immediately yields the definition (1.10) when  , is also a line in the complex
, is also a line in the complex  -plane from
-plane from  to
to  . The argument
. The argument  in the Definition (1.13) and elsewhere in this paper is obviously necessitated by the applicability of the definition (1.1) of the extended Beta function
in the Definition (1.13) and elsewhere in this paper is obviously necessitated by the applicability of the definition (1.1) of the extended Beta function  when we set
when we set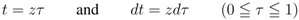
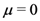 , we find from the second part of the Definition (1.13) (with
, we find from the second part of the Definition (1.13) (with  ) that
) that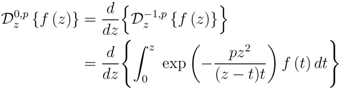
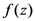 when
when  . Thus, in general, the natural connection of the Riemann–Liouville fractional derivative operator
. Thus, in general, the natural connection of the Riemann–Liouville fractional derivative operator 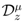 defined by (1.10) with ordinary derivatives when the order
defined by (1.10) with ordinary derivatives when the order  is zero or a positive integer is lost by the extended fractional derivative operator in Definition (1.13) and its further generalizations which we have considered in our present investigation.
is zero or a positive integer is lost by the extended fractional derivative operator in Definition (1.13) and its further generalizations which we have considered in our present investigation.1.3. Extended Appell Hypergeometric Functions in Two Variables
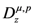 , Özarslan and Özergin [1] extended the familiar Appell hypergeometric functions
, Özarslan and Özergin [1] extended the familiar Appell hypergeometric functions 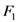 and
and 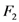 in two variables as follows:
in two variables as follows: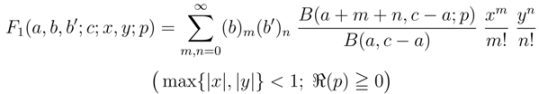
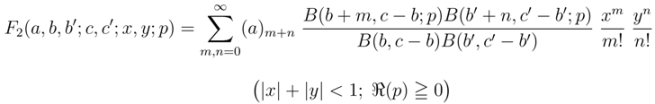
 , yield the familiar Appell hypergeometric functions
, yield the familiar Appell hypergeometric functions 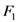 and
and 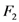 in two variables (see [13, p. 14]). For each of these extended Appell hypergeometric functions, such properties as their integral representations and relationships with the extended Riemann–Liouville fractional derivative operator
in two variables (see [13, p. 14]). For each of these extended Appell hypergeometric functions, such properties as their integral representations and relationships with the extended Riemann–Liouville fractional derivative operator 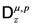 defined by (1.13) can also be found in the work of Özarslan and Özergin [1].
defined by (1.13) can also be found in the work of Özarslan and Özergin [1].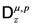 defined by (1.13) and apply the generalized operator to derive generating relations for hypergeometric functions in one, two and more variables. We first introduce, in Section 2, the following further generalizations of the extended Appell’s hypergeometric functions:
defined by (1.13) and apply the generalized operator to derive generating relations for hypergeometric functions in one, two and more variables. We first introduce, in Section 2, the following further generalizations of the extended Appell’s hypergeometric functions: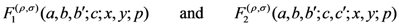
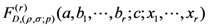
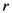 variables
variables 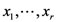 are defined and their integral representations are obtained. In Section 3, we introduce and study the properties and relationships associated with the above-mentioned further generalization of the extended fractional derivative operator
are defined and their integral representations are obtained. In Section 3, we introduce and study the properties and relationships associated with the above-mentioned further generalization of the extended fractional derivative operator 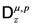 defined by Definition (1.13) and apply the generalized operator in order to obtain various generating relations in terms of the generalized extended Appell and Lauricella hypergeometric functions in two and more variables. Section 4 contains some results related to the Mellin transforms and the extended fractional derivative operator. In Section 5, some generating relations for generalized extended hypergeometric functions are obtained via the above-mentioned further generalized fractional derivative operator by following the lines which are detailed in the monograph by Srivastava and Manocha [14]. Finally, in Section 6, we conclude this paper by presenting a number of remarks and observations pertaining to our investigation here.
defined by Definition (1.13) and apply the generalized operator in order to obtain various generating relations in terms of the generalized extended Appell and Lauricella hypergeometric functions in two and more variables. Section 4 contains some results related to the Mellin transforms and the extended fractional derivative operator. In Section 5, some generating relations for generalized extended hypergeometric functions are obtained via the above-mentioned further generalized fractional derivative operator by following the lines which are detailed in the monograph by Srivastava and Manocha [14]. Finally, in Section 6, we conclude this paper by presenting a number of remarks and observations pertaining to our investigation here.2. The Generalized Extended Appell and Lauricella Functions
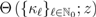 be analytic within the disk
be analytic within the disk 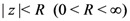 and let its Taylor–Maclaurin coefficients be explicitly denoted (for convenience) by the sequence
and let its Taylor–Maclaurin coefficients be explicitly denoted (for convenience) by the sequence  . Suppose also that the function
. Suppose also that the function 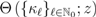 can be continued analytically in the right half-plane
can be continued analytically in the right half-plane 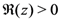 with the asymptotic property given as follows:
with the asymptotic property given as follows: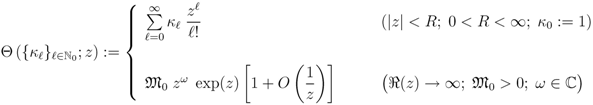
 and
and  depending essentially upon the sequence
depending essentially upon the sequence 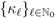 . Here, and in what follows, we assume that the series in the first part of the Definition (2.1) converges absolutely when
. Here, and in what follows, we assume that the series in the first part of the Definition (2.1) converges absolutely when  for some
for some  and represents the function
and represents the function  which is assumed to be analytic within the disk
which is assumed to be analytic within the disk 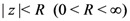 and which can be appropriately continued analytically elsewhere in the complex
and which can be appropriately continued analytically elsewhere in the complex 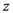 -plane with the order estimate provided in the second part of the Definition (2.1). For example, if we choose the sequence
-plane with the order estimate provided in the second part of the Definition (2.1). For example, if we choose the sequence 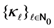 to be a suitable quotient of several
to be a suitable quotient of several 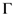 -products with arguments linear in
-products with arguments linear in 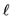 so that the function
so that the function  becomes identifiable with the familiar Fox–Wright
becomes identifiable with the familiar Fox–Wright 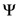 -function, we can easily determine the radius
-function, we can easily determine the radius  of the above-mentioned disk and, moreover, we can then appropriately continue the resulting function
of the above-mentioned disk and, moreover, we can then appropriately continue the resulting function 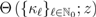 analytically by means of a suitable Mellin–Barnes contour integral (see, for details [12, p. 56 et seq.]). Such functions as
analytically by means of a suitable Mellin–Barnes contour integral (see, for details [12, p. 56 et seq.]). Such functions as 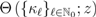 can indeed be specified on an ad hoc basis.
can indeed be specified on an ad hoc basis.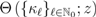 defined by (2.1), we now introduce a natural further generalization of the extended Gamma function
defined by (2.1), we now introduce a natural further generalization of the extended Gamma function 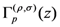 , the extended Beta function
, the extended Beta function  and the extended hypergeometric function
and the extended hypergeometric function  by
by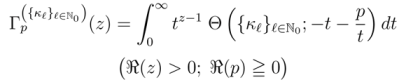
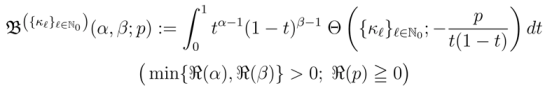
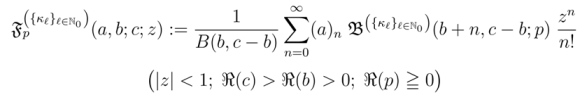
 , the definitions in (2.2–2.4) would reduce to (known or new) extensions of the Gamma, Beta and hypergeometric functions. In particular, if we set
, the definitions in (2.2–2.4) would reduce to (known or new) extensions of the Gamma, Beta and hypergeometric functions. In particular, if we set
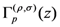 , the extended Beta function
, the extended Beta function  and the extended hypergeometric function
and the extended hypergeometric function  , respectively.
, respectively. defined by definition (2.1), it is not difficult to generalize the integral representation definition (1.8) to the following form:
defined by definition (2.1), it is not difficult to generalize the integral representation definition (1.8) to the following form: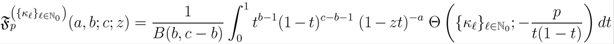
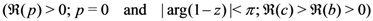
 and
and  , we propose these further generalizations of the extended Appell’s hypergeometric functions:
, we propose these further generalizations of the extended Appell’s hypergeometric functions: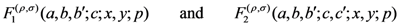
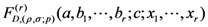
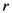 variables
variables 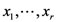 , which are defined by
, which are defined by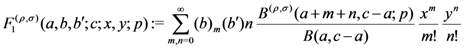
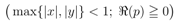
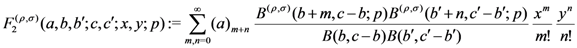
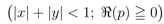
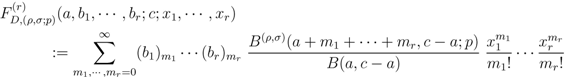
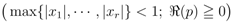
 is given by Definition (1.6). Clearly, the Definition (2.7) corresponds to the special case of the Definition (2.9) when
is given by Definition (1.6). Clearly, the Definition (2.7) corresponds to the special case of the Definition (2.9) when  . Moreover, in view of the relationship Definition (1.9), the Definitions (2.7) and (2.8) immediately yield the definitions in (1.14) and (1.15) when
. Moreover, in view of the relationship Definition (1.9), the Definitions (2.7) and (2.8) immediately yield the definitions in (1.14) and (1.15) when 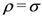 . More generally, in terms of the sequence
. More generally, in terms of the sequence 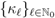 defined involved in (2.1), we have the following definitions:
defined involved in (2.1), we have the following definitions: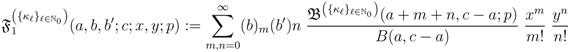
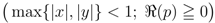
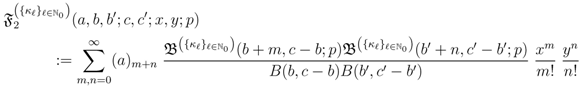

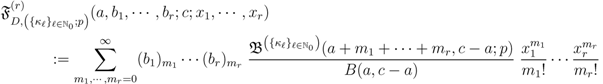
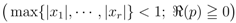
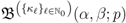 is given by Definition (2.3).
is given by Definition (2.3).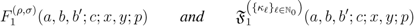
 and
and 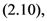 the following integral representations hold true:
the following integral representations hold true: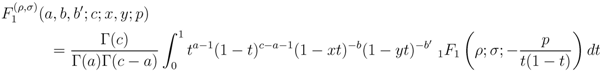
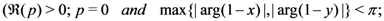
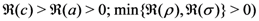
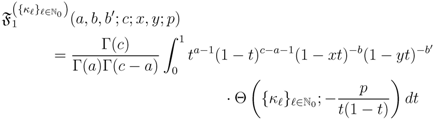
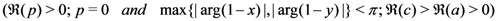
 and assume that
and assume that 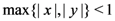 . Then, upon expressing
. Then, upon expressing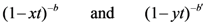
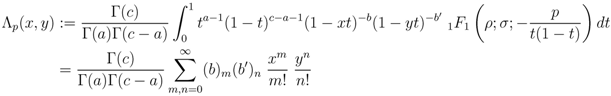
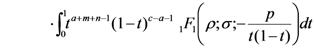
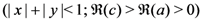
 above in (2.13) exists under the constraints which are listed already with (2.13).
above in (2.13) exists under the constraints which are listed already with (2.13).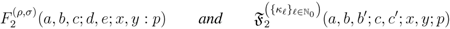
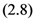 and
and 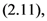 respectively, the following integral representations hold true:
respectively, the following integral representations hold true: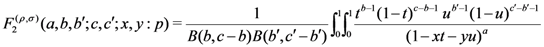
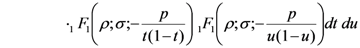
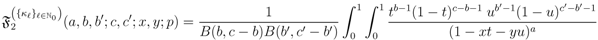
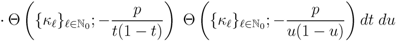
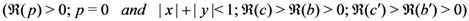
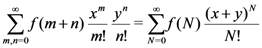
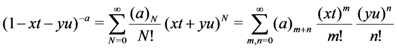
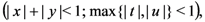
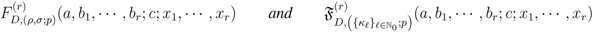
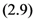 and
and 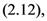 respectively, the following integral representations hold true:
respectively, the following integral representations hold true: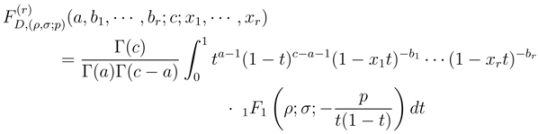
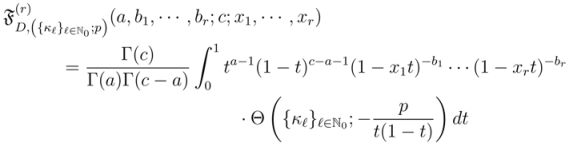
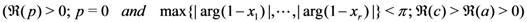
 . We, therefore, omit the details involved.
. We, therefore, omit the details involved.3. Applications of the Generalized Extended Riemann–Liouville Fractional Derivative Operator
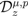 defined by (1.13):
defined by (1.13):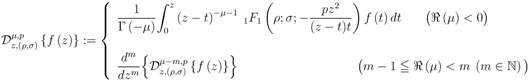
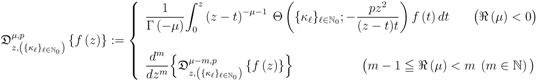
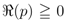 and the path of integration in each of the Definitions (3.1) and (3.2) is a line in the complex
and the path of integration in each of the Definitions (3.1) and (3.2) is a line in the complex  -plane from
-plane from 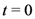 to
to  .
.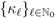 as in (2.5). Moreover, by using the specialization indicated in (1.9), the Definition (3.1) reduces immediately to (1.13). For
as in (2.5). Moreover, by using the specialization indicated in (1.9), the Definition (3.1) reduces immediately to (1.13). For  , the Definitions (1.13), (3.1) and (3.2) would obviously reduce at once to the familiar Riemann–Liouville Definition (1.10). Each of these and the aforementioned other specializations are fairly straightforward. Henceforth, therefore, we choose to state our results in their general forms only and leave the specializations as an exercise for the interested reader.
, the Definitions (1.13), (3.1) and (3.2) would obviously reduce at once to the familiar Riemann–Liouville Definition (1.10). Each of these and the aforementioned other specializations are fairly straightforward. Henceforth, therefore, we choose to state our results in their general forms only and leave the specializations as an exercise for the interested reader.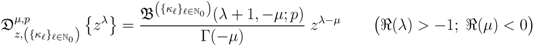
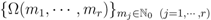 let the multivariable function
let the multivariable function 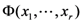 be defined by
be defined by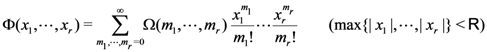

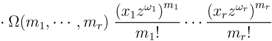
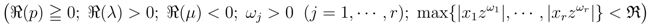
 exists.
exists.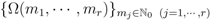 as follows:
as follows: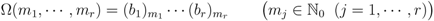

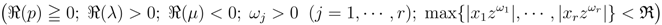
 exists.
exists. in the Definition (2.1), in its further special case when
in the Definition (2.1), in its further special case when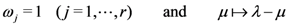
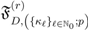 defined by (2.12), as follows:
defined by (2.12), as follows:
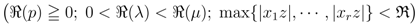
 or (alternatively) for
or (alternatively) for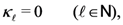
 ) case of the Definition (3.4), we set
) case of the Definition (3.4), we set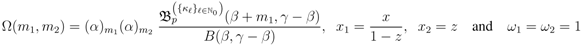
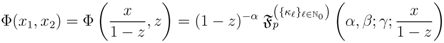
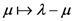 ) to
) to 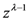 times the
times the  -function given by (3.9), we are led to the following result:
-function given by (3.9), we are led to the following result: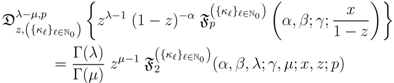
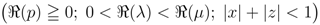
 .
. or (alternatively) for
or (alternatively) for
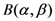 defined (for
defined (for 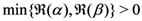 ) by
) by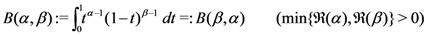
 as follows (see, for example, [14, p. 26, Equation 1.1(48)]):
as follows (see, for example, [14, p. 26, Equation 1.1(48)]):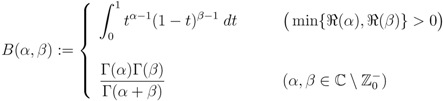

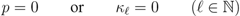
 in (3.3), (3.5) and (3.7), and
in (3.3), (3.5) and (3.7), and 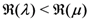 in (3.8) and (3.10), can be dropped fairly easily by applying both cases of the definition in (3.2).
in (3.8) and (3.10), can be dropped fairly easily by applying both cases of the definition in (3.2).4. Mellin Transforms of the Generalized Extended Fractional Derivatives
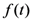 with index
with index 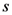 is defined, as usual, by
is defined, as usual, by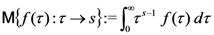
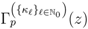 defined by
defined by 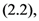 the Mellin transforms of the following generalized extended fractional derivatives defined by
the Mellin transforms of the following generalized extended fractional derivatives defined by 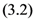 are given by
are given by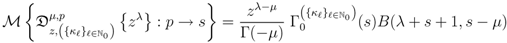
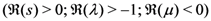
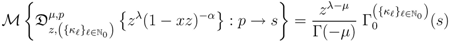
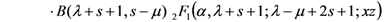
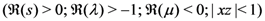
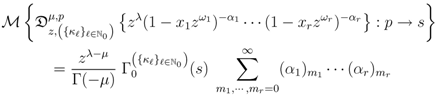
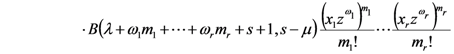
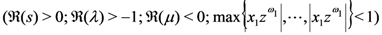
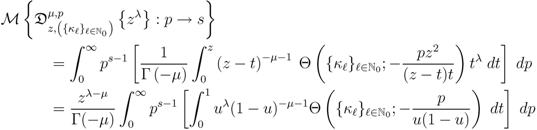
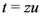 and
and 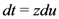 in the inner
in the inner  -integral. Upon interchanging the order of integration in (4.5), which can easily be justified by absolute convergence of the integrals involved under the constraints state with (4.2), we get
-integral. Upon interchanging the order of integration in (4.5), which can easily be justified by absolute convergence of the integrals involved under the constraints state with (4.2), we get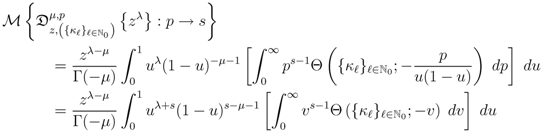
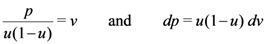
 -integral. We now interpret the
-integral. We now interpret the 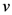 -integral and the
-integral and the 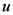 -integral in (4.6) by means of the Definitions (2.2) (with
-integral in (4.6) by means of the Definitions (2.2) (with  ) and (3.12), respectively. This evidently completes our derivation of the Mellin transform Formula (4.2) asserted by Theorem 5.
) and (3.12), respectively. This evidently completes our derivation of the Mellin transform Formula (4.2) asserted by Theorem 5.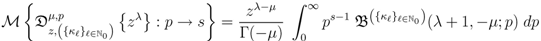
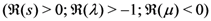
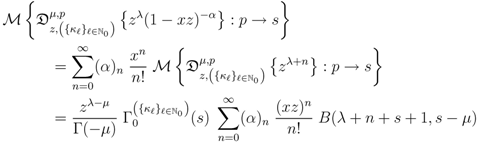
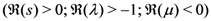
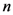 -series in the last member of (4.7) as a Gauss hypergeometric function
-series in the last member of (4.7) as a Gauss hypergeometric function 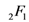 .
.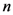 -series is to be replaced by the multiple
-series is to be replaced by the multiple 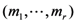 -series, the demonstration of the third Assertion (4.4) of Theorem 5 would run parallel to that of the second Assertion (4.3). The details involved may thus be omitted here.
-series, the demonstration of the third Assertion (4.4) of Theorem 5 would run parallel to that of the second Assertion (4.3). The details involved may thus be omitted here.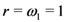 of the general Result (4.4). Moreover, in its special case when
of the general Result (4.4). Moreover, in its special case when  (or when
(or when  ), (4.3) would reduce at once to the Mellin transform Formula (4.2).
), (4.3) would reduce at once to the Mellin transform Formula (4.2).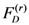 of
of 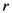 variables (see, for details, [14, p. 60, Equation 1.7(4)], the special case of the assertion (4.4) of Theorem 5 when
variables (see, for details, [14, p. 60, Equation 1.7(4)], the special case of the assertion (4.4) of Theorem 5 when 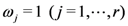 yields the following Mellin transform formula:
yields the following Mellin transform formula: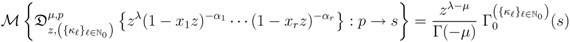
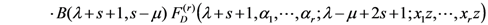
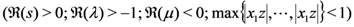
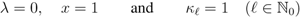
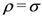 ), we obtain
), we obtain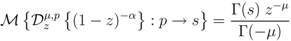
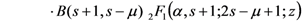
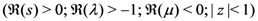
5. A Set of Generating Functions
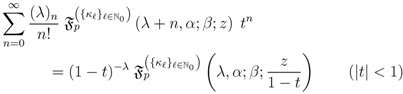
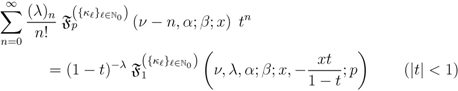
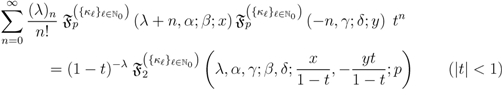
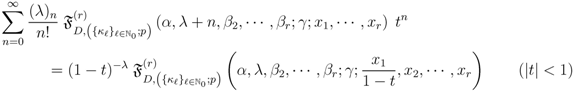
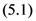 to
to  exists.
exists.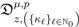 defined by (3.2). We first rewrite the elementary identity:
defined by (3.2). We first rewrite the elementary identity: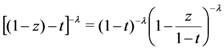
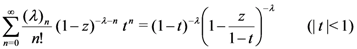
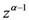 , if we apply the generalized extended fractional derivative operator
, if we apply the generalized extended fractional derivative operator 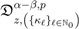 on each member of the resulting equation, we find that
on each member of the resulting equation, we find that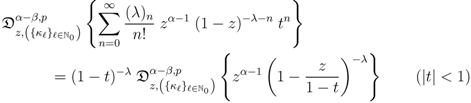

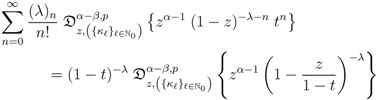
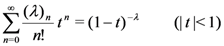
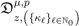 defined by (3.2), can be given along the following lines:
defined by (3.2), can be given along the following lines: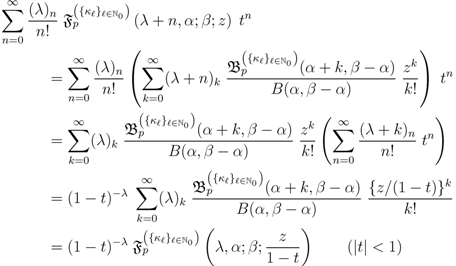
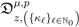 defined by (3.2) together with the following elementary identity:
defined by (3.2) together with the following elementary identity: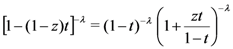
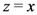 and
and 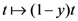 in (5.1), if we multiply the resulting equation by
in (5.1), if we multiply the resulting equation by 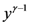 and then apply the generalized extended fractional derivative operator
and then apply the generalized extended fractional derivative operator 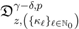 together with the elementary Identity (5.11), we find that
together with the elementary Identity (5.11), we find that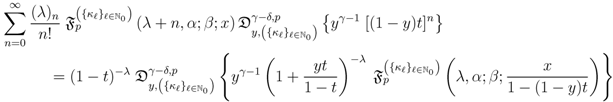
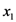 in (5.4) can be assumed instead by any of the other arguments
in (5.4) can be assumed instead by any of the other arguments 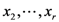 .
.6. Concluding Remarks and Observations
 (with
(with  . Thus, in terms of the
. Thus, in terms of the 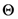 -function given by (2.1), we can introduce a further extension of the generalized extended Beta function in (2.3) as follows:
-function given by (2.1), we can introduce a further extension of the generalized extended Beta function in (2.3) as follows: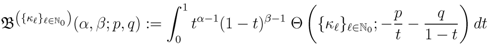
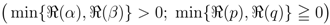
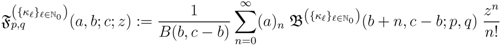

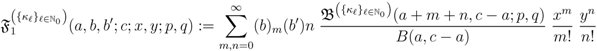
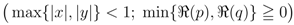
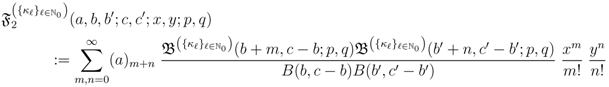
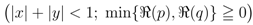
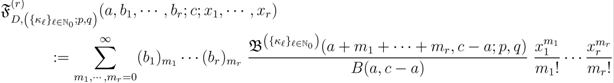
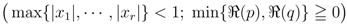
 defined by (3.2) can be further extended as follows:
defined by (3.2) can be further extended as follows: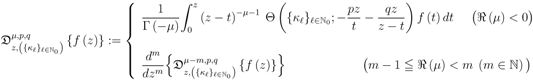
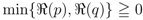 and, as also in (1.10), (1.13), (3.1) and (3.2), the path of integration in the Definition (6.6) is a line in the complex
and, as also in (1.10), (1.13), (3.1) and (3.2), the path of integration in the Definition (6.6) is a line in the complex  -plane from
-plane from 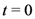 to
to  .
.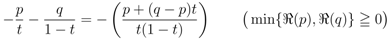
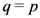 . Most (if not all) of the properties and results, which we have investigated in this paper in the
. Most (if not all) of the properties and results, which we have investigated in this paper in the 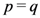 case, can indeed be considered analogously for the
case, can indeed be considered analogously for the 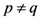 case in a rather simple and straightforward manner. The details involved may, therefore, be left as an exercise for the interested reader.
case in a rather simple and straightforward manner. The details involved may, therefore, be left as an exercise for the interested reader.References
- Özarslan, M.A.; Özergin, E. Some generating relations for extended hypergeometric function via generalized fractional derivative operator. Math. Comput. Model. 2010, 52, 1825–1833. [Google Scholar] [CrossRef]
- Chaudhry, M.A.; Temme, N.M.; Veling, E.J.M. Asymptotic and closed form of a generalized incomplete gamma function. J. Comput. Appl. Math. 1996, 67, 371–379. [Google Scholar] [CrossRef]
- Chaudhry, M.A.; Qadir, A.; Rafique, M.; Zubair, S.M. Extension of Euler’s beta function. J. Comput. Appl. Math. 1997, 78, 19–32. [Google Scholar] [CrossRef]
- Chaudhry, M.A.; Zubair, S.M. Generalized incomplete gamma functions with applications. J. Comput. Appl. Math. 1994, 55, 99–124. [Google Scholar] [CrossRef]
- Chaudhry, M.A.; Zubair, S.M. On the decomposition of generalized incomplete gamma functions with applications of Fourier transforms. J. Comput. Appl. Math. 1995, 59, 253–284. [Google Scholar] [CrossRef]
- Miller, A.R. Reduction of a generalized incomplete gamma function, related Kampé de Fériet functions, and incomplete Weber integrals. Rocky Mountain J. Math. 2000, 30, 703–714. [Google Scholar] [CrossRef]
- Özergin, E.; Özarslan, M.A.; Altn, A. Extension of gamma, beta and hypergeometric functions. J. Comput. Appl. Math. 2011, 235, 4601–4610. [Google Scholar] [CrossRef]
- Chaudhry, M.A.; Qadir, A.; Srivastava, H.M.; Paris, R.B. Extended hypergeometric and confluent hypergeometric functions. Appl. Math. Comput. 2004, 159, 589–602. [Google Scholar] [CrossRef]
- Chaudhry, M.A.; Zubair, S.M. On a Class of Incomplete Gamma Functions with Applications; CRC Press (Chapman and Hall): Boca Raton, FL, USA, 2002. [Google Scholar]
- Erdélyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F.G. Tables of Integral Transforms, Volume II; McGraw-Hill Book Company: New York, NY, USA, 1954. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications, Translated from the Russian: Integrals and Derivatives of Fractional Order and Some of Their Applications (“Nauka i Tekhnika", Minsk, 1987); Gordon and Breach Science Publishers: Reading, UK, 1993. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations. North-Holland Mathematical Studies; Elsevier (North-Holland) Science Publishers: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Appell, P.; Kampé de Fériet, J. Fonctions Hypergéométriques et Hypersphériques: Polynômes d’Hermite; Gauthier-Villars: Paris, France, 1926. [Google Scholar]
- Srivastava, H.M.; Manocha, H.L. A Treatise on Generating Functions; Halsted Press (Ellis Horwood Limited, Chichester), John Wiley and Sons: New York, NY, USA, 1984. [Google Scholar]
- Srivastava, H.M.; Saxena, R.K. Operators of fractional integration and their applications. Appl. Math. Comput. 2001, 118, 1–52. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Srivastava, H.M.; Parmar, R.K.; Chopra, P. A Class of Extended Fractional Derivative Operators and Associated Generating Relations Involving Hypergeometric Functions. Axioms 2012, 1, 238-258. https://doi.org/10.3390/axioms1030238
Srivastava HM, Parmar RK, Chopra P. A Class of Extended Fractional Derivative Operators and Associated Generating Relations Involving Hypergeometric Functions. Axioms. 2012; 1(3):238-258. https://doi.org/10.3390/axioms1030238
Chicago/Turabian StyleSrivastava, H. M., Rakesh K. Parmar, and Purnima Chopra. 2012. "A Class of Extended Fractional Derivative Operators and Associated Generating Relations Involving Hypergeometric Functions" Axioms 1, no. 3: 238-258. https://doi.org/10.3390/axioms1030238




