1. Introduction
Minerals flotation systems are by definition a complex assemblage of chemical, hydrodynamic and engineering parameters involving simultaneous interactions of aqueous solution, mineral surfaces and froth or bubbles. We focus here on two approaches that are pre-requisite for reliability and robustness of minerals processing studies with specific focus on minerals chemistry. Firstly, it is important that appropriate statistical procedures be routinely incorporated into the flotation investigation methodology to ensure that conclusions are robust and defensible. These can be divided into three classes:
Quoting the uncertainty (confidence interval) in any important measured or calculated quantity, and comparing such quantities rigorously.
Adopting the appropriate experimental design, both for laboratory experiments and plant trials. The correct design leads directly to an appropriate method of data analysis.
Using robust modelling methods to describe and compare data where necessary.
These all generally require that experiments be replicated to generate estimates of experimental error, a practice which the flotation research community has not enthusiastically embraced in the past (with some honorable exceptions, e.g., [
1]).
We also focus on factors that affect mineral surface chemistry and how these can be examined with emphasis on the behavior of real and therefore by definition complex ores. To understand the chemical processes taking place within a flotation system it is necessary to understand the mineralogy, and surface and solution speciation. It is only by doing this that an overall definition of the chemical processes taking place can be achieved. However, it is necessary to put in place analytical approaches that provide feed-back loops and to recognize the strengths and weaknesses of all analytical technologies. It has been the frequent and unfortunate practice in many past studies to ignore one or more of these critical aspects resulting in the exclusion of information necessary for the proper understanding of the flotation systems being studied.
To illustrate the necessity to consider both flotation statistics and mineral surface chemistry in any comprehensive flotation study we draw on both previously published case studies and new unpublished analyses.
2. Ensuring Statistical Rigour in Making Conclusions
The uncertainty in any replicated measurement is easily estimated using the usual
t-based formula for the confidence interval at a chosen level of confidence, and this should always be done [
2,
3]. An associated formula is available for determining the sample size required to estimate a mean value to a desired margin of uncertainty. This formula is
n = (
zσ/
m)
2 where
n is the required sample size,
z is the 2-sided normal deviate for a given confidence level (1.96 for 95% confidence),
σ is the standard deviation (assumed known) and
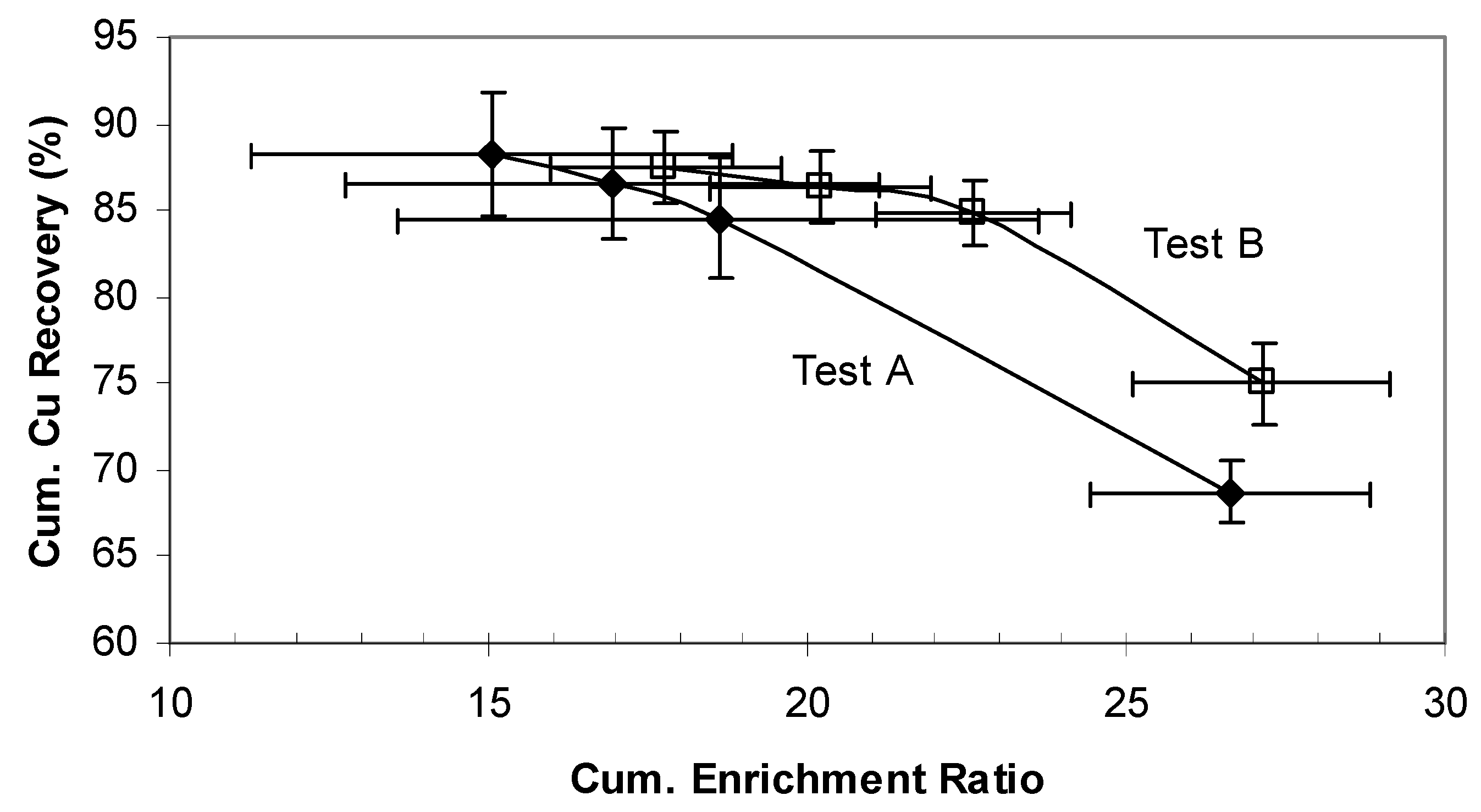
m is the desired margin of uncertainty. Uncertainties calculated in this way should be shown as error bars on graphs, as in
Figure 1 which shows 90% confidence intervals on individual points on two triply replicated batch flotation grade-recovery curves comparing two different collectors (Tests A and B). The uncertainties are quite large but not at all unusual in experiments of this kind. Comparisons between mean values are usually best formalised using the 2-sample or paired
t-test depending on how the experiments were obtained [
2].
Figure 1.
Ninety percent confidence intervals on two batch flotation grade-recovery curve points (from [
4] with permission).
Figure 1.
Ninety percent confidence intervals on two batch flotation grade-recovery curve points (from [
4] with permission).
Batch flotation grade-recovery curves such as those in
Figure 1 are commonly used to compare chemical conditions in flotation. In such cases care should be taken to make these comparisons robust and statistically defensible. Napier-Munn [
3] has recently proposed an appropriate methodology for this purpose. It involves fitting a model to the grade-recovery curve (grade is usually best represented by enrichment ratio, defined as the ratio of concentrate grade to feed grade), or the rate curve. The model is then bootstrapped using the replicate data to generate a large number of estimates of the model parameters and other important quantities. The distribution of these values represents the uncertainty in the original data, and simple hypothesis tests can be used to formalize comparisons between them.
Figure 2 shows the 95% confidence intervals calculated on the two grade-recovery curves of
Figure 1 using bootstrapping. The model fitted can be either that proposed by Vera
et al. [
5] or Bruey’s re-parameterisation of Vera’s model [
3].
In considering appropriate experimental designs we should distinguish between laboratory experiments (and sometimes pilot plant tests), in which conditions can be relatively easily controlled, and plant trials, which present some additional challenges. Laboratory flotation experiments lend themselves to factorial designs, which remain the most efficient way of evaluating the magnitude and significance of the effects of the factors of interest [
6]. Most importantly, factorials are the only real option for unequivocally estimating factor interaction which is not uncommon in flotation. Interaction between factors A and B exists when the dependence of the response on factor A depends in turn on the level of factor B. Thus recovery may depend significantly on the choice of collector at low pH but not at high pH. Another important advantage of factorials is that every run contributes information about every factor, unlike the traditional ‘one variable at a time’ approach which can be particularly misleading in flotation testing and should not be used. Factorials are also the most efficient way of collecting data for modeling.
Figure 2.
Bootstrapped 95% confidence intervals on the grade-recovery curves of
Figure 1 (from [
3] with permission).
Figure 2.
Bootstrapped 95% confidence intervals on the grade-recovery curves of
Figure 1 (from [
3] with permission).
Sometimes what is required is simply a description of the response surface of the flotation system to allow 3D graphs to be drawn to illustrate the complex relationships, or predictions to be made of the response at particular values of the factors of interest. In these cases an appropriate design is the CCRD (central composite rotatable design [
6]) which allows the development of arbitrary regression models incorporating non-linear trends and interactions, whilst needing less runs than a full (3-level) factorial.
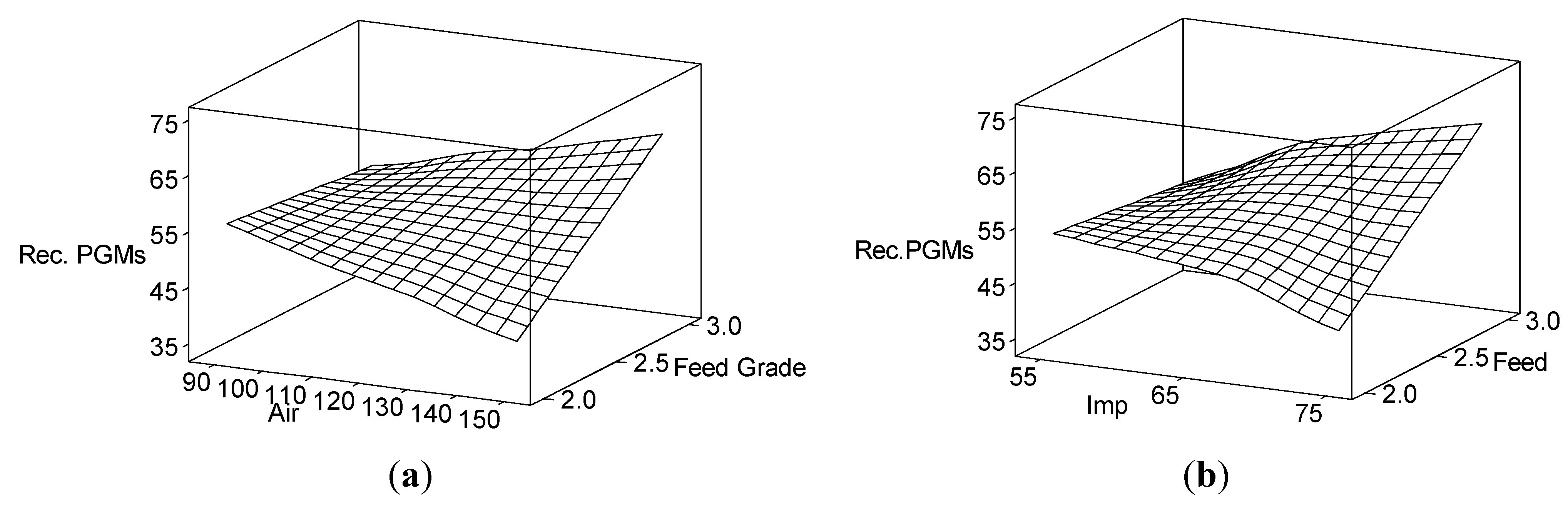
Figure 3 shows the 3D graphs drawn using the model obtained from a CCRD to study PGM (platinum group metal) recovery as a function of air rate, impeller speed and feed grade in a pilot flotation plant. The complex nature of the response surfaces is clear (and interesting).
Figure 3.
Response surfaces showing the dependency of PGM recovery on feed grade, air rate and impeller speed in a flotation pilot plant CCRD (data from [
7]). (
a) PGM recovery versus air versus feed grade and (
b) PGM recovery versus impeller speed versus feed grade.
Figure 3.
Response surfaces showing the dependency of PGM recovery on feed grade, air rate and impeller speed in a flotation pilot plant CCRD (data from [
7]). (
a) PGM recovery versus air versus feed grade and (
b) PGM recovery versus impeller speed versus feed grade.
A special case of a factorial experiment is the mixtures experiment which is appropriate when mixtures of components are being tested. These may be mixtures of reagents (e.g., two collectors in different proportions) or ores. An example of a study of the effect of four different ore types on PGM recovery in batch flotation testing is described in [
8]. Other statistical procedures are available to help in establishing important effects which otherwise might be difficult to infer from voluminous and complex data. A good example is the use of principal components analysis (PCA) for interpreting data from time of flight secondary ion mass spectrometry (ToF-SIMS) [
1].
When a new reagent or conditioning regime is established in the laboratory it is then necessary to test its efficacy in the plant. Here the challenge is to tease out the beneficial effects of the change against the background ‘noise’ of the production data. The magnitude of the improvement is usually quite small compared to the noise and therefore tends to be overwhelmed in the data. Conditions cannot be controlled as in a laboratory experiment and so precautions must be taken against uncontrolled factors that are known to influence plant performance such as feed conditions. The perils of not taking such precautions are well illustrated in
Figure 4 which shows a ‘before and after’ plant trial of a new reagent in a copper-gold concentrator, which appeared to show an astonishing 7% improvement in recovery following introduction of a new reagent. It is clear from a simple time series plot however that the improvement cannot be attributed to the reagent; in fact there is some evidence that the introduction of the reagent actually stopped the improvement that had been happening anyway (probably due to changed feed). This is a bad experiment and should not be contemplated in such trials.
Figure 4.
Daily gold recovery before and after the introduction of a new flotation reagent.
Figure 4.
Daily gold recovery before and after the introduction of a new flotation reagent.
These problems can be overcome by using paired experiments (when two conditions are to be compared, e.g., old and new reagent) or a randomized block design (when more than two conditions are of interest, e.g., reagents A, B and C). Pairing or blocking is done either across parallel circuits or in short periods of time (e.g., a shift or a day); the order (in time or across circuits) must be randomized. It is easy to calculate the number of pairs required to detect a given change in performance with a given confidence, which assists in planning the trial. It is also easy to calculate the confidence interval on the observed change in performance (
i.e., the improvement). The paired design tends to subtract out common variation within the pairs, making the effect being sought more obvious, and the randomized block extends the idea to more conditions. The paired trial is analyzed by a paired
t-test and the randomized block design by a 2-way analysis of variance, both of which are available in Excel. Full details can be found in [
2,
9].
With a little thought almost any plant trial of chemical factors in flotation can be arranged to suit a paired or randomized block design. In the rare cases where this is not possible, and the data has a more happenstance character (for example the use of historical data), then appropriate modeling of the data combined with other tools such as cumulative sum charts can usually identify the desired effects. Details can be found in [
2,
10,
11].
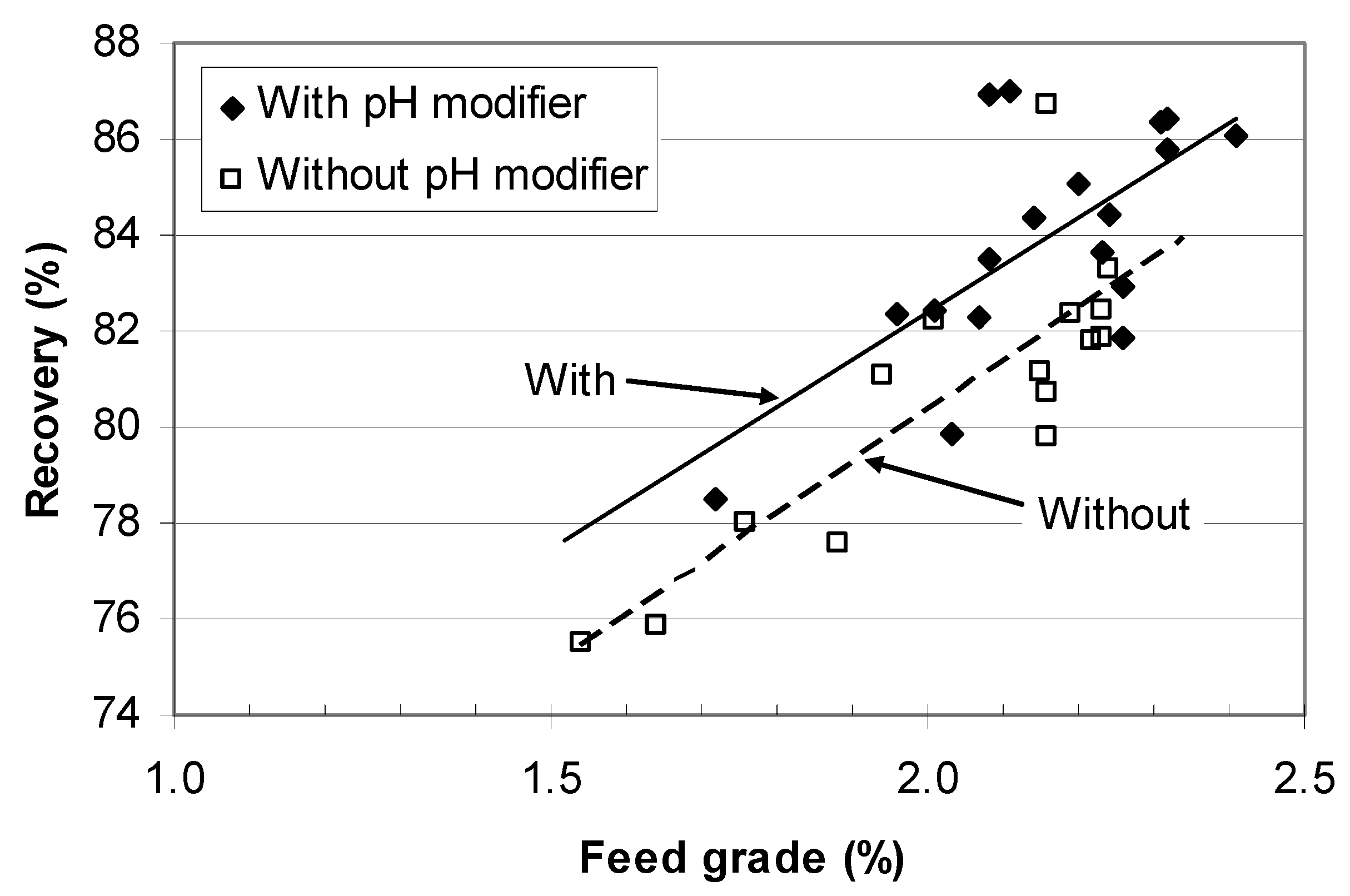
Figure 5 shows the comparison of two recovery-feed grade trend lines before and after a pH modifier was introduced into a nickel flotation circuit. Using the method described in [
8] it is possible to show rigorously that the pH modifier produced a statistically significant increase of 2% in nickel recovery, and that we are 90% confident that the increase is at least 1%. This is a very useful number in carrying out cost-benefit analysis of a change, and easy to determine. The important feature of this method is that the conclusion applies to the wide range of feed grades encountered in the trial, and the interfering effect of feed grade on recovery has been effectively removed by modelling it out. However, note that almost always such analyses are not as powerful (that is, they are less likely to detect a significant improvement) as those from a formal experimental design such as a paired test.
Figure 5.
Comparison of two trend lines with and without a pH modifier in a nickel flotation circuit.
Figure 5.
Comparison of two trend lines with and without a pH modifier in a nickel flotation circuit.
3. Analytical Approaches to the Study of the Chemistry of Minerals Flotation Systems
The aqueous environment interacts with mineral surfaces affecting the elemental composition, oxidation states, speciation and spatial relationships between species. Thus the resulting hydrophobic/hydrophilic species balance present on a value mineral is, in part, a function of the aqueous environment. Parameters that need to be considered to understand solution speciation are redox potential (Eh), which is frequently neglected, pH, concentrations, including those of collectors, depressants, dispersants etc. and saturation indices. The last factor takes into account species that are under-saturated and may dissolve into solution and solution species that are super-saturated and may precipitate. Mineral surface speciation is also a function of the prior treatment of the mineral phase, including interaction with grinding media and weathering (as may result from stock piling), which may result in the formation of surface layers, including partially leached and/or oxidized layers. These in turn are clearly a function of the mineral phase, impurities present, crystallinity and lattice distortions.
3.1. Solution Speciation
Basic determination of solution speciation is frequently readily analytically accessible but is often neglected. There exist a considerable number of speciation simulation programs, e.g., GEOCHEM-EZ [
12], PHREEQC [
13], MINTEQ [
14]
etc. Solution concentrations, pH, E
h and temperature must be input. Other parameters that may be included are gas partial pressures and the presence of solids. The computer programs, almost always come with their own databases of equilibrium constants including solubility products and redox couples. However data relating to more obscure species may not be listed.
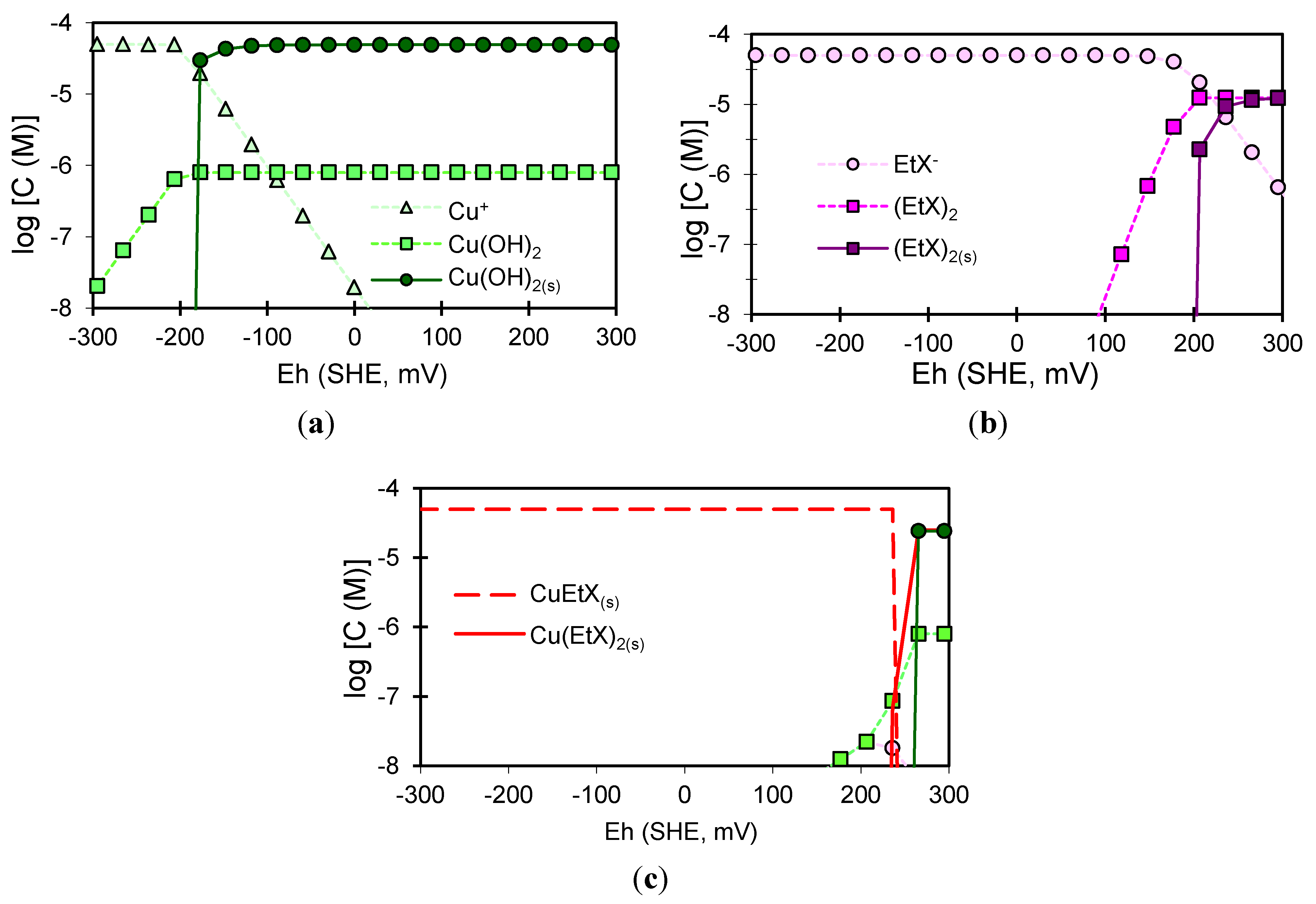
The most frequent mode of use of these simulation programs for minerals processing scenarios is to take a ‘snap-shot’ of the system, assuming equilibrium, so that under-saturated or supersaturated solids may be identified. While this does not provide proof that precipitation either has or will take place it does provide strong evidence. A simplified example of the utilization of such an approach is shown in
Figure 6 (adapted from [
15] with permission). It can be seen from these simulations that the addition of a typical concentration of Cu
2+ for metal sulfide activation for flotation may lead to the precipitation of Cu(OH)
2 if the kinetics of precipitation are more rapid than the kinetics of surface adsorption. The addition of 10
−5 M xanthate may lead to the formation of ethylxanthate precipitate at high E
h. However, on simultaneous addition of both xanthate and Cu
2+ the predicted speciation is significantly altered so that copper ethylxanthate (CuEtX) precipitate is the predominant species predicted at moderate E
h, whereas a mixture of Cu(OH)
2 and Cu(EtX)
2 are predicted to precipitate at high E
h, assuming that surface adsorption is not occurring faster than these precipitation processes are taking place. Clearly, this example is examining a model system however the same approach could be just as easily applied to real flotation liquor.
While there are numerous examples of the use of such simulation programs for environmental studies, particular for adsorption and examination of oxidation states for toxic elements (e.g., [
16]), there are surprising few applications for mineral flotation studies. A recent example of the incorporation of solution speciation simulations into a minerals flotation study is the simulation of Cu and Pb speciation as a function of contrasting E
h and pH conditions utilized during grinding [
17]. Calculations were carried out both with and without allowed precipitation and these were coupled to flotation studies as well as zeta potential, X-ray photoelectron spectroscopy (XPS) and ethylene diamine tetraacetic acid (EDTA) extraction analyses to provide a more complete interpretation of the mineral activation processes taking place. A further example of solution speciation simulation of more complicated synthetic plant liquor has been described in Gerson
et al. [
18] where speciation calculations were utilized to interpret whether the flotation liquor resulting from the processing contrasting ores may give rise to the precipitation of hydrophilic species.
On undertaking a thorough minerals flotation study the outcomes of solution analyses should be related to surface analyses. As these two phases are in intimate contact they must reasonably relate closely. For instance a high solution or surface loading of cations would reasonably relate to the presence of these species in the other phase. Moreover the presence of surface species should be commensurate with solution Eh, pH and relative super-saturations bearing in mind the kinetics of processes occurring.
Figure 6.
Solution speciation simulations of (a) 10−5 M Cu2+; (b) 10−5 M ethylxanthate, and (c) 10−5 M Cu2+ and elthylyxanthate, all as a function of Eh at pH 9. The legend in (c) is simplified to only include species not already defined in (a) and (b).
Figure 6.
Solution speciation simulations of (a) 10−5 M Cu2+; (b) 10−5 M ethylxanthate, and (c) 10−5 M Cu2+ and elthylyxanthate, all as a function of Eh at pH 9. The legend in (c) is simplified to only include species not already defined in (a) and (b).
3.2. Surface Analysis
There are numerous forms of surface analyses available but here we discuss only those commonly applied to minerals flotation studies of real ores. Almost by definition surface analysis is carried out under conditions of medium to high vacuum. As the measurement must probe only the first few molecular layers the resulting signals/species are of relatively low energy, so as not to emerge from the bulk, and consequently would have a limited mean free path through air. Surface sensitivity necessitates careful sample handing and preparation to ensure that the sample surface is as representative as possible of the mineral particles as they were in the flotation slurry [
19].
A pre-requisite for the effective study of real flotation products is the need for spatial resolution. Without this, while surface species may be measurable, it is not possible to differentiate the species location as a function of the many value and gangue minerals typically present in a real ore. As, clearly the aim of minerals flotation is to manipulate relative hydrophobicity/hydrophilicity as a function of the minerals present surface measurements that lack spatial resolution are of reduced value and on some occasions could be readily replaced by a technically much-simpler chemical-based analysis, e.g., EDTA extraction (e.g
., [
20]).
Laboratory X-ray photoelectron spectroscopy (XPS) has been widely applied to the studies of minerals. However, as spatial resolution is difficult to achieve, even when technically possible, due mostly to the length of time required to achieve adequate data quality, studies are generally limited to model systems. Moreover, until recently XPS analysis has been problematic for the analysis of insulating samples with only the advent of more effective charge neutralization systems making the analysis of many mineral types now possible [
21]. A recent example of such a study is the application of chitosan as a selective depressant of chalcopyrite during the flotation of galena [
22]. In this case XPS was used to examine the adsorption of chitosan (containing amine) onto the two single mineral systems where the N 1
s spectra were used to examine the form of attachment of the chitosan to the mineral surface. A further example of the same nature is the examination of S 2
p spectra to investigate the attachment of thiosulfate to chalcopyrite and tennantite single mineral samples at pH 4 and 9 [
23].
Synchrotron PEEM and SPEM (photoelectron emission spectroscopy and scanning photoelectron spectroscopy) are both relatives to laboratory XPS that do enable highly spatially resolved measurements, often in the order of 10 nm [
24]. However, both of these techniques require flat sample surfaces and hence are not applicable to the products of real mineral flotation systems. Auger electron spectroscopy (AES) has also been used for the study of mineral systems and is also related to XPS. However, where XPS measures the kinetic energy of an ejected core or valence electron, AES is the measure of the kinetic energy of electrons that are ejected due to the subsequent filling of the core hole resulting from ejection of the XPS electron. Surface mapping is made possible using AES as the source of primary excitation is an electron beam, as opposed to an X-ray beam as for XPS. The former are more easily focused and of greater intensity thus enabling mapping, however, as for XPS, AES suffers from sample surface charging if the material being analyzed is not sufficiently conducting.
ToF-SIMS has been increasingly utilized over the last 10 years for minerals analysis and is particularly applicable for mixed mineral or real ore systems. ToF-SIMS is based on the partial fragmentation of sample surfaces due to bombardment with an ion beam. The mass of the fragments, either positively or negatively charged, is then determined on the basis of the ‘time-of-flight’ required to reach the detector. The ion beam is rastered across the sample and at each location a full mass spectrum is collected. Static SIMS, utilizing a pulsed ion beam of low current (pA), results in minimal damage to the sample surfaces and thus interrogates only the top one to two molecular layers whereas dynamic SIMS utilizes an ion beam of greater current (nA) which results in a surface sputtering processes (up to 100 Å/min). In neither case is there a requirement for the samples to be conducting and highly spatially (<100 nm) and mass (>10,000 m/Δm) resolved data is readily achievable. While, dynamic SIMS can result in quantitative surface analyses this is not the case for the less destructive static SIMS. However, it is the latter that is generally of more interest in the highly surface sensitive process of minerals flotation and it is this technique which we focus on further.
As the data arising from static ToF-SIMS is not directly quantifiable, due to species fragmentation being matrix dependent, and the difficulty in interpreting the enormous quantities of data typically collected on analysis of a single sample area (typically full mass spectra at 256 × 256 pixels) statistical methodologies have been developed. While there has been progressive development as to the approach taken [
25,
26,
27] we discuss here the most recent published iteration [
28] and subsequent developments. As mentioned previously principal component analysis (PCA) has been applied to ToF-SIMS data sets to enable identification of correlated species. Mineral identification may be inferred from knowledge of the mineralogy and the presence of specific elements, for instance, Cu, Fe and S for chalcopyrite or bornite, Si and Mg for talc, Al and Si for kaolinite
etc. Surfaces containing particular elements are then further correlated, using PCA, to the occurrence of either hydrophobic species, e.g
., polysulfide and collector fragments, or to hydrophilic species,
e.g. oxides and hydroxides. In this way, by comparative analysis across a flotation circuit, or part thereof, it is possible to assess the changes in surface hydrophobic to hydrophilic species as a function of mineral type. We provide, as an example (previously unpublished), in
Figure 7 of ToF-SIMS images of Ag-containing particles with correlations to S, Fe, Cu and in particular CN.
Figure 7.
ToF-SIMS image (250 × 250 μm) of (a) Ag; (b) Cu; (c) Zn; (d) S; and (e) CN. (f) Graph of factor loadings for Principal Component 2 for this area of ToF-SIMS data showing clear statistical correlation of Ag to CN, as well as Cu, Zn and S, suggesting flotation depression of these value components.
Figure 7.
ToF-SIMS image (250 × 250 μm) of (a) Ag; (b) Cu; (c) Zn; (d) S; and (e) CN. (f) Graph of factor loadings for Principal Component 2 for this area of ToF-SIMS data showing clear statistical correlation of Ag to CN, as well as Cu, Zn and S, suggesting flotation depression of these value components.
3.3. Mineralogy
The most direct approach to the measurement of mineralogy is to carry out powder X-ray diffraction (XRD) analysis. This technique is a direct measure of crystallographic structure and does not infer mineralogical phase from composition in contrast to the scanning electron microscopy-based techniques discussed below. However, even the best X-ray diffraction data is limited by sensitivity to trace phases, particularly where there may be a highly complex mineralogical assemblage. Moreover extracting reliable quantitative information by application of Rietveld analysis is a skilled and at times laborious process. With care good results can be forthcoming e.g.,
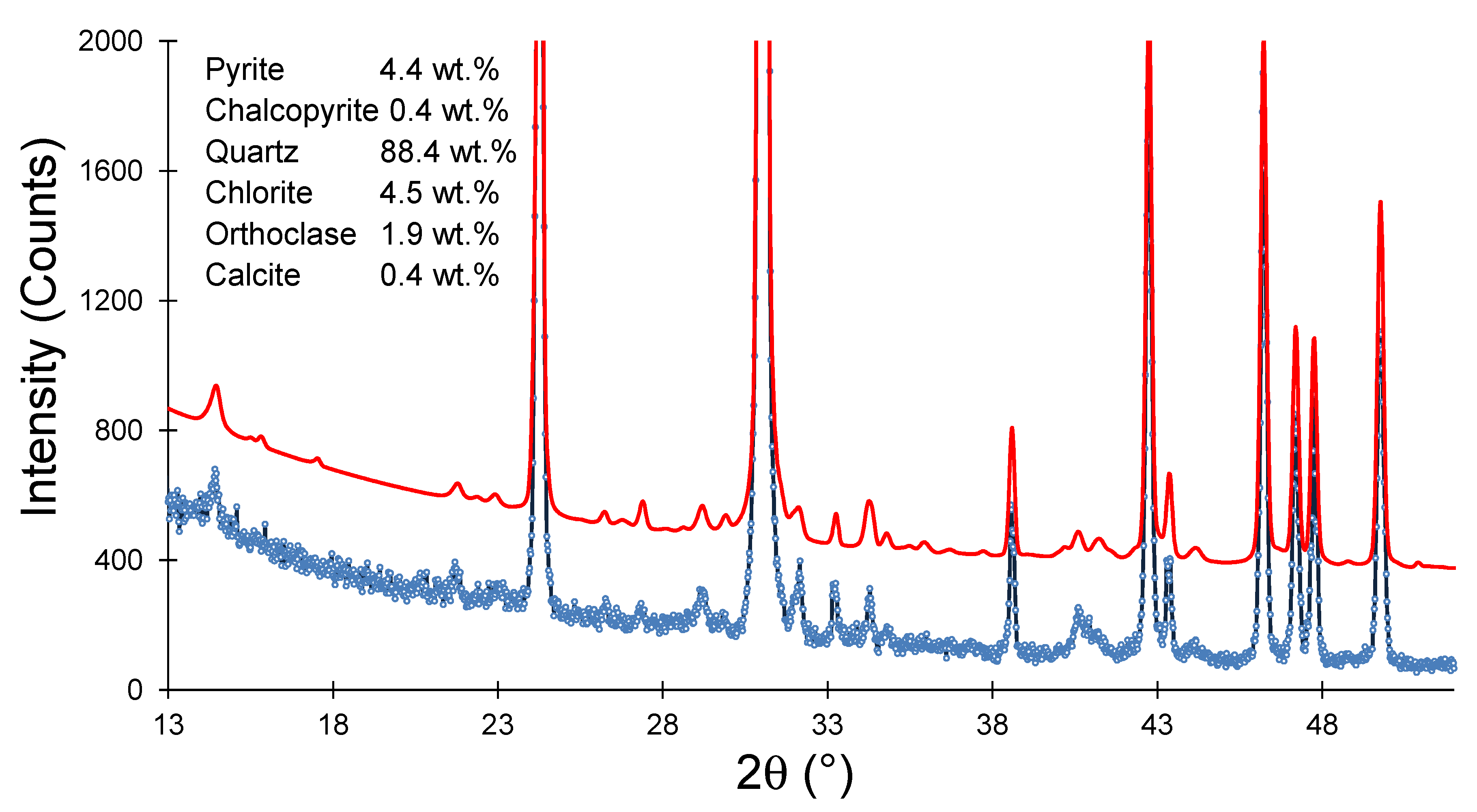
Figure 8 (previously unpublished). The sensitivity to the presence of low concentration phases may be increased by utilizing synchrotron X-ray sources; however, this overall limitation remains, due to the basic approach being taken of bulk mineralogical measurement.
Figure 8.
Rietveld analysis of standard laboratory XRD data of a simple Cu bearing ore, showing sensitivity to low wt % mineral fractions. The lower line represents the experimental data whereas the upper line (displaced by 300 in y for clarity) represents the simulated data.
Figure 8.
Rietveld analysis of standard laboratory XRD data of a simple Cu bearing ore, showing sensitivity to low wt % mineral fractions. The lower line represents the experimental data whereas the upper line (displaced by 300 in y for clarity) represents the simulated data.
An alternate approach is to carry out micro-diffraction analysis using a highly focused incident X-ray beam. Beam sizes as small as 10 μm are now available using laboratory facilities but to be practical these diffractometers need to be specifically designed for this purpose with maximized X-ray flux generally being supplied by a rotating anode X-ray source. Incident X-ray beam sizes of 1 μm or less are now routinely available at synchrotron facilities. The experimental approach generally taken is to either identify regions of interest using X-ray fluorescence mapping, or at laboratory facilities using scanning electron microscopy, and then to examine these areas. Alternatively entire regions may be mapped but frequently much of the data collected using this approach will not be of interest. Examples of the micro-diffraction analysis of specific regions may be found in [
29] and [
30] both of which are studies of Ni-containing mineralogy.
Indirect methods for examining mineralogy, in that they did not measure crystal structure directly, but infer mineralogy from stoichiometry, are those methods based on scanning electron microscopy. These consist of Minerals Liberation Analysis (MLA) and Quantitative Evaluation of Minerals by SCANing electron microscopy (QEMSCAN). These methods offer the great advantage in that they provide high spatial resolution, enabling very minor phases to be identified, and are also highly automated. They are both routinely used for liberation analysis of minerals flotation systems with very good and useful results obtained (e.g., [
31]). However, there are some limitations under some circumstances to these approaches:
They do not recognize differing degrees of crystallinity. As these techniques are based on analysis of stoichiometry it is assumed that all parts of all samples are crystalline. In reality mineral behavior can vary markedly as a function of crystalline disorder with amorphous phases generally being more readily soluble and reactive than their crystalline counterparts.
The analysis of fine fractions is limited by the ability to disperse these adequately within the sample and the tendency of the impacting electron beam and outgoing photoelectrons to spread within the sample.
Polymorphs or minerals that are part of a complex solid solution series are difficult to distinguish. For instance it is very difficult to differentiate between the polymorphs anatase and rutile, both TiO2, or sphalerite and wurtzite, both ZnS.
These techniques have difficulty ‘seeing’ either surface films or surface contaminants due to their depth of measurement and are not a replacement for surface analytical techniques. Also, where precious elements, e.g., Ag, Au, Pt group metals, are present in dilute solid solutions within other minerals they may be missed.
These analyses are also dependent on a comprehensive mineral database. The absence of key minerals in this database can and does lead to misinterpretations.
For application of relatively accessible lab-based techniques it is recommended that both diffraction and QEMSCAN (or MLA) be carried out, at least initially, to ensure the compatibility of the mineralogy resulting, which should be further reconciled to elemental analysis.
3.4. Selected Real Ore Case Studies
For a recently published study, solution, surface species and mineralogical analyses were examined in order to diagnose loss of recovery of Cu-containing phases and molybdenite on blending of ores [
15]. Mineralogical size-by-size analysis was carried out using QEMSCAN with additional XRD analysis of the fine size fraction (<5 μm). The smallest size fraction examined by QEMSCAN was <20 μm. Although the analyses weren’t of the same size fraction, as the QEMSCAN data suggested that identifiable size related trends were not observable, some mineralogical comparability should result. However, significant differences in the silicate phase quantification were apparent with the QEMSCAN estimates being, on the whole, considerably greater than the XRD estimates. Most notably XRD analysis suggested a 60 wt % amorphous content in the <5 μm fraction. This in turn suggests that a portion of the <20 μm silicate mineralogy observed by QEMSCAN was amorphous (as would be determined by XRD) and highlights the contrasting, but useful, mineralogy that may result from application of different analytical approaches. Along with flotation experiments and mineralogical analysis, solution speciation simulation of the flotation liquors and PCA ToF-SIMS of the resultant concentrates and tails were carried out enabling identification of the source of the fine particles causing the molybdenite poisoning. Only by carrying out this multifaceted approach was it possible to rule out precipitation of colloidal species.
A further study that has attempted a statistical surface analysis of a real ore is the study by Jasieniak and Smart [
32] which utilized statistical ToF-SIMS and SEM/EDX analyses. It was demonstrated, using ToF-SIMS that the chromite, found to report to a PGM concentrate, was affected by residual hydrophobic talc-like Mg and Si containing layers. However, SEM (and hence this would also be the case for QEMSCAN/MLA) was unable to detect these residual surface layers as the depth of analysis is too great. Smeink
et al. [
33] utilized mineralogical analysis by SEM and XRD of real ore and obtained good correlation. They also examined the distribution of the polymeric depressant Depramin
® using ToF-SIMS and were able to make semi-quantitative analysis of relative adsorption between mineral types, identified by their elemental mass fragments, by correlating solution depletion measurements to relative depressant fragment intensities. In a rare study utilising (quantitative) XPS imaging Biesinger
et al. [
34] examined the loss of selectivity between chalcocite from heazelwoodite. By combining this approach with traditional XPS and SEM/EDX it was possible to distinguish contrasting levels of oxidation between the two minerals in the rougher feed and tails as well as the principal sites of adsorption of the collector molecules.
4. Conclusions
There are a diminishingly small number of published case studies on real ore that have utilized statistical analysis of flotation or other mineral processing systems in conjunction with an analytical approach encompassing mineral phase, surface analysis and solution speciation. In order to understand, on a non-phenomenological basis, the impact of process change on a flotation system it is clearly necessary to determine whether the change is statistically significant and it is also necessary to identify what specifically has affected the change in a way that does not bias the results by the limited choice of analytical approaches made. In order to make scientific progress that is of direct relevance to industry this is clearly a direction for future focus.
Many of the analytical techniques described are commonly available internally within mineral processing companies, e.g., XRD and MLA/QEMSCAN, and if not available can be readily accessed externally. Both XRD and MLA/QEMSCAN can now be done in a highly routine and automated manner particularly for ores that have been previously well characterized. Solution speciation simulation software can be either accessed freely or for low cost but is very rarely utilized. In the absence of more sophisticated surface analytical techniques EDTA extraction is a cheap and simple method for examination of surface speciation that could be undertaken by almost any industrial analytical facility, but again is rarely utilized. ToF-SIMS is generally less accessible as the number of these instruments is limited and at times not accompanied by mineral processing expertise in the host laboratory. However, ToF-SIMS measurements are very rapid (each area analyzed taking <10 min) with the time required mostly being taken in the data analyses, although this too is now becoming more routine.
The key conclusion from this review is that methods are available to allow rigorous interpretation of data from flotation investigations. They are powerful and relatively easy to use, so there is no excuse for not using them. They should be routinely integrated into the investigative methodology, rather than being seen as exotic panaceas to be used when all else has failed.