Low Scale Saturation of Effective NN Interactions and Their Symmetries

Abstract

The Skyrme force parameters can be uniquely determined by coarse graining the Nucleon-Nucleon (NN) interactions at a characteristic momentum scale. We show how exact $V_{\mathrm{lowk}}$ potentials to second order in momenta are saturated with physical NN scattering threshold parameters at Center of Mass (CM) cut-off scales of about $\Lambda =250\mathrm{MeV}$ for the S-waves and $\Lambda =100\mathrm{MeV}$ for the P-waves. The pattern of Wigner and Serber symmetries unveiled previously and suggested by Quantum Chromodynamics (QCD) large $N_c$ contracted symmetry emerges at these scales.

1. Introduction

The derivation of effective interactions from NN dynamics has been a major task in Nuclear Physics ever since the pioneering works of Moshinsky [1] and Skyrme [2]. The use of those effective potentials, referred to as Skyrme forces, in mean field calculations can hardly be exaggerated due to the enormous simplifications that are implied as compared to the original many-body problem [3,4,5,6]. Similar ideas advanced by Moszkowski and Scott [7] (see also [8] for an udated view) have become rather useful in shell model calculations [9,10]. The Skyrme (pseudo)potential is usually written in coordinate space and contains delta functions and its derivatives [2]. In momentum space, it corresponds to a power expansion in the CM momenta $(p^{\prime }$ and $p)$, corresponding to the initial and final state, respectively. To second order in momenta, the potential reads

$$\begin{array}{ccc}\hfill V(p^{\prime },p)& =& \int d^{3}x{d}^3{x}^{\prime }{e}^{-i{\mathbf{x}}^{\prime }·p^{\prime }+ip·\mathbf{x}}V({\mathbf{x}}^{\prime },\mathbf{x}),\hfill \\ & =& t_0(1+x_0{P}_{\sigma })+\frac{t_1}{2}(1+x_1{P}_{\sigma })(p^{\prime 2}+p^2)+t_2(1+x_2{P}_{\sigma })p^{\prime }·p+i{W}_0({\sigma }_1+{\sigma }_2)·(p^{\prime }\wedge p)\hfill \\ & +& \frac{t_T}{2}\left[{\sigma }_1·p{\sigma }_2·p+{\sigma }_1·p^{\prime }{\sigma }_2·p^{\prime }-\frac{1}{3}{\sigma }_1·{\sigma }_2({p^{\prime }}^2+p^2)\right]\hfill \\ & +& \frac{t_U}{2}\left[{\sigma }_1·p{\sigma }_2·p^{\prime }+{\sigma }_1·p^{\prime }{\sigma }_2·p-\frac{2}{3}{\sigma }_1·{\sigma }_2{p}^{\prime }·p\right]+\mathcal{O}(p^4,{p^{\prime }}^4,p^2{p^{\prime }}^2),\hfill \end{array}$$

(1)

where $P_{\sigma }=(1+{\sigma }_1·{\sigma }_2)/2$ is the spin exchange operator with eigenvalues $P_{\sigma }=-1$ for spin singlet $S=0$ and $P_{\sigma }=1$ for spin triplet $S=1$ states, and ${\sigma }_1$ and ${\sigma }_2$ are the Pauli matrices. For a local potential $V\left(\mathbf{x}\right)$, our convention is such that $V({\mathbf{x}}^{\prime },\mathbf{x})=V\left(\mathbf{x}\right){\delta }^{\left(3\right)}(\mathbf{x}-{\mathbf{x}}^{\prime })$. In practice, these effective forces are parameterized in terms of a few constants which encode the relevant physical information and should be deduced directly from the elementary and underlying NN interactions. Unfortunately, there is a huge variety of Skyrme forces depending on the fitting strategy employed (see e.g., [11,12]). This lack of uniqueness may indicate that the systematic and/or statistical uncertainties within the various schemes are not accounted for completely. Interestingly, the natural units for those parameters have been outlined in Ref. [13,14] yielding the correct order of magnitude. A microscopic basis [15,16] for the Density Functional Theory (DFT) approach has also been set up, but uncertainties still remain. Conversely, while this is a two-body interaction, the connection with the free NN-force is not obvious. Therefore, Skyrme forces, while extremely useful in practice are neither uniquely defined nor obviously related to NN-scattering. A recent work discriminates positively 16 out of 240 sets of Skyrme parameters from nuclear matter constraints [17]. Energy density functionals implying density dependent parameters have been derived from chiral low two- and three nucleon interactions [18,19].

The Skyrme pseudo-potential in Equation (2) may and has been taken literally in mean field calculations, a procedure that makes sense due to the finite extension of the nucleus and, of course, under the assumption that such an extension is sufficiently large as not to unduly amplify short distance components of the pseudo-potential. However, its interpretation in the simplest two-body problem requires some regularization to give a precise meaning to the Dirac delta interactions. The standard view of a pseudo-potential (in the sense of Fermi) is that it corresponds to the potential,which, in the Born approximation, yields the real part of the full scattering amplitude. This is a prescription which implements unitarity of the S-matrix, but necessarily fails at low energies when the scattering length is unnaturally large as it is the case for NN interactions. The reason is that the Born approximation is no longer valid.

On the contrary, the Wilsonian viewpoint corresponds to a coarse graining of the NN interaction to a certain energy scale. There are several schemes to coarse grain interactions in Nuclear Physics. The traditional way has been by using the oscillator shell model, where matrix elements of NN interactions are evaluated with oscillator constants of about $b=1.4-2\mathrm{fm}$ [10]. A modern way of coarse graining nuclear interactions is represented by the $V_{\mathrm{lowk}}$ method [20] (for a review, see [21,22]) where all momentum scales above $2{\mathrm{fm}}^{-1}$ are integrated out. The recent Euclidean Lattice Effective Field Theory (EFT) calculations (for a review see e.g., [23]), although breaking rotational symmetry explicitly, provide a competitive scheme where coarse grained interactions allow ab initio calculations combining the insight of EFT and Monte-Carlo lattice experience, with lattice spacings as large as $a=2\mathrm{fm}$. These length scales match the typical inter-particle distance of nuclear matter $d=1/{\rho }^{\frac{1}{3}}\sim 2\mathrm{fm}$. Actually, the three approaches feature energy-, momentum- and configuration space coarse graining, respectively, and ignore explicit dynamical effects below distances $\sim b\sim 1/\Lambda \sim a$ (These are qualitative relations. A more quantitative determination is discussed in Ref. [24], where it is found that, at low energies, the CM cut-off Λ can be related with a short distance cut-off $r_c$ by the relation $\Lambda =\pi /2r_c$.), which advantageously sidesteps the problems related to the hard core and confirms the modern view that ab initio calculations are subjected to larger systematic uncertainties than assumed hitherto. Clearly, any computational setup implementing the coarse graining philosophy yields by itself a unique definition of the effective interaction. However, there is no universal effective interaction definition. For definiteness, we will follow here the $V_{\mathrm{lowk}}$ scheme to determine the effective parameters because, within this framework, some underlying old nuclear symmetries, namely those implied by Wigner and Serber forces, are vividly displayed [25,26,27,28].

A particular implementation of the coarse graining idea [29] has facilitated benchmarking partial wave analyses of the NN interaction and has also provided an alternative way to define the effective couplings as a function of the maximal fitting CM momentum $p\le {\Lambda }_{\mathrm{Fit}}$ [30], including different One Pion Exchange (OPE) and Chiral Two Pion Exchange (χTPE) [31,32] and an evaluation of uncertainties of both statistical and systematic origin [33].

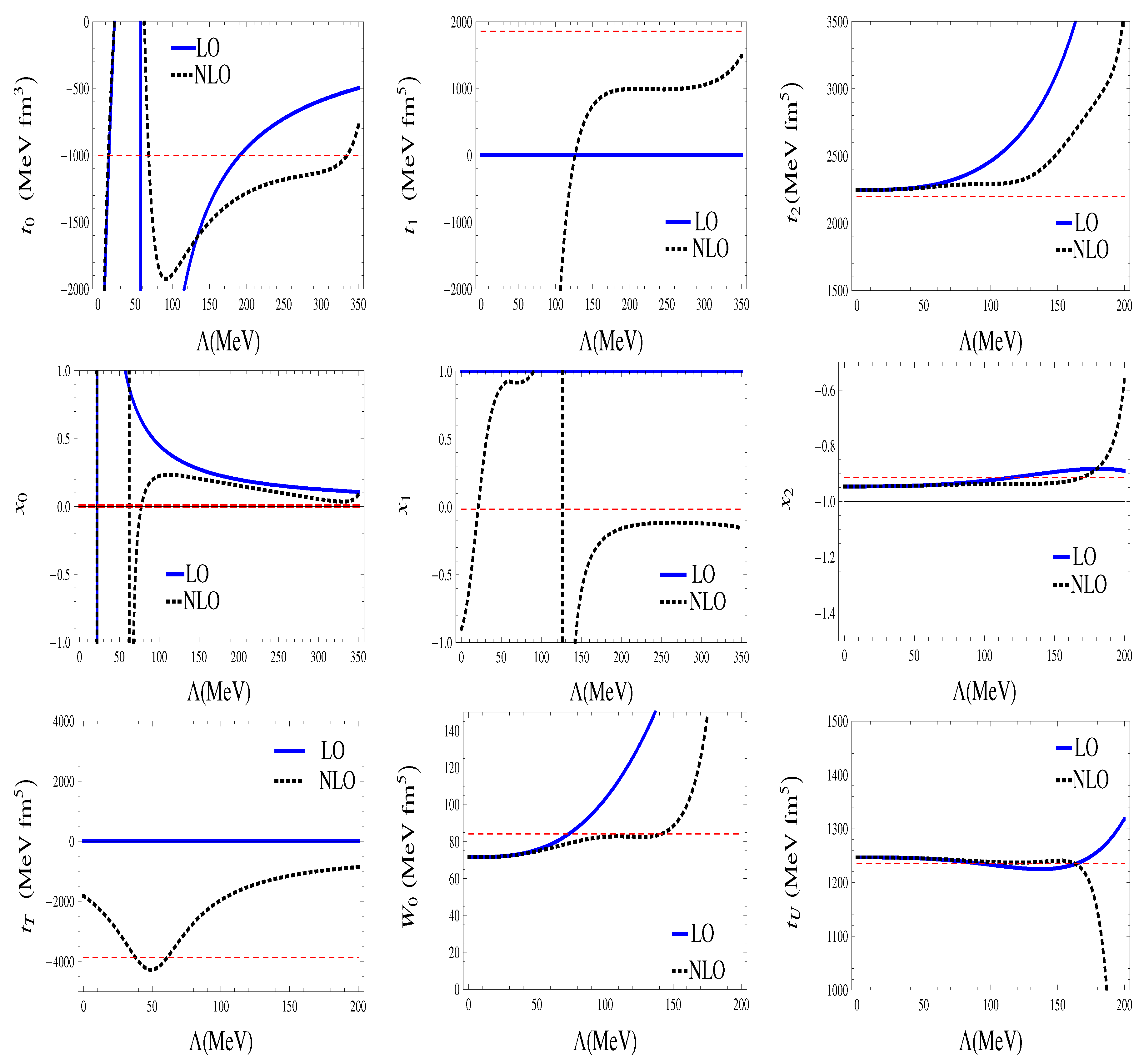
In the present paper, we want to show that, in fact, these parameters can uniquely be determined from known NN scattering threshold parameters by rather simple calculations where the interaction is just coarse grained over all wavelengths larger than the typical ones occurring in finite nuclei. As we will show, this introduces a momentum scale Λ in the nine effective parameters $t_{0,1,2}$, $x_{0,1,2}$ and $t_{U,T,V}$ ($t_V=W_0$), which allow for connecting the two body problem to the many body problem. Of course, for a finite nucleus, higher order corrections to the two body interaction as well as few body forces will be needed, and just stopping to second order in momenta will not be sufficient (see e.g., Ref. [34] for a calculation to $\mathcal{O}\left(p^6\right)$). However, going beyond Equation (2) requires further information than just two-body low energy scattering, in particular knowledge about three and four body forces and their scale dependence consistently inherited from their NN counterpart. The finite $k_F$ situation relevant for heavy nuclei and nuclear matter involves mixing between operators with different particle numbers and, in principle, could be conveniently tackled with the method outlined in Ref. [35], where the lack of genuine medium effects is manifestly built in.

The method we will be using is the implicit renormalization approach described already in Ref. [36,37,38], which has been positively tested for a simple toy model with just S-waves with the Block Diagonal (BD) formulation of the Similarity Renormalization Group (SRG) [39], which is an upgraded version of the $V_{\mathrm{lowk}}$-approach (see also [40] for a review). In previous work [36,37,38], it has explicitly been shown that the scale dependence deduced for the parameters of Equation (2) is not expected to change when higher orders in the expansion are included in a wide range of cut-offs Λ. This is our motivation to pursue the present analysis.

The paper is organized as follows. In Section 2, we review the $V_{\mathrm{lowk}}$ approach, with a particular stress on the low energy expansion and the connection to the threshold parameters in the relevant partial waves. In Section 3, we clarify the important distinction between pesudopotentials and $V_{\mathrm{lowk}}$ potentials as well its significance in coordinate space. In Section 4, we provide the pertinent partial wave decomposition of the Skyrme interaction, Equation (2), which becomes suitable to simplify the solution of the scattering problem. The analysis of the counterterms, and hence on the dependence of the Skyrme force parameters on the scale, is carried out in Section 4.2. Finally, in Section 5, we come to the conclusions. Further results are presented in the Appendix.

2. The ${\mathit{V}}_{\mathbf{lowk}}$ Approach

For completeness, we review here the $V_{\mathrm{lowk}}$ approach [21] in a way that our points can be easily stated. The starting point is a given phenomenological NN potential, V, and usually denominated bare potential, whence the scattering amplitude or T matrix is obtained as the solution of the Lippmann–Schwinger (LS) coupled channel equation in the CM system

$$\begin{array}{ccc}& & T_{l^{\prime },l}^{JS}(p^{\prime },p;k^2)=V_{l^{\prime },l}^{JS}(p^{\prime },p)\hfill \\ & & +\sum _{l^{\prime \prime }}{\int }_0^{\infty }\frac{M_N}{{\left(2\pi \right)}^3}\frac{dq{q}^2}{k^2-q^2}{V}_{l^{\prime },l^{\prime \prime }}^{JS}(p^{\prime },q)T_{l^{\prime \prime },l}^{JS}(q,p;k^2),\hfill \end{array}$$

(2)

where J is the total angular momentum, S the total spin and $l,l^{\prime }$ are orbital angular momentum quantum numbers, $p,p^{\prime },q$ are CM momenta, $M_N$ is the Nucleon mass, and $k^2/M_N$ is the CM energy. Solutions can be obtained just from the half off-shell T-matrix, taking, for instance, $k=p$.

For later reference, we also quote our convention for the relation with a local potential $V_{l^{\prime }l}^{JS}\left(r\right)$ with the momentum space case,

$$\begin{array}{c}\hfill V_{l^{\prime },l}^{JS}(p^{\prime },p)={\left(4\pi \right)}^2{\int }_0^{\infty }dr{r}^2{j}_{l^{\prime }}\left(p^{\prime }r\right)j_l\left(pr\right)V_{l^{\prime }l}^{JS}\left(r\right),\end{array}$$

(3)

where $j_l\left(x\right)$ are spherical Bessel funcions. Using the Bessel function expansion for small argument $j_l\left(x\right)=x^l/(2l+1)!![1-x^2/2(2l+3)+\cdots ]$, we get a low momentum expansion of the potential matrix elements. We keep up to total order $\mathcal{O}(p^4,p^{\prime 4},p^2{p}^{\prime 2})$ corresponding to S-, P- and D-waves as well as S-D and P-F mixing parameters,

$$\begin{array}{ccc}\hfill V_{00}^{JS}(p^{\prime },p)& =& {\tilde{C}}_{00}^{JS}+C_{00}^{JS}(p^2+p^{\prime 2})+D_{00}^1{}^{JS}(p^4+p^{\prime 4})+D_{00}^2{}^{JS}{p}^2{p}^{\prime 2}+\cdots ,\hfill \\ \hfill V_{11}^{JS}(p^{\prime },p)& =& p{p}^{\prime }{C}_{11}^{JS}+p{p}^{\prime }(p^2+p^{\prime 2})D_{11}^{JS}+\cdots ,\hfill \\ \hfill V_{22}^{JS}(p^{\prime },p)& =& p^2{p}^{\prime }{}^2{D}_{22}^{JS}+\cdots \hfill \\ \hfill V_{20}^{JS}(p^{\prime },p)& =& p^{\prime }{}^2{C}_{20}^{JS}+p^{\prime }{}^2{p}^2{D}_{20}^1{}^{JS}+p^{\prime }{}^4{D}_{20}^2{}^{JS}+\cdots ,\hfill \\ \hfill V_{31}^{JS}(p^{\prime },p)& =& p^{\prime }{}^{3}p{D}_{31}^{JS}+\cdots .\hfill \end{array}$$

(4)

To facilitate comparison, we will use below the usual spectroscopic NN notation ${}^{2S+1}{L}_J$ for diagonal channels and $E_J$ for off-diagonal channels. We will call the coefficients in the expansion counterterms, although, properly speaking, the name is justified when the potential $v(p^{\prime },p)$ is used to solve the problem in a restricted Hilbert space $p,p^{\prime }\le \Lambda$, which means, in particular, fitting scattering data up to CM momentum $p\le \Lambda$ [36] and providing a prescription to ensure hermiticity of the interaction. If a is the range of the interaction, only under these conditions is a truly universal behavior of the counterterms guaranteed for $\Lambda \sim 1/a$ as will be shown below.

The unitary (coupled channel) S-matrix is obtained as usual:

$$\begin{array}{c}\hfill S_{l^{\prime },l}^{JS}\left(p\right)={\delta }_{l^{\prime },l}-\mathrm{i}\frac{p{M}_N}{8{\pi }^2}{T}_{l^{\prime },l}^{JS}(p,p).\end{array}$$

(5)

Using the matrix representation $S^{JS}=(M^{JS}-i\mathbf{1}){(M^{JS}+i\mathbf{1})}^{-1}$ with ${\left(M^{JS}\right)}^{†}=M^{JS}$, a hermitian coupled channel matrix (also known as the K-matrix), at low energies, the effective range theory for coupled channels reads

$$\begin{array}{c}\hfill p^{l+l^{\prime }+1}{M}_{l^{\prime },l}^{JS}\left(p\right)=-{\left({\alpha }^{-1}\right)}_{l,l^{\prime }}^{JS}+\frac{1}{2}{\left(r\right)}_{l,l^{\prime }}^{JS}{p}^2+{\left(v\right)}_{l,l^{\prime }}^{JS}{p}^4+\cdots ,\end{array}$$

(6)

which, in the absence of mixing and using $S_l\left(p\right)=e^{2i{\delta }_l\left(p\right)}$, reduces to the well-known expression

$$\begin{array}{c}\hfill p^{2l+1}cot{\delta }_l\left(p\right)=-\frac{1}{{\alpha }_l}+\frac{1}{2}{r}_l{p}^2+v_l{p}^4+\cdots .\end{array}$$

(7)

An extensive study and determination of the low energy parameters for all partial waves has been carried out in Ref. [41] for both the NijmII and the Reid93 potentials [42] and also the AV18 [43] and the six modern Granada potentials in Ref. [33], yielding similar numerical results. Dropping these coupled channel indices for simplicity, the $V_{\mathrm{lowk}}$ potential is then defined by the equation:

$$\begin{array}{ccc}& & T(p^{\prime },p;p^2)=V_{\mathrm{lowk}}(p^{\prime },p)\hfill \\ & & +{\int }_0^{\Lambda }\frac{M_N}{{\left(2\pi \right)}^3}\frac{dq{q}^2}{p^2-q^2}{V}_{\mathrm{lowk}}(p^{\prime },q)T(q,p;p^2),\hfill \end{array}$$

(8)

where $(p,p^{\prime })\le \Lambda$. We use here a sharp three-dimensional cut-off Λ to separate between low and high momenta since results are not sensitive to the specific form of the regularization. Note, however, that the sharp function separates explicitly the model space from the rest in terms of orthogonal projection operators P and Q fulfilling $P^2=P$ and $Q^2=Q$ and $PQ=QP=0$, which is only fullfilled by the step functions $P=\theta (\Lambda -p)$ and $Q=1-\theta (\Lambda -p)$, and hence the total Hilbert space separates as $\mathcal{H}={\mathcal{H}}_P\oplus {\mathcal{H}}_Q$. Moreover, this definition does not provide a hermitean $V_{\mathrm{lowk}}$ potential, and usually a specific choice is made in order to restore hermiticity. Note that, in this context, such a prescription is equivalent to fulfill off-shell unitarity for the two body problem, a condition which proves essential for the three-body unitarity. However, there is generally an ambiguity in defining a restricted model space potential. The lack of uniqueness is not sufficiently emphasized in most $V_{\mathrm{lowk}}$ works. The Block Diagonal formulation of the Similarity Renormalization group (BD-SRG) [39] provides a suitable implementation of hermiticity at any stage of the calculation. In our case, and to the level of approximation of Equation (2), we will explicitly see that there is no ambiguity. Thus, eliminating the T matrix, we get the equation for the effective potential, which evidently depends on the cut-off scale Λ and corresponds to the effective interaction which nucleons see when all momenta higher than the momentum scale Λ are integrated out. It has been found [21] that high precision potential models, i.e., fitting the NN data to high accuracy and incorporating One Pion Exchange (OPE) at large distances and describing the deuteron form factors, collapse into a unique self-adjoint nonlocal potential for $\Lambda \sim 400-450\mathrm{MeV}$. This is not an unreasonable result since all the potentials provide a rather satisfactory description of elastic NN scattering data up to the pion production threshold $p\sim \sqrt{M_N{m}_{\pi }}\sim 360\mathrm{MeV}$. Note that this universality requires a marginal effect of off-shell ambiguities (beyond OPE off-shellness), which is a great advantage as this is a traditional source for uncertainties in nuclear structure.

Actually, in the extreme limit when $\Lambda \to 0$, one is left with zero energy on-shell scattering yielding $T_0(p,p)\to {\left(4\pi \right)}^2{\alpha }_0/M_N$. Moreover, for sufficiently small Λ, the potential which comes out from eliminating high energy modes can be accurately represented as the sum of the truncated original potential and a polynomial in the momentum [44]. However, as discussed in [26], a more convenient representation is to separate off all polynomial dependence explicitly from the original potential:

$$\begin{array}{c}\hfill V_{\mathrm{lowk}}(p^{\prime },p)={\overline{V}}_{\mathrm{NN}}(p^{\prime },p)+{\overline{V}}_{\mathrm{CT}}^{\Lambda }(p^{\prime },p),\end{array}$$

(9)

with $(p,p^{\prime })\le \Lambda$, so that, if ${\overline{V}}_{\mathrm{CT}}^{\Lambda }(p^{\prime },p)$ contains up to $\mathcal{O}\left(p^n\right)$, then ${\overline{V}}_{\mathrm{NN}}(p^{\prime },p)$ starts off at $\mathcal{O}\left(p^{n+1}\right)$, i.e., the next higher order. This way, the departures from a pure polynomial may be viewed as true and explicit effects due to the potential, and, more precisely, from the logarithmic left cut located at CM momentum $p=im/2$ at the partial wave amplitude level due to particle exchange with mass m. Thus, the coefficients in Equation (5) universally include all contributions to the effective interaction at low energies. Although we cannot calculate them ab initio, we may relate them to low energy scattering data for any value of Λ, in harmony with the expectation that off-shell effects are marginal in this energy regime. Not surprisingly, the physics encoding the effective interaction in Equation (5) will be related to the threshold parameters defined by Equation (6). Thus, the relevance of specific microscopic nuclear effective (coarse grained) forces has to do with the extent to which these threshold parameters are described by the underlying forces and not so much with their detailed structure. We will discuss below the limitations to this universal pattern.

In Ref. [45], an interesting study was conducted regarding the saturation of the short distance contributions due to heavy resonance exchange, namely $\sigma ,\rho ,\omega ,\delta ,\eta$. While this approach is, in principle, very appealing, it does not specify what the relevant scale is. Quite generally, the coefficients are scale dependent and this separation is scale dependent. In fact, the method used in Ref. [45] retains only the leading perturbative contribution in the resonance exchange. This procedure would be legitimate for peripheral waves, but certainly not for central S-waves where non-perturbative effects become crucial. As we will see, the Wilsonian renormalization point of view befits the situation in a more satisfactory manner.

A further objection to attempt the separation explicitly concerns the long distance pionic physics (see also [25,26,27,28]). Actually, we may separate the pionic contributions as follows:

$$\begin{array}{c}\hfill C_{\mathrm{Total}}(\Lambda )=C_{\mathrm{Short}}(\Lambda )+C_{1\pi }+C_{2\pi }+\cdots .\end{array}$$

(10)

There is the subtle issue on how to define numerically the pionic contribution. For instance, in Refs. [31,32], this separation is made in coordinate space as a function of the short distance cut radius $r_c$ in the range where the pionic contributions are proven to be indispensable when the fit is undertaken up to a maximum CM momentum, ${\Lambda }_{\mathrm{Fit}}$. Thus, the separation is done as

$$\begin{array}{c}\hfill C_{\mathrm{Total}}\left({\Lambda }_{\mathrm{Fit}}\right)=C_{\mathrm{Short}}(r<r_c)+C_{1\pi }(r>r_c)+C_{2\pi }(r>r_c)+\cdots .\end{array}$$

(11)

The potentials diverge like powers at large momenta, and, therefore, they become singular at short distances. Besides these extreme cases, the region around $r_c\sim 2\mathrm{fm}$ and ${\Lambda }_{\mathrm{Fit}}\sim 300\mathrm{MeV}$ does not map so easily. In fact, the numerical values quoted in [31,32,45] are not very similar when separations implied by either Equation (10) or Equation (11) are invoked, respectively.

3. ${\mathit{V}}_{\mathbf{highr}}$ vs. ${\mathit{V}}_{\mathbf{lowk}}$ Potentials

The most astonishing feature of the original $V_{\mathrm{lowk}}$ approaches, which made them so popular, was the universality of all potentials which have an OPE potential tail and simultaneously fit the phase-shifts up to pion production threshold with a ${\chi }^2/\mathrm{dof}\sim 1$. It is important to address here why the $V_{\mathrm{lowk}}$ approach works, i.e., why there is a universal and approximately scale independent behavior at $\Lambda \sim 2.1{\mathrm{fm}}^{-1}$. As we see, such a situation corresponds to a model space where particles do not interact, i.e., where $V_{\mathrm{lowk}}=0$, for CM momenta $p,p^{\prime }>\Lambda$ whence the original Lippmann–Schwinger equation directly reduces to the $V_{\mathrm{lowk}}$ equation. If we think of the ${}^1{S}_0$ channel, the traditional interpretation is that the vanishing of the phase shift at $p\sim 300$ MeV is an indication of the core of the interaction. Of course, an additional interpretation of a vanishing phase is that the interaction is weak. As already mentioned, in the BD-SRG version of the $V_{\mathrm{lowk}}$ approach, the Hilbert space is separated into the P and Q orthogonal subspaces, and hence both components of the Hilbert space are kept and thus phase equivalence is preserved. However, if we choose Λ such that $\delta (\Lambda )=0$ and neglect the Q space, we expect some stability against variations in Λ. As a matter of fact, much of the usefulness of the $V_{\mathrm{lowk}}$ approach has to do with the relative insensitivity to the change of the separation scale between the P and the Q spaces.

While renormalization issues are often posed in momentum space, one can provide an equivalent and insightful point of view in coordinate space [46] keeping the Wilsonian spirit (see also [47] for a nice presentation within the context of power counting). Actually, these features were anticipated in coordinate space long ago by the separation method of Moszkowski and Scott [7] (see a contextualized view in Ref. [8]). Indeed, while the standard view is that NN potentials present a repulsive core below a certain distance, $r\le a_{\mathrm{core}}\sim 0.5-0.6\mathrm{fm}$, the basic observation is that there is a given length scale, the separation distance, $d>a_{\mathrm{core}}$ below which one can instead replace the NN-interaction by a small potential. The typical values that one finds are in the range $d\sim 1\mathrm{fm}$. Let us see how this happens in the particular case of the ${}^1{S}_0$-channel where the core effects become more visible. Higher partial waves are already suppressed due to the centrifugal barrier, so we expect them to become less sensitive to short range repulsion of the central force.

In coordinate space, one has to look for regular solutions at the origin of the Schrödinger equation for positive energy states with scattering boundary conditions:

$$\begin{array}{ccc}\hfill -u_p^{\prime \prime }\left(r\right)+U\left(r\right)u_p\left(r\right)& =& p^2{u}_p\left(r\right),\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill u_p\left(r\right)& \to & \frac{sin(pr+{\delta }_0\left(p\right))}{sin{\delta }_0\left(p\right)},r\gg a,\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill u_p\left(r\right)& \to & A\left(p\right)r,r\to 0,\hfill \end{array}$$

(14)

where $U\left(r\right)=2\mu V\left(r\right)=MV\left(r\right)$ is the reduced NN-potential, $a\sim 3\mathrm{fm}$ is the range of the interaction and $A\left(p\right)$ is a constant which is fixed by the long distance normalization. Let us consider first the zero energy wave function, which corresponds to take $p\to 0$ and ${\delta }_0\left(p\right)\to -{\alpha }_{0}p$, fulfilling

$$\begin{array}{ccc}\hfill -u_0^{\prime \prime }\left(r\right)+U\left(r\right)u_0\left(r\right)& =& 0,\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill u_0\left(r\right)& \to & 1-\frac{r}{{\alpha }_0},r\gg a.\hfill \end{array}$$

(16)

As is well-known, the scattering length is defined by the intersection with the x-axis of the asymptotic zero energy wave function. For an interaction which is attractive at long distances, $U\left(r\right)<0$, we have that $u_0^{\prime \prime }\left(r\right)/u_0\left(r\right)=U\left(r\right)<0$, meaning that the function is concave in the attractive regime. The regular non interacting solution at the origin behaves as $u_{0,\mathrm{free}}\left(r\right)\sim r$, and it may happen that there is a distance d where the integrated-in full wave function matches a free solution, which means

$$\begin{array}{c}\hfill \frac{u_0^{\prime }\left(d\right)}{u_0\left(d\right)}=\frac{u_{0,\mathrm{free}}^{\prime }\left(d\right)}{u_{0,\mathrm{free}}\left(d\right)}=\frac{1}{d}.\end{array}$$

(17)

If this d exists, one can replace the zero energy scattering problem by the truncated original potential, which, following [25,26,27], we denote as the $V_{\mathrm{highr}}$ potential. The corresponding reduced potential, $U_{\mathrm{highr}}\left(r\right)=M{V}_{\mathrm{highr}}\left(r\right)$, reads

$$\begin{array}{c}\hfill U_{\mathrm{highr}}\left(r\right)=U\left(r\right)\theta (r-d).\end{array}$$

(18)

The situation is illustrated in Figure 1 for the Granada Gauss–OPE potential [48]. As we see, the inflexion point $u^{\prime \prime }\left(r_i\right)=0$ corresponds to the vanishing potential value $U\left(r_i\right)=0$, $r_i\sim 0.8$ fm, before the short distance repulsion sets in. Of course, this will generally not be true for finite momenta, and the picture gets somewhat modified. We will analyze, for illustration purposes, two possible schemes that we label as $U_{\mathrm{highr}}^{\mathrm{I}}$ and $U_{\mathrm{highr}}^{\mathrm{II}}$ and treat the short distances differently.

The simplest possibility is to make the separation distance d, below which the interaction can be taken to be zero, depending on p. This can be done by means of the modified relation:

$$\begin{array}{c}\hfill \frac{u_p^{\prime }\left(d\left(p\right)\right)}{u_p\left(d\left(p\right)\right)}=\frac{u_{p,\mathrm{free}}^{\prime }\left(d\left(p\right)\right)}{u_{p,\mathrm{free}}\left(d\left(p\right)\right)}=pcot\left(pd\left(p\right)\right),\end{array}$$

(19)

where we have taken, up to an irrelevant normalization, $u_{p,\mathrm{free}}\left(r\right)=sin\left(pr\right)$. Actually, we expect this change to be very small for $pd\ll 1$, as can be seen in Figure 2 (left panel). The resulting Vhighr potential becomes

$$\begin{array}{c}\hfill U_{\mathrm{highr}}^I(r,p)=U\left(r\right)\theta (r-d\left(p\right)).\end{array}$$

(20)

As we see, the $d\left(p\right)\to \infty$ for the critical value $p=1.78{\mathrm{fm}}^{-1}$, which is the value where the ${}^1{S}_0$ phase vanishes.

In another alternative scheme, one may keep the value of d at zero energy and add a (small) constant short distance square well potential

$$\begin{array}{c}\hfill U_{\mathrm{highr}}^{\mathrm{II}}(r,p)=U\left(r\right)\theta (r-d)+U_{\mathrm{short}}\left(p\right)\theta (d-r),\end{array}$$

(21)

where we have the condition $U_{\mathrm{short}}\left(0\right)=0$. The result is shown in Figure 2 (right panel), where we compare the computed values with a fit $V_{\mathrm{Short}}\left(p\right)=-8.75557p^2-0.676744p^4$ (V in MeV, p in fm${}^{-1}$). As we see from Figure 2, the short distance contribution of the effective potential $U_{\mathrm{short}}\left(p\right)$ remains moderate over the values of p compared to the core displayed by the original potential (see Figure 1). Note that the two different representations of the $V_{\mathrm{highr}}$ interaction, Equations (18) and (21), produce exactly the same phase-shifts by construction.

The existence of this separation scale and the smooth dependence on the energy at low energies is ubiquitous for NN interactions, but not a general feature of any potential; it depends on whether Equation (17) admits a solution. Integrating in from large distances to short distances, one finds for the ${}^1{S}_0$ channel and different potentials, the following separation distances:

$$\begin{array}{c}\hfill d^{\mathrm{Nijm}\mathrm{II}}=1.2\mathrm{fm},d^{\chi \mathrm{TPE}}=1.14\mathrm{fm},d^{\mathrm{Gauss}-\mathrm{OPE}}=1.05\mathrm{fm}.\end{array}$$

(22)

As a matter of fact, the coarse grained potentials used to make the most recent combined pp+np partial wave analyses allow taking vanishing potentials at distances numerically around these d values [49,50,51].

Once we have the $V_{\mathrm{highr}}$ interaction, we can compute the integrals and compare Equation (3) with the low momentum expansion, Equation (27) for $p^{\prime }=p$,

$$\begin{array}{ccc}\hfill V_{{}^1{S}_0}(p,p)& =& {\left(4\pi \right)}^2{\int }_0^{\infty }{r}^{2}dr{V}_{\mathrm{highr}}(r,p){\left[j_0\left(pr\right)\right]}^2,\hfill \end{array}$$

(23)

$$\begin{array}{ccc}& =& {\tilde{C}}_{{}^1{S}_0}+2p^2{C}_{{}^1{S}_0}+\cdots ,\hfill \end{array}$$

(24)

and similarly for the ${}^3{S}_1$ state. We get the values $({\tilde{C}}_{{}^1{S}_0},{\tilde{C}}_{{}^3{S}_1})=(-0.15,-0.13)\times {10}^4{\mathrm{GeV}}^{-2}$ and $(C_{{}^1{S}_0},C_{{}^3{S}_1})=(4.26,4.08)\times {10}^4{\mathrm{GeV}}^{-4}$ in fair agreement with the results of

Table 1. Counterterms obtained from the low energy threshold parameters compiled in Ref. [33] and compared with the corresponding potential integrals in different partial waves compiled in Ref. [52] for six different potentials which fit 6713 np and pp scattering data up to $T_{\mathrm{LAB}}\le 350\mathrm{MeV}$. Errors quoted for each potential are statistical; errors in the last column are systematic and correspond to the sample standard deviation of the six previous columns. See main text for details on the calculation of systematic errors. Units are: $\tilde{C}$’s are in ${10}^4$${\mathrm{GeV}}^{-2}$, C’s are in ${10}^4$${\mathrm{GeV}}^{-4}$. Λ is the renormalization scale, ${\Lambda }_{\mathrm{lowk}}$ the Vlowk cut-off and ${\Lambda }_{\mathrm{Fit}}$ the maximum CM fitting momentum used to determine the interaction (all in fm${}^{-1}$).

	Λ	Λ	Λ	Λ	Λ	${\Lambda }_{\mathrm{Vlowk}}=2.1$	${\Lambda }_{\mathrm{Vlowk}}=2.1$	${\Lambda }_{\mathrm{Fit}}<2$	${\Lambda }_{\mathrm{Fit}}<1.25$
	$0.25$	$0.5$	$0.75$	1	$1.25$	N3LO	AV18	6 Gr	χ TPE
${\tilde{C}}_{{}^1{S}_0}$	–0.3825	–0.241	–0.198	–0.178	–0.174	–0.168	–0.164	–0.13 (1)	–0.15 (1)
$C_{{}^1{S}_0}$	–28.06	1.08	2.538	2.436	2.333	4.105	3.997	4.15 (6)	4.20 (8)
${\tilde{C}}_{{}^3{S}_1}$	0.795	–0.381	–0.297	–0.243	–0.214	–0.168	–0.164	–0.045 (19)	–0.006 (19)
$C_{{}^3{S}_1}$	–450	–15.6	0.588	1.767	1.843	3.689	3.851	3.7 (2)	3.34 (4)
$C_{E_1}$	8.530	–3.905	–2.297	–1.714	–1.468	–7.912	–7.716	–8.42 (7)	–8.72 (6)
$C_{{}^1{P}_1}$	6.233	6.690	8.353	16.18	–29.63	6.092	5.939	6.47 (6)	6.45 (3)
$C_{{}^3{P}_0}$	–5.248	–4.962	–4.323	–3.457	–2.599	–4.296	–4.456	–4.89 (5)	–4.94 (1)
$C_{{}^3{P}_1}$	3.324	3.449	3.844	4.946	9.376	3.452	3.411	3.68 (6)	3.72 (3)
$C_{{}^3{P}_2}$	–0.617	–0.612	–0.602	–0.581	–0.551	–0.559	–0.556	–0.43 (1)	–0.486 (8)

. For the coefficients $C_{{}^1{S}_0}$ and $C_{{}^3{S}_1}$, the $V_{\mathrm{short}}\left(p\right)$ contribution is negligible. As we see, at the separation scale, the Wigner symmetry is well reproduced as a long distance effect, i.e., for $r>d$. This is a general pattern which has been found in recent fits [31] in the Skyrme parameters and the counterterms contributions for distances larger than $r_c=1.8\mathrm{fm}$. This pattern will reappear in our $V_{\mathrm{lowk}}$ analysis below, where $\Lambda \sim \pi /2d$ roughly marks the onset of the reported universality regime unveiled in the early works [21].

4. Skyrme Forces from Renormalization

4.1. Partial Waves Decomposition

Using the partial wave projection [53], we get the potentials in different angular momentum channels. These parameters can be related to the spectroscopic notation used in Ref. [45,54] (we call here $E_1$ their ${ϵ}_1$). Our identifications with Equation (5) are ${\tilde{C}}_{{}^1{S}_0}={\tilde{C}}_{00}^{00}$, ${\tilde{C}}_{{}^3{S}_1}={\tilde{C}}_{00}^{11}$, $C_{{}^1{S}_0}=C_{00}^{00}$, $C_{{}^3{S}_1}=C_{00}^{11}$, $C_{E_1}=C_{02}^{11}$, $C_{{}^3{P}_0}=C_{11}^{01}$, $C_{{}^3{P}_1}=C_{11}^{11}$, $C_{{}^3{P}_2}=C_{11}^{21}$, $C_{{}^1{P}_1}=C_{11}^{10}$ and similar identificatons hold with the threshold parameters α and r in the coupled channel effective range expansion, Equation (6). The S-wave potentials are

$$\begin{array}{ccc}\hfill V_{{}^1{S}_0}(p^{\prime },p)& =& {\tilde{C}}_{{}^1{S}_0}+C_{{}^1{S}_0}(p^{\prime 2}+p^2),\hfill \\ \hfill V_{{}^3{S}_1}(p^{\prime },p)& =& {\tilde{C}}_{{}^3{S}_1}+C_{{}^3{S}_1}(p^{\prime 2}+p^2),\hfill \\ \hfill V_{E_1}(p^{\prime },p)& =& C_{E_1}{p}^2,\hfill \end{array}$$

(25)

whereas the P-wave potentials read

$$\begin{array}{ccc}\hfill V_{{}^3{P}_0}(p^{\prime },p)& =& C_{{}^3{P}_0}{p}^{\prime }p,\hfill \\ \hfill V_{{}^3{P}_1}(p^{\prime },p)& =& C_{{}^3{P}_1}{p}^{\prime }p,\hfill \\ \hfill V_{{}^3{P}_2}(p^{\prime },p)& =& C_{{}^3{P}_2}{p}^{\prime }p,\hfill \\ \hfill V_{{}^1{P}_1}(p^{\prime },p)& =& C_{{}^1{P}_1}{p}^{\prime }p.\hfill \end{array}$$

(26)

The nine effective parameters depend on the scale Λ and can be related to the effective force representation $t_{0,1,2}$, $x_{0,1,2}$ and $t_{U,T}$ and $W_0$ of Equation (2) by the following explicit relations:

$$\begin{array}{ccc}\hfill t_0& =& \frac{1}{8\pi }\left({\tilde{C}}_{{}^3{S}_1}+{\tilde{C}}_{{}^1{S}_0}\right),\hfill \\ \hfill x_0& =& \frac{{\tilde{C}}_{{}^3{S}_1}-{\tilde{C}}_{{}^1{S}_0}}{{\tilde{C}}_{{}^3{S}_1}+{\tilde{C}}_{{}^1{S}_0}},\hfill \\ \hfill t_1& =& \frac{1}{8\pi }\left(C_{{}^3{S}_1}+C_{{}^1{S}_0}\right),\hfill \\ \hfill x_1& =& \frac{C_{{}^3{S}_1}-C_{{}^1{S}_0}}{C_{{}^3{S}_1}+C_{{}^1{S}_0}},\hfill \\ \hfill t_2& =& \frac{1}{32\pi }\left(9C_{{}^1{P}_1}+C_{{}^3{P}_0}+3C_{{}^3{P}_1}+5C_{{}^3{P}_2}\right),\hfill \\ \hfill x_2& =& \frac{-9C_{{}^1{P}_1}+C_{{}^3{P}_0}+3C_{{}^3{P}_1}+5C_{{}^3{P}_2}}{9C_{{}^1{P}_1}+C_{{}^3{P}_0}+3C_{{}^3{P}_1}+5C_{{}^3{P}_2}},\hfill \\ \hfill t_T& =& -\frac{3}{4\sqrt{2}\pi }{C}_{E_1},\hfill \\ \hfill W_0& =& \frac{1}{32\pi }\left(2C_{{}^3{P}_0}+3C_{{}^3{P}_1}-5C_{{}^3{P}_2}\right),\hfill \\ \hfill t_U& =& \frac{1}{16\pi }\left(-2C_{{}^3{P}_0}+3C_{{}^3{P}_1}-C_{{}^3{P}_2}\right).\hfill \end{array}$$

(27)

The result for $W_0$ can already be found in Ref. [55] and finite density corrections to it compare favorably with “empirical” estimates.

4.2. Analysis of Counterterms

The corresponding T-matrices are conveniently solved by factoring out the centrifugal terms that reduce the LS equation to a finite set of algebraic equations that are analytically solvable (see e.g., Ref. [24] and references therein). In the Appendix, we show how this is readily done. In the simplest case, where only the lowest order coefficients are taken into account, the explicit solutions for S- and P-waves are,

$$\begin{array}{ccc}\hfill {\tilde{C}}_S(\Lambda )& =& \frac{16{\pi }^2{\alpha }_0}{M_N(1-2{\alpha }_0\Lambda /\pi )},\hfill \\ \hfill C_P(\Lambda )& =& \frac{16{\pi }^2{\alpha }_1}{M_N(1-2{\alpha }_1{\Lambda }^3/3\pi )},\hfill \end{array}$$

(28)

where ${\alpha }_0$(${\alpha }_1$) is the scattering length (volume) defined by Equation (7). The Equation (28) illustrates the difference between a Fermi pseudo-potential and a coarse grained potential as the former corresponds to ${\alpha }_0\Lambda \ll 1$, where ${\tilde{C}}_S(\Lambda )\sim 16{\pi }^2{\alpha }_0/M_N$. In the case of ${\alpha }_0\Lambda \gg 1$, one has instead ${\tilde{C}}_S(\Lambda )\sim -8\pi /(M\Lambda )$. Full solutions including the Cs are also analytical, although a bit messier, so we do not display them explicitly. They rely on Equation (6), with ${\alpha }_{{}^1{S}_0}$, ${\alpha }_{{}^3{S}_1}$ being the S-wave scattering lengths in the ${}^1{S}_0$ and ${}^3{S}_1$ channels, respectively, ${\alpha }_{{}^3{P}_0}$, ${\alpha }_{{}^3{P}_1}$, ${\alpha }_{{}^3{P}_2}$, ${\alpha }_{{}^1{P}_1}$ being the P-waves scattering volumes in the ${}^3{P}_0$, ${}^3{P}_0$, ${}^3{P}_1$, ${}^3{P}_2$ and ${}^1{P}_1$, respectively, ${\alpha }_{E_1}$ being the mixing scattering volume in the ${}^3{S}_1{-}^3{D}_1$ channel, and $r_{{}^3{S}_1}$ and $r_{{}^1{S}_0}$ the effective ranges in the ${}^1{S}_0$ and ${}^3{S}_1$ channels, respectively. We refer to Ref. [41] for useful formulas and for numerical values for NijmII and Reid93 potentials and [33] for the six Granada potentials. At the order considered here, we just mention that, while all P-waves constants run independently of each other, with Λ, the spin-singlet parameters ${\tilde{C}}_{{}^1{S}_0}$, $C_{{}^1{S}_0}$ on the one hand and the spin-triplet parameters ${\tilde{C}}_{{}^3{S}_1}$, $C_{{}^3{S}_1}$ and $C_{E_1}$, on the other hand, are intertwined.

4.3. Numerical Results

We now turn to our numerical results. As can be seen from Figure 3 (see also Table 1 for numerical values), the comparison of contact interactions using threshold parameters with $V_{\mathrm{lowk}}$ results evolved to $\Lambda =420\mathrm{MeV}$ [21] (note the different normalization) from the Argonne-V18 bare potential [43] are saturated for $\Lambda =250\mathrm{MeV}$ for S-waves and for much lower cut-offs for P-waves. Note that this holds regardless of the details of the potential, as we only need the low energy threshold parameters as determined e.g., in Ref. [41]. The strong dependence observed at larger Λ values just reflects the inadequacy of the second order truncation in Equation (27). This also reflects in the $25\%$–$50\%$ inaccuracy off the exact $V_{\mathrm{lowk}}$ of the Ds themselves despite showing plateaus, and thus will not be discussed any further.

The close identities ${\tilde{C}}_{{}^1{S}_0}(\Lambda )\sim {\tilde{C}}_{{}^3{S}_1}(\Lambda )$ and $C_{{}^1{S}_0}(\Lambda )\sim C_{{}^3{S}_1}(\Lambda )$ for $\Lambda \ge 250\mathrm{MeV}$ feature the appearance of Wigner symmetry as pointed out in Ref. [25], but now we see that this does not depend on details of the force. Actually, the effect of the ${}^3{S}_1{-}^3{D}_1$ wave mixing represented by a non-vanishing off diagonal potential $V_{E_1}(p^{\prime },p)$ becomes essential to achieve this identity (a fact disregarded in Ref. [56]). As can be seen from Figure 3, there is a large mismatch at values of $\Lambda \sim 200-300\mathrm{MeV}$ when $C_{E_1}$ is set to zero (and hence ${\alpha }_{E_1}=0$) as compared with the case $C_{E_1}\ne 0$.

The scale dependence of the Skyrme interaction parameters (not involving the Ds) can be seen in Figure 4 in comparison with the $V_{\mathrm{lowk}}$ potentials [21] deduced from the Argonne-V18 bare potentials [43]. The plateaus observed in the different partial waves are corroborated here as well as a remarkable accuracy in reproducing the exact $V_{\mathrm{lowk}}$ numbers. Moreover, the weak cut-off dependence of the spin orbit interaction observed in Figure 4 suggests taking $\Lambda \to 0$, in which case:

$$\begin{array}{c}\hfill W_0=\frac{\pi }{2M_N}\left(2{\alpha }_{{}^3{P}_0}+3{\alpha }_{{}^3{P}_1}-5{\alpha }_{{}^3{P}_2}\right),\end{array}$$

(29)

which, upon using Ref. [41], yields $W_0=72{\mathrm{MeV}\mathrm{fm}}^5$. This numerical value reproduces within less than $10\%$ the exact $V_{\mathrm{lowk}}$ value, which illustrates the scale saturation. Nonetheless, it is $40\%$ smaller than nuclear structure mean field calculations based on Skyrme forces, which are generally rather stable and yield $W_0=120\pm 10{\mathrm{MeV}\mathrm{fm}}^5$ (see e.g., [55] for a compilation). As can be seen from Figure 4, the effective range correction $r_1$ provides, via additional D coefficients, the missing contribution. This is a bit lower than what it is found in phenomenological approaches from the $p_{3/2}-p_{1/2}$ level splitting in ${}^{16}$O [6]. In any case, the comparison with phenomenological approaches based on mean field calculations may be tricky since, as already mentioned, not all the terms are always kept, and selective fits to finite nuclear properties may overemphasize the role played by specific terms.

It has been argued that counterterms are fingerprints of long distance symmetries [25,26,27]. This remarkable result holds regardless of the nature of the forces and applies, in particular, to both Wigner and Serber symmetries. We confirm that, to great accuracy, $x_0=0$ (Wigner symmetry) and $x_2=-1$ (Serber symmetry). The astonishing large-$N_c$ ($N_c$ is the number of colors in QCD) relations discussed in Refs. [25,26,27,28] provide a direct link to the underlying quark and gluon dynamics and [57] suggests a $1/N_c^2$ accuracy of the Wigner symmetry in even-L partial waves. Wigner symmetry has proven crucial in nuclear coarse lattice ($a\sim 2\mathrm{fm}$) calculations [23] in sidestepping the sign problem for fermions. As we see for the scales typically involved there, this works with great accuracy already at $\Lambda \sim 250\mathrm{MeV}$. Taking into account that we are dealing with low energies, it is thus puzzling that chiral interactions to N${}^3$LO [58] having chiral cut-offs ${\Lambda }_{\chi }\sim 600\mathrm{MeV}$ tend to violate Wigner symmetry in the $V_{\mathrm{lowk}}$ sense, i.e., $C_{{}^1{S}_0}^{\chi }\ne C_{{}^3{S}_1}^{\chi }$, whereas smaller values ${\Lambda }_{\chi }\sim 450\mathrm{MeV}$ [26] are preferred. We also note that SRG studies do find accurate verification of Wigner symmetry [59,60,61].

On a more phenomenological level, there exist recent N3LO calculations (including terms to sixth order in momenta) [34,62,63] where the Skyrme parameters have been determined within a DFT framework. Typically, the number of terms is so large that additional symmetries have been implemented to reduce them. As we mentioned in the introduction, results vary depending on the calculational scheme and the fitting strategy. According to our view, the scale dependence of these higher order contributions in the two-body sector is intertwined with the scale dependence of three and higher nucleon forces. Error and correlation analyses may prove essential to gain further information from this viewpoint [64,65]. Our interpretation not only provides a unique definition of the DFT parameters but also indicates that they depend on the renormalization scale Λ, which clearly varies for different nuclei and neutron and nuclear matter. Density dependence of the parameters can only be regarded within our framework as many body interactions, a point emphasized within DFT recently in Ref. [66]. Extending our calculation to include many body interactions would be possible but numerically cumbersome and is left for future research.

5. Conclusions

In the present paper, we have provided a Wilsonian renormalization scale argument on how the much used effective interaction parameters of the venerable Skyrme interaction can be understood as coarse grained NN interactions over the suitable wavelengths. A mapping of these scale dependent parameters to counterterms usually employed in the NN interaction scattering analyses becomes possible. This view befits the idea that, even in the lightest nuclei, where density effects are negligible, nucleons interact with each other in an average fashion, sampling only the low energies relevant for nuclear binding or equivalently resolving only the physical effects for distances above the corresponding de Broglie wavelength. The typical momentum scales increase as one goes to heavier nuclei and nuclear and neutron matter where density effects become more visible. We have seen that, regarding the renormalization group, when running the parameters, there is scale saturation, i.e., above a certain scale, the effective interaction parameters do not depend strongly on the scale in a regime where most of the strength can be deduced from low energy NN scattering information regardless of the underlying forces. The fulfillment of the previously reported and well fulfilled Wigner and Serber symmetries in the effective interactions is reassuring and indicates that many of the main features of the effective interaction are kept. Of course, for heavier nuclei, many-body effects set in, and the number of terms in the effective interaction, and hence the number of parameters, grow rapidly. At the same time, explicit finite range effects such as pion exchange corrections will become relevant for higher dimensional terms beyond the second order in momenta analyzed here. The weak scale dependence not only provides a rationale for fitting strategies in mean field nuclear structure calculations, but also shows that, for $\Lambda \sim k_F$, one should distinguish between density effects due to many body forces and scale dependence due to finite wavelength resolution. We expect that a more clear disentanglement of both properties might provide further insight into the modern DFT approach to nuclear physics.

Our results can be improved and extended in several ways. Within the low energy expansion, we have neglected terms $\mathcal{O}({p^{\prime }}^4,p^4,{p^{\prime }}^2{p}^2)$, which correspond to P-waves and S-wave range corrections. In configuration space, this corresponds to a dimensional expansion, since $\delta \left({\overrightarrow{r}}_{12}\right)=\mathcal{O}\left({\Lambda }^3\right)$ and $\{P^2,\delta \left({\overrightarrow{r}}_{12}\right)\}=\mathcal{O}\left({\Lambda }^5\right)$, $\{P^4,\delta \left({\overrightarrow{r}}_{12}\right)\}=\mathcal{O}\left({\Lambda }^7\right)$. Within such a scheme, going to higher orders also requires including three-body interactions, $\sim \delta \left(r_{12}\right)\delta \left(r_{13}\right)=\mathcal{O}\left({\Lambda }^6\right)$. Actually, at the two-body level, there are more potential parameters than low energy threshold parameters. For instance, in the ${}^1{S}_0$ channel, one has two independent hermitean operators, ${p^{\prime }}^4+p^4$ and $2{p^{\prime }}^2{p}^2$ (which are on-shell equivalent), but only one $v_{{}^1{S}_0}$ threshold parameter in the low energy expansion (see Equation (6)). As it was shown in Ref. [67] (see also Ref. [68]), these two features are interrelated since this two body off-shell ambiguity is cancelled when a three body observable, like e.g., the triton binding energy, is fixed. An intriguing aspect of the present investigation is the modification induced by potential tails due to e.g., pion exchange, which cannot be represented by a polynomial since particle exchange generates a cut in the complex energy plane. The important issue, however, is that the low scale saturation unveiled in the present paper works accurately just to the second order as long as the low energy parameters determined from on-shell scattering are properly reproduced. Along these lines, we also expect that higher order two-body derivative terms accounting for higher energies will become more sensitive to the long range features of the interaction, and more specifically to pion exchanges. Finally, it would be very interesting to check this behavior of the counterterms by the explicit renormalization method based on the Block-Diagonal Similarity Renormalization Group, as was done in a toy model in Ref. [36,37], as the problem becomes extremely stiff and computationally expensive for $\Lambda \ll 1{\mathrm{fm}}^{-1}$. There, it was found that the simple analytical formulas overlap in the physically interesting $\Lambda \sim 1{\mathrm{fm}}^{-1}$ region and allow for sidestepping the stiff equations for lower values. Work along these lines is in progress.