Recent Advances in Microscopic Approaches to Nuclear Matter and Symmetry Energy
Abstract
:1. Introduction
2. The Symmetry Energy
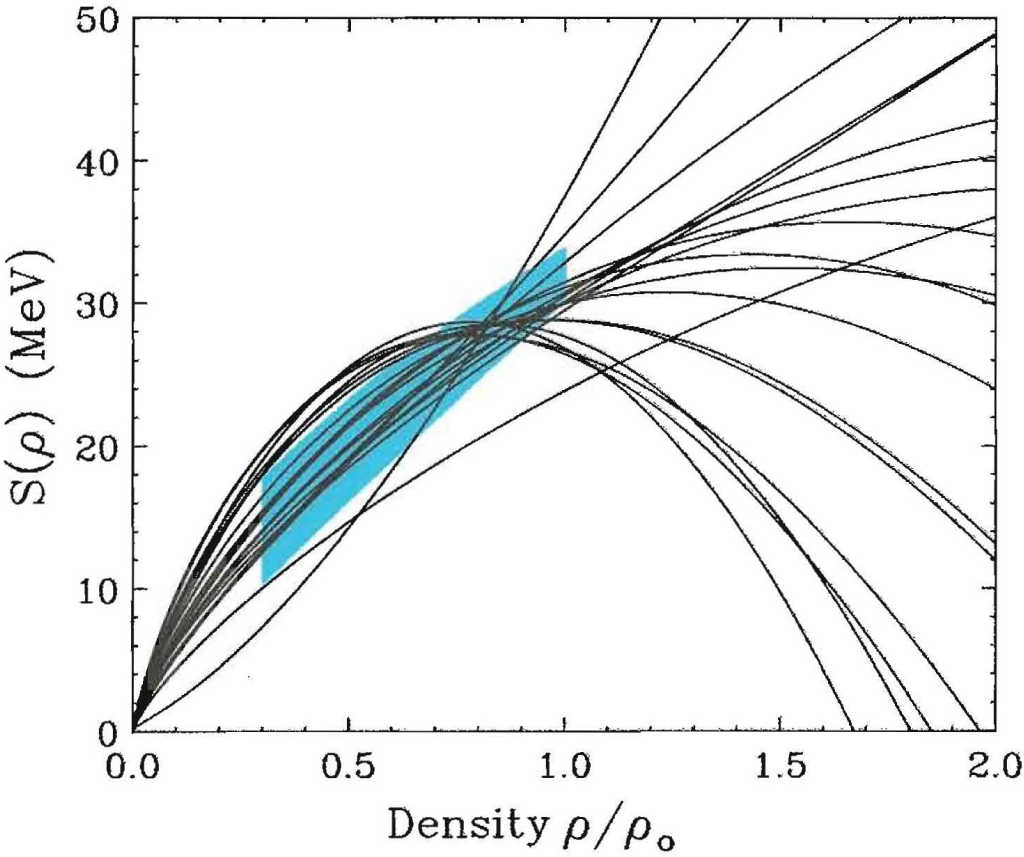
2.1. Empirical Facts
2.2. Experimental Constraints on the Symmetry Energy
Heavy ion collisions:
Nuclear binding energies:
Neutron skin measurements with hadronic or electroweak probes:
Electric dipole strength function:
2.3. The Slope of the Symmetry Energy and the Radii of Neutron Stars
3. Our Microscopic Approach to Isospin-Asymmetric Nuclear Matter
3.1. Brief Review of the Model
3.2. Microscopic Predictions of the EoS and Related Quantities
4. A Different Approach: Chiral Interactions
5. Summary and Conclusions
Acknowledgments
Conflicts of Interest
References
- Bethe, H.A.; Bacher, R.F. Nuclear Physics A. Stationary states of nuclei. Rev. Mod. Phys 1936, 8. [Google Scholar] [CrossRef]
- Von Weizäcker, C.F. Zur theorie der kernmassen. Z. Phys 1935, 96, 431–458. [Google Scholar]
- Machleidt, R. The meson theory of nuclear forces and nuclear structure. Adv. Nucl. Phys 1989, 19, 189–376. [Google Scholar]
- Oyamatsu, K.; Tanihata, I.; Sugahara, Y.; Sumiyoshi, K.; Toki, H. Can the equation of state of asymmetric nuclear matter be studied using unstable nuclei? Nucl. Phys. A 1998, 634, 3–14. [Google Scholar]
- Furnstahl, R.J. Neutron radii in mean-field models. Nucl. Phys. A 2002, 706, 85–110. [Google Scholar]
- Sammarruca, F.; Liu, P. Neutron skin of 208Pb and density dependence of the symmetry energy. Phys. Rev. C 2009. [Google Scholar]
- Brueckner, K.A.; Levinson, C.A.; Mahmoud, H.M. Two-body forces and nuclear saturation. I. Central forces. Phys. Rev 1954, 95, 217–228. [Google Scholar]
- Bethe, H.A. Nuclear Many-body problem. Phys. Rev 1956, 103, 1353–1366. [Google Scholar]
- Goldstone, J. Derivation of the Brueckner many-body theory. Proc. R. Soc. London Ser. A 1957, 239, 267–279. [Google Scholar]
- Bethe, H.A. Theory of nuclear matter. Annu. Rev. Nucl. Sci 1971, 21, 93–244. [Google Scholar]
- Haftel, M.I.; Tabakin, F. Nuclear saturation and the smoothness of nucleon-nucleon potentials. Nucl. Phys. A 1970, 158, 1–42. [Google Scholar]
- Sprung, D.W.L. Nuclear matter calculations. Adv. Nucl. Phys 1972, 5, 225–343. [Google Scholar]
- Pandharipande, V.R.; Wiringa, R.B. Variations on a theme of nuclear matter. Rev. Mod. Phys 1979, 51, 821–859. [Google Scholar]
- Lagaris, I.E.; Pandharipande, V.R. Variational calculations of realistic models of nuclear matter. Nucl. Phys. A 1981, 359, 349–364. [Google Scholar]
- Day, B.D.; Wiringa, R.B. Brueckner-Bethe and variational calculations of nuclear matter. Phys. Rev. C 1985. [Google Scholar]
- Anastasio, M.R.; Celenza, L.S.; Pong, W.S.; Shakin, C.M. Relativistic nuclear structure physics. Phys. Rep 1983, 100, 327–392. [Google Scholar]
- Horowitz, C.J.; Serot, B.D. Two-nucleon correlations in a relativistic theory of nuclear matter. Phys. Lett. B 1984, 137, 287–293. [Google Scholar]
- Horowitz, C.J.; Serot, B.D. The relativistic two-nucleon problem in nuclear matter. Nucl. Phys. A 1987, 464, 613–699. [Google Scholar]
- Brockmann, R.; Machleidt, R. Nuclear saturation in a relativistic Brueckner–Hartree–Fock approach. Phys. Lett. B 1984, 149, 283–287. [Google Scholar]
- Brockmann, R.; Machleidt, R. Relativistic nuclear structure. I. Nuclear matter. Phys. Rev. C 1990. [Google Scholar]
- Sugahara, Y.; Toki, H. Relativistic mean-field theory for unstable nuclei with non-linear σ and ω terms. Nucl. Phys. A 1994, 579, 557–572. [Google Scholar]
- Lalazissis, G.A.; König, J.; Ring, P. New parametrization for the Lagrangian density of relativistic mean field theory. Phys. Rev. C 1997. [Google Scholar]
- Kubis, S.; Kutschera, M. Nuclear matter in a relativistic mean field theory with isovector scalar meson. Phys. Lett. B 1997, 399, 191–195. [Google Scholar]
- Mueller, H.; Serot, B.D. Relativistic mean-field theory and the high-density nuclear equation of state. Nucl. Phys. A 1996, 606, 508–537. [Google Scholar]
- Stone, J.R.; Miller, J.C.; Koncewicz, R.; Stevenson, P.D. Nuclear matter and neutron star properties calculated with the Skyrme interaction. Phys. Rev. C 2003. [Google Scholar]
- Stone, J.R.; Reinhard, P.-G. The Skyrme interaction in finite nuclei and nuclear matter. Prog. Part. Nucl. Phys 2007, 58, 587–657. [Google Scholar]
- Das, C.B.; Gupta, S.D.; Gale, C.; Li, B.A. Momentum dependence of symmetry potential in asymmetric nuclear matter for transport model calculations. Phys. Rev. C 2003. [Google Scholar]
- Chappert, F.; Girad, M.; Hilaire, S. Toward a new parametrization of the Gogny force: Neutron matter and nuclear binding energies. Phys. Lett. B 2008, 668, 420–424. [Google Scholar]
- Gandolfi, S.; Yu Illarionov, A.; Schmidt, K.E.; Pederiva, F.; Fantoni, S. Quantum Monte Carlo calculation of the equation of state of neutron matter. Phys. Rev. C 2009. [Google Scholar]
- Baldo, M.; Polls, A.; Rios, A.; Schulze, H.-J.; Vidana, I. Comparative study of neutron and nuclear matter with simplified Argonne nucleon-nucleon potentials. Phys. Rev. C 2012, 86. [Google Scholar] [CrossRef]
- Weinberg, S. Phenomenological Lagrangians. Physica A 1979, 96, 327–340. [Google Scholar]
- Weinberg, S. Nuclear forces from chiral lagrangians. Phys. Lett. B 1990, 251, 288–292. [Google Scholar]
- Simenel, C.; Chomaz, P.H.; de France, G. Fusion process studied with a preequilibrium giant dipole resonance. Phys. Rev. C 2007. [Google Scholar]
- Brown, B.A. Neutron Radii in Nuclei and the Neutron equation of State. Phys. Rev. Lett 2000. [Google Scholar]
- Ko, C.M.; Oh, Y.; Xu, J. Medium effects on charged pion ratio in heavy ion collisions. Int. J. Mod. Phys. E 2010, 19, 1763–1772. [Google Scholar]
- Tsang, M.B.; Stone, J.R.; Camera, F.; Danielewicz, P.; Gandolfi, S.; Hebeler, K.; Horowitz, C.J.; Lee, J.; Lynch, W.G.; Kohley, Z.; et al. Constraints on the symmetry energy and neutron skins from experiments and theory. Phys. Rev. C 2012. [Google Scholar]
- Lane, A.M. Isobaric spin dependence of the optical potential and quasi-elastic (p,n) reaction. Nucl. Phys 1962, 35, 676–685. [Google Scholar]
- Zenihiro, J.; Sakaguchi, H.; Murakami, T.; Yosoi, M.; Yasuda, Y.; Terashima, S.; Iwao, Y.; Takeda, H.; Itoh, M.; Yoshida, H.P.; et al. Neutron density distributions of 204,206,208Pb deduced via proton elastic scattering at Ep = 295 MeV. Phys. Rev. C 2010. [Google Scholar]
- 208Pb Radius Experiment PREX. Available online: hallaweb.jlab.org/parity/prex accessed on 20 July 2014.
- C-REX Workshop. Available online: http://www.jlab.org/conferences/crex accessed on 20 July 2014.
- Reinhard, P.-G.; Nazarewicz, W. Information content of a new observable: The case of the nuclear neutron skin. Phys. Rev. C 2010. [Google Scholar]
- Sedrakian, A. The physics of dense hadronic matter and compact stars. Prog. Part. Nucl. Phys 2007, 58, 168–246. [Google Scholar]
- Champion, D.J.; Ransom, S.M.; Lazarus, P.; Camilo, F.; Bassa, C.; Kaspi, V.M.; Nice, D.J.; Freire, P.C.C.; Stairs, I.H.; van Leeuwen, J.; et al. An eccentric Binary Millisecond Pulsar in the Galactic Plane. Science 2008, 320, 1309–1312. [Google Scholar]
- Demorest, P.; Pennucci, T.; Ransom, S.; Roberts, M.; Hessels, J. Shapiro delay measurement of a two solar mass neutron star. Nature 2010, 468, 1081–1083. [Google Scholar]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 1–9. [Google Scholar]
- Lattimer, J. M.; Prakash, M. Neutron star observations: Prognosis for equation of state constraints. Phys. Rep 2007, 442, 109–165. [Google Scholar]
- Faulkner, A.J.; Kramer, M.; Lyne, A.G.; Manchester, R.N.; McLaughlin, M.A.; Stairs, I.H.; Hobbs, G.; Possenti, A.; Lorimer, D.R.; D’Amico, N.; et al. A new relativistic double neutron star system. Astrophys. J. Lett 2004, 618, L119–L122. [Google Scholar]
- Weber, F. Pulsars as Astrophysical Laboratories for Nuclear and Particle Physic; Institute of Physics Publishing: Bristol, UK; Philadelphia, PA, USA, 1999. [Google Scholar]
- Fattoyev, F.J.; Piekarewicz, J. Neutron skins and neutron stars. Phys. Rev. C 2012. [Google Scholar]
- Li, Z.H.; Lombardo, U.; Schulze, H.-J. Consistent nucleon-nucleon potentials and three-body forces. Phys. Rev. C 2008. [Google Scholar]
- Li, Z.H.; Schulze, H.-J. Neutron star structure with modern nucleonic three-body forces. Phys. Rev. C 2008. [Google Scholar]
- Wiringa, R.B.; Stocks, V.G.J.; Schiavilla, R. Accurate nucleon-nucleon potential with charge-independence breaking. Phys. Rev. C 1995. [Google Scholar]
- Stocks, V.G.J.; Klomp, R.A.M.; Terheggen, C.P.F.; de Swart, J.J. Construction of high-quality NN potential models. Phys. Rev. C 1994. [Google Scholar]
- Pieper, S.C.; Pandharipande, V.R.; Wiringa, R.B.; Carlson, J. Realistic models of pion-exchange three-nucleon interactions. Phys. Rev. C 2001. [Google Scholar]
- Harrison, B.K.; Thorne, K.S.; Wakano, M.; Wheeler, J.A. Gravitation Theory and Gravitational Collapse; University of Chicago Press: Chicago, IL, USA, 1965. [Google Scholar]
- Negele, J.W.; Vautherin, D. Neutron star matter at sub-nuclear densities. Nucl. Phys. A 1973, 207, 298–320. [Google Scholar]
- Machleidt, R. High-precision, charge-dependent Bonn nucleon-nucleon potential. Phys. Rev. C 2001. [Google Scholar]
- Thompson, R.H. Bethe-Salpeter Equation Applied to the Nucleon-Nucleon Interaction. Phys. Rev. D 1970. [Google Scholar]
- Salpeter, E.E.; Bethe, H.A. A Relativistic Equation for Bound-State Problems. Phys. Rev 1951, 84, 1232–1242. [Google Scholar]
- Sammarruca, F. The microscopic approach to nuclear matter and neutron star matter. Int. J. Mod. Phys. E 2010, 19, 1259–1313. [Google Scholar]
- Sammarruca, F. Analysis of the symmetry energy in a microscopic approach. Int. J. Mod. Phys. E 2013, 22, 1–37. [Google Scholar]
- Danielewicz, P.; Lacey, R.; Lynch, W.G. Determination of the equation of state of dense matter. Science 2002, 298, 1592–1596. [Google Scholar]
- Sammarruca, F. Contribution of isovector mesons to the symmetry energy in a microscopic model. Phys. Rev. C 2011. [Google Scholar]
- Sakurai, J.J. Currents and Mesons; University of Chicago Press: Chicago, IL, USA, 1969. [Google Scholar]
- Höhler, G.; Pietarinen, E. The ρ NN vertex in the vector-dominance model. Nucl. Phys 1975, B95, 210–230. [Google Scholar]
- Fujita, J.I.; Miyazawa, H. Pion theory of three-body forces. Prog. Theor. Phys 1957, 17, 360–365. [Google Scholar]
- Weinberg, S. Nonlinear realization of chiral symmetry. Phys. Rev 1968, 166, 1568–1577. [Google Scholar]
- Machleidt, R.; Entem, D.R. Chiral effective field theory and nuclear forces. Phys. Rep 2011, 503, 1–75. [Google Scholar]
- Epelbaum, E. Few-nucleon forces and systems in chiral effective field theory. Prog. Part. Nucl. Phys 2006, 57, 654–741. [Google Scholar]
- Epelbaum, E.; Hammer, H.-W.; Meissner, U.-G. Modern theory of nuclear forces. Rev. Mod. Phys 2009, 81, 1773–1825. [Google Scholar]
- Entem, D.R.; Machleidt, R. Accurate charge-dependent nucleon-nucleon potential at fourth order of chiral perturbation theory. Phys. Rev. C 2003. [Google Scholar]
- Epelbaum, E. Four-nucleon force using the method of unitary transformation. Eur. Phys. J 2007, A34, 197–214. [Google Scholar]
- Rozpedzik, D.; Golak, J.; Skibinski, R.; Witala, H. A. First Estimation of Chiral Four-Nucleon Force Effects in 4He. Acta Phys. Polon 2006, B37, 2889–2904. [Google Scholar]
- Holt, J.W.; Kaiser, N.; Weise, W. Density-dependent effective nucleon-nucleon interaction from chiral three-nucleon forces. Phys. Rev. C 2010. [Google Scholar]
- Marcucci, L.E.; Kievsky, A.; Rosati, S.; Schiavilla, R.; Viviani, M. Chiral effective field theory predictions for muon capture on deuteron and 3He. Phys. Rev. Lett 2012. [Google Scholar]
- Coraggio, L.; Holt, J.W.; Itaco, N.; Machleidt, R.; Marcucci, L.E.; Sammarruca, F. Nuclear matter equation of state with consistent two- and three-body perturbative chiral interactions. Phys. Rev. C 2014. [Google Scholar]
- Kaiser, N.; Fritsch, S.; Weise, W. Chiral dynamics and nuclear matter. Nucl. Phys. A 2002, 697, 255–276. [Google Scholar]
- Fritsch, S.; Kaiser, N.; Weise, W. Chiral approach to nuclear matter: Role of two-pion exchange with virtual delta-isobar excitation. Nucl. Phys. A 2005, 750, 259–293. [Google Scholar]
- Kaiser, N. Isovector part of nuclear energy density functional from chiral two- and three-nucleon forces. Eur. Phys. J 2012, A48, 36–49. [Google Scholar]
- Holt, J.W.; Kaiser, N.; Weise, W. Nuclear chiral dynamics and thermodynamics. Prog. Part. Nucl. Phys 2013, 73, 35–83, and references therein. [Google Scholar]
- Bogner, S.K.; Furnstahl, R.J.; Schwenk, A. From low-momentum interactions to nuclear structure. Prog. Part. Nucl. Phys 2010, 65, 94–147. [Google Scholar]
- Hebeler, K.; Bogner, S.K.; Furnstahl, R.J.; Nogga, A.; Schwenk, A. Improved nuclear matter calculations from chiral low-momentum interactions. Phys. Rev. C 2011. [Google Scholar]













| Physical property A | Correlation coefficient between A and the neutron skin thickness in 208 Pb |
|---|---|
| L | 0.9952 |
| 0.9882 | |
| 0.8016 | |
| R0.6 | 0.9953 |
| R0.8 | 0.9931 |
| R1.0 | 0.9866 |
| R1.4 | 0.9486 |
| R1.6 | 0.8361 |
| Λ (MeV) | n | c1 | c3 | c4 | cD | cE |
|---|---|---|---|---|---|---|
| 450 | 3 | −0.81 | −3.40 | 3.40 | −0.24 | −0.11 |
| 500 | 2 | −0.81 | −3.20 | 5.40 | 0.0 | −0.18 |
| 600 | 2 | −0.81 | −3.20 | 5.40 | −0.19 | −0.833 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sammarruca, F. Recent Advances in Microscopic Approaches to Nuclear Matter and Symmetry Energy. Symmetry 2014, 6, 851-879. https://doi.org/10.3390/sym6040851
Sammarruca F. Recent Advances in Microscopic Approaches to Nuclear Matter and Symmetry Energy. Symmetry. 2014; 6(4):851-879. https://doi.org/10.3390/sym6040851
Chicago/Turabian StyleSammarruca, Francesca. 2014. "Recent Advances in Microscopic Approaches to Nuclear Matter and Symmetry Energy" Symmetry 6, no. 4: 851-879. https://doi.org/10.3390/sym6040851




