The Almost Periodic Rigidity of Crystallographic Bar-Joint Frameworks
1. Introduction
 , in the Euclidean spaces, ℝd, with respect to periodic first order flexes is determined by a finite matrix, the associated periodic rigidity matrix. For essentially generic frameworks of this type in two dimensions, there is a deeper combinatorial characterisation, which is a counterpart of Laman's characterisation of the infinitesimal rigidity of generic placements of finite graphs in the plane. See Ross [1]. For related results and characterisations of other forms of periodic infinitesimal rigidity, see Borcea and Streinu [2,3], Connelly, Shen and Smith [4], Malestein and Theran [5], Owen and Power [6], Power [7,8] and Ross, Schulze and Whiteley [9].
, in the Euclidean spaces, ℝd, with respect to periodic first order flexes is determined by a finite matrix, the associated periodic rigidity matrix. For essentially generic frameworks of this type in two dimensions, there is a deeper combinatorial characterisation, which is a counterpart of Laman's characterisation of the infinitesimal rigidity of generic placements of finite graphs in the plane. See Ross [1]. For related results and characterisations of other forms of periodic infinitesimal rigidity, see Borcea and Streinu [2,3], Connelly, Shen and Smith [4], Malestein and Theran [5], Owen and Power [6], Power [7,8] and Ross, Schulze and Whiteley [9]. ), of the d-torus,
), of the d-torus,
 d, or as an equivalent subset of [0, 1)d, which arises from a choice of translation group
d, or as an equivalent subset of [0, 1)d, which arises from a choice of translation group
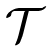 . This set of multi-phases is determined by a matrix-valued function, Φ
. This set of multi-phases is determined by a matrix-valued function, Φ  (z), on
(z), on
 d with the value at z = 1̂ = (1, 1, … , 1) providing the corresponding periodic rigidity matrix for
d with the value at z = 1̂ = (1, 1, … , 1) providing the corresponding periodic rigidity matrix for
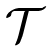 .
. as an infinite bar-joint framework. It is shown that
as an infinite bar-joint framework. It is shown that
 is almost periodically infinitesimally rigid if and only if for some choice of translation group, it is periodically infinitesimally rigid, and the corresponding RUM spectrum is the minimal set {1̂}. More generally, we show how the almost periodic infinitesimal flexes of
is almost periodically infinitesimally rigid if and only if for some choice of translation group, it is periodically infinitesimally rigid, and the corresponding RUM spectrum is the minimal set {1̂}. More generally, we show how the almost periodic infinitesimal flexes of
 are determined in terms of the matrix function, Φ
are determined in terms of the matrix function, Φ  (z).
(z). ) =
) =
 3. We show that for crystal frameworks whose RUM spectrum decomposes into a finite union of linear components, there is a corresponding vector space decomposition of the almost periodic flex space. The flexes in these subspaces are periodic in specific directions associated with certain symmetries of the crystallographic point group.
3. We show that for crystal frameworks whose RUM spectrum decomposes into a finite union of linear components, there is a corresponding vector space decomposition of the almost periodic flex space. The flexes in these subspaces are periodic in specific directions associated with certain symmetries of the crystallographic point group.2. Crystal Frameworks and the RUM Spectrum
Definition 1
 , is a bar-joint framework (G, p) for which there exist finite subsets, Fv ⊆ p(V) and Fe ⊆ p(E), and a full rank translation group,
, is a bar-joint framework (G, p) for which there exist finite subsets, Fv ⊆ p(V) and Fe ⊆ p(E), and a full rank translation group,
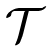 , such that:
, such that: . The elements of Fv are called motif vertices, and the elements of Fe are called motif edges. The translation group,
. The elements of Fv are called motif vertices, and the elements of Fe are called motif edges. The translation group,
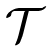 , is necessarily of the form:
, is necessarily of the form:
 is said to be
is said to be
- local if u(v, k) ≠ 0 for at least one and at most finitely many (v, k) ∈ Fv × ℤd;
- strictly periodic if u(v, k) = u(v, 0) for all (v, k) ∈ Fv × ℤd;
- supercell periodic if u(v, k) = u(v, 0) for each motif vertex v ∈ Fv and for all k in a full rank subgroup of ℤd of the form m1ℤ × ⋯ × mdℤ.
2.1. The Symbol Function and Rigidity Matrix
 (z), of a crystal framework and the rigidity matrix, R(
(z), of a crystal framework and the rigidity matrix, R(
 ), from which it is derived. The d-dimensional torus is
), from which it is derived. The d-dimensional torus is
 d = {(z1, …, zd) ∈ ℂd : |z1| = ⋯ = |zd| = 1}. For k ∈ Zd, the associated monomial function, f :
d = {(z1, …, zd) ∈ ℂd : |z1| = ⋯ = |zd| = 1}. For k ∈ Zd, the associated monomial function, f :
 d → ℂ, given by
, is written simply as zk.
d → ℂ, given by
, is written simply as zk.Definition 2
 be a crystal framework in ℝd with motif (Fv, Fe), and for e = (v, k)(w, l) ∈ Fe, let p(e) = p(v, k) − p(w, l). Then, Φ
be a crystal framework in ℝd with motif (Fv, Fe), and for e = (v, k)(w, l) ∈ Fe, let p(e) = p(v, k) − p(w, l). Then, Φ  (z) is a matrix-valued function on
(z) is a matrix-valued function on  d, which assigns a finite |Fe| × d|Fv| matrix to each z ∈
d, which assigns a finite |Fe| × d|Fv| matrix to each z ∈
 d. The rows of Φ
d. The rows of Φ  (z) are labelled by the edges of Fe, and the columns are labelled by the vertex-coordinate pairs in Fv × {1,…, d}. The row for an edge e = (v, k)(w, l) with v ≠ w takes the form,
(z) are labelled by the edges of Fe, and the columns are labelled by the vertex-coordinate pairs in Fv × {1,…, d}. The row for an edge e = (v, k)(w, l) with v ≠ w takes the form,Definition 3
 be a crystal framework in ℝd with motif (Fv, Fe), and for e = vw ∈ Fe, let p(e) = p(v) − p(w). Then, R(
be a crystal framework in ℝd with motif (Fv, Fe), and for e = vw ∈ Fe, let p(e) = p(v) − p(w). Then, R(
 ) is the infinite matrix, whose rows are labelled by the edges, (e, k) in Fe × ℤd, and whose columns are labelled by the pairs, (v, k) in Fv × ℤd. The row for an edge (e, k) = (v, l + k)(w, m + k), with e = (v, l)(w, m) ∈ Fe, takes the form:
) is the infinite matrix, whose rows are labelled by the edges, (e, k) in Fe × ℤd, and whose columns are labelled by the pairs, (v, k) in Fv × ℤd. The row for an edge (e, k) = (v, l + k)(w, m + k), with e = (v, l)(w, m) ∈ Fe, takes the form: if and only if R(
if and only if R(
 ) u = 0.
) u = 0.2.2. The RUM Spectrum
 d. A velocity vector u : Fv × ℤd → ℂd is said to be ω-phase-periodic if u(v, k) = ωku(v, 0) for all (v, k) ∈ Fv × ℤd. Here, ωk is the product
. We also write u = b ⊗ eω for this vector, where b is the vector (u(v, 0))v in ℂd|Fv| and eω is the multi-sequence (ωk)k∈ℤd. We refer to ω as a multi-phase for u. The velocity vector u is said to be phase-periodic if it is ω-phase-periodic for some multi-phase ω ∈
d. A velocity vector u : Fv × ℤd → ℂd is said to be ω-phase-periodic if u(v, k) = ωku(v, 0) for all (v, k) ∈ Fv × ℤd. Here, ωk is the product
. We also write u = b ⊗ eω for this vector, where b is the vector (u(v, 0))v in ℂd|Fv| and eω is the multi-sequence (ωk)k∈ℤd. We refer to ω as a multi-phase for u. The velocity vector u is said to be phase-periodic if it is ω-phase-periodic for some multi-phase ω ∈
 d.
d.Theorem 1
 be a crystal framework in ℝd; let ω ∈
be a crystal framework in ℝd; let ω ∈
 d and let u = b ⊗ eω, with b ∈ Fv × ℂd, be a ω-phase-periodic velocity vector. Then, the following conditions are equivalent:
d and let u = b ⊗ eω, with b ∈ Fv × ℂd, be a ω-phase-periodic velocity vector. Then, the following conditions are equivalent:- (i)
- R(
)u = 0;
- (ii)
- Φ
(ω̅)b = 0.
 ), of
), of
 is defined to be the set of multi-phases, ω, for which there exists a nonzero phase-periodic infinitesimal flex for
is defined to be the set of multi-phases, ω, for which there exists a nonzero phase-periodic infinitesimal flex for
 as an infinite-bar-joint framework, or, equivalently, as the set of multi-phases for which the rank of the matrix, Φ
as an infinite-bar-joint framework, or, equivalently, as the set of multi-phases for which the rank of the matrix, Φ  (ω̅), is less than d|Fv|.
(ω̅), is less than d|Fv|. are, by definition, precisely the phase-periodic velocity vectors, which have multi-phase 1̂ = (1,…, 1) ∈
are, by definition, precisely the phase-periodic velocity vectors, which have multi-phase 1̂ = (1,…, 1) ∈
 d. Evidently, the RUM spectrum must always contain the point, 1̂ ∈
d. Evidently, the RUM spectrum must always contain the point, 1̂ ∈
 d, as every constant velocity vector, u, is a phase-periodic infinitesimal flex with multi-phase 1̂. Thus, the RUM spectrum of
d, as every constant velocity vector, u, is a phase-periodic infinitesimal flex with multi-phase 1̂. Thus, the RUM spectrum of
 is a singleton (i.e., it contains only the single point, 1̂ if and only if every phase-periodic infinitesimal flex for
is a singleton (i.e., it contains only the single point, 1̂ if and only if every phase-periodic infinitesimal flex for
 is strictly periodic.
is strictly periodic.Corollary 1
 be a crystal framework in ℝd with translation group
be a crystal framework in ℝd with translation group 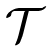 . Then, the following statements are equivalent:
. Then, the following statements are equivalent:- (i)
- The
-periodic real infinitesimal flexes of
are trivial;
- (ii)
- The
-periodic complex infinitesimal flexes of
are trivial;
- (iii)
- The periodic rigidity matrix Φ
(1,…, 1) has rank equal to d|Fv| − d.
3. Almost Periodic Rigidity
3.1. Almost Periodic Sequences
 . Partial counterparts of the Fejér kernel functions, Kn (x), are given by the Fejér sequences:
. Partial counterparts of the Fejér kernel functions, Kn (x), are given by the Fejér sequences:
Theorem 2
 d, is the pure frequency sequence eω1 ⊗ ⋯ ⊗ eωd in AP(ℤd, ℂ) with:
d, is the pure frequency sequence eω1 ⊗ ⋯ ⊗ eωd in AP(ℤd, ℂ) with:
 d, which we freely identify with a countable subset of points, λ, in [0, 2π)d. For notational convenience, we state the general theorem only in the case d = 2.
d, which we freely identify with a countable subset of points, λ, in [0, 2π)d. For notational convenience, we state the general theorem only in the case d = 2.Theorem 3
3.2. Almost Periodic Rigidity
 , with full rank translation group
, with full rank translation group
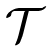 , various linear transformations may be associated with the rigidity matrix, R(
, various linear transformations may be associated with the rigidity matrix, R(
 ). These transformations are restrictions of the induced linear transformation:
). These transformations are restrictions of the induced linear transformation:
 ) is the vector space of complex-valued functions on the set of edges.
) is the vector space of complex-valued functions on the set of edges. ) for the integral vector, l in ℤd, are denoted by
and
, respectively. Here, the right shift of a sequence, h(k, κ), by l is the sequence, h(k − l, κ). We note that:
) for the integral vector, l in ℤd, are denoted by
and
, respectively. Here, the right shift of a sequence, h(k, κ), by l is the sequence, h(k − l, κ). We note that:
Definition 4
- An integral vector, l in ℤd, is an ε-translation vector for h if.
- The velocity field, h, is Bohr almost periodic if for every ∊ > 0, the set of ∊-translation vectors, l, is relatively dense in ℝd.
Lemma 1
 , then each component sequence aω ⊗ eω is a nonzero ω-phase-periodic infinitesimal flex.
, then each component sequence aω ⊗ eω is a nonzero ω-phase-periodic infinitesimal flex.Proof
 d and N ∈ ℕ, let RV (ω, N) be the linear map on the normed space ℓ∞(ℤd × Fv, ℂd) given in terms of the right shift operators,
, k ∈ ℤd, by:
d and N ∈ ℕ, let RV (ω, N) be the linear map on the normed space ℓ∞(ℤd × Fv, ℂd) given in terms of the right shift operators,
, k ∈ ℤd, by:
 ) is a bounded linear transformation from ℓ∞(ℤd × Fv, ℂd) to ℓ∞(ℤd × Fe, ℂ), which commutes with the right shift operators. Thus, if ω is a multi-frequency for g, then:
) is a bounded linear transformation from ℓ∞(ℤd × Fv, ℂd) to ℓ∞(ℤd × Fe, ℂ), which commutes with the right shift operators. Thus, if ω is a multi-frequency for g, then:
Lemma 2
 in AP(ℤd × Fv, ℂd). Then, the mean convolution multi-sequence g : ℤd × Fv → ℂd given by g(k, vκ) = [h, Rk(K)]ℤd is an infinitesimal flex for
in AP(ℤd × Fv, ℂd). Then, the mean convolution multi-sequence g : ℤd × Fv → ℂd given by g(k, vκ) = [h, Rk(K)]ℤd is an infinitesimal flex for  .
.Proof
 )gN = 0 for each N and, hence, that R(
)gN = 0 for each N and, hence, that R(
 )g = 0.
)g = 0.Theorem 4
 be a crystallographic bar-joint framework in ℝd. The following statements are equivalent:
be a crystallographic bar-joint framework in ℝd. The following statements are equivalent:- (i)
- Every almost periodic infinitesimal flex of
is trivial;
- (ii)
- Every strictly periodic infinitesimal flex of
is trivial, and Ω(
) = {1̂}.
Proof
 , and so, by Lemma 1, each gn is a finite linear combination of phase-periodic infinitesimal flexes of
, and so, by Lemma 1, each gn is a finite linear combination of phase-periodic infinitesimal flexes of
 . By hypothesis, the RUM spectrum, Ω(
. By hypothesis, the RUM spectrum, Ω(
 ), contains the single multi-phase, 1̂, and so, every phase-periodic infinitesimal flex is strictly periodic. In particular, gn is strictly periodic. It follows that u is strictly periodic and, hence, trivial, as desired.
), contains the single multi-phase, 1̂, and so, every phase-periodic infinitesimal flex is strictly periodic. In particular, gn is strictly periodic. It follows that u is strictly periodic and, hence, trivial, as desired.Proposition 5
 be a crystallographic bar-joint framework in ℝd. Then, the space of supercell periodic infinitesimal flexes for m-fold periodicity with m = (m1,…, md) is equal to the linear span of:
be a crystallographic bar-joint framework in ℝd. Then, the space of supercell periodic infinitesimal flexes for m-fold periodicity with m = (m1,…, md) is equal to the linear span of: ) is the finite subset of the RUM spectrum given by the multi-phases ω, whose k-th component is an mk–th root of unity.
) is the finite subset of the RUM spectrum given by the multi-phases ω, whose k-th component is an mk–th root of unity. is an almost periodic infinitesimal flex for
is an almost periodic infinitesimal flex for  .
. , is the finite or countable set given by:
, is the finite or countable set given by:
 ) is contained in the RUM spectrum of
) is contained in the RUM spectrum of
 . Furthermore, since phase-periodic flexes are almost periodic, it follows that the RUM spectrum as a subset of [0, 1)d is the union of the Bohr spectra of all almost periodic infinitesimal flexes. Note that the spectra here depend on the translation group in the following manner. If
. Furthermore, since phase-periodic flexes are almost periodic, it follows that the RUM spectrum as a subset of [0, 1)d is the union of the Bohr spectra of all almost periodic infinitesimal flexes. Note that the spectra here depend on the translation group in the following manner. If
 ′ has the same underlying bar-joint framework as
′ has the same underlying bar-joint framework as
 , but full rank translation group
, but full rank translation group
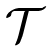 ′ ⊆
′ ⊆
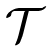 , then the infinitesimal flex, u, is represented anew as a sequence in
, where
is a vertex motif for
, then the infinitesimal flex, u, is represented anew as a sequence in
, where
is a vertex motif for
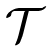 ′. The Bohr spectrum, Λ(u,
′. The Bohr spectrum, Λ(u,
 ), is then the image of Λ(u,
), is then the image of Λ(u,
 ) under the surjective map,
) under the surjective map,
 d →
d →
 d, induced by the inclusion,
d, induced by the inclusion,
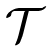 ′ ⊆
′ ⊆
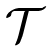 . This follows the same relationship as that for the RUM spectrum noted in [8]. It also follows from this that the dimension of Ω(
. This follows the same relationship as that for the RUM spectrum noted in [8]. It also follows from this that the dimension of Ω(
 ), as a topological space or as an algebraic variety, is independent of the translation group, and we refer to this integer, which takes values between zero and d, as the RUM dimension of
), as a topological space or as an algebraic variety, is independent of the translation group, and we refer to this integer, which takes values between zero and d, as the RUM dimension of
 .
. ), as a subset of [0, 1)d, often decomposes as a union of linear components. This is the case, for example, in two dimensions if Φ
), as a subset of [0, 1)d, often decomposes as a union of linear components. This is the case, for example, in two dimensions if Φ  (z) is a square matrix function, whose determinant polynomial, det Φ
(z) is a square matrix function, whose determinant polynomial, det Φ  (z), either vanishes identically or factorises into simple factors of the form (zn − λwm) with |λ| = 1. It follows that each almost periodic flex, u, of
(z), either vanishes identically or factorises into simple factors of the form (zn − λwm) with |λ| = 1. It follows that each almost periodic flex, u, of
 admits a finite sum decomposition u1 + ⋯ + ur in which each component, ui, is an almost periodic flex, whose Bohr spectrum lies in the i-th linear component. Such component flexes are partially periodic, being periodic in certain directions of translational symmetry.
admits a finite sum decomposition u1 + ⋯ + ur in which each component, ui, is an almost periodic flex, whose Bohr spectrum lies in the i-th linear component. Such component flexes are partially periodic, being periodic in certain directions of translational symmetry.4. Gallery of Crystal Frameworks
 d.
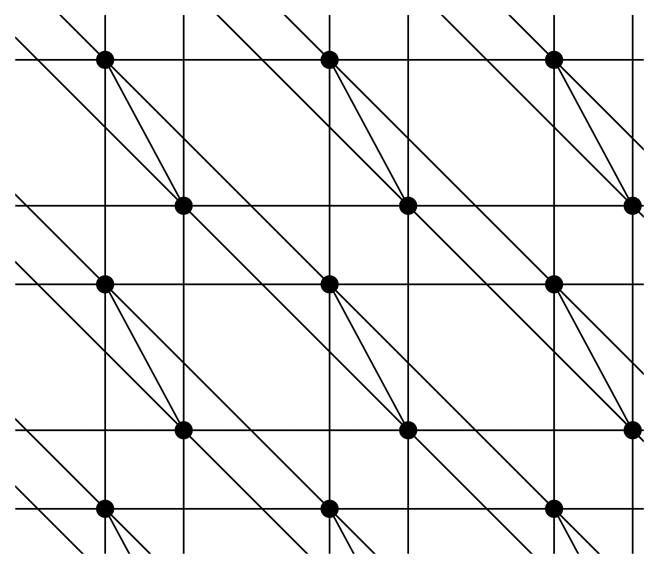
d.Example 1
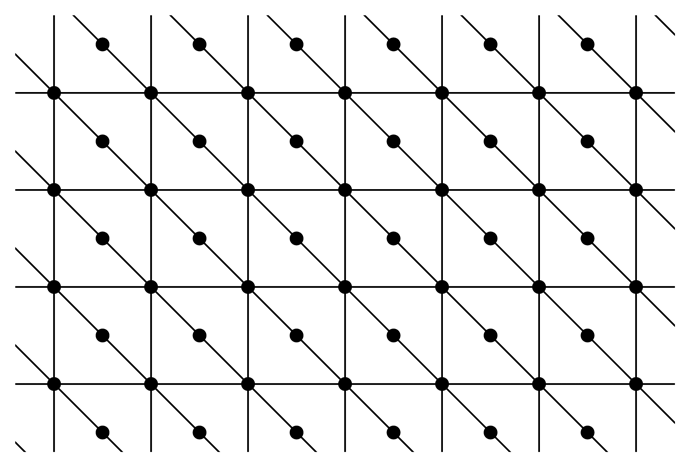
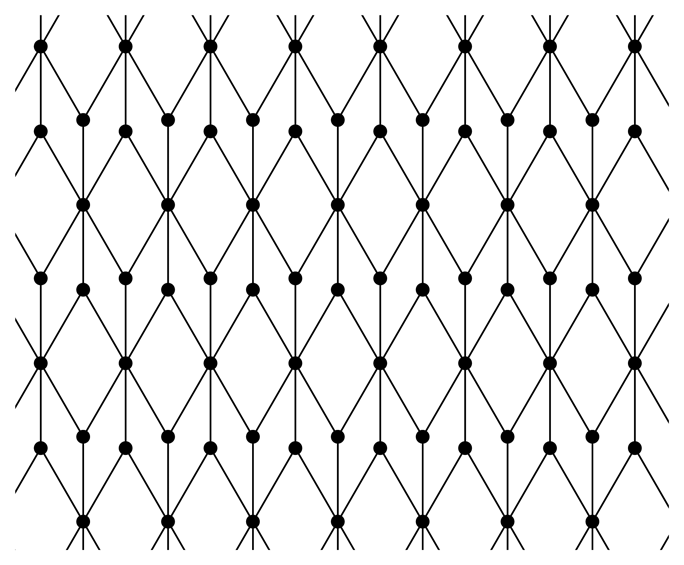
 = (G, p) be the crystallographic bar-joint framework with motif (Fv, Fe) and translation group
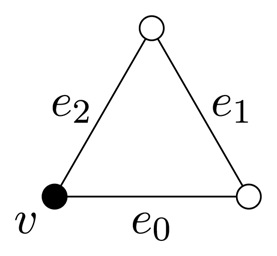
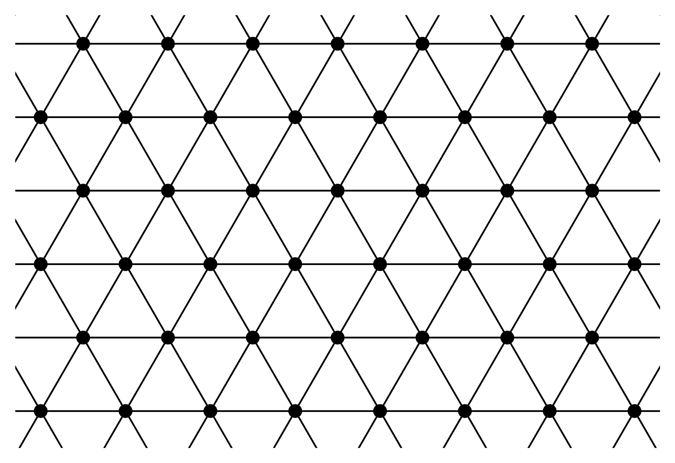
= (G, p) be the crystallographic bar-joint framework with motif (Fv, Fe) and translation group 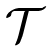 indicated in Table 1. Simplifying earlier notation, the motif vertex is labelled v and the motif edges are labelled e0 = v(0, 0)v(1, 0), e1 = v(1, 0)v(0, 1) and e2 = v(0, 0)v(0, 1). The translation group is
indicated in Table 1. Simplifying earlier notation, the motif vertex is labelled v and the motif edges are labelled e0 = v(0, 0)v(1, 0), e1 = v(1, 0)v(0, 1) and e2 = v(0, 0)v(0, 1). The translation group is  = {k1a1 + k2a2 : k1,k2 ∈ ℤ}, where a1 = (1, 0) and. The symbol function for
= {k1a1 + k2a2 : k1,k2 ∈ ℤ}, where a1 = (1, 0) and. The symbol function for  is,
is,
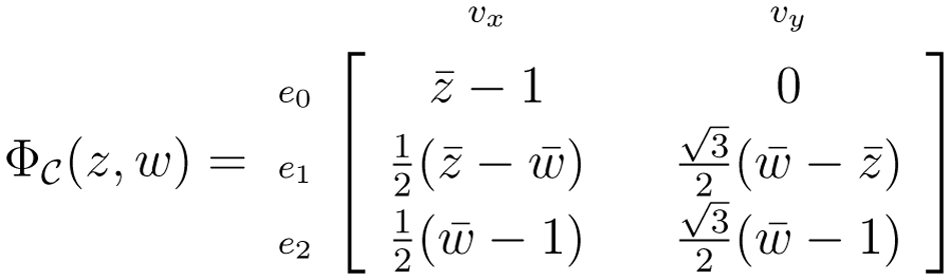
 (z, w) has rank two unless z = w = 1, and so, the RUM spectrum of
(z, w) has rank two unless z = w = 1, and so, the RUM spectrum of  is the singleton, (1, 1) ∈
is the singleton, (1, 1) ∈
 2. Furthermore, there are no non-trivial strictly periodic infinitesimal flexes of
2. Furthermore, there are no non-trivial strictly periodic infinitesimal flexes of  , and so, by Theorem 4,
, and so, by Theorem 4,  is almost periodically infinitesimally rigid.
is almost periodically infinitesimally rigid. is sequentially infinitesimally rigid in the sense that there exists an increasing chain of finite subgraphs G1 ⊂ G2 ⊂ ⋯ of G, such that every vertex of G is contained in some Gn and each sub-framework (Gn, p) is infinitesimally rigid. For example, for each n, take Gn to be the vertex-induced subgraph on {v(k1, k2) : (k1, k2) ∈ ℤ2, |ki| ≤ n}. It follows that
is sequentially infinitesimally rigid in the sense that there exists an increasing chain of finite subgraphs G1 ⊂ G2 ⊂ ⋯ of G, such that every vertex of G is contained in some Gn and each sub-framework (Gn, p) is infinitesimally rigid. For example, for each n, take Gn to be the vertex-induced subgraph on {v(k1, k2) : (k1, k2) ∈ ℤ2, |ki| ≤ n}. It follows that  admits no nontrivial infinitesimal flexes and, so, is (absolutely) infinitesimally rigid as a bar-joint framework. In [22], we obtain a general characterisation of countable simple graphs, G, whose locally generic placements are infinitesimally rigid in this sense. The condition is that G should contain a vertex-complete chain of (2, 3)-tight subgraphs. The crystal framework,
admits no nontrivial infinitesimal flexes and, so, is (absolutely) infinitesimally rigid as a bar-joint framework. In [22], we obtain a general characterisation of countable simple graphs, G, whose locally generic placements are infinitesimally rigid in this sense. The condition is that G should contain a vertex-complete chain of (2, 3)-tight subgraphs. The crystal framework,  , may be viewed as a non-generic placement of such a graph, which remains infinitesimally rigid despite the crystallographic symmetry.
, may be viewed as a non-generic placement of such a graph, which remains infinitesimally rigid despite the crystallographic symmetry.Example 2
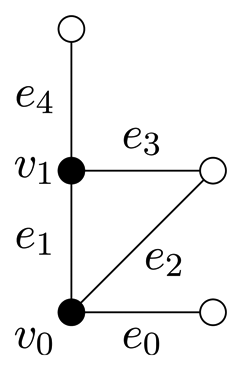
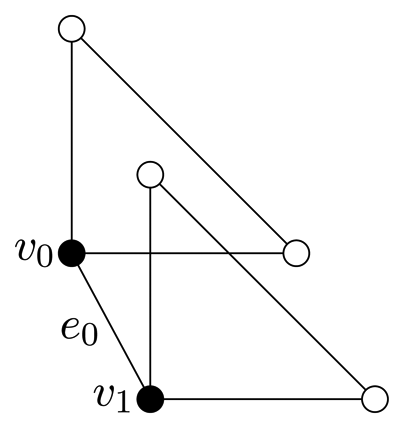
 , with the motif and translation group shown in Table 2. The motif vertices are v0 = (0, 0) and. The motif edges are e0 = v0(0, 0)v0(1, 0), e1 = v0(0, 0)v0(0, 1), e2 = v0(0, 1)v1(0, 0) and e3 = v0(1, 0)v1(0, 0). Note that the symbol function, Φ
, with the motif and translation group shown in Table 2. The motif vertices are v0 = (0, 0) and. The motif edges are e0 = v0(0, 0)v0(1, 0), e1 = v0(0, 0)v0(0, 1), e2 = v0(0, 1)v1(0, 0) and e3 = v0(1, 0)v1(0, 0). Note that the symbol function, Φ  (z,w), is a square matrix,
(z,w), is a square matrix,
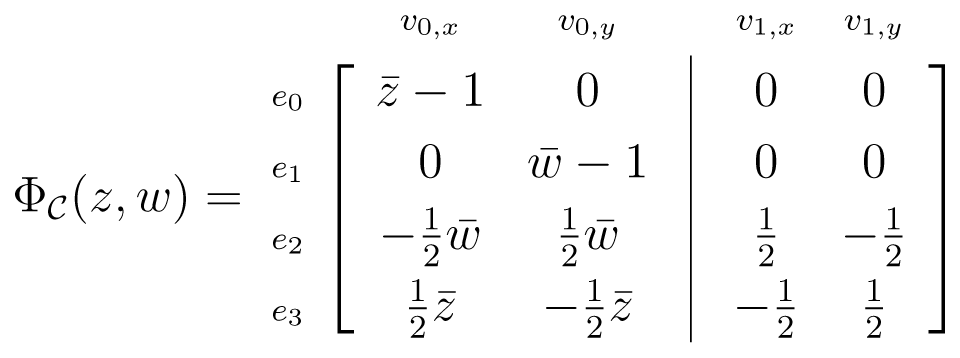
 (z, w) vanishes identically, and so, the RUM spectrum of
(z, w) vanishes identically, and so, the RUM spectrum of  is
is  2. A local infinitesimal flex of
2. A local infinitesimal flex of
 is evident by defining u(v1) = (1, 1) and uv = 0 for all v ≠ v1. A phase-periodic infinitesimal flex of
is evident by defining u(v1) = (1, 1) and uv = 0 for all v ≠ v1. A phase-periodic infinitesimal flex of
 for ω = (ω1, ω2) is obtained by taking u(v0, k) = 0 and for each k = (k1, k2) ∈ ℤ2. In particular, any finite linear combination of such phase-periodic flexes will be an almost periodic infinitesimal flex for
for ω = (ω1, ω2) is obtained by taking u(v0, k) = 0 and for each k = (k1, k2) ∈ ℤ2. In particular, any finite linear combination of such phase-periodic flexes will be an almost periodic infinitesimal flex for  .
. , if u(vκ, 0) = u(vκ, k) for each motif vertex, vκ, and all k in a full rank subgroup of ℤd.
, if u(vκ, 0) = u(vκ, k) for each motif vertex, vκ, and all k in a full rank subgroup of ℤd.Example 3
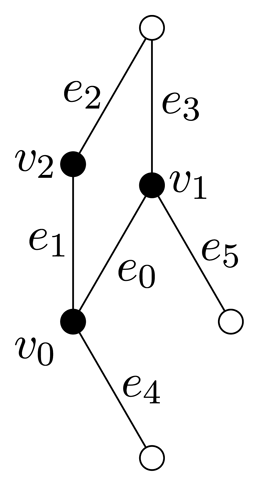
 be the crystallographic bar-joint framework with motif (Fv, Fe) and translation group
be the crystallographic bar-joint framework with motif (Fv, Fe) and translation group
 indicated in Table 3. Note that
indicated in Table 3. Note that
 has symbol function,
has symbol function,
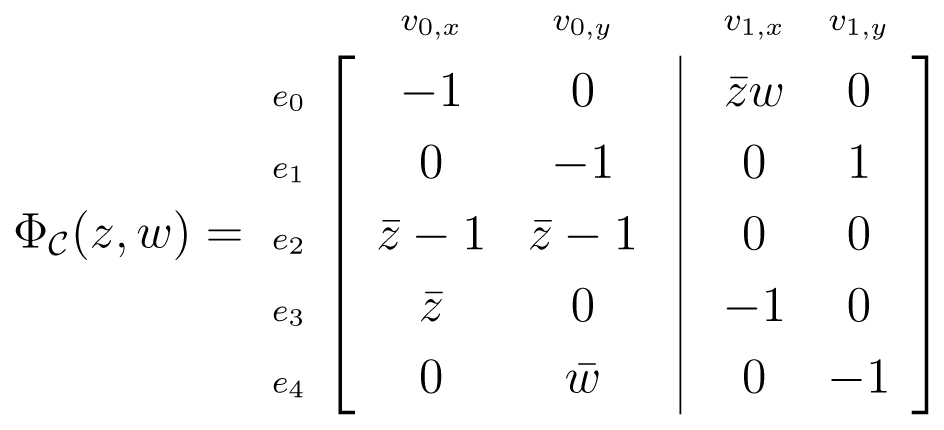
 is Ω(
is Ω(
 ) = {(1, 1), (−1, 1)}. Note that
) = {(1, 1), (−1, 1)}. Note that
 does not admit any non-trivial infinitesimal flexes, which are strictly periodic with respect to
does not admit any non-trivial infinitesimal flexes, which are strictly periodic with respect to
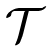 . However,
. However,
 does admit non-trivial supercell periodic infinitesimal flexes, which may be constructed from the motif and RUM spectrum Assign velocity vectors u(v0, 0) and u(v1, 0) to the motif vertices and consider the multi-phase ω = (ω1, ω2) = (−1, 1) ∈ Ω(
does admit non-trivial supercell periodic infinitesimal flexes, which may be constructed from the motif and RUM spectrum Assign velocity vectors u(v0, 0) and u(v1, 0) to the motif vertices and consider the multi-phase ω = (ω1, ω2) = (−1, 1) ∈ Ω(
 ). Define for each k = (k1, k2) ∈ ℤ2,
). Define for each k = (k1, k2) ∈ ℤ2,
 . Note that u consists of alternating rotational motions. In the notation of Proposition 5, u has m-fold periodicity, where we have taken m = (2, 1); the multi-phase ω = (−1, 1) is contained in,
. Note that u consists of alternating rotational motions. In the notation of Proposition 5, u has m-fold periodicity, where we have taken m = (2, 1); the multi-phase ω = (−1, 1) is contained in,
 (ω̅).
(ω̅).Example 4
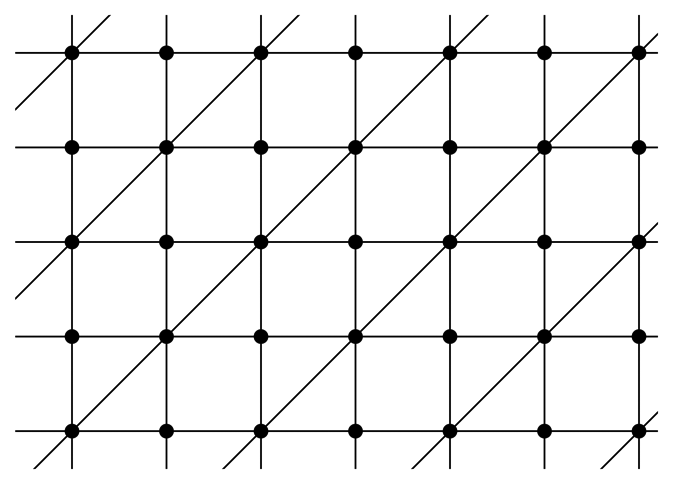
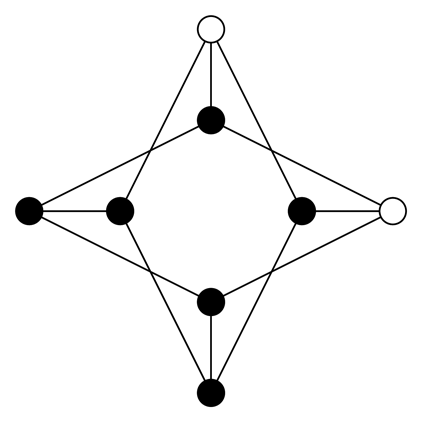
 be the crystallographic bar-joint framework in ℝ2, which is indicated in Table 4. The motif vertices are p(v0) = (0, 0) and. The symbol function, Φ
be the crystallographic bar-joint framework in ℝ2, which is indicated in Table 4. The motif vertices are p(v0) = (0, 0) and. The symbol function, Φ  (z, w) is,
(z, w) is,
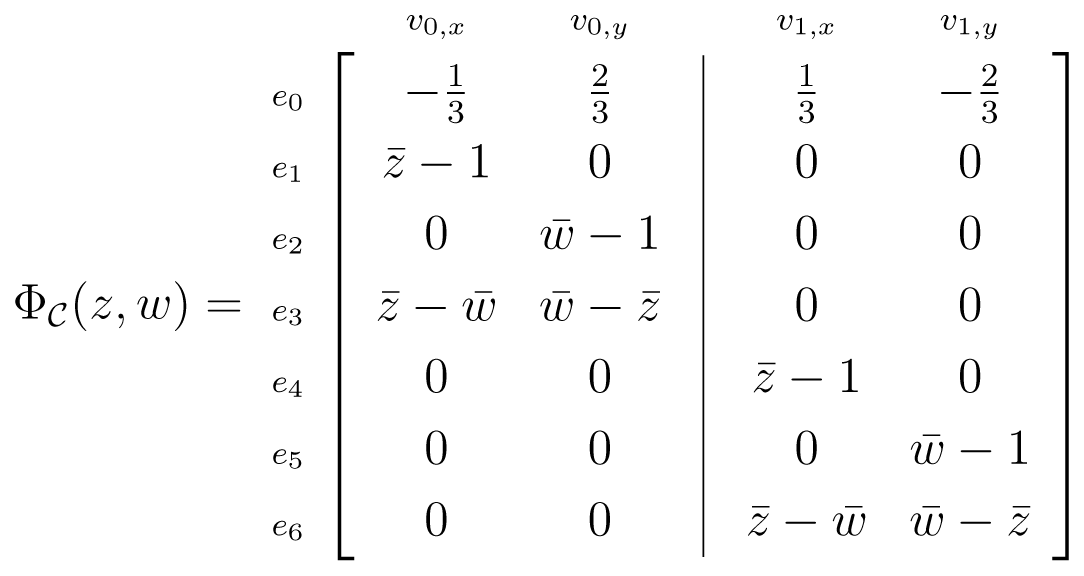
 ), is the singleton, (1, 1) ∈
), is the singleton, (1, 1) ∈
 2. However, every strictly periodic velocity field, u, with (p(v0)−p(v1))·(u(v0)−u(v1)) = 0 and u(v0) = u(v1) is a non-trivial strictly periodic infinitesimal flex of
2. However, every strictly periodic velocity field, u, with (p(v0)−p(v1))·(u(v0)−u(v1)) = 0 and u(v0) = u(v1) is a non-trivial strictly periodic infinitesimal flex of  .
. , is the dimension of the RUM spectrum, Ω(
, is the dimension of the RUM spectrum, Ω(
 ), as a real algebraic variety (see [8]).
), as a real algebraic variety (see [8]).Example 5
 , illustrated in Table 5 has motif vertices v0 = (0,0),
and v2 = (0, 1). The symbol function is a square matrix,
, illustrated in Table 5 has motif vertices v0 = (0,0),
and v2 = (0, 1). The symbol function is a square matrix,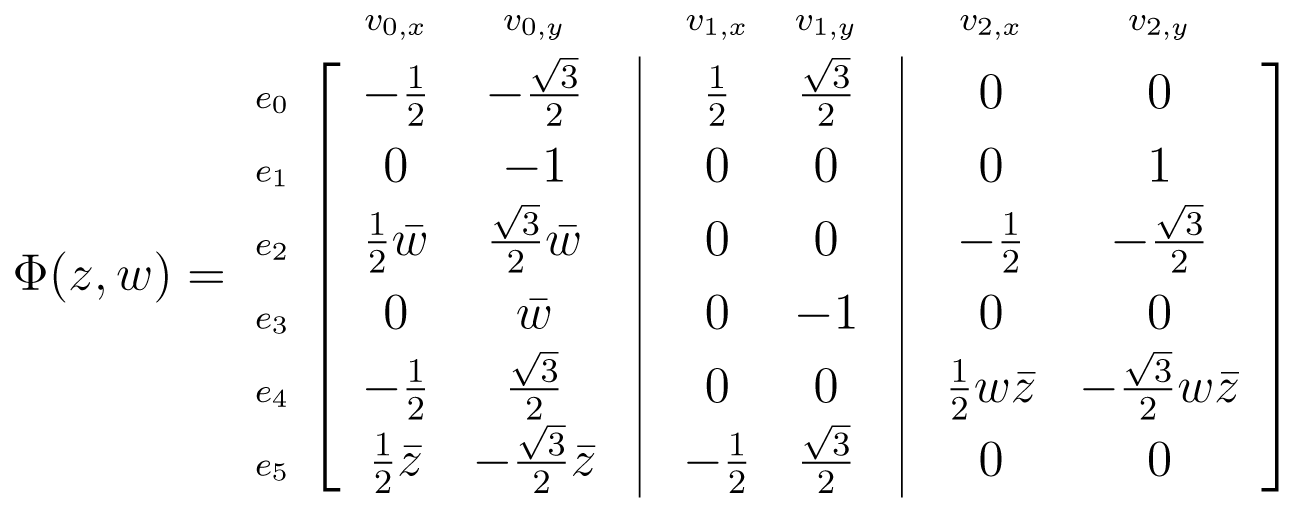
 2, whose representation in [0, 1)2 consists of the points (s,t) in the line segments given by:
2, whose representation in [0, 1)2 consists of the points (s,t) in the line segments given by: is almost periodically infinitesimally flexible, but has no local infinitesimal flexes. Furthermore, the RUM dimension of
is almost periodically infinitesimally flexible, but has no local infinitesimal flexes. Furthermore, the RUM dimension of
 is one. It follows that every almost periodic infinitesimal flex decomposes as a sum u1 + u2 + u3 of three almost periodic flexes corresponding to this ordered decomposition. Furthermore, u1, with the Bohr spectrum in the line s = 0, is periodic in the direction of the period vector a1 = (1, 0), while u2, with the Bohr spectrum in the line t = 0, is periodic in the direction of the period vector, and u3, with the Bohr spectrum, in the line s = t is periodic in the direction a1 − a2.
is one. It follows that every almost periodic infinitesimal flex decomposes as a sum u1 + u2 + u3 of three almost periodic flexes corresponding to this ordered decomposition. Furthermore, u1, with the Bohr spectrum in the line s = 0, is periodic in the direction of the period vector a1 = (1, 0), while u2, with the Bohr spectrum in the line t = 0, is periodic in the direction of the period vector, and u3, with the Bohr spectrum, in the line s = t is periodic in the direction a1 − a2.Example 6
 be the crystal framework illustrated in Table 6. The symbol function, Φ(z, w), is the square matrix,
be the crystal framework illustrated in Table 6. The symbol function, Φ(z, w), is the square matrix,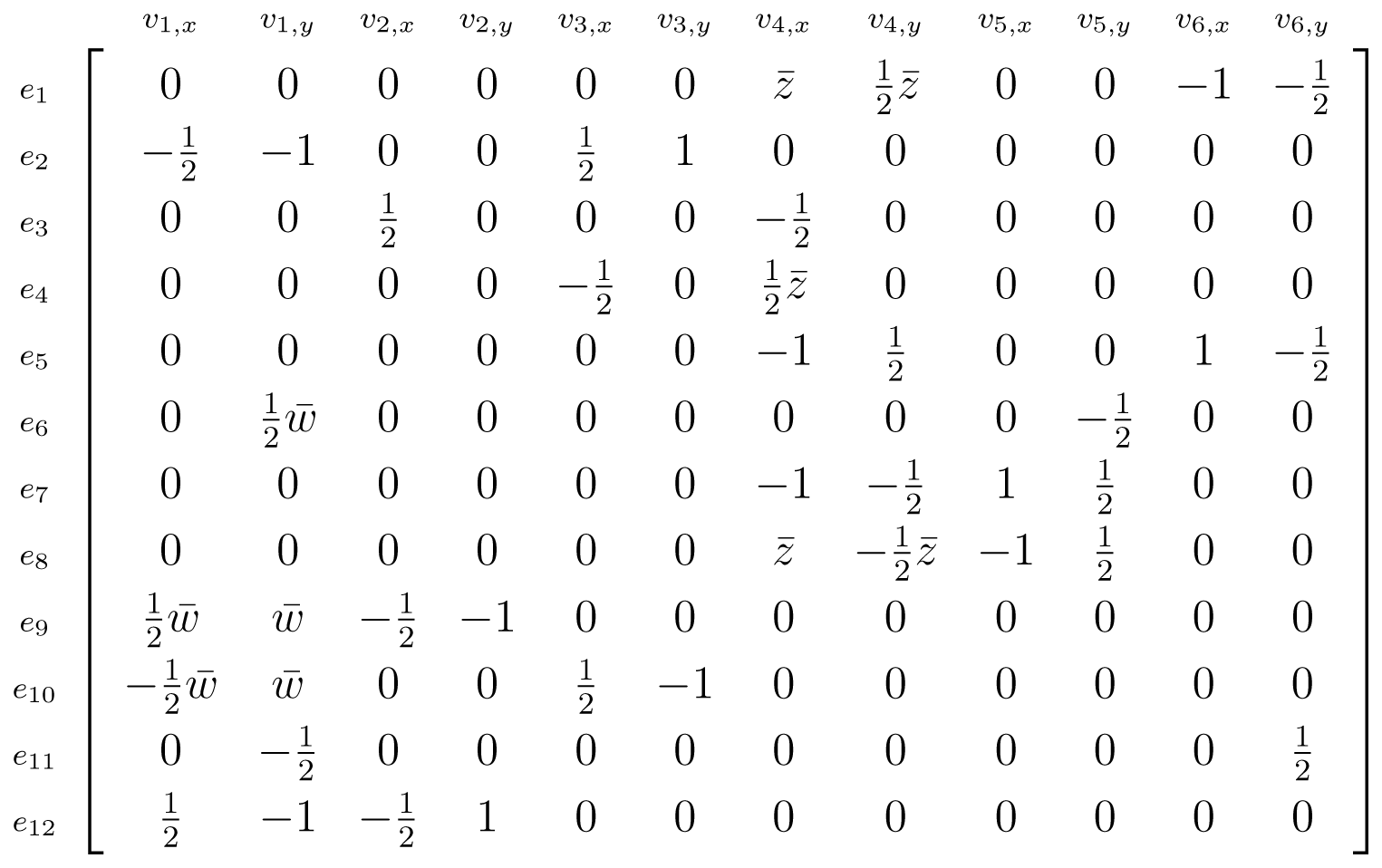
 2v. However, the former has RUM dimension one and is linearly indecomposable while the latter has RUM dimension zero. Note that four-regular crystal frameworks such as these have a square symbol function.
2v. However, the former has RUM dimension one and is linearly indecomposable while the latter has RUM dimension zero. Note that four-regular crystal frameworks such as these have a square symbol function.Example 7
 be the crystal framework with |Fe| = d|Fv| illustrated in Table 7. The symbol function, Φ
be the crystal framework with |Fe| = d|Fv| illustrated in Table 7. The symbol function, Φ  (z,w), is,
(z,w), is,Example 8
 be the crystal framework illustrated in Table 8. The framework motif satisfies |Fe| = d|Fv|, and so, the symbol function, Φ
be the crystal framework illustrated in Table 8. The framework motif satisfies |Fe| = d|Fv|, and so, the symbol function, Φ  (z,w), is a square matrix,
(z,w), is a square matrix,Example 9
 2 that satisfy ℜ(w) = aℜ(z) + (1 − a) for either or. This set is illustrated in Figure 1 as a subset of the torus [0, 1)2, which consists of four closed curves with the common intersection point (0,0).
2 that satisfy ℜ(w) = aℜ(z) + (1 − a) for either or. This set is illustrated in Figure 1 as a subset of the torus [0, 1)2, which consists of four closed curves with the common intersection point (0,0).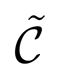 be the basic one-dimensional grid framework for the lattice, ℤ in ℝ. For any crystal framework,
be the basic one-dimensional grid framework for the lattice, ℤ in ℝ. For any crystal framework,
 in ℝd, one may construct a product framework
in ℝd, one may construct a product framework
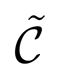 =
=
 ×
×
 ℤ in ℝd+1, whose intersection with the hyperplanes ℝd × {n} are copies of
ℤ in ℝd+1, whose intersection with the hyperplanes ℝd × {n} are copies of
 and where these copies are connected by the edges ((p(v), n), (p(v), n + 1)). In the case that
and where these copies are connected by the edges ((p(v), n), (p(v), n + 1)). In the case that
 has square matrix symbol function Φ
has square matrix symbol function Φ  (z1,…,zd), it is straightforward to verify that:
(z1,…,zd), it is straightforward to verify that:
 3 of such frameworks. Further, three-dimensional examples not of this product form may be found in Power [8] and Wegner [12].
3 of such frameworks. Further, three-dimensional examples not of this product form may be found in Power [8] and Wegner [12].Example 10
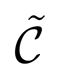 be the three-dimensional framework derived from the regular octagon framework of Example 9. Then the crystal polynomial admits a three-fold factorisation and it follows that the RUM spectrum has the topological structure of four two-dimensional tori connected over the common circle of points (1, 1, z) in
be the three-dimensional framework derived from the regular octagon framework of Example 9. Then the crystal polynomial admits a three-fold factorisation and it follows that the RUM spectrum has the topological structure of four two-dimensional tori connected over the common circle of points (1, 1, z) in  3.
3.Further Work
Acknowledgments
Conflicts of Interest
References
- Ross, E. The rigidity of periodic body-bar frameworks on the fixed torus. Phil. Trans. R. Soc. A 2014, 372. [Google Scholar] [CrossRef]
- Borcea, C.S.; Streinu, I. Periodic frameworks and flexibility. Proc. R. Soc. A 2010, 466, 2633–2649. [Google Scholar]
- Borcea, C.S.; Streinu, I. Frameworks with crystallographic symmetry. Phil. Trans. R. Soc. A 2014, 372. [Google Scholar] [CrossRef]
- Connelly, R.; Shen, J.D.; Smith, A.D. Ball packings with periodic constraints. Available online: http://arxiv.org/abs/1301.0664 (accessed on 18 April 2014).
- Malestein, J.; Theran, L. Generic combinatorial rigidity of periodic frameworks. Adv. Math. 2013, 233, 291–331. [Google Scholar]
- Owen, J.C.; Power, S.C. Infinite bar-joint frameworks, crystals and operator theory. N. Y. J. Math. 2011, 17, 445–490. [Google Scholar]
- Power, S.C. Crystal frameworks, symmetry and affinely periodic flexes. Available online: http://arxiv.org/pdf/1103.1914v3.pdf (accessed on 18 April 2014).
- Power, S.C. Polynomials for crystal frameworks and the rigid unit mode spectrum. Phil. Trans. R. Soc. A 2014, 372. [Google Scholar] [CrossRef]
- Ross, E.; Schulze, B.; Whiteley, W. Finite motions from periodic frameworks with added symmetry. Int. J. Solids Struct. 2011, 48, 1711–1729. [Google Scholar]
- Dove, M.T.; Pryde, A.K.A.; Heine, V.; Hammonds, K.D. Exotic distributions of rigid unit modes in the reciprocal spaces of framework aluminosilicates. J. Phys. Condens. Matter 2007, 19. [Google Scholar] [CrossRef]
- Giddy, A.P.; Dove, M.T.; Pawley, G.S.; Heine, V. The determination of rigid unit modes as potential soft modes for displacive phase transitions in framework crystal structures. Acta Crystallogr. 1993, A49, 697–703. [Google Scholar]
- Wegner, F. Rigid-unit modes in tetrahedral crystals. J. Phys. Condens. Matter 2007, 19, 406–218. [Google Scholar]
- Kapko, V.; Dawson, C.; Rivin, I.; Treacy, M.M.J. Density of Mechanisms within the Flexibility Window of Zeolites. Phys. Rev. Lett. 2011, 107. [Google Scholar] [CrossRef]
- Power, S.C. Crystal frameworks, matrix-valued functions and rigidity operators, Operator Theory: Advances and Applications. In Concrete Operators, Spectral Theory, Operators in Harmonic Analysis and Approximation: 22nd International Workshop in Operator Theory and Its Application; Springer: Birkhäuser Basel, Switzerland, 2014; Volume 236. [Google Scholar]
- Partington, J.R. Linear operators and linear systems. An analytical approach to control theory. In London Mathematical Society Student Texts, 60; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Besicovitch, A.S.; Bohr, H. Almost periodicity and general trigonometric series. Acta Math. 1931, 57, 203–292. [Google Scholar]
- Besicovitch, A.S. Almost Periodic Functions; Dover Publications, Inc.: New York, NY, USA, 1955. [Google Scholar]
- Bochner, S.; von Neumann, J. Almost periodic functions in groups. II. Trans. Amer. Math. Soc. 1935, 37, 21–50. [Google Scholar]
- Levitan, B.M.; Zhikov, V.V. Almost Periodic Functions and Differential Equations; Cambridge University Press: Cambridge, UK, 1982; Longdon, L. W., Translator. [Google Scholar]
- Loomis, L.H. An Introduction to Abstract Harmonic Analysis; D. Van Nostrand Company, Inc.: New York, NY, USA, 1953. [Google Scholar]
- Šubin, M.A. Almost periodic functions and partial differential operators. Russ. Math. Surv. 1978, 33. [Google Scholar] [CrossRef]
- Kitson, D.; Power, S.C. The rigidity of infinite graphs. Available online: http://arxiv.org/abs/1310.1860 (accessed on 18 April 2014).

| Motif | Translation group | Crystal framework |
|---|---|---|
 | 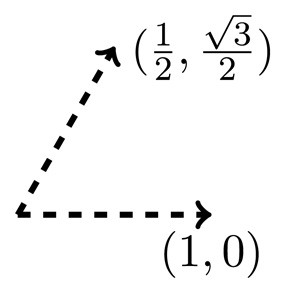 |  |
| Motif | Translation group | Crystal framework |
|---|---|---|
 |  |  |
| Motif | Translation group | Crystal framework |
|---|---|---|
 |  |  |
| Motif | Translation group | Crystal framework |
|---|---|---|
 |  |  |
| Motif | Translation group | Crystal framework |
|---|---|---|
 | 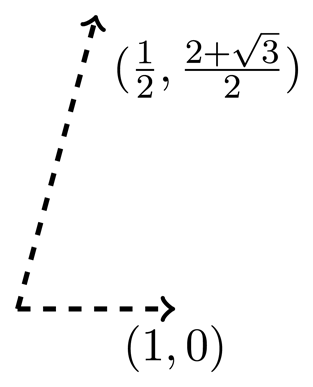 |  |
| Motif | Translation group | Crystal framework |
|---|---|---|
 |  | 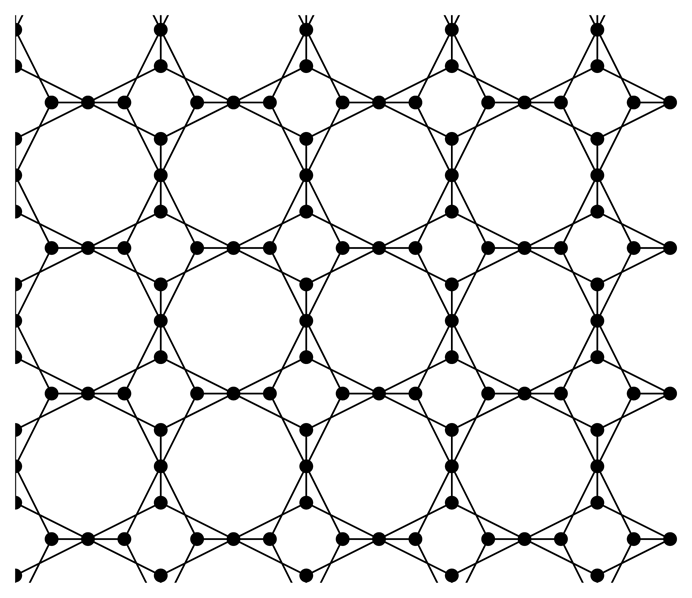 |
| Motif | Translation group | Crystal framework |
|---|---|---|
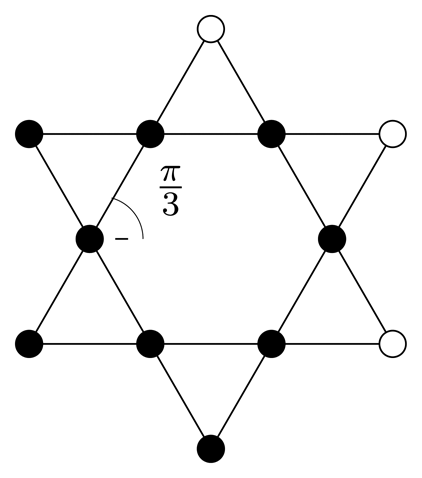 |  |  |
| Motif | Translation group | Crystal framework |
|---|---|---|
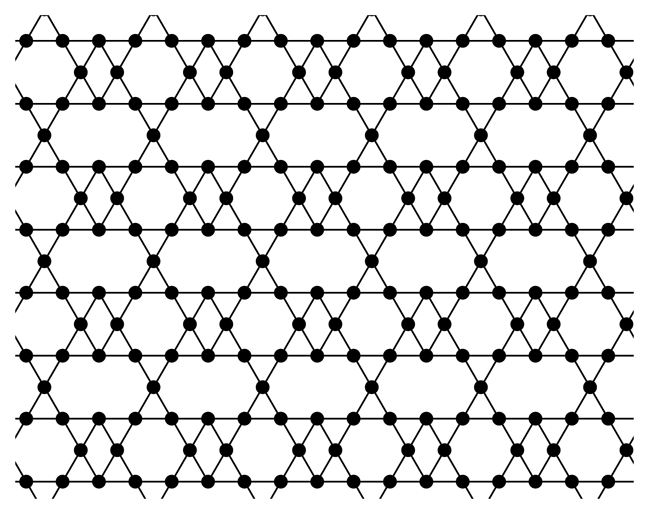
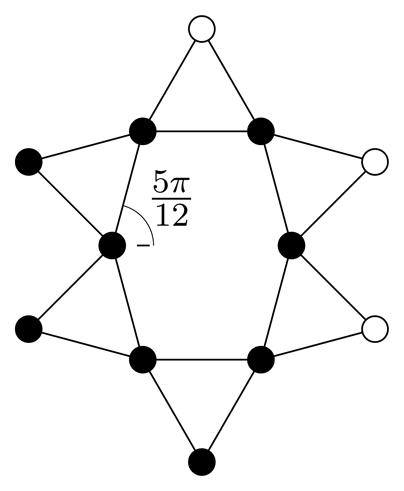 |  | 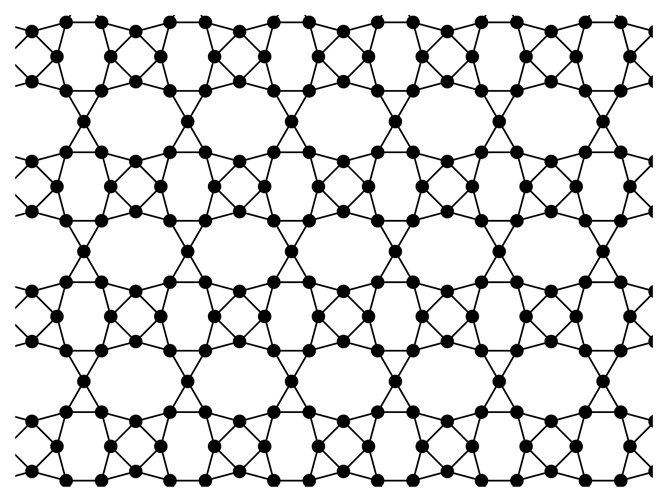 |
| Motif | Translation group | Crystal framework |
|---|---|---|
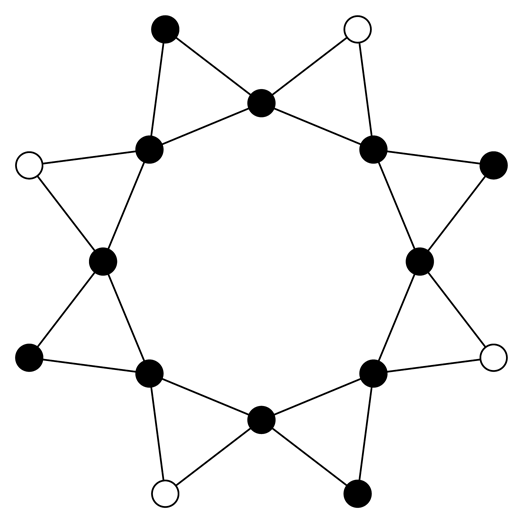 |  | 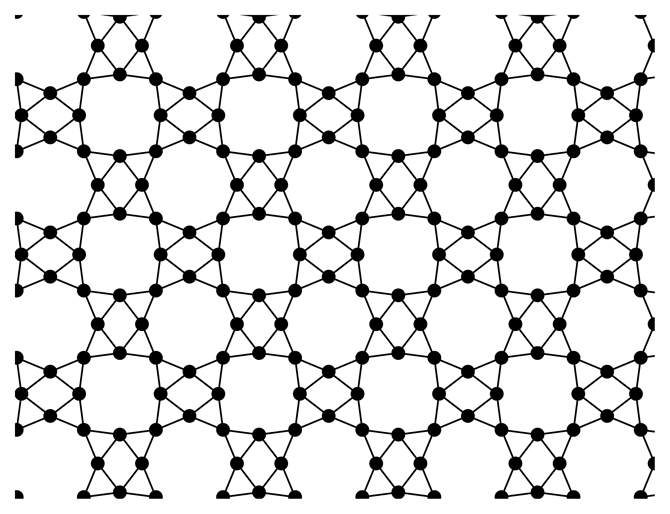 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Badri, G.; Kitson, D.; Power, S.C. The Almost Periodic Rigidity of Crystallographic Bar-Joint Frameworks. Symmetry 2014, 6, 308-328. https://doi.org/10.3390/sym6020308
Badri G, Kitson D, Power SC. The Almost Periodic Rigidity of Crystallographic Bar-Joint Frameworks. Symmetry. 2014; 6(2):308-328. https://doi.org/10.3390/sym6020308
Chicago/Turabian StyleBadri, Ghada, Derek Kitson, and Stephen C. Power. 2014. "The Almost Periodic Rigidity of Crystallographic Bar-Joint Frameworks" Symmetry 6, no. 2: 308-328. https://doi.org/10.3390/sym6020308




