Thermodynamic Response of Beams on Winkler Foundation Irradiated by Moving Laser Pulses
Abstract
:1. Introduction
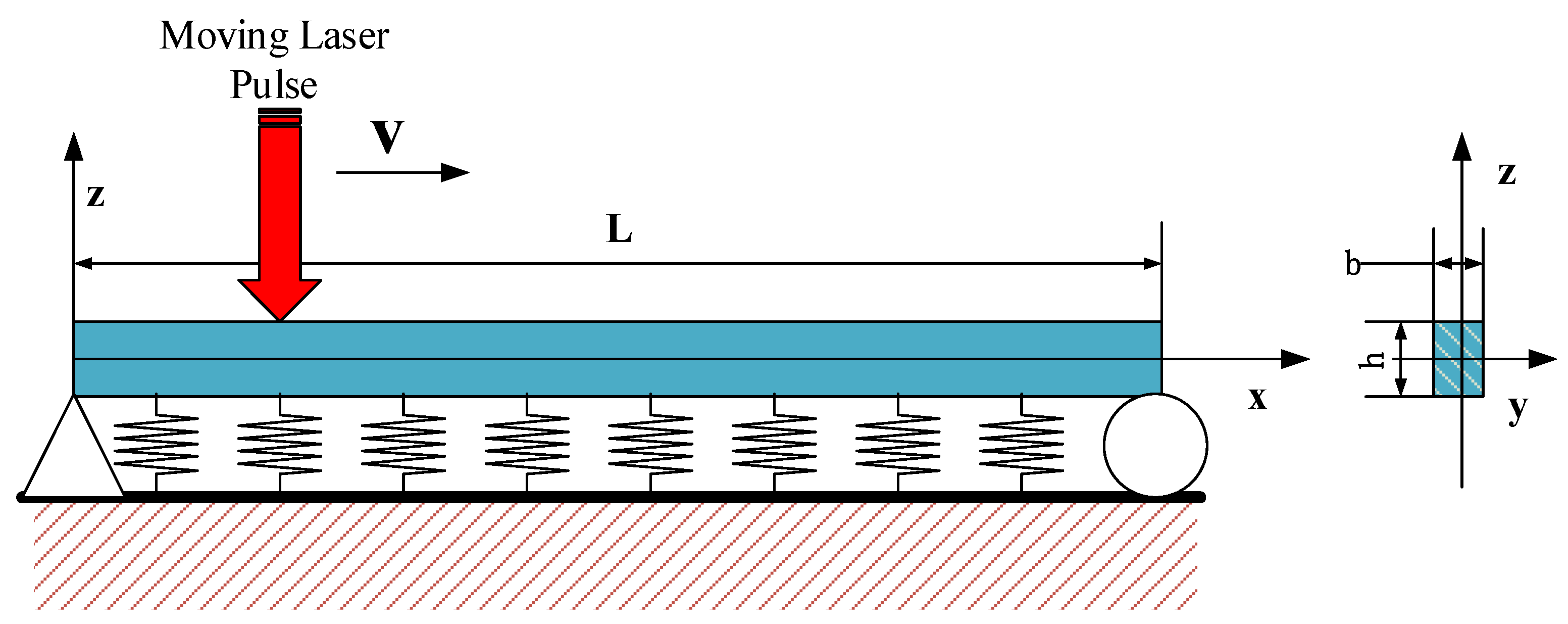
2. Basic Formulations of the Problem
3. Derivation of Temperature Rise
4. Solution of Vibration Equation
5. Results and Discussions
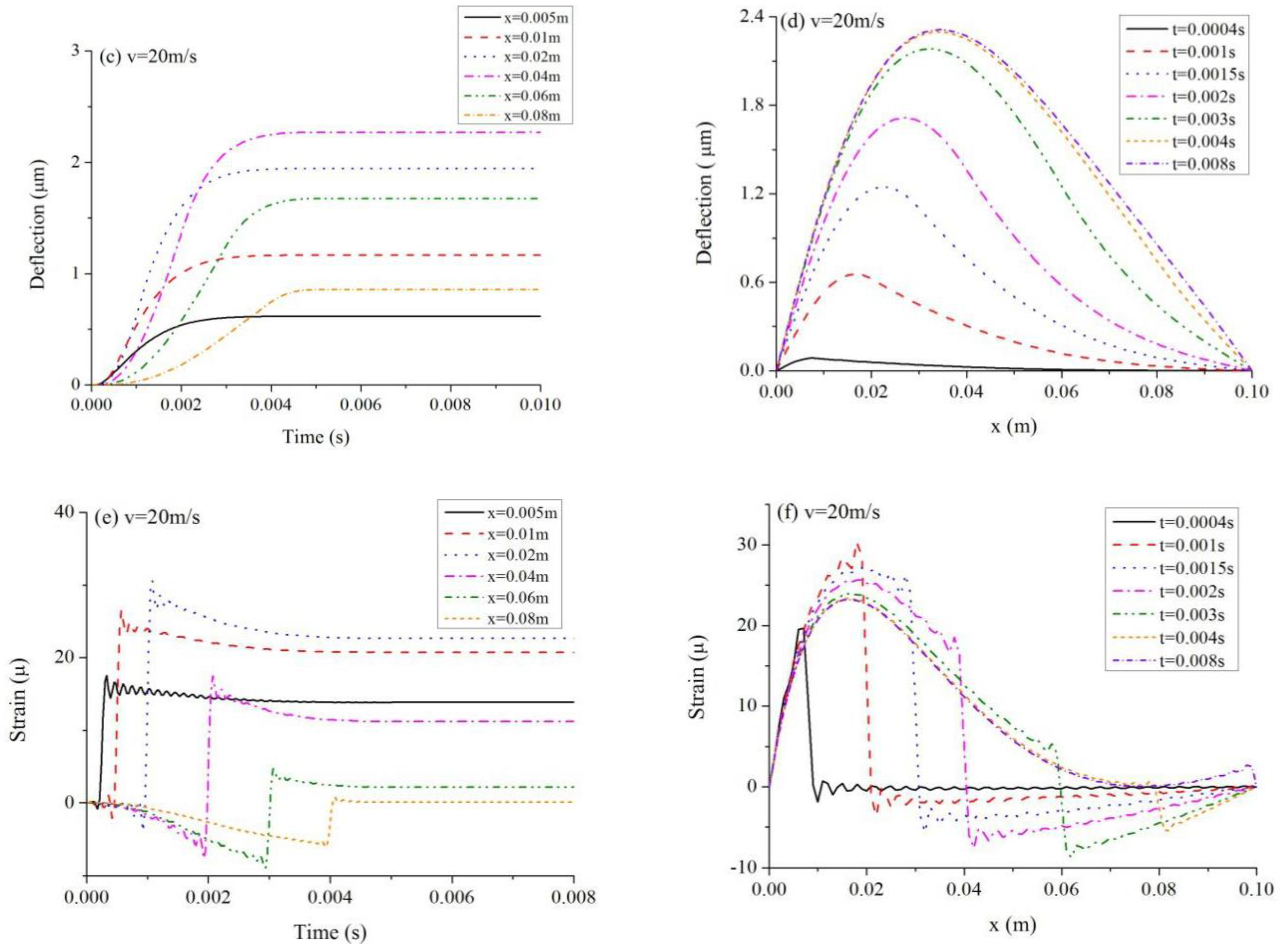
5.1. Example Results of Temperature, Deflection and Strain
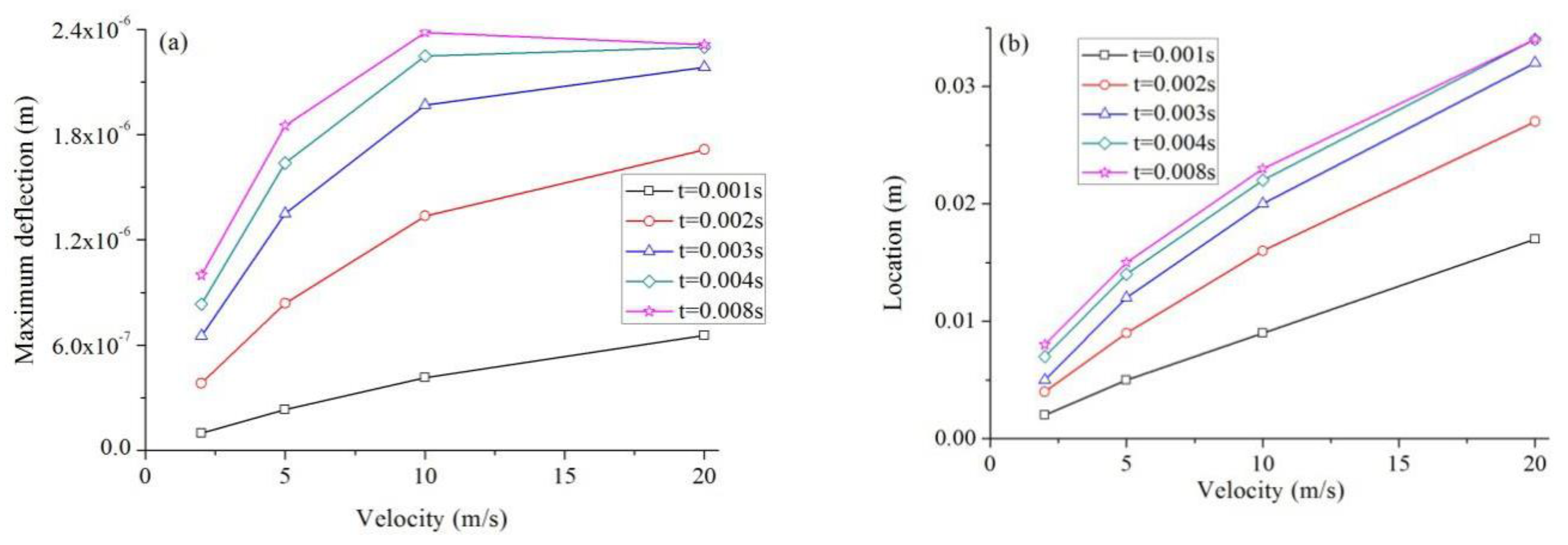
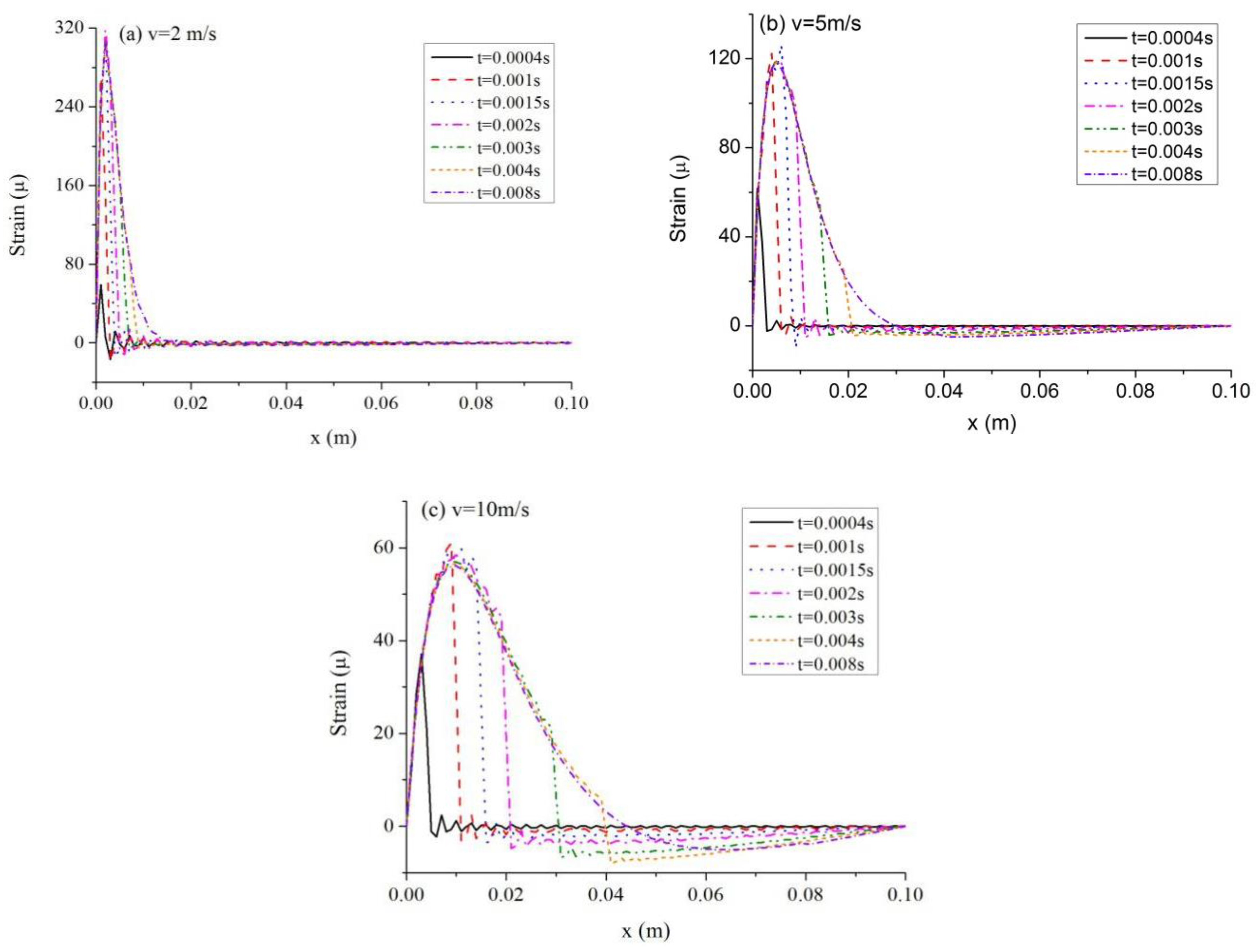
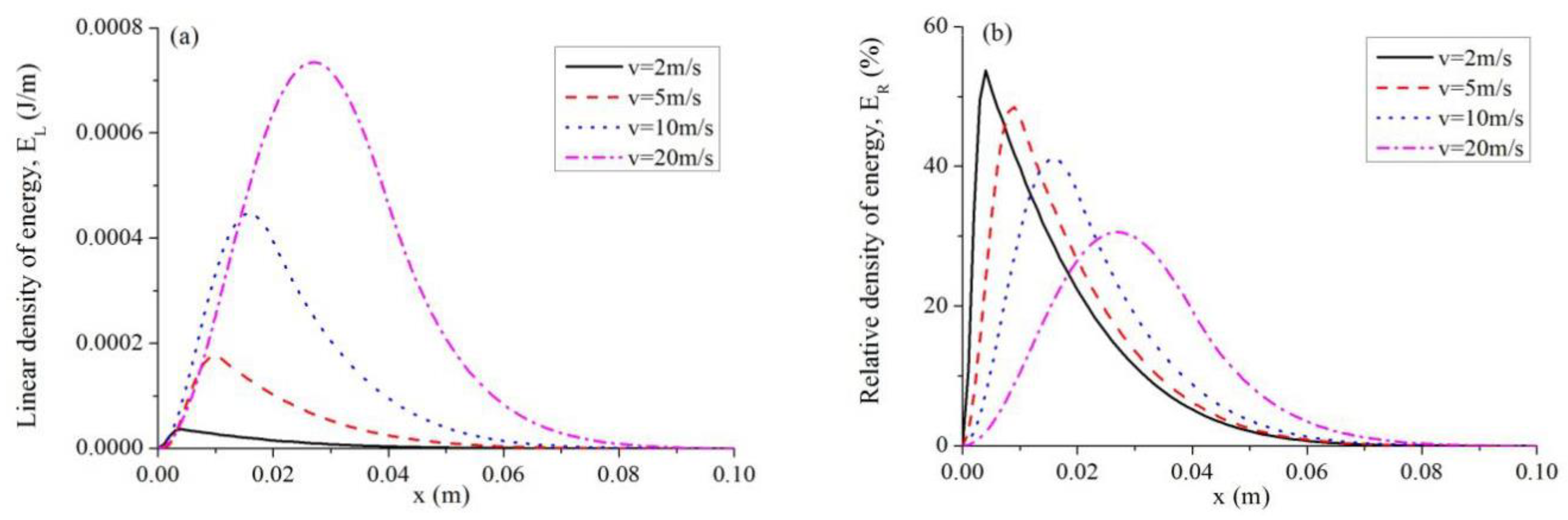
5.2. Influence of Laser Pulse Speed
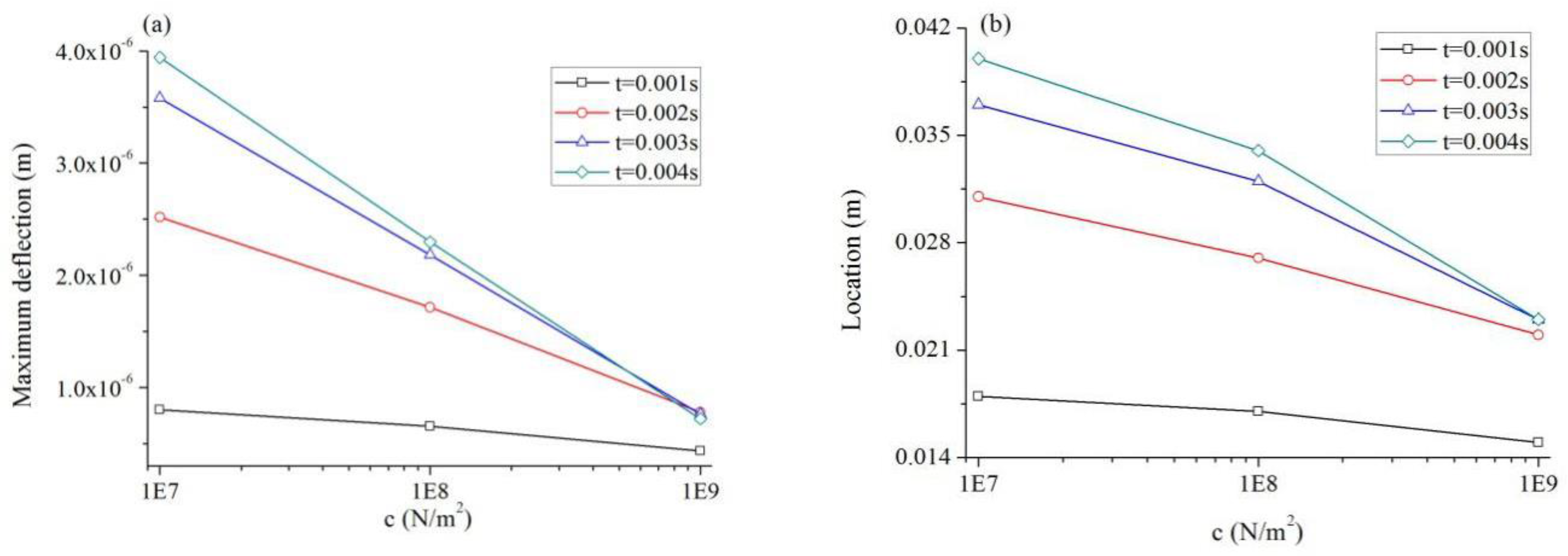
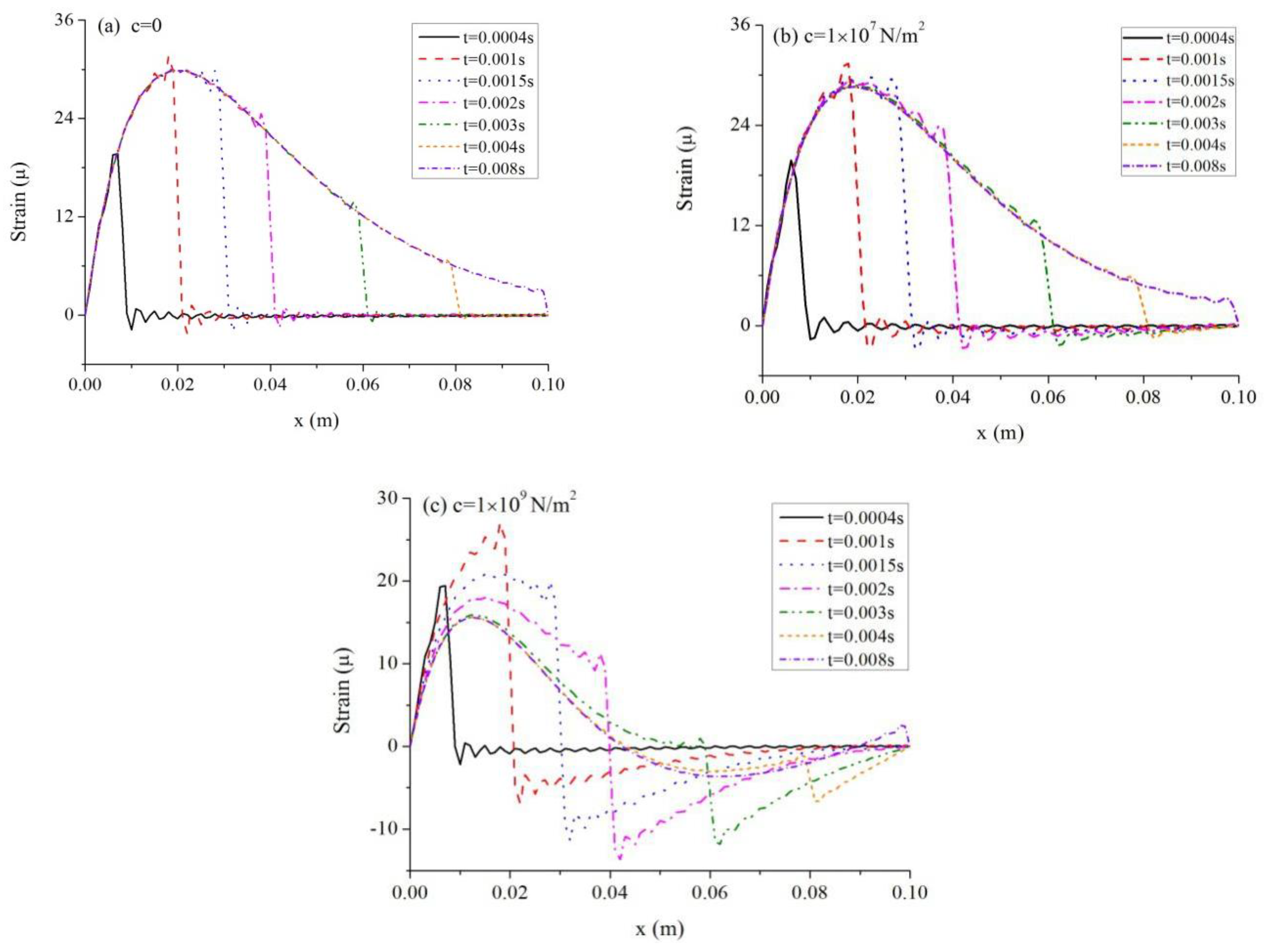
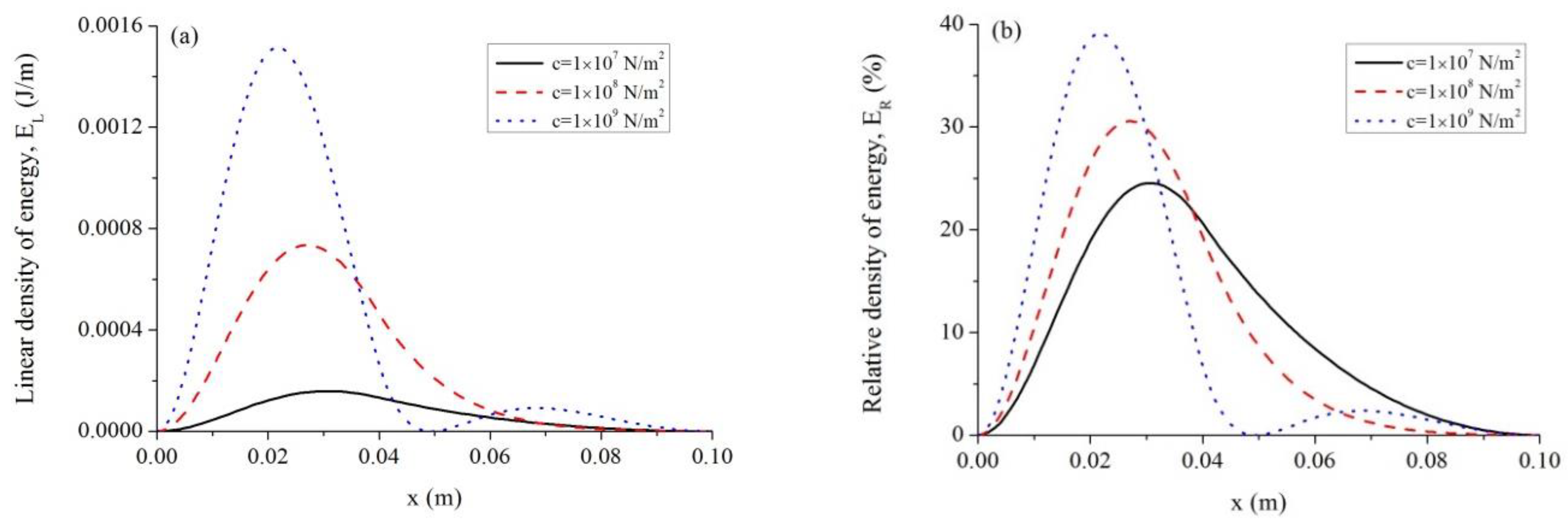
5.3. Influence of Modulus of Elastic Foundation Reaction
5.4. Influence of Duration Time of Laser Pulse
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Cline, H.E.; Anthony, T.R. Heat treating and melting material with a scanning laser or electron beam. J. Appl. Phys. 1977, 48, 3895–3900. [Google Scholar] [CrossRef]
- Mercier, R.J.; Malkin, S.; Mollendorf, J.C. Thermal stresses from a moving band source of heat on the surface of a semi-infinite solid. J. Eng. Ind. 1978, 100, 43–48. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Ohta, A.; Matsuoka, K.; Suzuki, N.; Maeda, Y. Analytic solutions for transient temperature of semi-infinite body subjected to 3-D moving heat sources. Weld. Res. 1999, 8, 265–274. [Google Scholar]
- Elsen, M.V.; Baelmans, M.; Mercelis, P.; Kruth, J.P. Solutions for modelling moving heat sources in a semi-infinite medium and applications to laser material processing. Int. J. Heat Mass Trans. 2007, 50, 4872–4882. [Google Scholar] [CrossRef]
- Sun, Y.X.; Ma, J.X.; Wang, X.; Soh, A.K.; Yang, J.L. Thermoelastic response of a one-dimensional semi-infinite rod heated by a moving laser pulse. Can. J. Phys. 2016, 94, 953–959. [Google Scholar] [CrossRef]
- Ootao, Y.; Tanigawa, Y. Three-dimensional solution for transient thermal stresses offunctionally graded rectangular plate due to nonuniform heat supply. Int. J. Mech. Sci. 2005, 47, 1769–1788. [Google Scholar] [CrossRef]
- Yang, X.F.; Ma, J.X.; Liu, S.B.; Xing, Y.; Yang, J.L.; Sun, Y.X. Exact analytical solution for thermoelastic response of clamped beams subjected to a movable laser pulse. Symmetry 2018, 10, 139. [Google Scholar] [CrossRef]
- Sun, Y.X.; Ma, J.X.; Liu, S.B.; Yang, J.L. Analytical solution of transient heat conduction in a bi-layered circular plate irradiated by laser pulse. Can. J. Phys. 2017, 95, 322–330. [Google Scholar] [CrossRef]
- Abbas, I.A. The effects of relaxation times and a moving heat source on a two-temperature generalized thermoelastic thin slim strip. Can. J. Phys. 2015, 93, 585–590. [Google Scholar] [CrossRef]
- Kenney, J.T. Steady-state vibrations of beam on elastic foundation for moving load. J. Appl. Mech. 1954, 21, 359–364. [Google Scholar]
- Sun, L. A closed-form solution of beam on viscoelastic subgrade subjected to moving loads. Comput. Struct. 2002, 80, 1–8. [Google Scholar] [CrossRef]
- Kim, S.M. Vibration and stability of axial loaded beams on elastic foundation under moving harmonic loads. Eng. Struct. 2004, 26, 95–105. [Google Scholar] [CrossRef]
- Basu, D.; Rao, V.K. Analytical solutions for Euler–Bernoulli beam on visco-elastic foundation subjected to moving load. Int. J. Numer. Anal. Meth. Geomech. 2013, 37, 945–960. [Google Scholar] [CrossRef]
- Brown, T.; Du, S.K.; Eruslu, H.; Sayas, F.J. Analysis of models for viscoelastic wave propagation. Appl. Math. Nonlinear Sci. 2018, 3, 55–96. [Google Scholar] [Green Version]
- .Żur, K.K. Green’s function approach to frequency analysis of thin circular plates. Bull. Polish Acad. Sci. Tech. Sci. 2016, 64, 181–188. [Google Scholar] [Green Version]
- Żur, K.K. Free vibration analysis of elastically supported functionally graded annular plates via quasi-Green’s function method. Comp. Part B Eng. 2018, 144, 37–55. [Google Scholar] [CrossRef]
- Żur, K.K. Green’s function for frequency analysis of thin annular plates with nonlinear variable thickness. Appl. Math. Model. 2016, 40, 3601–3619. [Google Scholar] [CrossRef]
- Żur, K.K. Green’s function in frequency analysis of circular thin plates of variable thickness. J. Theor. Appl. Mech. 2015, 53, 873–884. [Google Scholar] [CrossRef]
- Żur, K.K. Quasi-Green’s function approach to free vibration analysis of elastically supported functionally graded circular plates. Comput. Struct. 2018, 183, 600–610. [Google Scholar] [CrossRef]
- Zhao, X.; Hu, Q.J.; Crossley, W.; Du, C.C.; Li, Y.H. Analytical solutions for the coupled thermoelastic vibrations of the cracked Euler-Bernoulli beams by means of Green’s functions. Int. J. Mech. Sci. 2017, 128–129, 37–53. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, E.C.; Li, Y.H. Analytical solutions for the coupled thermoelastic vibrations of Timoshenko beams by means of Green’s functions. Int. J. Mech. Sci. 2017, 128, 37–53. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, Y.R.; Gao, X.Z.; Li, X.Y.; Li, Y.H. Green’s functions for the forced vibrations of cracked Euler–Bernoulli beams. Mech. Syst. Signal Process. 2016, 68–69, 155–175. [Google Scholar] [CrossRef]
- Chen, T.; Su, G.Y.; Shen, Y.S.; Gao, B.; Li, X.Y.; Müller, R. Unified Green’s functions of forced vibration of axially loaded Timoshenko beam: Transition parameter. Int. J. Mech. Sci. 2016, 113, 211–220. [Google Scholar] [CrossRef]
- Hozhabrossadati, S.M.; Sani, A.A.; Mehri, B.; Mofid, M. Green’s function for uniform Euler–Bernoulli beams at resonant condition: introduction of Fredholm alternative theorem. Appl. Math. Model. 2015, 39, 3366–3379. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Rajabzadeh-Safaei, N.; Hozhabrossadati, S.M. Three-dimensional deformations of a curved circular beam subjected to thermo-mechanical loading using green’s function method. Int. J. Mech. Sci. 2018, 142, 163–175. [Google Scholar] [CrossRef]
- Li, S.Q.; Yuan, H. Quasi-Green’s function method for free vibration of clamped thin plates on Winkler foundation. Appl. Math. Mech. Engl. Ed. 2011, 32, 265–276. [Google Scholar] [CrossRef]
- Sun, Y.X.; Ma, J.X.; Yang, X.F.; Liu, S.B.; Yang, J.L. Thermoelastic response of a simply supported beam irradiated by a movable laser pulse. Can. J. Phys. 2017, 95, 1012–1022. [Google Scholar] [CrossRef]
- Ma, J.X.; Sun, Y.X.; Yang, J.L. Analytical solution of dual-phase-lag heat conduction in a finite medium subjected to a moving heat source. Int. J. Therm. Sci. 2018, 125, 34–43. [Google Scholar] [CrossRef]
- Ma, J.X.; Yang, X.F.; Liu, S.B.; Sun, Y.X.; Yang, J.L. Exact solution of thermal response in a three-dimensional living bio-tissue subjected to a scanning laser beam. Int. J. Heat Mass Trans. 2018, 124, 1107–1116. [Google Scholar] [CrossRef]
- Ozisik, M.N. Heat Conduction, 1st ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1980. [Google Scholar]
- Warburton, G.B. The Dynamical Behavior of Structures, 2nd ed.; Pergamon Press Ltd.: Oxford, UK, 1976. [Google Scholar]
- Zhou, H.F.; Jiang, J.Q.; Zhang, T.Q. Steady-state response of infinite beam on Kelvin foundation under moving loads. J. Zhejiang Univ. (Eng. Sci.) 2004, 38, 1328–1333. (In Chinese) [Google Scholar]
- Stakgold, I. Green’s Functions and Boundary Value Problems, 2nd ed.; Wiley-Interscience: New York, NY, USA, 1997. [Google Scholar]
- Sun, Y.X.; Jiang, Y.; Yang, J.L. Thermoelastic damping of the axisymmetric vibration of laminated trilayered circular plate resonators. Can. J. Phys. 2014, 92, 1026–1032. [Google Scholar] [CrossRef]



| Velocity (m/s) | 2 | 5 | 10 | 20 |
|---|---|---|---|---|
| (K) | 537.65 | 336.78 | 227.14 | 151.93 |
| (ms) | () | Location (m) |
|---|---|---|
| 0.8 | 39.1766 | 0.014 |
| 1 | 29.7347 | 0.014 |
| 1.2 | 25.0138 | 0.018 |
| 1.5 | 19.3491 | 0.028 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Liu, S.; Rao, Z.; Li, Y.; Yang, J. Thermodynamic Response of Beams on Winkler Foundation Irradiated by Moving Laser Pulses. Symmetry 2018, 10, 328. https://doi.org/10.3390/sym10080328
Sun Y, Liu S, Rao Z, Li Y, Yang J. Thermodynamic Response of Beams on Winkler Foundation Irradiated by Moving Laser Pulses. Symmetry. 2018; 10(8):328. https://doi.org/10.3390/sym10080328
Chicago/Turabian StyleSun, Yuxin, Shoubin Liu, Zhangheng Rao, Yuhang Li, and Jialing Yang. 2018. "Thermodynamic Response of Beams on Winkler Foundation Irradiated by Moving Laser Pulses" Symmetry 10, no. 8: 328. https://doi.org/10.3390/sym10080328





