Effective Saturated Hydraulic Conductivity for Representing Field-Scale Infiltration and Surface Soil Moisture in Heterogeneous Unsaturated Soils Subjected to Rainfall Events
Abstract
:1. Introduction
2. Materials and Methods
Field-Scale Solution
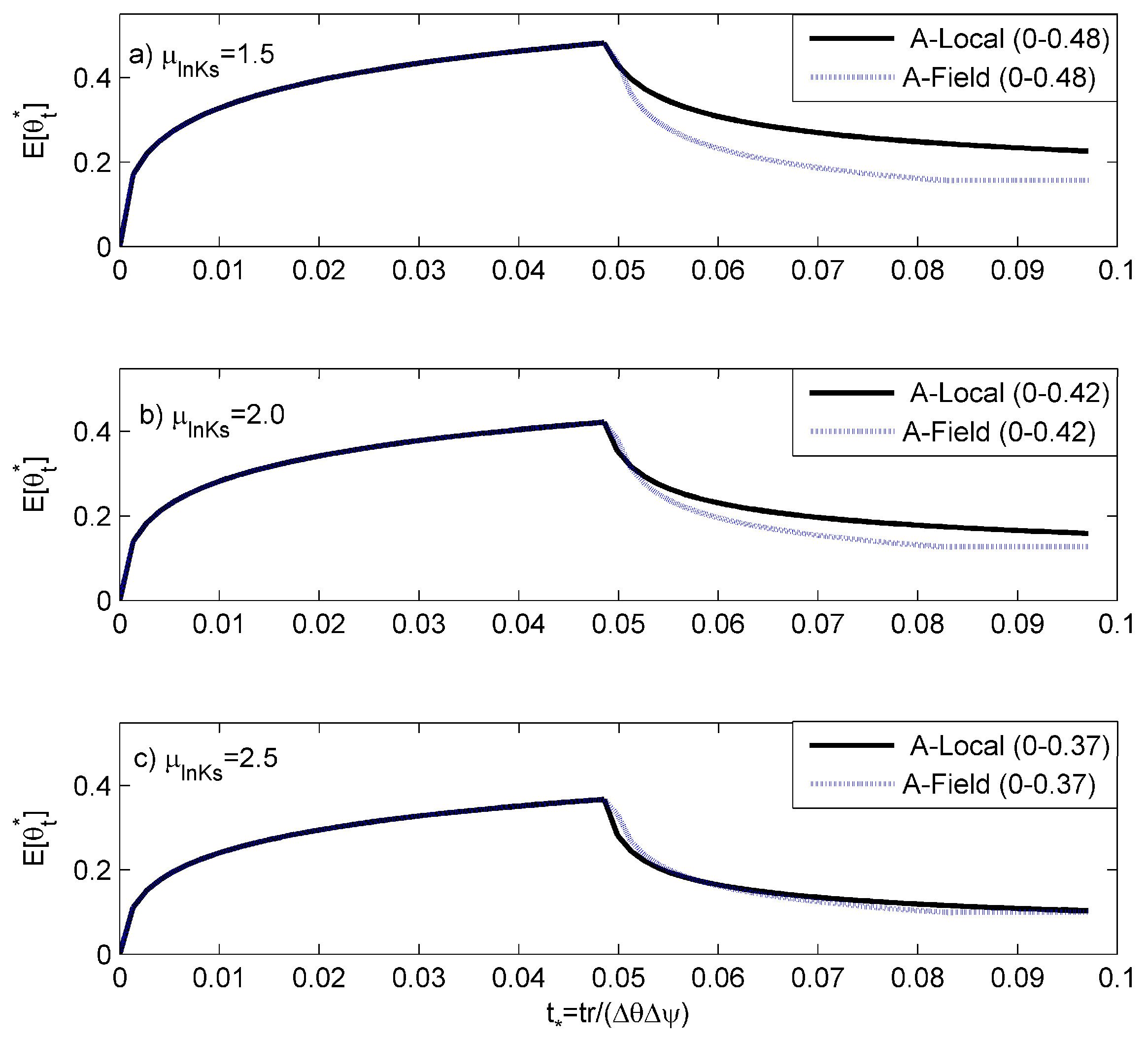
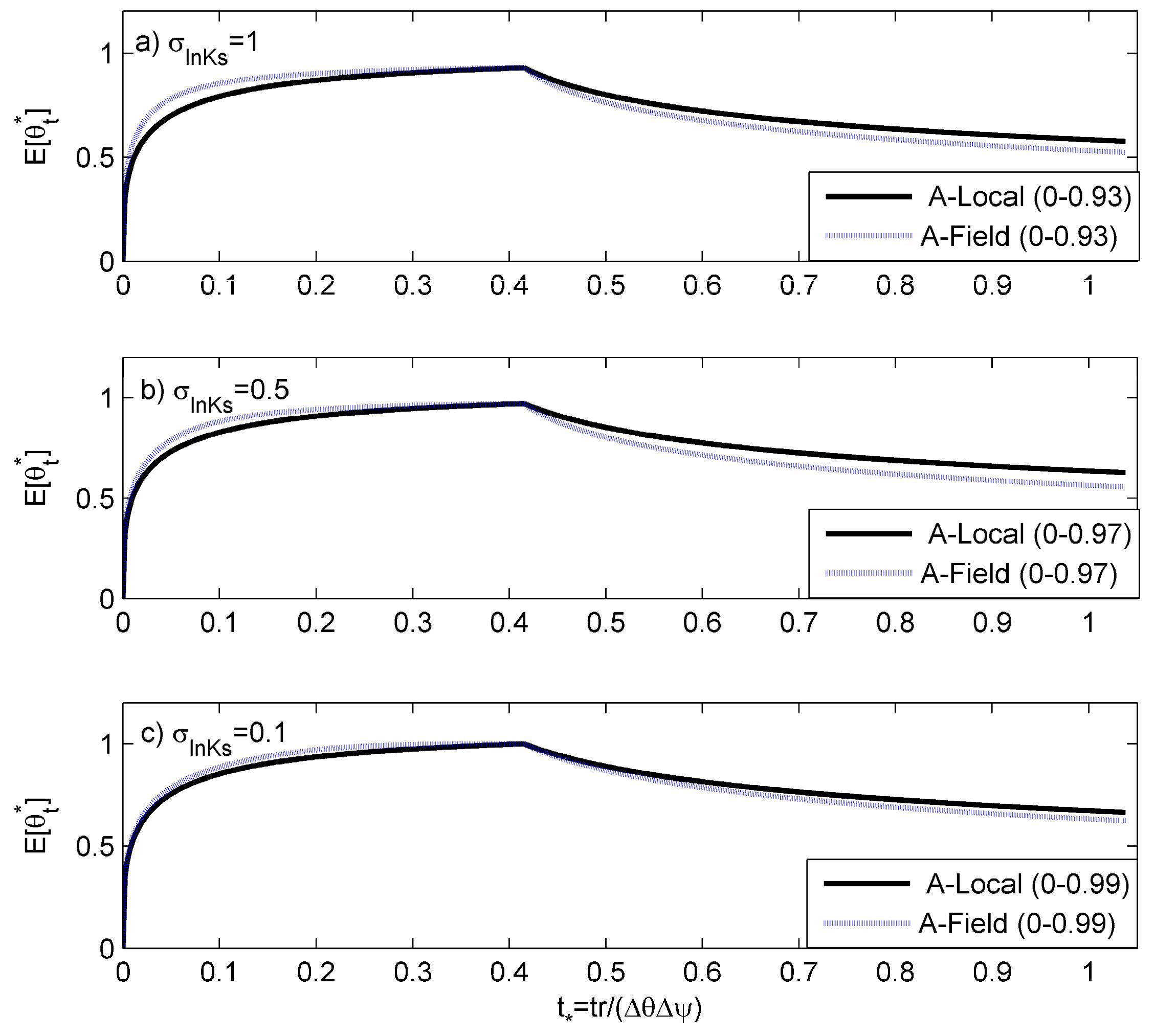
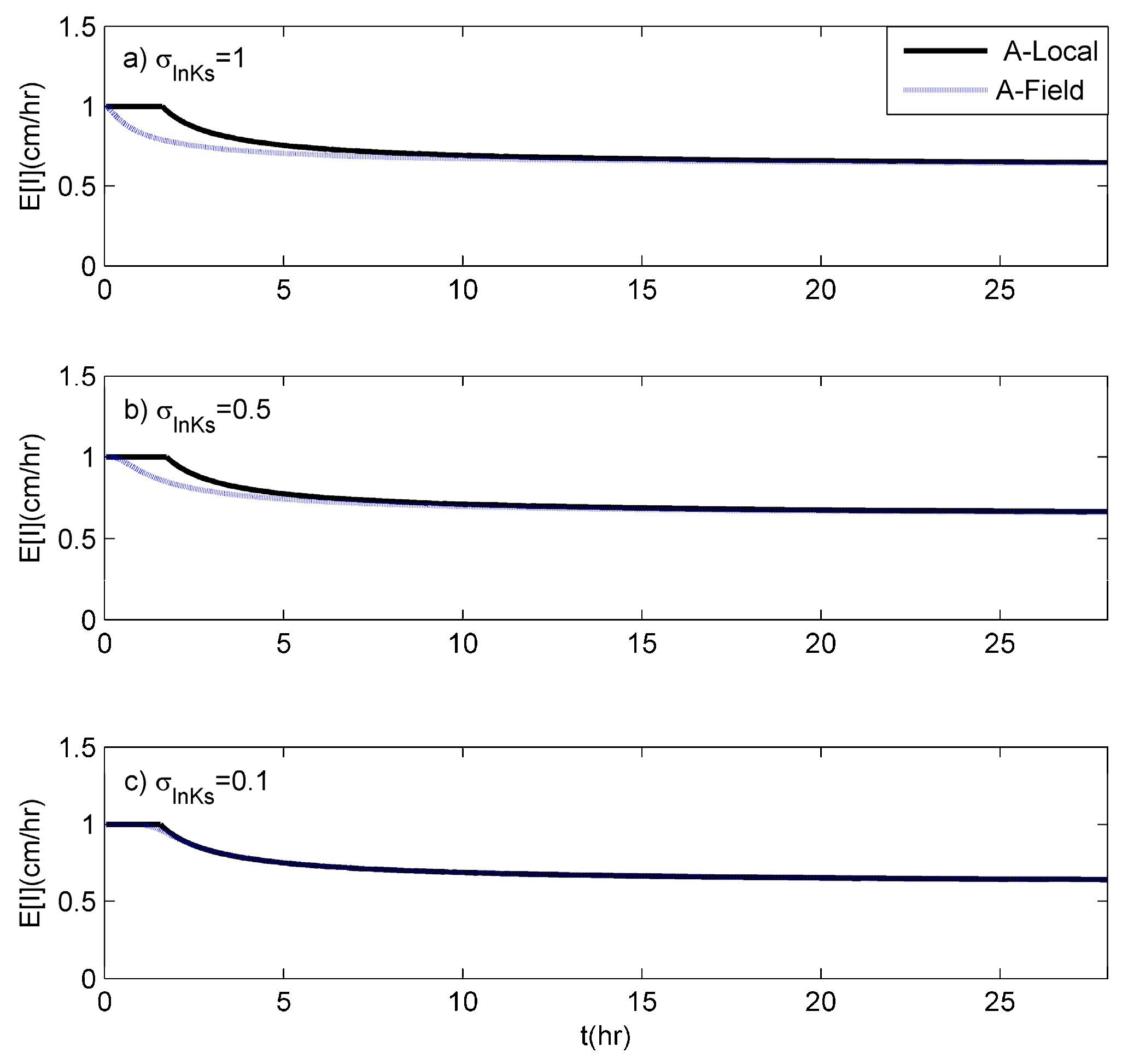
Effective Value for Replicating Field-Scale Infiltration Rates
Effective Value for Replicating Surface Soil Moisture
3. Design of Numerical Schemes
- (a)
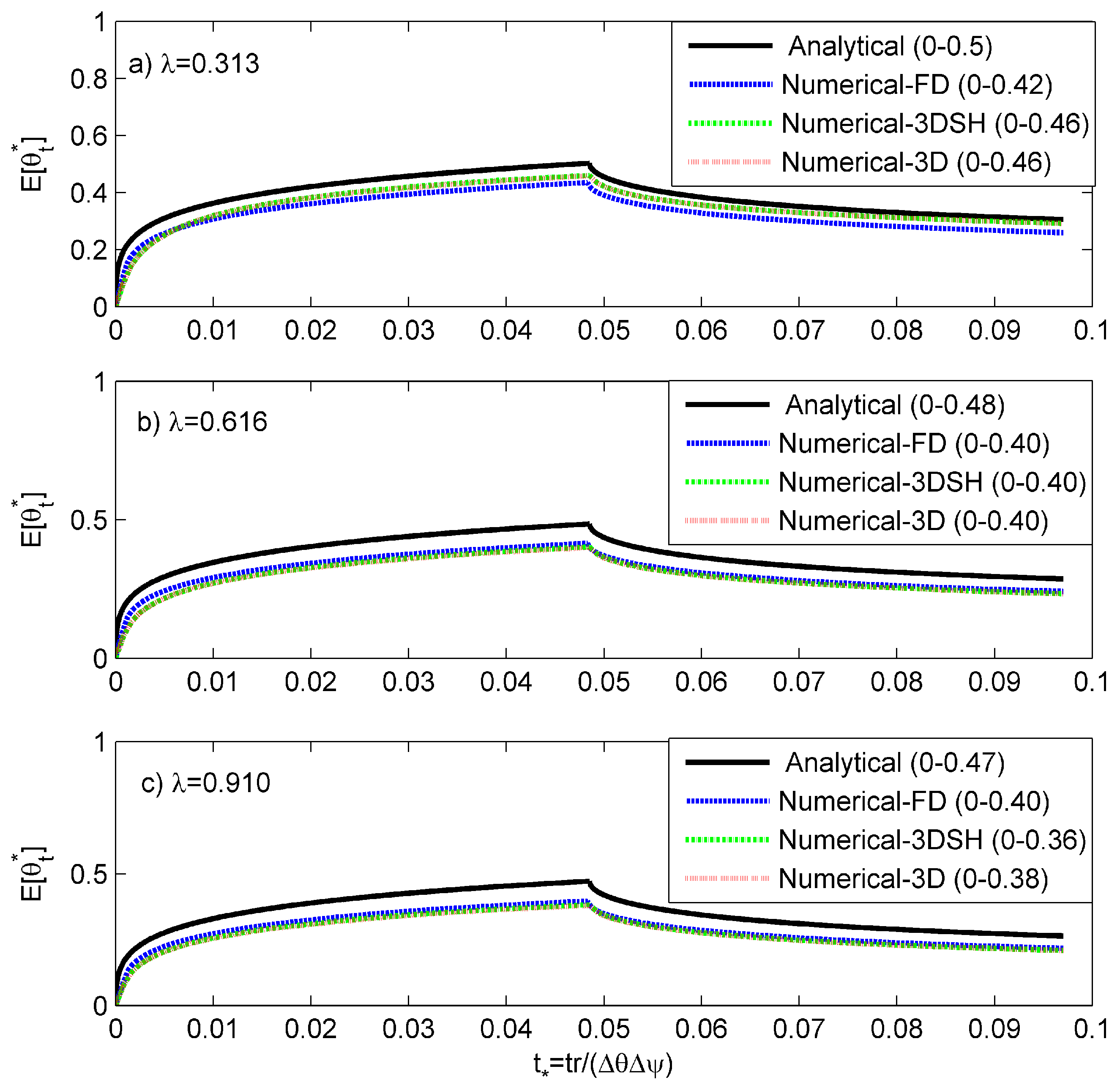
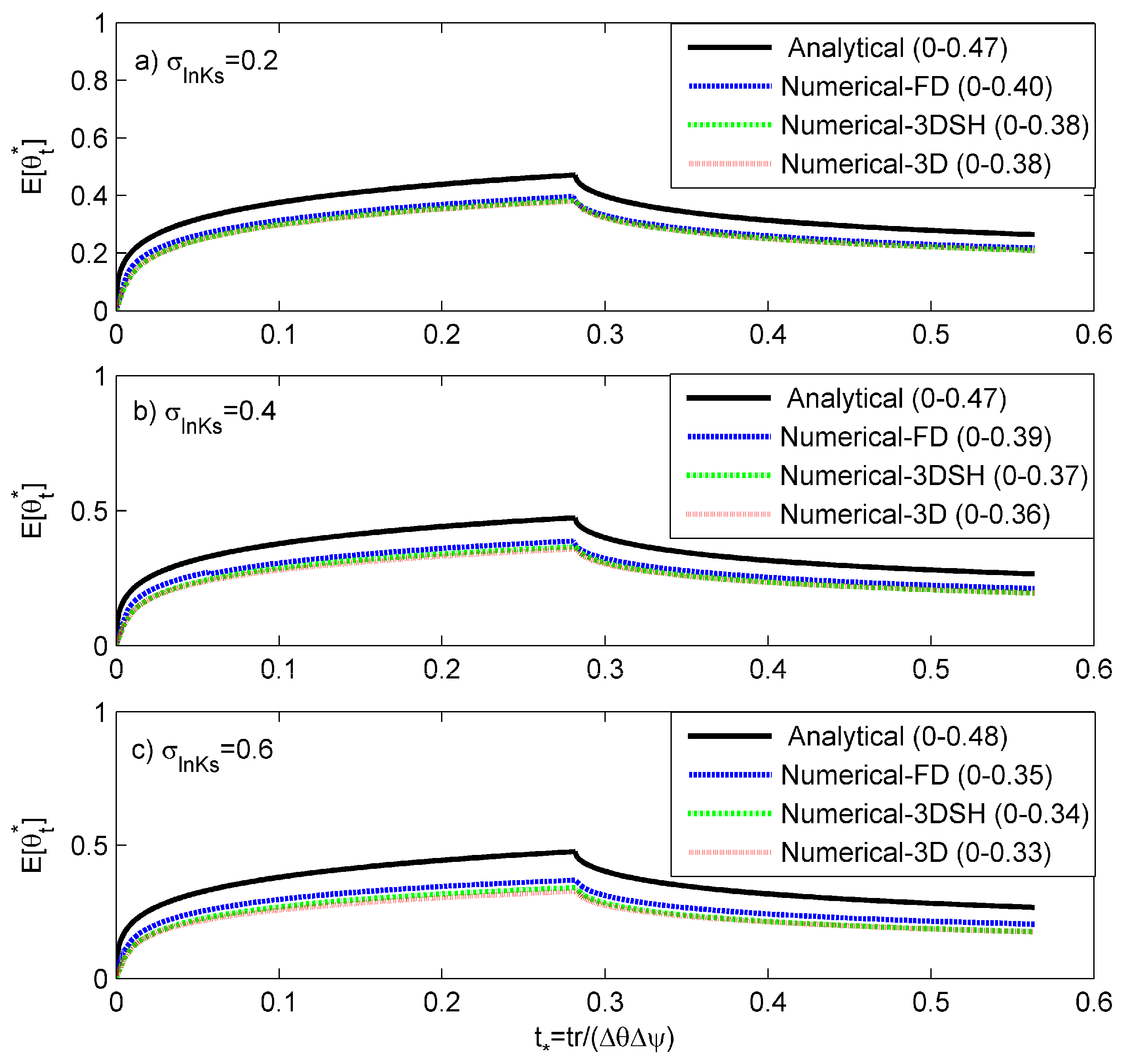
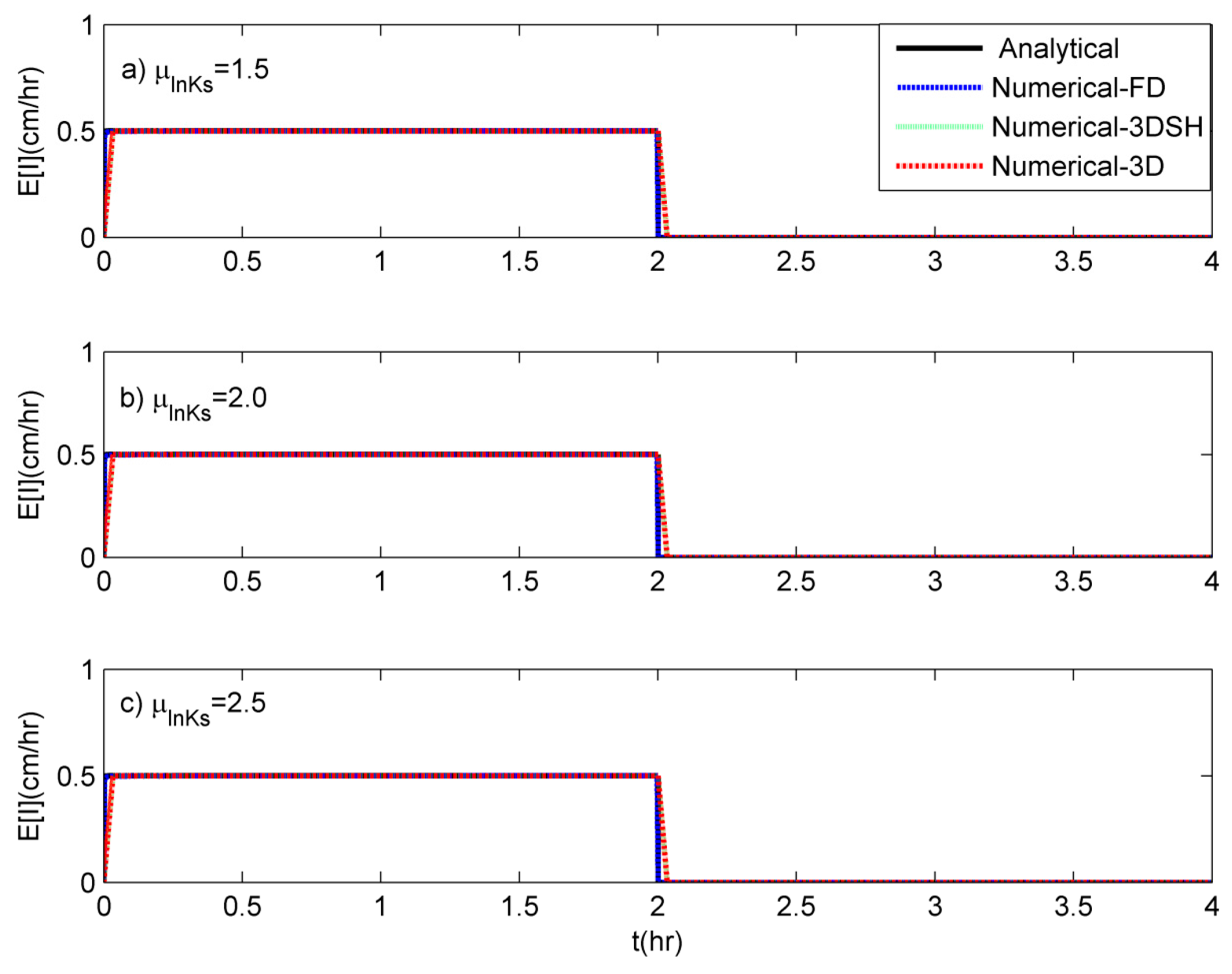
- Numerical-FD: A numerical scheme denoted as “Numerical-FD” was implemented for Monte-Carlo simulations. In this scheme, from a prescribed lognormal distribution, a random value of was drawn. Further, the numerical solution of the Richards equation (Equations (1)–(3)) was obtained using an implicit finite difference scheme. The water content, , fields so generated were stored for this single realization of , and 2000 such Monte Carlo simulations were utilized to obtain the field-scale surface soil moisture, and infiltration rates, .
- (b)
- Numerical 3DSH: A 3-D layered domain of dimensions 12 m × 12 m × 3 m was set up in Hydrus-3D [44], with 80 horizontal layers. Finite element mesh was generated, with fine spacing near the soil surface to capture the sharp fronts. In the horizontal plane the average size of triangular elements was 25 cm, leading to a total of 3691 finite element nodes in one horizontal layer. The layered 3-D model allows for setting up a spatially heterogeneous and vertically homogeneous or heterogeneous soil models. Initially, a 2-D spatially heterogeneous domain with the specified parameters for was generated. To set-up a spatially heterogeneous and vertically homogeneous physical domain, the generated values of were assigned to each element for all horizontal layers of the 3D-domain. A no-flux boundary condition was assigned to the vertical side walls and at the bottom boundary. At the soil surface, before ponding is achieved, the boundary condition is of surface flux equal to the constant rainfall intensity. After ponding, a fixed pressure head of zero is applied at the surface node.
- (c)
- Numerical-3D: The above mentioned 1-D and 3-D numerical schemes only consider horizontal heterogeneity; whereas, in realistic field-conditions heterogeneity exists in both horizontal and vertical directions. Therefore, a 3-D numerical scheme in Hydrus-3D, with heterogeneity in both horizontal and vertical directions was also considered for comparison. For this scheme, uncorrelated saturated hydraulic conductivity values were generated in both horizontal and vertical directions with the specified parameters of . The dimensions of the 3-D domain, mesh-spacing, parameters and boundary conditions are similar to those adopted for “Numerical-3DSH” scheme.
4. Results
4.1. Surface Soil Moisture
4.1.1. Comparisons with Numerical Results
4.1.2. Comparisons with Analytical Results
4.2. Infiltration Rates
4.2.1. Comparisons with Numerical Results
4.2.2. Comparisons with Analytical Results
5. Conclusions
Author Contributions
Conflicts of Interest
Appendix A. Expressions for Soil Moisture Content and Infiltration Rate
Appendix A.1. Soil Moisture Content Variation for Initially Dry Soils
Appendix A.1.1. Local-Scale
Appendix A.1.2. Field-Scale Solution
Appendix A.2. Expected Field-Scale InfiltrationRates
References
- Brocca, L.; Melone, F.; Moramarco, T.; Morbidelli, R. Spatial-temporal variability of soil moisture and its estimation across scales. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Corradini, C.; Flammini, A.; Morbidelli, R.; Govindaraju, R.S. A conceptual model for infiltration in two-layered soils with a more permeable upper layer: From local to field scale. J. Hydrol. 2011, 410, 62–72. [Google Scholar] [CrossRef]
- Srivastava, R.; Yeh, T.-C.J. Analytical solutions for one-dimensional, transient infiltration toward the water table in homogeneous and layered soils. Water Resour. Res. 1991, 27, 753–762. [Google Scholar] [CrossRef]
- Govindaraju, R.S.; Morbidelli, R.; Corradini, C. Areal Infiltration Modeling over Soils with Spatially Correlated Hydraulic Conductivities. J. Hydrol. Eng. 2001, 6, 150–158. [Google Scholar] [CrossRef]
- Govindaraju, R.S.; Corradini, C.; Morbidelli, R. A semi-analytical model of expected areal-average infiltration under spatial heterogeneity of rainfall and soil saturated hydraulic conductivity. J. Hydrol. 2006, 316, 184–194. [Google Scholar] [CrossRef]
- Ojha, R.; Prakash, A.; Govindaraju, R.S. Local- and field-scale stochastic-advective vertical solute transport in horizontally heterogeneous unsaturated soils. Water Resour. Res. 2014, 50. [Google Scholar] [CrossRef]
- Western, A.W.; Grayson, R.B.; Blöschl, G. Scaling of Soil Moisture: A Hydrologic Perspective. Annu. Rev. Earth Planet. Sci. 2002, 30, 149–180. [Google Scholar] [CrossRef]
- Grayson, R.B.; Western, A.W. Towards areal estimation of soil water content from point measurements: Time and space stability of mean response. J. Hydrol. 1998, 207, 68–82. [Google Scholar] [CrossRef]
- Lai, J.; Ren, L. Estimation of effective hydraulic parameters in heterogeneous soils at field scale. Geoderma 2016, 264, 28–41. [Google Scholar] [CrossRef]
- Vereecken, H.; Kasteel, R.; Vanderborght, J.; Harter, T. Upscaling Hydraulic Properties and Soil Water Flow Processes in Heterogeneous Soils. Vadose Zone J. 2007, 6, 1–28. [Google Scholar] [CrossRef]
- Sadeghi, M.; Tuller, M.; Gohardoust, M.R.; Jones, S.B. Column-scale unsaturated hydraulic conductivity estimates in coarse-textured homogeneous and layered soils derived under steady-state evaporation from a water table. J. Hydrol. 2014, 519, 1238–1248. [Google Scholar] [CrossRef]
- Bolster, D.; Dentz, M.; Carrera, J. Effective two-phase flow in heterogeneous media under temporal pressure fluctuations. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Liu, Z.; Zha, Y.; Yang, W.; Kuo, Y.-M.; Yang, J. Large-Scale Modeling of Unsaturated Flow by a Stochastic Perturbation Approach. Vadose Zone J. 2016, 15. [Google Scholar] [CrossRef]
- Mantoglou, A.; Gelhar, L.W. Stochastic modeling of large-scale transient unsaturated flow systems. Water Resour. Res. 1987, 23, 37–46. [Google Scholar] [CrossRef]
- Ünlü, K.; Nielsen, D.R.; Biggar, J.W.; Morkoc, F. Statistical Parameters Characterizing the Spatial Variability of Selected Soil Hydraulic Properties. Soil Sci. Soc. Am. J. 1990, 54, 1537. [Google Scholar] [CrossRef]
- Zhang, D. Nonstationary stochastic analysis of transient unsaturated flow in randomly heterogeneous media. Water Resour. Res. 1999, 35, 1127–1141. [Google Scholar] [CrossRef]
- Bresler, E.; Dagan, G. Unsaturated flow in spatially variable fields: 2. Application of water flow models to various fields. Water Resour. Res. 1983, 19, 421–428. [Google Scholar] [CrossRef]
- Dagan, G.; Bresler, E. Unsaturated flow in spatially variable fields: 1. Derivation of models of infiltration and redistribution. Water Resour. Res. 1983, 19, 413–420. [Google Scholar] [CrossRef]
- Mohanty, B.P.; Zhu, J.; Mohanty, B.P.; Zhu, J. Effective Hydraulic Parameters in Horizontally and Vertically Heterogeneous Soils for Steady-State Land–Atmosphere Interaction. J. Hydrometeorol. 2007, 8, 715–729. [Google Scholar] [CrossRef]
- Zhu, J.; Mohanty, B.P. Upscaling of soil hydraulic properties for steady state evaporation and infiltration. Water Resour. Res. 2002, 38, 17-1–17-13. [Google Scholar] [CrossRef]
- Zhu, J.; Mohanty, B.P.; Das, N.N. On the Effective Averaging Schemes of Hydraulic Properties at the Landscape Scale. Vadose Zone J. 2006, 5, 308–316. [Google Scholar] [CrossRef]
- Foussereau, X.; Graham, W.D.; Rao, P.S.C. Stochastic analysis of transient flow in unsaturated heterogeneous soils. Water Resour. Res. 2000, 36, 891–910. [Google Scholar] [CrossRef]
- Ward, A.L.; Zhang, Z.F.; Gee, G.W. Upscaling unsaturated hydraulic parameters for flow through heterogeneous anisotropic sediments. Adv. Water Resour. 2006, 29, 268–280. [Google Scholar] [CrossRef]
- Ye, M.; Khaleel, R.; Yeh, T.-C.J. Stochastic analysis of moisture plume dynamics of a field injection experiment. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Yeh, T.-C.J.; Ye, M.; Khaleel, R. Estimation of effective unsaturated hydraulic conductivity tensor using spatial moments of observed moisture plume. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Nietsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. SWAT User Documentation, Version 2005. 2005. Available online: http://swat.tamu.edu/media/1292/swat2005theory.pdf (accessed on 17 February 2017).
- Downer, C.; Ogden, F. GSSHA: Model to simulated diverse streamflow producing processes. J. Hydrol. Eng. 2004, 9, 161–174. [Google Scholar] [CrossRef]
- KINEROS2: A Kinematic Runoff and Erosion Model. Available online: http://www.tucson.ars.ag.gov/kineros (accessed on 14 February 2017).
- Yang, J.; Zhang, D.; Lu, Z. Stochastic analysis of saturated–unsaturated flow in heterogeneous media by combining Karhunen-Loeve expansion and perturbation method. J. Hydrol. 2004, 294, 18–38. [Google Scholar] [CrossRef]
- Ojha, R.; Morbidelli, R.; Saltalippi, C.; Flammini, A.; Govindaraju, R.S. Scaling of surface soil moisture over heterogeneous fields subjected to a single rainfall event. J. Hydrol. 2014, 516. [Google Scholar] [CrossRef]
- Ojha, R.; Govindaraju, R.S. A physical scaling model for aggregation and disaggregation of field-scale surface soil moisture dynamics. Chaos 2015, 25. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Govindaraju, R.S.; Kavvas, M.L. Spatial averaging of unsaturated flow equations under infiltration conditions over areally heterogeneous fields 2. Numerical simulations. Water Resour. Res. 1994, 30, 535–548. [Google Scholar] [CrossRef]
- Chen, Z.; Govindaraju, R.S.; Kavvas, M.L. Spatial averaging of unsaturated flow equations under infiltration conditions over areally heterogeneous fields: 1. Development of models. Water Resour. Res. 1994, 30, 523–533. [Google Scholar] [CrossRef]
- Govindaraju, R.S.; Or, D.; Kavvas, M.L.; Rolston, D.E.; Biggar, J. Error analyses of simplified unsaturated flow models under large uncertainty in hydraulic properties. Water Resour. Res. 1992, 28, 2913–2924. [Google Scholar] [CrossRef]
- Destouni, G. The effect of vertical soil heterogeneity on field scale solute flux. Water Resour. Res. 1992, 28, 1303–1309. [Google Scholar] [CrossRef]
- Leij, F.J.; Sciortino, A.; Haverkamp, R.; Soria Ugalde, J.M. Aggregation of vertical flow in the vadose zone with auto- and cross-correlated hydraulic properties. J. Hydrol. 2007, 338, 96–112. [Google Scholar] [CrossRef]
- Russo, D. Field-scale transport of interacting solutes through the unsaturated zone: 1. Analysis of the spatial variability of the transport properties. Water Resour. Res. 1989, 25, 2475–2485. [Google Scholar] [CrossRef]
- Russo, D. Field-scale transport of interacting solutes through the unsaturated zone: 2. Analysis of the spatial variability of the field response. Water Resour. Res. 1989, 25, 2487–2495. [Google Scholar] [CrossRef]
- Kavvas, M.L.; Chen, Z.Q.; Govindaraju, R.S.; Rolston, D.E.; Koos, T.; Karakas, A.; Or, D.; Jones, S.; Biggar, J. Probability Distribution of Solute Travel Time for Convective Transport in Field-Scale Soils Under Unsteady and Nonuniform Flows. Water Resour. Res. 1996, 32, 875–889. [Google Scholar] [CrossRef]
- Russo, D.; Bresler, E. A univariate versus a multivariate parameter distribution in a stochastic-conceptual analysis of unsaturated flow. Water Resour. Res. 1982, 18, 483–488. [Google Scholar] [CrossRef]
- Nielsen, D.; Biggar, J.; Erh, K. Spatial variability of field-measured soil-water properties. Hilgardia 1973, 42, 215–259. [Google Scholar] [CrossRef]
- Brooks, R.J.; Corey, A.T. Hydraulic Properties of Porous Media; Hydrol. Pap. 3; Colorado State University: Fort Collins, CO, USA, 1964; 27p. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W.; Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Simůnek, J.; Genuchten, M.T.V.; Sejna, M. The Hydrus Soft-Ware Package for Simulating Two- and Three-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media: Technical Manual, version 1.0; PC-Progress: Prague, Czech Republic, 2006. [Google Scholar]
- Rawls, W.J.; Brakensiek, D.L.; Miller, N. Green-ampt Infiltration Parameters from Soils Data. J. Hydraul. Eng. 1983, 109, 62–70. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. Convective-dispersive transport of solutes involved in sequential first-order decay reactions. Comput. Geosci. 1985, 11, 129–147. [Google Scholar] [CrossRef]
- Charbeneau, R.J. Groundwater Hydraulics and Pollutant Transport; Prentice Hall: Upper Saddle River, NJ, USA, 2000; pp. 206–211. [Google Scholar]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ojha, R.; Corradini, C.; Morbidelli, R.; Govindaraju, R.S. Effective Saturated Hydraulic Conductivity for Representing Field-Scale Infiltration and Surface Soil Moisture in Heterogeneous Unsaturated Soils Subjected to Rainfall Events. Water 2017, 9, 134. https://doi.org/10.3390/w9020134
Ojha R, Corradini C, Morbidelli R, Govindaraju RS. Effective Saturated Hydraulic Conductivity for Representing Field-Scale Infiltration and Surface Soil Moisture in Heterogeneous Unsaturated Soils Subjected to Rainfall Events. Water. 2017; 9(2):134. https://doi.org/10.3390/w9020134
Chicago/Turabian StyleOjha, Richa, Corrado Corradini, Renato Morbidelli, and Rao S. Govindaraju. 2017. "Effective Saturated Hydraulic Conductivity for Representing Field-Scale Infiltration and Surface Soil Moisture in Heterogeneous Unsaturated Soils Subjected to Rainfall Events" Water 9, no. 2: 134. https://doi.org/10.3390/w9020134





