Bed Evolution under Rapidly Varying Flows by a New Method for Wave Speed Estimation
Abstract
:1. Introduction
2. Governing Equations
2.1. Hydrodynamic Component
2.2. Morphodynamic Component
2.2.1. Grass Formula
2.2.2. MPM Formula
3. Numerical Scheme
3.1. Flux Computation
3.2. Source Term Treatment
3.3. Wetting and Drying
3.4. Boundary Conditions
4. Applications
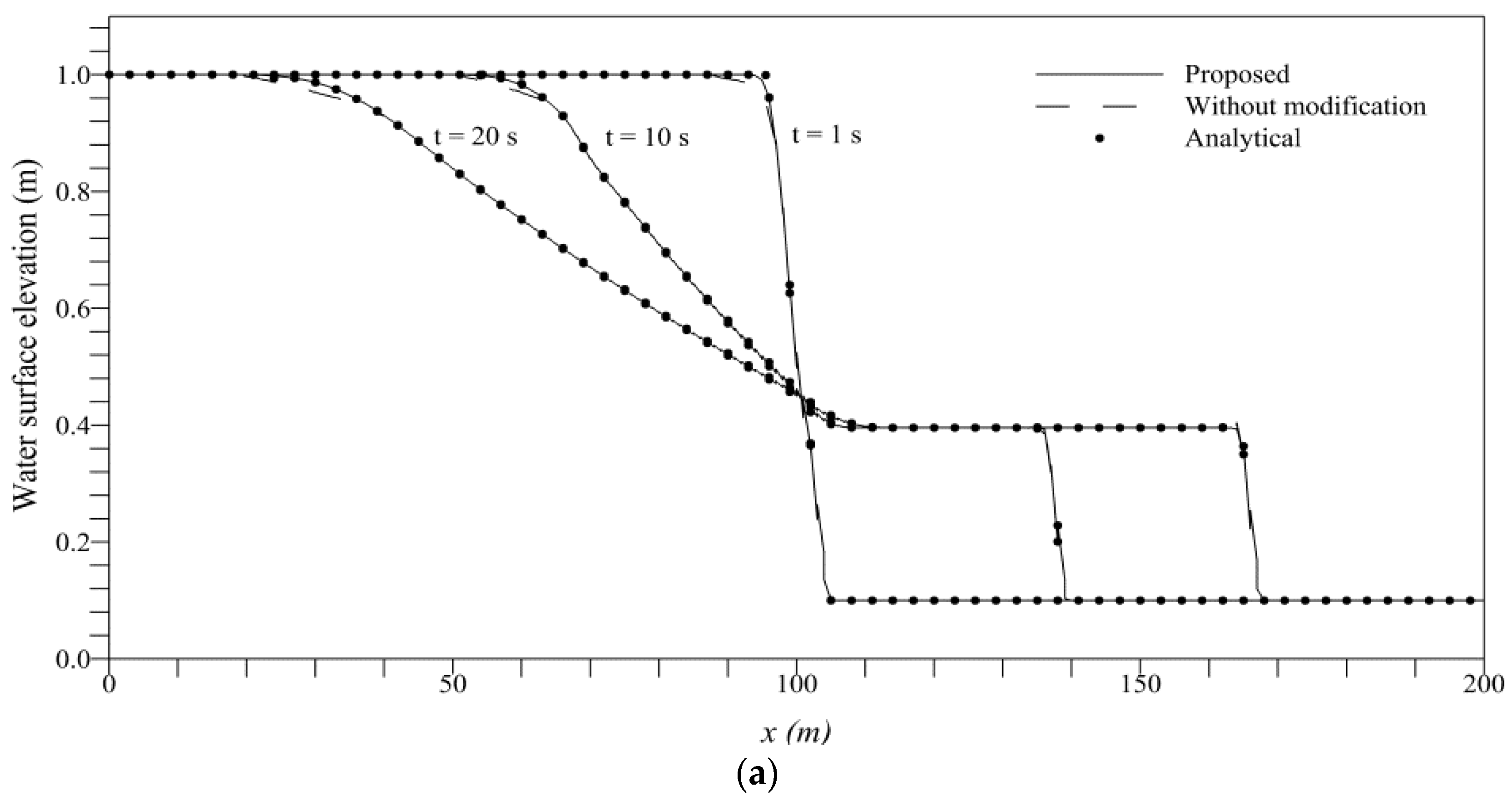
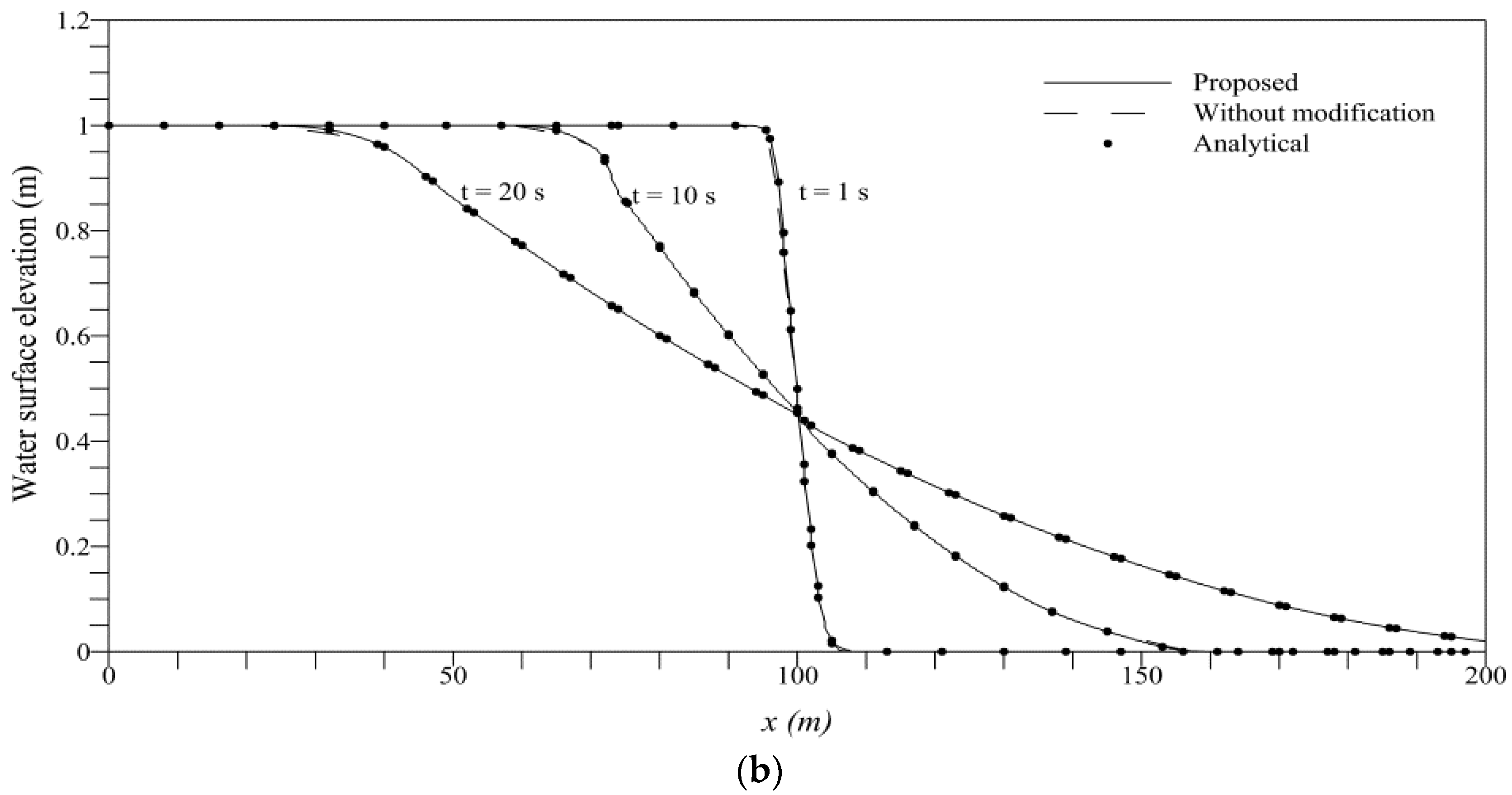
4.1. Dam-Break over a Rigid Bed
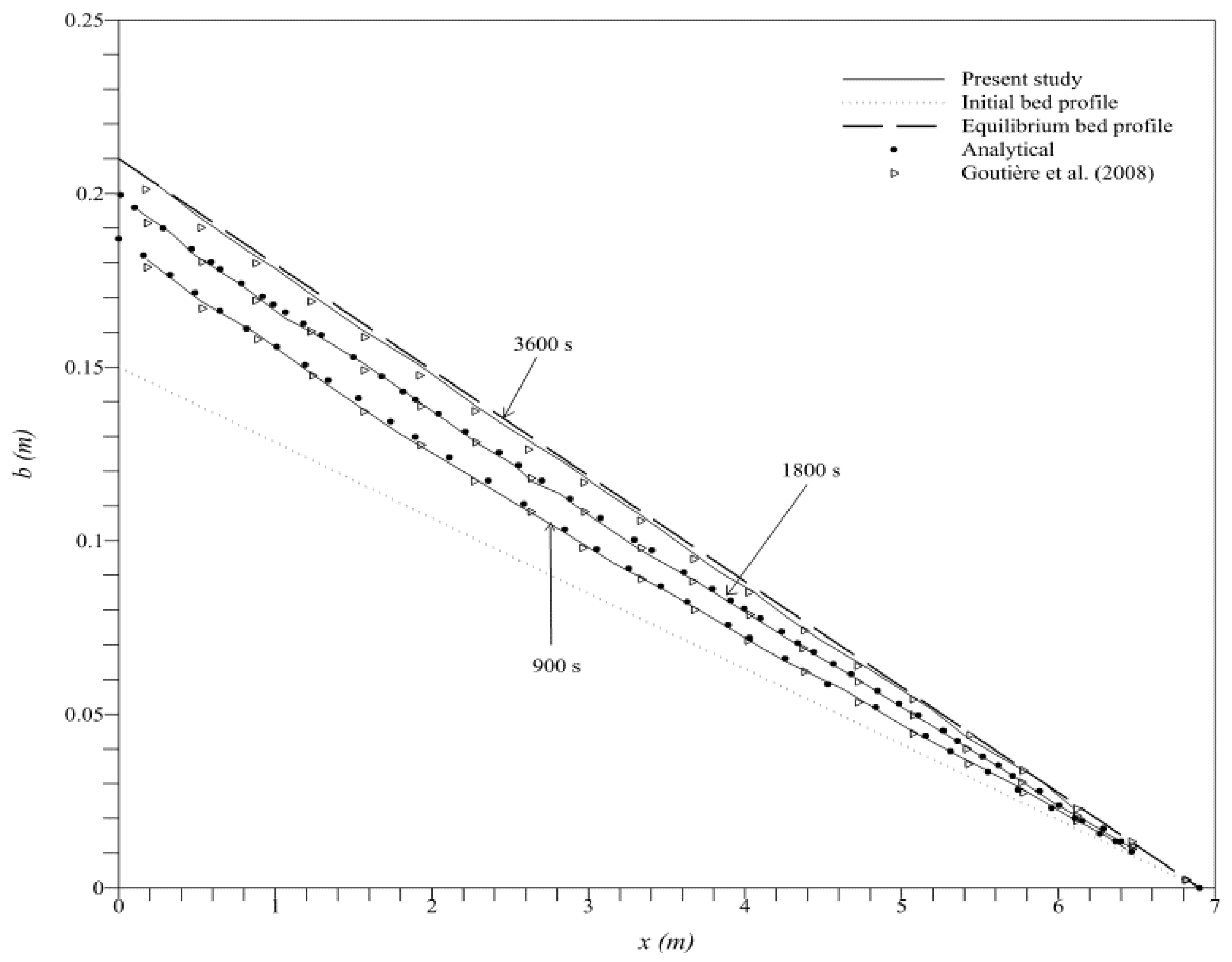
4.2. Bed-Slope Aggradation
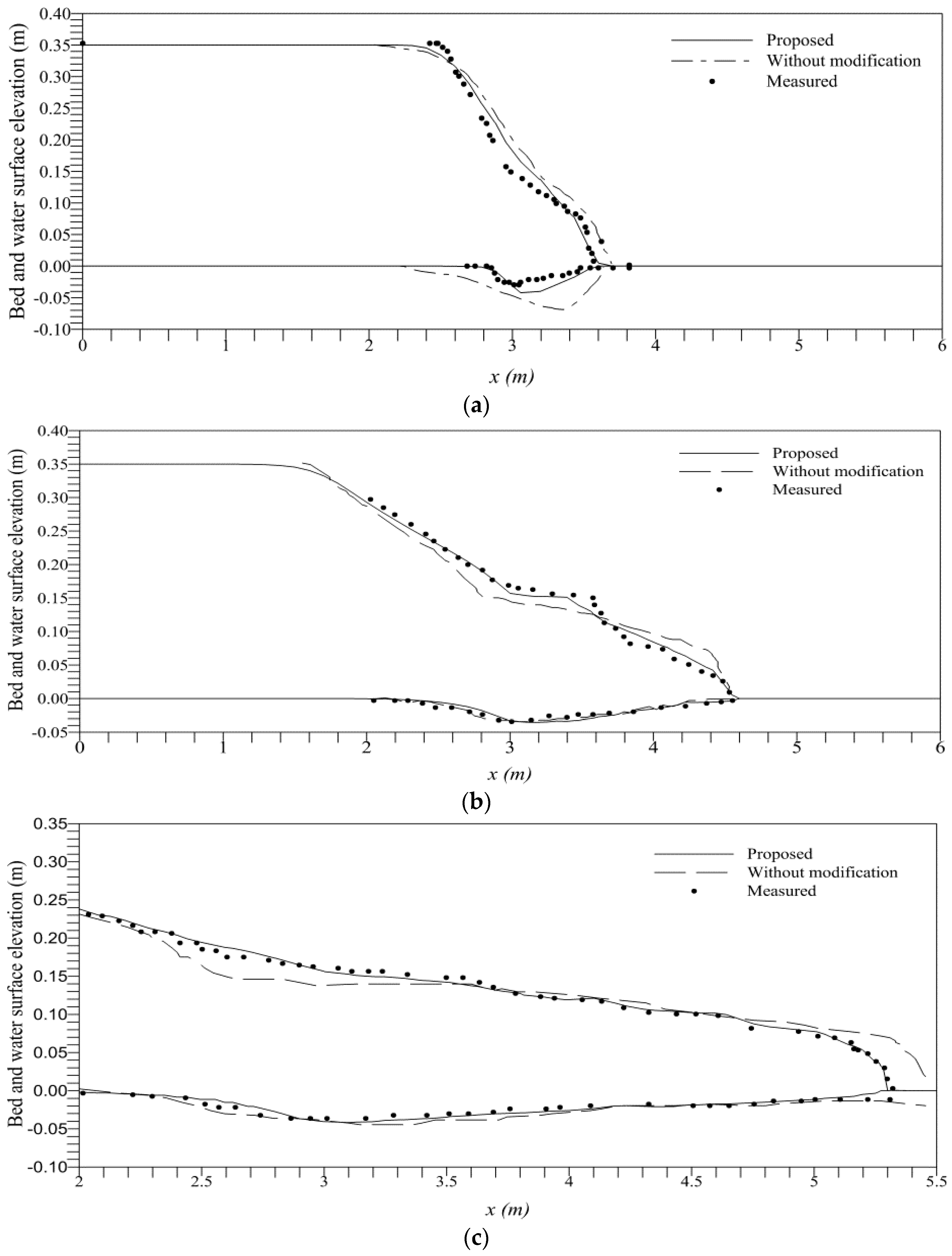
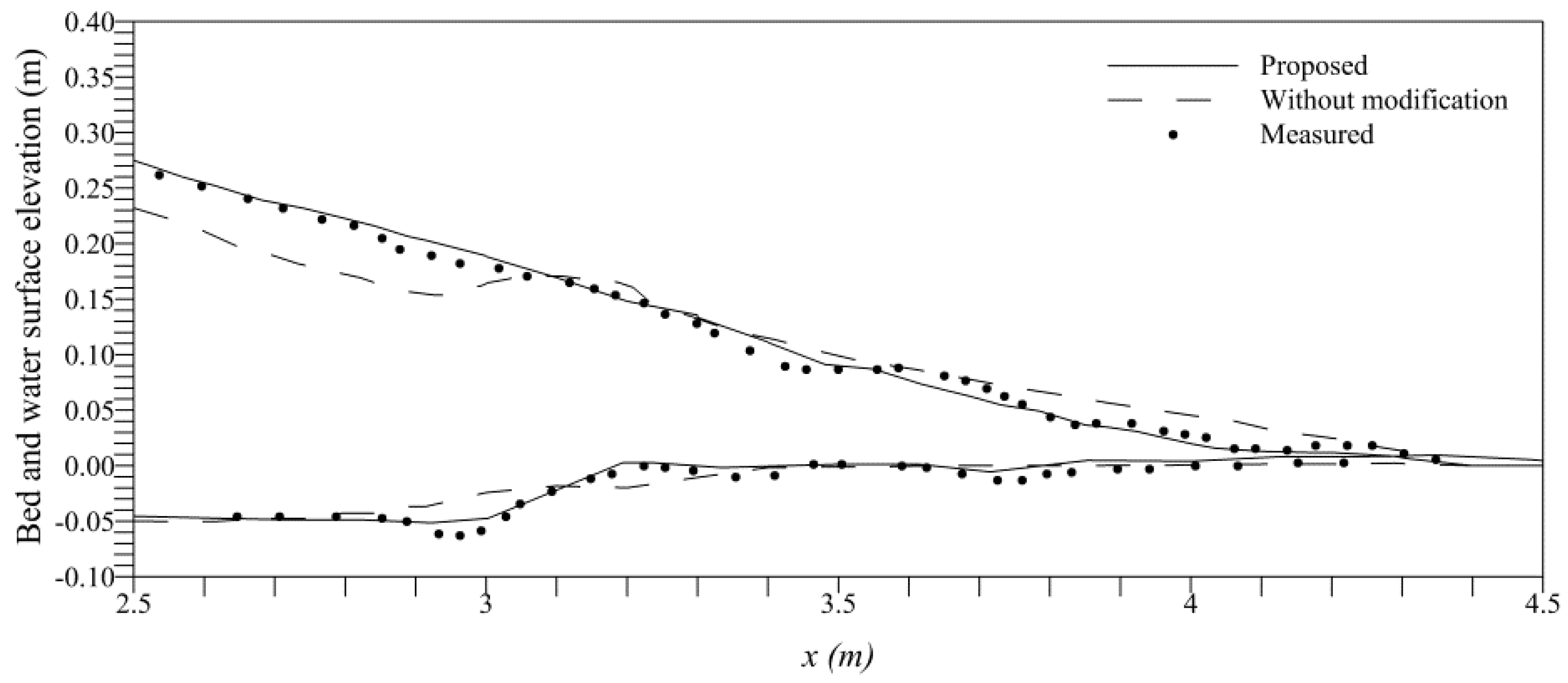
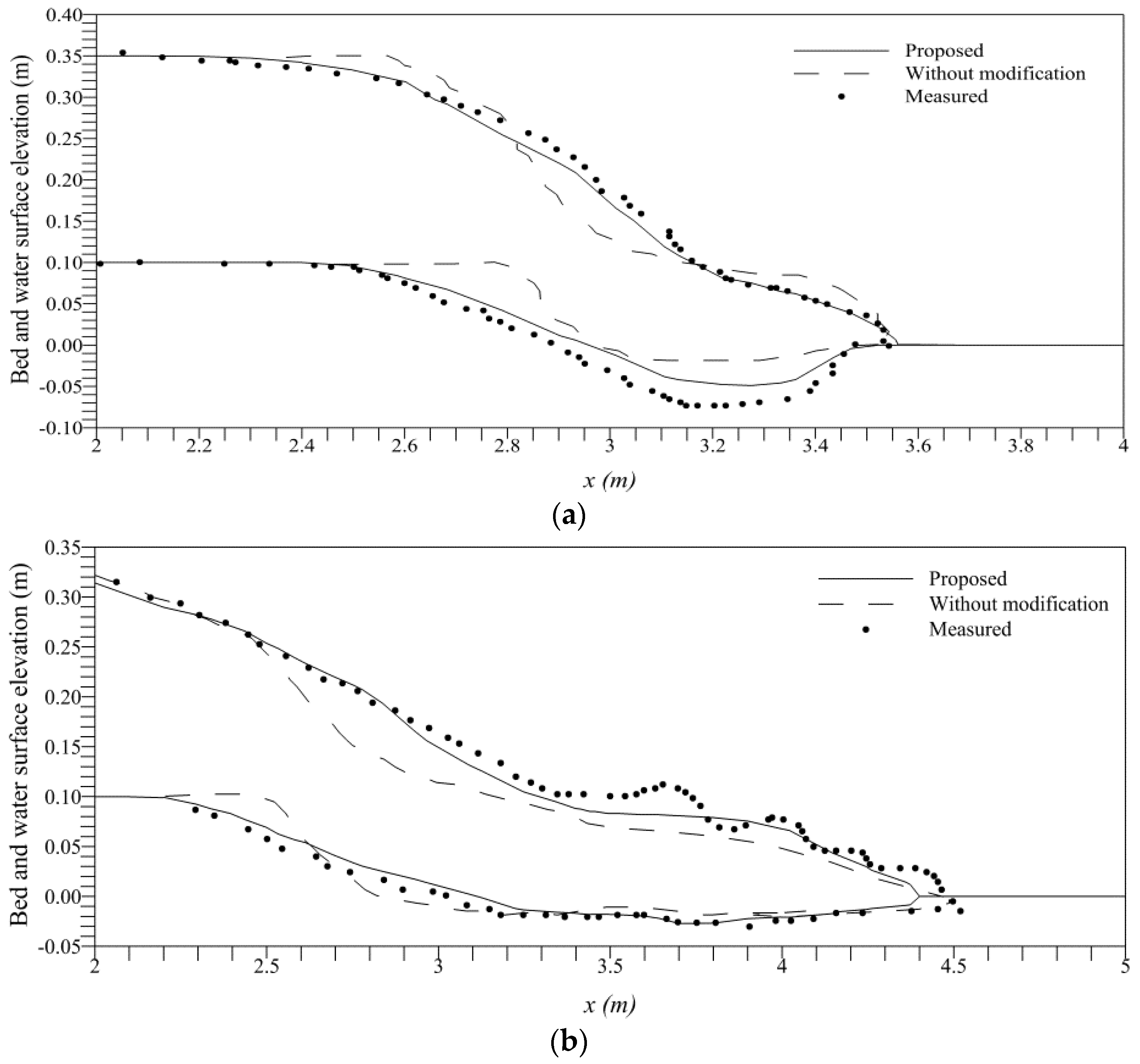
4.3. Dam-Break in an Erodible Channel
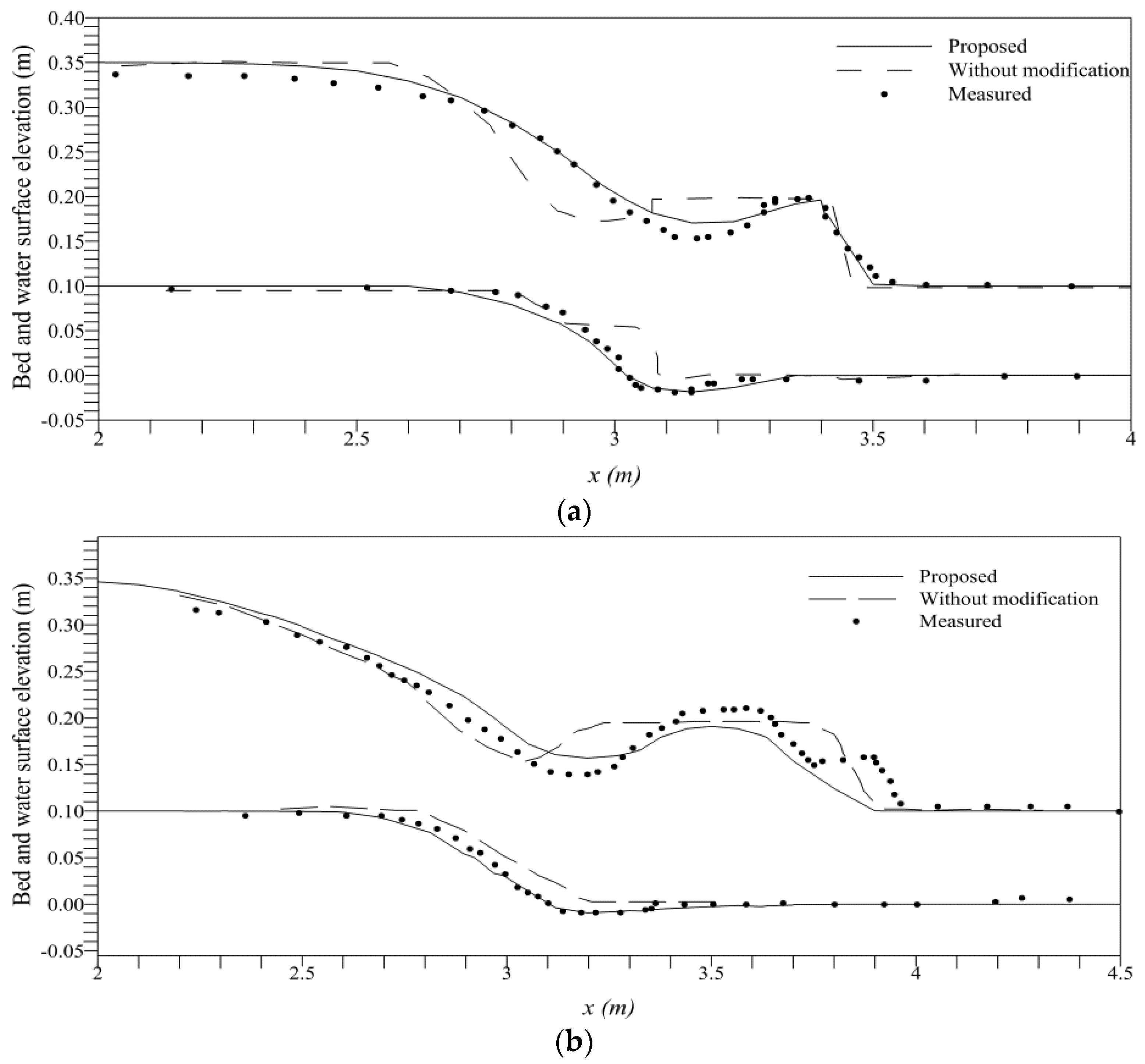
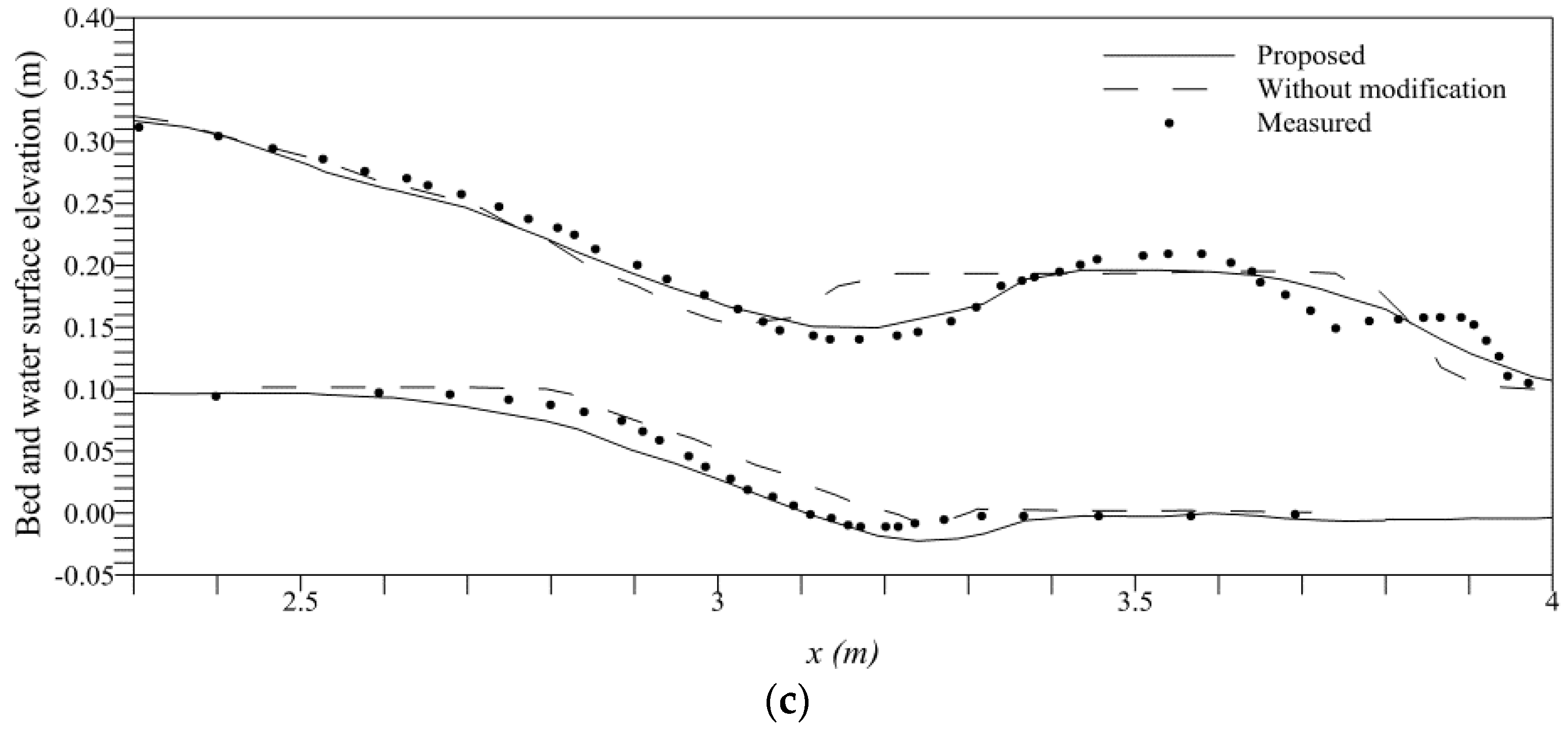
4.4. Dam-Break over Sand Bed
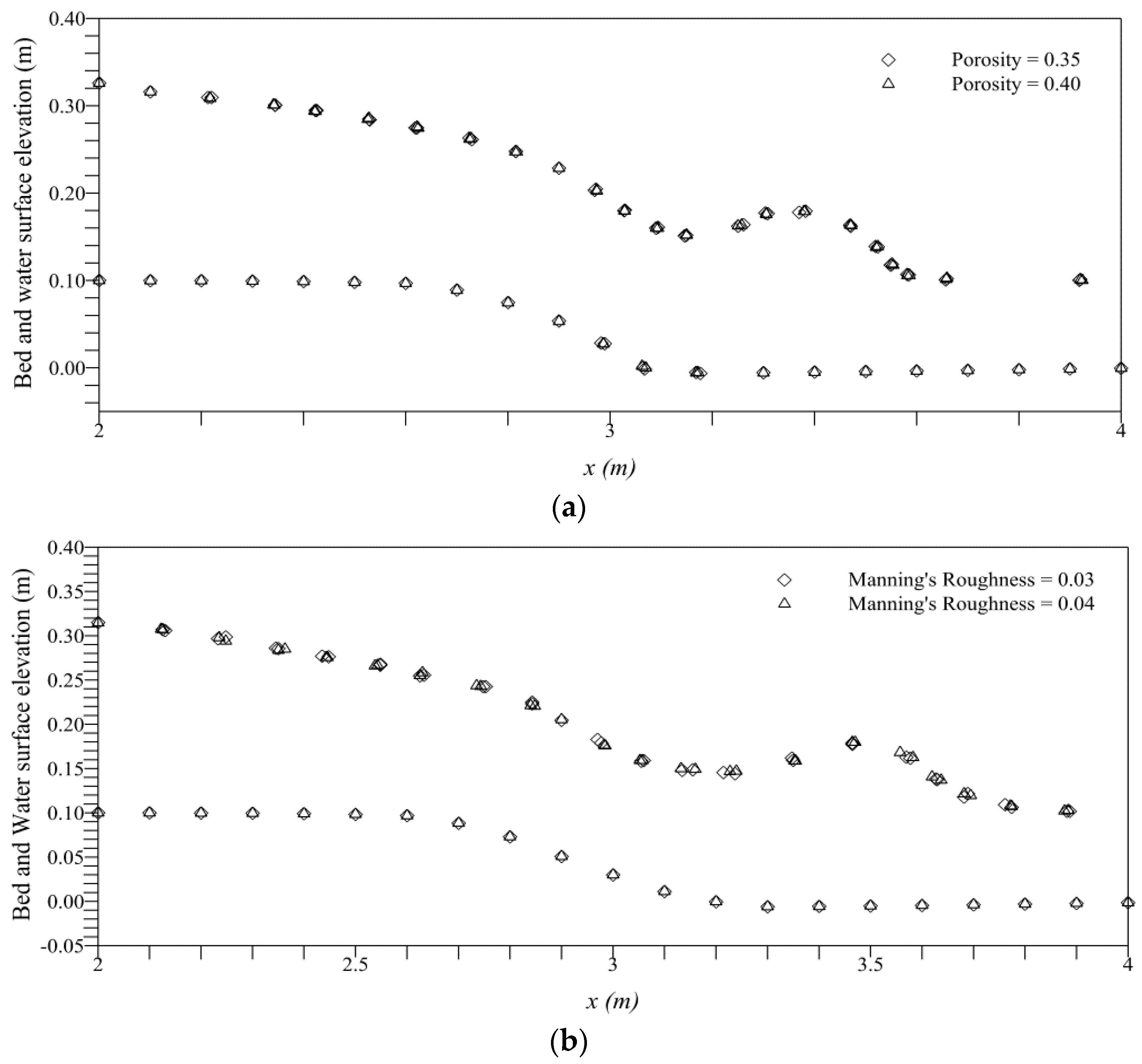
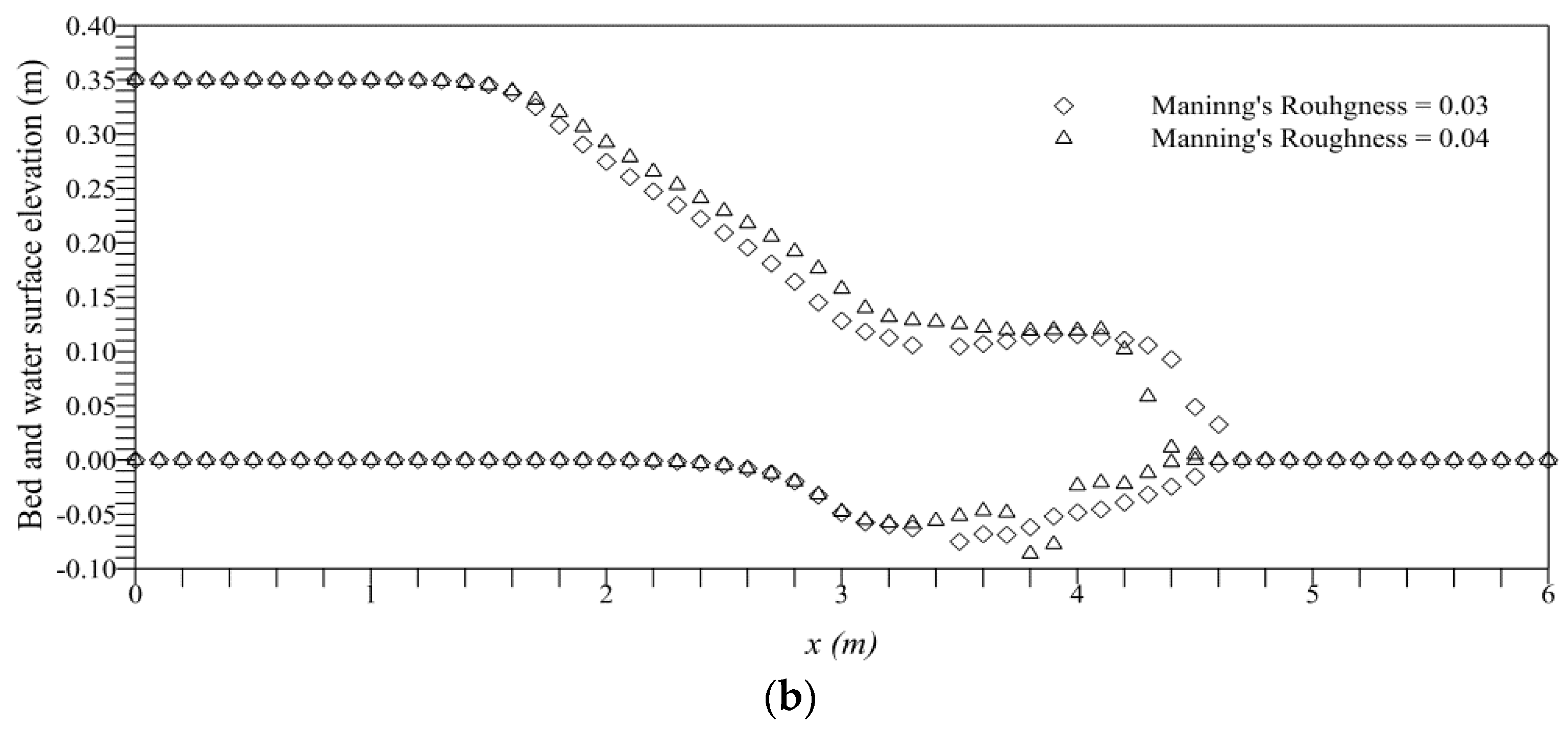
4.5. Sensitivity Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Carrivick, J.L.; Manville, V.; Graettinger, A.; Cronin, S.J. Coupled fluid dynamics-sediment transport modelling of a Crater Lake break-out lahar: Mt. Ruapehu, New Zealand. J. Hydrol. 2010, 388, 399–413. [Google Scholar] [CrossRef]
- Kim, J.; Ivanov, V.Y.; Katopodes, N.D. Modeling erosion and sedimentation coupled with hydrological and overland flow processes at the watershed scale. Water Resour. Res. 2013, 49, 5134–5154. [Google Scholar] [CrossRef]
- Guan, M.; Wright, N.G.; Sleigh, P.A.; Carrivick, L.J. Assessment of hydro-morphodynamic modelling and geomorphological impacts of a sediment-charged jökulhlaup, at Sólheimajökull, Iceland. J. Hydrol. 2015, 530, 336–349. [Google Scholar] [CrossRef]
- Huang, W.; Cao, Z.; Carling, P.; Pender, G. Coupled 2D hydrodynamic and sediment transport modeling of megaflood due to glacier dam-break in Altai Mountains, Southern Siberia. J. Mt. Sci. 2014, 11, 1442–1453. [Google Scholar] [CrossRef]
- Benkhaldoun, F.; Sahmim, S.; Seaïd, M. A two-dimensional finite volume morphodynamic model on unstructured triangular grids. Int. J. Numer. Methods Fluids 2010, 63, 1296–1327. [Google Scholar] [CrossRef]
- Hudson, J.; Damgaard, J.; Dodd, N.; Chesher, T.; Cooper, A. Numerical approaches for 1D morphodynamic modelling. Coast. Eng. 2005, 52, 691–707. [Google Scholar] [CrossRef]
- Liang, Q. A coupled morphodynamic model for applications involving wetting and drying. J. Hydrodyn. Ser. B 2011, 23, 273–281. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.S. One-dimensional modeling of dam-break flow over movable beds. J. Hydraul. Eng. ASCE 2007, 133, 48–58. [Google Scholar] [CrossRef]
- Cao, Z.; Pender, G.; Wallis, S.; Carling, P. Computational dam-break hydraulics over erodible sediment bed. J. Hydraul. Eng. ASCE 2004, 130, 689–703. [Google Scholar] [CrossRef]
- Xia, J.; Lin, B.; Falconer, R.A.; Wang, G. Modelling dam-break flows over mobile beds using a 2D coupled approach. Adv. Water Resour. 2010, 33, 171–183. [Google Scholar] [CrossRef]
- Campisano, A.; Creaco, E.; Modica, C. Experimental and numerical analysis of the scouring effects of flushing waves on sediment deposits. J. Hydrol. 2004, 299, 324–334. [Google Scholar] [CrossRef]
- Hudson, J. Numerical Techniques for Morphodynamic Modelling. Ph.D. Thesis, University of Reading, Reading, UK, October 2001. [Google Scholar]
- Goutière, L.; Soares-Frazão, S.; Savary, C.; Laraichi, T.; Zech, Y. One-dimensional model for transient flows involving bed-load sediment transport and changes in flow regimes. J. Hydraul. Eng. ASCE 2008, 134, 726–735. [Google Scholar] [CrossRef]
- Soares-Frazão, S.; Zech, Y. HLLC scheme with novel wave speed estimators appropriate for two dimensional shallow water flow on erodible bed. Int. J. Numer. Methods Fluids 2011, 66, 1019–1036. [Google Scholar] [CrossRef]
- Grass, A.J. Sediment Transport by Waves and Currents; University College London, Department of Civil Engineering: London, UK, 1981. [Google Scholar]
- Meyer-Peter, E.; Müller, R. Formulas for bed-load transport. In Proceedings of the 2nd Meeting of the International Association for Hydraulic Structures Research, Stockholm, Sweden, 7 June 1948.
- Van Rijn, L.C. Sediment transport, part I: Bed load transport. J. Hydraul. Eng. ASCE 1984, 110, 1431–1456. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Sediment transport, Part II: Suspended load transport. J. Hydraul. Eng. ASCE 1984, 110, 1613–1641. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Sediment transport, part III: Bed forms and alluvial roughness. J. Hydraul. Eng. ASCE 1984, 110, 1733–1754. [Google Scholar] [CrossRef]
- Nielsen, P. Coastal Bottom Boundary Layers and Sediment Transport; World Scientific: Tuck Link, Singapore, 1992; Volume 4. [Google Scholar]
- El Kadi Abderrezzak, K.; Paquier, A. Applicability of sediment transport capacity formulas to dam-break flows over movable beds. J. Hydraul. Eng. ASCE 2010, 137, 209–221. [Google Scholar] [CrossRef]
- Murillo, J.; García-Navarro, P. An Exner-based coupled model for two-dimensional transient flow over erodible bed. J. Comput. Phys. 2010, 229, 8704–8732. [Google Scholar] [CrossRef]
- Liu, X.; Landry, B.; García, M. Two-dimensional scour simulations based on coupled model of shallow water equations and sediment transport on unstructured meshes. Coast. Eng. 2008, 55, 800–810. [Google Scholar] [CrossRef]
- Murillo, J.; García-Navarro, P. Improved Riemann solvers for complex transport in two-dimensional unsteady shallow flow. J. Comput. Phys. 2011, 230, 7202–7239. [Google Scholar] [CrossRef]
- Hudson, J.; Sweby, P.K. Formulations for numerically approximating hyperbolic systems governing sediment transport. J. Sci. Comput. 2003, 19, 225–252. [Google Scholar] [CrossRef]
- Hudson, J.; Sweby, P.K. A high-resolution scheme for the equations governing 2D bed-load sediment transport. Int. J. Numer. Methods Fluids 2005, 47, 1085–1091. [Google Scholar] [CrossRef]
- Castro Díaz, M.J.; Fernández-Nieto, E.D.; Ferreiro, A.; Parés, C. Two-dimensional sediment transport models in shallow water equations. A second order finite volume approach on unstructured meshes. Comput. Methods Appl. Mech. Eng. 2009, 198, 2520–2538. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann problems and the WAF method for solving the two-dimensional shallow water equations. Philos. Trans. R. Soc. Lond. Ser. A Phys. Eng. Sci. 1992, 338, 43–68. [Google Scholar] [CrossRef]
- Batten, P.; Clarke, N.; Lambert, C.; Causon, D. On the choice of wavespeeds for the HLLC Riemann solver. SIAM J. Sci. Comput. 1997, 18, 1553–1570. [Google Scholar] [CrossRef]
- Roe, P. Approximate Riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 1997, 135, 250–258. [Google Scholar] [CrossRef]
- Mottura, L.; Vigevano, L.; Zaccanti, M. An evaluation of Roe’s scheme generalizations for equilibrium real gas flows. J. Comput. Phys. 1997, 138, 354–399. [Google Scholar] [CrossRef]
- Glaister, P. An approximate linearised Riemann solver for the Euler equations for real gases. J. Comput. Phys. 1988, 74, 382–408. [Google Scholar] [CrossRef]
- Hu, X.; Adams, N.; Iaccarino, G. On the HLLC Riemann solver for interface interaction in compressible multi-fluid flow. J. Comput. Phys. 2009, 228, 6572–6589. [Google Scholar] [CrossRef]
- Toro, E. Shock-Capturing Methods for Free-Surface Shallow Flows; Wiley: Chichester, UK, 2001. [Google Scholar]
- Holmes, D.; Connell, S.; Engines, G.A. Solution of the 2D Navier-Stokes Equations on Unstructured Adaptive Grids; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1989. [Google Scholar]
- Delis, A.; Skeels, C.; Ryrie, S. Evaluation of some approximate Riemann solvers for transient open channel flows. J. Hydraul. Res. 2000, 38, 217–231. [Google Scholar] [CrossRef]
- Kim, D.-H.; Cho, Y.-S.; Kim, H.-J. Well-Balanced Scheme between Flux and Source Terms for Computation of Shallow-Water Equations over Irregular Bathymetry. J. Eng. Mech. 2008, 134, 277–290. [Google Scholar] [CrossRef]
- Li, S.; Duffy, C.J. Fully coupled approach to modeling shallow water flow, sediment transport, and bed evolution in rivers. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Stoker, J.J. Water Waves: The Mathematical Theory with Applications; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 36. [Google Scholar]
- Bellal, M. Fluvial Morphodynamics in Super and Transcritical Flows: Experimental and Analytical Approaches. Ph.D. Thesis, University College London, London, UK, August 2012. [Google Scholar]
- Briganti, R.; Dodd, N.; Kelly, D.; Pokrajac, D. An efficient and flexible solver for the simulation of the morphodynamics of fast evolving flows on coarse sediment beaches. Int. J. Numer. Methods Fluids 2012, 69, 859–877. [Google Scholar] [CrossRef]
- Kelly, D.M.; Dodd, N. Floating grid characteristics method for unsteady flow over a mobile bed. Comput. Fluids 2009, 38, 899–909. [Google Scholar] [CrossRef]
- Spinewine, B.; Zech, Y. Small-scale laboratory dam-break waves on movable beds. J. Hydraul. Res. 2007, 45, 73–86. [Google Scholar] [CrossRef]
- Evangelista, S.; Altinakar, M.S.; Di Cristo, C.; Leopardi, A. Simulation of dam-break waves on movable beds using a multi-stage centered scheme. Int. J. Sediment Res. 2013, 28, 269–284. [Google Scholar] [CrossRef]
- Guan, M.; Wright, N.G.; Andrew Sleigh, P. Multimode morphodynamic model for sediment-laden flows and geomorphic impacts. J. Hydraul. Eng. ASCE 2015, 141. [Google Scholar] [CrossRef]





© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rehman, K.; Cho, Y.-S. Bed Evolution under Rapidly Varying Flows by a New Method for Wave Speed Estimation. Water 2016, 8, 212. https://doi.org/10.3390/w8050212
Rehman K, Cho Y-S. Bed Evolution under Rapidly Varying Flows by a New Method for Wave Speed Estimation. Water. 2016; 8(5):212. https://doi.org/10.3390/w8050212
Chicago/Turabian StyleRehman, Khawar, and Yong-Sik Cho. 2016. "Bed Evolution under Rapidly Varying Flows by a New Method for Wave Speed Estimation" Water 8, no. 5: 212. https://doi.org/10.3390/w8050212





