Understanding Persistence to Avoid Underestimation of Collective Flood Risk
Abstract
:1. Introduction
2. Data and Methodology
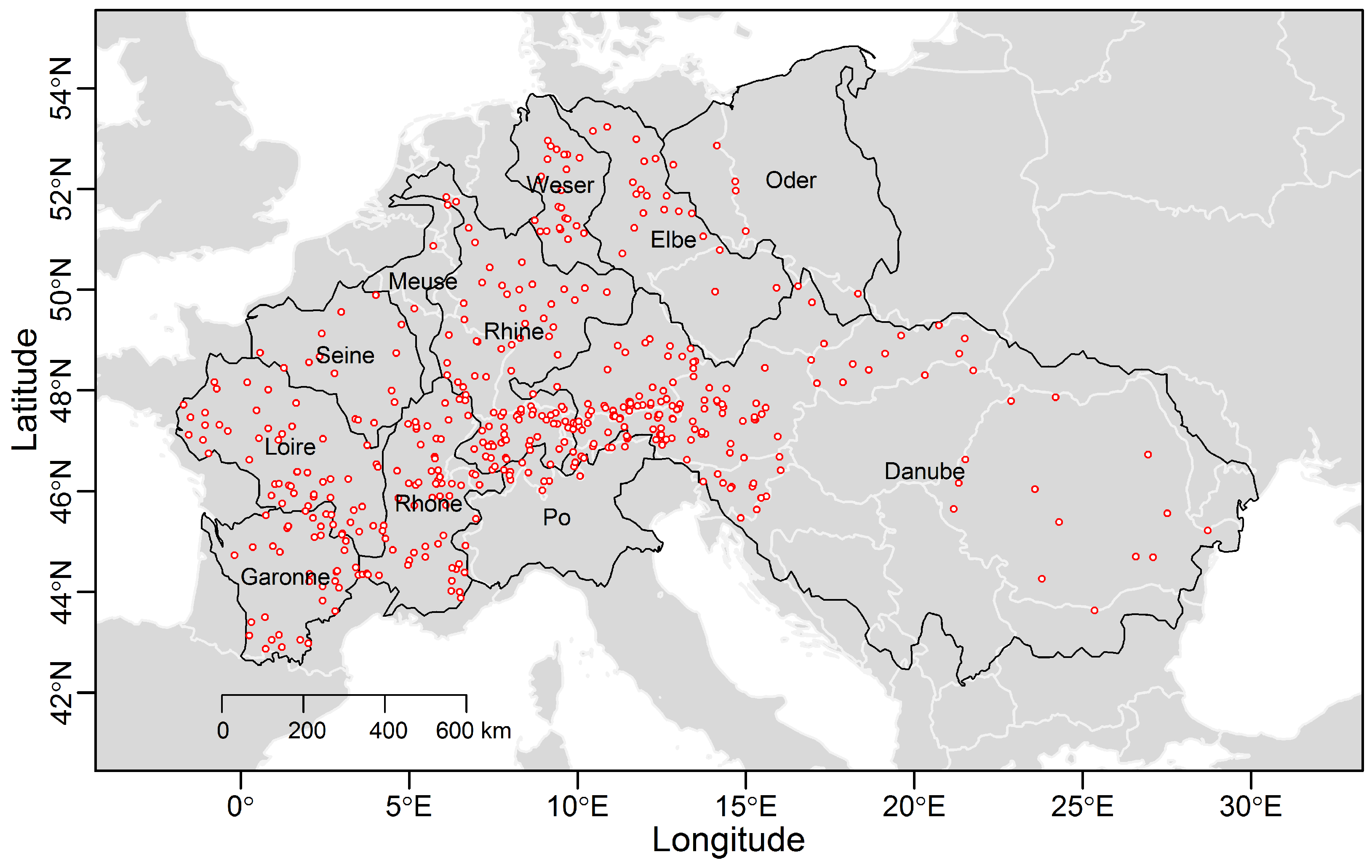
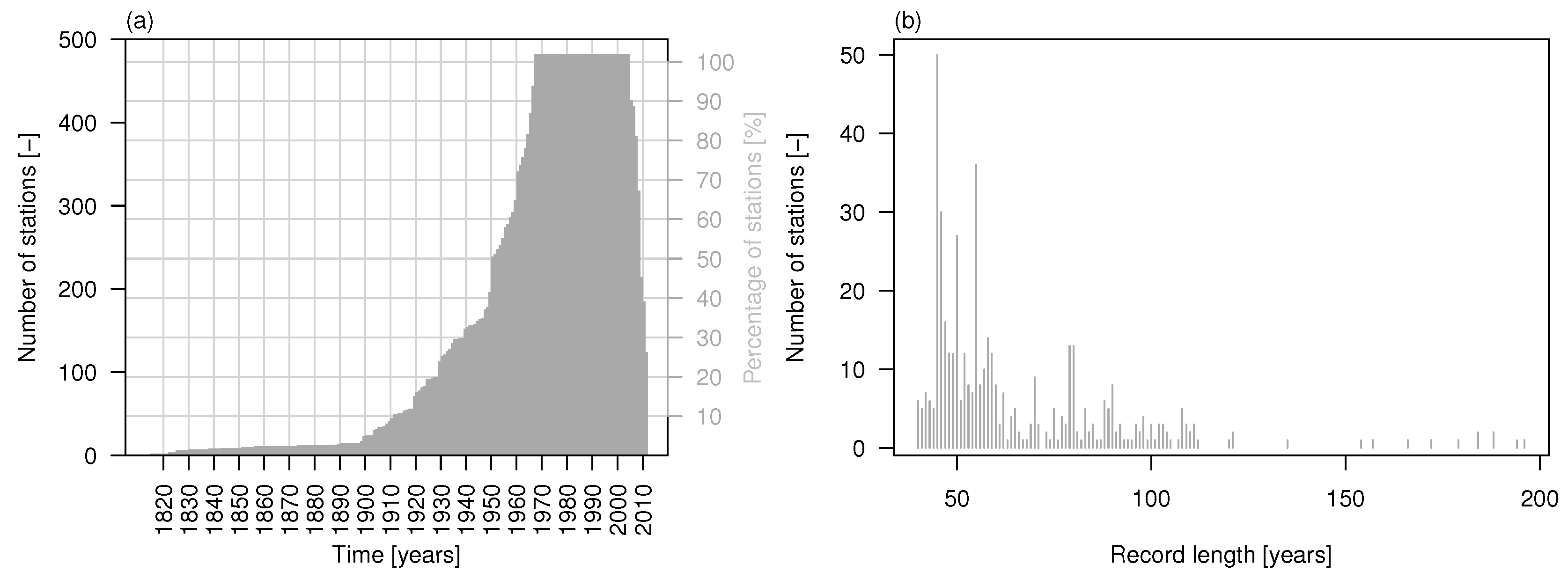
2.1. Data
2.2. Methods
3. Results
3.1. Preliminary Remarks
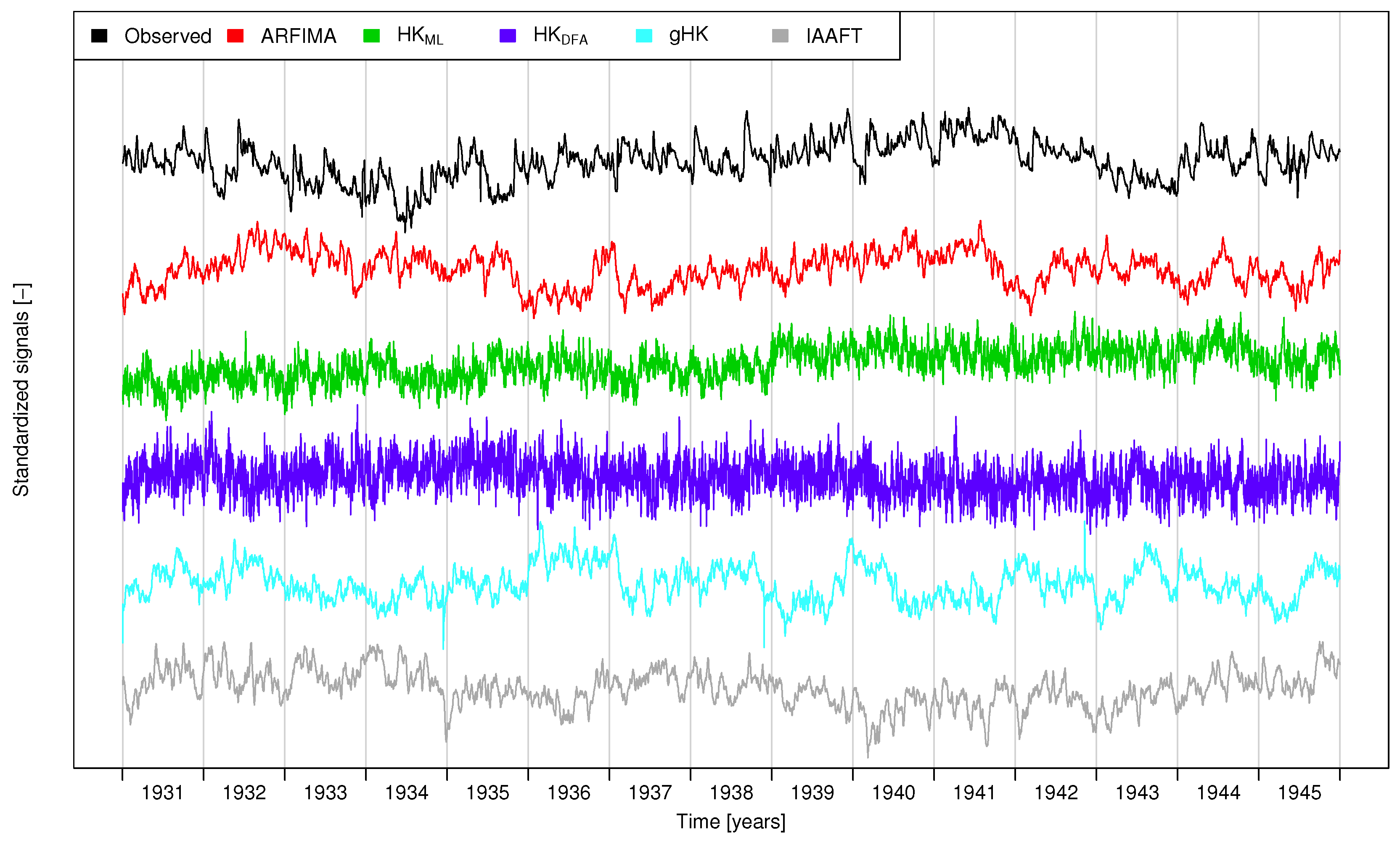
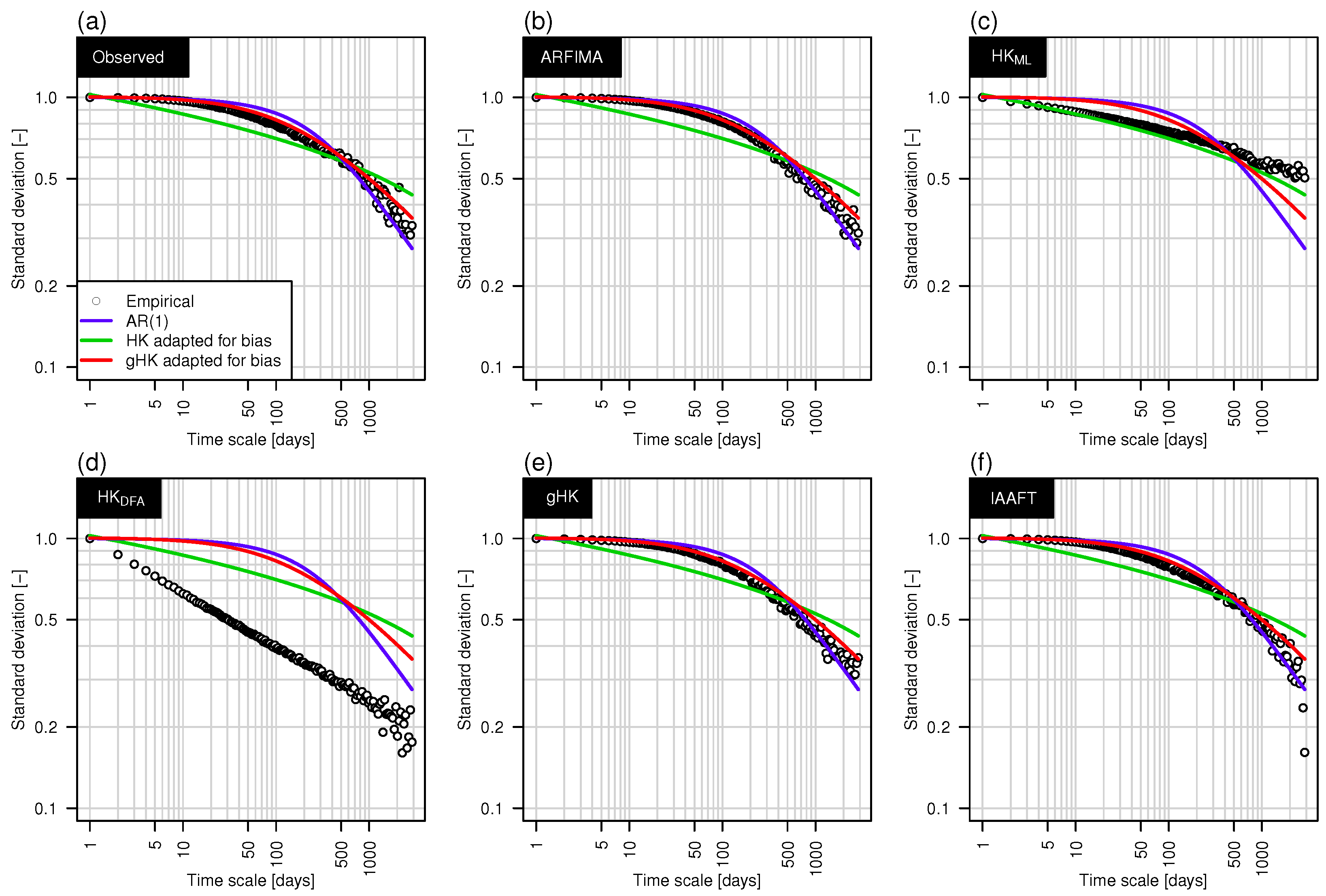
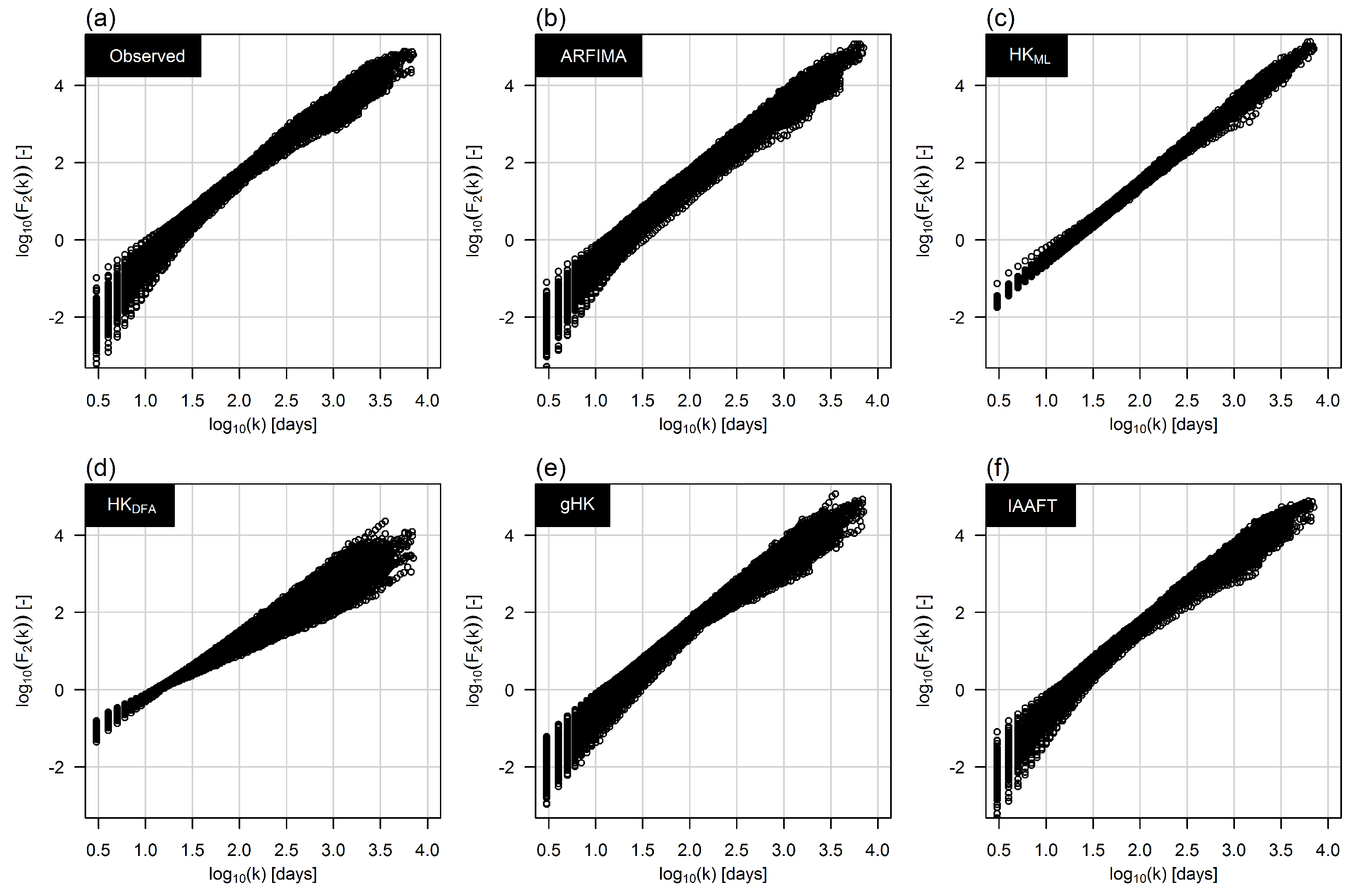
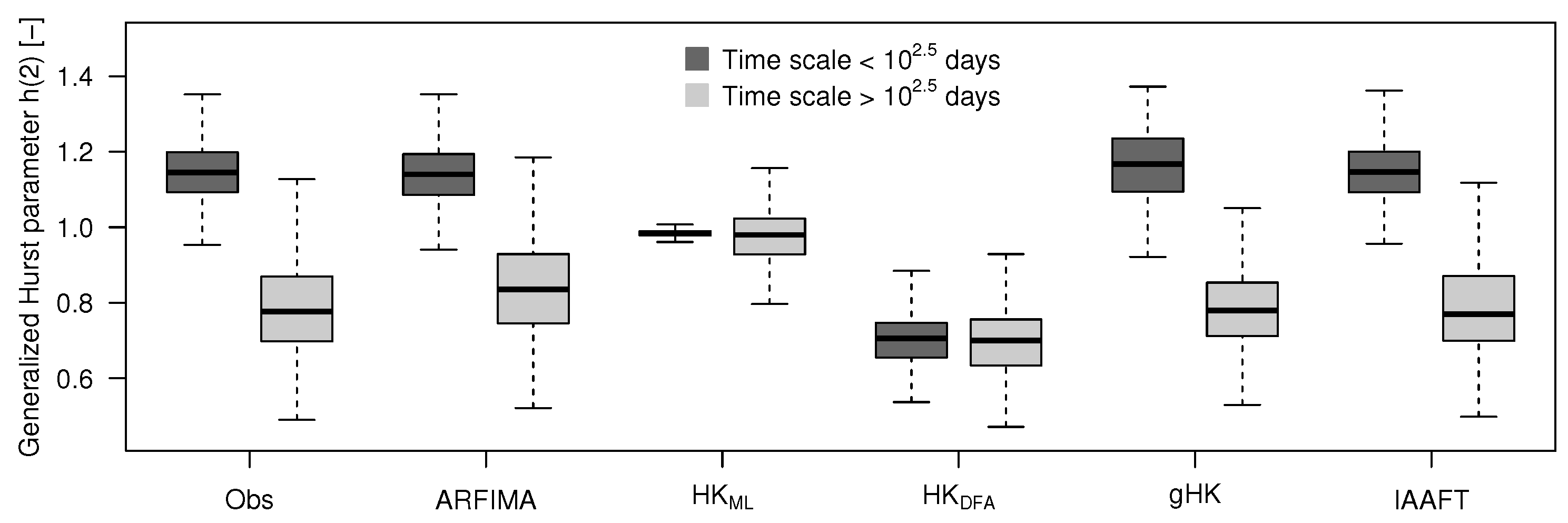
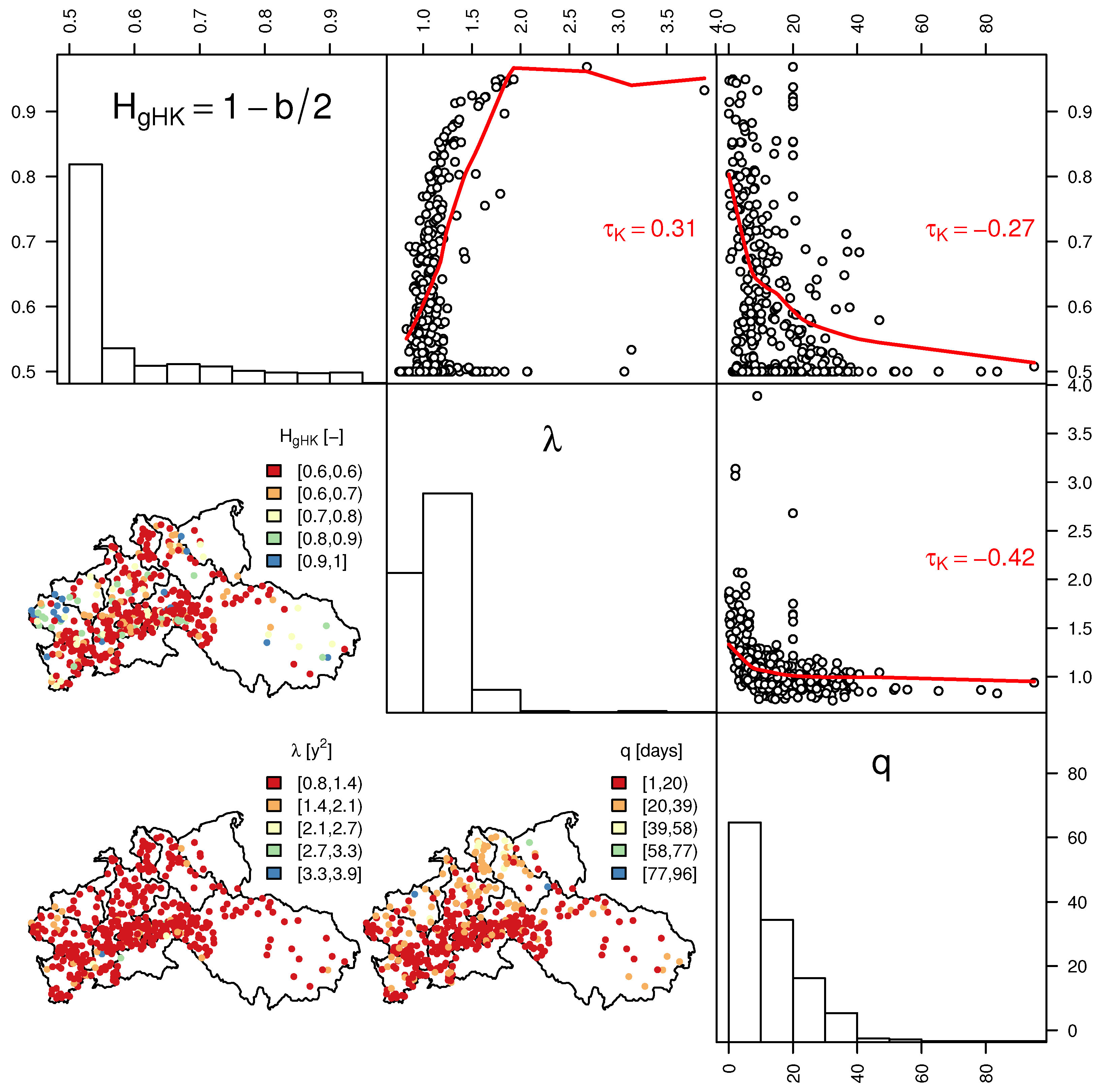
3.2. Climacogram Analysis and DFA: Highlighting SRD and LRD
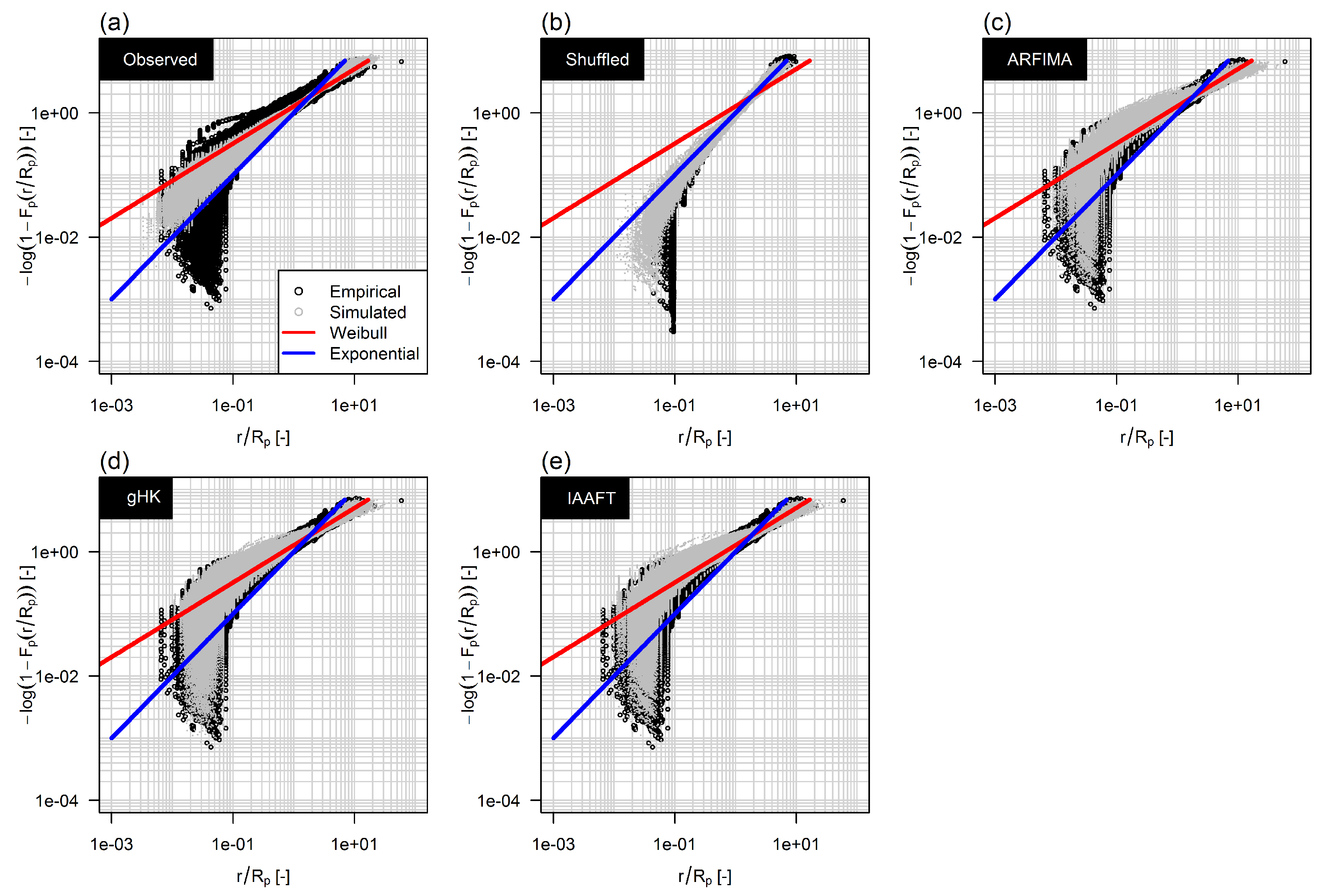
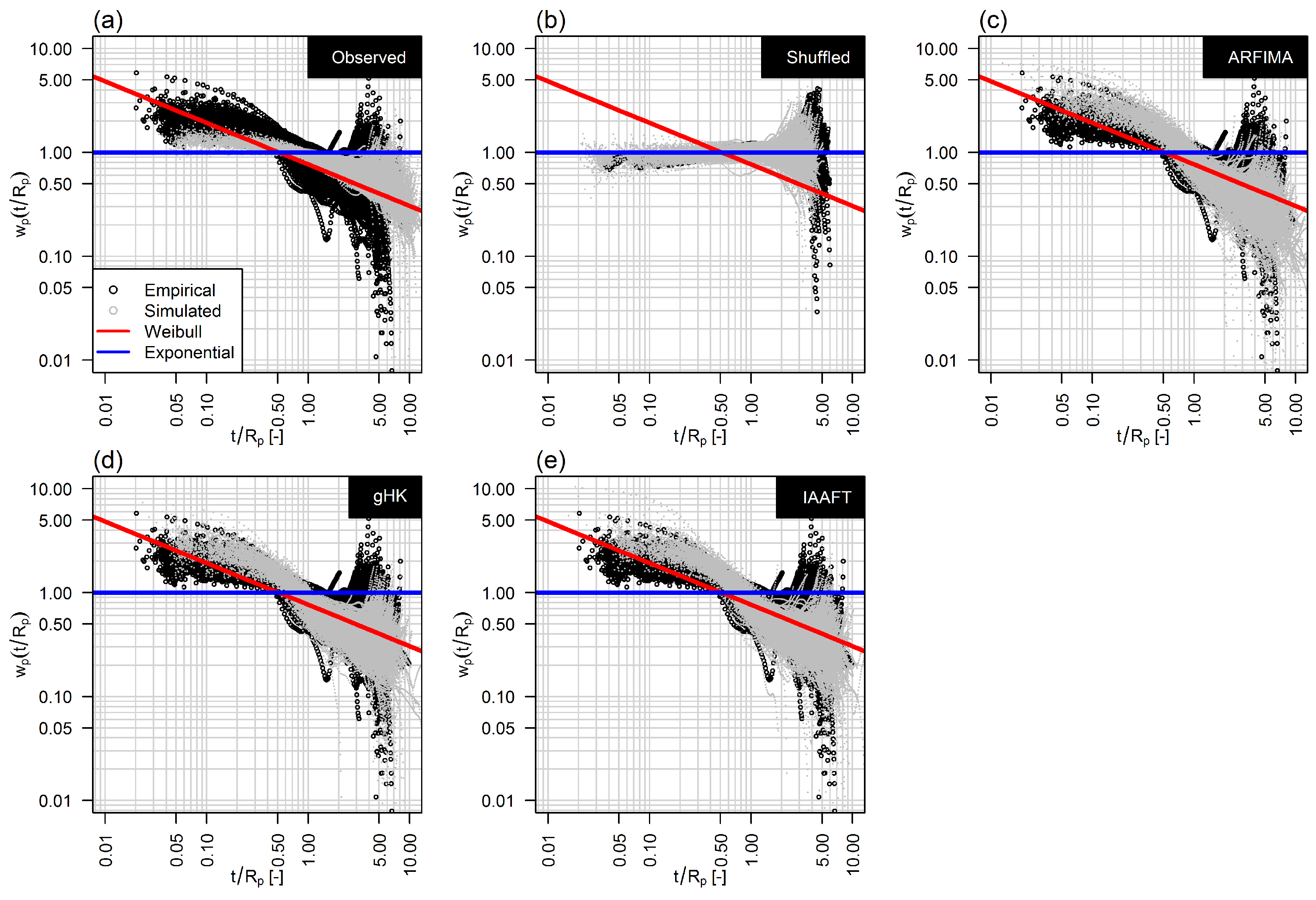
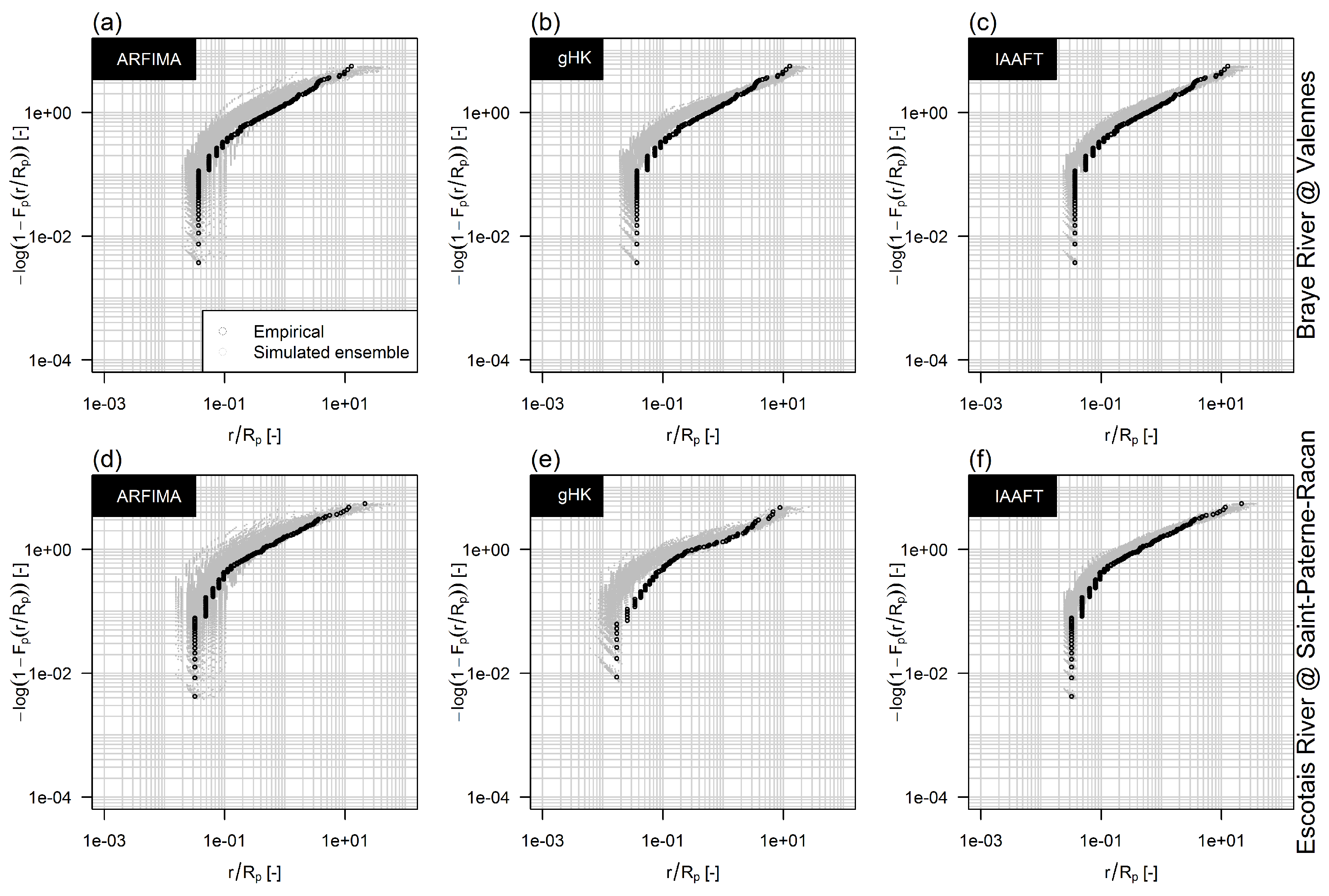
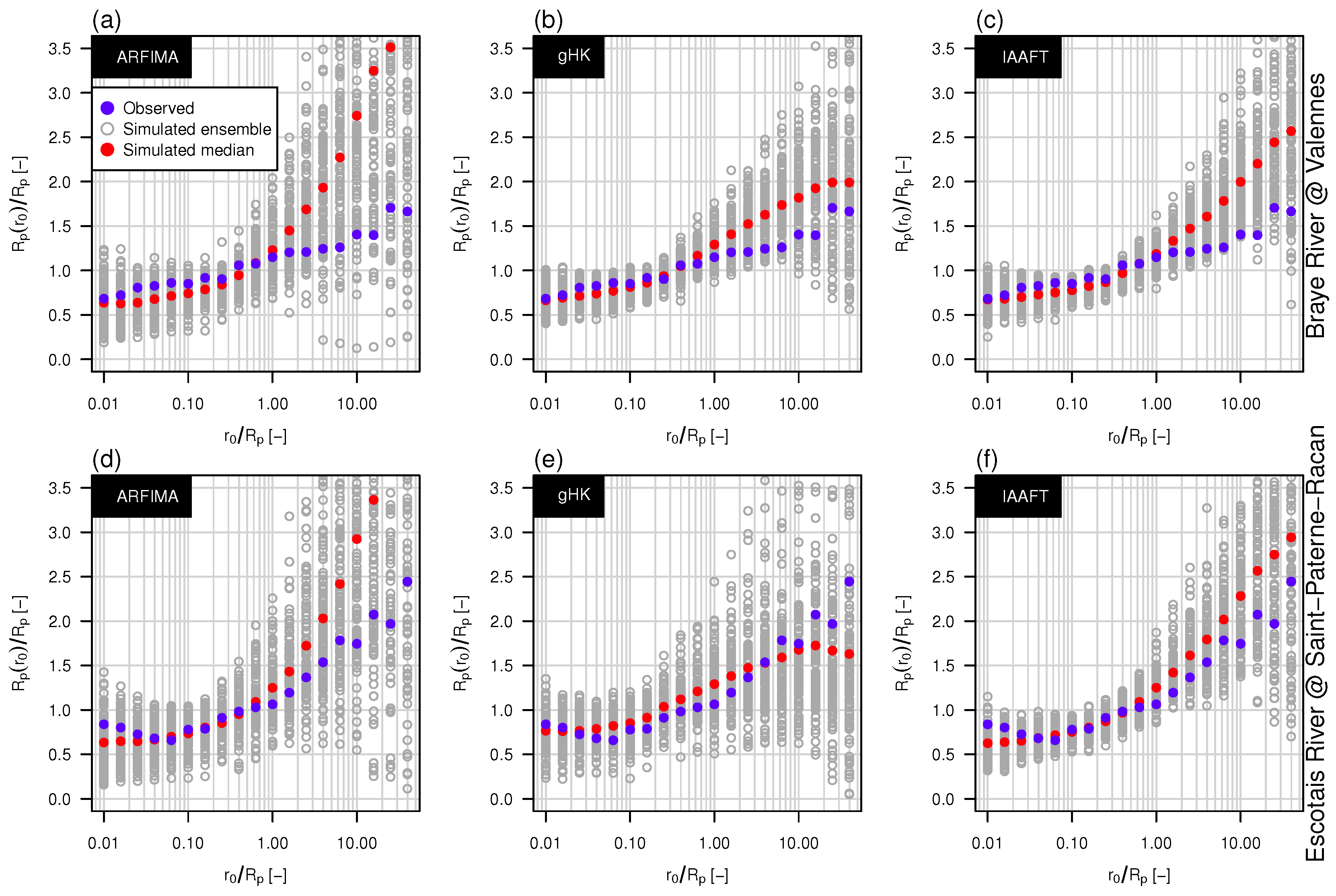
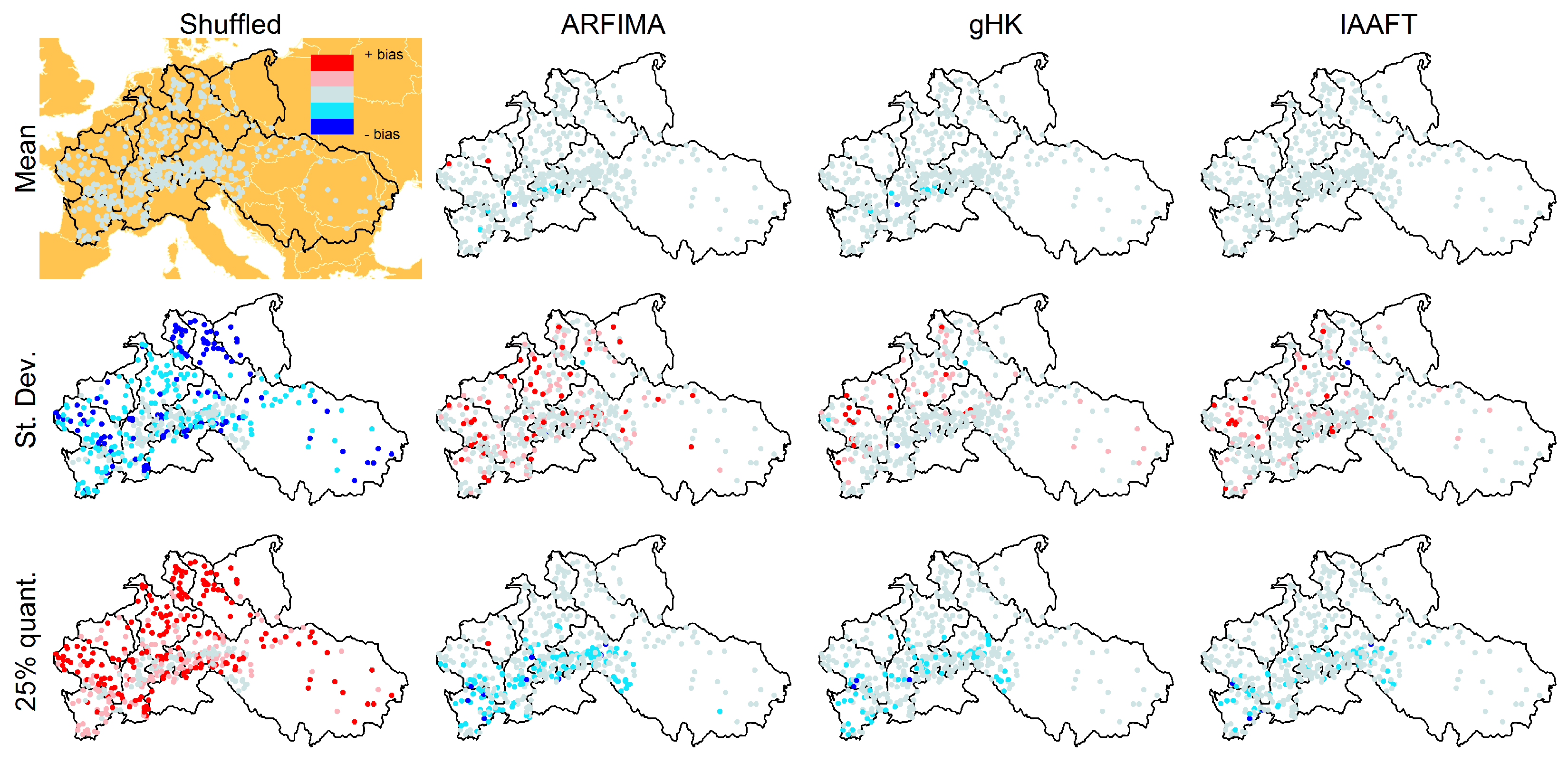
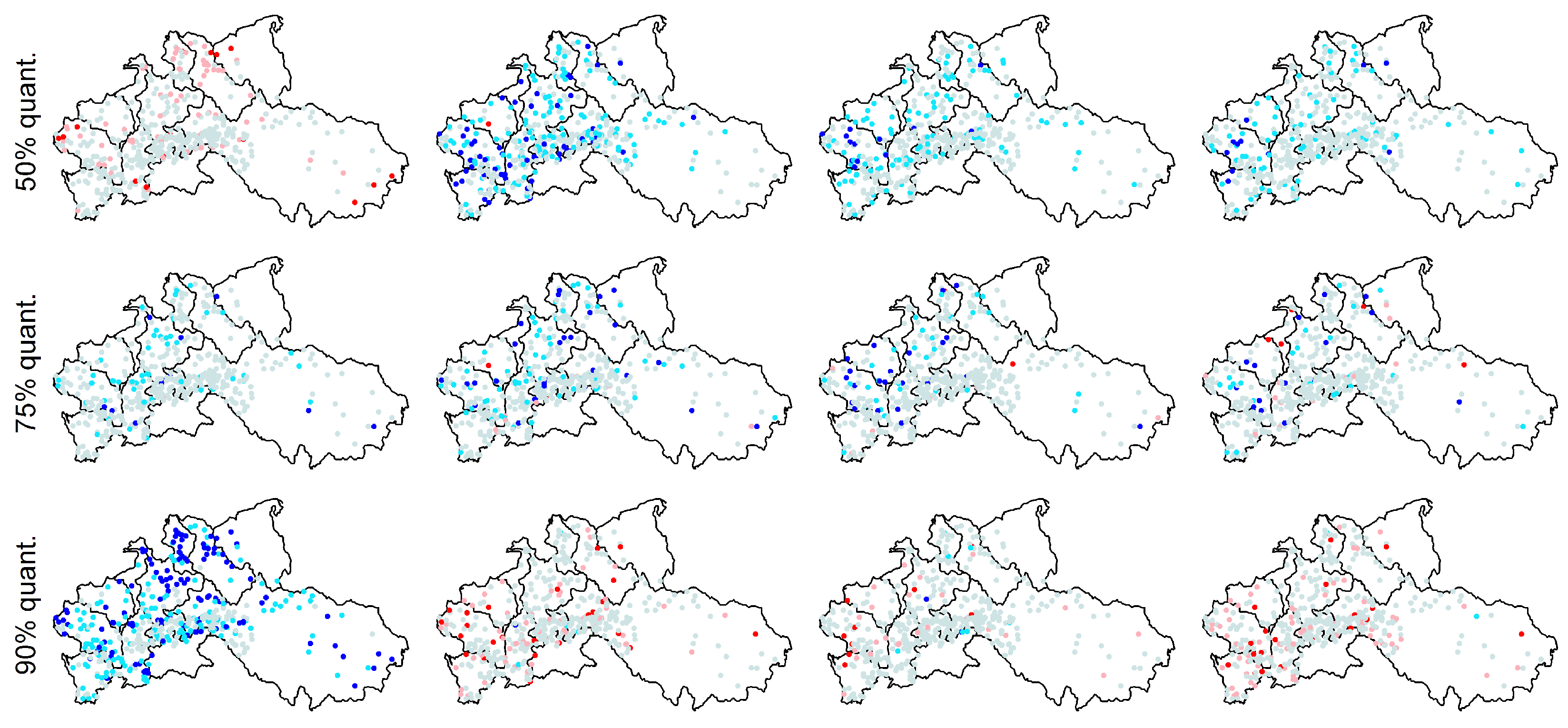
3.3. The Effect of Persistence on Return Intervals’ Statistics
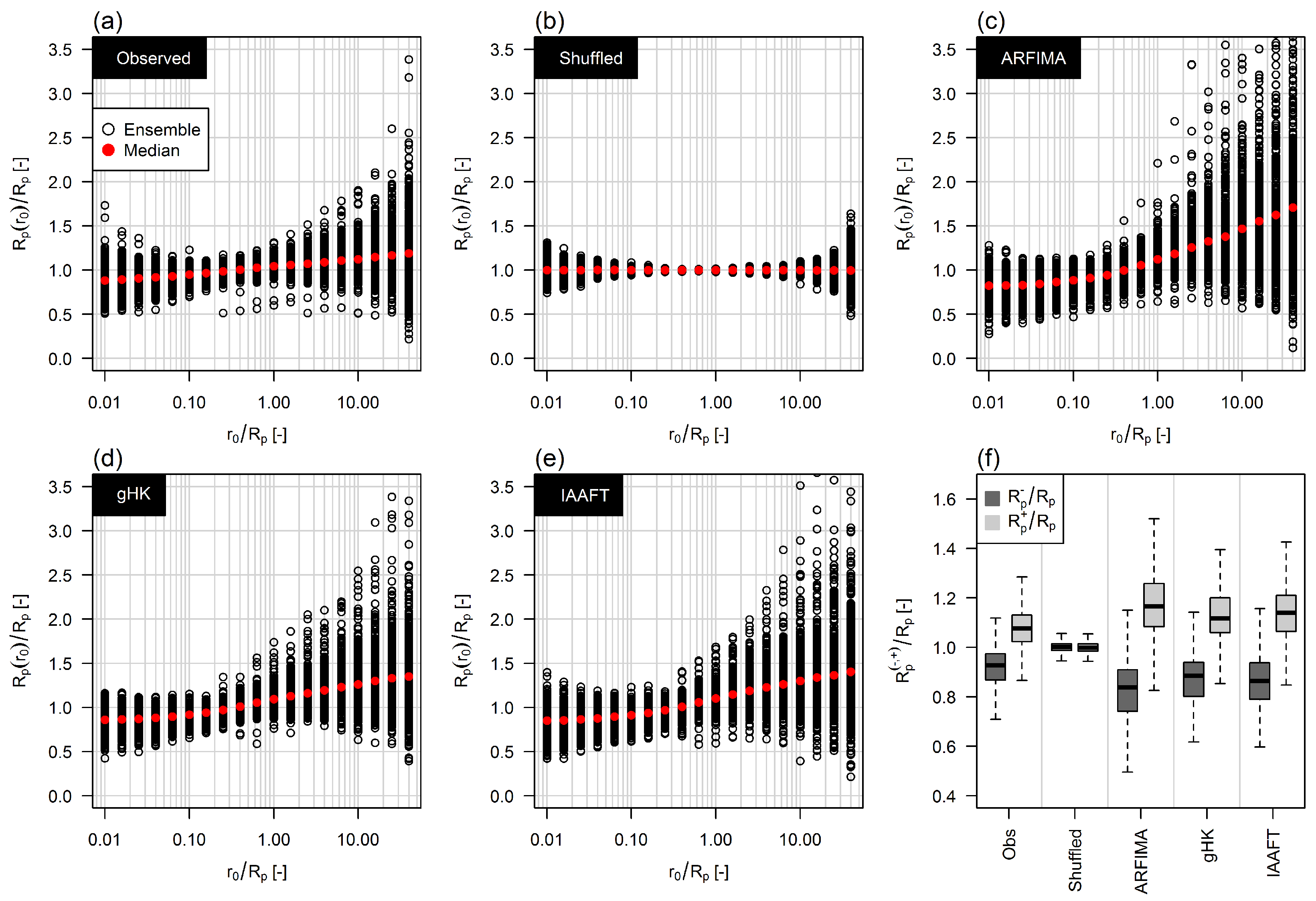
3.4. The Effect of Sampling Uncertainty of Return Intervals’ Statistics
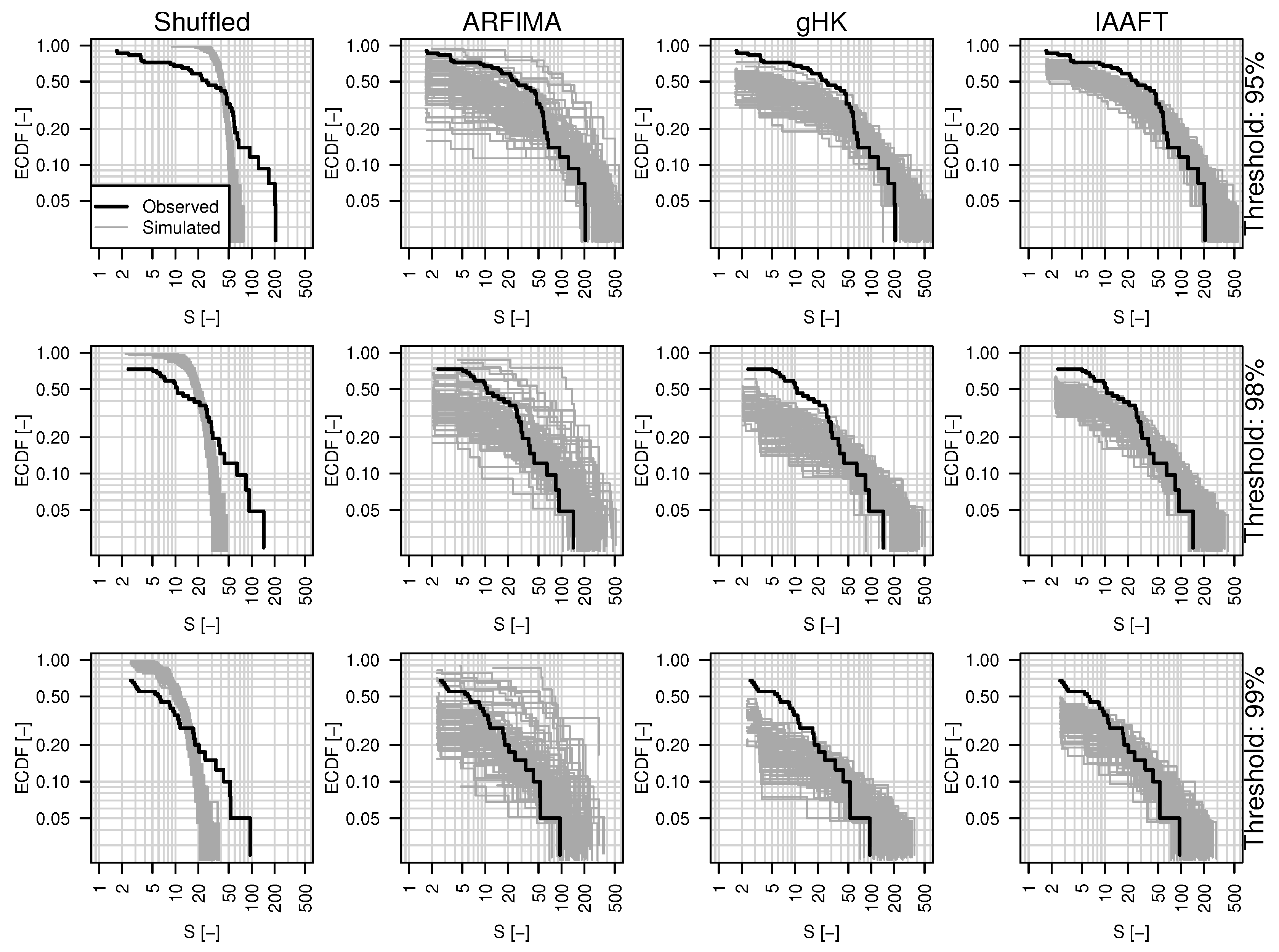
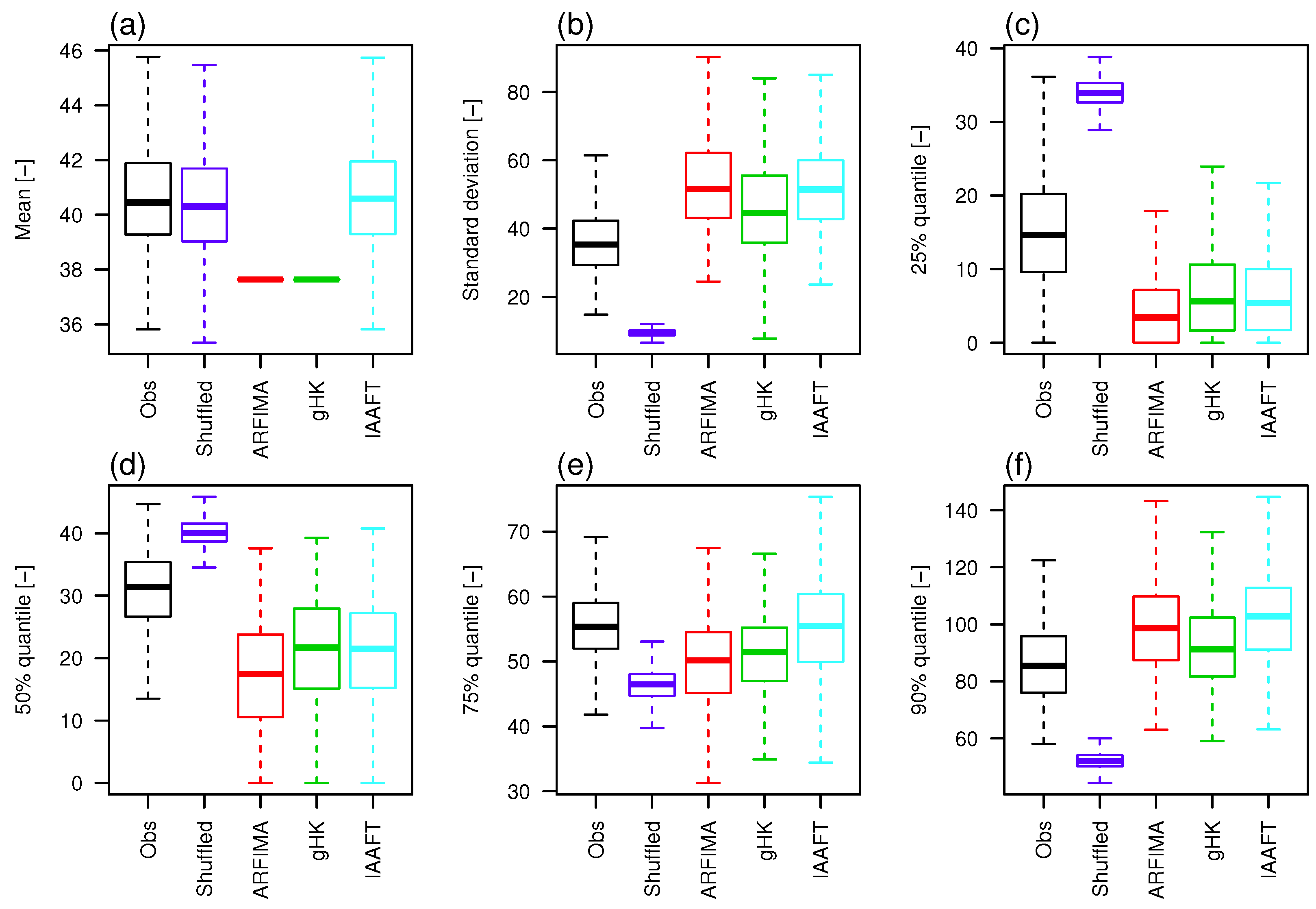
3.5. The Effect of Persistence on Collective Risk
4. Conclusions
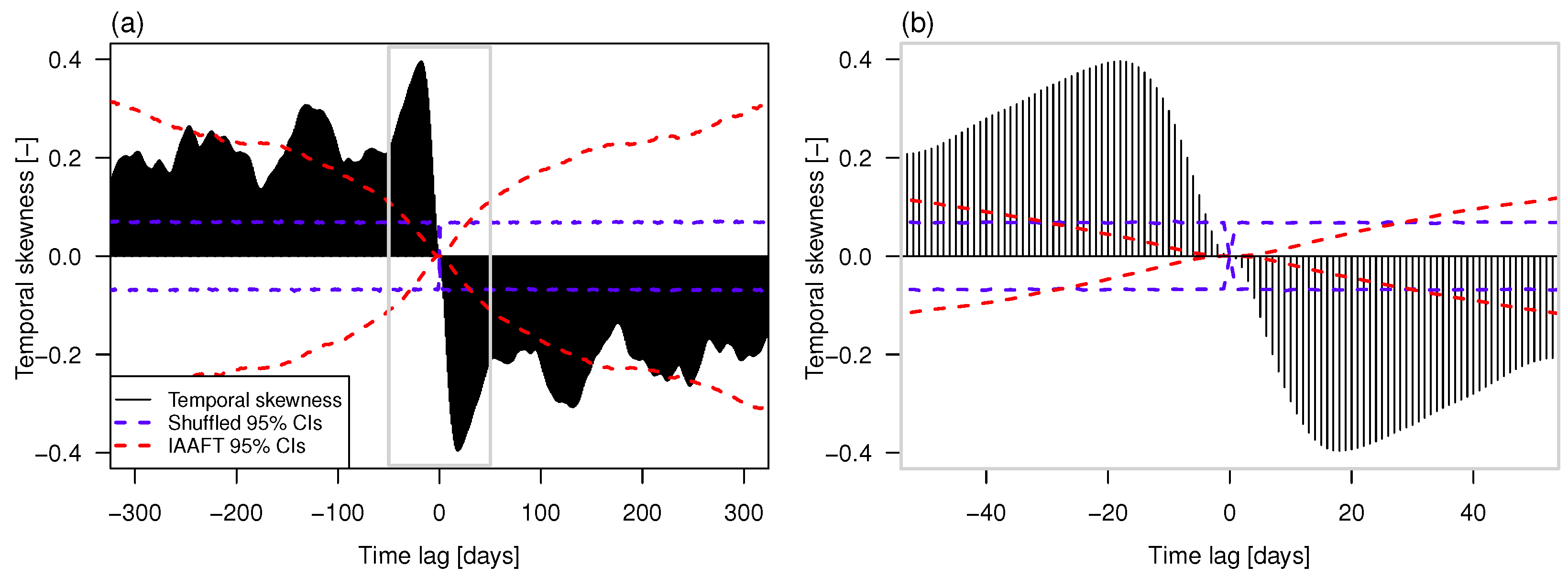
- Extending previous analyses [19] and resorting to recently proposed tools such as bias-corrected climacograms and gHK model (merging SRD and LRD), we strengthen the empirical evidence that the crossover in DFA patterns and the behavior of empirical climacograms of mean daily stream flow signals can be attributed to the interplay of SRD and LRD rather than residual seasonality as sometimes argued in the literature. This conclusion is confirmed by the results corresponding to synthetic signals showing only LRD (simulated by HK model) or SRD and LRD (simulated by ARFIMA and gHK models and the IAAFT resampling method). In particular, gHK seems to be a parsimonious, flexible and physically consistent option compared with highly-parameterized ARFIMA models. However, since all these models/methods are linear, they can reproduce flow characteristics up to the second order, thus excluding the observed temporal asymmetry, which can be measured by third-order temporal coefficient of skewness. Time irreversibility provides further evidence for nonlinearity of stream flow dynamics [73] , thus confirming by a different analysis the stream flow nonlinear behavior recognized by Kantelhardt et al. [19] by multifractal DFA. Our analyses also show that the recognition of possible LRD requires additional care and need to account for the effect of SRD, and use suitable processes as benchmark for comparisons and validations of empirical results.
- Focusing on the behavior of the return intervals between over-threshold values, our results further confirm the behavior previously highlighted by e.g., Bunde et al. [69], and Bogachev and Bunde [32] for less extensive stream flow data sets. Namely, return intervals tend to follow a sub-exponential (Weibull-like) distribution, implying a higher (smaller) probability of observing long (short) return intervals longer (shorter) than expected under independence (i.e., Poisson process with exponentially distributed inter-arrival times). Moreover, the statistics of conditional return periods (expected return intervals) show that the sequence of return intervals is no longer independent, meaning that short (long) return intervals tend to follow short (long) return intervals. This partly explains the so-called clustering of extreme events observed in many natural phenomena [69], and has important practical consequences. For example, reviewing factors influencing private flood mitigation behavior, Bubeck et al. [74] highlighted that experience with floods is often considered to have a great impact on the recognition of risk, resulting for instance in a positive relationship between individual flood risk perceptions in the Netherlands and demand for flood insurance [75]. Moreover, an important role is also played by the severity of the experienced negative consequences along with the timing of the previous experience, since it can be expected that floods experienced in the distant past have only a limited influence on individual risk perceptions and mitigation behavior later [74]. In this respect, Bubeck et al. [74] highlighted that the International Commission for the Protection of the Rhine (ICPR) estimates that flood awareness mostly diminishes within seven years after a flood and that only catastrophic disasters are remembered in the long term [76], and that flood damage is significantly lower in areas where people have recently experienced a flood event, which is attributed to a better preparedness of the population in the direct aftermath of a flood [77,78,79]. The better understanding of the causes of flood clustering is therefore paramount to set up effective mitigation strategies that are not affected by the flood risk perception related to the alternation of flood-rich and flood-poor periods.
- From a collective risk perspective, the previous remarks are further strengthened by the empirical evidence of the positive correlation of the average intensity of extreme flows and the number of events over one-year time windows, implying that years that are more active in terms of number of events tend to exhibit more extreme events also in terms of average magnitude. This behavior results in distributions of the cumulated flow (which can be seen as a proxy of the potential annual losses) characterized by a spike of probability at zero, which describes the probability of years with no events, and a heavier upper tail, which indicates a probability of more extreme annual losses larger than expected under independence. Concerning these aspects, the linear models used in this study only partly reproduce the observed behavior. In particular, since IAAFT preserves almost exactly both marginal distribution and the empirical power spectrum, we argue that nonlinearity might be the cause of the observed discrepancies between observations and simulations. However, other factors such as river training, dam building and operation, and other anthropogenic interventions cannot be excluded. Therefore, we suggest repeating the analyses reported in this study on data sets of (reasonably) natural stream flow records such as those of the U.S. Geological Survey Hydro-Climatic Data Network (HCDN-2009; [80]).
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
References
- Mudelsee, M.; Börngen, M.; Tetzlaff, G.; Grünewald, U. Extreme floods in central Europe over the past 500 years: Role of cyclone pathway “Zugstrasse Vb”. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Glaser, R.; Riemann, D.; Schönbein, J.; Barriendos, M.; Brázdil, R.; Bertolin, C.; Camuffo, D.; Deutsch, M.; Dobrovolný, P.; van Engelen, A.; et al. The variability of European floods since AD 1500. Clim. Chang. 2010, 101, 235–256. [Google Scholar] [CrossRef]
- Hall, J.; Arheimer, B.; Borga, M.; Brázdil, R.; Claps, P.; Kiss, A.; Kjeldsen, T.R.; Kriaučiūnienė, J.; Kundzewicz, Z.W.; Lang, M.; et al. Understanding flood regime changes in Europe: A state-of-the-art assessment. Hydrol. Earth Syst. Sci. 2014, 18, 2735–2772. [Google Scholar] [CrossRef] [Green Version]
- Barredo, J.I. Major flood disasters in Europe: 1950–2005. Nat. Hazards 2007, 42, 125–148. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Pinskwar, I.; Brakenridge, G.R. Large floods in Europe, 1985–2009. Hydrol. Sci. J. 2013, 58, 1–7. [Google Scholar] [CrossRef]
- Montanari, A. Hydrology of the Po River: Looking for changing patterns in river discharge. Hydrol. Earth Syst. Sci. 2012, 16, 3739–3747. [Google Scholar] [CrossRef]
- Hurst, H.E. Long–term storage capacity of reservoirs. Trans. Am. Soc. Civil Eng. 1951, 116, 770–808. [Google Scholar]
- Taqqu, M.S.; Teverovsky, V.; Willinger, W. Estimators for long-range dependence: An empirical study. Fractals 1995, 3, 785–798. [Google Scholar] [CrossRef]
- Malamud, B.D.; Turcotte, D.L. Self-affine time series: Measures of weak and strong persistence. J. Stat. Plan. Inference 1999, 80, 173–196. [Google Scholar]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Serinaldi, F. Use and misuse of some Hurst parameter estimators applied to stationary and non-stationary financial time series. Phys. A Stat. Mech. Appl. 2010, 389, 2770–2781. [Google Scholar] [CrossRef]
- Tyralis, H.; Koutsoyiannis, D. Simultaneous estimation of the parameters of the Hurst-Kolmogorov stochastic process. Stoch. Environ. Res. Risk Assess. 2011, 25, 21–33. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Ness, J.W.V. Fractional Brownian Motions, Fractional Noises and Applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Hosking, J.R.M. Fractional differencing. Biometrika 1981, 68, 165–176. [Google Scholar] [CrossRef]
- Beran, J. Statistics for Long-Memory Processes; Chapman & Hall/CRC Monographs on Statistics & Applied Probability: Taylor & Francis: Boca Raton, FL, USA, 1994. [Google Scholar]
- Hipel, K.W.; McLeod, A.I. Time Series Modelling of Water Resources and Environmental Systems; Developments in Water Science, Elsevier Science: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Dimitriadis, P.; Koutsoyiannis, D. Climacogram versus autocovariance and power spectrum in stochastic modelling for Markovian and Hurst-Kolmogorov processes. Stoch. Environ. Res. Risk Assess. 2015, 29, 1649–1669. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Rybski, D.; Zschiegner, S.A.; Braun, P.; Koscielny-Bunde, E.; Livina, V.; Havlin, S.; Bunde, A. Multifractality of river runoff and precipitation: Comparison of fluctuation analysis and wavelet methods. Phys. A Stat. Mech. Appl. 2003, 330, 240–245. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Koscielny-Bunde, E.; Rybski, D.; Braun, P.; Bunde, A.; Havlin, S. Long-term persistence and multifractality of precipitation and river runoff records. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Rao, A.; Bhattacharya, D. Effect of Short-Term Memory on Hurst Phenomenon. J. Hydrol. Eng. 2001, 6, 125–131. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Montanari, A. Statistical analysis of hydroclimatic time series: Uncertainty and insights. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Wang, W.; van Gelder, P.H.A.J.M.; Vrijling, J.K.; Chen, X. Detecting long-memory: Monte Carlo simulations and application to daily streamflow processes. Hydrol. Earth Syst. Sci. 2007, 11, 851–862. [Google Scholar] [CrossRef]
- Montanari, A.; Rosso, R.; Taqqu, M.S. Fractionally differenced ARIMA models applied to hydrologic time series: Identification, estimation, and simulation. Water Resour. Res. 1997, 33, 1035–1044. [Google Scholar] [CrossRef]
- Montanari, A.; Longoni, M.; Rosso, R. A seasonal long-memory stochastic model for the simulation of daily river flows. Phys. Chem. Earth B Hydrol. Oceans Atmos. 1999, 24, 319–324. [Google Scholar] [CrossRef]
- Montanari, A.; Rosso, R.; Taqqu, M.S. A seasonal fractional ARIMA model applied to the Nile River monthly flows at Aswan. Water Resour. Res. 2000, 36, 1249–1259. [Google Scholar] [CrossRef]
- Elek, P.; Márkus, L. A long range dependent model with nonlinear innovations for simulating daily river flows. Nat. Hazards Earth Syst. Sci. 2004, 4, 277–283. [Google Scholar] [CrossRef]
- Eichner, J.F.; Kantelhardt, J.W.; Bunde, A.; Havlin, S. Extreme value statistics in records with long-term persistence. Phys. Rev. E 2006, 73. [Google Scholar] [CrossRef] [PubMed]
- Eichner, J.F.; Kantelhardt, J.W.; Bunde, A.; Havlin, S. Statistics of return intervals in long-term correlated records. Phys. Rev. E 2007, 75, 011128. [Google Scholar] [CrossRef] [PubMed]
- Eichner, J.F.; Kantelhardt, J.W.; Bunde, A.; Havlin, S. The Statistics of Return Intervals, Maxima, and Centennial Events Under the Influence of Long-Term Correlations. In In Extremis; Kropp, J., Schellnhuber, H.J., Eds.; Springer: Berlin, Geramny; Heidelberg, Germany, 2011; pp. 2–43. [Google Scholar]
- Bogachev, M.I.; Eichner, J.F.; Bunde, A. Effect of nonlinear correlations on the statistics of return intervals in multifractal data sets. Phys. Rev. Lett. 2007, 99. [Google Scholar] [CrossRef] [PubMed]
- Bogachev, M.I.; Eichner, J.F.; Bunde, A. The effects of multifractality on the statistics of return intervals. Eur. Phys. J. Spec. Top. 2008, 161, 181–193. [Google Scholar] [CrossRef]
- Bogachev, M.I.; Bunde, A. Universality in the precipitation and river runoff. Europhys. Lett. 2012, 97. [Google Scholar] [CrossRef]
- Matsoukas, C.; Islam, S.; Rodriguez-Iturbe, I. Detrended fluctuation analysis of rainfall and streamflow time series. J. Geophys. Res. Atmos. 2000, 105, 29165–29172. [Google Scholar] [CrossRef]
- Labat, D.; Masbou, J.; Beaulieu, E.; Mangin, A. Scaling behavior of the fluctuations in stream flow at the outlet of karstic watersheds, France. J. Hydrol. 2011, 410, 162–168. [Google Scholar] [CrossRef]
- Serinaldi, F.; Zunino, L.; Rosso, O.A. Complexity-entropy analysis of daily stream flow time series in the continental United States. Stoch. Environ. Res. Risk Assess. 2014, 28, 1685–1708. [Google Scholar] [CrossRef]
- Szolgayova, E.; Laaha, G.; Blöschl, G.; Bucher, C. Factors influencing long range dependence in streamflow of European rivers. Hydrol. Processes 2014, 28, 1573–1586. [Google Scholar] [CrossRef]
- Kaas, R.; Goovaerts, M.; Dhaene, J.; Denuit, M. Modern Actuarial Risk Theory: Using R; Springer Science & Business Media: New York, NY, USA, 2008; Volume 128. [Google Scholar]
- Cleveland, W.S.; Devlin, S.J. Locally-Weighted Regression: An Approach to Regression Analysis by Local Fitting. J. Am. Stat. Assoc. 1988, 83, 596–610. [Google Scholar] [CrossRef]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. STL: A seasonal-trend decomposition procedure based on loess. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Bogachev, M.I.; Bunde, A. Improved risk estimation in multifractal records: Application to the value at risk in finance. Phys. Rev. E 2009, 80. [Google Scholar] [CrossRef] [PubMed]
- Bogachev, M.I.; Bunde, A. On the occurrence and predictability of overloads in telecommunication networks. Europhys. Lett. 2009, 86. [Google Scholar] [CrossRef]
- Hosking, J.R.M. Modeling persistence in hydrological time series using fractional differencing. Water Resour. Res. 1984, 20, 1898–1908. [Google Scholar]
- Mandelbrot, B.B.; Wallis, J.R. Computer experiments with fractional Gaussian noises: Part 1, averages and variances. Water Resour. Res. 1969, 5, 228–241. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Wallis, J.R. Computer experiments with fractional Gaussian noises: Part 2, rescaled ranges and spectra. Water Resour. Res. 1969, 5, 242–259. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Wallis, J.R. Computer experiments with fractional Gaussian noises: Part 3, mathematical appendix. Water Resour. Res. 1969, 5, 260–267. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. The Hurst phenomenon and fractional Gaussian noise made easy. Hydrol. Sci. J. 2002, 47, 573–595. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. A random walk on water. Hydrol. Earth Syst. Sci. 2010, 14, 585–601. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Hurst-Kolmogorov Dynamics and Uncertainty. J. Am. Water Resour. Assoc. 2011, 47, 481–495. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Improved Surrogate Data for Nonlinearity Tests. Phys. Rev. Lett. 1996, 77, 635–638. [Google Scholar] [CrossRef] [PubMed]
- Kugiumtzis, D. Test your surrogate data before you test for nonlinearity. Phys. Rev. E 1999, 60, 2808–2816. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Surrogate time series. Phys. D Nonlinear Phenom. 2000, 142, 346–382. [Google Scholar] [CrossRef]
- Venema, V.; Ament, F.; Simmer, C. A Stochastic Iterative Amplitude Adjusted Fourier Transform algorithm with improved accuracy. Nonlinear Processes Geophys. 2006, 13, 321–328. [Google Scholar] [CrossRef]
- Venema, V.; Bachner, S.; Rust, H.W.; Simmer, C. Statistical characteristics of surrogate data based on geophysical measurements. Nonlinear Processes Geophys. 2006, 13, 449–466. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Generic and parsimonious stochastic modelling for hydrology and beyond. Hydrol. Sci. J. 2016, 61, 225–244. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Hydrology and change. Hydrol. Sci. J. 2013, 58, 1177–1197. [Google Scholar] [CrossRef]
- Franzke, C. A novel method to test for significant trends in extreme values in serially dependent time series. Geophys. Res. Lett. 2013, 40, 1391–1395. [Google Scholar] [CrossRef]
- Livina, V.N.; Ashkenazy, Y.; Braun, P.; Monetti, R.; Bunde, A.; Havlin, S. Nonlinear volatility of river flux fluctuations. Phys. Rev. E 2003, 67. [Google Scholar] [CrossRef] [PubMed]
- Beran, J. A Test of Location for Data with Slowly Decaying Serial Correlations. Biometrika 1989, 76, 261–269. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simmons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef]
- Kantelhardt, J.W. Chapter Fractal and Multifractal Time Series. In Mathematics of Complexity and Dynamical Systems; Springer New York: New York, NY, USA, 2011; pp. 463–487. [Google Scholar]
- Moreira, I.G.; Kamphorst Leal da Silva, I.; Kamphorst, S.O. On the fractal dimension of self-affine profiles. J. Phys. A 1994, 27, 8079–8089. [Google Scholar] [CrossRef]
- Montanari, A.; Taqqu, M.S.; Teverovsky, V. Estimating long-range dependence in the presence of periodicity: An empirical study. Math. Comput. Model. 1999, 29, 217–228. [Google Scholar] [CrossRef]
- Marković, D.; Koch, M. Sensitivity of Hurst parameter estimation to periodic signals in time series and filtering approaches. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Ludescher, J.; Bogachev, M.I.; Kantelhardt, J.W.; Schumann, A.Y.; Bunde, A. On spurious and corrupted multifractality: The effects of additive noise, short-term memory and periodic trends. Phys. A Stat. Mech. Appl. 2011, 390, 2480–2490. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, Y.; Singh, V.P.; Chen, Y.D. Comparison of detrending methods for fluctuation analysis in hydrology. J. Hydrol. 2011, 400, 121–132. [Google Scholar] [CrossRef]
- Markonis, Y.; Koutsoyiannis, D. Climatic variability over time scales spanning nine orders of magnitude: Connecting Milankovitch cycles with Hurst-Kolmogorov dynamics. Surv. Geophys. 2013, 34, 181–207. [Google Scholar] [CrossRef]
- McLeod, A.I.; Hipel, K.W. Preservation of the rescaled adjusted range: 1. A reassessment of the Hurst Phenomenon. Water Resour. Res. 1978, 14, 491–508. [Google Scholar] [CrossRef]
- McLeod, A.I.; Yu, H.; Krougly, Z.L. Algorithms for Linear Time Series Analysis: With R Package. J. Stat. Softw. 2007, 23, 1–26. [Google Scholar] [CrossRef]
- Bunde, A.; Eichner, J.F.; Kantelhardt, J.W.; Havlin, S. Long-term memory: A natural mechanism for the clustering of extreme events and anomalous residual times in climate records. Phys. Rev. Lett. 2005, 94. [Google Scholar] [CrossRef] [PubMed]
- Bogachev, M.I.; Bunde, A. On the predictability of extreme events in records with linear and nonlinear long-range memory: Efficiency and noise robustness. Phys. A Stat. Mech. Appl. 2011, 390, 2240–2250. [Google Scholar] [CrossRef]
- Ashkenazy, Y.; Baker, D.R.; Gildor, H.; Havlin, S. Nonlinearity and multifractality of climate change in the past 420,000 years. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Markonis, Y.; Koutsoyiannis, D. Scale-dependence of persistence in precipitation records. Nat. Clim. Chang. 2015, in press. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G. Irreversibility and complex network behavior of stream flow fluctuations. Phys. A Stat. Mech. Appl. 2016, 450, 585–600. [Google Scholar] [CrossRef]
- Bubeck, P.; Botzen, W.J.W.; Aerts, J.C.J.H. A review of risk perceptions and other factors that influence flood mitigation behavior. Risk Anal. 2012, 32, 1481–1495. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Botzen, W.J.W.; van Den Bergh, J.C.J.M. Monetary valuation of insurance against flood risk under climate change. Int. Econ. Rev. 2012, 53, 1005–1026. [Google Scholar] [CrossRef]
- Egli, T.; Wehner, K.; International Commission for the Protection of the Rhine. Non Structural Flood Plain Management: Measures and Their Effectiveness; International Commission for the Protection of the Rhine: Koblenz, Germany, 2002. [Google Scholar]
- Engel, H. The flood events of 1993/1994 and 1995 in the Rhine River basin. In Destructive Water: Water-Caused Natural Disasters, Their Abatement and Control; Leavesly, G.H., Lins, H.F., Nobilis, F., Parker, R.S., Schneider, V.R., van der Ven, F.H.M., Eds.; IAHS-AISH Publication No. 239; IAHS Press: Wallingford, UK, 1997; pp. 21–32. [Google Scholar]
- Wind, H.G.; Nierop, T.M.; de Blois, C.J.; de Kok, J.L. Analysis of flood damages from the 1993 and 1995 Meuse Floods. Water Resour. Res. 1999, 35, 3459–3465. [Google Scholar] [CrossRef]
- Bubeck, P.; Botzen, W.J.W.; Kreibich, H.; Aerts, J.C.J.H. Long-term development and effectiveness of private flood mitigation measures: An analysis for the German part of the river Rhine. Nat. Hazards Earth Syst. Sci. 2012, 12, 3507–3518. [Google Scholar] [CrossRef] [Green Version]
- Lins, H. Hydro-Climatic Data Network 2009 (HCDN-2009); U.S. Geological Survey Fact Sheet 2012-3047; U.S. Geological Survey: Reston, VA, USA, 2012.
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
- Wuertz, D. fArma: ARMA Time Series Modelling; R Package Version 3010.79; Rmetrics: Zurich, Switzerland, 2013. [Google Scholar]
- McLeod, A.I.; Veenstra, J. FGN: Fractional Gaussian Noise, Estimation and Simulation; R Package Version 2.0; Rmetrics: Zurich, Switzerland, 2012. [Google Scholar]
- Fraley, C. fracdiff: Fractionally Differenced ARIMA aka ARFIMA(p,d,q) Models; R Package Version 1.4-2 (S original by Chris Fraley and U.Washington and Seattle. R port by Fritz Leisch at TU Wien; since 2003-12: Martin Maechler; fdGPH and fdSperio and etc. by Valderio Reisen and Artur Lemonte); Rmetrics: Zurich, Switzerland, 2012. [Google Scholar]
- Constantine, W.; Percival, D. fractal: Fractal Time Series Modeling and Analysis; R Package Version 2.0-0; Rmetrics: Zurich, Switzerland, 2014. [Google Scholar]
- Hess, K. muhaz: Hazard Function Estimation in Survival Analysis; R Package Version 1.2.5 (S original by Kenneth Hess and R port by R. Gentleman); Rmetrics: Zurich, Switzerland, 2010. [Google Scholar]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serinaldi, F.; Kilsby, C.G. Understanding Persistence to Avoid Underestimation of Collective Flood Risk. Water 2016, 8, 152. https://doi.org/10.3390/w8040152
Serinaldi F, Kilsby CG. Understanding Persistence to Avoid Underestimation of Collective Flood Risk. Water. 2016; 8(4):152. https://doi.org/10.3390/w8040152
Chicago/Turabian StyleSerinaldi, Francesco, and Chris G. Kilsby. 2016. "Understanding Persistence to Avoid Underestimation of Collective Flood Risk" Water 8, no. 4: 152. https://doi.org/10.3390/w8040152




