Innovative Analysis of Runoff Temporal Behavior through Bayesian Networks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Areas
2.1.1. Adaja River
2.1.2. Porma River
2.2. Data Description
2.3. Methodology
2.3.1. Stage 1. Traditional Time Analysis
2.3.2. Stage 2. ARMA Model Building
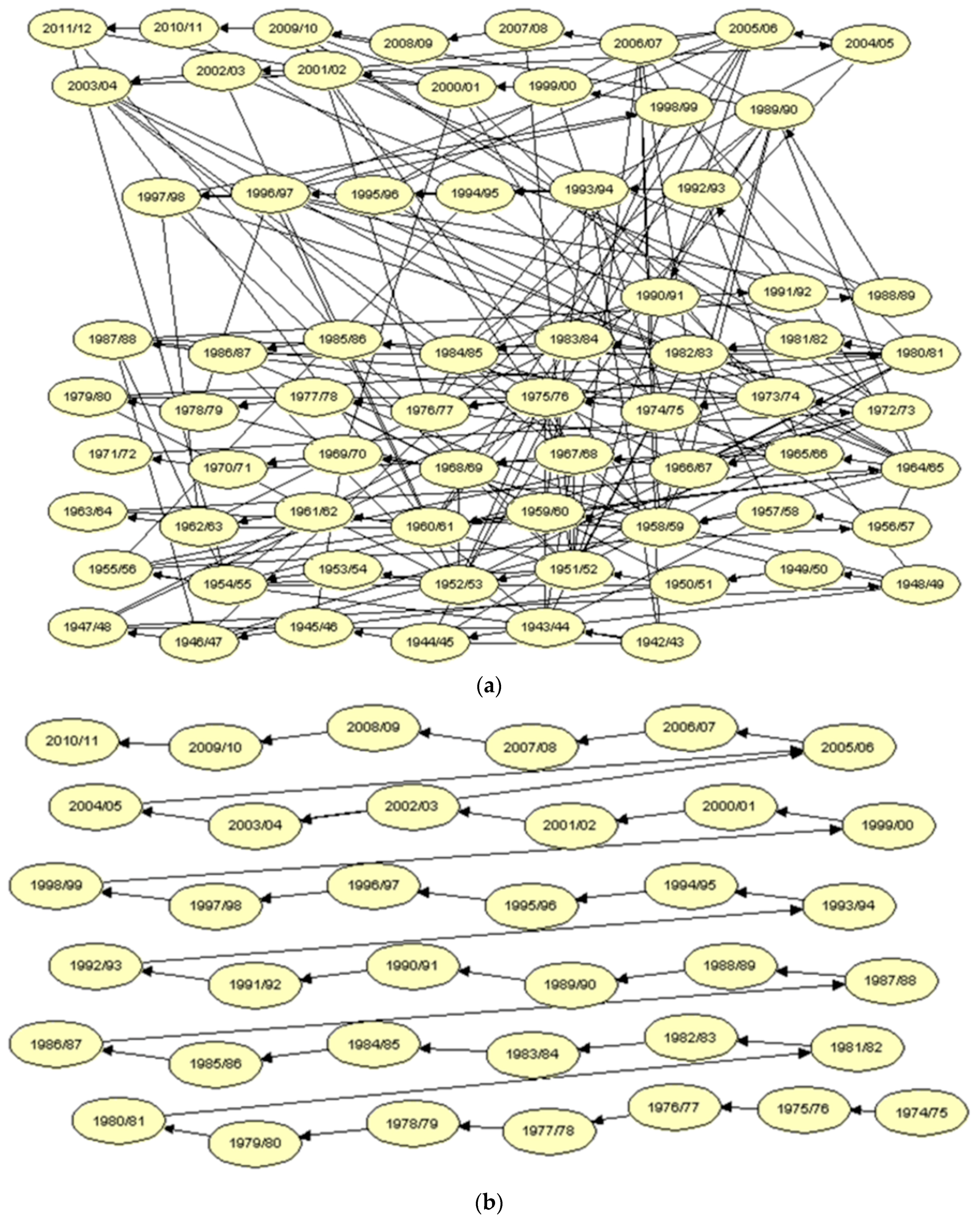
2.3.3. Stage 3. Bayesian Networks Building
3. Results
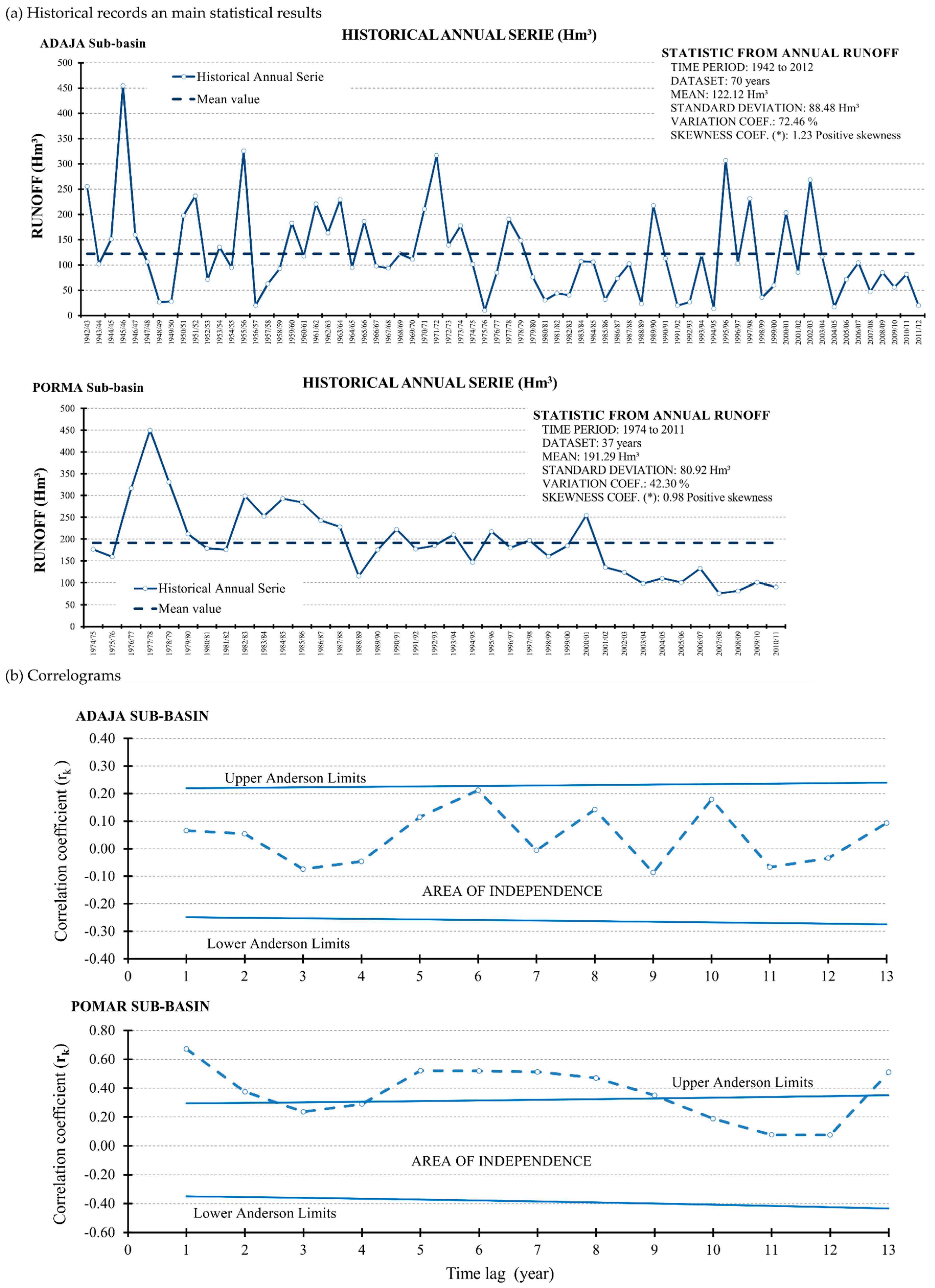
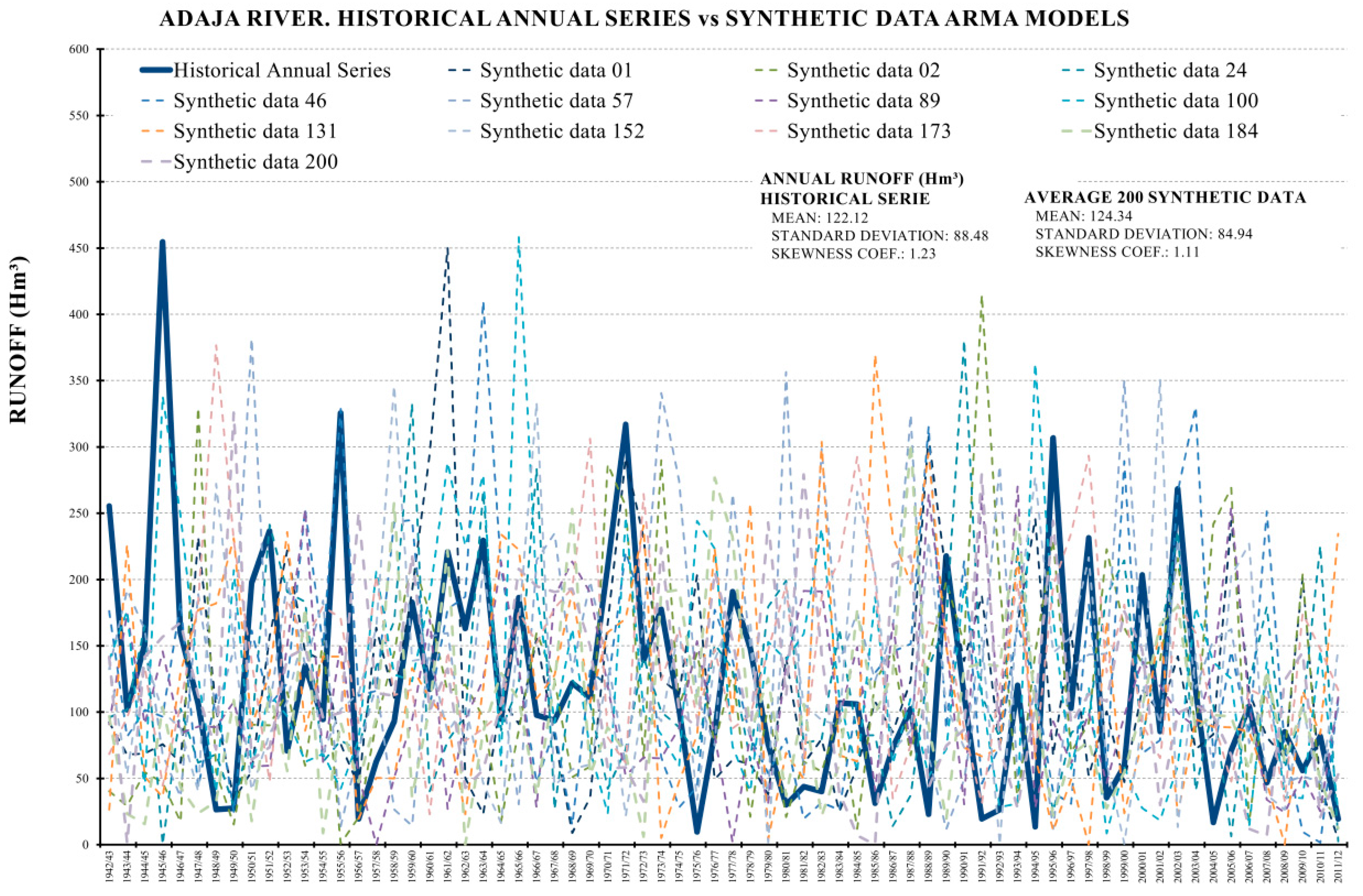
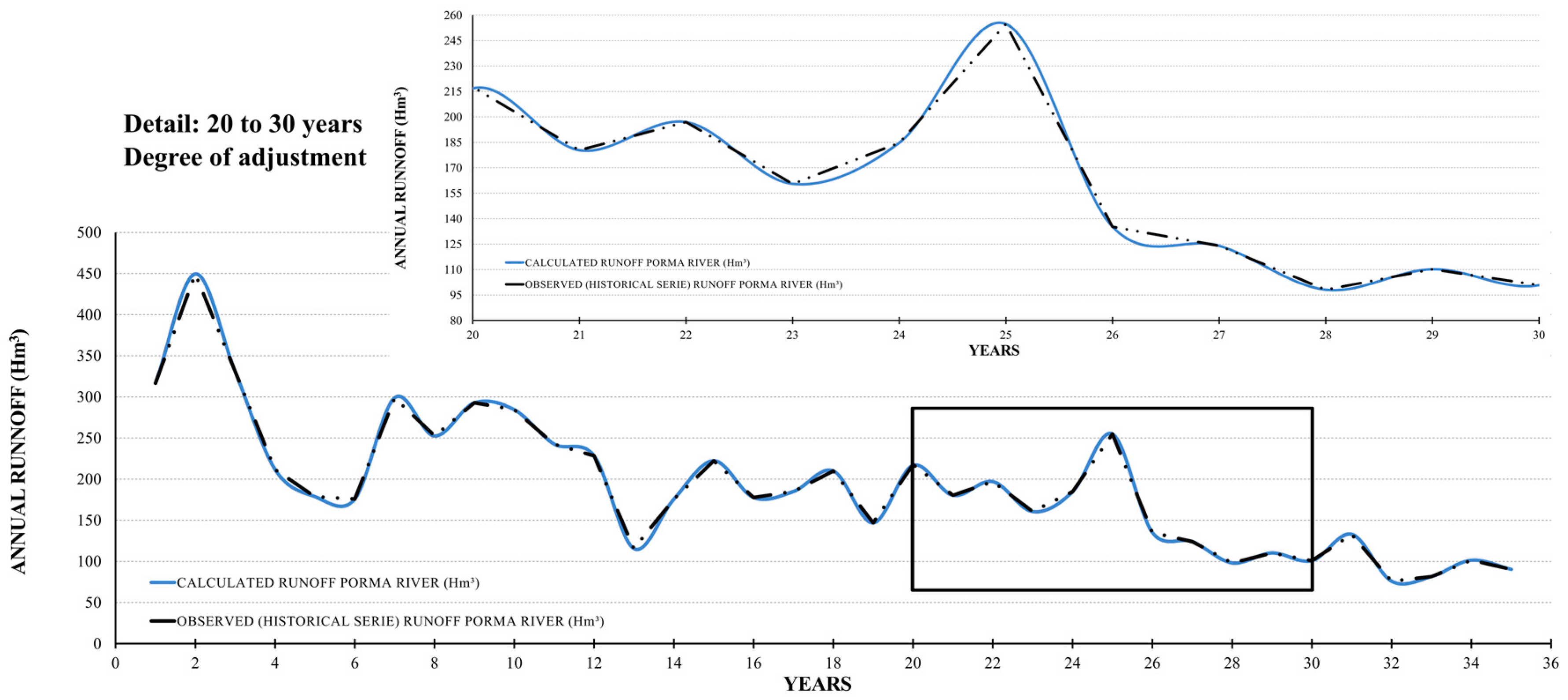
3.1. Traditional Time Analysis and Synthetic Series Prior Analyses
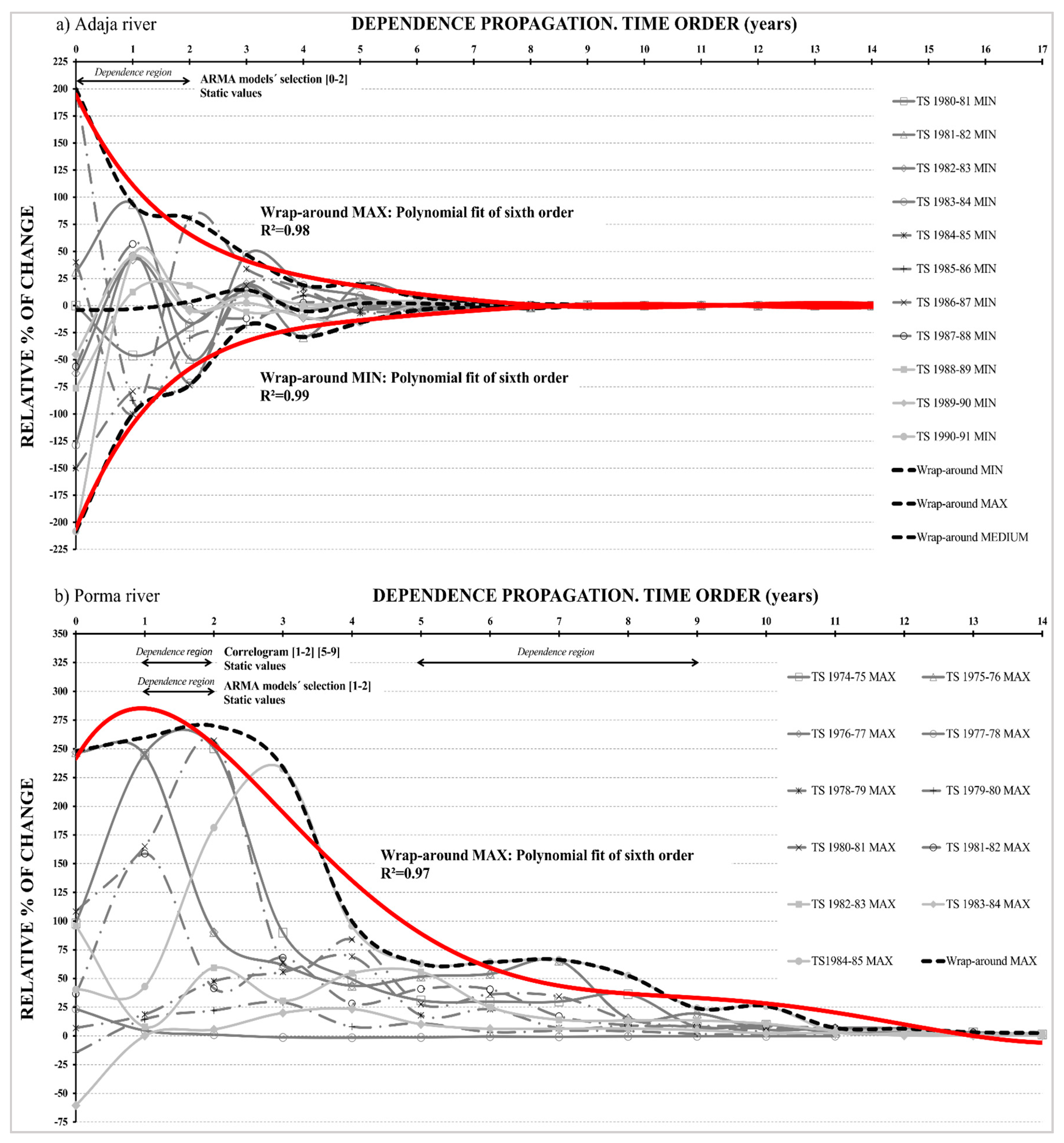
3.2. Hydrological Interpretation. Time Dependence Analysis
3.2.1. Adaja River
- Resulting symmetry on the shapes of wrap-around MAX and MIN practically coincides with the x-axis.
- Both wrap-around MAX and MIN tend (or decay) to zero rapidly (Figure 7a).
- There exists a very high goodness of fit of the shapes’ MAX and MIN of 0.98 and 0.99 respectively, measured by coefficient of determination R2.
- This fit corresponds to a sixth order function for all time steps.
3.2.2. Porma River
3.3. Time Order (Model Orden) Suitability Analysis
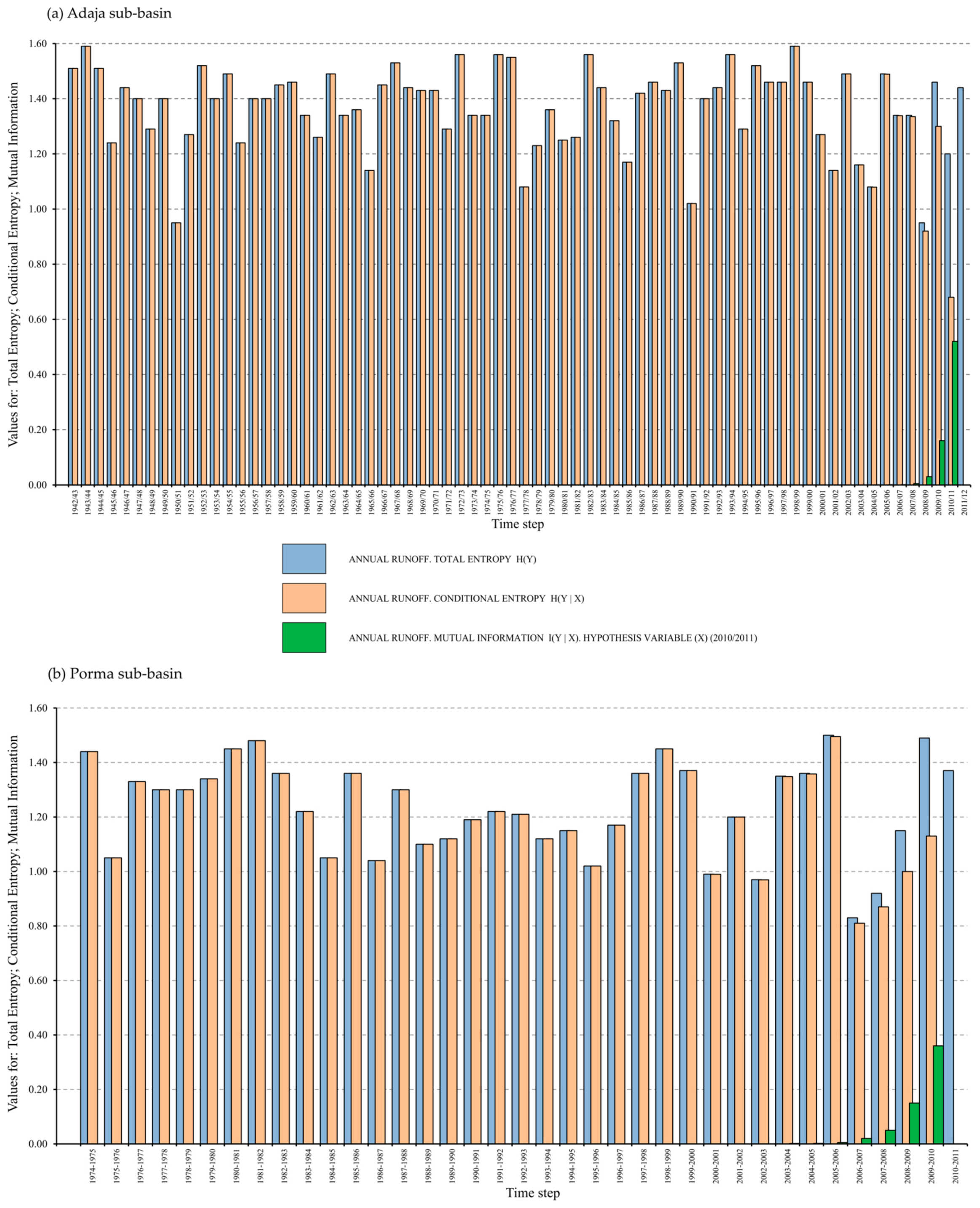
3.4. Consistency and Quality Assessment of the BNs Model and Its Analysis
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Reihan, A.; Kriauciuniene, J.; Meilutyte-Barauskiene, D.; Kolcova, T. Temporal Variation of Spring Flood in Rivers of the Baltic States. Hydrol. Res. 2012, 43, 301–314. [Google Scholar] [CrossRef]
- Yang, C.; Yu, Z.; Hao, Z.; Zhang, J.; Zhu, J. Impact of Climate Change on Flood and Drought Events in Huaihe River Basin, China. Hydrol. Res. 2012, 43, 14–22. [Google Scholar] [CrossRef]
- Pulido-Velazquez, D.; Luis Garcia-Arostegui, J.; Molina, J.; Pulido-Velazquez, M. Assessment of Future Groundwater Recharge in Semi-Arid Regions under Climate Change Scenarios (Serral-Salinas Aquifer, SE Spain). Could Increased Rainfall Variability Increase the Recharge Rate? Hydrol. Process. 2015, 29, 828–844. [Google Scholar] [CrossRef]
- Bogner, K.; Liechti, K.; Zappa, M. Post-Processing of Stream Flows in Switzerland with an Emphasis on Low Flows and Floods. Water 2016, 8, 115. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-Term Storage Capacity of Reservoirs. Trans. Am. Soc. Civ. Eng. (ASCE) 1951, 116, 770–808. [Google Scholar]
- Box, G.E.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1976; p. 575. [Google Scholar]
- Akintug, B.; Rasmussen, P.F. A Markov Switching Model for Annual Hydrologic Time Series. Water Resour. Res. 2005, 41, W09424. [Google Scholar] [CrossRef]
- Kim, T.W.; Valdes, J.B. Synthetic Generation of Hydrologic Time Series Based on Nonparametric Random Generation. J. Hydrol. Eng. 2005, 10, 395–404. [Google Scholar] [CrossRef]
- Stojkovic, M.; Prohaska, S.; Plavsic, J. Stochastic Structure of Annual Discharges of Large European Rivers. J. Hydrol. Hydromech. 2015, 63, 63–70. [Google Scholar] [CrossRef]
- Andreu, J. Capítulo 1: Reflexiones sobre la planificación hidrológica. In Conceptos y Métodos Para la Planificación Hidrológica, 1st ed.; Sauquillo Herraiz, A., Ed.; Centro Internacional de Métodos Numéricos en Ingeniería (CIMNE): Barcelona, Spain, 1993; pp. 2–3. [Google Scholar]
- Wang, W.; Chau, K.; Cheng, C.; Qiu, L. A Comparison of Performance of several Artificial Intelligence Methods for Forecasting Monthly Discharge Time Series. J. Hydrol. 2009, 374, 294–306. [Google Scholar] [CrossRef]
- Romano, E.; del Bon, A.; Petrangeli, A.B.; Preziosi, E. Generating Synthetic Time Series of Springs Discharge in Relation to Standardized Precipitation Indices. Case Study in Central Italy. J. Hydrol. 2013, 507, 86–99. [Google Scholar] [CrossRef]
- Díaz Caballero, F.F. Selección de Modelos Mediante Criterios de Información en Análisis Factorial: Aspectos Teóricos y Computacionales; Granada University: Granada, Spain, 2011; p. 28. [Google Scholar]
- Todini, E. History and Perspectives of Hydrological Catchment Modelling. Hydrol. Res. 2011, 42, 73–85. [Google Scholar] [CrossRef]
- Myung, I.J. The Importance of Complexity in Model Selection. J. Math. Psychol. 2000, 44, 190–204. [Google Scholar] [CrossRef] [PubMed]
- Kendall, D.R.; Dracup, J.A. A Comparison of Index-Sequential and Ar(1) Generated Hydrologic Sequences. J. Hydrol. 1991, 122, 335–352. [Google Scholar] [CrossRef]
- Lin, G.F.; Lee, F.C. Assessment of Aggregated Hydrologic Time-Series Modeling. J. Hydrol. 1994, 156, 447–458. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, X. Auto Regressive and Ensemble Empirical Mode Decomposition Hybrid Model for Annual Runoff Forecasting. Water Resour. Manag. 2015, 29, 2913–2926. [Google Scholar] [CrossRef]
- Burlando, P.; Rosso, R.; Cadavid, L.G.; Salas, J.D. Forecasting of Short-Term Rainfall using ARMA Models. J. Hydrol. 1993, 144, 193–211. [Google Scholar] [CrossRef]
- Karthikeyan, L.; Kumar, D.N. Predictability of Nonstationary Time Series using Wavelet and EMD Based ARMA Models. J. Hydrol. 2013, 502, 103–119. [Google Scholar] [CrossRef]
- Mohammadi, K.; Eslami, H.R.; Kahawita, R. Parameter Estimation of an ARMA Model for River Flow Forecasting using Goal Programming. J. Hydrol. 2006, 331, 293–299. [Google Scholar] [CrossRef]
- Salas, J.D. Analysis and modeling of hydrologic time series. In The McGraw Hill Handbook of Hydrology, 1st ed.; Maidment, D.R., Ed.; McGraw-Hill: New York, NY, USA, 1993; Chapter 19; pp. 1–72. [Google Scholar]
- Salas, J.D.; Boes, D.C.; Smith, R.A. Estimation of ARMA Models with Seasonal Parameters. Water Resour. Res. 1982, 18, 1006–1010. [Google Scholar] [CrossRef]
- Nourani, V.; Kisi, O.; Komasi, M. Two Hybrid Artificial Intelligence Approaches for Modeling Rainfall-Runoff Process. J. Hydrol. 2011, 402, 41–59. [Google Scholar] [CrossRef]
- Salas, J.; Delleur, J.; Yevjevich, V.; Lane, W.L. Applied Modeling of Hydrologic Time Series, 1st ed.; Water Resources Publications: Littleton, CO, USA, 1980; p. 484. [Google Scholar]
- Lee, T.; Salas, J.D.; Prairie, J. An Enhanced Nonparametric Streamflow Disaggregation Model with Genetic Algorithm. Water Resour. Res. 2010, 46, W08545. [Google Scholar] [CrossRef]
- Vogel, R.M.; Shallcross, A.L. The Moving Blocks Bootstrap versus Parametric Time Series Models. Water Resour. Res. 1996, 32, 1875–1882. [Google Scholar] [CrossRef]
- Srinivas, V.V.; Srinivasan, K. Hybrid Moving Block Bootstrap for Stochastic Simulation of Multi-Site Multi-Season Streamflows. J. Hydrol. 2005, 302, 307–330. [Google Scholar] [CrossRef]
- Srivastav, R.K.; Srinivasan, K.; Sudheer, K.P. Simulation-Optimization Framework for Multi-Season Hybrid Stochastic Models. J. Hydrol. 2011, 404, 209–225. [Google Scholar] [CrossRef]
- Ouarda, T.B.M.J.; Labadie, J.W.; Fontane, D.G. Indexed Sequential Hydrologic Modeling for Hydropower Capacity Estimation. J. Am. Water Resour. Assoc. 1997, 33, 1337–1349. [Google Scholar] [CrossRef]
- Sharma, A.; Tarboton, D.G.; Lall, U. Streamflow Simulation: A Nonparametric Approach. Water Resour. Res. 1997, 33, 291–308. [Google Scholar] [CrossRef]
- Lall, U.; Sharma, A. A Nearest Neighbor Bootstrap for Resampling Hydrologic Time Series. Water Resour. Res. 1996, 32, 679–693. [Google Scholar] [CrossRef]
- Rajagopalan, B.; Salas, J.D.; Lall, U. Stochastic methods for modeling precipitation and streamflow. In Advances in Data-Based Approaches for Hydrologic Modeling and Forecasting; Berndtsson, R., Sivakumar, B., Eds.; World Scientific: Singapore, 2010; Chapter 2; pp. 17–52. [Google Scholar]
- Adarnowski, J.F. Development of a Short-Term River Flood Forecasting Method for Snowmelt Driven Floods Based on Wavelet and Cross-Wavelet Analysis. J. Hydrol. 2008, 353, 247–266. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Teshnehlab, M. Using Adaptive Neuro-Fuzzy Inference System for Hydrological Time Series Prediction. Appl. Soft Comput. 2008, 8, 928–936. [Google Scholar] [CrossRef]
- Aqil, M.; Kita, I.; Yano, A.; Nishiyama, S. A Comparative Study of Artificial Neural Networks and Neuro-Fuzzy in Continuous Modeling of the Daily and Hourly Behaviour of Runoff. J. Hydrol. 2007, 337, 22–34. [Google Scholar] [CrossRef]
- Molina, J.; Pulido-Velazquez, D.; Luis Garcia-Arostegui, J.; Pulido-Velazquez, M. Dynamic Bayesian Networks as a Decision Support Tool for Assessing Climate Change Impacts on Highly Stressed Groundwater Systems. J. Hydrol. 2013, 479, 113–129. [Google Scholar] [CrossRef]
- Chan, T.U.; Hart, B.T.; Kennard, M.J.; Pusey, B.J.; Shenton, W.; Douglas, M.M.; Valentine, E.; Patel, S. Bayesian Network Models for Environmental Flow Decision Making in the Daly River, Northern Territory, Australia. River Res. Appl. 2012, 28, 283–301. [Google Scholar] [CrossRef]
- Molina, J.L.; Bromley, J.; Garcia-Arostegui, J.L.; Sullivan, C.; Benavente, J. Integrated Water Resources Management of Overexploited Hydrogeological Systems using Object-Oriented Bayesian Networks. Environ. Model. Softw. 2010, 25, 383–397. [Google Scholar] [CrossRef]
- Mamitimin, Y.; Feike, T.; Doluschitz, R. Bayesian Network Modeling to Improve Water Pricing Practices in Northwest China. Water 2015, 7, 5617–5637. [Google Scholar] [CrossRef]
- Castelletti, A.; Soncini-Sessa, R. Bayesian Networks and Participatory Modelling in Water Resource Management. Environ. Model. Softw. 2007, 22, 1075–1088. [Google Scholar] [CrossRef]
- Henriksen, H.J.; Barlebo, H.C. Reflections on the use of Bayesian Belief Networks for Adaptive Management. J. Environ. Manag. 2008, 88, 1025–1036. [Google Scholar] [CrossRef] [PubMed]
- Malekmohammadi, B.; Kerachian, R.; Zahraie, B. Developing Monthly Operating Rules for a Cascade System of Reservoirs: Application of Bayesian Networks. Environ. Model. Softw. 2009, 24, 1420–1432. [Google Scholar] [CrossRef]
- Varis, O.; Fraboulet-Jussila, S. Water Resources Development in the Lower Senegal River Basin: Conflicting Interests, Environmental Concerns and Policy Options. Int. J. Water Resour. Dev. 2002, 18, 245–260. [Google Scholar] [CrossRef]
- Bennett, J.C.; Wang, Q.J.; Pokhrel, P.; Robertson, D.E. The Challenge of Forecasting High Streamflows 1–3 Months in Advance with Lagged Climate Indices in Southeast Australia. Nat. Hazards Earth Syst. Sci. 2014, 14, 219–233. [Google Scholar] [CrossRef] [Green Version]
- Pokhrel, P.; Robertson, D.E.; Wang, Q.J. A Bayesian Joint Probability Post-Processor for Reducing Errors and Quantifying Uncertainty in Monthly Streamflow Predictions. Hydrol. Earth Syst. Sci. 2013, 17, 795–804. [Google Scholar] [CrossRef]
- Aviles, A.; Celleri, R.; Solera, A.; Paredes, J. Probabilistic Forecasting of Drought Events using Markov Chain- and Bayesian Network-Based Models: A Case Study of an Andean Regulated River Basin. Water 2016, 8, 37. [Google Scholar] [CrossRef]
- Wang, Q.J.; Robertson, D.E.; Chiew, F.H.S. A Bayesian Joint Probability Modeling Approach for Seasonal Forecasting of Streamflows at Multiple Sites. Water Resour. Res. 2009, 45, W05407. [Google Scholar] [CrossRef]
- Zhao, T.; Wang, Q.J.; Bennett, J.C.; Robertson, D.E.; Shao, Q.; Zhao, J. Quantifying Predictive Uncertainty of Streamflow Forecasts Based on a Bayesian Joint Probability Model. J. Hydrol. 2015, 528, 329–340. [Google Scholar] [CrossRef]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann: San Francisco, CA, USA, 1988. [Google Scholar]
- Jensen, F.V. An Introduction to Bayesian Networks; UCL Press: London, UK, 1996. [Google Scholar]
- See, L.; Openshaw, S. A Hybrid Multi-Model Approach to River Level Forecasting. Hydrol. Sci. J. 2000, 45, 523–536. [Google Scholar] [CrossRef]
- Sang, Y.; Shang, L.; Wang, Z.; Liu, C.; Yang, M. Bayesian-Combined Wavelet Regressive Modeling for Hydrologic Time Series Forecasting. Chin. Sci. Bull. 2013, 58, 3796–3805. [Google Scholar] [CrossRef]
- Jain, A.; Kumar, A.M. Hybrid Neural Network Models for Hydrologic Time Series Forecasting. Appl. Soft Comput. 2007, 7, 585–592. [Google Scholar] [CrossRef]
- MAGRAMA. 2016. Available online: http://www.magrama.gob.es/es/agua/temas/seguridad-de-presas-y-embalses/desarrollo (accessed on 11 November 2015).
- MAGRAMA. 2016. Available online: http://sig.magrama.es/saih/ (accessed on 14 August 2016).
- Mun, J. Modeling Risk: Applying Monte Carlo Risk Simulation, Strategic Real Options, Stochastic Forecasting, and Portfolio Optimization; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Peña, D. Análisis de Series Temporales; Alianza Editorial: Madrid, Spain, 2005. [Google Scholar]
- Steinskog, D.J.; Tjostheim, D.B.; Kvamsto, N.G. A Cautionary Note on the use of the Kolmogorov-Smirnov Test for Normality. Mon. Weather Rev. 2007, 135, 1151–1157. [Google Scholar] [CrossRef]
- Öztuna, D.; Elhan, A.H.; Tüccar, E. Investigation of Four Different Normality Tests in Terms of Type 1 Error Rate and Power Under Different Distributions. Turk. J. Med. Sci. 2006, 36, 171–176. [Google Scholar]
- HUGIN. Hugin Expert A/S. 2010, 7.3. Available online: http://www.hugin.com (accessed on 20 May 2016).
- Pollino, C.A.; Woodberry, O.; Nicholson, A.; Korb, K.; Hart, B.T. Parameterisation and Evaluation of a Bayesian Network for use in an Ecological Risk Assessment. Environ. Model. Softw. 2007, 22, 1140–1152. [Google Scholar] [CrossRef]
- Barton, D.N.; Saloranta, T.; Moe, S.J.; Eggestad, H.O.; Kuikka, S. Bayesian belief networks as a meta-modelling tool in integrated river basin management—Pros and cons in evaluating nutrient abatement decisions under uncertainty in a Norwegian river basin. Ecol. Econ. 2008, 66, 91–104. [Google Scholar] [CrossRef]


| (a) | Porma Sub-Basins. Synthetic Series | |||||||
| Synthetic annual runoff series | 01 | 02 | 07 | 18 | 27 | 62 | 94 | 104 |
| Test Statistic | 0.102 | 0.099 | 0.098 | 0.098 | 0.094 | 0.085 | 0.139 | 0.144 |
| Asymp. Sig (2-tailed), p-value (*) | 0.200 ** | 0.200 ** | 0.200 ** | 0.200 ** | 0.200 ** | 0.200 ** | 0.069 | 0.052 |
| Synthetic annual runoff series | 145 | 152 | 161 | 181 | 192 | 196 | 197 | 200 |
| Test Statistic | 0.101 | 0.139 | 0.101 | 0.126 | 0.139 | 0.072 | 0.103 | 0.115 |
| Asymp. Sig (2-tailed), p-value (*) | 0.200 ** | 0.069 | 0.200 ** | 0.147 | 0.069 | 0.200 ** | 0.200 ** | 0.200 ** |
| (b) | Porma Sub-Basins. ARMA Models | |||||||
| Annual runoff series | 01 | 02 | 07 | 18 | 27 | 62 | 94 | 104 |
| Mean | 173.85 | 186.84 | 205.07 | 182.69 | 169.84 | 243.98 | 203.08 | 223.99 |
| Standard deviation | 44.05 | 60.03 | 62.94 | 59.75 | 71.36 | 82.29 | 71.65 | 110.60 |
| Skewness Coefficient | 1.09 | 0.77 | 0.83 | 1.00 | 1.09 | 0.99 | 0.79 | 1.65 |
| Annual runoff series | 145 | 152 | 161 | 181 | 192 | 196 | 197 | 200 |
| Mean | 193.57 | 224.43 | 151.63 | 163.53 | 248.38 | 176.28 | 154.97 | 186.27 |
| Standard deviation | 49.51 | 101.10 | 50.49 | 63.23 | 105.83 | 83.20 | 53.64 | 75.93 |
| Skewness Coefficient | 0.86 | 0.96 | 0.99 | 0.91 | 1.30 | 0.80 | 0.89 | 1.21 |
| Average of All Annual Runoff Series | Historical Records | |||||||
| Mean | 192.59 | 191.29 | ||||||
| Standard deviation | 74.66 | 80.92 | ||||||
| Skewness Coefficient | 0.88 | 0.98 | ||||||
| Sub-Basins | ARMA Model | Schwarz Criteria | Akaike Information Criteria |
|---|---|---|---|
| Adaja | p = 0, q = 1 | 11.792 | 11.669 |
| p = 1, q = 1 | 11.981 | 11.795 | |
| p = 2, q = 0 | 12.083 | 11.895 | |
| p = 1, q = 0 | 12.245 | 12.121 | |
| p = 0, q = 2 | 12.580 | 12.394 | |
| p = 2, q = 0 | 12.764 | 12.573 | |
| Porma | p = 2, q = 0 | 11.025 | 10.720 |
| p = 0, q = 2 | 11.026 | 10.733 | |
| p = 2, q = 2 | 11.206 | 10.698 | |
| p = 1, q = 0 | 11.224 | 11.025 | |
| p = 1, q = 1 | 11.308 | 11.010 |
| Sub-Basins | Technique | ||
|---|---|---|---|
| Correlogram (*) | BNs (**) | Suitability Analysis. “p” Part of ARMA Models (*) | |
| Adaja | Full independent | 0 (Independent) | [0–2] (*) |
| Porma | [1–2] and [5–9] Discontinuous dependent behavior | [0–13] Continuous dependent behavior | [1–2] (*) Particular dependent behavior |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Molina, J.-L.; Zazo, S.; Rodríguez-Gonzálvez, P.; González-Aguilera, D. Innovative Analysis of Runoff Temporal Behavior through Bayesian Networks. Water 2016, 8, 484. https://doi.org/10.3390/w8110484
Molina J-L, Zazo S, Rodríguez-Gonzálvez P, González-Aguilera D. Innovative Analysis of Runoff Temporal Behavior through Bayesian Networks. Water. 2016; 8(11):484. https://doi.org/10.3390/w8110484
Chicago/Turabian StyleMolina, José-Luis, Santiago Zazo, Pablo Rodríguez-Gonzálvez, and Diego González-Aguilera. 2016. "Innovative Analysis of Runoff Temporal Behavior through Bayesian Networks" Water 8, no. 11: 484. https://doi.org/10.3390/w8110484









