A System Dynamics Model to Conserve Arid Region Water Resources through Aquifer Storage and Recovery in Conjunction with a Dam
Abstract
:1. Introduction
2. System Dynamics Modeling in ASR Using a Surface Water Reservoir
| Symbol | Name | Definition |
|---|---|---|
 | Arrow | Shows a directional relationship between two variables. |
 | Rate | Rate (or flow variable), also called a flow variable, represents change per unit time of a state variable; the cloud mark at the end or the beginning of the rate represents a sink or a source, respectively. These cloud marks can be replaced by a level, in which case, the rate will cause subtraction or accumulation at each time step. |
 | Level or Stock | Also called accumulation, stock or state, it represents accumulation. |
 | Auxiliary variable | Supporting variables that are constant. |
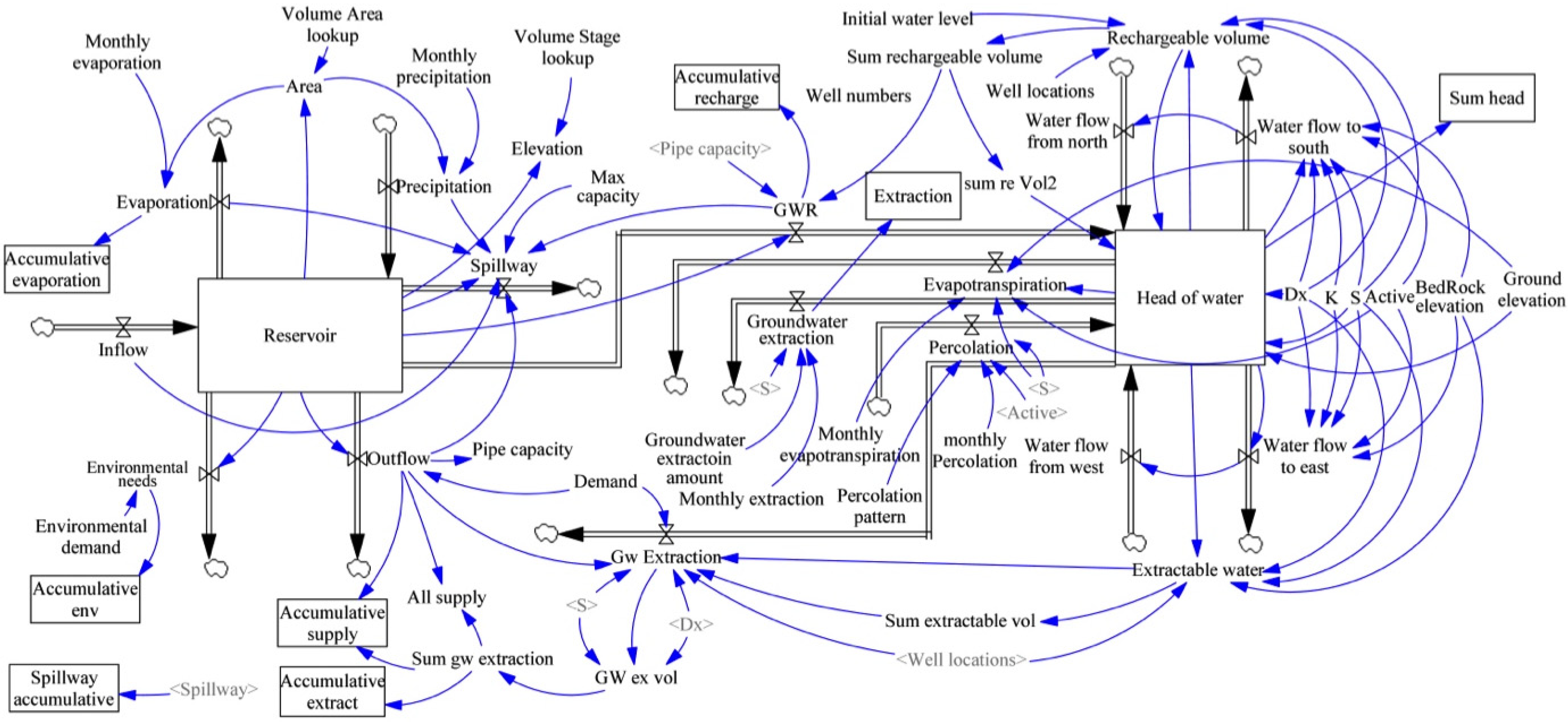
System Dynamics Model Conceptualization and Formulation

If (Inflow − Evaporation − Outflow + Precipitation + Reservoir) < Max capacity, then Spillway = 0)

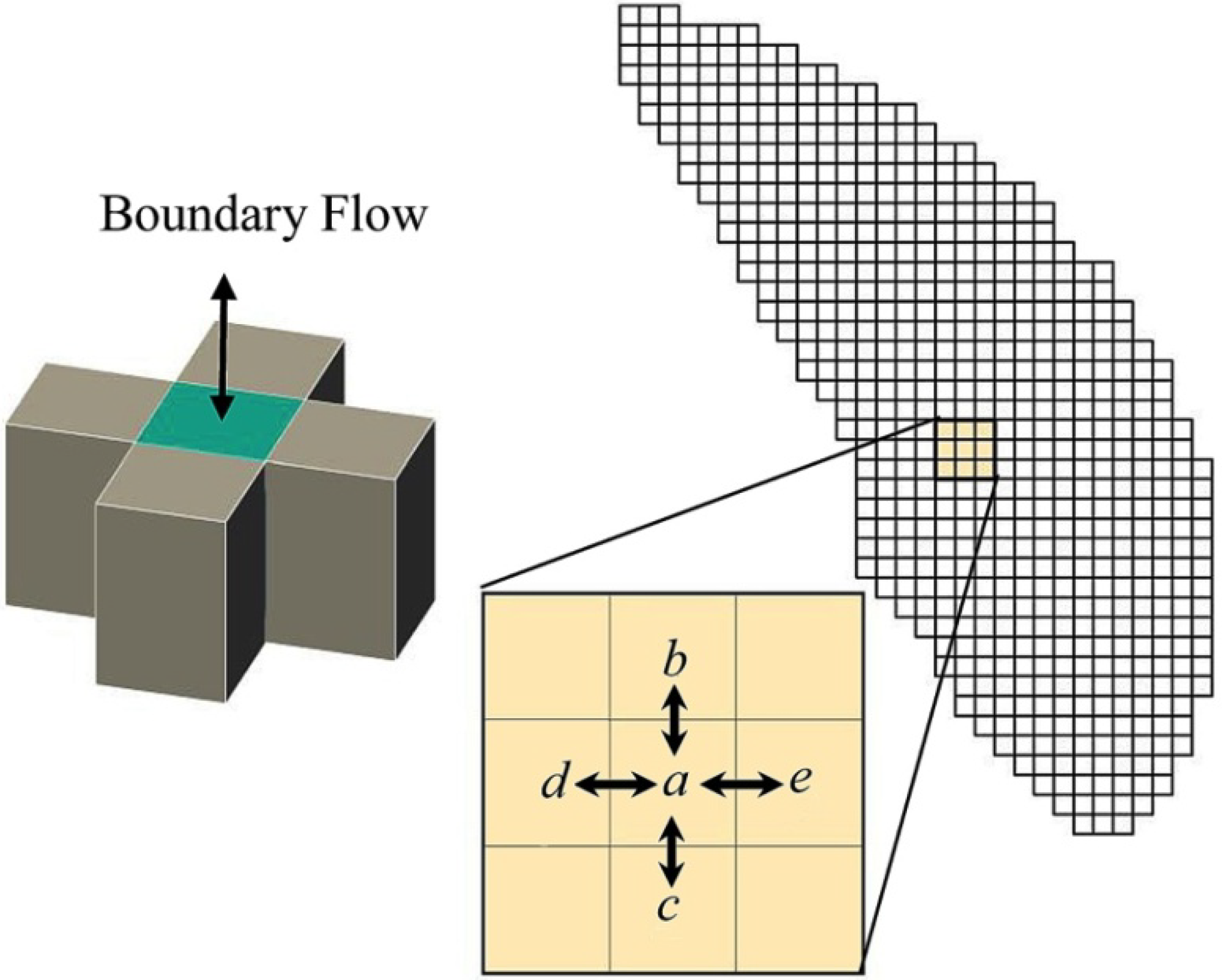
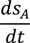 = Qab + Qac + Qad + Qae + QaB
= Qab + Qac + Qad + Qae + QaB
is the change in storage through time in cell a (L3·T−1);
- Qab,Qac,Qad,Qae is the flow into a from b, c, d and e, respectively, (L3·T−1); and
- QaB is the sum of boundary flows to cell a (L3·T−1).
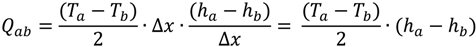
- ha is the head of water in cell a (L);
- hb is the head of water in cell b (L);
- Ta is the transmissivity of cell a (L2·T−1);
- Tb is the transmissivity of cell b (L2·T−1); and
- ∆x is the discrete distance used in the model (L).
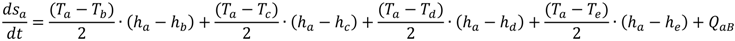
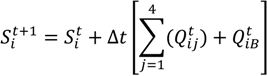
is the flow in or out of cell i from four adjacent cells (L3·T−1);
is the boundary flow (L3·T−1);
is the storage of cell i at time t (L3·T−1);
is the storage of cell i at time t + 1 (L3·T−1); and
- ∆t is the simulation time step (T).
- Sy is the specific yield of the aquifer ;
- Zbed is the bedrock elevation (L).
3. Study Area
3.1. Local Setting


3.2. Hydrogeology of the Aquifer
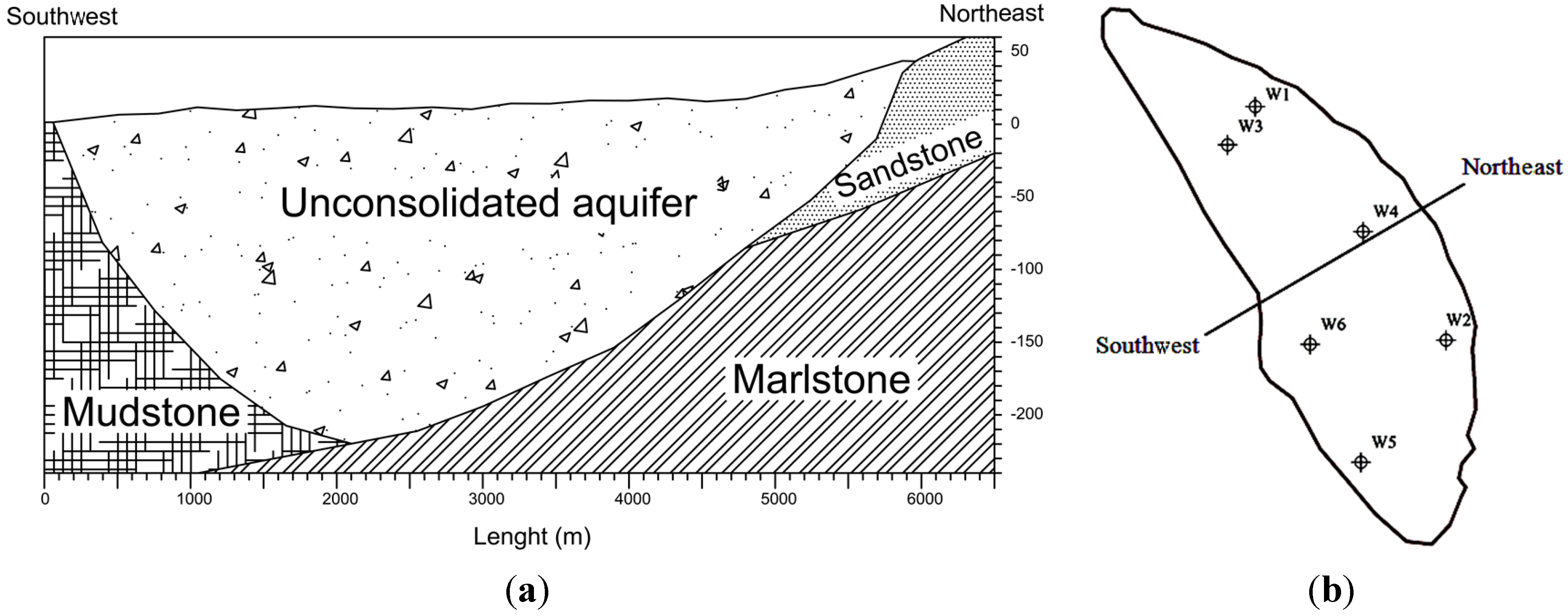
| Well name | Well depth (m) | Hydraulic conductivity (m2·s−1) | Specific yield |
|---|---|---|---|
| W1 | 50 | 8.4 × 10−5 | 0.05 |
| W2 | 40 | 8.7 × 10−5 | 0.06 |
| W3 | 70 | 1.1 × 10−6 | 0.08 |
| W4 | 70 | 1.3 × 10−6 | 0.011 |
| W5 | 60 | 5.6 × 10−6 | 0.011 |
| W6 | 90 | 4.7 × 10−6 | 0.014 |
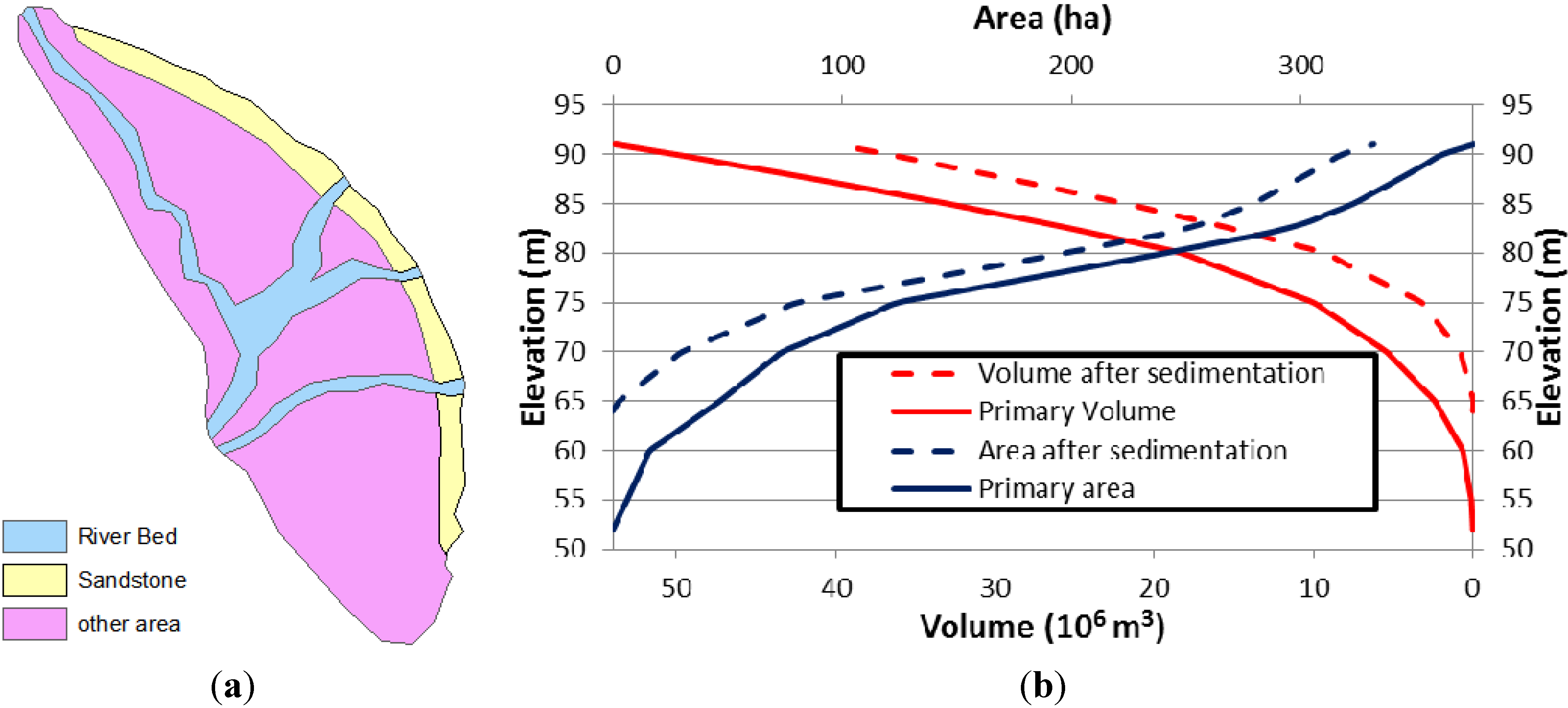
3.3. Dam/Reservoir Characteristics
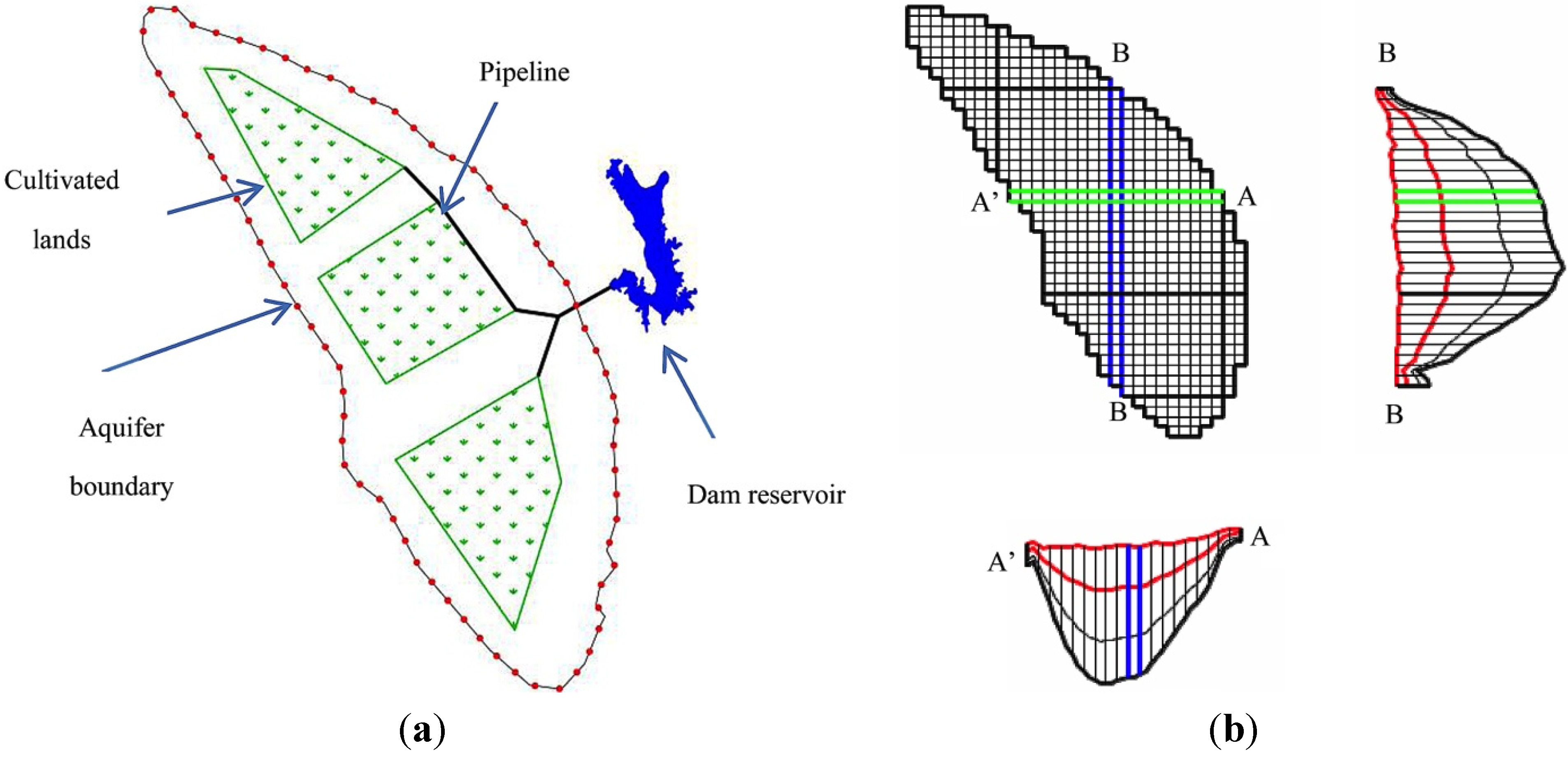
4. Methodology
4.1. Scenarios
4.2. Economic Analysis
| Economic Components | Value | Unit |
|---|---|---|
| Irrigation network | 6,500 | USD ha−1 |
| Installation of each injection well | 50,000 | USD per well |
| Building dam with 40 × 106 m3 reservoir | 22,239,000 | USD |
| Building dam with 20 × 106 m3 reservoir | 9,850,000 | USD |
| Modifying an existing well | 15,000 | USD |
| Dam lifetime | 50 | Years |
| Cost of operation and maintenance of dam | 2 | % of building cost per year |
| Cost of operation and maintenance of irrigation network | 5 | % of building cost per year |
| Construction duration | 2 | Years |
| Education of farmers towards using ASR in scenario 4 | 200,000 | USD |
| Interest rate | 7 | Percent |
| Engineering services | 8 | % of construction cost |
| Averaged agricultural gains | 3,556 | USD ha−1 |
5. Results
5.1. Results of Aquifer Model Implemented with MODFLOW

5.2. Comparison of VENSIM/MODFLOW Results
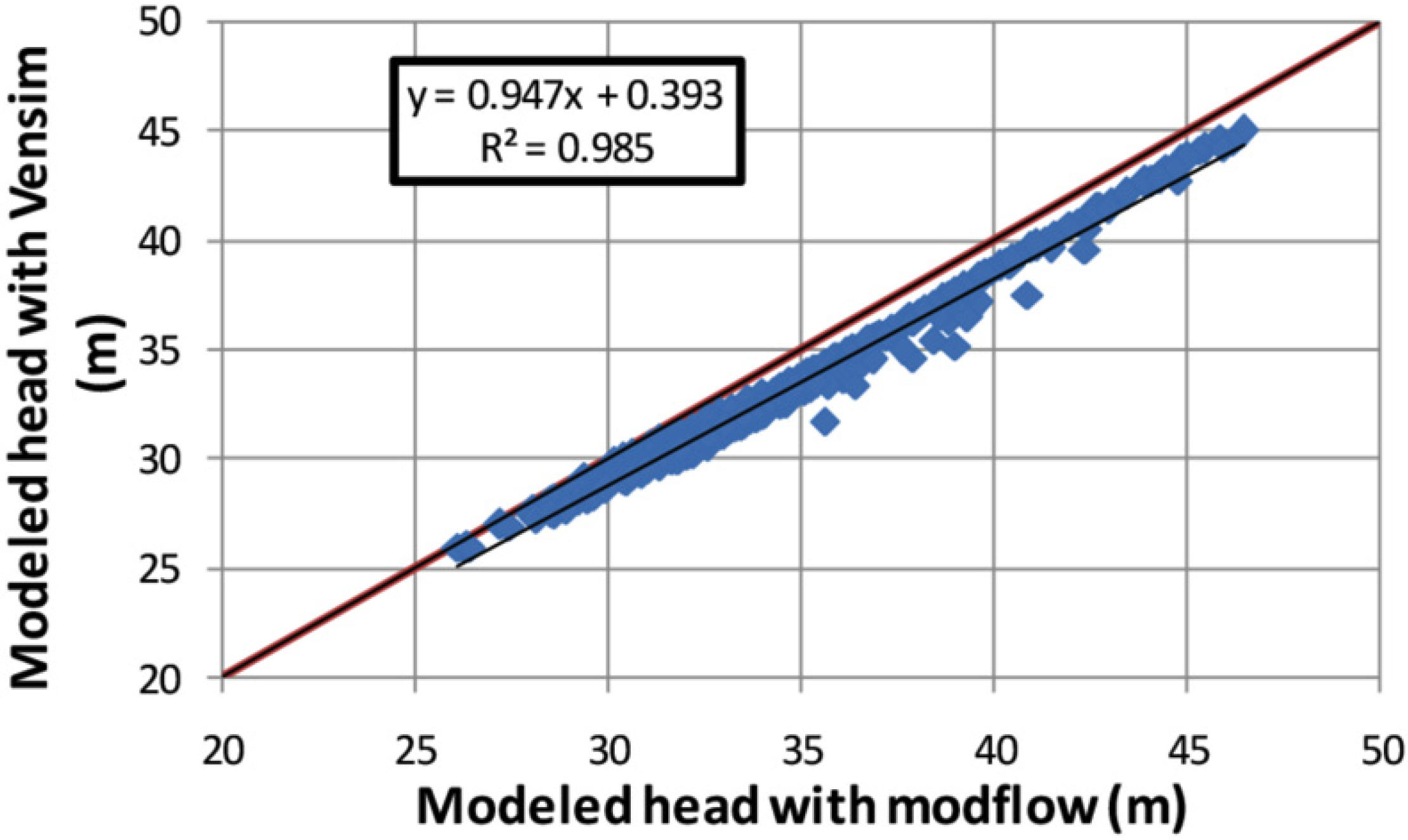
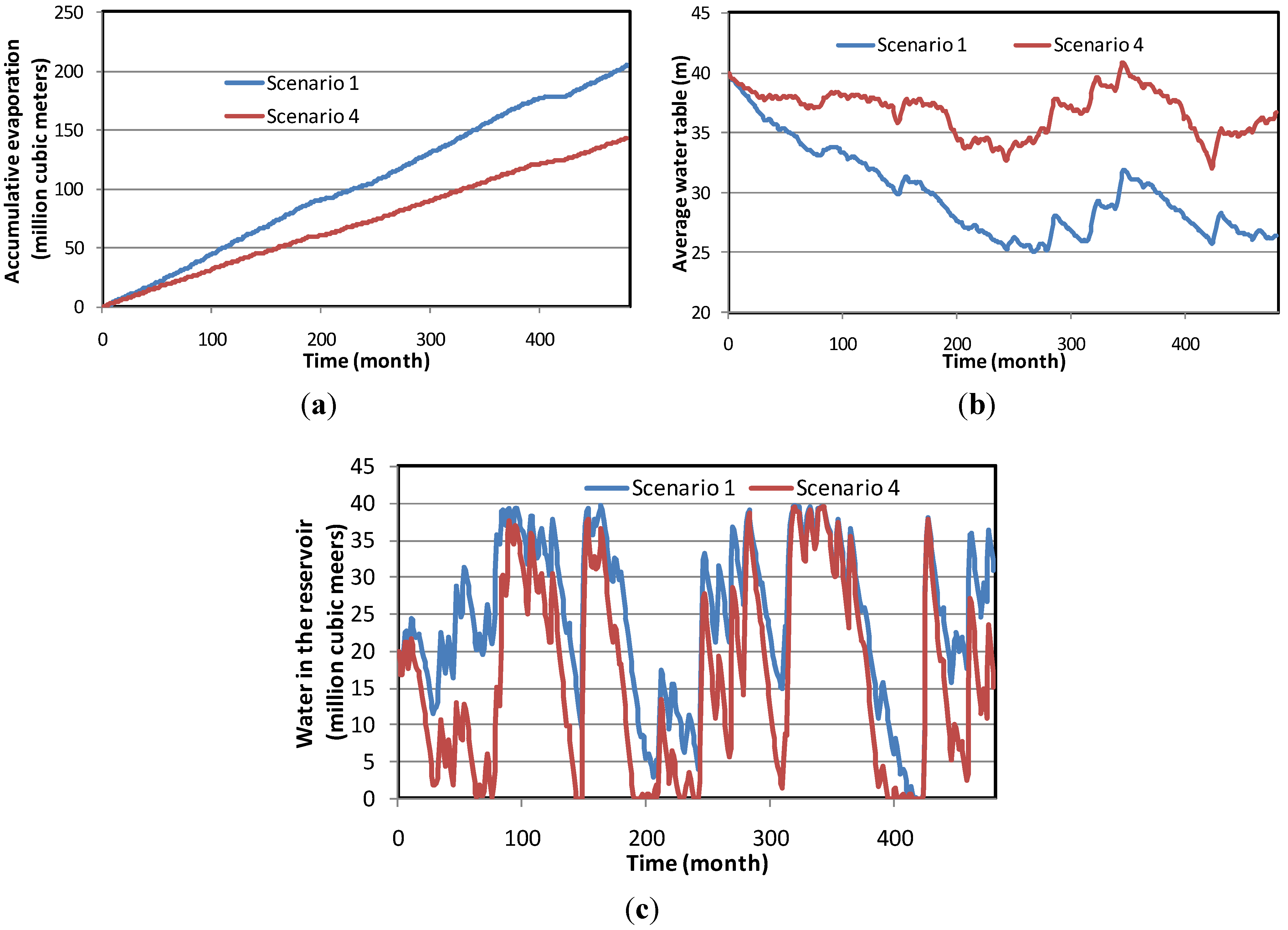
5.3. System Dynamics and Economic Analysis Results
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | |||||
|---|---|---|---|---|---|---|---|---|
| Initial reservoir volume (106 m3) | 40 | 20 | 40 | 20 | 40 | 20 | 40 | |
| Inflow (106 m3) | 1,036.5 | 1,036.5 | 1,036.5 | 1,036.5 | 1,036.5 | 1,036.5 | 1,036.5 | |
| Environmental flow (106 m3) | 153.4 | 130.7 | 144.5 | 117.0 | 130.3 | 129.9 | 143.6 | |
| Agriculture (106 m3) | 313.4 | 251.7 | 284.9 | 373.4 | 464.1 | 249.9 | 282.7 | |
| Command area (additional) (ha) | 1,000.0 | 1,000.0 | 1,000.0 | 1,000.0 | 1,000.0 | 1,000.0 | 1,000.0 | |
| Improved command area (ha) | 0.0 | 0.0 | 0.0 | 1,000.0 | 1,000.0 | 0.0 | 0.0 | |
| Existing area (no change) (ha) | 1,000.0 | 1,000.0 | 1,000.0 | 0.0 | 0.0 | 1,000.0 | 1,000.0 | |
| Evaporation (106 m3) | 205.1 | 100.1 | 156.9 | 71.7 | 118.2 | 98.6 | 153.5 | |
| Spillway (106 m3) | 423.6 | 342.0 | 227.3 | 290.9 | 186.0 | 340.5 | 222.7 | |
| Unregulated water (106 m3) | 577.0 | 472.7 | 371.8 | 407.8 | 316.2 | 470.4 | 366.2 | |
| Pumping (106 m3) | 0.0 | 67.9 | 34.6 | 265.77 | 175.1 | 69.7 | 36.9 | |
| Injection (106 m3) | 0.0 | 215.6 | 227.7 | 227.7 | 151.7 | 221.2 | 238.9 | |
| Average water table’s elevation | Start (m) | 39.9 | 39.9 | 39.9 | 39.9 | 39.9 | 39.9 | 39.9 |
| End (m) | 25.4 | 34.6 | 36.8 | 37.6 | 39.1 | 34.6 | 37.0 | |
| Average drawdown (m) | 14.5 | 5.4 | 3.2 | 2.4 | 0.9 | 5.3 | 3.0 | |
| Normal elevation of dam (m) | 91 | 85 | 91 | 85 | 91 | 85 | 91 | |
| Benefit (USD) | 49,075,000 | 49,075,000 | 49,075,000 | 56,436,000 | 56,437,000 | 49,075,000 | 49,075,000 | |
| Cost (USD) | 37,296,000 | 41,258,000 | 40,112,000 | 55,983,000 | 51,083,000 | 41,597,000 | 37,407,000 | |
| B/C | 1.32 | 1.19 | 1.22 | 1.01 | 1.10 | 1.18 | 1.31 | |
| B-C (USD) | 11,779,000 | 7,817,000 | 8,964,000 | 454,000 | 5,354,000 | 7,478,000 | 11,669,000 | |
6. Discussion
6.1. Consequences of “Business as Usual”
6.2. Scenario Selection Based on Cost/Benefit Analysis
6.3. Social Acceptability and Sustainability
6.4. Uncertainty Due to Climate Variability and Climate Change
7. Conclusions
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Giordano, M.; Villholth, K.G. The Agricultural Groundwater Revolution: Opportunities and Threats to Development; CABI (Commonwealth Agricultural Bureaux International): London, UK, 2007; p. 419. [Google Scholar]
- Gleeson, T.; VanderSteen, J.; Sophocleous, M.A.; Taniguchi, M.; Alley, W.M.; Allen, D.M.; Zhou, Y.X. Groundwater sustainability strategies. Nat. Geosci. 2010, 3, 378–379. [Google Scholar] [CrossRef]
- Theis, C.V. The source of water derived from wells essential factors controlling the response of an aquifer to development. Civil Eng. 1940, 10, 277–280. [Google Scholar]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice Hall Inc. Publishers: Upper Saddle River, NJ, USA, 1979; p. 604. [Google Scholar]
- Khana, S.; Mushtaqb, S.; Hanjraa, M.A.; Schaefferd, J. Estimating potential costs and gains from an aquifer storage and recovery program in australia. Agric. Water Manag. 2008, 95, 477–488. [Google Scholar] [CrossRef]
- Bouwer, H. Artificial recharge of groundwater: Hydrogeology and engineering. Hydrogeol. J. 2002, 10, 121–142. [Google Scholar] [CrossRef]
- Bouwer, H. Integrated water management: Emerging issues and challenges. Agric. Water Manag. 2000, 45, 217–228. [Google Scholar] [CrossRef]
- Sedighi, A. A Quasi-Analytical Model to Predict Water Quality during the Operation of an Aquifer Storage and Recovery System; University of Florida: Gainesville, FL, USA, 2003. [Google Scholar]
- Topper, R.; Barkmann, P.E.; Bird, D.A.; Sares, M.A. Artificial Recharge of Groundwater in Colorado; Colorado Geological Survey: Denver, CO, USA, 2004. [Google Scholar]
- Maliva, R.; Missimer, T. Arid Lands Water Evaluation and Management; Springer: Berlin/Heidelberg, Germany, 2012; Volume 1, p. 1076. [Google Scholar]
- Dillon, P. Future management of aquifer recharge. Hydrogeol. J. 2005, 13, 313–316. [Google Scholar] [CrossRef]
- Kalantari, N.; Rangzan, K.; Thigale, S.S.; Rahimi, M.H. Site selection and cost-benefit analysis for artificial recharge in the baghmalek plain, khuzestan province, southwest iran. Hydrogeol. J. 2010, 18, 761–773. [Google Scholar] [CrossRef]
- Todd, D.K.; Mays, L.W. Groundwater Hydrology, 3rd ed.; Wiley: Hoboken, USA, 2005. [Google Scholar]
- Pulido-Velazquez, M.; Jenkins, M.W.; Lund, J.R. Economic values for conjunctive use and water banking in southern california. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Kern Water Bank Authority. Available online: http://www.kwb.org/index.cfm/fuseaction/Pages.Page/id/330 (accessed on 20 March 2014).
- Sahuquillo, A.S. Conjunctive Use of Surface Water and Groundwater; Encyclopedia of Life Support Systems (EOLSS): Paris, France, 2004; Volume III. [Google Scholar]
- Stave, K. Participatory system dynamics modeling for sustainable environmental management: Observations from four cases. Sustainability 2010, 2, 2762–2784. [Google Scholar] [CrossRef]
- Geurts, J.L.A.; Joldersma, C. Methodology for participatory policy analysis. Eur. J. Oper Res. 2001, 128, 300–310. [Google Scholar] [CrossRef]
- Stave, K.A. Using system dynamics to improve public participation in environmental decisions. Syst. Dyn. Rev. 2002, 18, 139–167. [Google Scholar] [CrossRef]
- Winz, I.; Brierley, G.; Trowsdale, S. The use of system dynamics simulation in water resources management. Water Resour. Manag. 2009, 23, 1301–1323. [Google Scholar] [CrossRef]
- Giordano, R.; Brugnach, M.; Vurro1, M. System dynamic modelling for conflicts analysis in groundwater management. In International Congress on Environmental Modelling and Software, Managing Resources of a Limited Plane; Seppelt, R., Voinov, A.A., Lange, S., Bankamp, D., Eds.; International Environmental Modelling and Software Society (iEMSs): Leipzig, Germany, 2012; p. 10. [Google Scholar]
- Abbott, M.D.; Stanley, R.S. Modeling groundwater recharge and flow in an upland fractured bedrock aquifer. Syst. Dyn. Rev. 1999, 15, 163–184. [Google Scholar] [CrossRef]
- Leaver, J.D.; Unsworth, C.P. System dynamics modelling of spring behaviour in the orakeikorako geothermal field, New Zealand. Geothermics 2007, 36, 101–114. [Google Scholar] [CrossRef]
- Roach, J.; Tidwell, V. A compartmental-spatial system dynamics approach to ground water modeling. Ground Water 2009, 47, 686–698. [Google Scholar] [CrossRef]
- Langsdale, S.; Beall, A.; Carmichael, J.; Cohen, S.; Forster, C. An exploration of water resources futures under climate change using system dynamics modeling. Integr. Assess. J. 2007, 7, 51–79. [Google Scholar]
- Xu, Z.X.; Takeuchi, K.; Ishidaira, H.; Zhang, X.W. Sustainability analysis for yellow river water resources using the system dynamics approach. Water Resour. Manag. 2002, 16, 239–261. [Google Scholar] [CrossRef]
- Karavezyris, V.; Timpe, K.P.; Marzi, R. Application of system dynamics and fuzzy logic to forecasting of municipal solid waste. Math. Comput. Simul. 2002, 60, 149–158. [Google Scholar] [CrossRef]
- Ahmad, S.; Simonovic, S.P. Spatial system dynamics: New approach for simulation of water resources systems. J. Comput. Civil Eng. 2004, 18, 331–340. [Google Scholar] [CrossRef]
- Wang, X.-J.; Zhang, J.-Y.; Liu, J.-F.; Wang, G.-Q.; He, R.-M.; Elmahdi, A.; Elsawah, S. Water resources planning and management based on system dynamics: A case study of yulin city. Environ. Dev. Sustain. 2011, 13, 331–351. [Google Scholar] [CrossRef]
- Eberlein, R.L.; Peterson, D.W. Understanding models with vensim™. Eur. J. Oper Res. 1992, 59, 216–219. [Google Scholar] [CrossRef]
- Deal, B.; Farello, C.; Lancaster, M.; Kompare, T.; Hannon, B. A dynamic model of the spatial spread of an infectious disease: The case of fox rabies in illinois. Environ. Model. Assess. 2000, 5, 47–62. [Google Scholar] [CrossRef]
- Costanza, R.; Voinov, A.; Boumans, R.; Maxwell, T.; Villa, F.; Wainger, L.; Voinov, H. Integrated ecological economic modeling of the patuxent river watershed, maryland. Ecol. Monogr. 2002, 72, 203–231. [Google Scholar] [CrossRef]
- Morshedian, H. Feasibility Study of Merk Dam; Regional Water Co. Ministry of Energy: Tehran, Iran, 2012; p. 871. [Google Scholar]
- Neuman, S.P. Effect of partial penetration on flow in unconfined aquifers considering delayed gravity response. Water Resour. Res. 1974, 10, 303–312. [Google Scholar] [CrossRef]
- Harbaugh, A.W. MODFLOW-2005, the U.S. Geological Survey Modular Ground-Water Model—The Ground-Water Flow Process: U.S. Geological Survey Techniques and Methods 6-a16; USGS: Reston, VA, USA, 2005. [Google Scholar]
- Amiri, M.J.; Eslamian, S.S. Investigation of climate change in Iran. J. Environ. Sci. Technol. 2010, 3, 208–216. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Niazi, A.; Prasher, S.O.; Adamowski, J.; Gleeson, T. A System Dynamics Model to Conserve Arid Region Water Resources through Aquifer Storage and Recovery in Conjunction with a Dam. Water 2014, 6, 2300-2321. https://doi.org/10.3390/w6082300
Niazi A, Prasher SO, Adamowski J, Gleeson T. A System Dynamics Model to Conserve Arid Region Water Resources through Aquifer Storage and Recovery in Conjunction with a Dam. Water. 2014; 6(8):2300-2321. https://doi.org/10.3390/w6082300
Chicago/Turabian StyleNiazi, Amir, Shiv O. Prasher, Jan Adamowski, and Tom Gleeson. 2014. "A System Dynamics Model to Conserve Arid Region Water Resources through Aquifer Storage and Recovery in Conjunction with a Dam" Water 6, no. 8: 2300-2321. https://doi.org/10.3390/w6082300












