Setting Target Measurement Uncertainty in Water Analysis
Abstract
:1. Introduction
2. Selecting Inputs for Defining the Target Measurement Uncertainty
3. Using Inputs for Defining Target Measurement Uncertainty
3.1. Legislation or Product Specification
3.1.1. Defined Target Measurement Uncertainty

3.1.2. Defined Measurement Performance Parameters
| Performance parameter | Description |
|---|---|
| Limit of Detection (LD) | The Limit of Detection (LD) can be estimated in repeatability or intermediate precision conditions. For instrumental methods of analysis requiring daily calibration of the instrumentation, LD estimated in repeatability conditions is only applicable to the daily run. The LD estimated from the precision of measurements of different calibrations can be applicable to a larger time scale. At this quantity level, the measurement coefficient of variance is 33% or 30% if LD is calculated by multiplying precision standard deviation by 3 or 3.3, respectively. Since absolute precision is constant in a narrow quantity range, the precision estimated at LD can be used to estimate precision between LD and the Limit of Quantification (LQ) (3 or 3.3 times larger than LD). Only seldom relevant systematic effects affect measurements at this quantity range [LD, LQ[. Convergent (“[#” or “#]”) or divergent (“]#” or “#[”) brackets indicate the inclusion or exclusion of number “#” in the interval, respectively. A target limit of detection, LDtg, can be used to estimate a target standard deviation, stg, of precision under studied conditions. The stg is “LDtg/3” or “LDtg/3.3” depending on used convention for estimating LD. |
| Limit of Quantification (LQ) | The calculation of the Limit of Quantification (LQ) is similar to that involved to estimate LD where the multiplying factor of the standard deviation of measurement precision is 10 instead of 3 or 3.3. At this quantity level, systematic effects can be relevant. |
| Limit of Quantification (LQ) | A target limit of quantification, LQtg, can be used to define the target standard deviation, stg, of studied precision conditions (stg = LQtg/10). Typically, stg can be applied between LD and two to five times LQ. |
| Range of duplicate measurements | Whenever a target range of results of duplicate measurements is defined, the respective confidence level and involved precision conditions should be checked. If the confidence level is not reported, a value of 95% should be considered. Since the repeatability or intermediate precision limits [3], estimated for a confidence level of 95%, are 2.83 times larger than the standard deviation of measurements under the same precision conditions, the target range can be converted into a stg by dividing it by 2.83. Only if otherwise specified, this precision should refer to the global measurement. If a target range of more than two replicate results is defined, this range can be converted into stg by dividing it by the factor previously used to convert the standard deviation of single measurements in the critical range [3]. |
| Coefficient of variance | If a target coefficient of variance is defined without specifying the precision conditions considered (typically repeatability or intermediate precision conditions), it can be assumed that the more informative intermediate precision is reported. Many references of measurement performance parameters do not use terminology of the latest, or even previous, VIM [1] editions, requiring a careful check of the meaning of the terms. In the past, the term reproducibility was used for the concept designated as intermediate precision in the latest VIM edition. Some documents define precision requirements as a target value for two times the standard deviation of the precision in defined conditions [2]. The repeatability standard deviation only reflects random effects in specific environmental and operational (i.e., for an analyst/equipment combination) conditions. A target intermediate precision can be used to set the target standard uncertainty reflecting all relevant random effects affecting measurement results. This uncertainty component does not reflect relevant systematic effects like the so called laboratory or method bias [4]. |
| Mean error | Measurement error, E, calculated by the difference between estimated, x, and conventional true value, Xtrue, occurs as a result of the combination of a random, ε, and the systematic, Δ, errors (Figure 2). Although measurement uncertainty evaluation, following principles presented in the “Guide to the expression of uncertainty in measurement” (GUM) [5], involves the combination of the uncertainty associated with random and systematic effects using the same general propagation law, the single measured quantity value, x, comes from the sum of Xtrue with ε and Δ resulting from the uncertainty associated with independent effects. The mean error, E, occurs as a result of the combination of the same systematic error, Δ, affecting single measurements, with a random error of the mean εm resulting from an uncertainty component of random effects  times smaller than the one affecting single measurements (where n is the number of replicate measurements combined in the mean value) (Figure 3). As n increases, the error of the mean tends to be less affected by random effects. In most measurements in chemistry, if n ≥ 20 the mean error E describes, with acceptable reliability, the systematic error ( times smaller than the one affecting single measurements (where n is the number of replicate measurements combined in the mean value) (Figure 3). As n increases, the error of the mean tends to be less affected by random effects. In most measurements in chemistry, if n ≥ 20 the mean error E describes, with acceptable reliability, the systematic error (  Δ). Δ).Therefore, the target absolute mean error  of a specific measurement defines the target absolute systematic error. This target value can be converted into an uncertainty component described by a variable centred in zero with a maximum range of of a specific measurement defines the target absolute systematic error. This target value can be converted into an uncertainty component described by a variable centred in zero with a maximum range of  (0 ± (0 ±  ). Assuming a normal distribution associated with ). Assuming a normal distribution associated with  , this range is converted into a standard uncertainty by dividing it by a coverage factor of 2 (u = , this range is converted into a standard uncertainty by dividing it by a coverage factor of 2 (u =  ). If a rectangular or triangular distribution is assumed, the divisor 2 is replaced by ). If a rectangular or triangular distribution is assumed, the divisor 2 is replaced by  or or  , respectively. This component only reflects systematic effects. , respectively. This component only reflects systematic effects. |
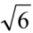 (
( 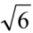 = stg). The standard deviation of measurement repeatability underestimates random effects observable in various runs.
= stg). The standard deviation of measurement repeatability underestimates random effects observable in various runs. can be used to estimate the target standard uncertainty associated with systematic effects
can be used to estimate the target standard uncertainty associated with systematic effects 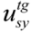 , as described in Table 1 (
, as described in Table 1 (  ; where divisor 2 can be substituted by
; where divisor 2 can be substituted by  or
or  ).
).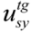 .
. , reflecting the combination of random and systematic effects, is calculated using uncertainty propagation law:
, reflecting the combination of random and systematic effects, is calculated using uncertainty propagation law:
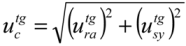
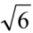 can be estimated from target values of the LD, LQ, coefficient of variation or range of replicate measurements, or any other parameter describing the same effect. The
can be estimated from target values of the LD, LQ, coefficient of variation or range of replicate measurements, or any other parameter describing the same effect. The 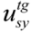 can be estimated from the target absolute mean error, mean analyte recovery tolerance or an equivalent parameter. If a relative target mean error is defined, it must be multiplied by the measured quantity value or the target quantity value before being combined with the random effect component in measurement result units.
can be estimated from the target absolute mean error, mean analyte recovery tolerance or an equivalent parameter. If a relative target mean error is defined, it must be multiplied by the measured quantity value or the target quantity value before being combined with the random effect component in measurement result units.
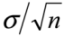 ) (where σ is the standard deviation of individual measurements, Figure 2).
) (where σ is the standard deviation of individual measurements, Figure 2).
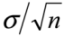 ) (where σ is the standard deviation of individual measurements, Figure 2).
) (where σ is the standard deviation of individual measurements, Figure 2).
 ) is to be compared with the combined standard uncertainty of performed measurements. The expansion of
) is to be compared with the combined standard uncertainty of performed measurements. The expansion of  , considering the typical coverage factor, in the expanded target measurement uncertainty
, considering the typical coverage factor, in the expanded target measurement uncertainty  allows the definition of criterion for the expanded measurement uncertainty. The comparison of the estimated with the target measurement uncertainty is discussed in Section 5.
allows the definition of criterion for the expanded measurement uncertainty. The comparison of the estimated with the target measurement uncertainty is discussed in Section 5.3.1.3. Defined Target Quantity Value
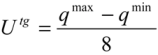
3.1.4. Defined Decision Risk
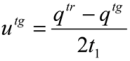
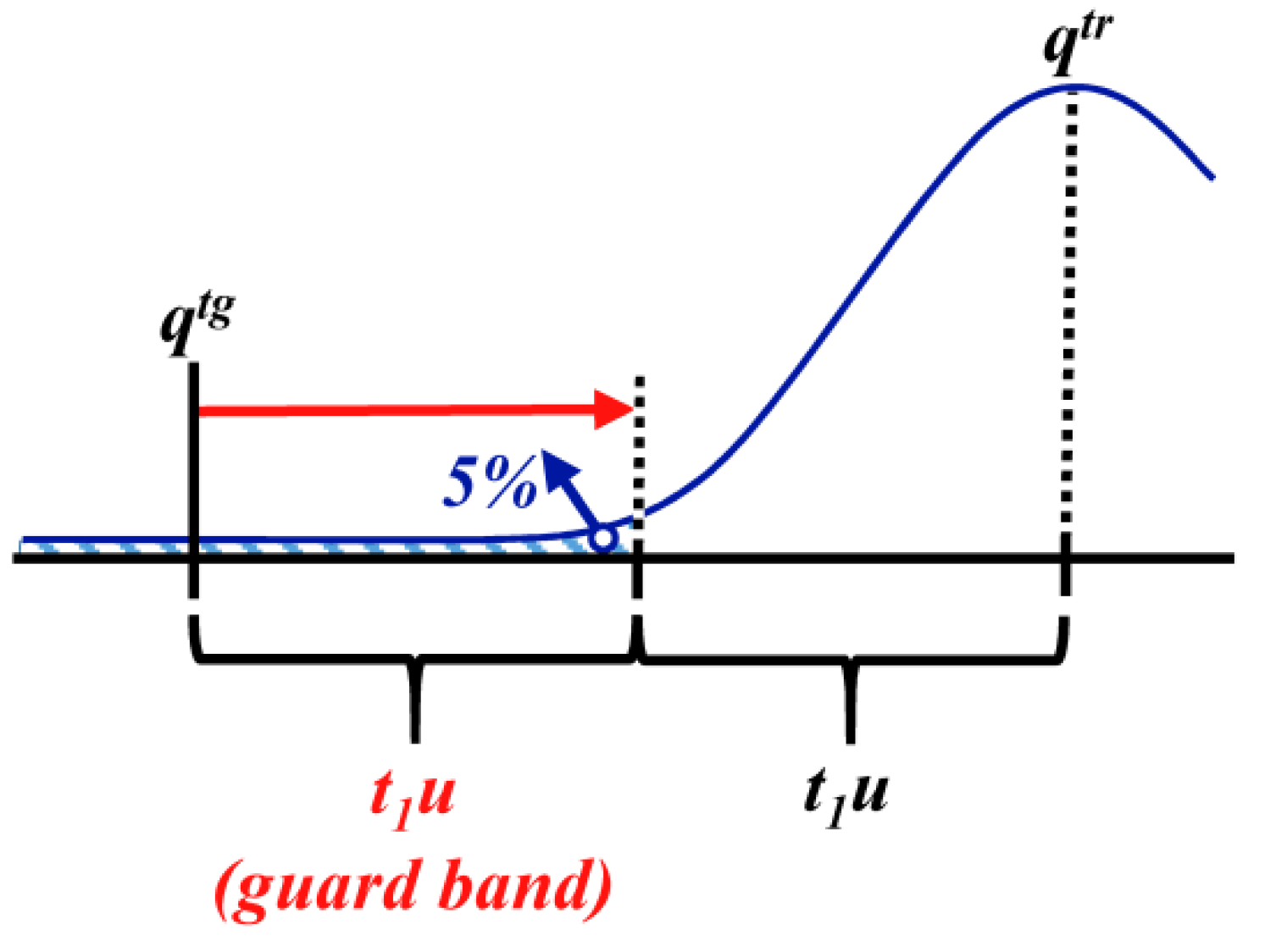

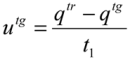
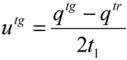
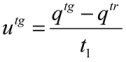
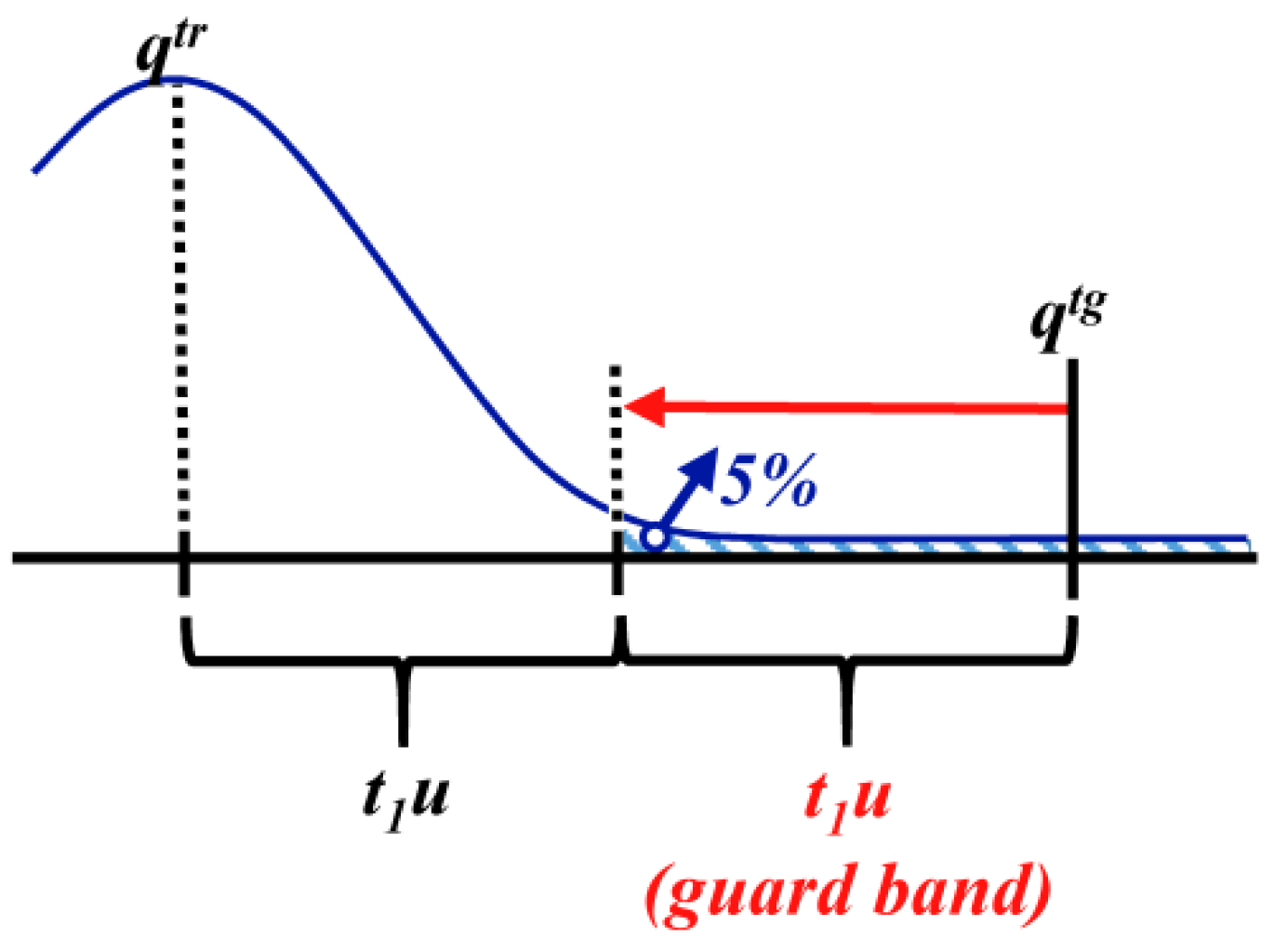
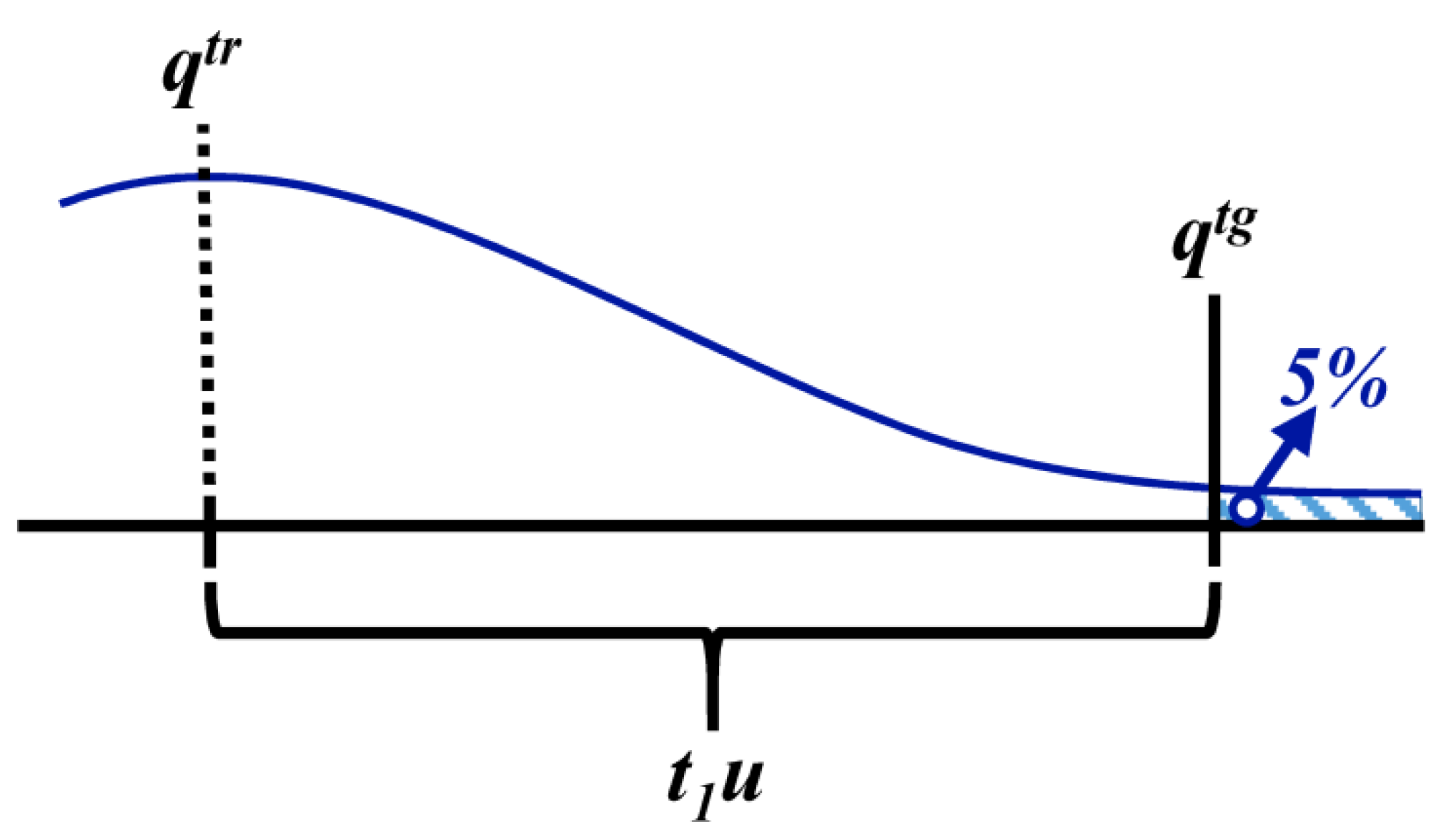
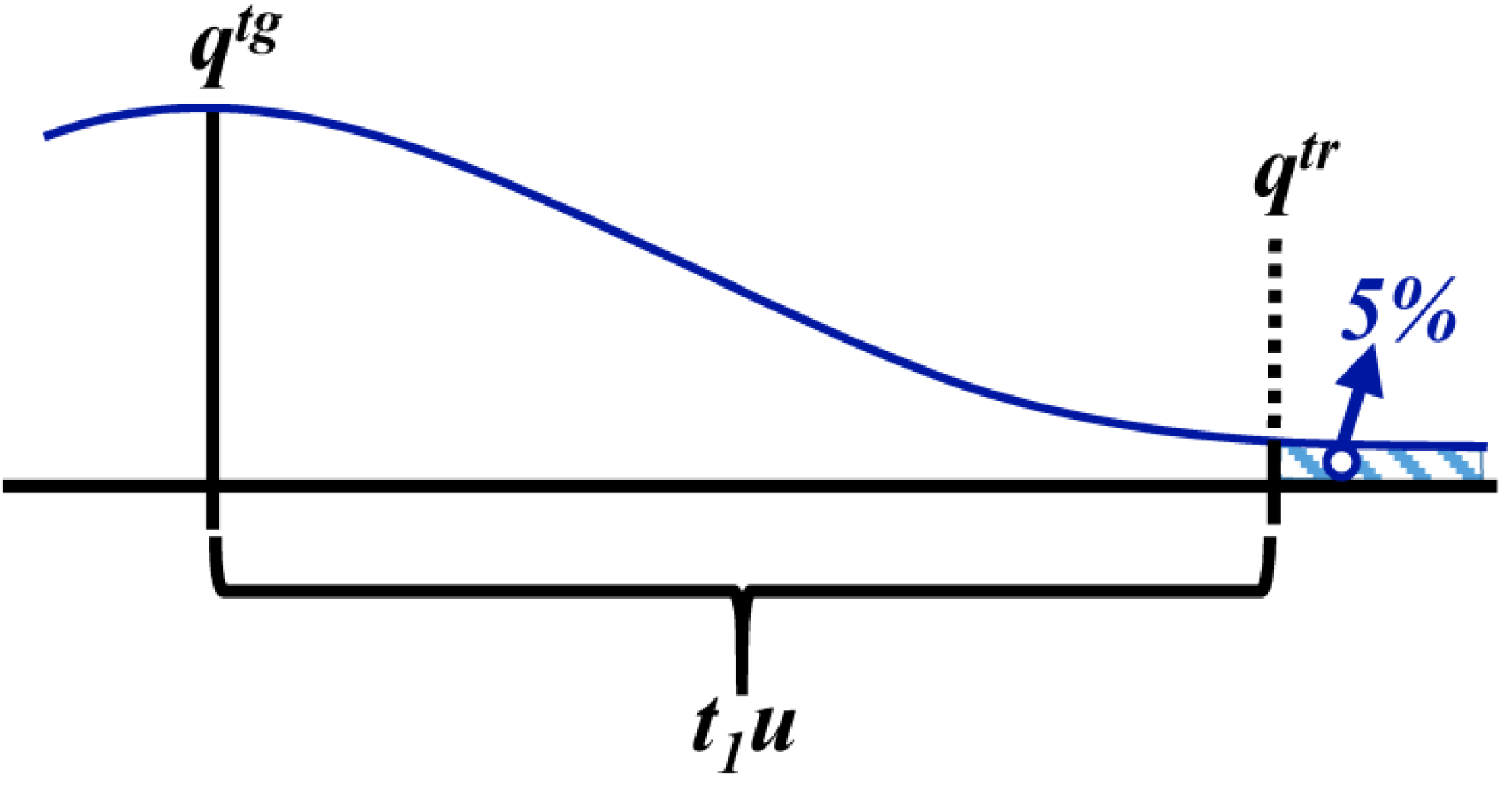

3.2. Proficiency Evaluation Criterion
3.2.1. Proficiency Tests
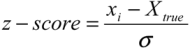
 ) for which a coverage factor of 2 can be used to expand to a confidence level of 95% (
) for which a coverage factor of 2 can be used to expand to a confidence level of 95% (  ).
).3.2.2. Measurement Reproducibility
 . If sR is estimated with a low number of degrees of freedom (νtg), this information should be considered in estimating the target expanded uncertainty Utg [
. If sR is estimated with a low number of degrees of freedom (νtg), this information should be considered in estimating the target expanded uncertainty Utg [  , where
, where  is the Student’s t for νtg degrees of freedom and 95% confidence level] and making a comparison with the estimated measurement uncertainty (see Section 5).
is the Student’s t for νtg degrees of freedom and 95% confidence level] and making a comparison with the estimated measurement uncertainty (see Section 5).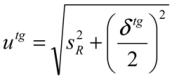
3.2.3. Maximum Error
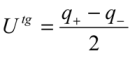
 ], analyst can decide to subtract this component to estimate a target measurement uncertainty independent of the uncertainty of the CRM value:
], analyst can decide to subtract this component to estimate a target measurement uncertainty independent of the uncertainty of the CRM value:
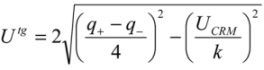
3.3. Magnitude of Studied Trends
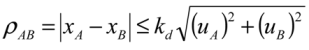
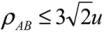
 ]; i.e., the u should be, at least, (3
]; i.e., the u should be, at least, (3  = 4.24) times smaller than the ρmin to distinguish this minim range. If ud is expected to be associated with a low number of degrees of freedom, the kd must be adjusted accordingly.
= 4.24) times smaller than the ρmin to distinguish this minim range. If ud is expected to be associated with a low number of degrees of freedom, the kd must be adjusted accordingly.3.4. Information from a Different Scope
4. Variation of the Target Measurement Uncertainty with the Quantity Value
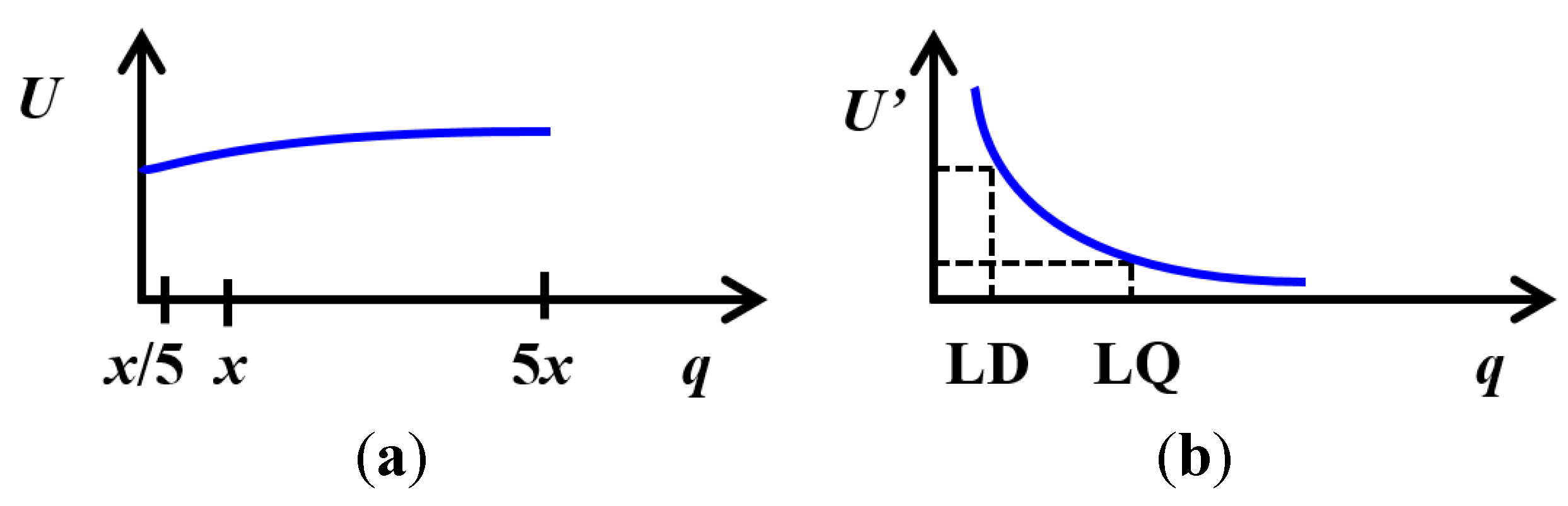
 represents the expected trend of U or U’ with the quality value, q.
represents the expected trend of U or U’ with the quality value, q.
 represents the expected trend of U or U’ with the quality value, q.
represents the expected trend of U or U’ with the quality value, q.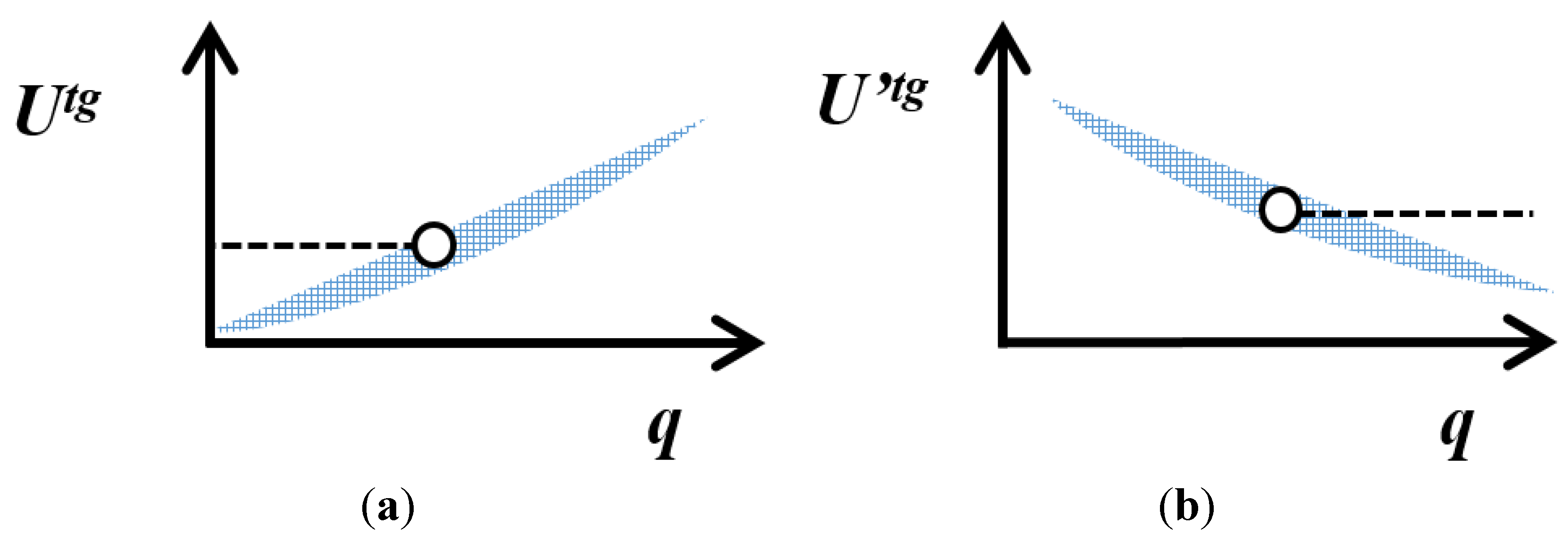
5. Comparison of the Estimated with the Target Measurement Uncertainty
 for the degrees of freedom associated with u, ν, and utg, νtg, and a confidence level of 95%.
for the degrees of freedom associated with u, ν, and utg, νtg, and a confidence level of 95%.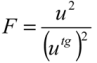
 , it can be assumed that there is no evidence that u is larger than utg. Assuming ν is larger than 50, a
, it can be assumed that there is no evidence that u is larger than utg. Assuming ν is larger than 50, a  of 1.35 can be used.
of 1.35 can be used.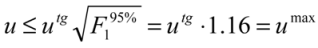
6. Measurement Uncertainty Optimization
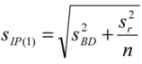
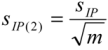
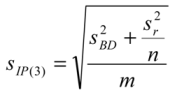
7. Examples
7.1. Defined Target Measurement Uncertainty
7.2. Defined Measurement Performance Parameters
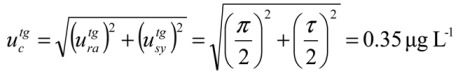
 =0.35
=0.35  ) (see Section 5). Nevertheless, if Cd results are estimated by the mean of duplicate measurement performed in two consecutive days (i.e., under intermediate precision conditions), the standard uncertainty can become fit for the intended use (see Section 6).
) (see Section 5). Nevertheless, if Cd results are estimated by the mean of duplicate measurement performed in two consecutive days (i.e., under intermediate precision conditions), the standard uncertainty can become fit for the intended use (see Section 6).7.3. Defined Target Quantity Value
7.4. Proficiency Tests
7.5. Measurements Reproducibility
7.6. Maximum Error

7.7. Magnitude of the Studied Trends
7.8. Information from a Different Scope
7.9. Variation of the Target Measurement Uncertainty with the Quantity Value
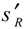 , estimated in three interlaboratory tests of the determination of copper in wastewaters by measurement procedure SMEWW3113B [22].
, estimated in three interlaboratory tests of the determination of copper in wastewaters by measurement procedure SMEWW3113B [22].
| Mass concentration of Cu (μg L−1) | 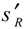 (%) (%) | |||
| Wastewater 1 | Wastewater 2 | Wastewater 3 | Maximum | |
| 234 | 21 | - | 26 | 26 |
| 300 | - | 14 | - | 14 |
| 1670 | - | 13 | - | 13 |
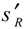 standard deviations of measurement reproducibility for various ranges, used to define the absolute utg or relative u'tg target standard uncertainty, respectively. The selectivity of the determination of copper in wastewater by ETAAS after an acid digestion of sample suggests measurement procedure bias is negligible and does not need to be considered in defining the target uncertainty. Convergent (“[#” or “#]”) or divergent (“]#” or “#[”) brackets indicate the inclusion or exclusion of the number “#” in the interval, respectively.
standard deviations of measurement reproducibility for various ranges, used to define the absolute utg or relative u'tg target standard uncertainty, respectively. The selectivity of the determination of copper in wastewater by ETAAS after an acid digestion of sample suggests measurement procedure bias is negligible and does not need to be considered in defining the target uncertainty. Convergent (“[#” or “#]”) or divergent (“]#” or “#[”) brackets indicate the inclusion or exclusion of the number “#” in the interval, respectively.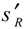 of measurements of copper in wastewater, following procedure SMEWW 3113B [22], with mass concentration of copper, used to define utg and
of measurements of copper in wastewater, following procedure SMEWW 3113B [22], with mass concentration of copper, used to define utg and 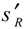 , respectively.
, respectively.
| Mass concentration of copper (μg L−1) | S R and utg (μg L−1) | 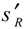 and u'tg(%) and u'tg(%) |
|---|---|---|
| [2.02, 10.1[ | 7.5 | - |
| [10.1, 234[ | - | 74 |
| [234, 300[ | - | 26 |
| [300, 1670[ | - | 14 |
| [1670, (…)[ | - | 13 |
| Mass concentration of copper (μg L−1) | umax (mg L−1) | u'max (%) |
|---|---|---|
| [2.02, 10.1[ | 8.7 | - |
| [10.1, 234[ | - | 86 |
| [234, 300[ | - | 30 |
| [300, 1670[ | - | 16 |
| [1670, (…)[ | - | 15 |
8. Conclusions
Conflicts of Interest
References
- International Vocabulary of Metrology—Basic and General Concepts and Associated Terms (VIM), 3rd ed.; International Bureau of Weights and Measures: Paris, France, 2008.
- Council Directive 98/83/EC of 3 November 1998 on the Quality of Water Intended for Human Consumption; Official Journal of the European Communities: Brussels, Belgium, 1998.
- International Organization for Standardization, Accuracy (Trueness and Precision) of Measurement Methods and Results—Part 6: Use in Practice of Accuracy Values—ISO5725-6; International Organization for Standardization: Geneva, Switzerland, 1994.
- Analytical Methods Committee, Uncertainty of measurement: Implications of its use in analytical science. In Analyst; 1995; Volume 120, pp. 2303–2308.
- Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement (GUM); International Bureau of Weights and Measures: Paris, France, 2008.
- Technical Material and Preparations: Guidance for Generating and Reporting Methods of Analysis in Support of Pre- and Post-Registration Data Requirements for Annex II (Part A, Section 4) and Annex III (Part A, Section 5) of Directive 91/414; SANCO/3030/99 rev.4 11/07/00; Directorate General for Health and Consumer Protection: Brussels, Belgium, 1999.
- EURACHEM/CITAC Guide: Use of Uncertainty Information in Compliance Assessment, 1st ed; Eurachem: Uppsala, Sweden, 2007.
- RELACRE, EAA—Ensaios De Aptidão De Águas—Programa De Execução; [in Portuguese]; RELACRE: Lisbon, Portugal, 2012.
- International Organization for Standardization, Guidance for the Use of Repeatability, Reproducibility and Trueness Estimates in Measurement Uncertainty Estimation—ISO21748; International Organization for Standardization: Geneva, Switzerland, 2010.
- Da Silva, R.J.N.B.; Santos, J.R.; Camões, M.F.G.F.C. A new terminology for the approaches to the quantification of the measurement uncertainty. Accred. Qual. Assur. 2006, 10, 664–671. [Google Scholar] [CrossRef]
- Ellison, S.L.R.; Barwick, V.J.; Farrant, T.J.D. Practical Statistics for the Analytical Scientist: A Bench Guide; Royal Society of Chemistry: London, UK, 2009. [Google Scholar]
- Council Directive 75/440/EEC of 16 June 1975 Concerning the Quality Required of Surface Water Intended for the Abstraction of Drinking Water in the Member States; Official Journal of the European Communities: Brussels, Belgium, 1975.
- Council Directive 76/160/EEC of 8 December 1975 Concerning the Quality of Bathing Water; Official Journal of the European Communities: Brussels, Belgium, 1975.
- Council Directive 78/659/EEC of 18 July 1978 on the Quality of Fresh Waters Needing Protection or Improvement in order to Support Fish Life as Amended by Council Directive 91/692/EEC (further Amended by Council Regulation 1882/2003/EC), and Council Regulation 807/2003/EC; Official Journal of the European Communities: Brussels, Belgium, 1978.
- Council Directive 79/869/EEC of 9 October 1979 Concerning the Methods of Measurement and Frequencies of Sampling and Analysis of Surface Water Intended for the Abstraction of Drinking Water in the Member States; Official Journal of the European Communities: Brussels, Belgium, 1979.
- Council Directive 79/923/EEC of 30 October 1979 on the Quality Required of Shellfish Waters; Official Journal of the European Communities: Brussels, Belgium, 1979.
- Council Directive 84/491/EEC of 9 October 1984 on Limit Values and Quality Objectives for Discharges of Hexachlorocyclohexane; Official Journal of the European Communities: Brussels, Belgium, 1984.
- Council Directive 86/280/EEC of 12 June 1986 on Limit Values and Quality Objectives for Discharges of Certain Dangerous Substances Included in List I of the Annex to Directive 76/464/EEC; Official Journal of the European Communities: Brussels, Belgium, 1986.
- Council Directive 88/347/EEC of 16 June 1988 amending Annex II to Directive 86/280/EEC on Limit Values and Quality Objectives for Discharges of Certain Dangerous Substances Included in List I of the Annex to Directive 76/464/EEC; Official Journal of the European Communities: Brussels, Belgium, 1988.
- Silva, A.M.E.V.; Silva, R.J.N.B.; Camões, M.F.G.F.C. Optimization of the determination of chemical oxygen demand in wastewaters. Anal. Chim. Acta 2011, 699, 161–169. [Google Scholar] [CrossRef]
- De la Calle, M.B.; Robouch, P.; Bynens, S.; van de Kreeke, J.; Taylor, P. Report of the Second Interlaboratory Comparison Organised by the Community Reference Laboratory for Heavy Metals in Feed and Food—Total Cd, Pb and Hg in Mineral Water; Official Publications of the European Communities: Luxembourg, 2007. [Google Scholar]
- American Public Health AssociationAmerican Water Works AssociationWater Environment FederationStandard Methods for the Examination of Water & Wastewater; American Water Works Association: Denver, CO, USA, 2012.
- SCP Science, Certificate of Analysis, Certified Reference Material “EnviroMAT EU-H-1” of Mass Concentration of Metals in Wastewater; SCP Science: Beijing, China, 2005.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Da Silva, R.J.N.B. Setting Target Measurement Uncertainty in Water Analysis. Water 2013, 5, 1279-1302. https://doi.org/10.3390/w5031279
Da Silva RJNB. Setting Target Measurement Uncertainty in Water Analysis. Water. 2013; 5(3):1279-1302. https://doi.org/10.3390/w5031279
Chicago/Turabian StyleDa Silva, Ricardo J.N. Bettencourt. 2013. "Setting Target Measurement Uncertainty in Water Analysis" Water 5, no. 3: 1279-1302. https://doi.org/10.3390/w5031279




