Risk Analysis for Reservoir Real-Time Optimal Operation Using the Scenario Tree-Based Stochastic Optimization Method
Abstract
:1. Introduction
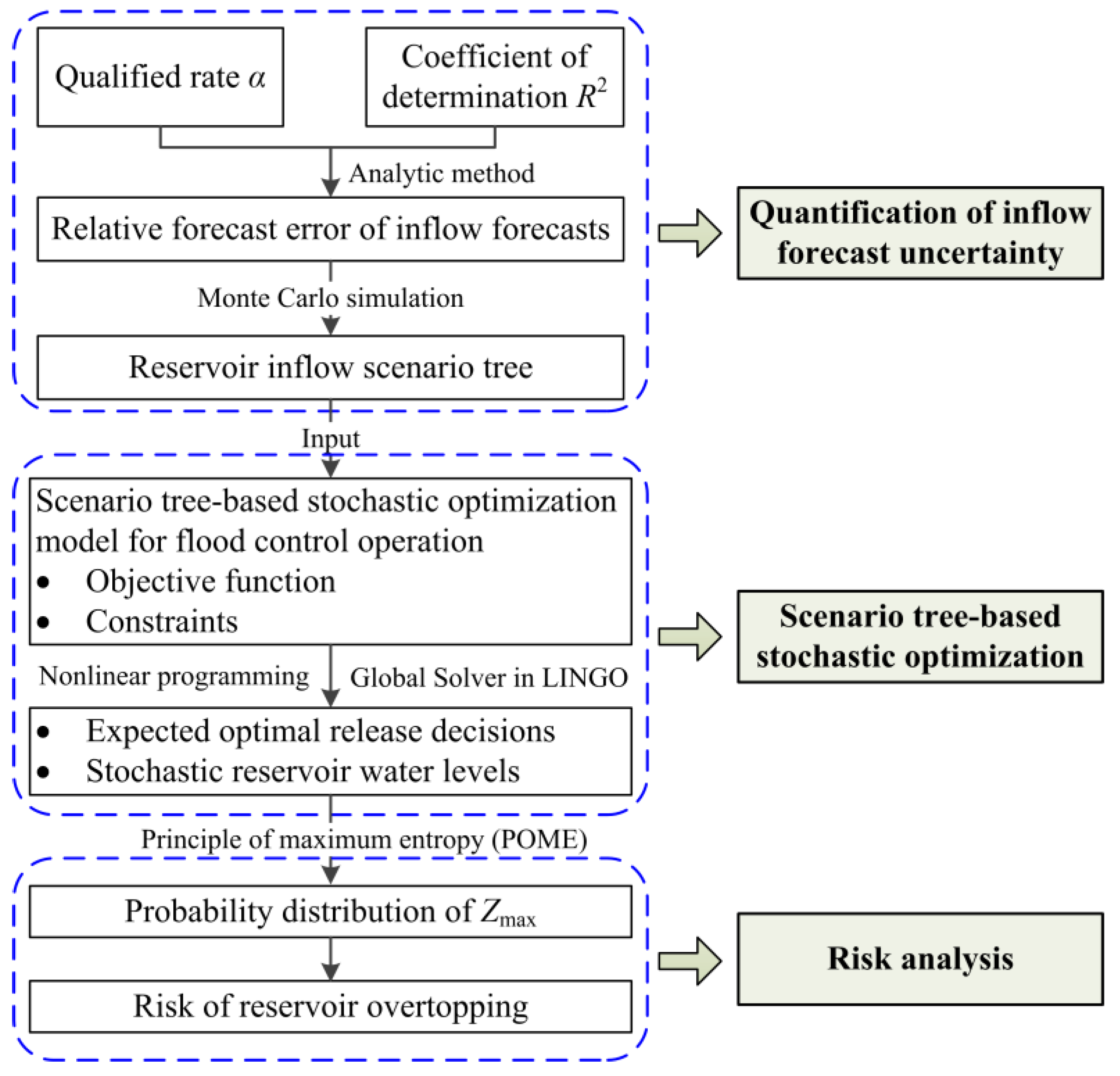
2. Methodology
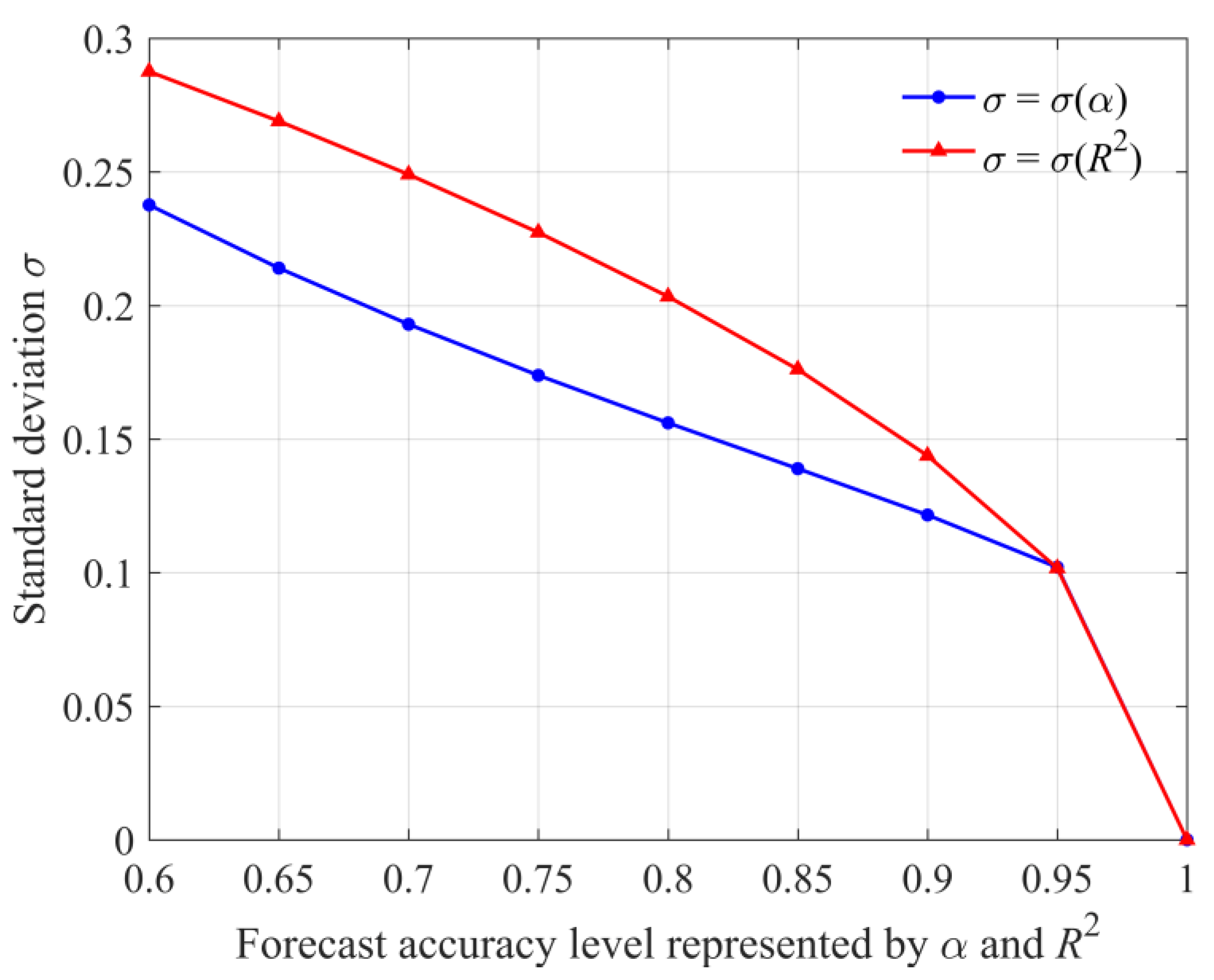
2.1. Quantify the Probability Distribution of Inflow Forecast Uncertainty
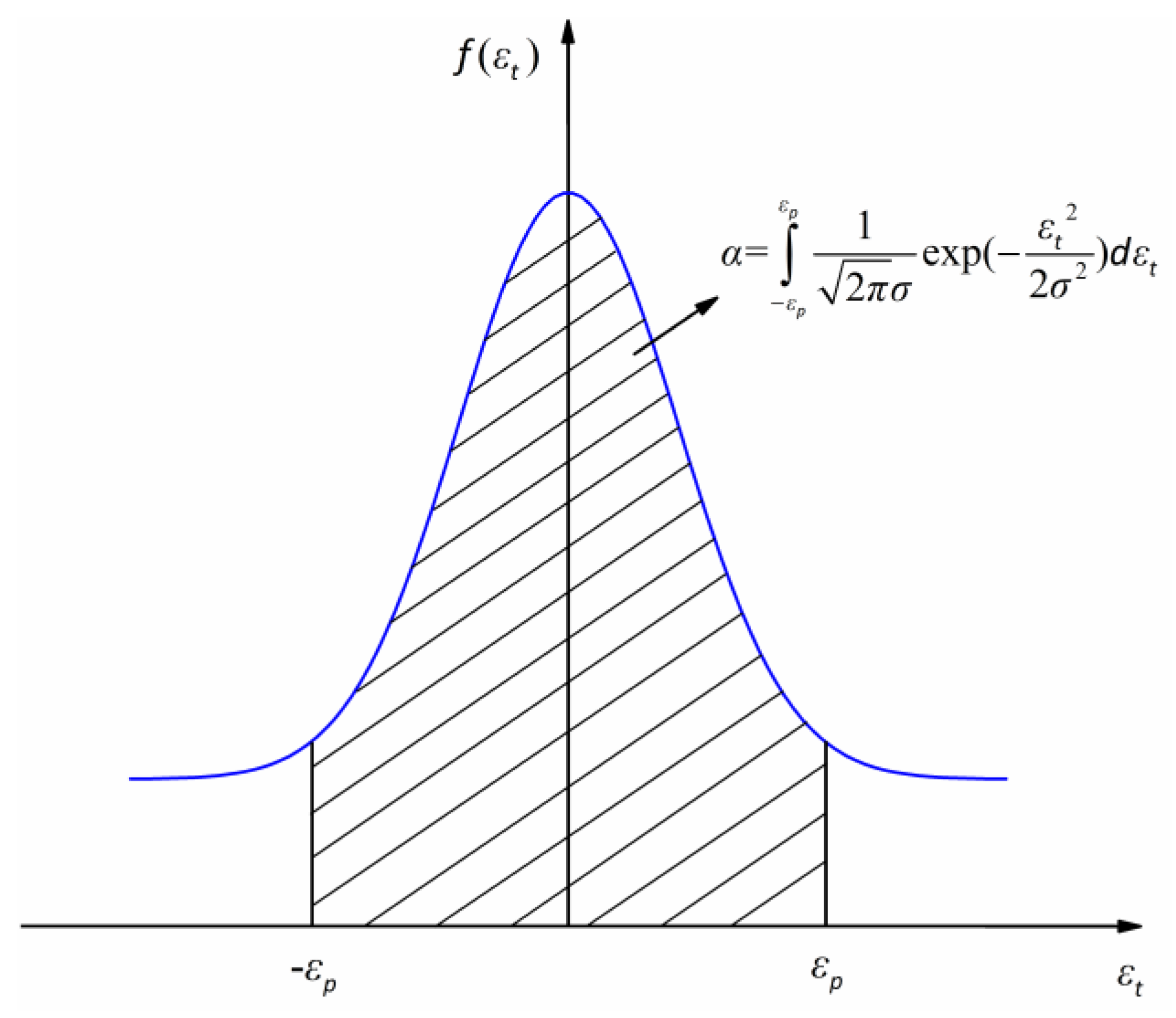
2.1.1. Based on the Qualified Rate
2.1.2. Based on the Coefficient of Determination
2.1.3. Inflow Scenario Tree Generation via Monte Carlo Simulation
2.2. Scenario Tree-Based Stochastic Optimization Model for Flood Control Operation
2.2.1. Objective Function
2.2.2. Constraints
- (1)
- Water balance equationwhere and are reservoir storage variables at the ending and beginning of time t − 1 under scenario , respectively (m3); and represent reservoir inflow and outflow at time t under scenario , respectively (m3/s); and is the time interval (s).
- (2)
- Reservoir water level boundswhere and are the lower and upper bounds of reservoir water level at time t, respectively (m).
- (3)
- Reservoir release limitswhere and are the lower and upper bounds of reservoir release at time t, respectively (m3/s).
- (4)
- Reservoir release capacity limitswhere is a function of the reservoir release capacity, which represents the maximum limit of outflow that can be released to the downstream river when all spillways reach their release capacities (m3/s).
- (5)
- Reservoir release fluctuation limitswhere is the permitted maximum release fluctuation (m3/s). To ensure the safety of downstream navigation and avoid the sediment erosion of levee systems, the reservoir release should not fluctuate sharply. We use this constraint to restrict the difference of reservoir release between two adjacent time periods within a given range.
- (6)
- Initial and boundary conditionswhere and represent the initial and target end water level, respectively (m). The end water level is expected to fall back to the target water level. For long-term hydropower operations, this should be a hard constraint which must be strictly satisfied. However, for short-term real-time flood control operations, this is usually treated as a soft constraint and loosened, since the end water level sometimes cannot reach the target water level in a limited operation horizon if the initial water level is high or the peak inflow discharge is huge and occurs late.
2.2.3. Algorithm
2.3. Risk Analysis Based on the Principle of Maximum Entropy (POME)
2.3.1. Risk Source of Reservoir Optimal Flood Control Operation
2.3.2. Risk Definition of Reservoir Optimal Flood Control Operation
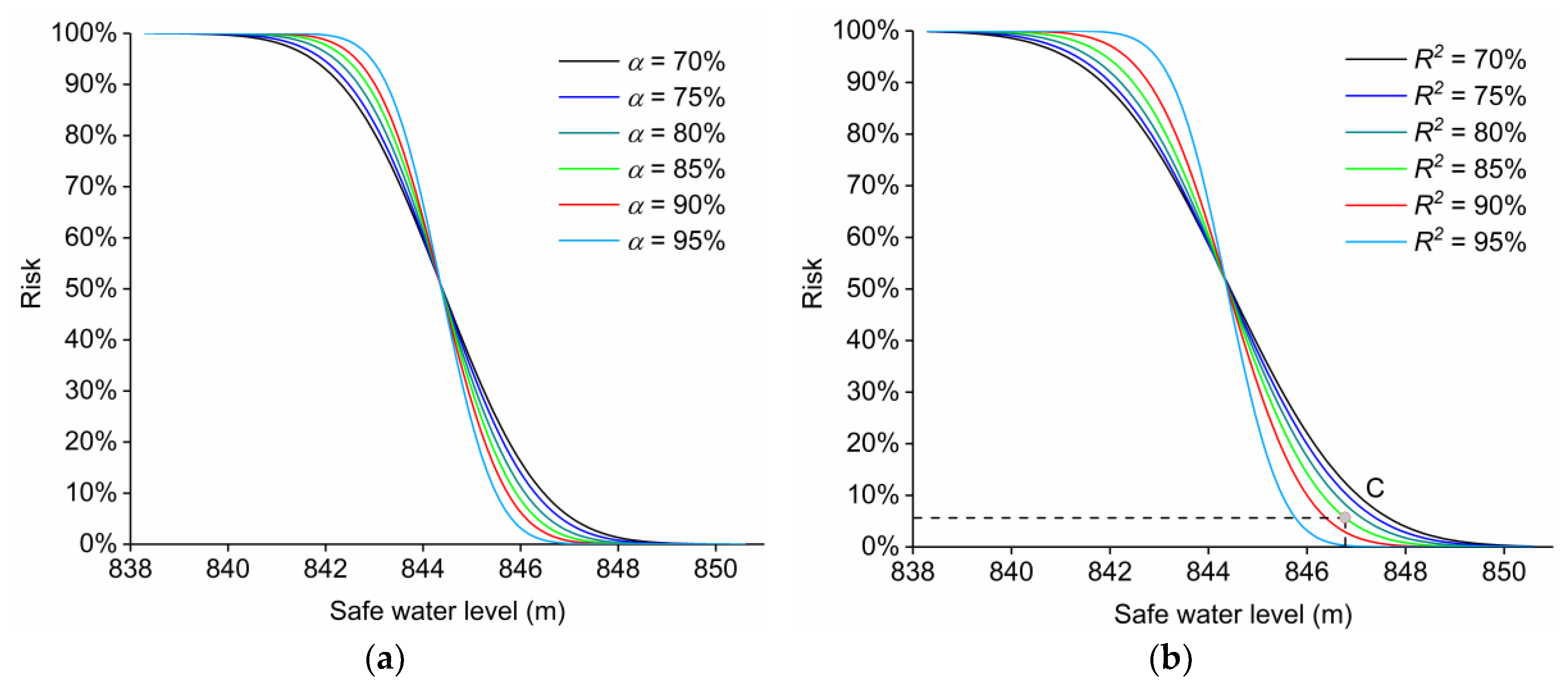
2.3.3. Derive the Probability Distribution of Zmax Using POME
3. Results and Discussion
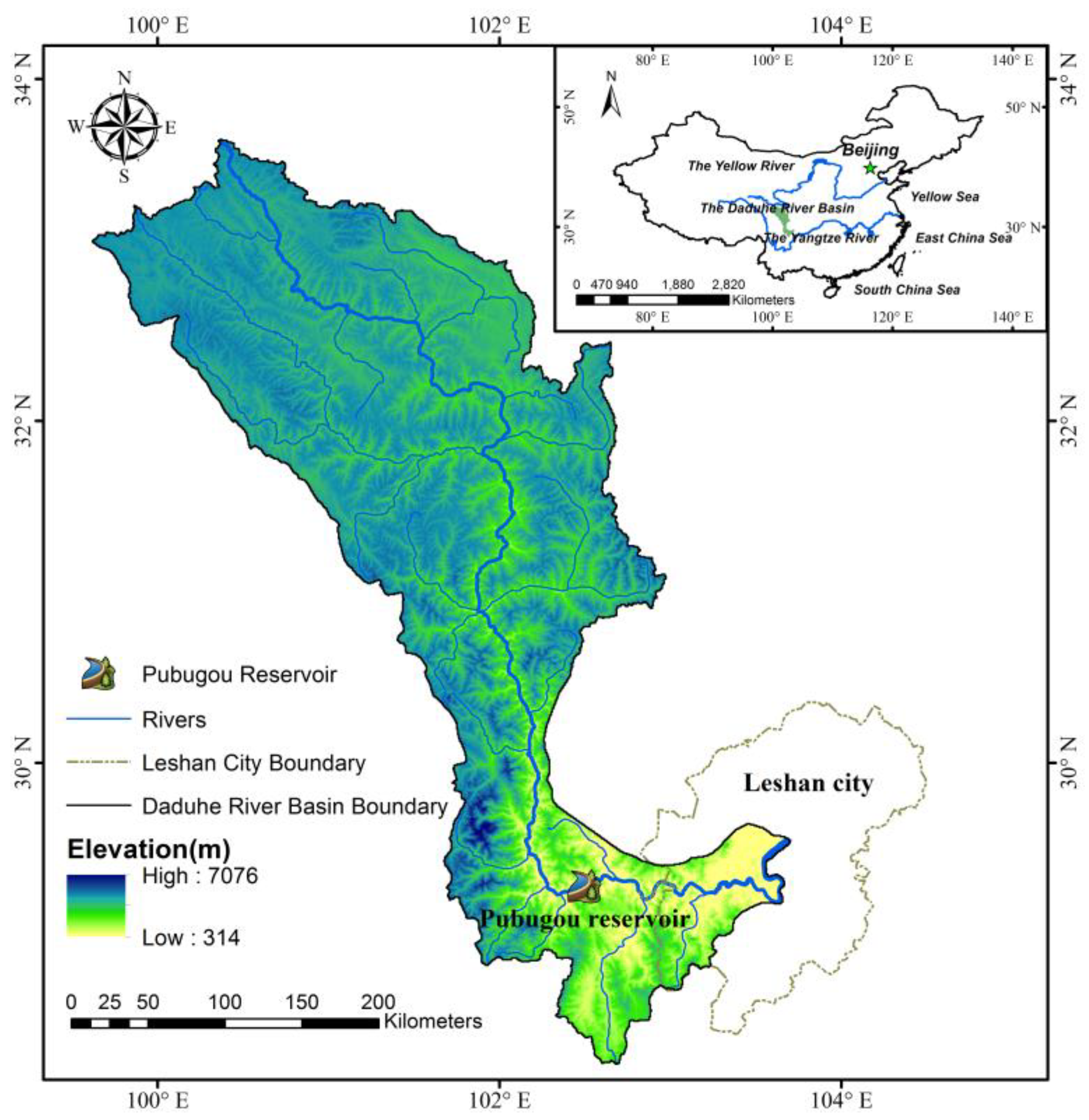
3.1. Introduction to the Study Area
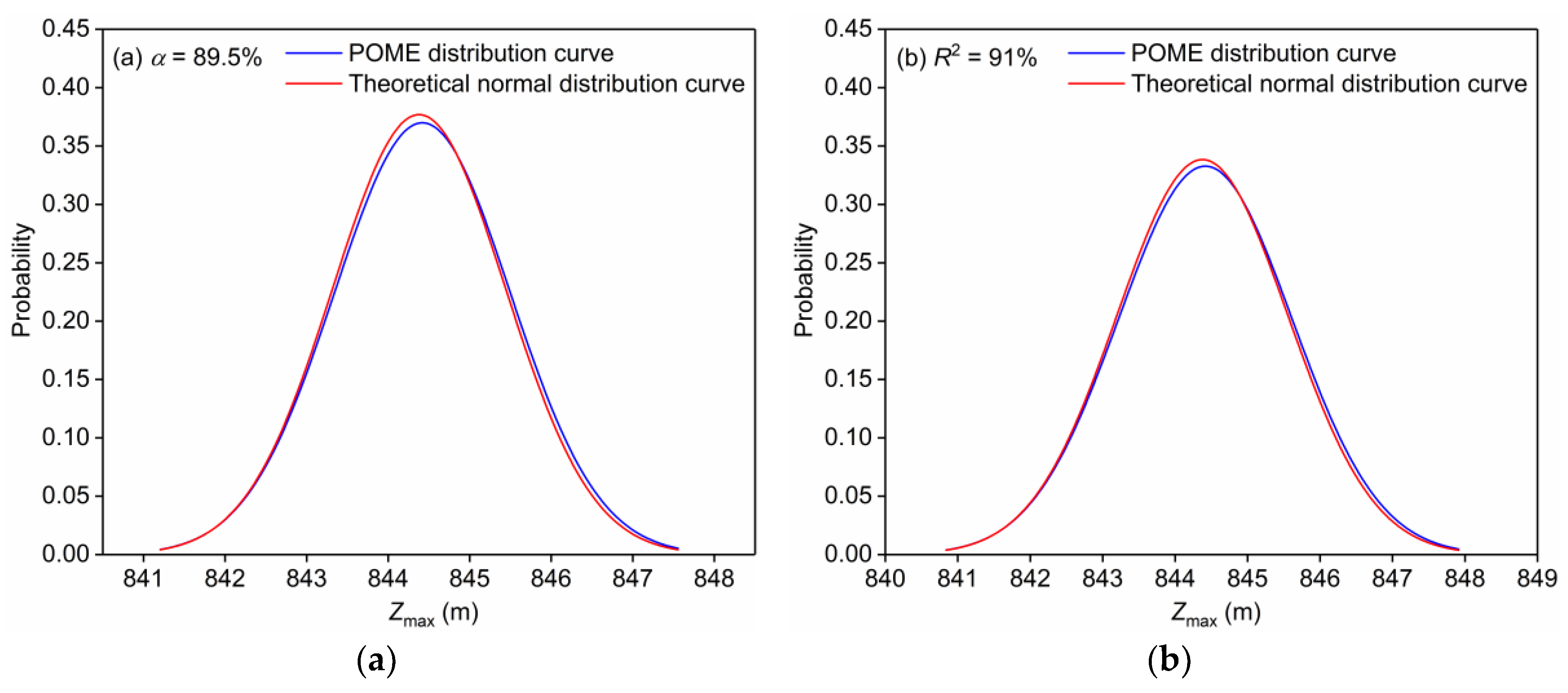
3.2. Demonstration of the Proposed Methodology
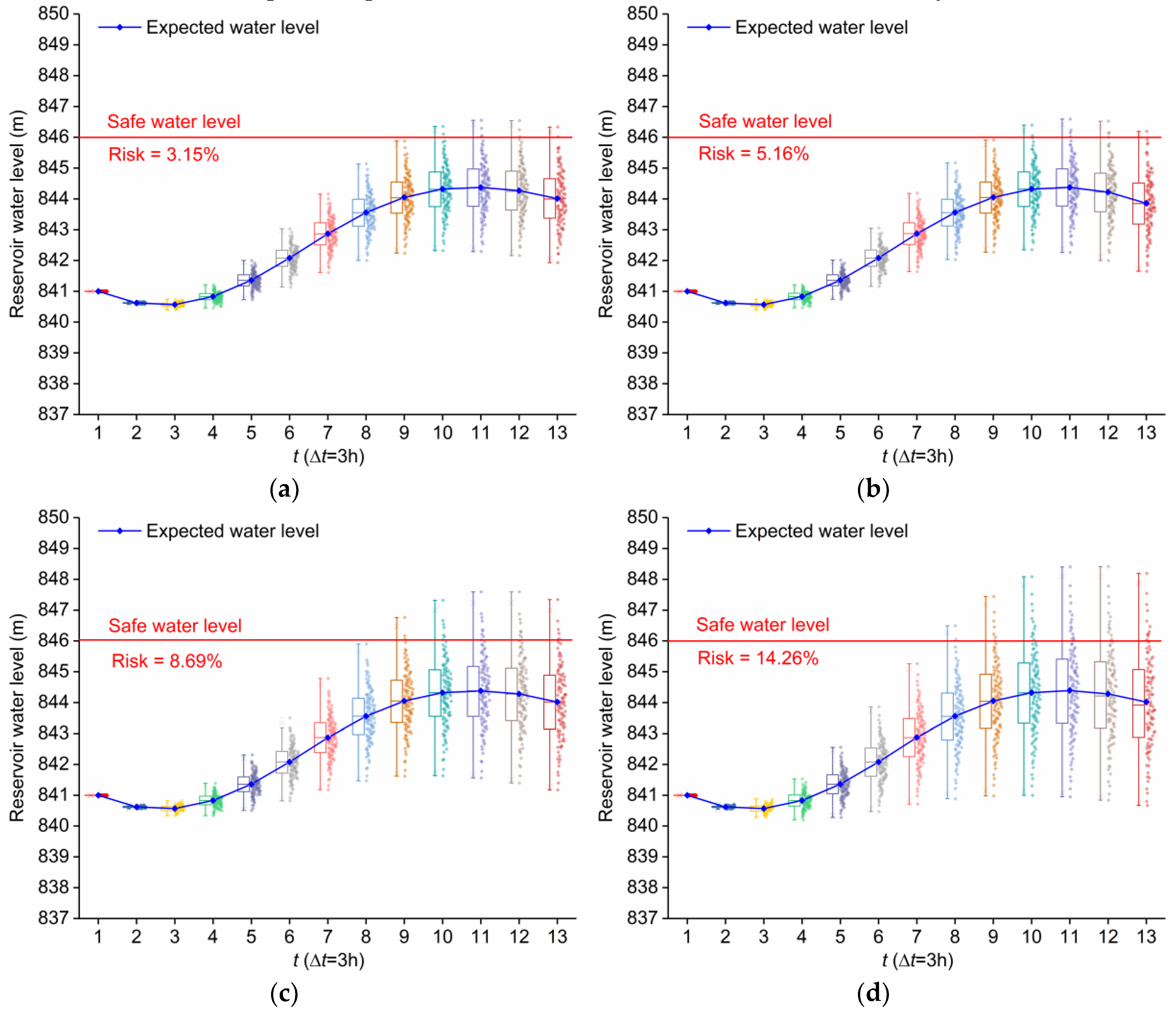
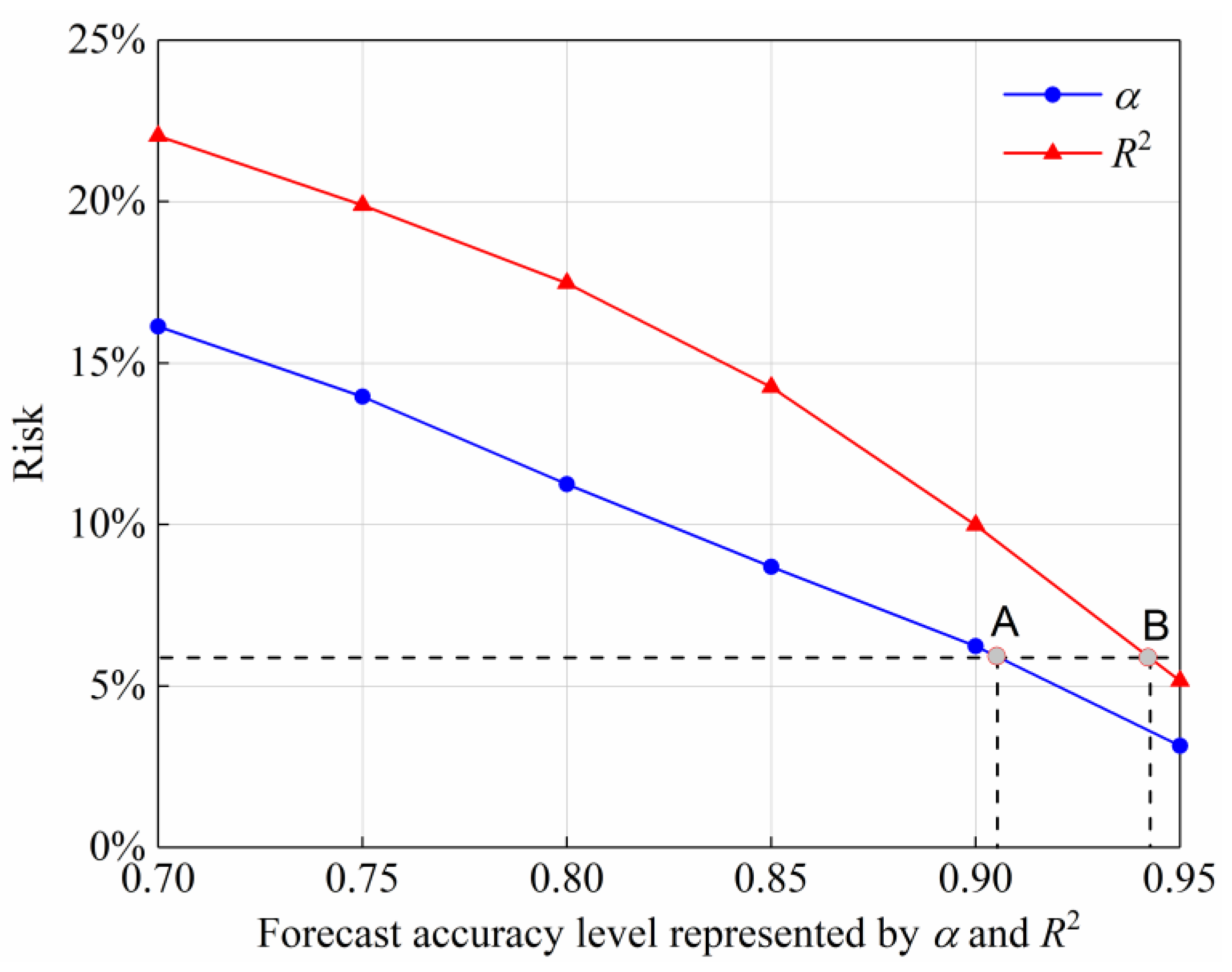
3.3. Effect of Forecast Accuracy Level on Optimal Flood Control Operation
4. Summary and Conclusions
- (1)
- We derived the probability distribution of inflow forecast uncertainty by developing the relationship between two forecast accuracy metrics (i.e., the qualified rate α and the coefficient of determination R2) and the standard deviation of relative forecast error. The inflow scenario tree, used to represent the uncertain inflow forecasts, was generated via Monte Carlo simulation.
- (2)
- We established the scenario tree-based stochastic optimization model to explicitly incorporate inflow forecast uncertainty into the stochastic optimization process. Nonlinear programming (the Global Solver available in LINGO 17.0) was employed to solve the model and to find the globally optimal solutions.
- (3)
- We carried out risk analysis to estimate the risk of reservoir overtopping based on the principle of maximum entropy (POME).
- (4)
- We applied the proposed methodology to the flood control system in the Daduhe River Basin, China. Additionally, we conducted numerical experiments to investigate the effect of two different forecast accuracy metrics and different forecast accuracy levels on reservoir optimal flood control operation as well as risk analysis.
Author Contributions
Funding
Conflicts of Interest
References
- Zhu, F.L.; Zhong, P.A.; Xu, B.; Wu, Y.N.; Zhang, Y. A multi-criteria decision-making model dealing with correlation among criteria for reservoir flood control operation. J. Hydroinf. 2016, 18, 531–543. [Google Scholar] [CrossRef]
- Zhu, F.L.; Zhong, P.A.; Sun, Y.M.; Xu, B. Selection of criteria for multi-criteria decision making of reservoir flood control operation. J. Hydroinf. 2017, 19, 558–571. [Google Scholar] [CrossRef]
- Yeh, W.W.G. Reservoir management and operations models: A state-of-the-art review. Water Resour. Res. 1985, 21, 1797–1818. [Google Scholar] [CrossRef]
- Chou, F.N.F.; Wu, C.W. Stage-wise optimizing operating rules for flood control in a multi-purpose reservoir. J. Hydrol. 2015, 521, 245–260. [Google Scholar] [CrossRef]
- Hsu, N.S.; Huang, C.L.; Wei, C.C. Multi-phase intelligent decision model for reservoir real-time flood control during typhoons. J. Hydrol. 2015, 522, 11–34. [Google Scholar] [CrossRef]
- Jia, B.Y.; Simonovic, S.P.; Zhong, P.A.; Yu, Z.B. A multi-objective best compromise decision model for real-time flood mitigation operations of multi-reservoir system. Water Resour. Manag. 2016, 30, 3363–3387. [Google Scholar] [CrossRef]
- Zhu, F.L.; Zhong, P.A.; Wu, Y.N.; Sun, Y.M.; Chen, J.; Jia, B.Y. SMAA-based stochastic multi-criteria decision making for reservoir flood control operation. Stoch. Environ. Res. Risk Assess. 2017, 31, 1485–1497. [Google Scholar] [CrossRef]
- Zhu, F.L.; Zhong, P.A.; Sun, Y.M. Multi-criteria group decision making under uncertainty: Application in reservoir flood control operation. Environ. Model. Softw. 2018, 100, 236–251. [Google Scholar] [CrossRef]
- Kumar, A.; Sharma, M.P. Assessment of risk of GHG emissions from Tehri hydropower reservoir, India. Hum. Ecol. Risk Assess. 2016, 22, 71–85. [Google Scholar] [CrossRef]
- Kumar, A.; Sharma, M.P. A modeling approach to assess the greenhouse gas risk in Koteshwar hydropower reservoir, India. Hum. Ecol. Risk Assess. 2016, 22, 1651–1664. [Google Scholar] [CrossRef]
- Bogner, K.; Pappenberger, F. Multiscale error analysis, correction, and predictive uncertainty estimation in a flood forecasting system. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Qu, B.; Zhang, X.N.; Pappenberger, F.; Zhang, T.; Fang, Y.H. Multi-model grand ensemble hydrologic forecasting in the Fu river basin using Bayesian model averaging. Water 2017, 9, 74. [Google Scholar] [CrossRef]
- Schoups, G.; Vrugt, J.A. A formal likelihood function for parameter and predictive inference of hydrologic models with correlated, heteroscedastic, and non-Gaussian errors. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- McInerney, D.; Thyer, M.; Kavetski, D.; Lerat, J.; Kuczera, G. Improving probabilistic prediction of daily streamflow by identifying Pareto optimal approaches for modeling heteroscedastic residual errors. Water Resour. Res. 2017, 53, 2199–2239. [Google Scholar] [CrossRef]
- Roy, T.; Serrat-Capdevila, A.; Gupta, H.; Valdes, J. A platform for probabilistic multimodel and multiproduct streamflow forecasting. Water Resour. Res. 2017, 53, 376–399. [Google Scholar] [CrossRef]
- Yan, B.W.; Guo, S.L.; Chen, L. Estimation of reservoir flood control operation risks with considering inflow forecasting errors. Stoch. Environ. Res. Risk Assess. 2014, 28, 359–368. [Google Scholar] [CrossRef]
- Kumar, A.; Sharma, M.P. Estimation of soil organic carbon in the forest catchment of two hydroelectric reservoirs in Uttarakhand, India. Hum. Ecol. Risk Assess. 2016, 22, 991–1001. [Google Scholar] [CrossRef]
- Rajaram, H.; Bahr, J.M.; Bloschl, G.; Cai, X.M.; Mackay, D.S.; Michalak, A.M.; Montanari, A.; Sanchez-Villa, X.; Sander, G. A reflection on the first 50 years of Water Resources Research. Water Resour. Res. 2015, 51, 7829–7837. [Google Scholar] [CrossRef] [Green Version]
- Zhu, F.L.; Zhong, P.A.; Sun, Y.M.; Yeh, W.W.G. Real-time optimal flood control decision making and risk propagation under multiple uncertainties. Water Resour. Res. 2017, 53, 10635–10654. [Google Scholar] [CrossRef]
- Chen, J.; Zhong, P.A.; Zhang, Y.; Navar, D.; Yeh, W.W.G. A decomposition-integration risk analysis method for real-time operation of a complex flood control system. Water Resour. Res. 2017, 53, 2490–2506. [Google Scholar] [CrossRef]
- Chen, J.; Zhong, P.A.; Wang, M.L.; Zhu, F.L.; Wan, X.Y.; Zhang, Y. A risk-based model for real-time flood control operation of a cascade reservoir system under emergency conditions. Water 2018, 10, 167. [Google Scholar] [CrossRef]
- Jiang, S. Application of stochastic differential equations in risk assessment for flood releases. Hydrol. Sci. J. 1998, 43, 349–360. [Google Scholar] [CrossRef]
- Li, X.; Guo, S.L.; Liu, P.; Chen, G.Y. Dynamic control of flood limited water level for reservoir operation by considering inflow uncertainty. J. Hydrol. 2010, 391, 124–132. [Google Scholar] [CrossRef]
- Chen, J.; Zhong, P.A.; Xu, B.; Zhao, Y.F. Risk analysis for real-time flood control operation of a reservoir. J. Water Resour. Plan. Manag. 2015, 141. [Google Scholar] [CrossRef]
- Chen, J.; Zhong, P.A.; Zhao, Y.F.; Xu, B. Risk analysis for the downstream control section in the real-time flood control operation of a reservoir. Stoch. Environ. Res. Risk Assess. 2015, 29, 1303–1315. [Google Scholar] [CrossRef]
- Labadie, J.W. Optimal operation of multireservoir systems: State-of-the-art review. J. Water Resour. Plan. Manag. 2004, 130, 93–111. [Google Scholar] [CrossRef]
- Xu, B.; Zhong, P.A.; Zambon, R.C.; Zhao, Y.F.; Yeh, W.W.G. Scenario tree reduction in stochastic programming with recourse for hydropower operations. Water Resour. Res. 2015, 51, 6359–6380. [Google Scholar] [CrossRef]
- Xu, B.; Boyce, S.E.; Zhang, Y.; Liu, Q.; Guo, L.; Zhong, P.A. Stochastic programming with a joint chance constraint model for reservoir refill operation considering flood risk. J. Water Resour. Plan. Manag. 2016, 143. [Google Scholar] [CrossRef]
- Bozorg-Haddad, O.; Azarnivand, A.; Hosseini-Moghari, S.M.; Loaiciga, H.A. Optimal operation of reservoir systems with the symbiotic organisms search (SOS) algorithm. J. Hydroinf. 2017, 19, 507–521. [Google Scholar] [CrossRef]
- Housh, M. Non-probabilistic robust optimization approach for flood control system design. Environ. Model. Softw. 2017, 95, 48–60. [Google Scholar] [CrossRef]
- Chen, D.; Leon, A.S.; Engle, S.P.; Fuentes, C.; Chen, Q.W. Offline training for improving online performance of a genetic algorithm based optimization model for hourly multi-reservoir operation. Environ. Model. Softw. 2017, 96, 46–57. [Google Scholar] [CrossRef]
- Liu, P.; Li, L.P.; Chen, G.J.; Rheinheimer, D.E. Parameter uncertainty analysis of reservoir operating rules based on implicit stochastic optimization. J. Hydrol. 2014, 514, 102–113. [Google Scholar] [CrossRef]
- Côté, P.; Leconte, R. Comparison of stochastic optimization algorithms for hydropower reservoir operation with ensemble streamflow prediction. J. Water Resour. Plan. Manag. 2016, 142. [Google Scholar] [CrossRef]
- Unami, K.; Abagale, F.K.; Yangyuoru, M.; Alam, A.H.M.B.; Kranjac-Berisavljevic, G. A stochastic differential equation model for assessing drought and flood risks. Stoch. Environ. Res. Risk Assess. 2010, 24, 725–733. [Google Scholar] [CrossRef]
- Camacho, R.A.; Martin, J.L.; Wool, T.; Singh, V.P. A framework for uncertainty and risk analysis in Total Maximum Daily Load applications. Environ. Model. Softw. 2018, 101, 218–235. [Google Scholar] [CrossRef]
- Joyce, J.; Chang, N.B.; Harji, R.; Ruppert, T. Coupling infrastructure resilience and flood risk assessment via copulas analyses for a coastal green-grey-blue drainage system under extreme weather events. Environ. Model. Softw. 2018, 100, 82–103. [Google Scholar] [CrossRef]
- Lam, D.; Thompson, C.; Croke, J.; Sharma, A.; Macklin, M. Reducing uncertainty with flood frequency analysis: The contribution of paleoflood and historical flood information. Water Resour. Res. 2017, 53, 2312–2327. [Google Scholar] [CrossRef]
- Cloke, H.L.; Pappenberger, F. Ensemble flood forecasting: A review. J. Hydrol. 2009, 375, 613–626. [Google Scholar] [CrossRef]




| Forecast Accuracy Metrics (%) | Grade A | Grade B | Grade C |
|---|---|---|---|
| Qualified rate | α ≥ 85 | 70 ≤ α < 85 | 60 ≤ α < 70 |
| Coefficient of determination | R2 ≥ 90 | 70 ≤ R2 < 90 | 50 ≤ R2 < 70 |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Crest elevation of dam | 856 m | Gross storage capacity | 53.32 × 108 m3 |
| Normal water level | 850 m | Regulation storage capacity | 38.85 × 108 m3 |
| Flood limit water level | 841 m | Dead storage capacity | 11.17 × 108 m3 |
| Dead water level | 790 m | Installed capacity | 3300 MW |
| Designed discharge capacity | 8464 m3/s |
| Forecast Accuracy | Total Variables | Nonlinear Variables | Total Constraints | Nonlinear Constraints | Iteration Numbers | CPU Time (s) |
|---|---|---|---|---|---|---|
| α = 89.5% | 3805 | 3600 | 9901 | 3600 | 18,522 | 61.4 |
| R2 = 91% | 3805 | 3600 | 9901 | 3600 | 18,325 | 60.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Zhu, F.; Chen, J.; Li, J. Risk Analysis for Reservoir Real-Time Optimal Operation Using the Scenario Tree-Based Stochastic Optimization Method. Water 2018, 10, 606. https://doi.org/10.3390/w10050606
Sun Y, Zhu F, Chen J, Li J. Risk Analysis for Reservoir Real-Time Optimal Operation Using the Scenario Tree-Based Stochastic Optimization Method. Water. 2018; 10(5):606. https://doi.org/10.3390/w10050606
Chicago/Turabian StyleSun, Yimeng, Feilin Zhu, Juan Chen, and Jinshu Li. 2018. "Risk Analysis for Reservoir Real-Time Optimal Operation Using the Scenario Tree-Based Stochastic Optimization Method" Water 10, no. 5: 606. https://doi.org/10.3390/w10050606




