The Importance of Lateral Boundaries, Surface Forcing and Choice of Domain Size for Dynamical Downscaling of Global Climate Simulations
Abstract
: Dynamical downscaling by atmospheric Regional Climate Models (RCMs) forced with low-resolution data should produce climate details and add quality and value to the low-resolution data. The aim of this study was to explore the importance of (i) the oceanic surface forcing (sea-surface temperature (SST) and sea-ice), (ii) the lateral boundary condition data, and (iii) the size of the integration domain with respect to improved quality and value in dynamically downscaled data. Experiments addressing the three aspects were performed and the results were investigated for mean sea level pressure (mslp), 2 m air temperature (T2m) and daily precipitation. Although changes in SST gave a clear response locally, changes in the lateral boundary data and the size of the integration domain turned out to be more important with our geographical scope being Norway. The T2m turned out less sensitive to the changes in lateral forcing and the size of the integration domain than mslp and precipitation. The sensitivity for all three variables differed between Norwegian regions; northern parts of Norway were the most sensitive. Even though the sensitivities found in this study might be different in other regions and for other RCMs, these results call for careful consideration when choosing integration domain and driving lateral boundary data when performing dynamical downscaling.1. Introduction
State-of-science climate predictions are based on scenarios for future natural and societal developments which influence the external forcing of processes in the climate system. These processes are modelled mathematically by the use of General Circulation Models (GCMs) or Earth System Models (ESMs) if bio-geochemical processes are included on-line. Typical horizontal resolutions of the GCMs used in the 3rd Assessment Report from IPCC were 250–300 km in the atmosphere [1] and 100–150 km in the oceans [2]. In the 4th Assessment Report (AR4) from IPCC, the resolutions were increased by a factor 1.5–2 by some of the GCMs [3]. This is still insufficient for characterizing most regional and local impacts of climate change, and the coarse resolution constitutes an important source of errors in the global climate simulations and predictions.
Regionalization of global climate predictions by applying statistical and dynamical methods is therefore common. Dynamical downscaling, which is the subject of the present paper, employs Regional Climate Models (RCMs) with higher spatial resolution than contemporary GCMs, but in general only for selected physical compartments of the climate system and over selected geographical regions. By applying nesting [4,5], information from outside the RCM-domains is provided by the GCMs (or ESMs) through the open lateral boundaries of the RCMs, which define their geographical scope. For atmospheric RCMs, information from the global models is also provided through the lower boundary. An atmospheric RCM normally includes a dynamical land-surface model for the upper soil layers, including vegetation and simplified surface hydrology, whilst sea surface temperatures (SST) and sea-ice cover (SIC) are prescribed from the global model [6]. Similarly, oceanic regional models can be applied for dynamical downscaling over limited ocean regions by providing atmospheric fluxes from the GCM as upper boundary conditions [7]. In recent years, RCMs which couple atmospheric and oceanic processes on-line have been developed [8,9], but they are still not widely applied.
In this paper we focus on the use of atmospheric RCMs for dynamical downscaling of global climate simulations. A basic pre-requisite for a successful dynamical downscaling is that the atmospheric RCM produces data which refine and add value to the driving input data provided by the GCM. Such refinements can be partly due to higher resolution and better description of the ground surface forcing, and partly to an improved description of the internal atmospheric dynamics and physics [10,11]. One possible way to evaluate the enhanced quality of atmospheric RCMs is to perform Perfect Boundary Experiments (PBEs) [12,13], while the nesting method itself can be assessed through Big Brother Experiments [14,15].
There are several issues that need to be addressed concerning the nesting strategy [16]. One is the importance of the quality of the imposed driving data for the RCMs. Several studies suggest that RCM results for large scale variables, e.g. mean sea level pressure, depend crucially on the lateral boundary data [4,17,18]. On the other hand, for variables predominantly influenced by local conditions, e.g., 2 m temperature, the quality of the lateral data is less important. Furthermore, the importance of the lateral forcing generally decreases with the size of the integration domain [15].
In an atmospheric RCM the driving data provided by a coarse resolution GCMs can be divided into a part provided through the lower boundary conditions (in particular sea surface variables) and another part governing the lateral boundaries. In re-constructions of the present-day climate by atmospheric GCMs, sea ice surface variables are prescribed. In an experiment with four different data-sets for the sea ice climatology which all were considered to represent the true situation equally well, high local sensitivities to the differences in sea ice properties were found, considerably smaller impacts were found remotely [19]. One reason for the small remote impact was linked to the fact that the same prescribed sea surface temperature (SST) was used in all simulations.
Significant effects of extra tropical SST anomalies at middle and high latitudes on atmospheric circulation patterns have been reported in existing literature [20,21]. Both of these studies showed a response in the North Atlantic circulation due to SST anomalies in the Labrador Sea. Furthermore, extra-tropical SST anomalies do indeed influence the atmosphere outside of the boundary layer, but this influence may be masked by the internal atmospheric variability [22]. The highest sensitivity to surface forcing is diagnosed during winter due to the relatively strong fluxes of latent and sensible heat in this period. Differences in sea-ice cover (SIC) will in particular enhance the sensitivities with respect to these fluxes along the Arctic boundaries. This is due to the very large temperature difference between the cold Arctic air and the underlying sea surface often observed during incidents of Arctic air outflow.
In a study, an evaluation of 14 GCMs from IPCC AR4 in the Arctic was performed and the penetration of the North Atlantic storm tracks into the Barents Sea was consistently missing or seriously underestimated [23]. In particular this shortcoming was seen in combination with too much sea-ice in the same area. It was not possible to conclude on the causes of this deficiency, but the combination of errors suggested that there is a connection between the state of the sea surface and the atmospheric dynamics. Such connections may limit the possibilities for dynamic downscaling with atmospheric RCMs in the Arctic.
There are relatively few published studies that focus the role of SST and SIC in atmospheric RCM simulations [24,25], even though the sea surface state shows impacts on the atmospheric dynamics in regional models. In addition, the sea surface temperatures have a profound impact on the precipitation in RCM simulations for the Baltic Sea area and the Anatolian Peninsula, respectively [26,27]. Another interesting issue in this connection is to what extent the importance of the surface forcing depends on the size of the integration domain. Several studies have concluded that the size of the integration domain is of importance and that the proper size may differ for different variables [28]. Closely linked to this is the relative importance of data imposed at the lateral boundaries versus at the ground surface as a function of the integration domain size. There are several reasons why this is an important issue. First, the relative importance of ground surface versus lateral boundary forcing in RCM's is not firmly established. Second, if the surface forcing is important, this will constitute an additional source of uncertainty in downscaled climate scenarios. Whilst the importance of the quality of the atmospheric lateral boundary data is recognised and widely studied, the quality of the ground-surface data, including the ocean surface, should be considered more carefully in connection with dynamical downscaling. Thus, a significant sensitivity to surface forcing would imply that a coupled RCM with an improved description of the sea surface forcing should further improve the atmospheric flows and physics compared to pure atmospheric downscaling with fixed coarse resolution surface forcing.
The aim of this study is to explore the importance of data for ground surface forcing (e.g., sea surface temperature (SST) and sea ice concentration (SIC)) relative to data for lateral boundary forcing in atmospheric RCMs. The importance of the forcing is of course closely connected to the employed models, but also closely coupled to the more universal issue with limited area models, what is the proper size and location of the RCM domain. In this context we therefore also discuss the relevance of the size of the integration domain for dynamical downscaling
In Section 2 a description of the employed RCM is given, before the experiments are described in Section 3. Results are presented and discussed in Section 4 before the investigation is summarized and conclusions are drawn in Section 5.
2. Model Description
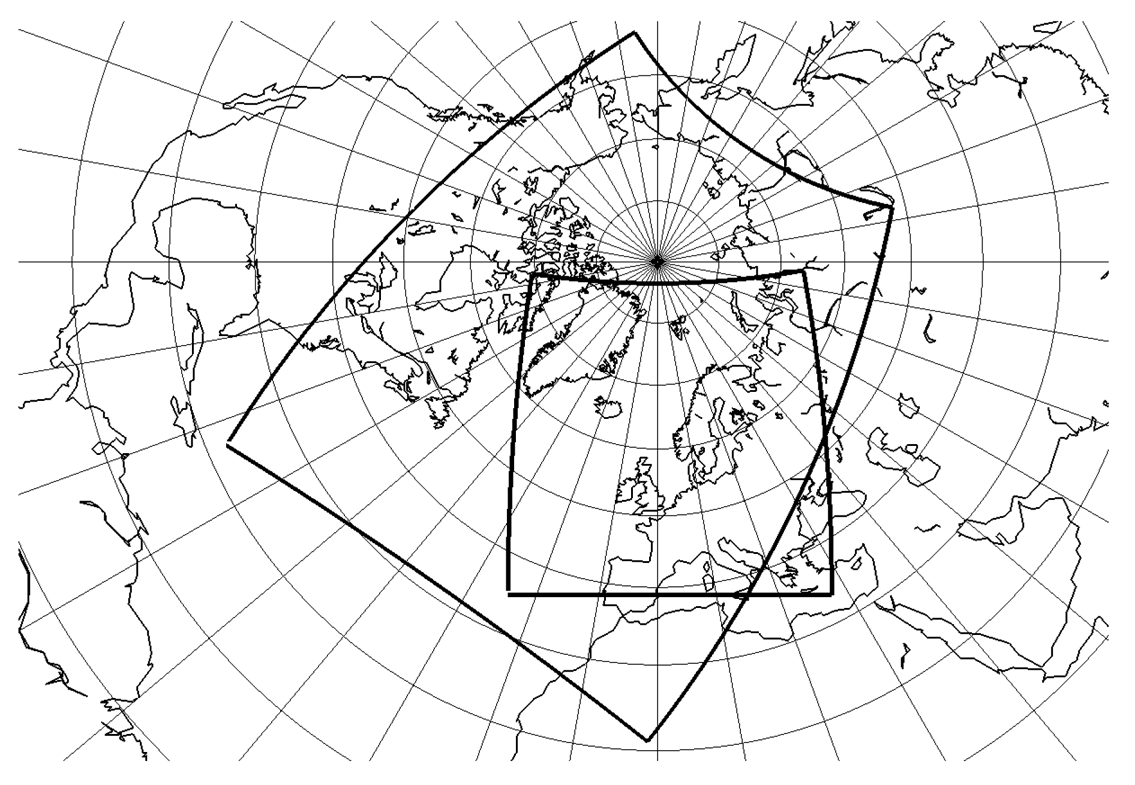
The regional climate model HIRHAM consists of the HIRLAM Eulerian grid-point model [29] and the ECHAM4 physical parameterization routine [30]. A description, with some minor modifications, is also available [31]. The model was used for dynamical downscaling of global climate scenarios over Northern Europe and parts of the adjacent North-Atlantic and Arctic oceans [32]. In this study the model makes use of a rotated spherical grid with mesh width 0.5 degree (∼55 km) in the horizontal direction and 19 levels in the vertical. Two different integration domains are used, see Figure 1.
The model dynamics are quasi-hydrostatic, and include prognostic equations for specific humidity and the cloud water. Physical processes are only partly resolved, and therefore include parameterizations. The turbulent vertical fluxes from the sea surface to the atmospheric boundary layer, which are particularly important in connection with the studies in this paper, are calculated using bulk transfer relations in the atmospheric surface layer [30]. The roughness parameter for turbulent momentum over open ocean is computed from the Charnock formula whilst assigned a constant value over the ice-covered ocean. The roughness parameter for heat and moisture are approximated by an empirical relation to the momentum roughness parameter [30].
The lateral boundary conditions employs a relaxation scheme [33] over 7 grid points (also used in 6 out of 8 RCMs in the Arctic Model Intercomparison [24]). At the lateral boundaries the prognostic variables are relaxed towards the imposed data by a nudging coefficient which puts full weight on model-calculated values in the inner parts of the domain and gradually increase the weight towards a full weight on the externally imposed values across a relaxation zone along the lateral boundary. SST and SIC are entirely specified from the externally global data; i.e., these variables are not calculated by the RCM.
3. Description of Experiments
In this study a set of dynamical downscaling experiments is done with the HIRHAM model. All experiments are valid for the climate during the period 1960–1990. The first year is omitted in the analysis to avoid spin-up effects in the model results. The driving data are from the ECHAM4 GCM (The Max Planck Institute for Meteorology in Hamburg, Germany) and from the Hadley GCM (The Hadley Centre at the UK MetOffice). Hereafter we use the following naming conventions: HL for lateral boundary data from the Hadley GCM, HS for ground surface forcing data from the Hadley GCM, ML for lateral boundary data from the ECHAM4 GCM, and finally MS for ground surface forcing data from the ECHAM4 GCM.
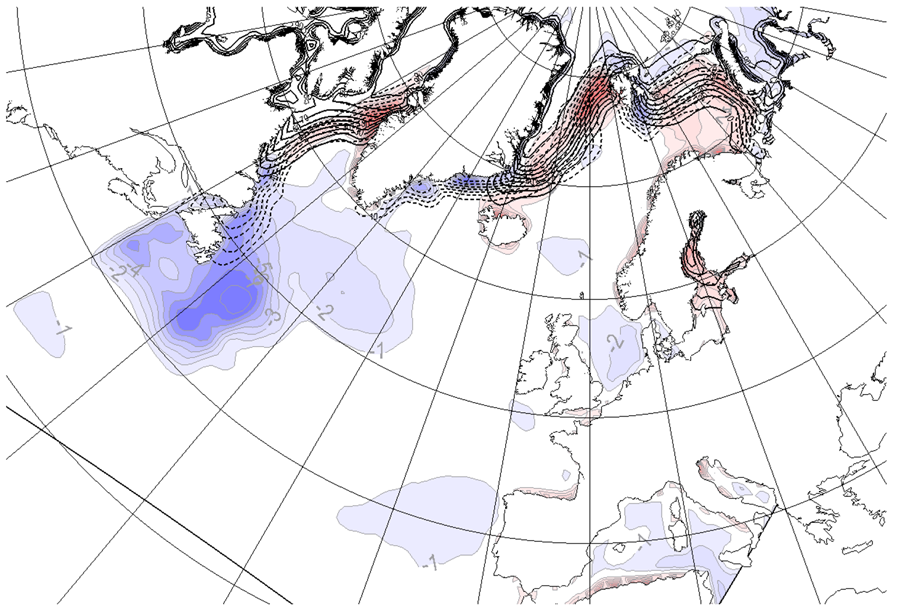
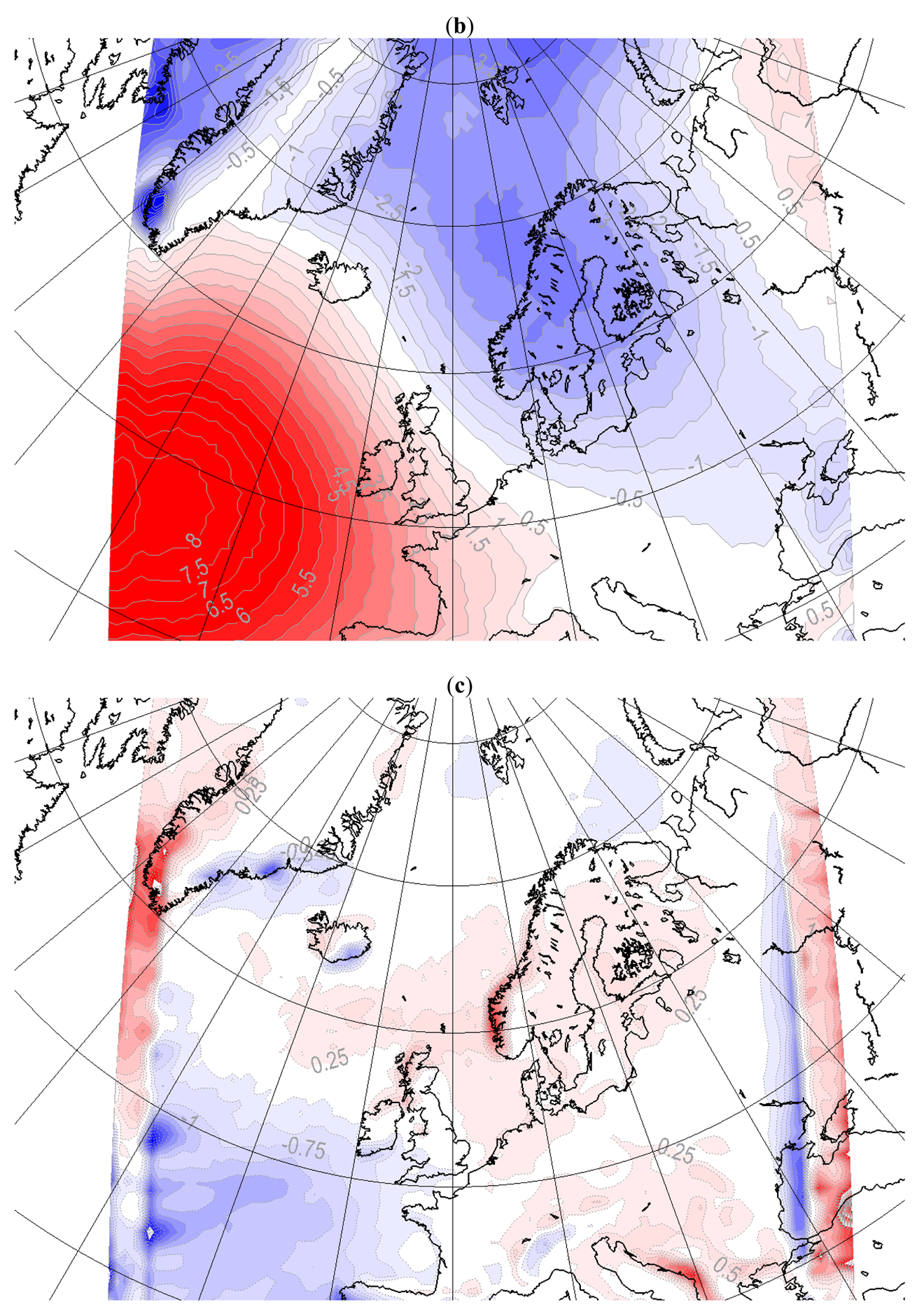
The experiments are performed using a small and a large integration domain (Figure 1). The large domain consists of 150 × 165 grid points, while the small domain consists of 96 × 96 grid points. For the experiments in which HS replaces MS, this is only done for parts of the domain (30° W to 40° E). The differences in SST and SIC between MS and HS are seen throughout the whole year but are most pronounced during the winter seasons. In winter (December, January and February, DJF) the HS surface temperatures are considerable lower than for MS south of Greenland, while it is opposite near the sea ice edge along the eastern Greenland coast and in the Barents Sea (Figure 2). While the former differences are associated with the location of the warm North-Atlantic current (the “Gulf stream”), the latter are mainly due to the different location of the sea ice edge, and thereby the surface temperature. In addition there are differences along the coasts.
Five experiments are performed: (1) MLMS on the small domain; (2) MLHS on the small domain; (3) MLMS on the large domain; (4) MLHS on the large domain; and finally (5) HLHS on the small domain. The experiments are summed up in Table 1. For a straightforward interpretation of the results, we mainly focus the comparison between combinations involving only one difference in the external variables (i.e., different surface forcing only, different lateral boundary forcing only, or different domains only, see Table 1). Each experiment is run for 30 years and designed to be representative of the 1960–1990 climate.
4. Results
In this section a comparison of the 30 year long averages of mean sea level pressure (MSLP), 2 m air temperature (T2m) and daily amounts of precipitation from the different RCM simulations is presented. The attention will be on how the differences in the size of the integration domain and in the lateral- and surface forcing (referred to as external forcing of the RCM) alter the simulation results. The external forcing and RCM response is present throughout the entire year, but with a pronounced annual cycle. The results are presented for the winter season (DJF) when the differences in surface forcing and in the response are largest. These winter maxima are also found in other studies [19,24], and can be explained by larger latent and sensible heat fluxes from open water compared to the radiative forcing during the winter.
A general overview of the differences in the simulated climate from the different experiments is given below, before the impacts on selected Norwegian regions are discussed in more detail.
4.1. Differences in Simulated Climate due to Different Surface Forcing
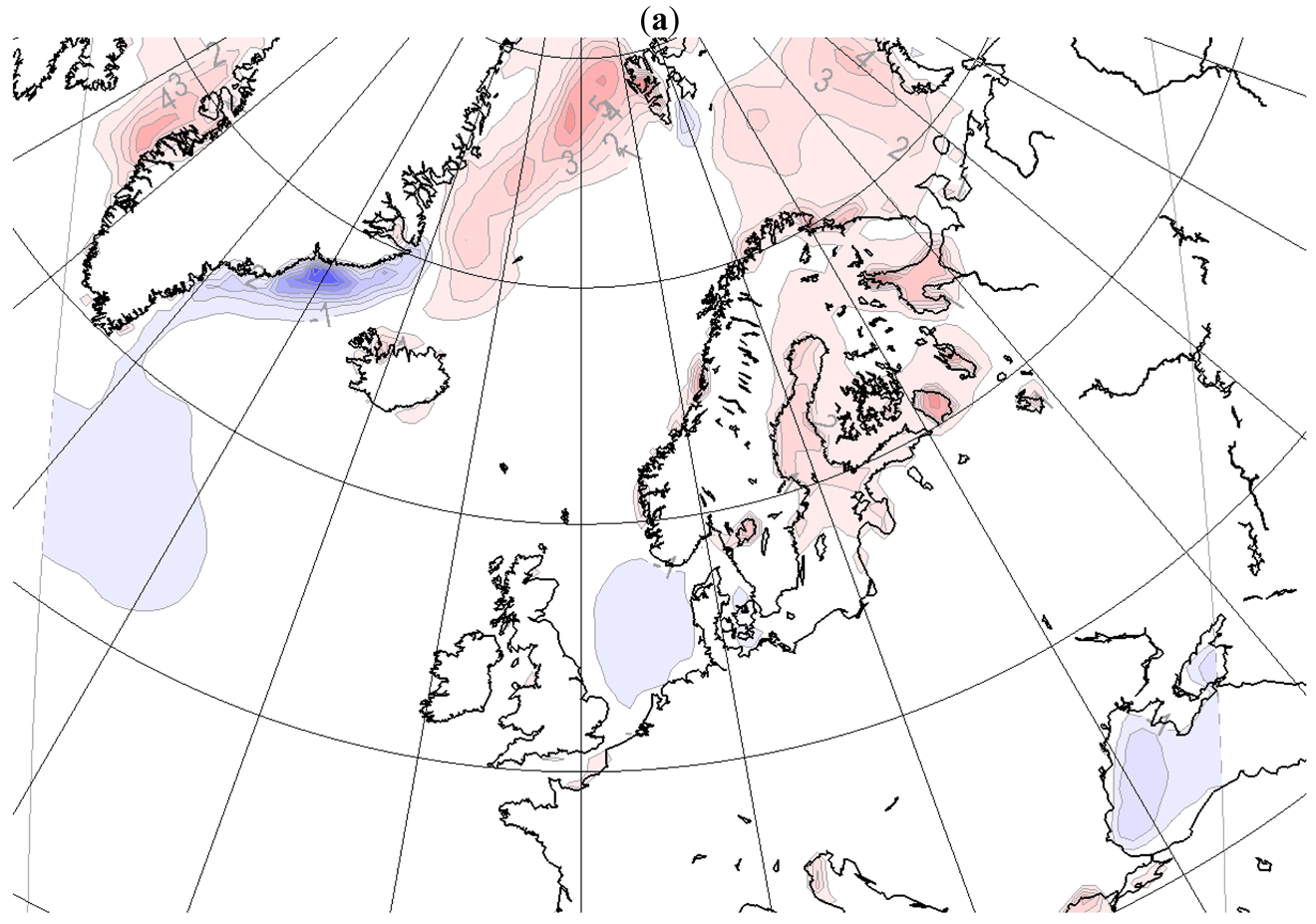
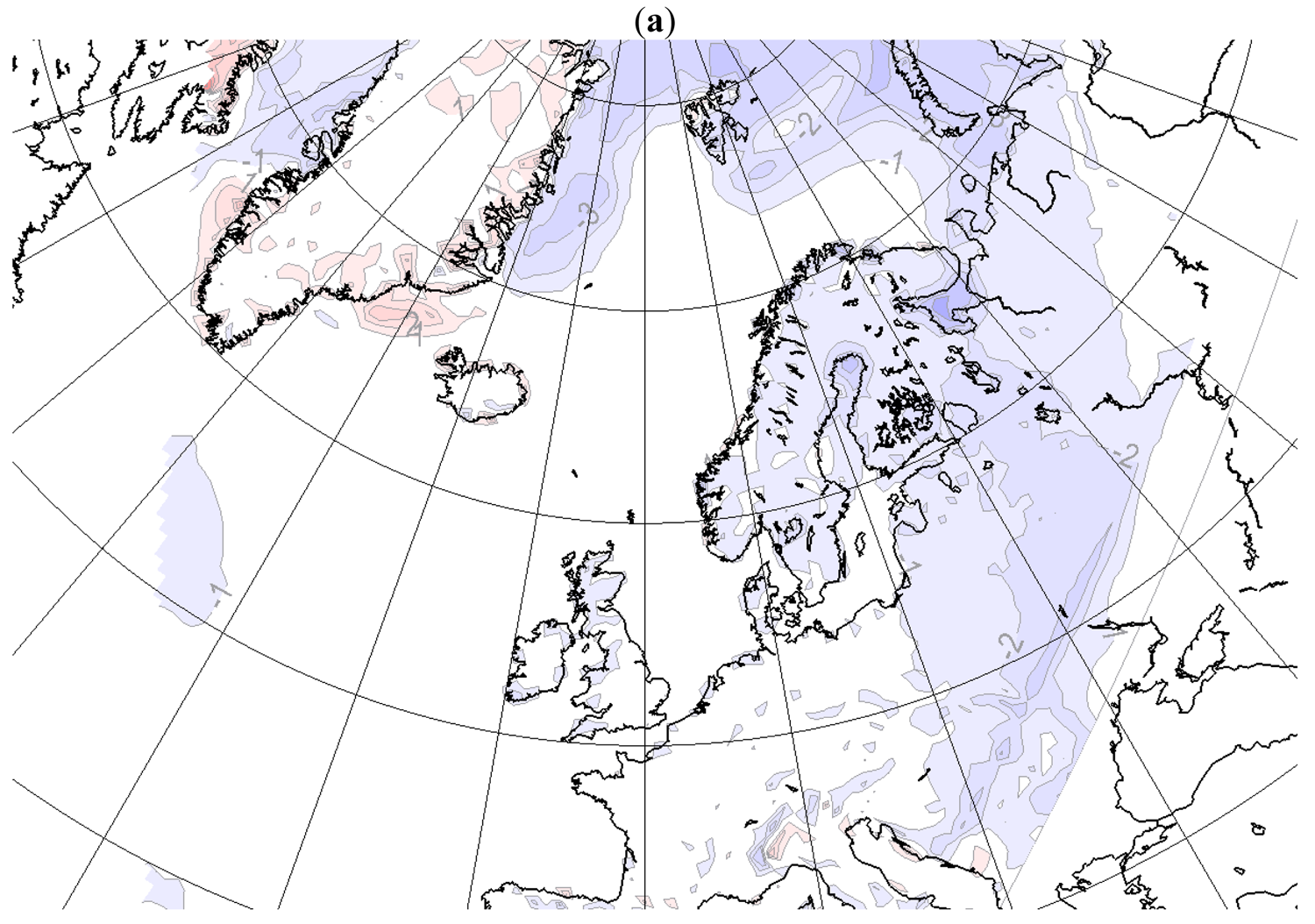
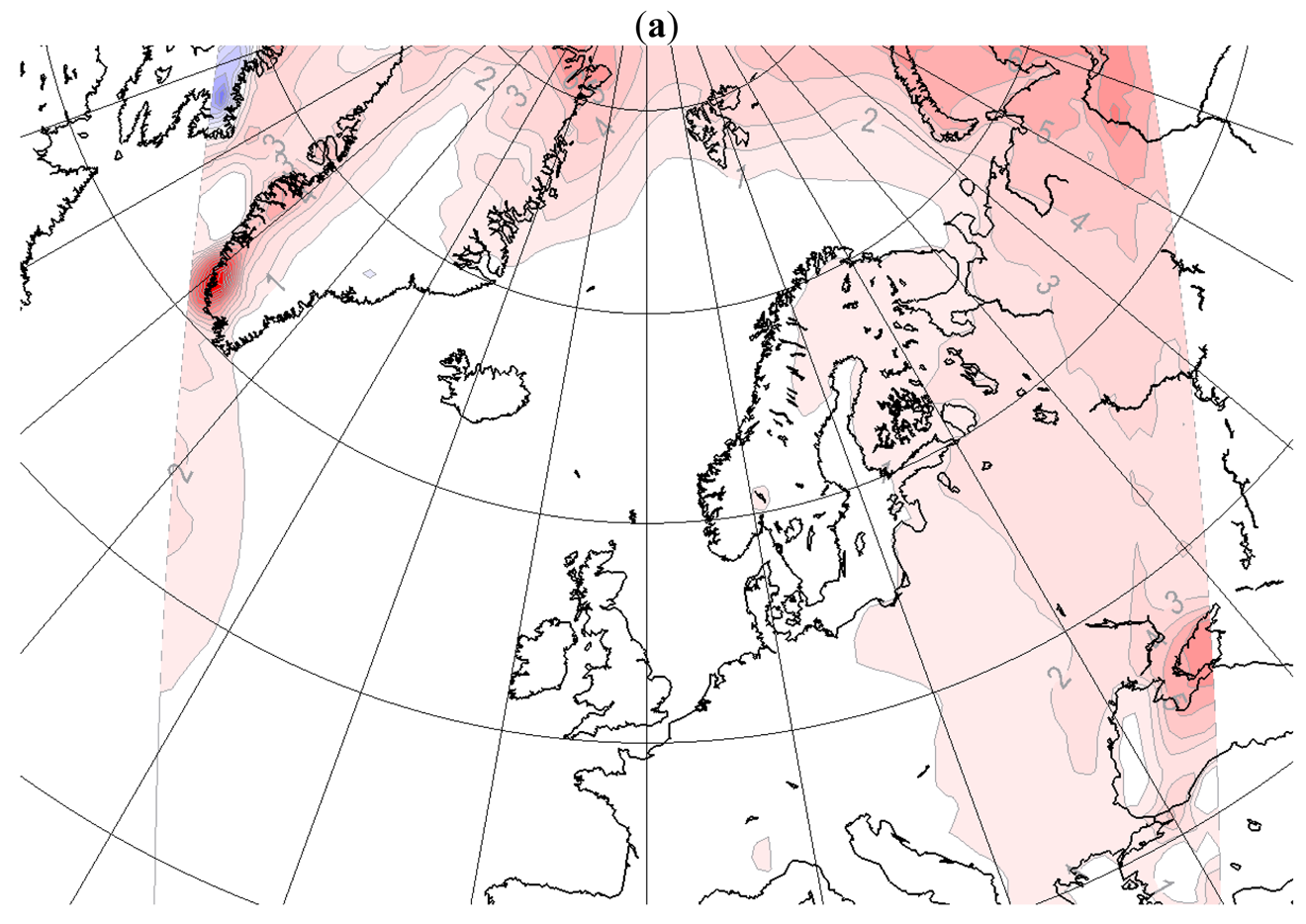
The responses in T2m due to changed surface forcing are concentrated close to the areas of large forcing differences in both integration domains (Figure 3a and 4a shows the difference in response due to MLHS instead of MLMS forcing, small and large domain, respectively). The differences in surface forcings are shown in Figure 2. There is a local and apparent one-to-one relationship between the differences in SST and the differences in T2m. The strong local response is expected because the T2m is estimated applying a stability dependent interpolation between the surface temperature (here SST) and the temperature in the lowest model level. The latter is between 50–150 m above ground in climate models. Effects of the lateral forcing are also seen as the response to the SST difference in the small domain is slightly weaker than in the large domain. Similar behaviour is found in the T2m response for other seasons; the local response dominates with similar patterns in both domains, but with larger amplitude in the large (not shown). However, the differences in T2m are more modest downstream in the prevailing westerly winds of the areas with large SST differences. This is in agreement with earlier findings which reported a modest non-local response to surface forcing [6]. This finding is explained by the fact that the prescription of more similar SSTs downstream effectively constrains the effect of the changes. However, other studies report larger remote responses, both in coupled models [34] and pure atmospheric models [20]. Also the shape and scale of the surface forcing can be important for the nature of the response [21].
A response to surface forcing in Mean Sea Level Pressure is mainly seen in autumn and winter, and the response is clearly most pronounced in the large domain (Figure 3b and 4b, small and large domain, respectively). The MSLP response in the large domain is high locally, but is also seen in remote areas (e.g., over central Europe). The surface pressure increase (up to 2 hPa) over colder water and a reduction of about 1hPa is found in areas with warmer water. This implies a change in the north-south gradient of the MSLP for the Atlantic and changes in flow patterns when replacing MS with HS. Smaller response is calculated close to the lateral boundaries. In the Barents Sea the response is not sensitive to the size of the integration domain.
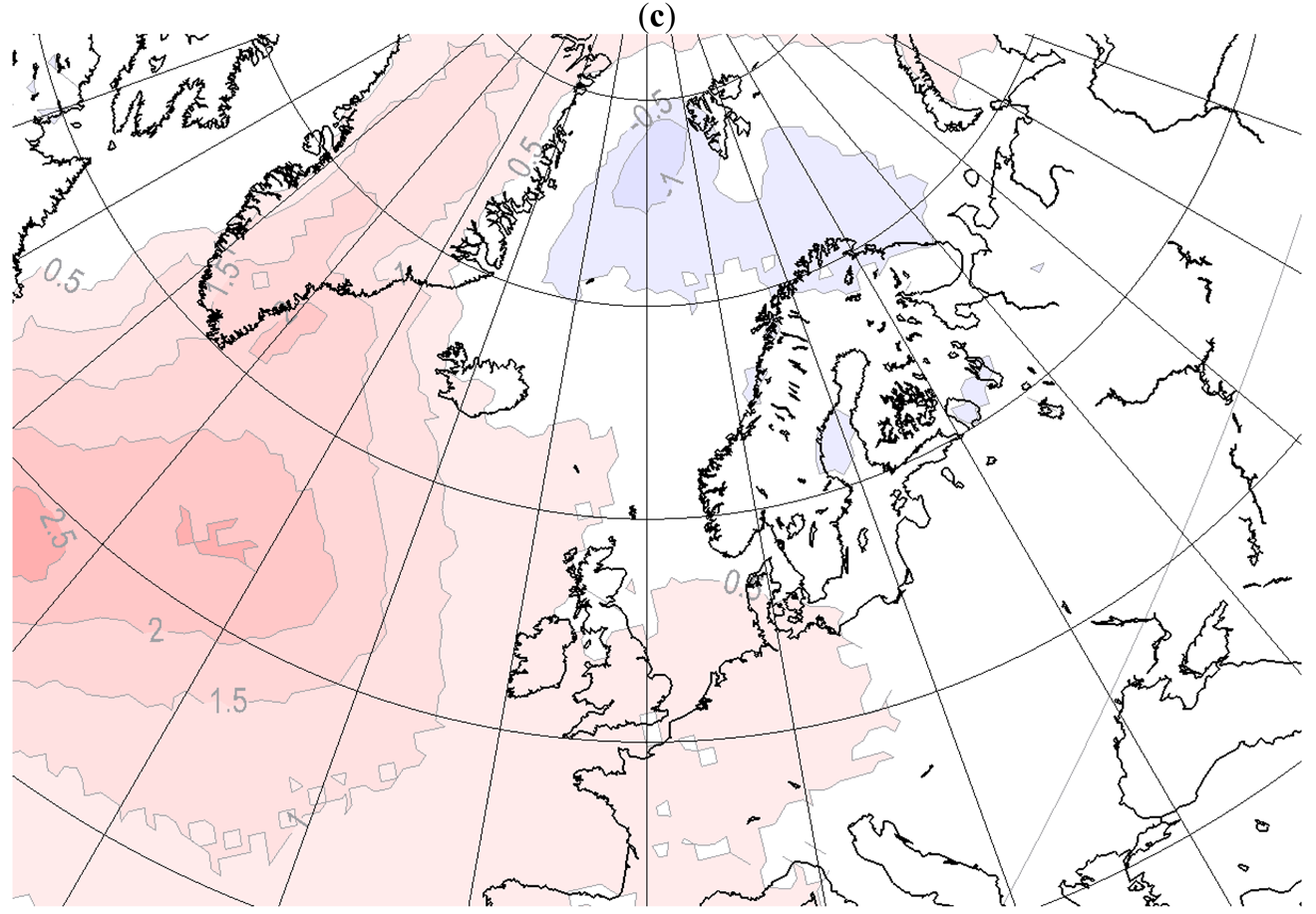
As for mslp, the response in precipitation is mainly seen in autumn and winter (Figure 3c and 4c, small and large domain, respectively). The patterns appear independent of the size of the integration domain, but the amplitudes are larger with the large domain. During winter, an increased surface temperature and reduced surface pressure is correlated with increased precipitation. The increased precipitation amounts to 1mm/day in regions with 2–4° increased SST (south of Greenland). The precipitation response is predominantly local to the surface forcing, but there are also changes in precipitation remotely at the Norwegian coast. The latter is likely to be connected with the changes found in the pressure gradients. In the large integration domain even more remote response in precipitation is seen over locations not included in the small domain, such as areas near the Alps. A possible explanation for this response might be a change in humidity in air flowing across the Mediterranean due to changed SST. However, this area is also situated close to the lateral boundary and might be influenced by the lateral boundary treatment.
So far, only the response in surface fields is studied, and figures for free tropospheric responses are not included. However, investigation of the thickness of the 1,000 hpa to 850 hPa layer and 850 hPa to 500 hPa layer reveals differences up to 10 m. Mainly, a reduction is seen in thickness south and east of the south tip of Greenland due to the colder surface in HS. Locally, the main difference is found in the lower part of the troposphere, whilst downstream of the forcing the main difference is found in the mid-troposphere. Close to the sea ice edge, an increase in thickness is found. In the lower parts of the atmosphere the response is closely linked to the surface forcing, whilst the response in mid-troposphere is more homogenous.
4.2. Differences in Climatology due to Different Size of the Integration Domain
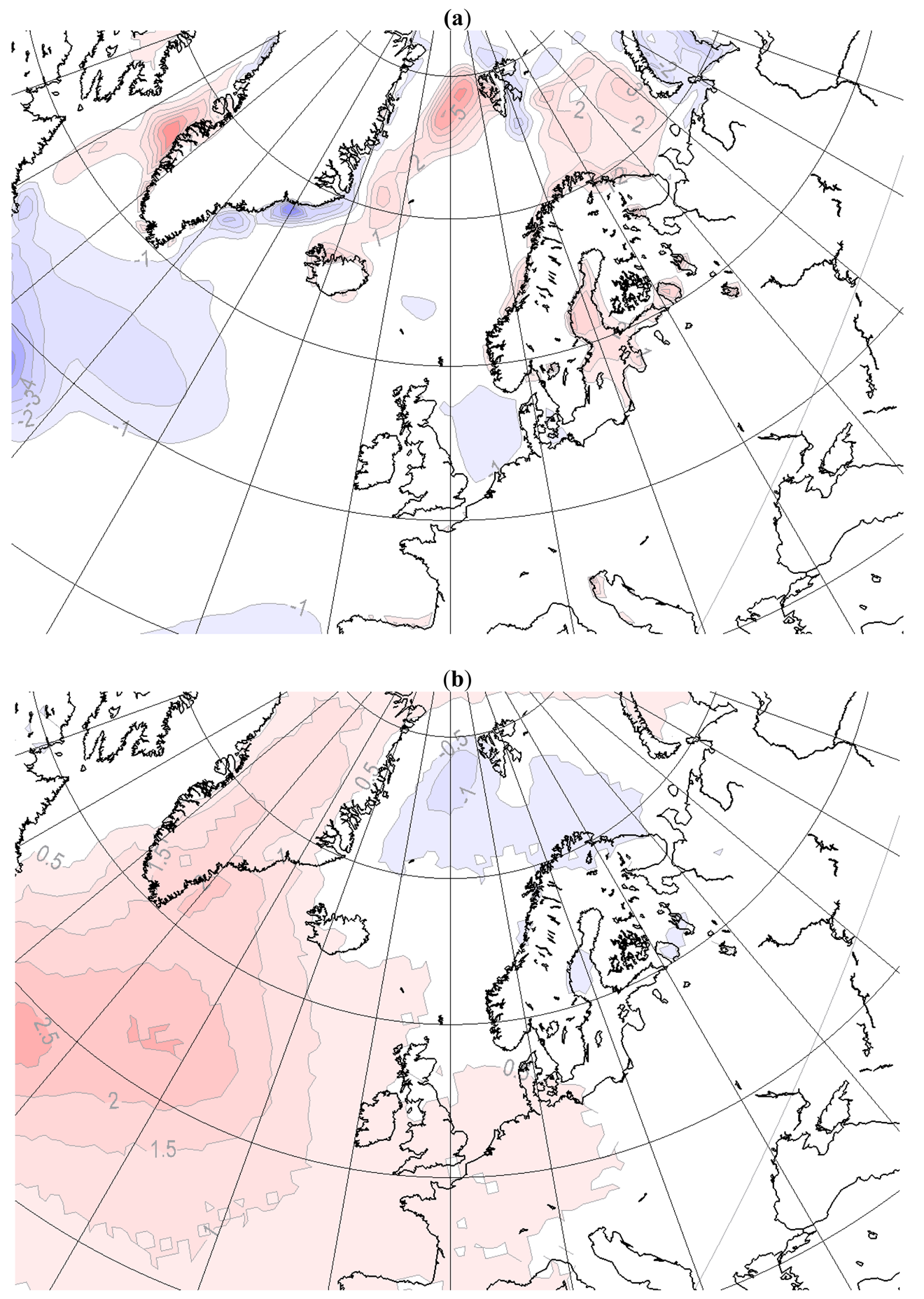
The MLMS and MLHS data sets are downscaled with the HIRHAM RCM both in a “small” and a “large” integration domain. Differences in mean values valid for DJF between the large and the small integration domain are shown in Figure 5 (MLMS driven) and 6 (MLHS driven). The differences between the large and the small integration domain are almost independent on the surface forcing, since there are similar patterns in Figure 5 as in Figure 6. In the small domain, the Icelandic low is deeper and associated with a stronger westerly flow over Northern Europe than for the solution in the large domain. The increased low level advection of relatively warm air from the North Atlantic Ocean over Northern Europe, contributes to the 0.5–1.5 °K increase of the T2m in Scandinavia in the small domain. There are also temperature differences in the Arctic (not shown), which can be a consequence of changed circulation patterns and the proximity to the lateral boundary in the small domain. Similar explanations are plausible for the differences in precipitation in southern Europe and close to the Alps. At the Norwegian coast, the response in the small domain produces approximately 0.5–1.0 mm/day more precipitation than in the large domain. The maximum precipitation differences are around 10% of the daily precipitation in the downscaled MLMS in the small domain.
Although the results presented here can be specific to the employed RCM and the geographical area, they suggest that RCM results are highly sensitive to the choice of integration domain size. The optimal choice of integration domain depends on one's perspective on the purposes of dynamical downscaling. One perspective is that downscaling should mainly introduce small-scale features that are not resolved in GCMs, whilst the large scale features resolved in the driving GCM are kept unaltered. This is a linear perspective on the role of downscaling which can be achieved by choosing sufficiently small integration domains [5] so that the large scale circulation is restricted by the lateral boundaries, but still large enough for small scale features to develop by the RCM. Alternatively, so-called spectral nudging can be applied in the RCM to control the larger scales [35,36]. Another perspective on the role of regional climate modelling is more non-linear, in that the increased resolution in the RCM may introduce fine-scale features which may develop and upscale and thus contribute to improve the description of features on the larger scales that are resolved by the GCM providing the driving data. In this perspective, large integration domains are preferred in order to allow the upscale development in the RCM, and thus to potentially improve the large scale as well as the small scale features [15,37]. These different perspectives are discussed in more detail in existing literature [16].
4.3. Differences in Climatology due to Different GCM Driving Data
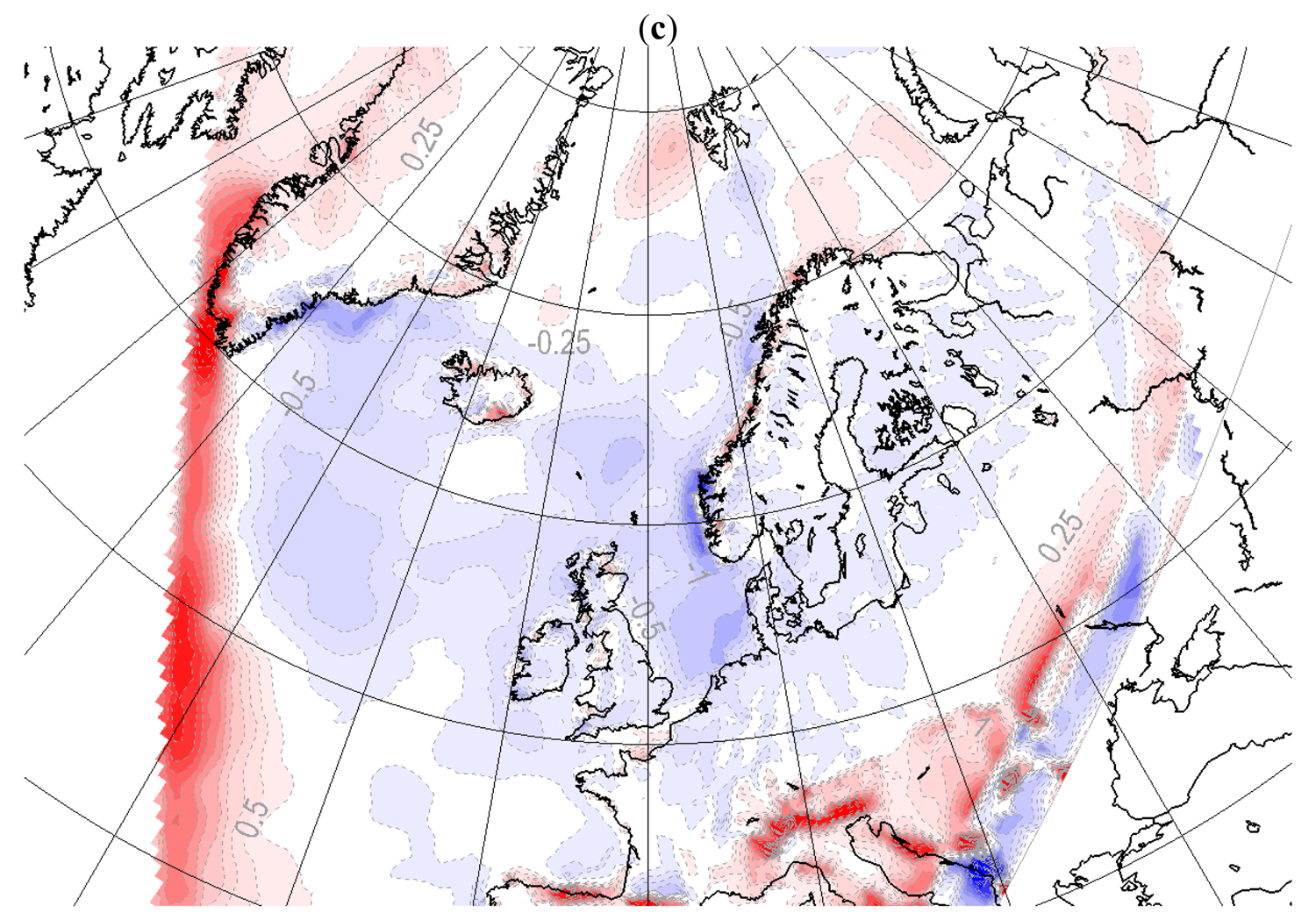
In Figure 7, the differences in simulated winter climate (DJF) due to different lateral driving data but similar surface forcing (MLHS versus HLHS) are shown. This can be compared to another experiment (MLMS versus HLHS) shown in Figure 8. All simulations are done in the small integration domain. The differences are very similar and independent on the employed surface forcing (except locally over the ocean), implying that with this integration domain the lateral boundary forcing strongly constrains the flow and is of higher importance than the surface boundary conditions.
The ML driven RCM shows a considerable lower surface pressure in the Arctic and Northern Europe, while higher pressure are obtained south west of Iceland compared to the HL driven simulation. The differences mean that the Icelandic low is moved north-eastward in the ML driven simulation. This gives an increased on-shore wind component in southern Norway and an off-shore component in the more northerly parts of Norway. In conjunction with the Norwegian orography, this results in ∼2mm/day more precipitation at the Norwegian west coast in the ML driven simulation. Temperature differences are smaller and mainly seen locally over the sea and sea ice where the surface forcing differs, as well as close to the lateral boundaries.
In these experiments there is little doubt that the large-scale parts of the RCM solutions strongly depend on the driving data. However, for more locally forced variables, such as near surface temperatures and parts of the precipitation, the solutions are less dependent on the lateral forcing data. An interesting question is whether the results of the RCM would converge with increasing integration domain, but this is left for further investigation.
4.4. The Impacts of RCM Set-up on the Simulated Climate in Norwegian Regions
In this section, the RCM results for different regions in Norway are examined. We will investigate how the external forcing alters the RCM results with respect to mean value and month-to-month variability. The analysis is done for the three regions shown in Figure 9. The three regions have considerably different climates as illustrated with the MLMS driven RCM-climate for MSLP, T2m, and daily precipitation in winter (Figure 9). Eastern Norway has a pronounced continental climate with warm summers, cold winters and moderate annual precipitation amounts. Both Western and Northern parts of Norway are dominated by a coast line that is exposed to the westerly winds from the North Atlantic Ocean. Annual precipitation amounts are large while the difference between summer and winter temperatures is moderate. In addition, Northern Norway is strongly influenced by the proximity to the Arctic, even though the surrounding ocean is open all year. The three regions are hereafter denoted north, west and east Norway.
The results are presented as the mean differences between the different simulations and the ratio of month-to-month variance between different experiments for north Norway (Table 2), west Norway (Table 3) and east Norway (Table 4).
For north Norway (Table 2), large differences in the surface pressure are found in the comparison of results from different integration domains and with different lateral boundary conditions. The latter reflect the difference in the driving data since the small domain is employed. The higher surface pressure with the large domain (but similar lateral data set) is also noticed in an earlier study [15]. The reason for this behaviour of the RCM is not known. We believe that the increased surface pressure is RCM dependent, but illustrate that with larger integration domain the RCM becomes less constrained by the lateral driving data. The differences between the small and the large integration domain are less than the differences with completely (lateral and surface) different driving data for the small domain. For the daily precipitation there are relatively large differences between the different simulations (maximum of 0.42 mm/day between MLHS and HLHS on the small domain, the MLMS climate give approximately 4 mm/day). The T2m show minor differences (maximum 0.72 °C between MLHS and HLHS on the small domain).
The month-to-month variability of the mslp is smaller in the large domain than in the small, a result also seen for precipitation. This is a result that contradicts an earlier study which states that in general the internal variability increases with domain size [38]. However, the ground surface boundary conditions are important in generating large scale variability in RCMs, and the importance increases as the integration domain increases [39]. Thus, large scale atmospheric variability tends to be increasingly underestimated as the domain size increases when the lower boundary conditions are prescribed. The month-to-month variability for T2m is less sensitive to the external forcing than the surface pressure and precipitation.
The differences in mean MSLP, T2m, and daily precipitation for west Norway are less than in north Norway (Table 3). However, there are still large differences in the mean sea level pressure when the integration domain is changed and when the lateral boundary conditions are changed. Associated with these differences we also see differences in precipitation with a maximum of 0.79 mm/day (MLHS versus HLHS on the small domain), which is between 5 and 10% of the total precipitation amount in the region. The T2m is remarkably similar in all simulations and seems almost independent of the external forcing of the RCM. This is in agreement with earlier findings that local forced variables, like T2m, are partly controlled by internal processes in the RCM [15].
The external forcing has little impact on the month-to-month variability when comparing results from similar integration domain (Table 3). However, for west Norway we find a substantial reduction in the variability for MSLP and precipitation when a different integration domain is employed.
The differences of mean MSLP, T2m and daily precipitation for east Norway (Table 4) are similar to the other regions with a pronounced difference in the MSLP between large and small integration domains. In this connection, the precipitation is slightly higher in the small domain, i.e., approximately 0.25 mm/day whilst the MLMS winter mean is approximately 3.5 mm/day. For T2m, there is one major difference compared to the other regions. RCM simulations with ML lateral forcing are up to 1 °C warmer than simulations with HL lateral boundaries.
As for the other regions, the month-to-month variability is substantially lower for MSLP and daily precipitation when employing the large integration domain (Table 4), whilst the variability of the T2m shows little sensitivity to external forcing of the RCM. In general, the sensitivity in month-to-month variability depending on variable and geographical region is in agreement with earlier findings [38].
A statistical t-test for significance has been performed to evaluate if the probability that the mean values of the data sets differ by chance are smaller than 5%, i.e., if the differences are significant at the 5% level and not due to noise (i.e., high month-to-month variability of the mean value). There is a significant difference between ML and HL forced RCM results in the small domain for MSLP in all three regions. The differences between RCM-results in the large and small domains are also significant. Simulated precipitation in north and west Norway are significantly different with respect to different domain size and different surface forcing. For T2m the HL forced RCM simulation is statistically different from the ML forced simulation for north and east Norway. Summarizing the statistical tests we find that at least one combination of the investigated variables and change in the external forcing creates statistical significant differences for one or more Norwegian regions.
5. Summary and Conclusions
The aim of this study was to explore (i) the importance of the surface forcing (e.g., sea surface temperature and sea ice), (ii) the importance of the lateral boundary forcing, and (iii) the importance of the size of the integration domain for dynamical downscaling with the HIRHAM RCM. This has been done through a set of experiments where the three sources of differences have been systematically varied. The lateral boundary and surface forcings are taken either from simulations with the Hadley Centre GCM or the Max-Planck-Institute GCM, while the two integration domains are shown in Figure 1. The main purpose for all simulations was to simulate the Norwegian climate for the period 1961–1990. In principle, there should only be insignificant differences between the results since they are supposed to simulate the same climate. The highest sensitivity of the RCM results to the external forcing is found during winter, and the results for December-January-February were the subject of the analysis.
The analysis shows that the RCM climate is sensitive to both the lateral boundary and surface forcing, as well as to the size of the integration domain. For different Norwegian regions, several of the differences in response are significant. Changing the surface forcing shows a very strong local response, 2 m air temperature is immediately affected, but response is also seen in mean sea level pressure and precipitation. More remote response is also seen, although with considerably smaller amplitude.
For changes in the lateral boundary forcing there is a clear response in RCM simulated MSLP. The response is most pronounced in connection with the main storm tracks. A Change in the circulation pattern has in turn an effect on the geographical distribution of precipitation. The difference in daily precipitation amounts is around 10% at the Norwegian coast during winter. Elsewhere only minor precipitation impacts are found. Only minor differences (up to 0.5–1.0 °K in some regions) are found for the typically more local variable T2m.
Changing the size of the integration domain also alters the MSLP and the large scale circulation pattern. Also in this case an up to 10% change in daily RCM-estimated precipitation is found in coastal regions in Norway, whilst the local variable T2m is less sensitive. Results over Norway also indicate that the month-to-month variability decreases with increasing integration domain in a RCM. The surface forcing is important for generating variability [39], and a carefully designed coupled atmosphere-ocean RCM should be considered for a better simulation of the variability. Another approach for controlling the variability with integration domains of different sizes might be to apply the spectral nudging approach [35-36] in addition to lateral boundary forcing.
In many aspects the results generated in this work support earlier findings. For example, in a large integration domain the RCM-results are less constrained by the lateral forcing than in a smaller domain [5,15]. This study also demonstrates that changes in surface forcing create local and remote responses, where the former is most pronounced. Similar results are reported for GCMs earlier in the literature [34].
Concerning remote responses in RCMs, considerably fewer studies are published. A plausible reason for this is that RCMS often employs integration domains that are too small to truly produce remote responses. In addition, the effect of differences in local forcing is damped downstream of areas with large differences. The smaller differences in surface forcing downstream act to relax the differences between the lower-level variables in the atmosphere.
In this paper, we have emphasized investigating the response in fields directly associated with weather and climate (2 m temperature, precipitation), since these variables are the main targets for dynamical downscaling of global data. The tropospheric response in the geopotential height of isobaric surfaces as well as the thickness fields are interesting in view of classical theory for extratropical, planetary-scale response to surface temperature anomalies, e.g., [40,41]. The difference between the experiments MLHS and MLMS can be viewed as study of the response of a negative temperature anomaly south and east of the south tip of Greenland, and a positive anomaly along the sea-ice edge of the northern rim of the Nordic and Barents Seas. However, the calculated response is clearly influenced by the constant lateral boundary conditions.
The cold anomaly is situated in the westerly wind-system over the North-Atlantic Ocean, whilst the latter is in a region with less pronounced background flow. There is a clear response in the 1,000 hPa geopotential height with a ridge-pattern slightly downstream of the cold anomaly increasing the warm air advection over it. A similar pattern with increased cold air advection is seen at 1,000 hPa over the warm anomalies. Higher up, the response is better characterized in terms of thickness in geopotential heights. Thus the thickness fields between 1,000 hpa and 850 hPa and between 850 hPa and 500 hPa (not shown) reveal mainly a reduction south and east of the south tip of Greenland. Close to the anomalies the main response is developed in the lower part of the troposphere, whilst downstream the main difference is found in the mid-troposphere. In connection with the warm anomalies close to the sea-ice edge where the background flow is weak, the thickness increases throughout the lower troposphere.
It is worth noting that different variables show different sensitivity to changed external forcing. Large scale variables like MSLP are sensitive to lateral forcing and size of integration domain, but less sensitive to surface forcing. However, more local forced variables like T2m are less sensitive outside regions of changed surface forcing. This is in agreement with earlier studies [15].
This study employs only a few different sets of forcing (e.g., only lateral- and surface forcing from two different GCM, and only two different integration domains). However, the results suggest that the choice of lateral driving data and size of integration might be of equal importance, while the RCM is less sensitive to changed surface forcing, although the latter also play a role. In agreement with an earlier study [38] there are indications that surface forcing is especially important for the simulated variability. Due to this, a coupled RCM would probably give higher variability compared to only an atmosphere RCM.
In this study the simulation of the Norwegian climate is more sensitive to external forcing than other regions. From a methodology perspective this can be explained since Norway is situated well inside the integration domains and thereby experiences less restriction by the lateral boundaries than other regions closer to the lateral boundaries. However, from a physical perspective, Norway is situated in the North-Atlantic Storm track and might be more sensitive to small perturbations of the mean flow. Several of the different simulations give a statistical different climate for different variables for Norwegian regions. The Norwegian regions also show different sensitivities to changes in the external forcing with north Norway experience the highest sensitivity.
This study, together with previous studies suggests that the set up of a RCM should be done with care. This might even be of higher importance for some regions than for other regions. The choices made concerning size of integration domain and lateral- and surface forcing in dynamical downscaling may contribute to uncertainties in future climate scenarios.






| MLMS small domain | MLHS small domain | MLMS large domain | MLHS large domain | HLHS small domain | |
|---|---|---|---|---|---|
| MLMS small domain | SFC on small domain | Domain size | Domain size & SF | Driving data (SFC and LBC) | |
| MLHS small domain | SFC on small domain | Domain size & SFC | Domain size | LBC on small domain | |
| MLMS large domain | Domain size | Domain size & SFC | SFC on a large domain | Driving data (SFC & LBC) and domain size | |
| MLHS large domain | Domain size & SFC | Domain size | SFC on a large domain | LBC and domain size | |
| HLHS small domain | Driving data (SFC & LBC) on small domain. | LBC on small domain | Driving data (SFC & lateral) and domain size | LBC and domain size |
| MLMS Small domain | MLHS Small domain | MLMS Large domain | MLHS Large domain | HLHS Small domain | |
|---|---|---|---|---|---|
| MLMS Small domain | Mean difference: | Mean difference: | Mean difference: | Mean difference: | |
| MSLP = 0.33 | MSLP = −2.84 | MSLP = −2.71 | MSLP = −3.86 | ||
| T2m = −0.47 | T2m = 0.14 | T2m = −0.22 | T2m = 0.25 | ||
| Prec = −0.21 | Prec = 0.08 | Precip = 0.03 | Precip = 0.20 | ||
| Variance ratio: | Variance ratio: | Variance ratio: | Variance ratio: | ||
| MSLP = 0.96 | MSLP = 2.11 | MSLP = 1.89 | MSLP = 1.10 | ||
| T2m = 1.35 | T2m = 0.93 | T2m = 1.11 | T2m = 1.13 | ||
| Prec = 1.07 | Precip = 6.08 | Precip = 5.27 | Precip = 1.16 | ||
| MLHS Small domain | Mean difference: | Mean difference: | Mean difference: | Mean difference: | |
| MSLP = −0.33 | MSLP = −3.17 | MSLP = −3.04 | MSLP = −4.19 | ||
| T2m = 0.47 | T2m = 0.61 | T2m = 0.25 | T2m = 0.72 | ||
| Precip = 0.21 | Precip = 0.29 | Precip = 0.24 | Precip = 0.42 | ||
| Variance ratio: | Variance ratio: | Variance ratio: | Variance ratio: | ||
| MSLP = 1.04 | MSLP = 2.19 | MSLP = 1.96 | MSLP = 1.14 | ||
| T2m = 0.74 | T2m = 0.69 | T2m = 0.82 | T2m = 0.83 | ||
| Precip = 0.94 | Precip = 5.67 | Precip = 4.91 | Precip = 1.09 | ||
| MLMS Large domain | Mean difference: | Mean difference: | Mean difference: | Mean difference: | |
| MSLP = 2.84 | MSLP = 3.17 | MSLP = 0.13 | MSLP = −1.02 | ||
| T2m = −0.14 | T2m = −0.61 | T2m = −0.36 | T2m = 0.11 | ||
| Precip = −0.08 | Precip = −0.29 | Precip = −0.05 | Precip = −0.12 | ||
| Variance ratio: | Variance ratio: | Variance ratio: | Variance ratio: | ||
| MSLP = 0.47 | MSLP = 0.46 | MSLP = 0.9 | MSLP = 0.52 | ||
| T2m = 1.08 | T2m = 1.45 | T2m = 1.2 | T2m = 1.21 | ||
| Precip = 0.16 | Precip = 0.18 | Precip = 0.87 | Precip = 0.19 | ||
| MLHS Large domain | Mean difference: | Mean difference: | Mean difference: | Mean difference: | |
| MSLP = 2.71 | MSLP = 3.04 | MSLP = −0.13 | MSLP = −1.15 | ||
| T2m = 0.22 | T2m = −0.25 | T2m = 0.36 | T2m = 0.47 | ||
| Precip = −0.03 | Precip = −0.24 | Precip = 0.05 | Precip = 0.17 | ||
| Variance ratio: | Variance ratio: | Variance ratio: | Variance ratio: | ||
| MSLP = 0.53 | MSLP = 0.51 | MSLP = 1.11 | MSLP = 0.58 | ||
| T2m = 0.90 | T2m = 1.22 | T2m = 0.83 | T2m = 1.01 | ||
| Precip = 0.19 | Precip = 0.20 | Precip = 1.15 | Precip = 0.22 | ||
| HLHS Small domain | Mean difference: | Mean difference: | Mean difference: | Mean difference: | |
| MSLP = 3.86 | MSLP = 4.19 | MSLP = 1.02 | MSLP = 1.15 | ||
| T2m = −0.25 | T2m = −0.72 | T2m = −0.11 | T2m = −0.47 | ||
| Precip = −0.20 | Precip = −0.42 | Precip = 0.12 | Precip = −0.17 | ||
| Variance ratio: | Variance ratio: | Variance ratio: | Variance ratio: | ||
| MSLP = 0.91 | MSLP = 0.88 | MSLP = 1.92 | MSLP = 1.72 | ||
| T2m = 0.88 | T2m = 1.20 | T2m = 0.83 | T2m = 0.99 | ||
| Precip = 0.86 | Precip = 0.92 | Precip = 5.26 | Precip = 4.54 | ||
| MLMS Small domain | MLHS Small domain | MLMS Large domain | MLHS Large domain | HLHS Small domain | |
|---|---|---|---|---|---|
| MLMS Small domain | Mean difference: | Mean difference: | Mean difference: | Mean difference: | |
| MSLP = 0.10 | MSLP = −2.1 | MSLP = −1.97 | MSLP = −2.4 | ||
| T2m = −0.04 | T2m = 0.12 | T2m = 0.18 | T2m = 0.22 | ||
| Precip =−0.09 | Precip = 0.38 | Precip = 0.38 | Precip = 0.70 | ||
| Variance ratio: | Variance ratio: | Variance ratio: | Variance ratio: | ||
| MSLP = 0.98 | MSLP = 2.55 | MSLP = 2.67 | MSLP = 1.05 | ||
| T2m=1.17 | T2m = 0.98 | T2m = 1.01 | T2m = 1.06 | ||
| Precip= 0.90 | Precip = 4.98 | Precip = 1.03 | Precip = 1.03 | ||
| MLHS Small domain | Mean difference: | Mean difference: | Mean difference: | Mean difference: | |
| MSLP = −0.10 | MSLP = −2.21 | MSLP = −2.07 | MSLP = −2.51 | ||
| T2m = 0.04 | T2m = 0.17 | T2m = 0.23 | T2m = 0.27 | ||
| Precip = 0.09 | Precip = 0.47 | Precip = 0.47 | Precip = 0.79 | ||
| Variance ratio: | Variance ratio: | Variance ratio: | Variance ratio: | ||
| MSLP = 1.02 | MSLP = 2.61 | MSLP = 2.73 | MSLP = 1.08 | ||
| T2m = 0.85 | T2m = 0.83 | T2m = 0.86 | T2m = 0.90 | ||
| Precip = 1.11 | Precip = 5.52 | Precip = 5.02 | Precip = 1.14 | ||
| MLMS Large domain | Mean difference: | Mean difference: | Mean difference: | Mean difference: | |
| MSLP = 2.1 | MSLP = 2.21 | MSLP = 0.14 | MSLP = −0.30 | ||
| T2m = −0.12 | T2m = −0.17 | T2m = 0.06 | T2m = 0.10 | ||
| Precip = −0.38 | Precip = −0.47 | Precip = 0.0 | Precip = 0.32 | ||
| Variance ratio: | Variance ratio: | Variance ratio: | Variance ratio: | ||
| MSLP = 0.39 | MSLP = 0.38 | MSLP = 1.05 | MSLP = 0.41 | ||
| T2m = 1.02 | T2m = 1.20 | T2m = 1.04 | T2m = 1.08 | ||
| Precip = 0.20 | Precip = 0.18 | Precip = 0.91 | Precip = 0.21 | ||
| MLHS Large domain | Mean difference: | Mean difference: | Mean difference: | Mean difference: | |
| MSLP = 1.97 | MSLP = 2.07 | MSLP = −0.14 | MSLP = −0.44 | ||
| T2m = −0.18 | T2m = −0.23 | T2m = −0.06 | T2m = 0.04 | ||
| Precip = −0.38 | Precip = −0.47 | Precip = 0.0 | Precip = 0.32 | ||
| Variance ratio: | Variance ratio: | Variance ratio: | Variance ratio: | ||
| MSLP = 0.37 | MSLP = 0.37 | MSLP = 0.95 | MSLP = 0.39 | ||
| T2m = 0.99 | T2m = 1.16 | T2m = 0.96 | T2m = 1.04 | ||
| Precip = 0.97 | Precip = 0.20 | Precip = 1.10 | Precip = 0.23 | ||
| HLHS Small domain | Mean difference: | Mean difference: | Mean difference: | Mean difference: | |
| MSLP = 2.4 | MSLP = 2.51 | MSLP = 0.30 | MSLP = 0.44 | ||
| T2m = −0.22 | T2m = −0.27 | T2m = −0.10 | T2m = −0.04 | ||
| Precip = −0.70 | Precip = −0.79 | Precip = −0.32 | Precip = −0.32 | ||
| Variance ratio: | Variance ratio: | Variance ratio: | Variance ratio: | ||
| MSLP = 0.67 | MSLP = 0.93 | MSLP = 0.49 | MSLP = 2.56 | ||
| T2m = 0.94 | T2m = 1.11 | T2m = 0.93 | T2m = 0.96 | ||
| Precip = 0.97 | Precip = 0.88 | Precip = 4.76 | Precip = 4.35 | ||
| MLMS small domain | MLHS Small domain | MLMS Large domain | MLHS Large domain | HLHS Small domain | |
|---|---|---|---|---|---|
| MLMS Small domain | Mean difference: | Mean difference: | Mean difference: | Mean difference: | |
| MSLP = 0.19 | MSLP = −1.77 | MSLP = −1.65 | MSLP = −2.12 | ||
| T2m = −0.04 | T2m = −0.05 | T2m = −0.15 | T2m = 0.85 | ||
| Precip = −0.28 | Precip = −0.06 | Precip = −0.01 | Precip = −0.03 | ||
| Variance ratio: | Variance ratio: | Variance ratio: | Variance ratio: | ||
| MSLP = 0.99 | MSLP = 2.75 | MSLP = 3.02 | MSLP = 0.90 | ||
| T2m = 1.09 | T2m = 0.95 | T2m = 0.97 | T2m = 0.99 | ||
| Precip = 0.73 | Precip = 8.41 | Precip = 9.66 | Precip = 1.10 | ||
| MLHS Small domain | Mean difference: | Mean difference: | Mean difference: | Mean difference: | |
| MSLP = −0.19 | MSLP = −1.97 | MSLP = −1.84 | MSLP = −2.32 | ||
| T2m = 0.04 | T2m = −0.02 | T2m = −0.12 | T2m = 0.89 | ||
| Precip = 0.28 | Precip = 0.22 | Precip = 0.26 | Precip = 0.24 | ||
| Variance ratio: | Variance ratio: | Variance ratio: | Variance ratio: | ||
| MSLP = 1.01 | MSLP = 2.78 | MSLP = 3.06 | MSLP = 0.92 | ||
| T2m = 0.92 | T2m = 0.87 | T2m = 0.89 | T2m = 0.91 | ||
| Precip = 1.37 | Precip = 11.50 | Precip = 13.21 | Precip = 1.50 | ||
| MLMS Large domain | Mean difference: | Mean difference: | Mean difference: | Mean difference: | |
| MSLP = 1.77 | MSLP = 1.97 | MSLP = 0.13 | MSLP = −0.35 | ||
| T2m = 0.05 | T2m = 0.02 | T2m = −0.10 | T2m = 0.90 | ||
| Precip = 0.06 | Precip = −0.22 | Precip = 0.05 | Precip = 0.02 | ||
| Variance ratio: | Variance ratio: | Variance ratio: | Variance ratio: | ||
| MSLP = 0.36 | MSLP = 0.36 | MSLP = 1.10 | MSLP = 0.33 | ||
| T2m = 1.05 | T2m = 1.15 | T2m = 1.02 | T2m = 1.04 | ||
| Precip = 0.12 | Precip = 0.09 | Precip = 1.15 | Precip = 0.13 | ||
| MLHS Large domain | Mean difference: | Mean difference: | Mean difference: | Mean difference: | |
| MSLP = 1.65 | MSLP = 1.84 | MSLP = −0.13 | MSLP = −0.48 | ||
| T2m = 0.15 | T2m = 0.12 | T2m = 0.10 | T2m = 1.01 | ||
| Precip = 0.01 | Precip = −0.26 | Precip = −0.05 | Precip = −0.02 | ||
| Variance ratio: | Variance ratio: | Variance ratio: | Variance ratio: | ||
| MSLP = 0.33 | MSLP = 0.33 | MSLP = 0.91 | MSLP = 0.3 | ||
| T2m = 1.03 | T2m = 1.12 | T2m = 0.98 | T2m = 1.02 | ||
| Precip = 0.10 | Precip = 0.08 | Precip = 0.67 | Precip = 0.11 | ||
| HLHS Small domain | Mean difference: | Mean difference: | Mean difference: | Mean difference: | |
| MSLP = 2.12 | MSLP = 2.32 | MSLP = 0.35 | MSLP = 0.48 | ||
| T2m = −0.85 | T2m = −0.89 | T2m = −0.90 | T2m = −1.01 | ||
| Precip = 0.03 | Precip = −0.24 | Precip = −0.02 | Precip = 0.02 | ||
| Variance ratio: | Variance ratio: | Variance ratio: | Variance ratio: | ||
| MSLP = 1.11 | MSLP = 1.09 | MSLP = 3.03 | MSLP = 3.33 | ||
| T2m = 1.01 | T2m = 1.10 | T2m = 0.96 | T2m = 0.98 | ||
| Precip = 0.91 | Precip = 0.67 | Precip = 7.69 | Precip = 9.1 | ||
Acknowledgments
The work reported here is funded in part by the Norwegian Research Council, through grant no. 120656/720 to the Norwegian Meteorological Institute/RegClim. Computational costs are covered by a grant from the Research Council's Programme for Supercomputing.
References
- IPCC, Climate Change 2001: The Scientific Basis; Houghton, J.T., Ding, Y., Griggs, D.J., Noguer, M., van der Linden, P.J., Dai, X., Maskell, K., Johnson, C.A., Eds.; Cambridge University Press: Cambridge, UK, 2001; p. 881.
- Lambert, S.J.; Boer, G.J. CMIP1 evaluation and intercomparison of coupled climate models. Clim. Dynam. 2001, 17, 83–106. [Google Scholar]
- Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. In IPCC, Climate Change 2007: The Physical Science Basis; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK and New York, NY, USA, 2007; p. 996.
- Noguer, M.; Jones, R.; Murphy, J. Sources of systematic errors in the climatology of a regional climate model over Europe. Clim. Dynam. 1998, 14, 691–712. [Google Scholar]
- Jones, R.G.; Murphy, J.M.; Noguer, M. Simulation of climate change over Europe using a nested regional-climate model. I: Assessment of control climate, including sensitivity to location of lateral boundaries. Quart. J. Roy. Meteorol. Soc. 1995, 121, 1413–1449. [Google Scholar]
- Christensen, J.H.; Hewitson, B.; Busuioc, A.; Chen, A.; Gao, X.; Held, R.; Jones, R.; Kolli, R.K.; Kwon, W.K.; Laprise, R.; et al. Contribution of working group I to the fourth assessment report of the intergovernmental panel on climate change. In Regional Climate Projections, Climate Change, 2007: The Physical Science Basis; Cambridge University Press: Cambridge, UK and New York, NY, USA, 2007; Chapter 11; pp. 847–940. [Google Scholar]
- Ådlandsvik, B. Marine downscaling of a future climate scenario for the North Sea. Tellus 2008, 60A, 451–458. [Google Scholar]
- Rinke, A.; Gerdes, R.; Dethloff, K.; Kandlbinder, T.; Karcher, M.; Kauker, F.; Frickenhaus, S; Köberle, C.; Hiller, W. A case study of the anomalous Arctic sea ice conditions during 1990: Insights from coupled and uncoupled regional climate model simulations. J. Geophys. Res. 2003, 108(D9), 4275. [Google Scholar]
- Döscher, R.; Willen, U.; Jones, C.; Rutgersson, A.; Meier, H.E.M.; Hansson, U.; Graham, L.P. The development of the coupled regional ocean-atmosphere model RCAO. Boreal Environ. Res. 2002, 7, 1221–1234. [Google Scholar]
- Anthes, R.A. The General Question of Predictability. In Chapter 27 in Mesoscale Meteorology and Forecasting; Ray, P.S., Ed.; The American Meteorological Society: Boston, MA, USA, 1986; pp. 636–656. [Google Scholar]
- Boer, G.J. Predictability regimes in atmospheric flow. Mon. Weather Rev. 1994, 122, 2285–2295. [Google Scholar]
- Christensen, J.H.; Machenhauer, B.; Jones, R.G.; Schar, C.; Ruti, P.M.; Castro, M.; Visconti, G. Validation of present-day regional climate simulations over Europe: LAM simulations with observed boundary conditions. Clim. Dynam. 1997, 13, 489–506. [Google Scholar]
- Rinke, A.; Dethloff, K.; Spekat, A.; Enke, W.; Christensen, J.H. High resolution climate simulations over the Arctic. Polar Res. 1999, 18, 1–9. [Google Scholar]
- Denis, B.; Laprise, R; Caya, D.; Cote, J. Downscaling ability of one-way nested regional climate models: The big-brother experiment. Clim. Dynam. 2002, 18, 627–646. [Google Scholar]
- Køltzow, M.; Iversen, T.; Haugen, J.E. On abilities and limitations of atmospheric dynamical downscaling of global climate scenarios. Tellus 2008, 60A, 398–410. [Google Scholar]
- Laprise, R.; de Elía, R.; Caya, D.; Biner, S.; Lucas-Picher, P.H.; Diaconescu, E.P.; Leduc, M.; Alexandru, A.; Separovic, L. Challenging some tenets of regional climate modelling. Meteorol. Atmos. Phys. 2008, 100, 3–22. [Google Scholar]
- Leduc, M.; Laprise, R. Regional climate model sensitivity to domain size. Clim. Dynam. 2009, 32, 833–854. [Google Scholar]
- Diaconescu, E.P.; Laprise, R.; Sushama, L. The impact of lateral boundary data errors on the simulated climate of a nested regional climate model. Clim. Dynam. 2007, 28, 333–350. [Google Scholar]
- Singarayer, J.S.; Valdes, P.J.; Bamber, J.L. The atmospheric impact of uncertainties in recent Arctic sea ice reconstructions. J. Clim. 2005, 18, 3996–4012. [Google Scholar]
- Lopez, P.; Schmith, T.; Kaas, E. Sensitivity of the Northern Hemisphere circulation to North Atlantic SSTs in the ARPEGE Climate AGCM. Clim. Dynam. 2000, 16, 535–547. [Google Scholar]
- Kvamstø, N.G.; Skeie, P.; Stephenson, D.B. Impact of labrador sea-ice extent on the North Atlantic Oscillation. Int. J. Climatol. 2004, 24, 603–612. [Google Scholar]
- Kushnir, Y.W.; Robinson, A.; Blade, I.; Hall, N.M.J.; Peng, S.; Sutton, R. Atmospheric GCM response to extratropical SST Anomalies: Synthesis and evaluation. J. Climate 2002, 15, 2233–2256. [Google Scholar]
- Chapman, W.L.; Walsh, J.E. Simulations of arctic temperature and pressure by global coupled models. J. Climate 2007, 20, 609–632. [Google Scholar]
- Rinke, A.; Maslowski, W.; Dethloff, K.; Clement, J. Influence of sea ice on the atmosphere: A study with an Arctic atmospheric regional climate model. J. Geophys. Res. 2006, 111, D16103. [Google Scholar]
- Semmler, T.; Jacob, D.; Heinke Schlunzen, K.; Podzun, R. Influence of sea ice treatment in a regional climate model on boundary layer values in the fraim strait region. Mon. Weather Rev. 2004, 132, 985–999. [Google Scholar]
- Kjellstrøm, E.; Ruosteenoja, K. Present-day and future precipitation in the Baltic Sea region as simulated in a suite of regional climate models. Clim. Change 2007, 81, 281–291. [Google Scholar]
- Bozkurt, D.; Sen, O.L. Precipitation in the Anatolian peninsula: Sensitivity to increased SSTs in the surrounding seas. Clim. Dynam. 2009, 36, 711–726. [Google Scholar]
- Vannitsem, S.; Chome, F. One-way nested regional climate simulations and domain size. J. Clim. 2005, 18, 229–233. [Google Scholar]
- Gustafsson, N. The HIRLAM2 Final Report; HIRLAM Technical Report No. 9; Swedish Meteorological and Hydrological Institute: Norrkoping, Sweden, 1993. [Google Scholar]
- Roeckner, E.; Arpe, K.; Bengtsson, L.; Christoph, M.; Claussen, M.; Dümenil, L.; Esch, M.; Giorgetta, M.; Schlese, U.; Schulzweida, U. The Atmospheric General Circulation Model ECHAM4: Model Description and Simulation of Present-Day Climate; MPI Report No. 218; MPI für Meteorologie: Hamburg, Germany, 1996. [Google Scholar]
- Christensen, J.H.; Christensen, O.B.; Lopez, P.; van Meijgaard, E.; Botzet, M. The HIRHAM4, Regional Atmospheric Climate Model; Scientific Report No. 96-4; Danish Meteorological Institute: Copenhagen, Denmark, 1996. [Google Scholar]
- Bjørge, D.; Haugen, J.E.; Nordeng, T.E. Future climate in Norway; DNMI Research Rep. No. 103; Norwegian Meteorological Institute: Oslo, Norway, 2000; p. 41. [Google Scholar]
- Davies, H.C. A lateral boundary formulation for multi-level prediction models. Quart. J. Roy. Meteorol. Soc. 1976, 102, 405–418. [Google Scholar]
- Dethloff, K.; Rinke, A.; Benkel, A.; Køltzow, M.; Sokolova, E.; Kumar Saha, S.; Handorf, D.; Dorn, W.; Rockel, B.; von Storch, H.; et al. A dynamical link between the Arctic and the global climate system, Geophys. Res. Lett. 2006, 33, L03703. [Google Scholar]
- Kida, H.; Koide, T.; Sasaki, H.; Chiba, M. A new approach to coupling a limited area model with a GCM for regional climate simulation. J. Meteor. Soc. Japan 1991, 69, 723–728. [Google Scholar]
- von Storch, H.; Langenberg, H.; Feser, F. A spectral nudging technique for dynamical downscaling purposes. Mon. Weather Rev. 2000, 128, 3664–3673. [Google Scholar]
- Mesinger, F.; Brill, K.; Chuang, H.; DiMego, G.; Rogers, E. Limited Area Predictability: Can “Upscaling'” Also Take Place? In Research Activities in Atmospheric and Oceanic Modelling; Ritchie, H., Ed.; World Meteorological Organization: Geneva, Switzerland, 2002. [Google Scholar]
- Alexandru, A.; de Elía, R.; Laprise, R. Internal variability in regional climate downscaling at the seasonal time scale. Mon. Weather Rev. 2007, 135, 3221–3238. [Google Scholar]
- Castro, C.L.; Pielke, R.A., Sr.; Leoncini, G. Dynamical downscaling: Assessment of value retained and added using the regional atmospheric modeling system (RAMS). J. Geophys. Res. 2005, 110, D05108. [Google Scholar]
- Held, I.M. Stationary and Quasi-stationary Eddies in the Extratropical Atmosphere: Theory. In Large Scale Dynamical Processes in the Atmosphere; Hoskins, B.J., Pearce, R.P., Eds.; Academic Press: Burlington, MA, USA, 1983; pp. 127–168. [Google Scholar]
- Hoskins, B.J.; Karoly, D.J. The steady linear response of a spherical atmosphere to thermal and orographic forcing. J. Atmos. Sci. 1981, 38, 1179–1196. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Køltzow, M.A.Ø.; Iversen, T.; Haugen, J.E. The Importance of Lateral Boundaries, Surface Forcing and Choice of Domain Size for Dynamical Downscaling of Global Climate Simulations. Atmosphere 2011, 2, 67-95. https://doi.org/10.3390/atmos2020067
Køltzow MAØ, Iversen T, Haugen JE. The Importance of Lateral Boundaries, Surface Forcing and Choice of Domain Size for Dynamical Downscaling of Global Climate Simulations. Atmosphere. 2011; 2(2):67-95. https://doi.org/10.3390/atmos2020067
Chicago/Turabian StyleKøltzow, Morten A.Ø., Trond Iversen, and Jan Erik Haugen. 2011. "The Importance of Lateral Boundaries, Surface Forcing and Choice of Domain Size for Dynamical Downscaling of Global Climate Simulations" Atmosphere 2, no. 2: 67-95. https://doi.org/10.3390/atmos2020067




