Modeling Long-Term Trends in Russet Burbank Potato Growth and Development in Wisconsin
Abstract
:1. Introduction
2. Experimental Setup
2.1. Data Analysis



| Parameter | Definition |
|---|---|
| α | The maximum value or upper asymptote of the response variable (Average Tuber Length (mm) or Average Tuber Number). |
| α0 | Estimated intercept parameter of the linear function describing the dependence of α on the explanatory variable. |
| αstems | Estimated slope parameter of the linear function describing the dependence of α on the explanatory variable. |
| β | The inflection point where the response variable reaches half of its maximum value. |
| γ | The scaling factor that governs how rapidly the response variable reaches its maximum value. |
| γ0 | Estimated intercept parameter of the linear function describing the dependence of γ on the explanatory variable. |
| γstems | Estimated slope parameter of the linear function describing the dependence of γ on the explanatory variable. |
| Stems | Average stem number per plant. |
| t | Thermal time, here measured as growing degree days accumulated over the potato growing season using a base of 4.4 °C. |
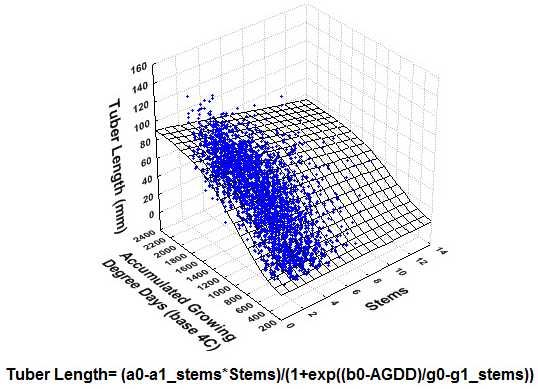
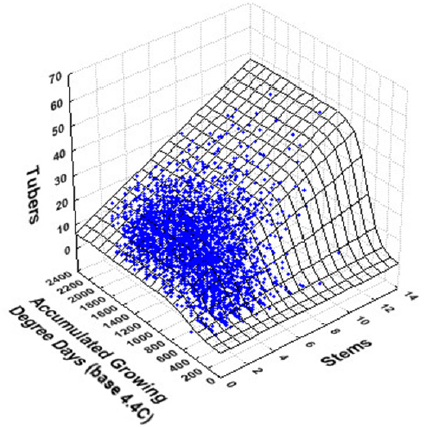
3. Experimental Results
| Average Tuber Length (mm) | Average Tuber Number per Plant | |||
|---|---|---|---|---|
| Variance Explained: 76.6% | Variance Explained: 45.1% | |||
| R = 0.875 | R = 0.672 | |||
| Parameter | Estimate | SE | Estimate | SE |
| * Significant at the 0.05 probability level; ** Significant at the 0.01 probability level; *** Significant at the 0.001 probability level. | ||||
| αor α0 | 89.23 *** | 1.54 | 6.22 ** | 0.27 |
| αstems | 1.85 *** | 0.27 | 2.92 ** | 0.07 |
| β | 960.95 *** | 11.33 | 528.89 ** | 6.55 |
| γor γ0 | 274.95 *** | 17.31 | 102.56 ** | 6.25 |
| γstems | -8.19 * | 4.11 | NS | -- |
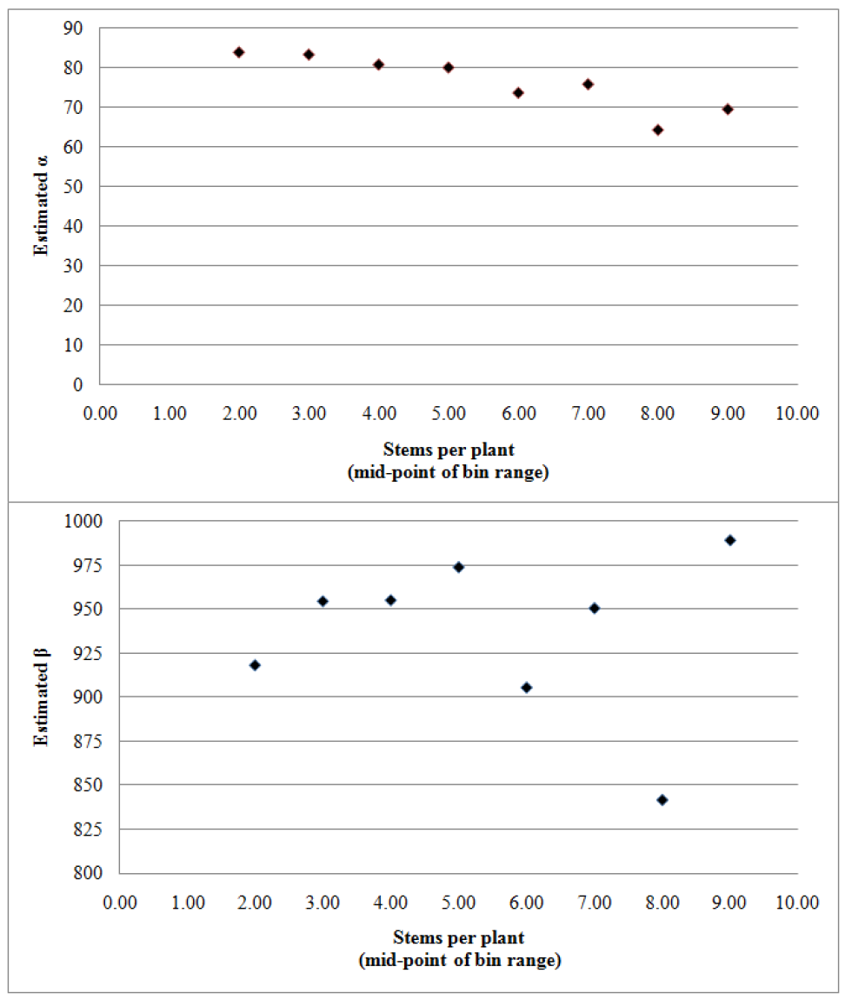
| α0 | αstem | β | γ | |||||
|---|---|---|---|---|---|---|---|---|
| Year | Estimate | SE | Estimate | SE | Estimate | SE | Estimate | SE |
| * Significant at the 0.05 probability level; ** Significant at the 0.01 probability level; *** Significant at the .001 probability level. | ||||||||
| 1979 | 80.38 ** | 6.29 | 1.69 | 0.92 | 1005.19 ** | 40.50 | 245.69 ** | 17.24 |
| 1980 | 75.60 ** | 2.68 | 2.72 ** | 0.80 | 834.48 ** | 16.49 | 197.86 ** | 10.02 |
| 1981 | 114.22 ** | 6.91 | 4.73 ** | 1.29 | 1168.62 ** | 43.69 | 309.51 ** | 19.68 |
| 1982 | 63.21 ** | 2.54 | 1.67 | 0.89 | 922.05 ** | 19.74 | 205.39 ** | 10.74 |
| 1983 | 96.37 ** | 3.89 | 3.77 ** | 0.84 | 998.60 ** | 36.56 | 322.32 ** | 22.54 |
| 1984 | 77.84 ** | 3.83 | 1.42 ** | 0.54 | 968.51 ** | 28.28 | 264.93 ** | 19.98 |
| 1985 | 80.91 ** | 5.45 | 1.62 ** | 0.48 | 719.91 ** | 30.69 | 265.56 ** | 61.68 |
| 1986 | 91.17 ** | 3.99 | 2.35 ** | 0.85 | 866.74 ** | 27.07 | 287.48 ** | 15.61 |
| 1987 | 98.79 ** | 2.98 | 2.95 ** | 0.81 | 887.25 ** | 13.71 | 214.31 ** | 7.77 |
| 1988 | 96.74 ** | 3.25 | 2.78 ** | 0.65 | 1143.67 ** | 23.71 | 302.34 ** | 15.10 |
| 1989 | 93.62 ** | 3.47 | 1.99 ** | 0.70 | 978.20 ** | 20.13 | 251.11 ** | 14.57 |
| 1990 | 63.78 ** | 2.94 | 0.68 | 0.57 | 898.94 ** | 20.30 | 228.44 ** | 15.67 |
| 1991 | 86.49 ** | 3.10 | 2.63 ** | 0.63 | 932.97 ** | 26.22 | 287.13 ** | 20.73 |
| 1992 | 90.90 ** | 2.65 | 3.06 ** | 0.52 | 762.02 ** | 16.82 | 226.32 ** | 14.96 |
| 1993 | 84.24 ** | 2.53 | 2.38 ** | 0.58 | 784.20 ** | 17.64 | 239.93 ** | 13.38 |
| Residual Square Error = 0.870 |





4. Conclusions
Acknowledgements
References
- Mulligan, M.; Wainwright, J. In Environmental Modeling,Finding Simplicity in Complexity; 2004; John Wiley : Chinchester, UK. [Google Scholar]
- Cubeta, M.A.; Crozier, C.R.; Creamer, N.G. Influence of seedpiece spacing and population on yield, internal quality, and economic performance of Atlantic, Superior, and Snowden potato varieties in Eastern North Carolina. Am. J. Potato Res. 1999, 76, 257–261. [Google Scholar] [CrossRef]
- Thompson-Johns, A.; Love, S.L. Seed piece spacing influences yield, tuber size distribution, stem and tuber density, and net returns of three processing potato cultivars. HortScience 1999, 34, 629–633. [Google Scholar]
- Thornton, R.E.; Iritani, W.M.; Schotzko, R.T. The economics of Russet Burbank seed size and spacing. Am. Potato J. 1984, 61, 57–66. [Google Scholar] [CrossRef]
- Blackmore, K.W.; Strange, P.C. Effect of whole seed tubers, cut seed and within row spacing on potato (cv. Sebago) tuber yield. Aust. J. Exp. Agric 1990, 30, 427–431. [Google Scholar] [CrossRef]
- Drilias, M.J.; Copas, M.E.; Mitchell, P.D.; Bussan, A.J. Evaluation of the Effect of Density on Potato Yield and Tuber Size Distribution. Crop Sci. 2007, 47, 2462–2472. [Google Scholar] [CrossRef]
- Kawchuk, L.M.; Kozub, G.C.; Lynch, D.R. The relationship between yield, mainstem number, and tuber number in five maincrop and two early-maturing cultivars. Am. J. Potato Res. 2001, 78, 83–90. [Google Scholar] [CrossRef]
- Knowles, L.O.; Knowles, N.R. Manipulating stem number, tuber set, and yield relationships for northern and southern-grown potato seed lots. Crop Sci. 2006, 46, 284–296. [Google Scholar] [CrossRef]
- Wierzbicka, A.; Lutomirska, B.; Mazurcyk, W. Relation between air temp and length of vegetation period of potato crops. Agric. For. Meterol. 2003, 118, 169–172. [Google Scholar] [CrossRef]
- Bierman, P.M.; Rosen, C.J. Potato yield and tuber set as affected by phosphorus fertilization. Am. J. Pot. Res. 2008, 85, 110–120. [Google Scholar] [CrossRef]
- Struik, P.C.; Kooman, P.L.; Van Dam, J. Effects of temperature and photoperiod on early growth and final number of tubers in potato (Solanum tuberosum L.). Pot. Res 1996, 39, 51–62. [Google Scholar] [CrossRef]
- Haverkort, A.J.; Pecio, A.; van Delden, A. Temperature response of early foliar expansion of potato and wheat. Ann. Bot. 2000, 86, 355–369. [Google Scholar] [CrossRef]
- Allen, E.J.; Fellows, J.R.; Wurr, D.C.E. An approach to determining optimum tuber planting densities in early potato varieties. J. Agric. Sci. 1993, 120, 63–70. [Google Scholar] [CrossRef]
- Swallow, W.H.; Haynes, F.L.; Haynes, K.G. Temperature and Photoperiod effects on Tuber Production and Specific Gravity in Diploid Potatoes. HortScience 1988, 23, 562–565. [Google Scholar]
- Allen, E.J.; Sutherland, R.A.; Fellows, J.R.; Wurr, D.C.E. Determination of optimum tuber planting density for production of tubers in processing ware grades in potato variety. Record. J. Agric. Sci. 1990, 114, 11–18. [Google Scholar]
- Sanderson, J.B.; Arsenault, W.J.; Zebarth, B.J. Effect of seedpiece spacing and nitrogen fertilization on tuber yield, yield components, and nitrogen use efficiency parameters of two potato cultivars. Am. J. Potato Res. 2006, 83, 289–296. [Google Scholar] [CrossRef]
- Dellai, J.; Heldwein, A.B.; Bisognin, D.A.; Matielo de Paula, F.L.; Streck, N.A. Simulating the development of field grown potato (Solanum tuberosum L.). Agric. For. Meterol 2007, 142, 1–11. [Google Scholar] [CrossRef]
- Tooming, H.; Kadaja, J. Potato production model based on principle of maximum plant productivity. Agric. For. Meterol. 2004, 127, 17–33. [Google Scholar] [CrossRef]
- Bland, W.L.; Yuan, F.M. Light and temperature modulated expolinear growth model for potato (Solanum tuberosum L.). Agric. For. Meterol 2004, 121, 141–151. [Google Scholar] [CrossRef]
- Miller, P.R.; Maxwell, B.D.; Bussan, A.J.; Holman, J.D. Spring wheat, canola, and sunflower response to Persian darnel (Lolium persicum) interference. Weed Technol 2004, 18, 509–520. [Google Scholar] [CrossRef]
- Stahlman, P.W.; Seefeldt, S.S.; Ogg, A.G.; Morishita, D.W.; Miller, S.D.; Lyons, D.J.; Evans, J.O.; Anderson, R.L.; Maxwell, B.D.; Jasieniuk, M. Evaluation of model predicting winter wheat yield as a function of winter wheat and jointed goatgrass density. Weed Sci. 2001, 49, 48–60. [Google Scholar] [CrossRef]
- Masiunas, J.B.; Williams, M.M. Functional relationships between giant ragweed (Ambrosia trifida) interference and sweet corn yield and ear traits. Weed Sci. 2006, 54, 948–953. [Google Scholar] [CrossRef]
- II. Ascough, J.C.; Dunn, G.H.; McMaster, G.S.; Erskine, R.H.; Wiles, L.J.; Canner, S.R. Modeling with limited data, the influence of crop rotation and management on weed communities and crop yield loss. Weed Sci. 2009, 57, 175–186. [Google Scholar] [CrossRef]
- Moorby, J.; Milthrope, F.L. An Introduction to Crop Physiology1979, 2nd ed; Cambridge University Press: Cambridge, UK. [Google Scholar]
- Scholtz, R.V., III; Martin, F.G., III; Overman, A.R. Defense of the Extended Logistic Model of Crop Production. Comm. In Soil Sci. Plant Anal 2003, 34, 851–864. [Google Scholar]
- Brock, K.H.; Overman, A.R. Model analysis of Corn Response to Applied Nitrogen and Tillage. Comm. In Soil Sci. Plant Anal. 2003, 34, 2177–2191. [Google Scholar] [CrossRef]
- Dobermannm, A.; Cassman, K.G.; Specht, J.E.; Weiss, A.; Setiyono, T.D. Leaf area index simulation in soybean grown under high-yield conditions. Field Crops Res. 2008, 108, 82–92. [Google Scholar] [CrossRef]
- Ferreira, M.E.; de Melo-Abreu, J.P.; De Varennes, A. Predicting the concentration and uptake of nitrogen, phosphorus, and potassium by field grown green beans under non-limiting conditions. Eur. J. Agron. 2002, 17, 63–72. [Google Scholar] [CrossRef]
- Ruark, M.D.; Mahr, D.L.; Heider, D.J.; Groves, R.L.; Gevens, A.J.; Flashinski, R.A.; Cullen, E.M.; Colquhoun, J.B.; Bussan, A.J.; Boerboom, C.M. Commercial Vegetable Production in Wisconsin; 2009; Bullution No. A3422; University of Wisconsin Extension: Madison, WI, USA. [Google Scholar]
- Bouvier, A.; Hennequet, C.; Huet, S.; Robert, N. Methodology for choosing a model for wheat kernel growth. Agronomie 1999, 19, 405–417. [Google Scholar] [CrossRef]
- Bates, D.M.; Pienhero, J.C. In Mixed-Effects Models in S and S-Plus; 2000; Springer Press: New York, NY, USA. [Google Scholar]
- Allen, E.J.; Fellows, J.R.; Wurr, D.C.E. Determination of optimum tuber planting density in the potato varieties Pentland Squire, Cara, Estima, Maris Piper, and King Edward. J. Agric. Sci. 1992, 199, 35–44. [Google Scholar]
- Garcia del Moral, L.F.; Guillen, A.; De la Morena, I. Yield development in potatoes as influenced by cultivar and the timing and level of nitrogen fertilization. Am. Potato J. 1994, 71, 165–173. [Google Scholar] [CrossRef]
- Welham, S.J.; Hide, G.A. Observations on the bulking and development of tuber size distribution in maincrop potatoes at Rothamsted in 1964–75. Potato Res. 1992, 35, 235–247. [Google Scholar] [CrossRef]
- Lynn, J.R.; Hambidge, A.J.; Akehurst, J.M.; Fellows, J.R.; Wurr, D.C.E. The effect of cultural and environmental factors on potato seed tuber morphology and subsequent sprout and stem development. J. Agric. Sci. 2001, 136, 56–63. [Google Scholar]
- Workneh, T.S.; Tekalign, T.; Asmamaw, Y. Specific gravity, dry matter concentration, pH, and crisp-making potential of Ethiopian Potato (Solanum tuberosum L.) cultivars as influenced by growing environment and length of storage under ambient conditions. Potato Res. 2010, 53, 95–109. [Google Scholar] [CrossRef]
- Caliskan, C.F.; Yildirim, M.B. Genotype × environment interactions in potato (Solanum tuberosum L.). Am. Potato J. 1985, 62, 371–375. [Google Scholar] [CrossRef]
- Wurr, D.C.E.; Allen, E.J. The Potato Crop: The Scientific Basis for Improvement; Ed., Harris, P.M., Eds.; 1992; p. 292. Chapman and Hall: London, UK. [Google Scholar]
- Crop Production. United States Department of Agriculture, National Agricultural Statistics Service (NASS): Washington, DC, USA, 2010. Available online: http://usda.mannlib.cornell.edu/usda/nass/CropProd//2010s/2010/CropProd-09-10-2010.pdf (accessed on 1 March 2012).
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Goeser, N.J.; Mitchell, P.D.; Esker, P.D.; Curwen, D.; Weis, G.; Bussan, A.J. Modeling Long-Term Trends in Russet Burbank Potato Growth and Development in Wisconsin. Agronomy 2012, 2, 14-27. https://doi.org/10.3390/agronomy2010014
Goeser NJ, Mitchell PD, Esker PD, Curwen D, Weis G, Bussan AJ. Modeling Long-Term Trends in Russet Burbank Potato Growth and Development in Wisconsin. Agronomy. 2012; 2(1):14-27. https://doi.org/10.3390/agronomy2010014
Chicago/Turabian StyleGoeser, Nicholas J., Paul D. Mitchell, Paul D. Esker, David Curwen, Gavin Weis, and Alvin J. Bussan. 2012. "Modeling Long-Term Trends in Russet Burbank Potato Growth and Development in Wisconsin" Agronomy 2, no. 1: 14-27. https://doi.org/10.3390/agronomy2010014