Scattering and Gaussian Fluctuation Theory for Semiflexible Polymers
Abstract
:1. Introduction
2. Structure Factor of a Single Worm-Like Chain (WLC)
2.1. Rigid and Flexible Limit
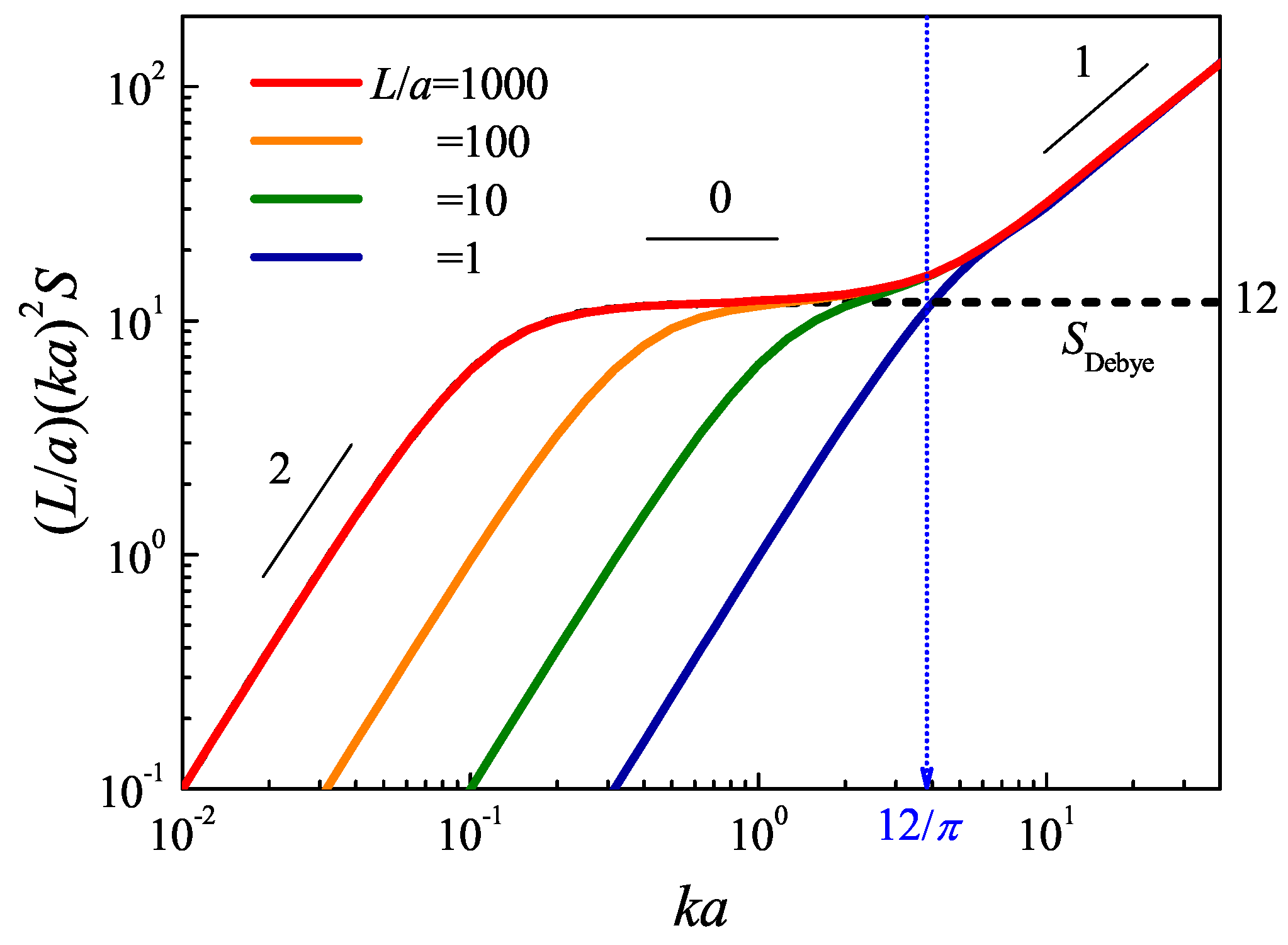
2.2. Asymptotic Behavior of the Structure Factor in Small and Large Wavenumbers
2.3. Structure Factor of WLC with Finite L/a
3. Structure Factor in the Orientational Field
4. Gaussian Fluctuation Theory and the Random Phase Approximation
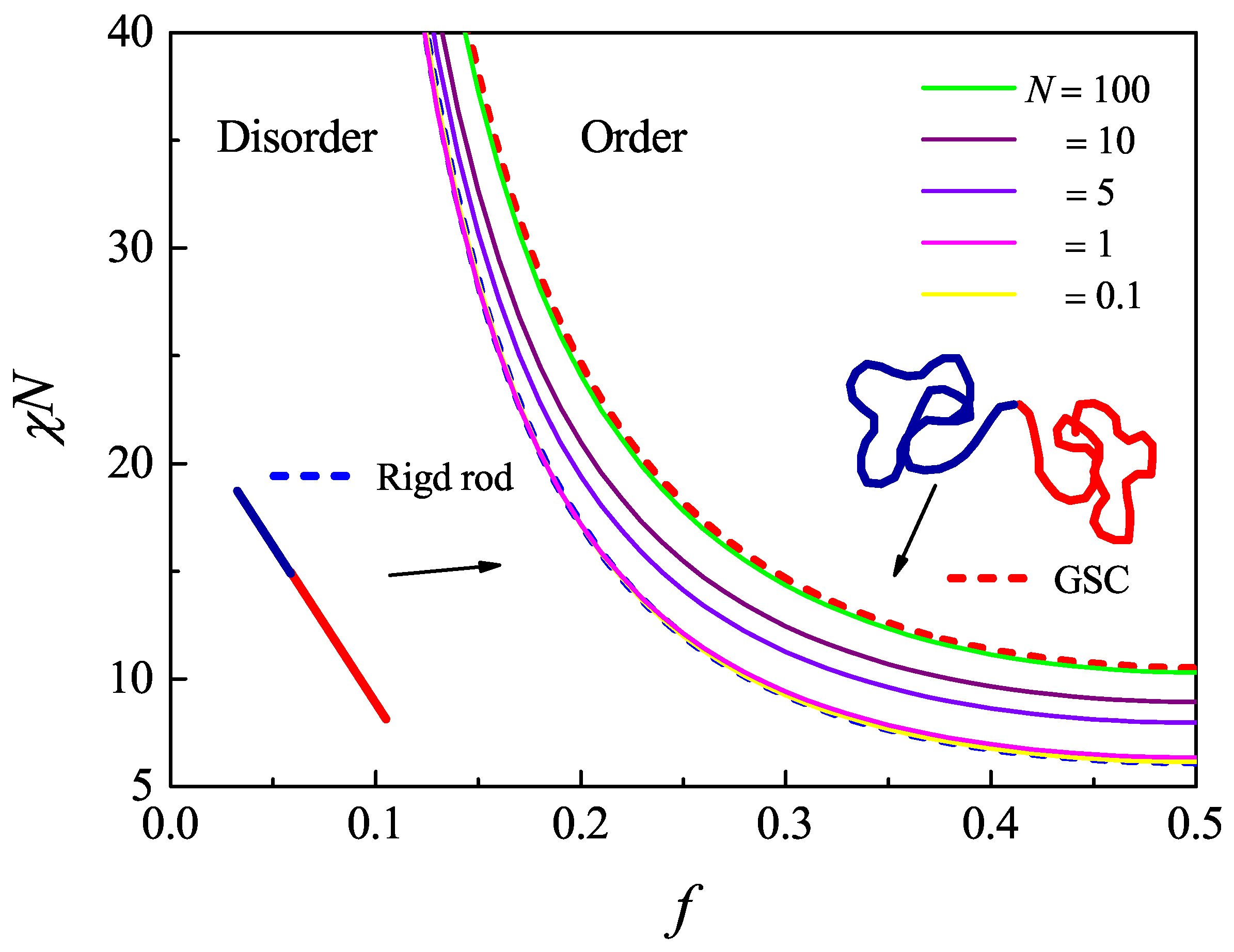
4.1. Gaussian Fluctuation Theory of the Worm-Like Diblock Copolymer
4.2. Worm-Like Diblock Polymer with δ Interaction Potential
4.3. Effects of the Finite Interaction Range
5. Summary
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| GSC | Gaussian chain |
| MDE | modified diffusion equation |
| RPA | random phase approximation |
| SCFT | self-consistent field theory |
| WLC | worm-like chain |
References
- Netz, R.R.; Orland, H. Variational theory for a single polyelectrolyte chain. Eur. Phys. J. B 1999, 8, 81–98. [Google Scholar] [CrossRef]
- Bates, C.M.; Maher, M.J.; Janes, D.W.; Ellison, C.J.; Willson, C.G. Block copolymer lithography. Macromolecules 2014, 47, 2–12. [Google Scholar] [CrossRef]
- Schmid, F.; Schick, M. Liquid phases of Langmuir monolayers. J. Chem. Phys. 1995, 102, 2080. [Google Scholar] [CrossRef]
- Katsov, K.; Müller, M.; Schick, M. Field theoretic study of bilayer membrane fusion. I. Hemifusion mechanism. Biophys. J. 2004, 87, 3277–3290. [Google Scholar] [CrossRef] [PubMed]
- Tanner, P.; Baumann, P.; Enea, R.; Onaca, O.; Palivan, C.; Meier, W. Polymeric vesicles: From drug carriers to nanoreactors and artificial organelles. Acc. Chem. Res. 2011, 44, 1039–1049. [Google Scholar] [CrossRef] [PubMed]
- Singh, C.; Goulian, M.; Liu, A.; Fredrickson, G.H. Phase behavior of semiflexible diblock copolymers. Macromolecules 1994, 27, 2974–2986. [Google Scholar] [CrossRef]
- Marques, C. M.; Fredrickson, G. H. Rigid gaussian chains I: The scattering function. J. Phys. II Fronce 1997, 7, 1805–1816. [Google Scholar] [CrossRef]
- Kratky, O.; Porod, G. Röntgenuntersuchung glöster Fagenmoleküle. Recl. Trav. Chim. 1949, 68, 1106–1122. [Google Scholar] [CrossRef]
- Saito, N.; Takahashi, K.; Yunoki, Y. The statistical mechanical theory of stiff chains. J. Phys. Soc. Jpn. 1967, 22, 219–226. [Google Scholar] [CrossRef]
- Liu, A.J.; Fredrickson, G.H. Free energy functionals for liquid crystalline polymer solutions and blends. Macromolecules 1993, 26, 2817–2824. [Google Scholar] [CrossRef]
- Cui, S.M.; Akcakir, O.; Chen, Z.Y. Isotropic-nematic interface of liquid-crystalline polymers. Phys. Rev. E 1995, 51, 4548. [Google Scholar] [CrossRef]
- Düchs, D.; Sullivan, D.E. Entropy-induced smectic phases in rod-coil copolymers. J. Phys. Condens. Matter 2002, 14, 12189. [Google Scholar]
- Jiang, Y.; Chen, Z.Y. Isotropic-nematic interface in a lyotropic system of worm-like chains with the Onsager interaction. Macromolecules 2010, 43, 10668–10678. [Google Scholar] [CrossRef]
- Fredrickson, G.H. The Equilibrium Theory of Inhomogeneous Polymers; Clarendon: Oxford, UK, 2006. [Google Scholar]
- Higgins, J.S.; Benoit, H.C. Polymers and Neutron Scattering; Clarendon: Oxford, UK, 1994. [Google Scholar]
- Flory, P.J. Principles of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953. [Google Scholar]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Clarendon Press: Oxford, UK, 1986. [Google Scholar]
- Benoit, H.; Doty, P. Light scattering from non-gaussian chains. J. Phys. Chem. 1953, 57, 958–963. [Google Scholar] [CrossRef]
- Hermans, J.J.; Ullman, R. The statistics of stiff chains, with applications to light scattering. Physica 1952, 18, 951–971. [Google Scholar] [CrossRef]
- Hammouda, B.; Doty, P. SANS from Homogeneous polymer mixtures: A unified overview. Adv. Polym. Sci. 1993, 106, 87–133. [Google Scholar]
- Yeung, C.; Shi, A.C.; Noolandi, J.; Desai, R.C. Anisotropic fluctuations in ordered copolymer phases. Macromol. Theory Simul. 1996, 5, 291–298. [Google Scholar] [CrossRef]
- Leibler, L. Theory of microphase separation in block copolymers. Macromolecules 1980, 13, 1602–1617. [Google Scholar] [CrossRef]
- Shi, A.-C.; Noolandi, J.; Desai, R.D. Theory of anisotropic fluctuations in ordered block copolymer phases. Macromolecules 1996, 29, 6487–6504. [Google Scholar] [CrossRef]
- Fredrickson, G.H.; Helfand, E. Fluctuation effects in the theory of microphase separation in block copolymers. J. Phy. Chem. 1987, 87, 697–705. [Google Scholar] [CrossRef]
- Schweizer, K.S.; Curro, J.G. Integral equation theories of the structure, thermodynamics, and phase transitions of polymer fluids. Adv. Chem. Phys. 1997, 98, 1–142. [Google Scholar]
- Netz, R.R.; Andelman, D. Neutral and charged polymers at interfaces. Phys. Rep. 2003, 380, 1–95. [Google Scholar] [CrossRef]
- Semenov, A.N. Adsorption of a semiflexible worm-like chain. Eur. Phys. J. E 2002, 9, 353–363. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, I.; Shi, A.C.; Wang, Z.G. Ion solvation in liquid mixtures: Effects of solvent reorganization. Phys. Rev. Lett. 2012, 109, 257802. [Google Scholar] [CrossRef] [PubMed]
- Sing, C.E.; Zwanikken, J.W.; de la Cruz, M.O. Electrostatic control of block copolymer morphology. Nat. Mater. 2014, 13, 694–698. [Google Scholar] [CrossRef] [PubMed]
- Ariel, G.; Andelman, D. Polyelectrolyte persistence length: Attractive effect of counterion correlations and fluctuations. Europhys. Lett. 2003, 61, 67–73. [Google Scholar] [CrossRef]
- Chen, K.; Saltzman, J.; Schweizer, K.S. Molecular theories of segmental dynamics and mechanical response in deeply supercooled polymer melts and glasses. Annu. Rev. Condens. Matter Phys. 2010, 1, 277–300. [Google Scholar] [CrossRef]
- Dell, Z.E.; Schweizer, K.S. Theory of localization and activated hopping of nanoparticles in cross-linked networks and entangled polymer melts. Macromolecules 2013, 47, 405–414. [Google Scholar] [CrossRef]
- Freed, K.F. Functional integrals and polymer statistics. Adv. Chem. Phys. 1972, 22, 1. [Google Scholar]
- Dogic, Z.; Zhang, J.; Lau, A.; Aranda-Espinoza, H.; Dalhaimer, P.; Discher, D.E.; Janmey, P.A.; Kamien, R.D.; Lubensky, T.C.; Yodh, A.G. Elongation and fluctuations of semiflexible polymers in a nematic solvent. Phys. Rev. Lett. 2004, 92, 125503. [Google Scholar] [CrossRef] [PubMed]
- Neugebauer, T. Berechnung der lichtzerstreuung von fadenkettenlösungen. Ann. Phys. 1943, 42, 509–533. [Google Scholar]
- Teraoka, I. Polymer Solutions: An Introduction to Physical Properties; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Feigin, L.A.; Svergun, D.I. Structure Analysis by Small-Angle X-ray and Neutron Scattering; Plenum Press: New York, NY, USA, 1987. [Google Scholar]
- Norisuye, T.; Fujita, H. Excluded-volum effects in dilute polymer solutions. XIII. Efffects of chain stiffness. Polym. J. 1982, 14, 143–147. [Google Scholar] [CrossRef]
- Hsu, H.-P.; Paul, W.; Binder, K. Polymer chain stiffness vs. excluded volume: A Monte Carlo study of the crossover towards the worm-like chain model. Europhys. Lett. 2010, 92, 28003. [Google Scholar] [CrossRef]
- Hsu, H.-P.; Paul, W.; Binder, K. Understanding the multiple length scales describing the structure of bottle-brush polymers by Monte Carlo simulation methods. Macromol. Theory Simul. 2011, 20, 510–525. [Google Scholar] [CrossRef]
- Hsu, H.-P.; Paul, W.; Binder, K. Estimation of persistence lengths of semiflexible polymers: Insight from simulations. Polym. Sci. Ser. C 2013, 55, 39–59. [Google Scholar] [CrossRef]
- Hsu, H.-P.; Binder, K. Stretching semiflexible polymer chains: Evidence for the importance of excluded volume effects from Monte Carlo simulation. J. Chem. Phys. 2012, 136, 024901. [Google Scholar] [CrossRef] [PubMed]
- Kholodenko, A.L. Fermi-bose transmutation: From semiflexible polymers to superstrings. Ann. Phys. 1990, 202, 186–225. [Google Scholar] [CrossRef]
- Kholodenko, A.L. Persistence length and related conformational properties of semiflexible polymers from Dirac propagator. J. Chem. Phys. 1992, 96, 700–713. [Google Scholar] [CrossRef]
- Kholodenko, A.L. Analytical calculation of the scattering function for polymers of arbitrary flexibility using the Dirac propagator. Macromolecules 1993, 26, 4179–4183. [Google Scholar] [CrossRef]
- Bawendi, M.G.; Freed, K.F. A wiener integral model for stiff polymer chains. J. Chem. Phys. 1985, 83, 2491. [Google Scholar] [CrossRef]
- Ghosh, K.; Muthukumar, M. Scattering properties of a single semiflexible polyelectrolyte. J. Polym. Sci. Part B Polym. Phys. 2001, 39, 2644–2652. [Google Scholar] [CrossRef]
- Yoshizaki, T.; Yamakawa, H. Scattering functions of worm-like and helical worm-like chains. Macromolecules 1980, 13, 1518–1525. [Google Scholar] [CrossRef]
- Pedersen, J.S.; Schurtenberger, P. Scattering functions of semiflexible polymers with and without excluded volume effects. Macromolecules 1996, 29, 7602–7612. [Google Scholar] [CrossRef]
- FISH. Available online: http://www.diamond.ac.uk/Home/Beamlines/small-angle/SAXS-Software/CCP13/FISH/Models.html (accessed on 7 January 2003).
- SASFIT. Available online: http://sasfit.ingobressler.net/manual/KholodenkoWorm (accessed on 13 May 2011).
- Yamakawa, H. Worm-Like Chains in Polymer Solutions; Springer-Verla: New York, NY, USA, 1997. [Google Scholar]
- Stepanow, S.; Schütz, G.M. The distribution function of a semiflexible polymer and random walks with constraints. Europhys. Lett. 2002, 60, 546–551. [Google Scholar] [CrossRef]
- Stepanow, S. Statistical mechanics of semiflexible polymers. Eur. Phys. J. B 2004, 39, 499–512. [Google Scholar] [CrossRef]
- Spakowitz, A.J.; Wang, Z.-G. Exact results for a semiflexible polymer chain in an aligning field. Macromolecules 2004, 37, 5814–5823. [Google Scholar] [CrossRef]
- Mehraeen, S.; Sudhanshu, B.; Koslover, E.F.; Spakowitz, A.J. End-to-end distribution for a worm-like chain in arbitrary dimensions. Phys. Rev. E 2008, 77, 061803. [Google Scholar] [CrossRef] [PubMed]
- Tsubouchi, R.; Ida, D.; Yoshizaki, T.; Yamakawa, H. Scattering function of worm-like rings. Macromolecules 2014, 47, 1449–1454. [Google Scholar] [CrossRef]
- Zhang, X.H.; Jiang, Y.; Miao, B.; Chen, Y.L.; Yan, D.D.; Chen, J.Z.Y. The structure factor of a worm-like chain and the random-phase-approximation solution for the spinodal line of a diblock copolymer melt. Soft Matter 2014, 10, 5405–5416. [Google Scholar] [CrossRef] [PubMed]
- Deng, M.; Jiang, Y.; Liang, H.; Chen, J.Z.Y. Worm-like polymer brush: A self-consistent field treatment. Macromolecules 2010, 43, 3455–3464. [Google Scholar] [CrossRef]
- Fujii, M.; Yamakawa, H. Statistical mechanics of helical worm-like chains. III. Scattering functions. J. Chem. Phys. 1977, 66, 2578. [Google Scholar] [CrossRef]
- Maier, W.; Saupe, A. Eine einfache molekulare Theorie des nematischen kristallinflüssigen Zustandes. Z. Naturforsch. A 1958, 13, 564–566. [Google Scholar] [CrossRef]
- Maier, W.; Saupe, A. Eine einfache molekular-statistische Theorie der nematischen kristallinflüssigen Phase. Z. Naturforsch. A 1959, 14, 882–889. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, X.H.; Miao, B.; Yan, D.D. The study of the structure factor of a worm-like chain in an orientational external field. J. Chem. Phys. 2015, 142, 154901. [Google Scholar] [CrossRef] [PubMed]
- Benoit, H.; Hadziioannou, G. Scattering theory and properties of block copolymers with various architectures in the homogeneous bulk state. Macromolecules 1988, 21, 1449–1464. [Google Scholar] [CrossRef]
- Zhang, X.H.; Chen, Y.; Qu, L.J.; Yan, D.D. Effects of attractive colloids on the phase separation behaviors of binary polymer blends. J. Chem. Phys. 2013, 139, 074902. [Google Scholar] [CrossRef] [PubMed]
- Semenov, A.N.; Anastasiadis, S.H.; Boudenne, N.; Fytas, G.; Xenidou, M.; Hadjichristidis, N. Dynamic structure factor of diblock copolymers in the ordering regime. Macromolecules 1997, 30, 6280–6294. [Google Scholar] [CrossRef]
- Borsali, R.; Lecommandoux, S.; Pecora, R.; Benoit, H. Scattering Properties of rod-coil and once-broken rod block copolymers. Macromolecules 2001, 34, 4229–4234. [Google Scholar] [CrossRef]
- Matsen, M.W. Melts of semiflexible diblock copolymer. J. Chem. Phys. 1996, 104, 7758. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, W.Y.; Chen, J.Z.Y. Dependence of the disorder-lamellar stability boundary of a melt of asymmetric worm-like AB diblock copolymers on the chain rigidity. Phys. Rev. E 2011, 84, 041803. [Google Scholar] [CrossRef] [PubMed]
- Friedel, P.; John, A.; Pospiech, D.; Jehnichen, D.; Netz, R.R. Modelling of the phase separation behaviour of semiflexible diblock copolymers. Macromol. Theory Simul. 2002, 11, 785–793. [Google Scholar] [CrossRef]
- Tang, J.Z.; Jiang, Y.; Zhang, X.H.; Yan, D.D.; Chen, J.Z.Y. Phase diagram of rod-coil diblock copolymer melts. Macromolecules 2015, 48, 9060–9070. [Google Scholar] [CrossRef]
- Matsen, M.W. Self-consistent field theory for melts of low-molecular-weight diblock copolymer. Macromolecules 2012, 45, 8502–8509. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, X.H.; Miao, B.; Yan, D.D.; Chen, J.Z.Y. Microphase separation of short worm-like diblock copolymers with finite interaction range. Soft Matter 2016, 12, 2481–2490. [Google Scholar] [CrossRef] [PubMed]


| 1 | 1 | 5.33 | 5.53 | |
| 0.0625 | 0 | 3.95 |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bu, X.; Zhang, X. Scattering and Gaussian Fluctuation Theory for Semiflexible Polymers. Polymers 2016, 8, 301. https://doi.org/10.3390/polym8090301
Bu X, Zhang X. Scattering and Gaussian Fluctuation Theory for Semiflexible Polymers. Polymers. 2016; 8(9):301. https://doi.org/10.3390/polym8090301
Chicago/Turabian StyleBu, Xiangyu, and Xinghua Zhang. 2016. "Scattering and Gaussian Fluctuation Theory for Semiflexible Polymers" Polymers 8, no. 9: 301. https://doi.org/10.3390/polym8090301






