Semiflexible Biopolymers in Bundled Arrangements
Abstract
:1. Introduction
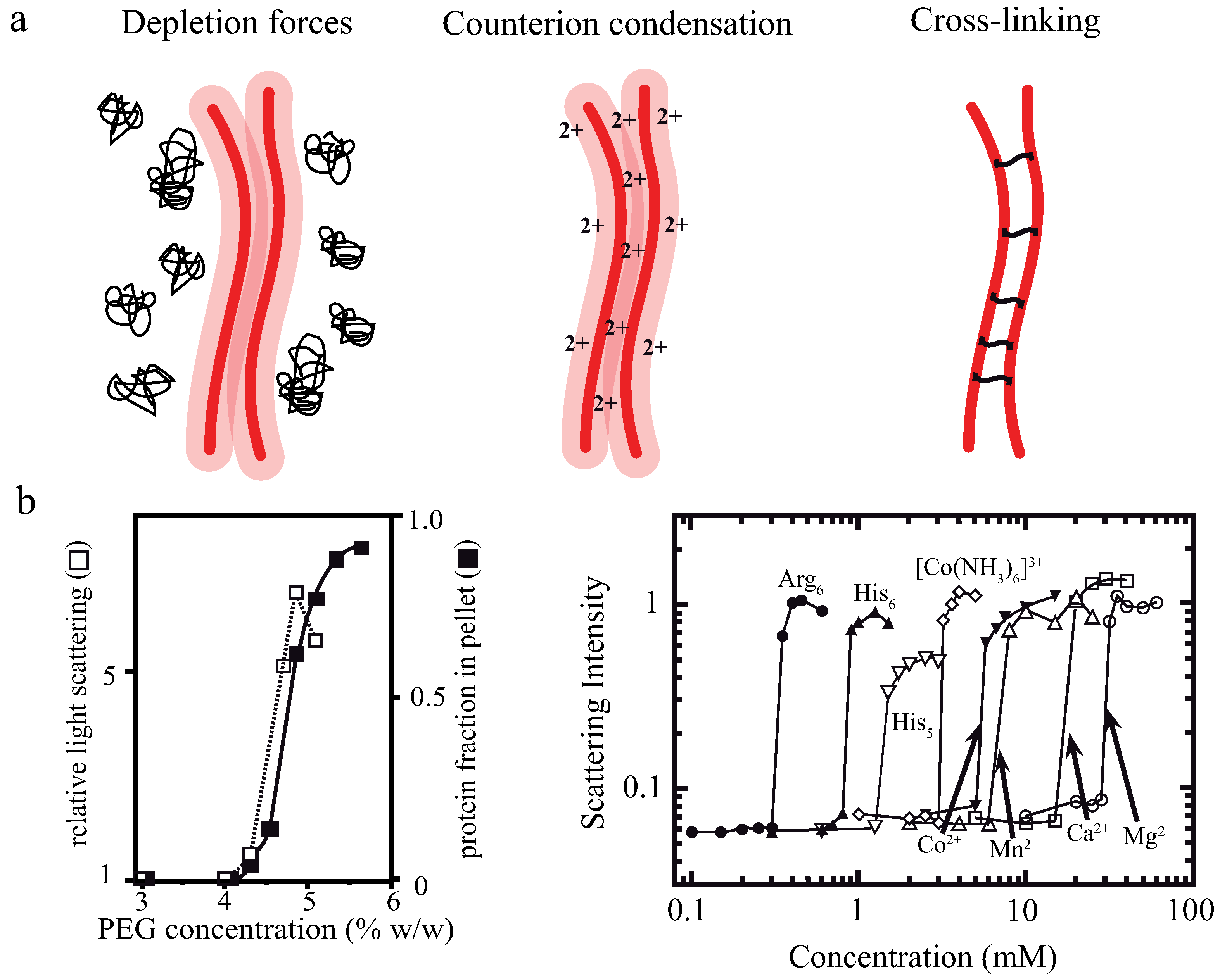
2. Bundle Formation
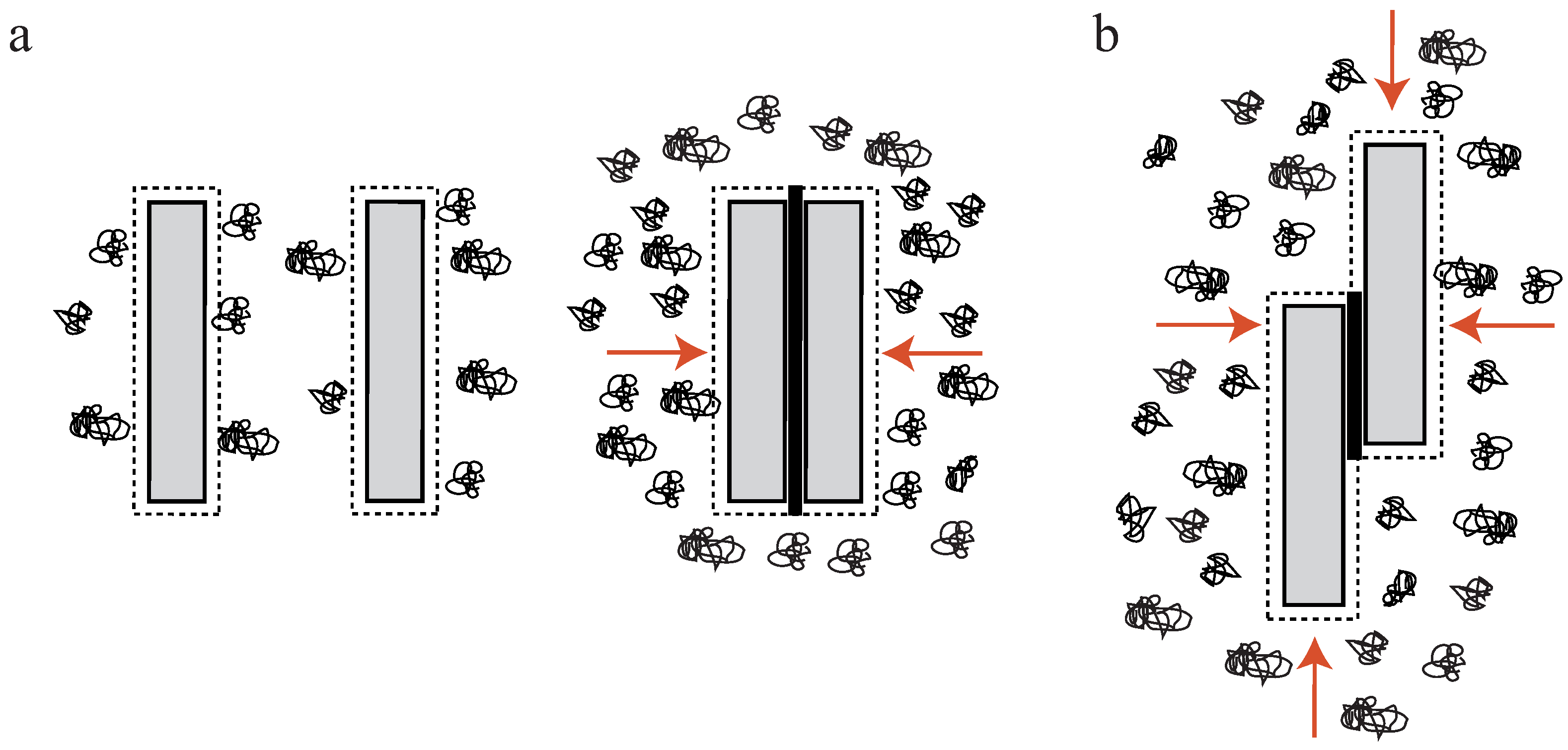
2.1. Depletion Interaction
2.2. Counterion Condensation
2.3. Crosslinkers
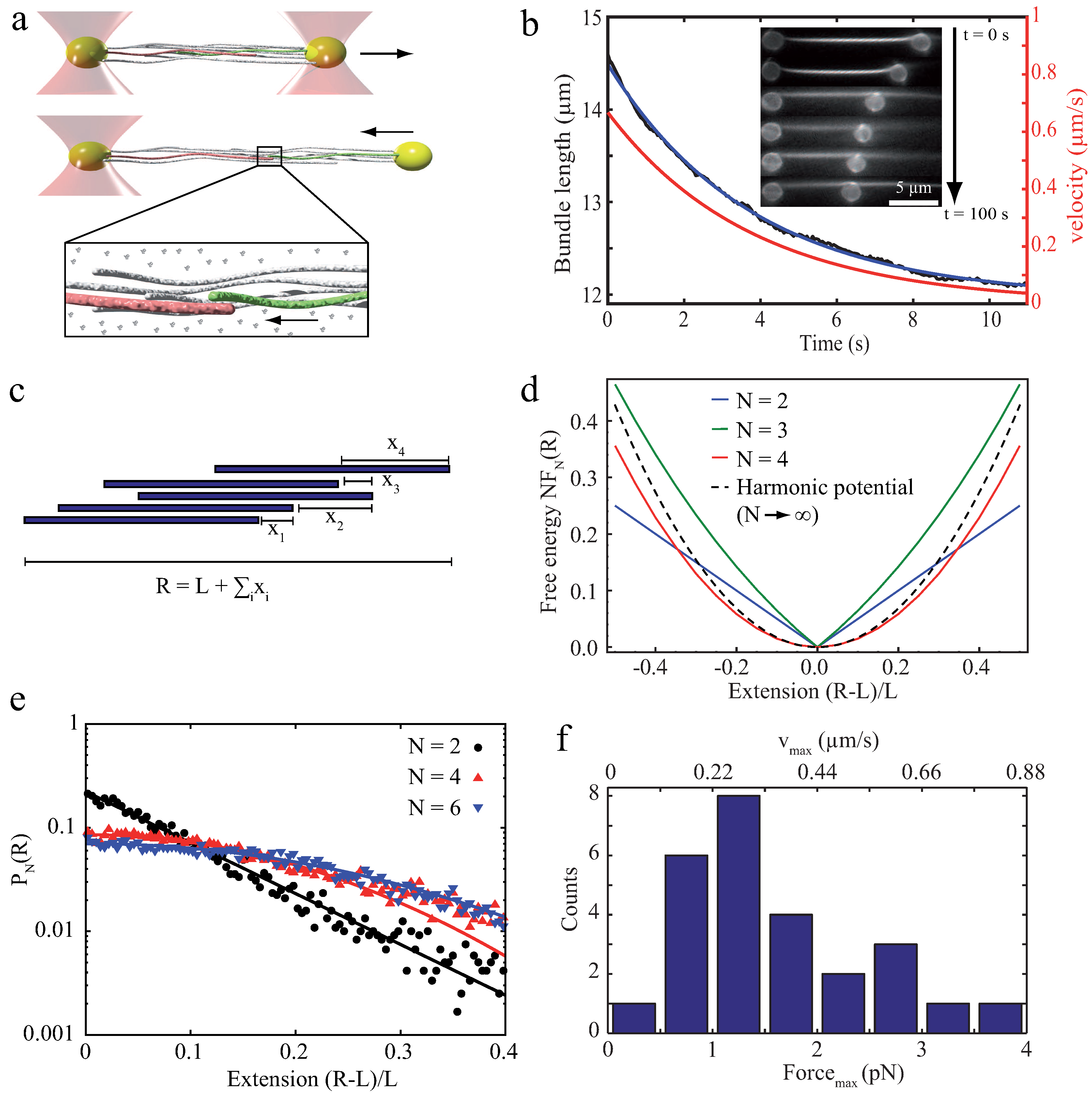
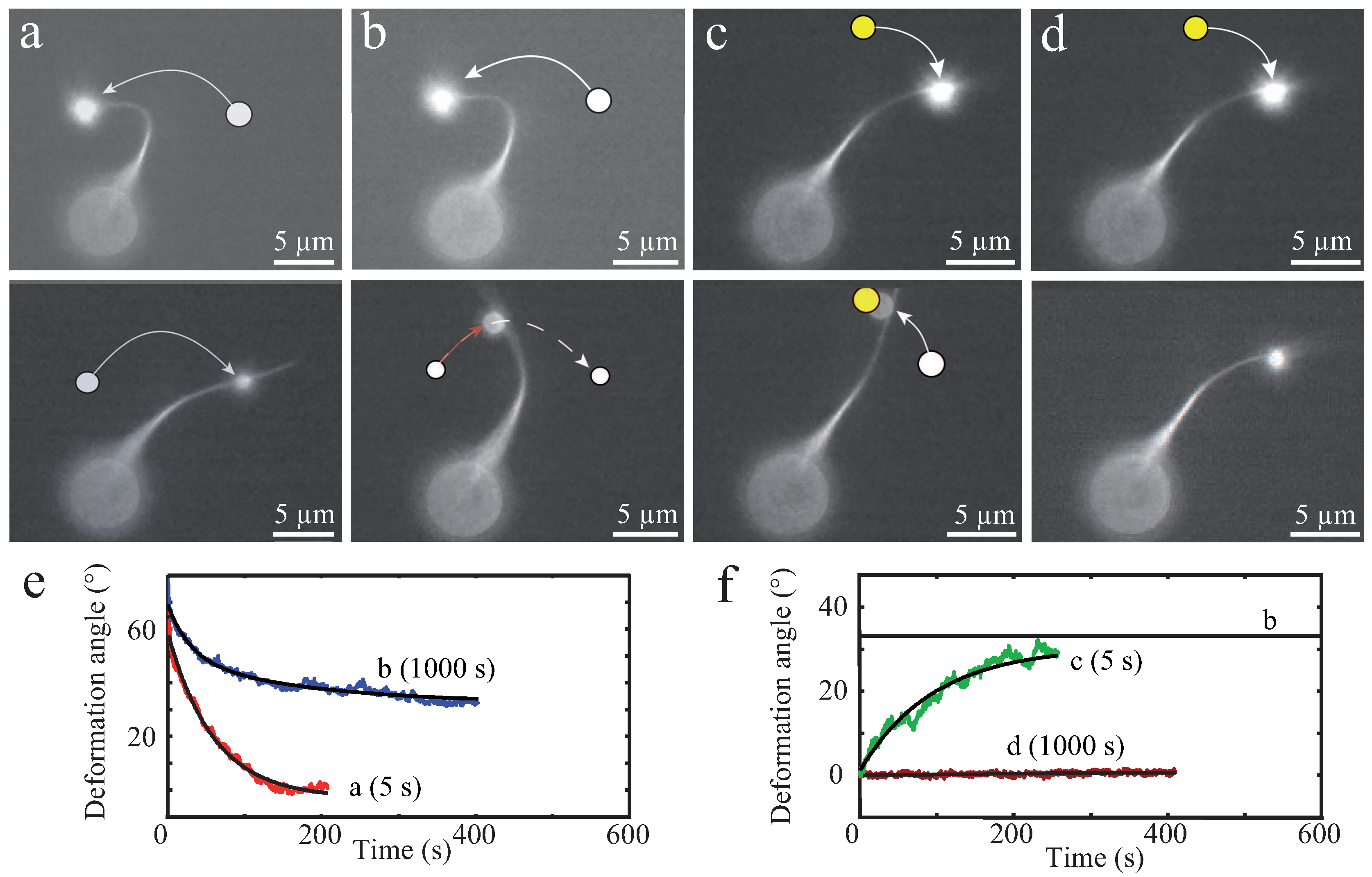
3. Dynamics in Uncrosslinked Bundles—Contractions Without Molecular Motors
4. Mechanical Properties of Bundles
4.1. Worm-Like Chain Model
4.2. Worm-Like Bundle Model
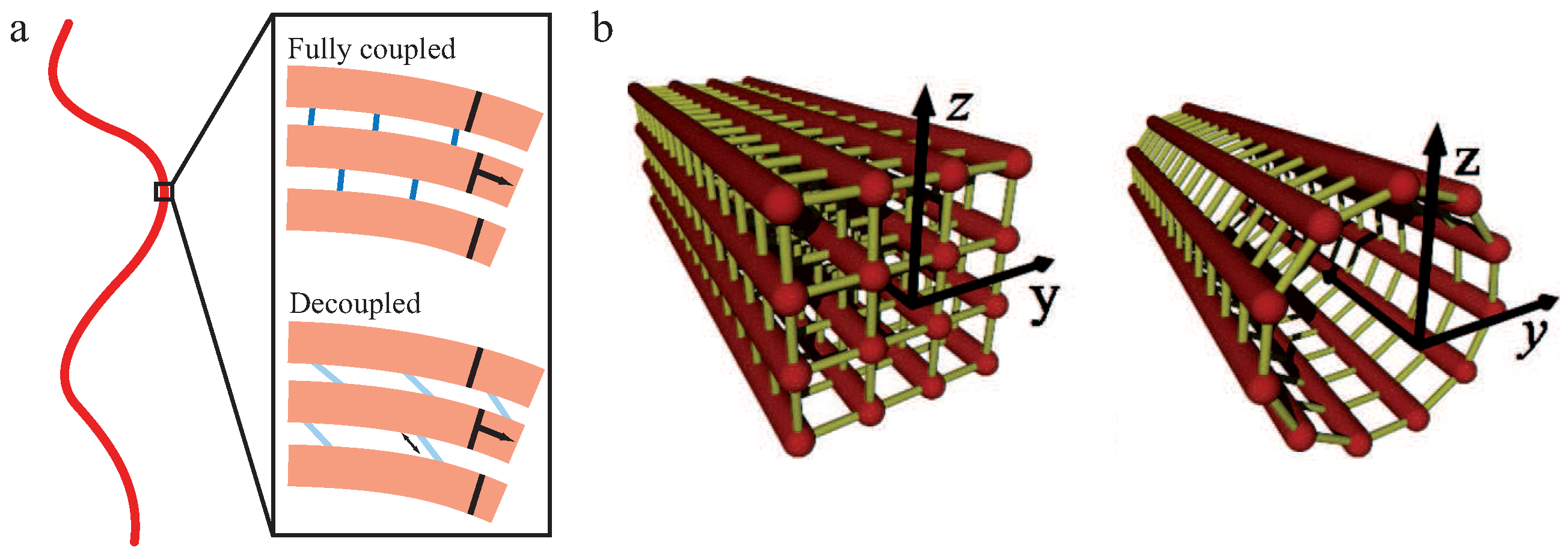
5. Transient Crosslinkers
5.1. Tunable Mechanical Responses of Transiently Crosslinked Actin Bundles
5.2. Unbundling/Rebundling of Crosslinked Bundles
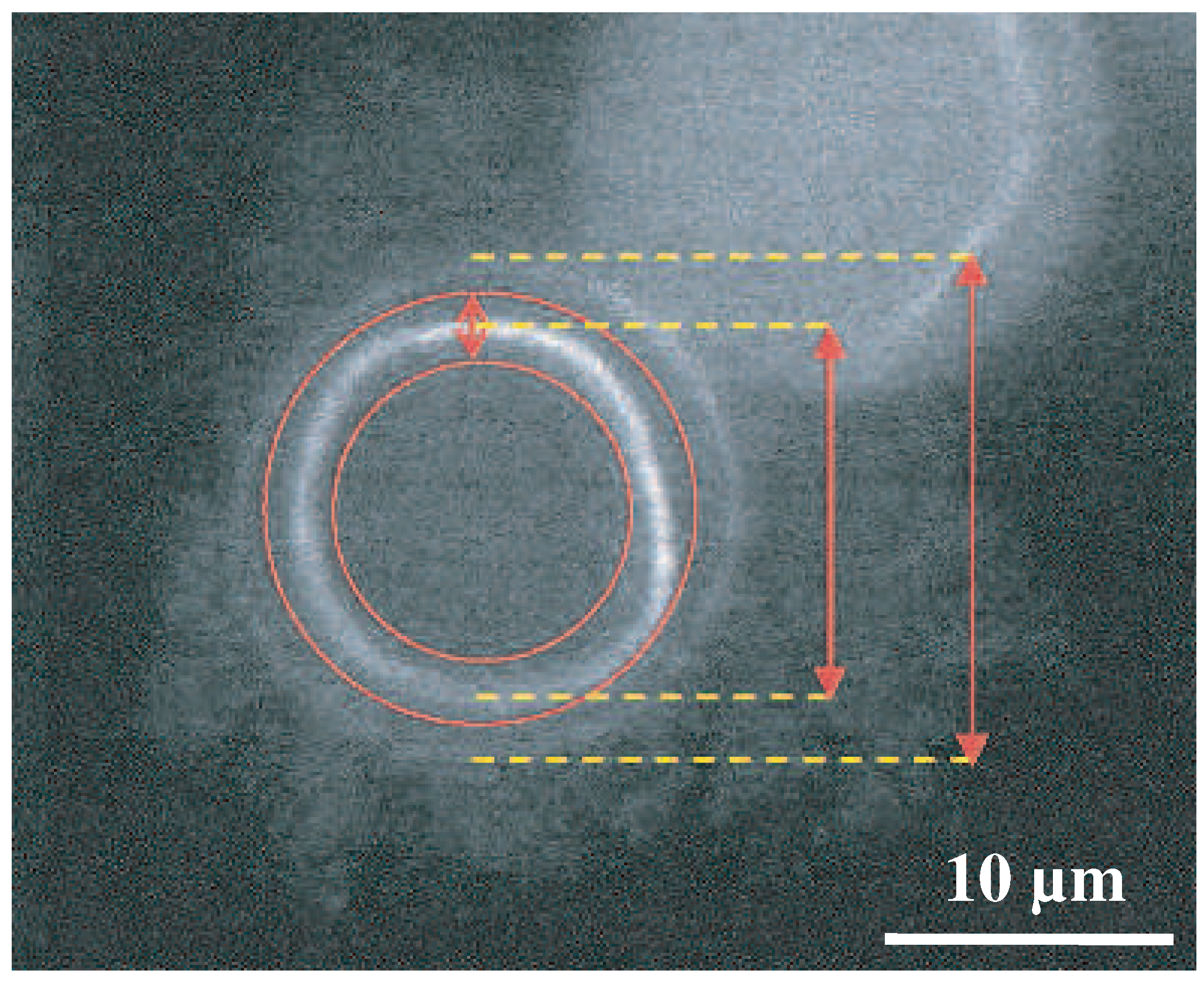
6. Finite Bundle Size
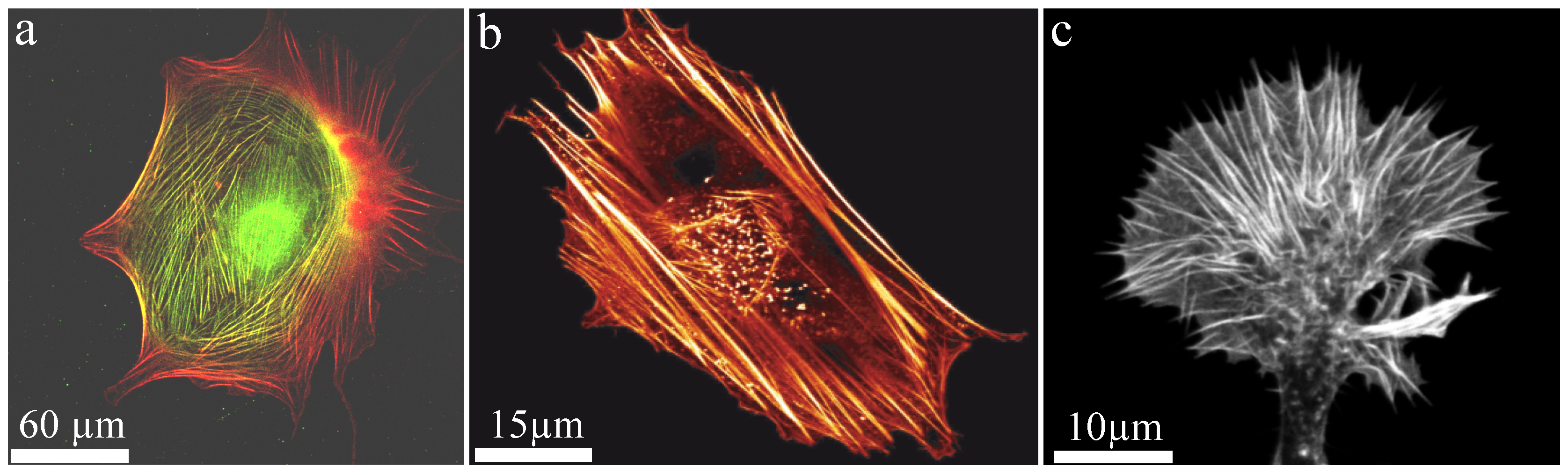
7. Bundles in Biological Systems
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| WLC | Worm-like chain |
| WLB | Worm-like bundle |
| PEG | Polyethylene glycol |
| Bending stiffness | |
| Persistence length |
References
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics (International Series of Monographs on Physics); Clarendon Press: Oxford, UK, 1988; Volume 73. [Google Scholar]
- Huber, F.; Schnauß, J.; Rönicke, S.; Rauch, P.; Müller, K.; Fütterer, C.; Käs, J. Emergent complexity of the cytoskeleton: From single filaments to tissue. Adv. Phys. 2013, 62, 1–112. [Google Scholar] [CrossRef] [PubMed]
- MacKintosh, F.; Käs, J.; Janmey, P. Elasticity of Semiflexible Biopolymer Networks. Phys. Rev. Lett. 1995, 75, 4425–4428. [Google Scholar] [CrossRef] [PubMed]
- Morse, D.C. Viscoelasticity of Concentrated Isotropic Solutions of Semiflexible Polymers. 2. Linear Response. Macromolecules 1998, 31, 7044–7067. [Google Scholar] [CrossRef]
- Morse, D. Tube diameter in tightly entangled solutions of semiflexible polymers. Phys. Rev. E 2001, 63. [Google Scholar] [CrossRef] [PubMed]
- Gardel, M.L.; Valentine, M.T.; Crocker, J.C.; Bausch, A.R.; Weitz, D.A. Microrheology of Entangled F-Actin Solutions. Phys. Rev. Lett. 2003, 91. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, D.A.; Mullins, R.D. Cell mechanics and the cytoskeleton. Nature 2010, 463, 485–492. [Google Scholar] [CrossRef] [PubMed]
- Broedersz, C.; MacKintosh, F. Modeling semiflexible polymer networks. Rev. Mod. Phys. 2014, 86, 995–1036. [Google Scholar] [CrossRef]
- Golde, T.; Schuldt, C.; Schnauß, J.; Strehle, D.; Glaser, M.; Käs, J. Fluorescent beads disintegrate actin networks. Phys. Rev. E 2013, 88. [Google Scholar] [CrossRef] [PubMed]
- Lieleg, O.; Claessens, M.M.A.E.; Heussinger, C.; Frey, E.; Bausch, A.R. Mechanics of Bundled Semiflexible Polymer Networks. Phys. Rev. Lett. 2007, 99. [Google Scholar] [CrossRef] [PubMed]
- Müller, K.W.; Bruinsma, R.F.; Lieleg, O.; Bausch, A.R.; Wall, W.A.; Levine, A.J. Rheology of Semiflexible Bundle Networks with Transient Linkers. Phys. Rev. Lett. 2014, 112. [Google Scholar] [CrossRef] [PubMed]
- Broedersz, C.P.; Depken, M.; Yao, N.Y.; Pollak, M.R.; Weitz, D.A.; MacKintosh, F.C. Cross-Link-Governed Dynamics of Biopolymer Networks. Phys. Rev. Lett. 2010, 105. [Google Scholar] [CrossRef] [PubMed]
- Claessens, M.; Bathe, M.; Frey, E.; Bausch, A.R. Actin-binding proteins sensitively meditate F-actin bundle stiffness. Nat. Mater. 2006, 5, 748–753. [Google Scholar] [CrossRef] [PubMed]
- Lai, G.H.; Coridan, R.; Zribi, O.V.; Golestanian, R.; Wong, G.C.L. Evolution of Growth Modes for Polyelectrolyte Bundles. Phys. Rev. Lett. 2007, 98. [Google Scholar] [CrossRef] [PubMed]
- Claessens, M.M.A.E.; Semmrich, C.; Ramos, L.; Bausch, A.R. Helical twist controls the thickness of F-actin bundles. Proc. Natl. Acad. Sci. USA 2008, 105, 8819–8822. [Google Scholar] [CrossRef] [PubMed]
- Strehle, D.; Schnauß, J.; Heussinger, C.; Alvarado, J.; Bathe, M.; Käs, J.; Gentry, B. Transiently crosslinked F-actin bundles. Eur. Biophys. J. 2011, 40, 93–101. [Google Scholar] [CrossRef] [PubMed]
- Schnauß, J.; Golde, T.; Schuldt, C.; Schmidt, B.S.; Glaser, M.; Strehle, D.; Händler, T.; Heussinger, C.; Käs, J.A. Transition from a Linear to a Harmonic Potential in Collective Dynamics of a Multifilament Actin Bundle. Phys. Rev. Lett. 2016, 116. [Google Scholar] [CrossRef] [PubMed]
- Shao, Z.; Shi, D.; Somlyo, A.V. Cryoatomic force microscopy of filamentous actin. Biophys. J. 2000, 78, 950–958. [Google Scholar] [CrossRef]
- Yang, L.; van der Werf, K.O.; Koopman, B.F.; Subramaniam, V.; Bennink, M.L.; Dijkstra, P.J.; Feijen, J. Micromechanical bending of single collagen fibrils using atomic force microscopy. J. Biomed. Mater. Res. Part A 2007, 82, 160–168. [Google Scholar] [CrossRef] [PubMed]
- Ikawa, T.; Hoshino, F.; Watanabe, O.; Li, Y.; Pincus, P.; Safinya, C.R. Molecular Scale Imaging of F-Actin Assemblies Immobilized on a Photopolymer Surface. Phys. Rev. Lett. 2007, 98. [Google Scholar] [CrossRef] [PubMed]
- Gilmore, J.L.; Kumeta, M.; Takeyasu, K. AFM Investigation of the Organization of Actin Bundles Formed by Actin-Binding Proteins. J. Surf. Eng. Mater. Adv. Technol. 2013, 3, 13–19. [Google Scholar] [CrossRef]
- Suzuki, A.; Yamazaki, M.; Ito, T. Polymorphism of F-actin assembly. 1. A quantitative phase diagram of F-actin. Biochemistry 1996, 35, 5238–5244. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.X.; Janmey, P.A. The Polyelectrolyte Nature of F-actin and the Mechanism of Actin Bundle Formation. J. Biol. Chem. 1996, 271, 8556–8563. [Google Scholar] [CrossRef] [PubMed]
- Schmid, M.F.; Agris, J.M.; Jakana, J.; Matsudaira, P.; Chiu, W. Three-dimensional structure of a single filament in the Limulus acrosomal bundle: Scruin binds to homologous helix-loop-beta motifs in actin. J. Cell Biol. 1994, 124, 341–350. [Google Scholar] [CrossRef] [PubMed]
- Haviv, L.; Gov, N.; Ideses, Y.; Bernheim-Groswasser, A. Thickness distribution of actin bundles in vitro. Eur. Biophys. J. 2007, 37, 447–454. [Google Scholar] [CrossRef] [PubMed]
- Nolting, J.F.; Möbius, W.; Köster, S. Mechanics of Individual Keratin Bundles in Living Cells. Biophys. J. 2014, 107, 2693–2699. [Google Scholar] [CrossRef] [PubMed]
- Shin, H.; Drew, K.R.P.; Bartles, J.R.; Wong, G.C.L.; Grason, G.M. Cooperativity and Frustration in Protein-Mediated Parallel Actin Bundles. Phys. Rev. Lett. 2009, 103. [Google Scholar] [CrossRef] [PubMed]
- Hémonnot, C.Y.J.; Reinhardt, J.; Saldanha, O.; Patommel, J.; Graceffa, R.; Weinhausen, B.; Burghammer, M.; Schroer, C.G.; Köster, S. X-rays Reveal the Internal Structure of Keratin Bundles in Whole Cells. ACS Nano 2016, 10, 3553–3561. [Google Scholar] [CrossRef] [PubMed]
- Heussinger, C.; Bathe, M.; Frey, E. Statistical mechanics of semiflexible bundles of wormlike polymer chains. Phys. Rev. Lett. 2007, 99. [Google Scholar] [CrossRef] [PubMed]
- Bathe, M.; Heussinger, C.; Claessens, M.M.A.E.; Bausch, A.R.; Frey, E. Cytoskeletal bundle mechanics. Biophys. J. 2008, 94, 2955–2964. [Google Scholar] [CrossRef] [PubMed]
- Benetatos, P.; Jho, Y. Bundling in semiflexible polymers: A theoretical overview. Adv. Colloid Interface Sci. 2016, 232, 114–126. [Google Scholar] [CrossRef] [PubMed]
- Heintzelman, M.B.; Mooseker, M.S. Assembly of the intestinal brush border cytoskeleton. Curr. Top. Dev. Biol. 1992, 26, 93–122. [Google Scholar] [PubMed]
- Bartles, J.R.; Zheng, L.; Li, A.; Wierda, A.; Chen, B. Small espin: A third actin-bundling protein and potential forked protein ortholog in brush border microvilli. J. Cell Biol. 1998, 143, 107–119. [Google Scholar] [CrossRef] [PubMed]
- Asakura, S.; Oosawa, F. On Interaction between Two Bodies Immersed in a Solution of Macromolecules. J. Chem. Phys. 1954, 22, 1255–1256. [Google Scholar]
- Asakura, S.; Oosawa, F. Interaction between particles suspended in solutions of macromolecules. J. Polym. Sci. 1958, 33, 183–192. [Google Scholar] [CrossRef]
- Hosek, M.; Tang, J.X. Polymer-induced bundling of F actin and the depletion force. Phys. Rev. E 2004, 69. [Google Scholar] [CrossRef] [PubMed]
- Kinoshita, M. Interaction between big bodies with high asphericity immersed in small spheres. Chem. Phys. Lett. 2004, 387, 47–53. [Google Scholar] [CrossRef]
- Galanis, J.; Nossal, R.; Harries, D. Depletion forces drive polymer-like self-assembly in vibrofluidized granular materials. Soft Matter 2010, 6, 1026–1034. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Ma, H.R. Depletion interactions between two spherocylinders. Eur. Phys. J. E Soft Matter 2005, 16, 225–231. [Google Scholar] [CrossRef] [PubMed]
- Hilitski, F.; Ward, A.R.; Cajamarca, L.; Hagan, M.F.; Grason, G.M.; Dogic, Z. Measuring Cohesion between Macromolecular Filaments One Pair at a Time: Depletion-Induced Microtubule Bundling. Phys. Rev. Lett. 2015, 114. [Google Scholar] [CrossRef] [PubMed]
- Ward, A.; Hilitski, F.; Schwenger, W.; Welch, D.; Lau, A.W.C.; Vitelli, V.; Mahadevan, L.; Dogic, Z. Solid friction between soft filaments. Nat. Mater. 2015, 14, 583–588. [Google Scholar] [CrossRef] [PubMed]
- Ellis, R. Macromolecular crowding: Obvious but underappreciated. Trends Biochem. Sci. 2001, 26, 597–604. [Google Scholar] [CrossRef]
- Janmey, P.A.; Slochower, D.R.; Wang, Y.H.; Wen, Q.; Cebers, A. Polyelectrolyte properties of filamentous biopolymers and their consequences in biological fluids. Soft Matter 2014, 10, 1439–1449. [Google Scholar] [CrossRef] [PubMed]
- Ray, J.; Manning, G.S. An attractive force between two rodlike polyions mediated by the sharing of condensed counterions. Langmuir 1994, 10, 2450–2461. [Google Scholar] [CrossRef]
- Grønbech-Jensen, N.; Mashl, R.J.; Bruinsma, R.F.; Gelbart, W.M. Counterion-Induced Attraction between Rigid Polyelectrolytes. Phys. Rev. Lett. 1997, 78, 2477–2480. [Google Scholar] [CrossRef]
- Ha, B.Y.; Liu, A.J. Counterion-Mediated Attraction between Two Like-Charged Rods. Phys. Rev. Lett. 1997, 79, 1289–1292. [Google Scholar] [CrossRef]
- Ha, B.Y.; Liu, A.J. Effect of Non-Pairwise-Additive Interactions on Bundles of Rodlike Polyelectrolytes. Phys. Rev. Lett. 1998, 81, 1011–1014. [Google Scholar] [CrossRef]
- Podgornik, R.; Parsegian, V.A. Charge-Fluctuation Forces between Rodlike Polyelectrolytes: Pairwise Summability Reexamined. Phys. Rev. Lett. 1998, 80, 1560–1563. [Google Scholar] [CrossRef]
- Barrat, J.L.; Joanny, J.F. Persistence Length of Polyelectrolyte Chains. EPL (Europhys. Lett.) 1993, 24, 333. [Google Scholar] [CrossRef]
- Ha, B.Y.; Thirumalai, D. Electrostatic Persistence Length of a Polyelectrolyte Chain. Macromolecules 1995, 28, 577–581. [Google Scholar] [CrossRef]
- Dobrynin, A.V. Electrostatic Persistence Length of Semiflexible and Flexible Polyelectrolytes. Macromolecules 2005, 38, 9304–9314. [Google Scholar] [CrossRef]
- Shklovskii, B.I. Wigner Crystal Model of Counterion Induced Bundle Formation of Rodlike Polyelectrolytes. Phys. Rev. Lett. 1999, 82, 3268–3271. [Google Scholar] [CrossRef]
- Manning, G.S. Limiting Laws and Counterion Condensation in Polyelectrolyte Solutions. III. An Analysis Based on the Mayer Ionic Solution Theory. J. Chem. Phys. 1969, 51, 3249–3252. [Google Scholar] [CrossRef]
- Stevens, M.J. Bundle Binding in Polyelectrolyte Solutions. Phys. Rev. Lett. 1999, 82, 101–104. [Google Scholar] [CrossRef]
- Lee, K.C.; Borukhov, I.; Gelbart, W.M.; Liu, A.J.; Stevens, M.J. Effect of Mono- and Multivalent Salts on Angle-Dependent Attractions between Charged Rods. Phys. Rev. Lett. 2004, 93. [Google Scholar] [CrossRef] [PubMed]
- Fazli, H.; Mohammadinejad, S.; Golestanian, R. Salt-induced aggregation of stiff polyelectrolytes. J. Phys. Condens. Matter 2009, 21. [Google Scholar] [CrossRef] [PubMed]
- Mohammadinejad, S.; Golestanian, R.; Fazli, H. Chiral structure of F-actin bundle formed by multivalent counterions. Soft Matter 2012, 8, 3649–3656. [Google Scholar] [CrossRef]
- Kierfeld, J.; Lipowsky, R. Unbundling and desorption of semiflexible polymers. EPL (Europhys. Lett.) 2003, 62, 285–291. [Google Scholar] [CrossRef]
- Benetatos, P.; Zippelius, A. Anisotropic Random Networks of Semiflexible Polymers. Phys. Rev. Lett. 2007, 99. [Google Scholar] [CrossRef] [PubMed]
- Kiemes, M.; Benetatos, P.; Zippelius, A. Orientational order and glassy states in networks of semiflexible polymers. Phys. Rev. E 2011, 83. [Google Scholar] [CrossRef] [PubMed]
- Ulrich, S.; Zippelius, A.; Benetatos, P. Random networks of cross-linked directed polymers. Phys. Rev. E 2010, 81. [Google Scholar] [CrossRef] [PubMed]
- Benetatos, P.; Ulrich, S.; Zippelius, A. Force-extension relation of cross-linked anisotropic polymer networks. New J. Phys. 2012, 14. [Google Scholar] [CrossRef]
- Zilman, A.G.; Safran, S.A. Role of cross-links in bundle formation, phase separation and gelation of long filaments. EPL (Europhys. Lett.) 2003, 63, 139–145. [Google Scholar] [CrossRef]
- Borukhov, I.; Bruinsma, R.F.; Gelbart, W.M.; Liu, A.J. Structural polymorphism of the cytoskeleton: A model of linker-assisted filament aggregation. Proc. Natl. Acad. Sci. USA 2005, 102, 3673–3678. [Google Scholar] [CrossRef] [PubMed]
- Kierfeld, J.; Kühne, T.; Lipowsky, R. Discontinuous Unbinding Transitions of Filament Bundles. Phys. Rev. Lett. 2005, 95. [Google Scholar] [CrossRef] [PubMed]
- Shin, H.; Grason, G.M. Structural reorganization of parallel actin bundles by crosslinking proteins: Incommensurate states of twist. Phys. Rev. E 2010, 82. [Google Scholar] [CrossRef] [PubMed]
- Dutta, S.; Benetatos, P.; Jho, Y.S. Bundle formation in parallel aligned polymers with competing interactions. EPL (Europhys. Lett.) 2016, 114. [Google Scholar] [CrossRef]
- Benetatos, P.; Terentjev, E.M.; Zippelius, A. Bundling in brushes of directed and semiflexible polymers. Phys. Rev. E 2013, 88. [Google Scholar] [CrossRef] [PubMed]
- Braun, M.; Lansky, Z.; Hilitski, F.; Dogic, Z.; Diez, S. Entropic forces drive contraction of cytoskeletal networks. Bioessays 2016, 38, 474–481. [Google Scholar] [CrossRef] [PubMed]
- Kroy, K.; Frey, E. Force-Extension Relation and Plateau Modulus for Wormlike Chains. Phys. Rev. Lett. 1996, 77, 306–309. [Google Scholar] [CrossRef] [PubMed]
- Heussinger, C.; Schüller, F.; Frey, E. Statics and dynamics of the wormlike bundle model. Phys. Rev. E 2010, 81. [Google Scholar] [CrossRef] [PubMed]
- Howard, J.; Ashmore, J.F. Stiffness of sensory hair bundles in the sacculus of the frog. Hear. Res. 1986, 23, 93–104. [Google Scholar] [CrossRef]
- Pampaloni, F.; Lattanzi, G.; Jonáš, A.; Surrey, T.; Frey, E.; Florin, E.L. Thermal fluctuations of grafted microtubules provide evidence of a length-dependent persistence length. Proc. Natl. Acad. Sci. USA 2006, 103, 10248–10253. [Google Scholar] [CrossRef] [PubMed]
- Everaers, R.; Bundschuh, R.; Kremer, K. Fluctuations and Stiffness of Double-Stranded Polymers: Railway-Track Model. EPL (Europhys. Lett.) 1995, 29, 263–268. [Google Scholar] [CrossRef]
- Taute, K.M.; Pampaloni, F.; Frey, E.; Florin, E.L. Microtubule Dynamics Depart from the Wormlike Chain Model. Phys. Rev. Lett. 2008, 100. [Google Scholar] [CrossRef] [PubMed]
- Von der Heydt, A.; Wilkin, D.; Benetatos, P.; Zippelius, A. Elasticity of cross-linked semiflexible biopolymers under tension. Phys. Rev. E 2013, 88. [Google Scholar] [CrossRef] [PubMed]
- Ylänne, J.; Scheffzek, K.; Young, P.; Saraste, M. Crystal Structure of the alpha-Actinin Rod Reveals an Extensive Torsional Twist. Structure 2001, 9, 597–604. [Google Scholar] [CrossRef]
- Aratyn, Y.; Schaus, T.; Taylor, E.; Borisy, G. Intrinsic dynamic behavior of fascin in filopodia. Mol. Biol. Cell 2007, 18, 3928–3940. [Google Scholar] [CrossRef] [PubMed]
- Lansky, Z.; Braun, M.; Lüdecke, A.; Schlierf, M.; ten Wolde, P.R.; Janson, M.E.; Diez, S. Diffusible Crosslinkers Generate Directed Forces in Microtubule Networks. Cell 2015, 160, 1159–1168. [Google Scholar] [CrossRef] [PubMed]
- Schnauß, J.; Glaser, M.; Schuldt, C.; Golde, T.; Händler, T.; Schmidt, B.U.S.; Diez, S.; Käs, J.A. Motor-free force generation in biological systems. Diffus. Fundam. 2015, 23, 1–15. [Google Scholar]
- Benetatos, P.; von der Heydt, A.; Zippelius, A. Tension-induced binding of semiflexible biopolymers. New J. Phys. 2014, 16. [Google Scholar] [CrossRef]
- Heussinger, C. Cooperative crosslink (un)binding in slowly driven bundles of semiflexible filaments. Phys. Rev. E 2011, 83. [Google Scholar] [CrossRef] [PubMed]
- Vink, R.L.C.; Heussinger, C. Cross-linked biopolymer bundles: Cross-link reversibility leads to cooperative binding/unbinding phenomena. J. Chem. Phys. 2012, 136. [Google Scholar] [CrossRef] [PubMed]
- Sadhukhan, P.; Schumann, O.; Heussinger, C. Elasto-plastic response of reversibly crosslinked biopolymer bundles. Eur. Phys. J. E 2014, 37, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Ha, B.Y.; Liu, A.J. Kinetics of bundle growth in DNA condensation. EPL (Europhys. Lett.) 1999, 46, 624–630. [Google Scholar] [CrossRef]
- Henle, M.L.; Pincus, P.A. Equilibrium bundle size of rodlike polyelectrolytes with counterion-induced attractive interactions. Phys. Rev. E 2005, 71. [Google Scholar] [CrossRef] [PubMed]
- Gov, N.S. Packing defects and the width of biopolymer bundles. Phys. Rev. E 2008, 78. [Google Scholar] [CrossRef] [PubMed]
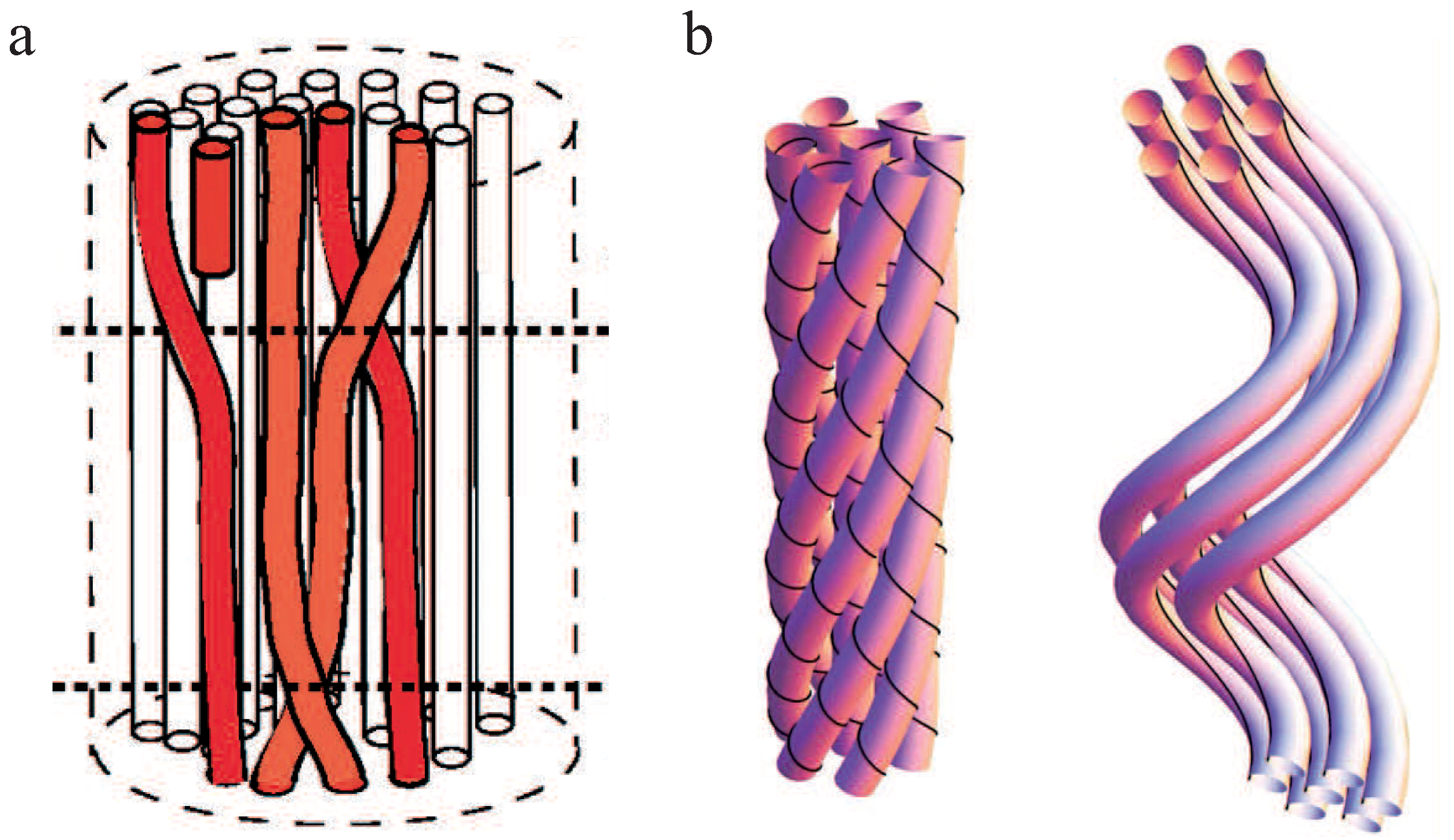
- Grason, G.M.; Bruinsma, R.F. Chirality and Equilibrium Biopolymer Bundles. Phys. Rev. Lett. 2007, 99. [Google Scholar] [CrossRef] [PubMed]
- Grason, G.M. Braided bundles and compact coils: The structure and thermodynamics of hexagonally packed chiral filament assemblies. Phys. Rev. E 2009, 79. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Meyer, R.B.; Hagan, M.F. Self-Limited Self-Assembly of Chiral Filaments. Phys. Rev. Lett. 2010, 104. [Google Scholar] [CrossRef] [PubMed]
- Heussinger, C.; Grason, G.M. Theory of crosslinked bundles of helical filaments: Intrinsic torques in self-limiting biopolymer assemblies. J. Chem. Phys. 2011, 135. [Google Scholar] [CrossRef] [PubMed]
- Romero, S.; Le Clainche, C.; Didry, D.; Egile, C.; Pantaloni, D.; Carlier, M.F. Formin is a processive motor that requires profilin to accelerate actin assembly and associated ATP hydrolysis. Cell 2004, 119, 419–429. [Google Scholar] [CrossRef] [PubMed]
- Kovar, D.R.; Pollard, T.D. Insertional assembly of actin filament barbed ends in association with formins produces piconewton forces. Proc. Natl. Acad. Sci. USA 2004, 101, 14725–14730. [Google Scholar] [CrossRef] [PubMed]
- Krause, W.J. Krause’s Essential Human Histology for Medical Students; Universal Publishers: Boca Raton, FL, USA, 2005. [Google Scholar]
- Tilney, M.S.; Tilney, L.G.; Stephens, R.E.; Merte, C.; Drenckhahn, D.; Cotanche, D.A.; Bretscher, A. Preliminary biochemical characterization of the stereocilia and cuticular plate of hair cells of the chick cochlea. J. Cell Biol. 1989, 109, 1711–1723. [Google Scholar] [CrossRef] [PubMed]
- Tilney, L.G.; Tilney, M.S.; DeRosier, D.J. Actin filaments, stereocilia, and hair cells: How cells count and measure. Ann. Rev. Cell Dev. Biol. 1992, 8, 257–274. [Google Scholar] [CrossRef] [PubMed]
- Bartles, J.R. Parallel actin bundles and their multiple actin-bundling proteins. Curr. Opin. Cell Biol. 2000, 12, 72–78. [Google Scholar] [CrossRef]
- Pickles, J.O. An Introduction to the Physiology of Hearing; Emerald Group Publishing: Bingley, UK, 2012. [Google Scholar]
- Roberts, W.M.; Howard, J.; Hudspeth, A.J. Hair cells: Transduction, tuning, and transmission in the inner ear. Ann. Rev. Cell Dev. Biol. 1988, 4, 63–92. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Wirtz, D.; Pollard, T.D. Dynamic cross-linking by alpha-actinin determines the mechanical properties of actin filament networks. J. Biol. Chem. 1998, 273, 9570–9576. [Google Scholar] [CrossRef] [PubMed]
- Fabry, B.; Maksym, G.; Butler, J.; Glogauer, M.; Navajas, D.; Fredberg, J. Scaling the Microrheology of Living Cells. Phys. Rev. Lett. 2001, 87. [Google Scholar] [CrossRef] [PubMed]
- Vignjevic, D.; Kojima, S.; Aratyn, Y.; Danciu, O.; Svitkina, T.; Borisy, G.G. Role of fascin in filopodial protrusion. J. Cell Biol. 2006, 174, 863–875. [Google Scholar] [CrossRef] [PubMed]
- Yamakita, Y.; Ono, S.; Matsumura, F.; Yamashiro, S. Phosphorylation of human fascin inhibits its actin binding and bundling activities. J. Biol. Chem. 1996, 271, 12632–12638. [Google Scholar] [CrossRef] [PubMed]
- Ono, S.; Yamakita, Y.; Yamashiro, S.; Matsudaira, P.T.; Gnarra, J.R.; Obinata, T.; Matsumura, F. Identification of an actin binding region and a protein kinase C phosphorylation site on human fascin. J. Biol. Chem. 1997, 272, 2527–2533. [Google Scholar] [PubMed]
- Romero, S.; Quatela, A.; Bornschlogl, T.; Guadagnini, S.; Bassereau, P.; Tran van Nhieu, G. Filopodium retraction is controlled by adhesion to its tip. J. Cell Sci. 2012, 125, 4999–5004. [Google Scholar] [CrossRef] [PubMed]
- Gentleman, E.; Lay, A.N.; Dickerson, D.A.; Nauman, E.A.; Livesay, G.A.; Dee, K.C. Mechanical characterization of collagen fibers and scaffolds for tissue engineering. Biomaterials 2003, 24, 3805–3813. [Google Scholar] [CrossRef]
- Yang, L.; Fitié, C.F.C.; van der Werf, K.O.; Bennink, M.L.; Dijkstra, P.J.; Feijen, J. Mechanical properties of single electrospun collagen type I fibers. Biomaterials 2008, 29, 955–962. [Google Scholar] [CrossRef] [PubMed]
- Dutov, P.; Antipova, O.; Varma, S.; Orgel, J.P.R.O.; Schieber, J.D. Measurement of Elastic Modulus of Collagen Type I Single Fiber. PLoS ONE 2016, 11, e0145711. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Schickel, M.E.; Stevenson, M.; Sarang-Sieminski, A.; Gooch, K.; Ghadiali, S.; Hart, R. Fibers in the Extracellular Matrix Enable Long-Range Stress Transmission between Cells. Biophys. J. 2013, 104, 1410–1418. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, H.; Janmey, P.A.; McCulloch, C.A. Lateral boundary mechanosensing by adherent cells in a collagen gel system. Biomaterials 2014, 35, 1138–1149. [Google Scholar] [CrossRef] [PubMed]
- Backouche, F.; Haviv, L.; Groswasser, D.; Bernheim-Groswasser, A. Active gels: Dynamics of patterning and self-organization. Phys. Biol. 2006, 3, 264–273. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.; Ziebert, F.; Humphrey, D.; Duggan, C.; Steinbeck, M.; Zimmermann, W.; Käs, J. Molecular motor-induced instabilities and cross linkers determine biopolymer organization. Biophys. J. 2007, 93, 4445–4452. [Google Scholar] [CrossRef] [PubMed]
- Huber, F.; Strehle, D.; Käs, J. Counterion-induced formation of regular actin bundle networks. Soft Matter 2012, 8, 931–936. [Google Scholar] [CrossRef]
- Huber, F.; Strehle, D.; Schnauß, J.; Käs, J. Formation of regularly spaced networks as a general feature of actin bundle condensation by entropic forces. New J. Phys. 2015, 17, 043029. [Google Scholar] [CrossRef]
- Köster, D.V.; Husain, K.; Iljazi, E.; Bhat, A.; Bieling, P.; Mullins, R.D.; Rao, M.; Mayor, S. Actomyosin dynamics drive local membrane component organization in an in vitro active composite layer. Proc. Natl. Acad. Sci. USA 2016, 113, E1645–E1654. [Google Scholar] [CrossRef] [PubMed]
- Nédélec, F.J.; Surrey, T.; Maggs, A.C.; Leibler, S. Self-organization of microtubules and motors. Nature 1997, 389, 305–308. [Google Scholar] [PubMed]
- Surrey, T.; Nedelec, F.; Leibler, S.; Karsenti, E. Physical properties determining self-organization of motors and microtubules. Science 2001, 292, 1167–1171. [Google Scholar] [CrossRef] [PubMed]
- Laan, L.; Pavin, N.; Husson, J.; Romet-Lemonne, G.; van Duijn, M.; López, M.P.; Vale, R.D.; Jülicher, F.; Reck-Peterson, S.L.; Dogterom, M. Cortical Dynein Controls Microtubule Dynamics to Generate Pulling Forces that Position Microtubule Asters. Cell 2012, 148, 502–514. [Google Scholar] [CrossRef] [PubMed]
- Yin, P.; Hariadi, R.F.; Sahu, S.; Choi, H.M.T.; Park, S.H.; LaBean, T.H.; Reif, J.H. Programming DNA Tube Circumferences. Science 2008, 321, 824–826. [Google Scholar] [CrossRef] [PubMed]
- Glaser, M.; Schnauß, J.; Tschirner, T.; Schmidt, B.U.S.; Moebius-Winkler, M.; Käs, J.A.; Smith, D.M. Self-assembly of hierarchically ordered structures in DNA nanotube systems. New J. Phys. 2016, 18. [Google Scholar] [CrossRef]
- Williams, M.A.K. Hey hey hey hey, it was the DNA. New J. Phys. 2016, 18. [Google Scholar] [CrossRef]
- Schiffels, D.; Liedl, T.; Fygenson, D.K. Nanoscale Structure and Microscale Stiffness of DNA Nanotubes. ACS Nano 2013, 7, 6700–6710. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schnauß, J.; Händler, T.; Käs, J.A. Semiflexible Biopolymers in Bundled Arrangements. Polymers 2016, 8, 274. https://doi.org/10.3390/polym8080274
Schnauß J, Händler T, Käs JA. Semiflexible Biopolymers in Bundled Arrangements. Polymers. 2016; 8(8):274. https://doi.org/10.3390/polym8080274
Chicago/Turabian StyleSchnauß, Jörg, Tina Händler, and Josef A. Käs. 2016. "Semiflexible Biopolymers in Bundled Arrangements" Polymers 8, no. 8: 274. https://doi.org/10.3390/polym8080274






