Dynamics of Polymer Translocation: A Short Review with an Introduction of Weakly-Driven Regime
Abstract
:1. Introduction
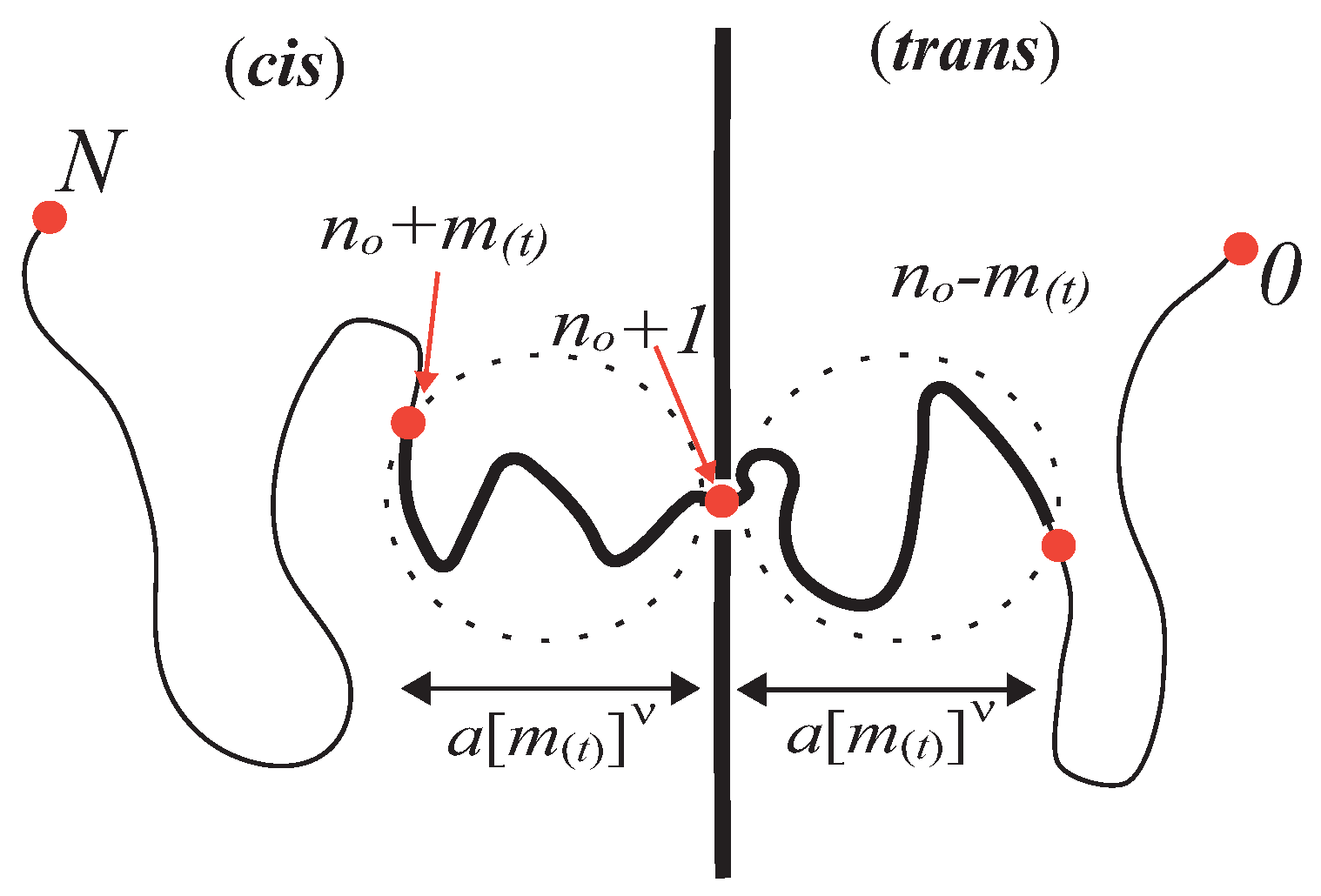
2. Unbiased Translocation
2.1. Memory Function for Stress Relaxation
2.2. Unbiased Translocation Dynamics
2.3. Traveled Fraction at
2.4. Post-Propagation Stage
3. Weakly-Driven Dynamics
3.1. Weakly-Driven Translocation Dynamics
3.2. Post-Propagation Stage
4. Strongly-Driven Dynamics
5. Summary and Discussions
5.1. Summary of the Scaling Formulae
5.1.1. Unbiased and Weakly-Driven Regimes
5.1.2. Strongly-Driven Regime
5.2. Discussion
Acknowledgments
Conflicts of Interest
Appendix A.
Appendix A.1.
Appendix A.2.
Appendix A.3.
Appendix A.4.
References
- Meller, A. Dynamics of polynucleotide transport through nanometre-scale pores. J. Phys. Condens. Matter 2003, 15, R581–R607. [Google Scholar] [CrossRef]
- Dekker, C. Solid-state nanopores. Nat. Nanotechnol. 2007, 2, 209. [Google Scholar] [CrossRef] [PubMed]
- Keyser, U.F. Controlling molecular transport through nanopores. J. R. Soc. Interface 2011, 8, 1369–1378. [Google Scholar] [CrossRef] [PubMed]
- Aksimentiev, A. Deciphering ionic current signatures of DNA transport through a nanopore. Nanoscale 2011, 2, 468–483. [Google Scholar] [CrossRef] [PubMed]
- Wanunu, M. Nanopores: A journey towards DNA sequencing. Phys. Life Rev. 2012, 9, 125–158. [Google Scholar] [CrossRef] [PubMed]
- Muthukumar, M. Polymer Translocation; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Panja, D.; Barkema, G.T.; Kolomeisky, A.B. Through the Eye of the Needle: Recent Advances in Understanding Biopolymer Translocation. J. Phys. Condens. Matter 2013, 25, 413101. [Google Scholar] [CrossRef] [PubMed]
- Palyulin, V.V.; Ala-Nissila, T.; Metzler, R. Polymer translocation: the first two decades and the recent diversification. Soft Matter 2014, 10, 9016–9037. [Google Scholar] [CrossRef] [PubMed]
- Branton, D.; Deamer, D.W.; Marziali, A.; Bayley, H.; Benner, S.A.; Butler, T.; Di Ventra, M.; Garaj, S.; Hibbs, A.; Huang, X.; et al. The potential and challenges of nanopore sequencing. Nat. Biotechnol. 2008, 26, 1146–1153. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Panja, D.; Barkema, G.T.; Ball, R.C. Anomalous dynamics of unbiased polymer translocation through a narrow pore. J. Phys. Condens. Matter 2007, 19, 432202. [Google Scholar] [CrossRef]
- Sakaue, T. Nonequilibrium dynamics of polymer translocation and straightening. Phys. Rev. E 2007, 76, 021803. [Google Scholar] [CrossRef] [PubMed]
- Sakaue, T. Sucking genes into pores: Insight into driven translocation. Phys. Rev. E 2010, 81, 041808. [Google Scholar] [CrossRef] [PubMed]
- Saito, T.; Sakaue, T. Dynamical diagram and scaling in polymer driven translocation. Eur. Phys. J. E 2011, 34, 135. [Google Scholar] [CrossRef] [PubMed]
- Lehtola, V.V.; Linna, R.P.; Kaski, K. Dynamics of forced biopolymer translocation. Europhys. Lett. 2009, 85, 58006. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Binder, K. Out-of-equilibrium characteristics of a forced translocating chain through a nanopore. Phys. Rev. E, 2010, 81, 041804. [Google Scholar] [CrossRef] [PubMed]
- Rowghanian, P.; Grosberg, A.Y. Force-Driven Polymer Translocation through a Nanopore: An Old Problem Revisited. J. Phys. Chem. B 2011, 115, 14127. [Google Scholar] [CrossRef] [PubMed]
- Ikonen, T.; Bhattacharya, A.; Ala-Nissila, T.; Sung, W. Influence of non-universal effects on dynamical scaling in driven polymer translocation. J. Chem. Phys. 2012, 137, 085101. [Google Scholar] [CrossRef] [PubMed]
- Dubbeldam, J.L.A.; Rostiashvili, V.G.; Milchev, A.; Vilgis, T.A. Forced translocation of a polymer: Dynamical scaling versus molecular dynamics simulation. Phys. Rev. E 2012, 85, 041801. [Google Scholar] [CrossRef] [PubMed]
- Saito, T.; Sakaue, T. Erratum to: Dynamical diagram and scaling in polymer driven translocation. Eur. Phys. J. E 2012, 35, 125. [Google Scholar] [CrossRef]
- Saito, T.; Sakaue, T. Two phase picture in driven polymer translocation. arXiv 2012. [Google Scholar]
- Saito, T.; Sakaue, T. Process time distribution of driven polymer transport. Phys. Rev. E 2012, 85, 061803. [Google Scholar] [CrossRef] [PubMed]
- Sarabadani, J.; Ikonen, T.; Ala-Nissila, T. Iso-flux tension propagation theory of driven polymer translocation: The role of initial configurations. J. Chem. Phys. 2014, 141, 214907. [Google Scholar] [CrossRef] [PubMed]
- Sung, W.; Park, P.J. Polymer Translocation through a Pore in a Membrane. Phys. Rev. Lett. 1996, 77, 783. [Google Scholar] [CrossRef] [PubMed]
- Muthukumar, M. Polymer translocation through a hole. J. Chem. Phys. 1999, 111, 10371. [Google Scholar] [CrossRef]
- Brochard-Wyart, F. Polymer Chains Under Strong Flows: Stems and Flowers. Europhys. Lett. 1995, 30, 387. [Google Scholar] [CrossRef]
- Sakaue, T.; Saito, T.; Wada, H. Dragging a polymer in a viscous fluid: Steady state and transient. Phys. Rev. E 2012, 86, 011804. [Google Scholar] [CrossRef] [PubMed]
- Grosberg, A.Y.; Nechaev, S.; Tamm, M.; Vasiyev, O. How long does it take to pull an ideal polymer into a small hole? Phys. Rev. Lett. 2006, 96, 228105. [Google Scholar] [CrossRef] [PubMed]
- Saito, T.; Sakaue, T. Cis-trans dynamical asymmetry in driven polymer translocation. Phys. Rev. E 2013, 88, 042606. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, R.; Bhattacharya, A. Driven translocation of a semi-flexible chain through a nanopore: A Brownian dynamics simulation study in two dimensions. J. Chem. Phys. 2013, 138, 204909. [Google Scholar] [CrossRef] [PubMed]
- Chuang, J.; Kantor, Y.; Kardar, M. Anomalous dynamics of translocation. Phys. Rev. E 2001, 65, 011802. [Google Scholar] [CrossRef] [PubMed]
- De Haan, H.W.; Slater, G.W. Memory effects during the unbiased translocation of a polymer through a nanopore. J. Chem. Phys. 2012, 136, 154903. [Google Scholar] [CrossRef] [PubMed]
- De Haan, H.W.; Slater, G.W. Using an incremental mean first passage approach to explore the viscosity dependent dynamics of the unbiased translocation of a polymer through a nanopore. J. Chem. Phys. 2012, 136, 204902. [Google Scholar] [CrossRef] [PubMed]
- Luo, K.; Ollila, S.T.T.; Huopaniemi, I.; Ala-Nissila, T.; Pomorski, P.; Karttunen, M.; Ying, S.-C.; Bhattacharya, A. Dynamical scaling exponents for polymer translocation through a nanopore. Phys. Rev. E 2008, 78, 050901. [Google Scholar] [CrossRef] [PubMed]
- Vocks, H.; Panja, D.; Barkema, G.T.; Ball, R.C. Pore-blockade times for field-driven polymer translocation. J. Phys. Condens. Matter 2008, 20, 095224. [Google Scholar] [CrossRef]
- Saito, T.; Sakaue, T. Driven anomalous diffusion: An example from polymer stretching. Phys. Rev. E 2015, 92, 012601. [Google Scholar] [CrossRef] [PubMed]
- Polson, M.J.; Dunn, T.R. Evaluating the applicability of the Fokker-Planck equation in polymer translocation: A Brownian dynamics study. J. Chem. Phys. 2014, 140, 184904. [Google Scholar] [CrossRef] [PubMed]

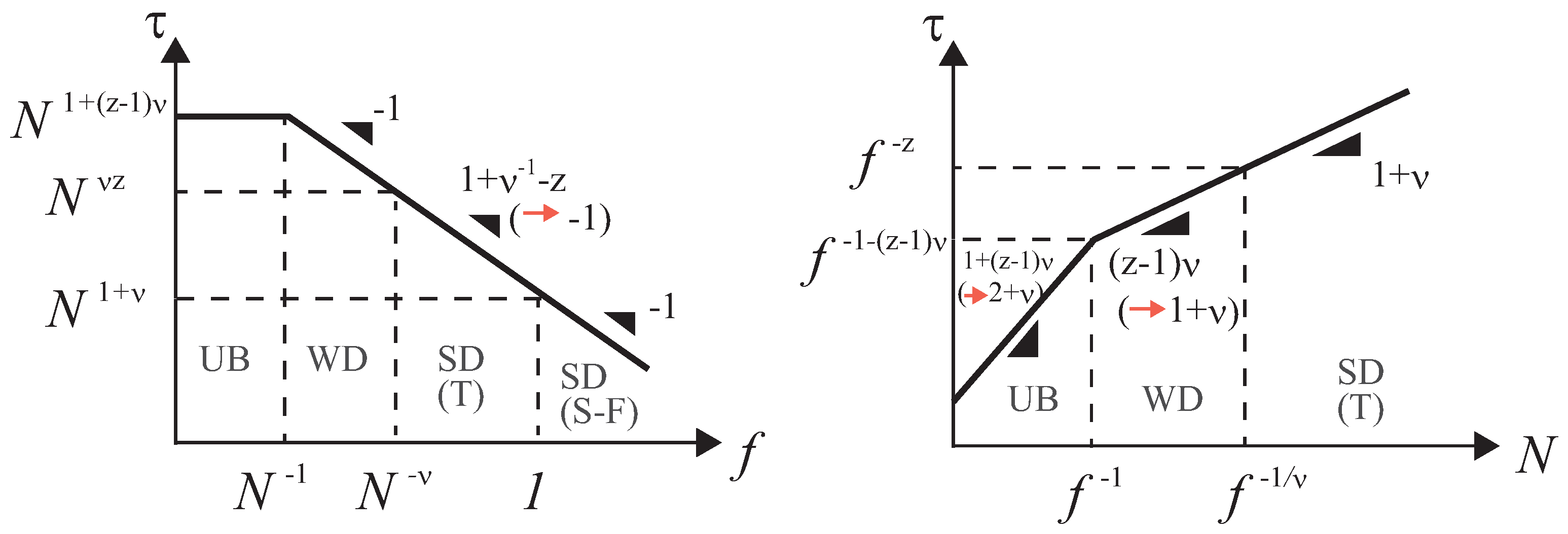
© 2016 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakaue, T. Dynamics of Polymer Translocation: A Short Review with an Introduction of Weakly-Driven Regime. Polymers 2016, 8, 424. https://doi.org/10.3390/polym8120424
Sakaue T. Dynamics of Polymer Translocation: A Short Review with an Introduction of Weakly-Driven Regime. Polymers. 2016; 8(12):424. https://doi.org/10.3390/polym8120424
Chicago/Turabian StyleSakaue, Takahiro. 2016. "Dynamics of Polymer Translocation: A Short Review with an Introduction of Weakly-Driven Regime" Polymers 8, no. 12: 424. https://doi.org/10.3390/polym8120424




