Efficient Determination of Slip-Link Parameters from Broadly Polydisperse Linear Melts
Abstract
:1. Introduction
2. Experiments
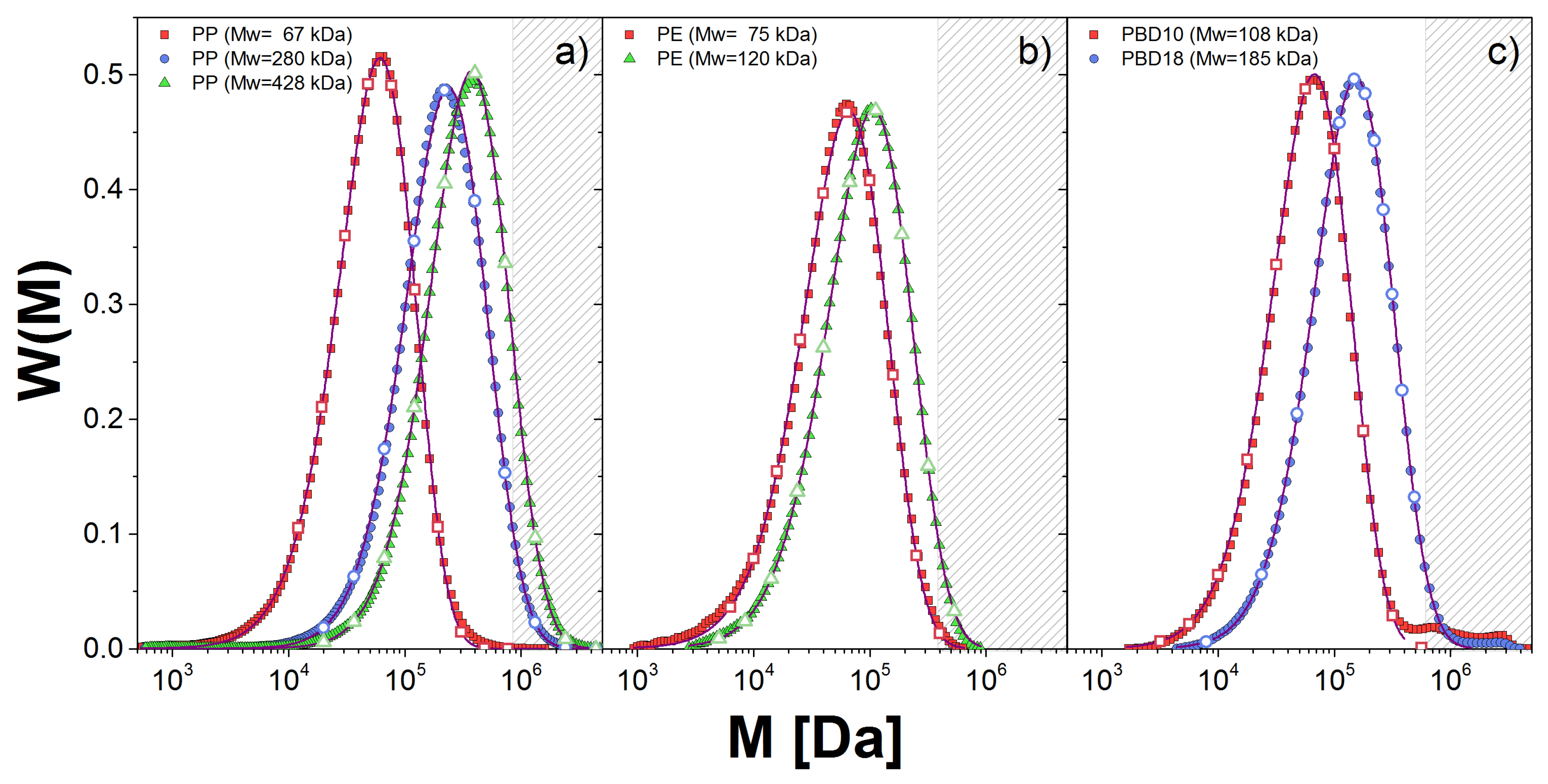
2.1. Samples
2.2. Characterization
2.3. Rheological Measurements
3. Double Reptation Model
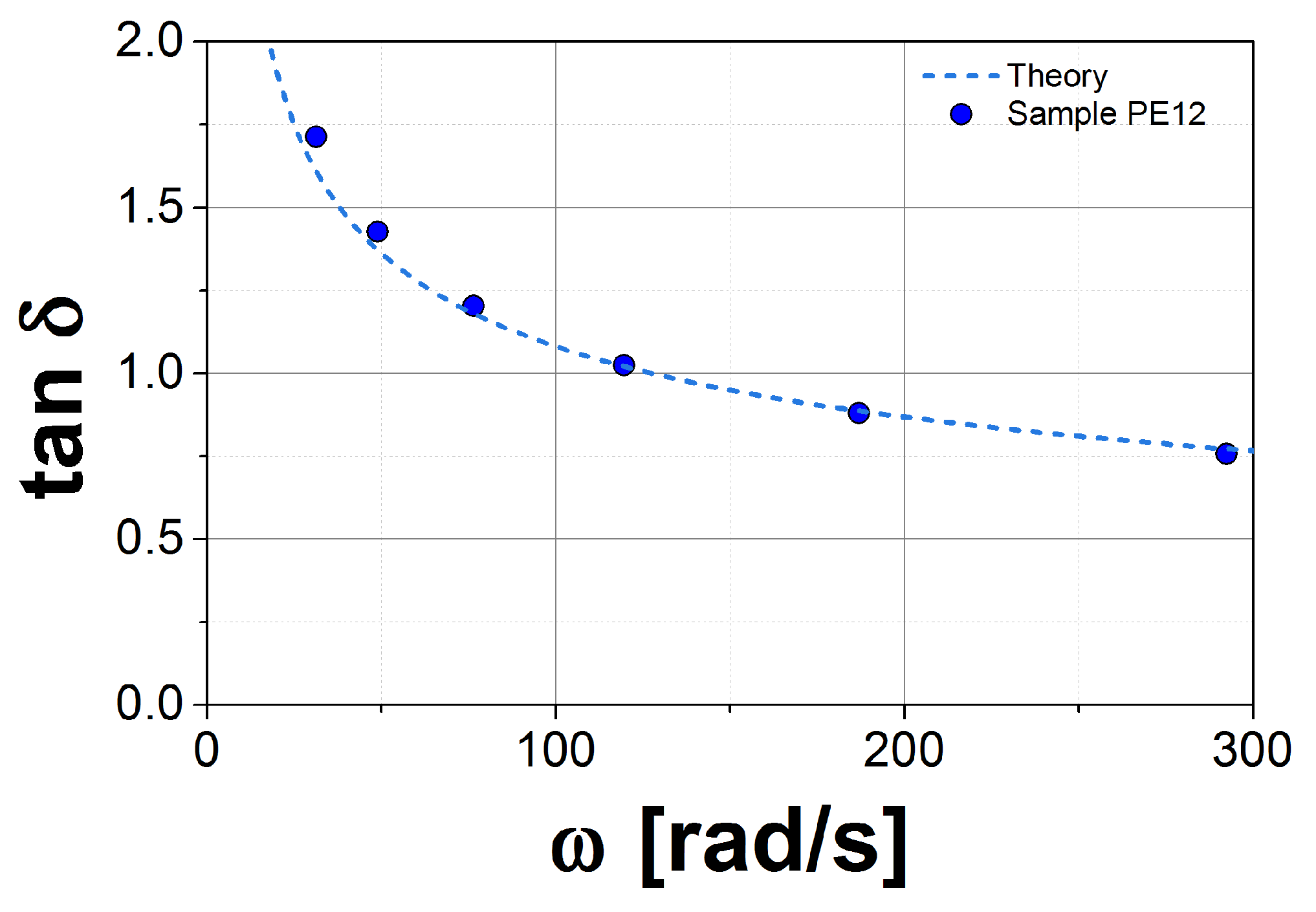
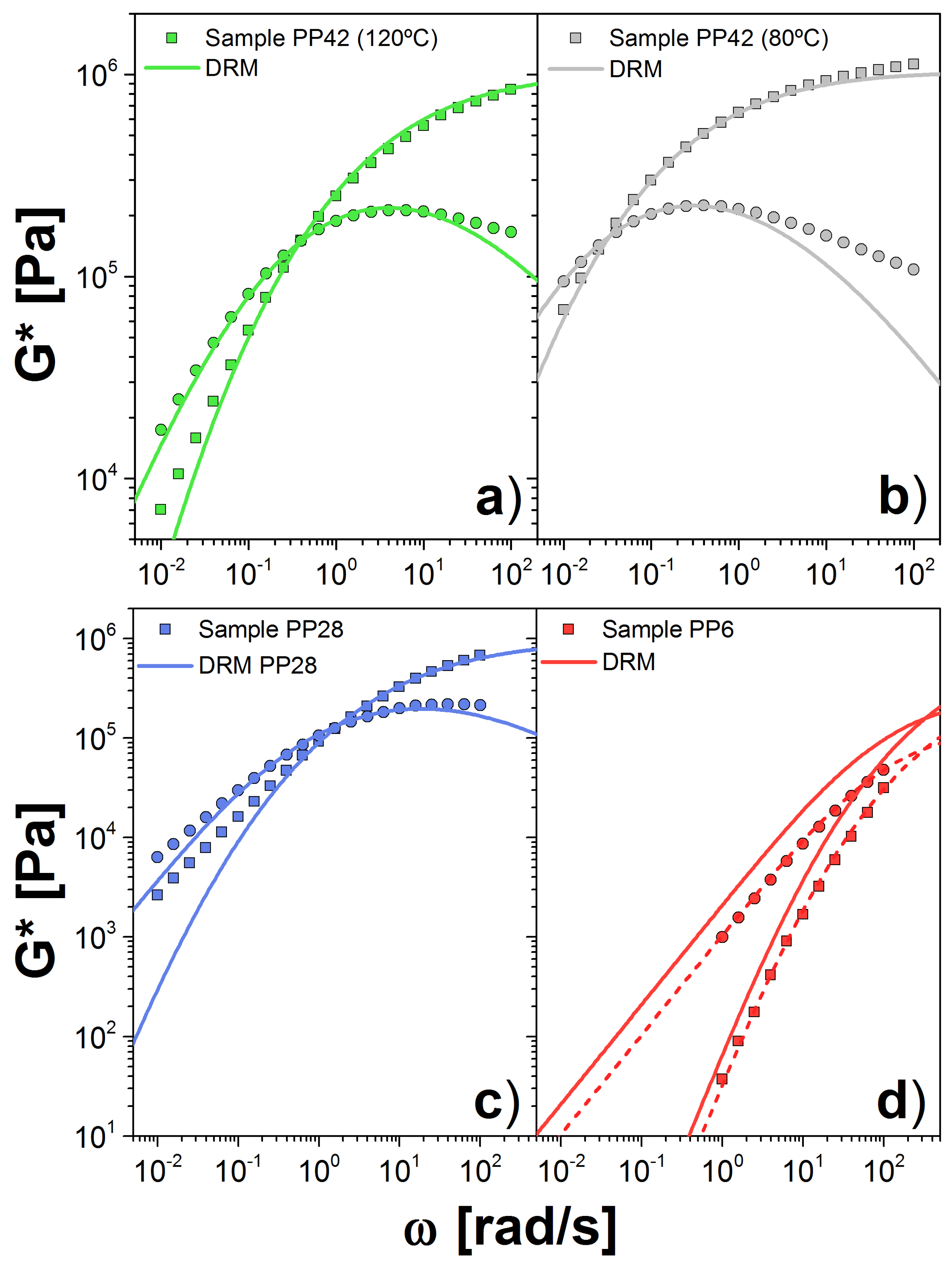
3.1. Results for the DRM
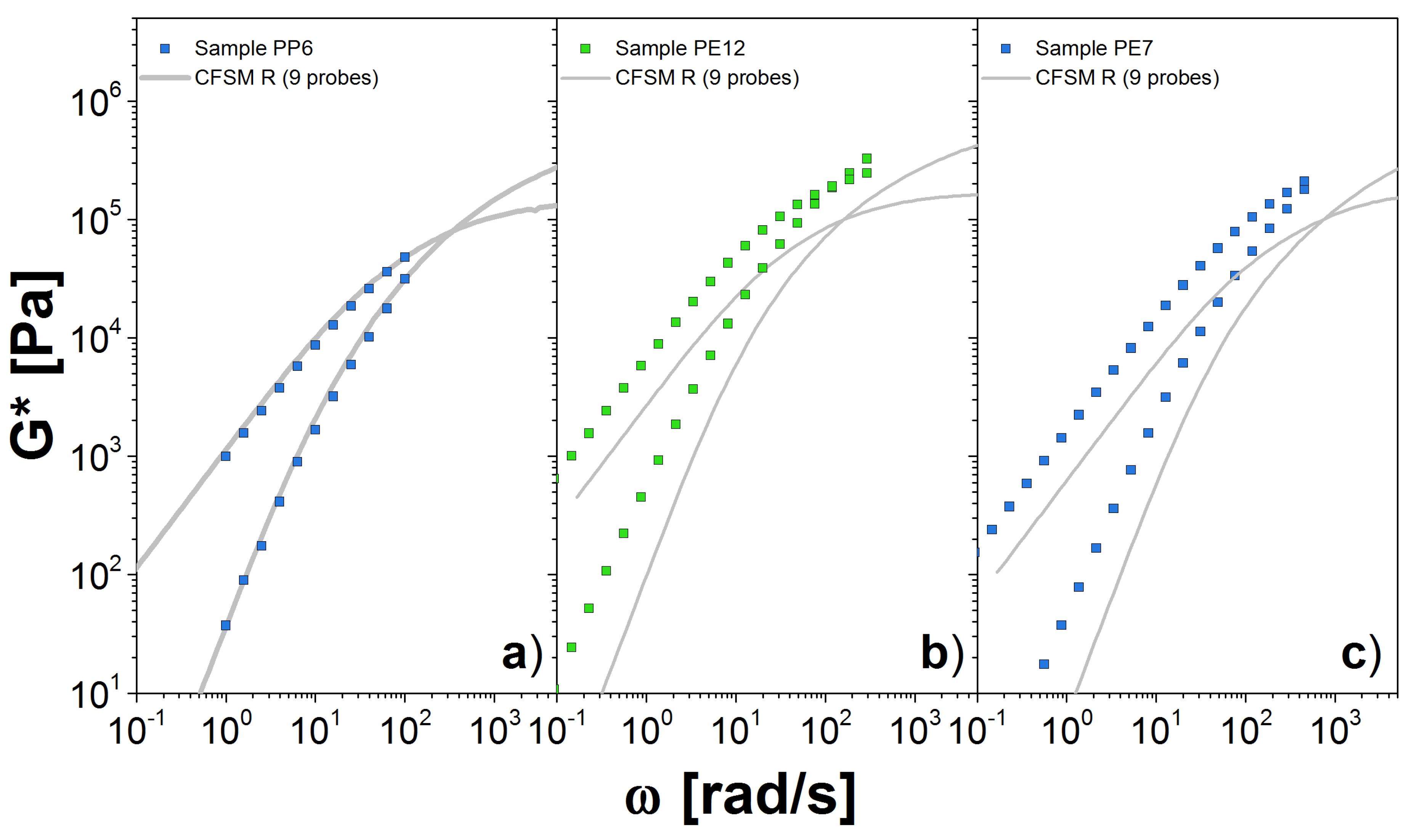
4. Clustered Fixed-Slip-Link Model
4.1. The Parameters
4.2. Implementation
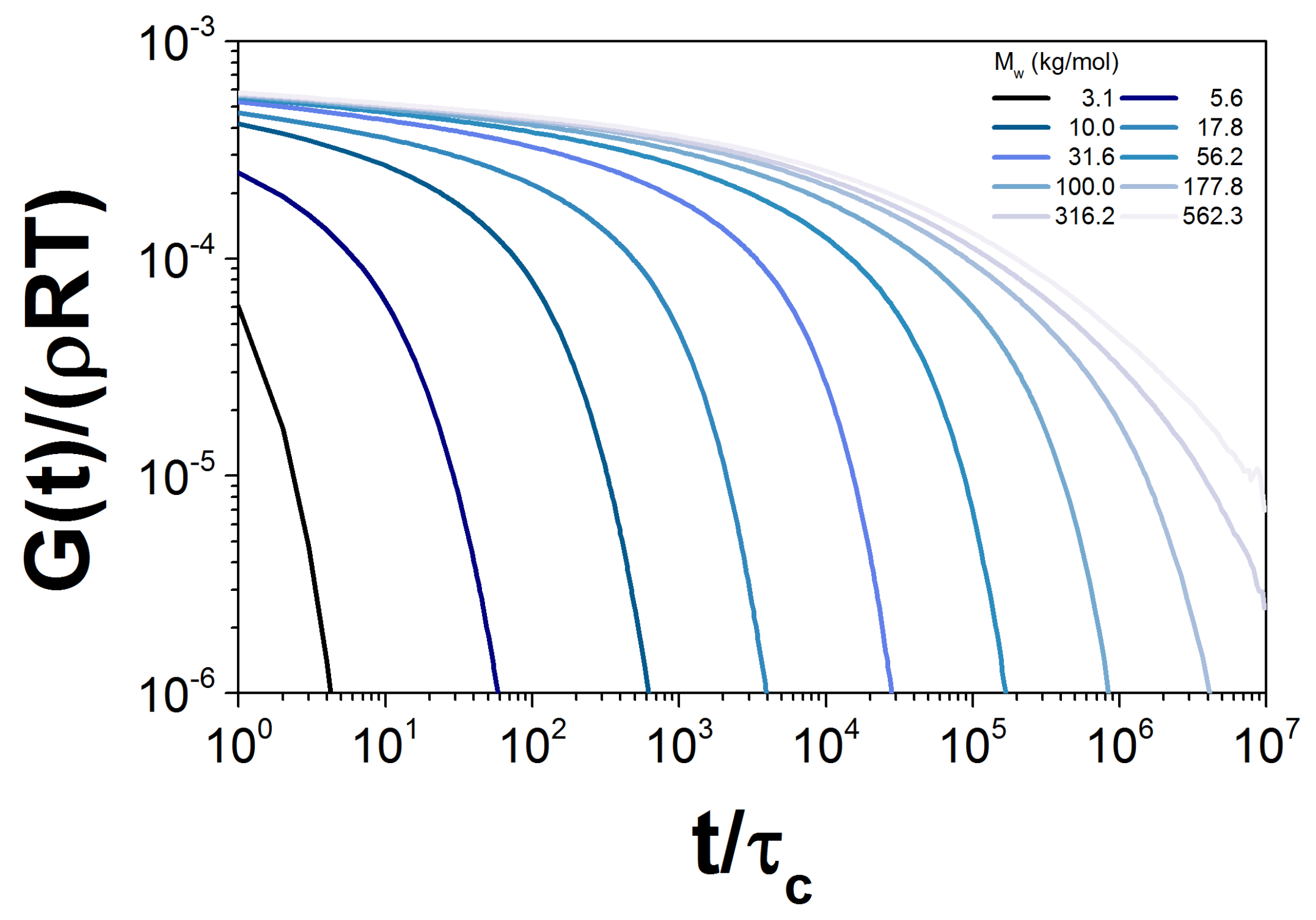
4.3. Results for the DSM
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DSM | discrete slip-link model |
| DRM | double-reptation model |
| PBD | polybutadiene |
| PP | polypropilene |
| PE | polyethylene |
| GEX | generalized exponential |
| PDI | polydisperse index |
| GPC | gel permeation chromatography |
| SAOS | small amplitude oscillatory shear |
| MWD | molecular weight distribution |
| CP | crossover point |
| CD | constraint dynamics |
| SD | sliding dynamics |
| CFSM | cluster fixed slip-link model |
References
- Ferry, J. Viscoelastic Properties of Polymers; Wiley: Hoboken, NJ, USA, 1980. [Google Scholar]
- Desai, P.S.; Kang, B.G.; Katzarova, M.; Hall, R.; Huang, Q.; Lee, S.; Shivokhin, M.; Chang, T.; Venerus, D.C.; Mays, J.; et al. Challenging Tube and Slip-Link Models: Predicting the Linear Rheology of Blends of Well-Characterized Star and Linear 1,4-Polybutadienes. Macromolecules 2016, 49, 4964–4977. [Google Scholar] [CrossRef]
- De Gennes, P. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Doi, M.; Edwards, S. The Theory of Polymer Dynamics; International Series of Monographs on Physics; Clarendon Press: Oxford, UK, 1988. [Google Scholar]
- Rubinstein, M.; Colby, R.H. Self-consistent theory of polydisperse entangled polymers: Linear viscoelasticity of binary blends. J. Chem. Phys. 1988, 89, 5291–5306. [Google Scholar] [CrossRef]
- Doi, M. Explanation for the 3.4 power law of viscosity of polymeric liquids on the basis of the tube model. J. Polym. Sci. Polym. Lett. Ed. 1981, 19, 265–273. [Google Scholar] [CrossRef]
- Tuminello, W.H. Molecular weight and molecular weight distribution from dynamic measurements of polymer melts. Polym. Eng. Sci. 1986, 26, 1339–1347. [Google Scholar] [CrossRef]
- Des Cloizeaux, J. Double Reptation vs. Simple Reptation in Polymer Melts. EPL (Europhys. Lett.) 1988, 5, 437. [Google Scholar] [CrossRef]
- Des Cloizeaux, J. Relaxation of entangled polymers in melts. Macromolecules 1990, 23, 3992–4006. [Google Scholar] [CrossRef]
- Tsenoglou, C. Molecular weight polydispersity effects on the viscoelasticity of entangled linear polymers. Macromolecules 1991, 24, 1762–1767. [Google Scholar] [CrossRef]
- Léonardi, F.; Majesté, J.C.; Allal, A.; Marin, G. Rheological models based on the double reptation mixing rule: The effects of a polydisperse environment. J. Rheol. 2000, 44, 675–692. [Google Scholar] [CrossRef]
- Van Ruymbeke, E.; Liu, C.Y.; Bailly, C. Quantitative Tube Model Predictions for the Linear Viscoelasticity of Linear Polymers. In Rheology Reviews; The British Society of Rheology: Swansea, UK, 2007; pp. 53–134. [Google Scholar]
- Kremer, K.; Grest, G.S.; Carmesin, I. Crossover from Rouse to Reptation Dynamics: A Molecular-Dynamics Simulation. Phys. Rev. Lett. 1988, 61, 566–569. [Google Scholar] [CrossRef] [PubMed]
- Kröger, M.; Hess, S. Rheological Evidence for a Dynamical Crossover in Polymer Melts via Nonequilibrium Molecular Dynamics. Phys. Rev. Lett. 2000, 85, 1128–1131. [Google Scholar] [CrossRef] [PubMed]
- Auhl, R.; Everaers, R.; Grest, G.S.; Kremer, K.; Plimpton, S.J. Equilibration of long chain polymer melts in computer simulations. J. Chem. Phys. 2003, 119, 12718–12728. [Google Scholar] [CrossRef]
- Schieber, J.D.; Neergaard, J.; Gupta, S. A full-chain, temporary network model with sliplinks, chain-length fluctuations, chain connectivity and chain stretching. J. Rheol. 2003, 47, 213–233. [Google Scholar] [CrossRef]
- Khaliullin, R.N.; Schieber, J.D. Self-Consistent Modeling of Constraint Release in a Single-Chain Mean-Field Slip-Link Model. Macromolecules 2009, 42, 7504–7517. [Google Scholar] [CrossRef]
- Khaliullin, R.N.; Schieber, J.D. Application of the Slip-Link Model to Bidisperse Systems. Macromolecules 2010, 43, 6202–6212. [Google Scholar] [CrossRef]
- Schieber, J.D.; Andreev, M. Entangled Polymer Dynamics in Equilibrium and Flow Modeled Through Slip Links. Annu. Rev. Chem. Biomol. Eng. 2014, 5, 367–381. [Google Scholar] [CrossRef] [PubMed]
- Andreev, M.; Feng, H.; Yang, L.; Schieber, J.D. Universality and speedup in equilibrium and nonlinear rheology predictions of the fixed slip-link model. J. Rheol. 2014, 58, 723–736. [Google Scholar] [CrossRef]
- Katzarova, M.; Yang, L.; Andreev, M.; Córdoba, A.; Schieber, J.D. Analytic slip-link expressions for universal dynamic modulus predictions of linear monodisperse polymer melts. Rheol. Acta 2015, 54, 169–183. [Google Scholar] [CrossRef]
- Andreev, M.; Schieber, J.D. Accessible and Quantitative Entangled Polymer Rheology Predictions, Suitable for Complex Flow Calculations. Macromolecules 2015, 48, 1606–1613. [Google Scholar] [CrossRef]
- Van Ruymbeke, E.; Coppola, S.; Balacca, L.; Righi, S.; Vlassopoulos, D. Decoding the viscoelastic response of polydisperse star/linear polymer blends. J. Rheol. 2010, 54, 507–538. [Google Scholar] [CrossRef]
- Fetters, L.J.; Lohse, D.J.; Colby, R.H. Chain Dimensions and Entanglement Spacings. In Physical Properties of Polymers Handbook; Mark, J.E., Ed.; Springer: New York, NY, USA, 2007; pp. 447–454. [Google Scholar]
- Guzmán, J.D.; Schieber, J.D.; Pollard, R. A regularization-free method for the calculation of molecular weight distributions from dynamic moduli data. Rheol. Acta 2005, 44, 342–351. [Google Scholar] [CrossRef]
- Thimm, W.; Friedrich, C.; Marth, M.; Honerkamp, J. An analytical relation between relaxation time spectrum and molecular weight distribution. J. Rheol. 1999, 43, 1663–1672. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; He, J.; van Ruymbeke, E.; Keunings, R.; Bailly, C. Evaluation of different methods for the determination of the plateau modulus and the entanglement molecular weight. Polymer 2006, 47, 4461–4479. [Google Scholar] [CrossRef]
- Struglinski, M.J.; Graessley, W.W. Effects of polydispersity on the linear viscoelastic properties of entangled polymers. 1. Experimental observations for binary mixtures of linear polybutadiene. Macromolecules 1985, 18, 2630–2643. [Google Scholar] [CrossRef]
- Santangelo, P.G.; Roland, C.M.; Puskas, J.E. Rheology of Star-Branched Polyisobutylene. Macromolecules 1999, 32, 1972–1977. [Google Scholar] [CrossRef] [Green Version]
- Aguilar, M.; Vega, J.; Na, B.P.; Martínez-Salazar, J. Novel features of the rheological behaviour of metallocene catalysed atactic polypropylene. Polymer 2003, 44, 1401–1407. [Google Scholar] [CrossRef]
- Van Ruymbeke, E.; Keunings, R.; Bailly, C. Prediction of linear viscoelastic properties for polydisperse mixtures of entangled star and linear polymers: Modified tube-based model and comparison with experimental results. J. Non-Newtonian Fluid Mech. 2005, 128, 7–22. [Google Scholar] [CrossRef]
- Stephanou, P.S.; Mavrantzas, V.G. Quantitative predictions of the linear viscoelastic properties of entangled polyethylene and polybutadiene melts via modified versions of modern tube models on the basis of atomistic simulation data. J. Non-Newtonian Fluid Mech. 2013, 200, 111–130. [Google Scholar] [CrossRef]
- Shivokhin, M.E.; Read, D.J.; Kouloumasis, D.; Kocen, R.; Zhuge, F.; Bailly, C.; Hadjichristidis, N.; Likhtman, A.E. Understanding Effect of Constraint Release Environment on End-to-End Vector Relaxation of Linear Polymer Chains. Macromolecules 2017, 50, 4501–4523. [Google Scholar] [CrossRef] [Green Version]
- Eckstein, A.; Suhm, J.; Friedrich, C.; Maier, R.D.; Sassmannshausen, J.; Bochmann, M.; Mülhaupt, R. Determination of Plateau Moduli and Entanglement Molecular Weights of Isotactic, Syndiotactic, and Atactic Polypropylenes Synthesized with Metallocene Catalysts. Macromolecules 1998, 31, 1335–1340. [Google Scholar] [CrossRef]
- Katzarova, M.; Andreev, M.; Sliozberg, Y.R.; Mrozek, R.A.; Lenhart, J.L.; Andzelm, J.W.; Schieber, J.D. Rheological predictions of network systems swollen with entangled solvent. AIChE J. 2014, 60, 1372–1380. [Google Scholar] [CrossRef]
- Kubo, R. Statistical-Mechanical Theory of Irreversible Processes. I. General Theory and Simple Applications to Magnetic and Conduction Problems. J. Phys. Soc. Jpn. 1957, 12, 570–586. [Google Scholar] [CrossRef] [Green Version]
- Baumgaertel, M.; Schausberger, A.; Winter, H.H. The relaxation of polymers with linear flexible chains of uniform length. Rheol. Acta 1990, 29, 400–408. [Google Scholar] [CrossRef]



| Polymer Name | T | |||||
|---|---|---|---|---|---|---|
| (g/mol) | (C) | (MPa) | (g/mL) | (g/mol) | ||
| PP6 | 0.67 | 2.02 | 120 | 0.47 | 0.791 | 183.4 |
| PP28 | 2.80 | 2.05 | 120 | 0.47 | 0.791 | 183.4 |
| PP42 | 4.28 | 1.98 | 120 | 0.47 | 0.791 | 183.4 |
| PP42 | 4.28 | 1.98 | 80 | 0.48 | 0.825 | 183.4 |
| PE7 | 0.75 | 2.20 | 190 | 2.6 | 0.785 | 150.4 |
| PE12 | 1.20 | 2.27 | 190 | 2.6 | 0.785 | 150.4 |
| PBD10 | 1.08 | 2.7 | 30 | 1.15 | 0.895 | 112.5 |
| PBD18 | 1.85 | 2.1 | 30 | 1.15 | 0.895 | 112.5 |
| PBD20 | 2.04 | 1.1 | 30 | 1.15 | 0.895 | 112.5 |
| Polymer Code | a | b | k | |||
|---|---|---|---|---|---|---|
| (g/mol) | (MPa) | (s(mol/g)) | () | |||
| PP6 | 1.33 (3) | 0.75 (1) | 13.7 (9) | 0.497 | 3.99 | 12.02 |
| PP28 | 2.2 (2) | 0.48 (4) | 5 (3) | 0.918 | 4.54 | 0.363 |
| PP42 * | 2.04 (8) | 0.54 (2) | 15 (4) | 1.000 | 4.51 | 19.05 |
| PP42 * | 2.04 (8) | 0.54 (2) | 15 (4) | 1.025 | 59.42 | 251.19 |
| PE7 | 1.26 (4) | 0.64 (1) | 9.1 (9) | 1.89 | 0.958 | 0.69 |
| PE12 * | 1.36 (2) | 0.61 (1) | 11.8 (6) | 1.44 | 1.02 | 1.82 |
| PBD10 | 1.48 (4) | 0.66 (1) | 9.3 (9) | 0.690 | 20.4 | 15.90 |
| PBD18 * | 1.96 (4) | 0.54 (1) | 6.7 (8) | 0.948 | 14.4 | 5.47 |
| PBD20 | - | - | - | - | - | - |
| Polymer Code | |||||
|---|---|---|---|---|---|
| (MPa) | (g/mol) | (g/mol) | (s) | ||
| PBD10 | 1.26 | 791.302 | 5.54 | 12.6 | 0.4 |
| PBD18 | 1.26 | 791.302 | 5.54 | 12.6 | 0.4 |
| PBD20 | 1.26 | 791.302 | – | 12.6 | 0.4 |
| PP6 | 1.00 | 1282.71 | 8.97 | 11.5 | 0.3 |
| PE12 | 1.44 | 1089.12 | 7.62 | 11.9 | 0.15 |
| PE7 | 1.44 | 1089.12 | 7.62 | 11.9 | 0.15 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valadez-Pérez, N.E.; Taletskiy, K.; Schieber, J.D.; Shivokhin, M. Efficient Determination of Slip-Link Parameters from Broadly Polydisperse Linear Melts. Polymers 2018, 10, 908. https://doi.org/10.3390/polym10080908
Valadez-Pérez NE, Taletskiy K, Schieber JD, Shivokhin M. Efficient Determination of Slip-Link Parameters from Broadly Polydisperse Linear Melts. Polymers. 2018; 10(8):908. https://doi.org/10.3390/polym10080908
Chicago/Turabian StyleValadez-Pérez, Néstor E., Konstantin Taletskiy, Jay D. Schieber, and Maksim Shivokhin. 2018. "Efficient Determination of Slip-Link Parameters from Broadly Polydisperse Linear Melts" Polymers 10, no. 8: 908. https://doi.org/10.3390/polym10080908





