Dynamics of a Complex Multilayer Polymer Network: Mechanical Relaxation and Energy Transfer
Abstract
:1. Introduction
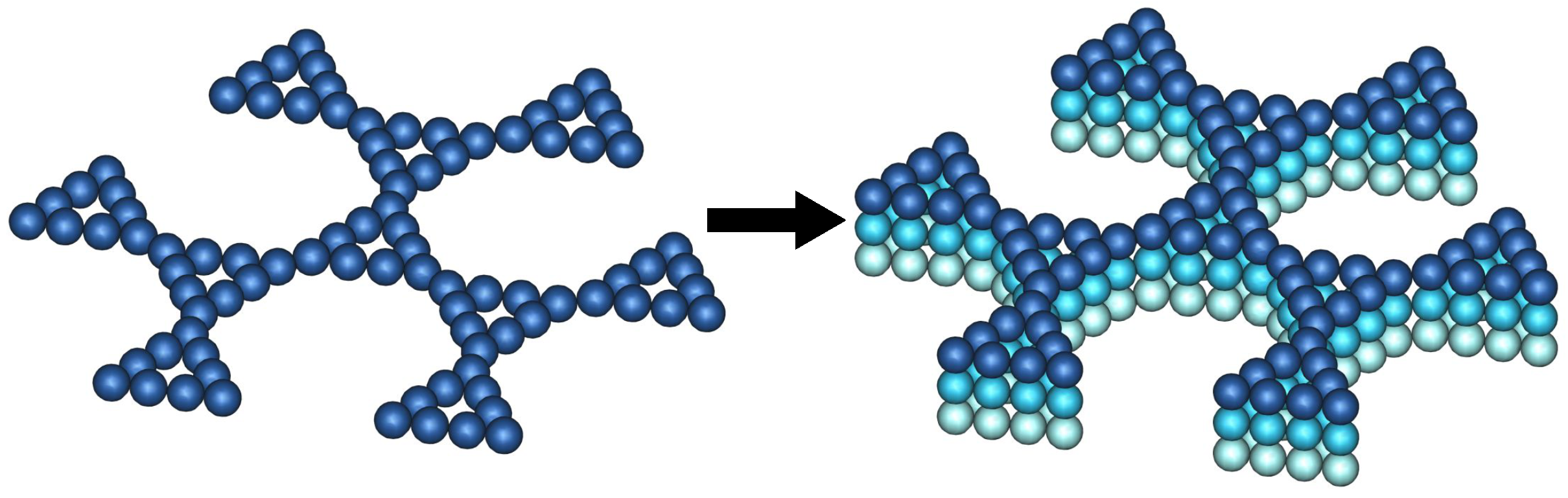
2. Generalized Gaussian Structures
3. The Multilayer Network and the Eigenvalue Spectrum
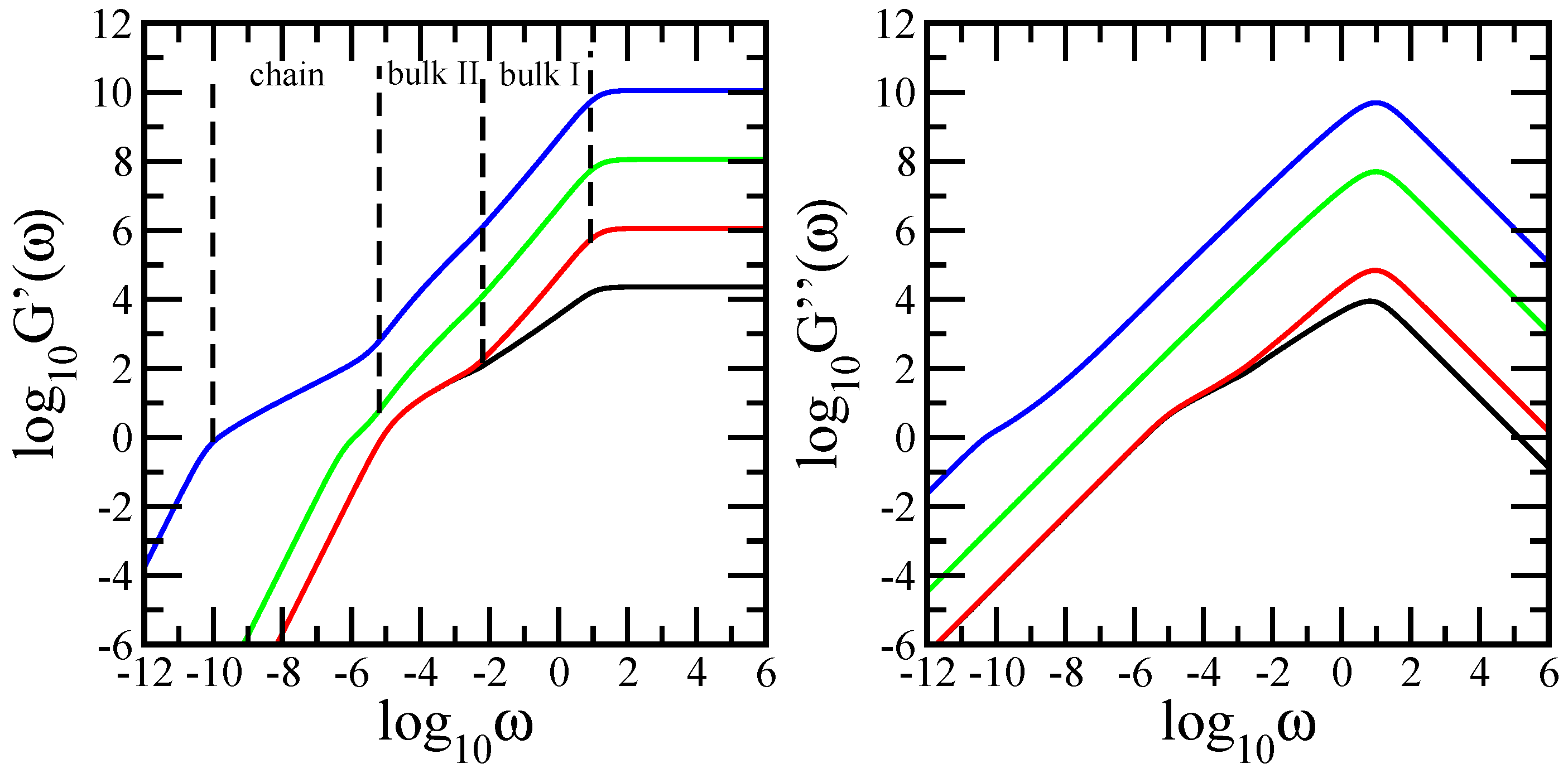
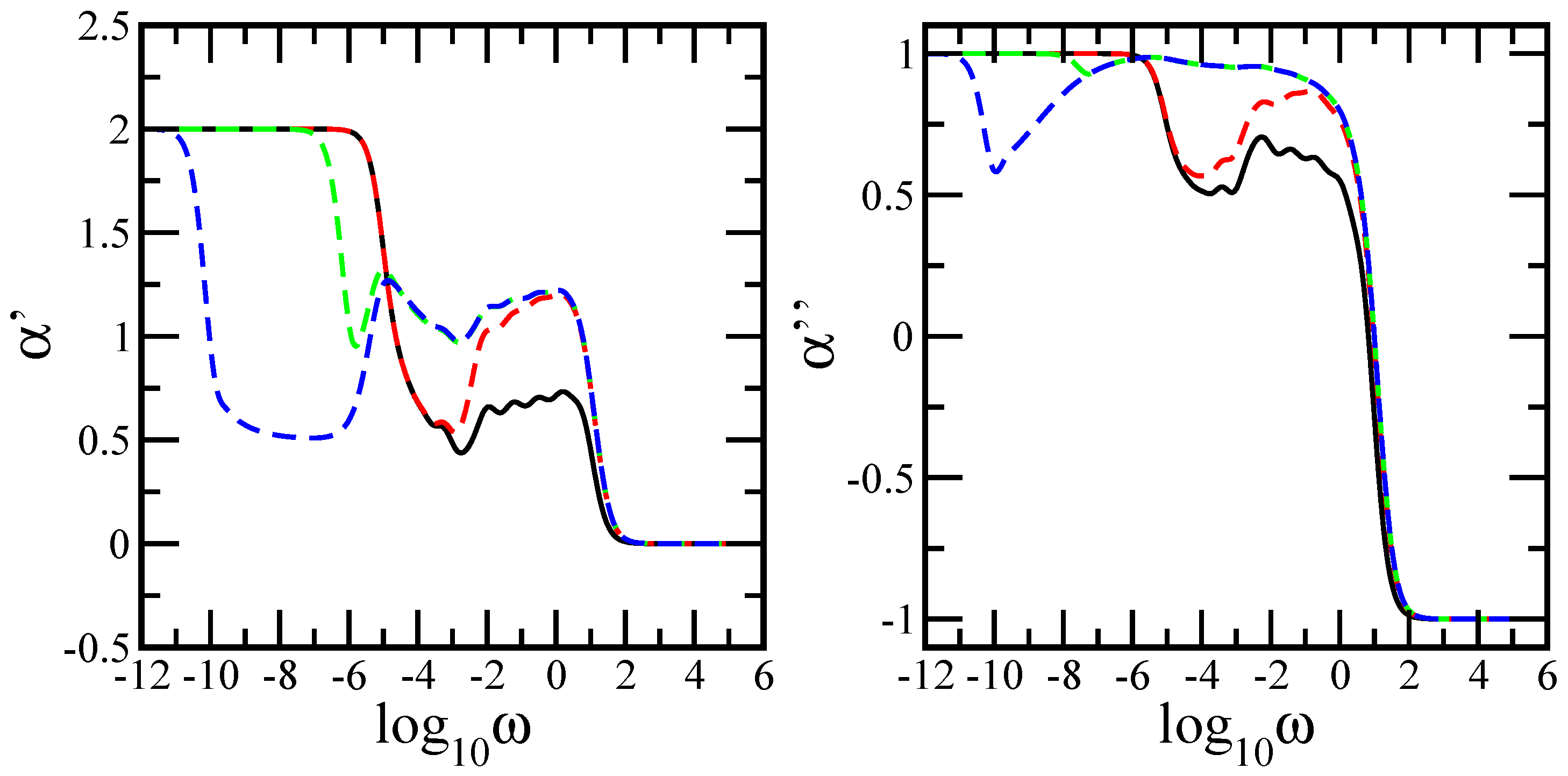
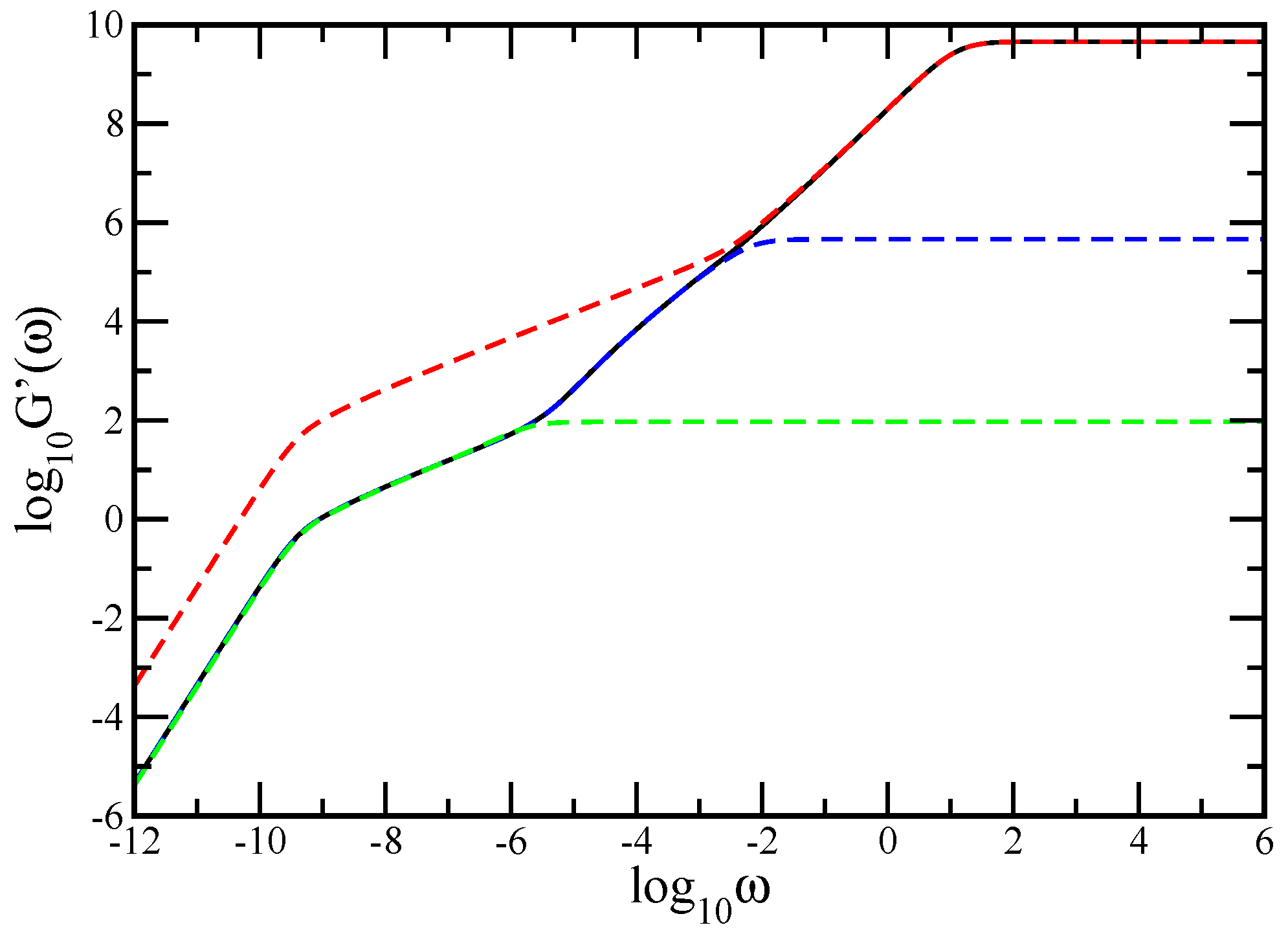
4. Relaxation Patterns
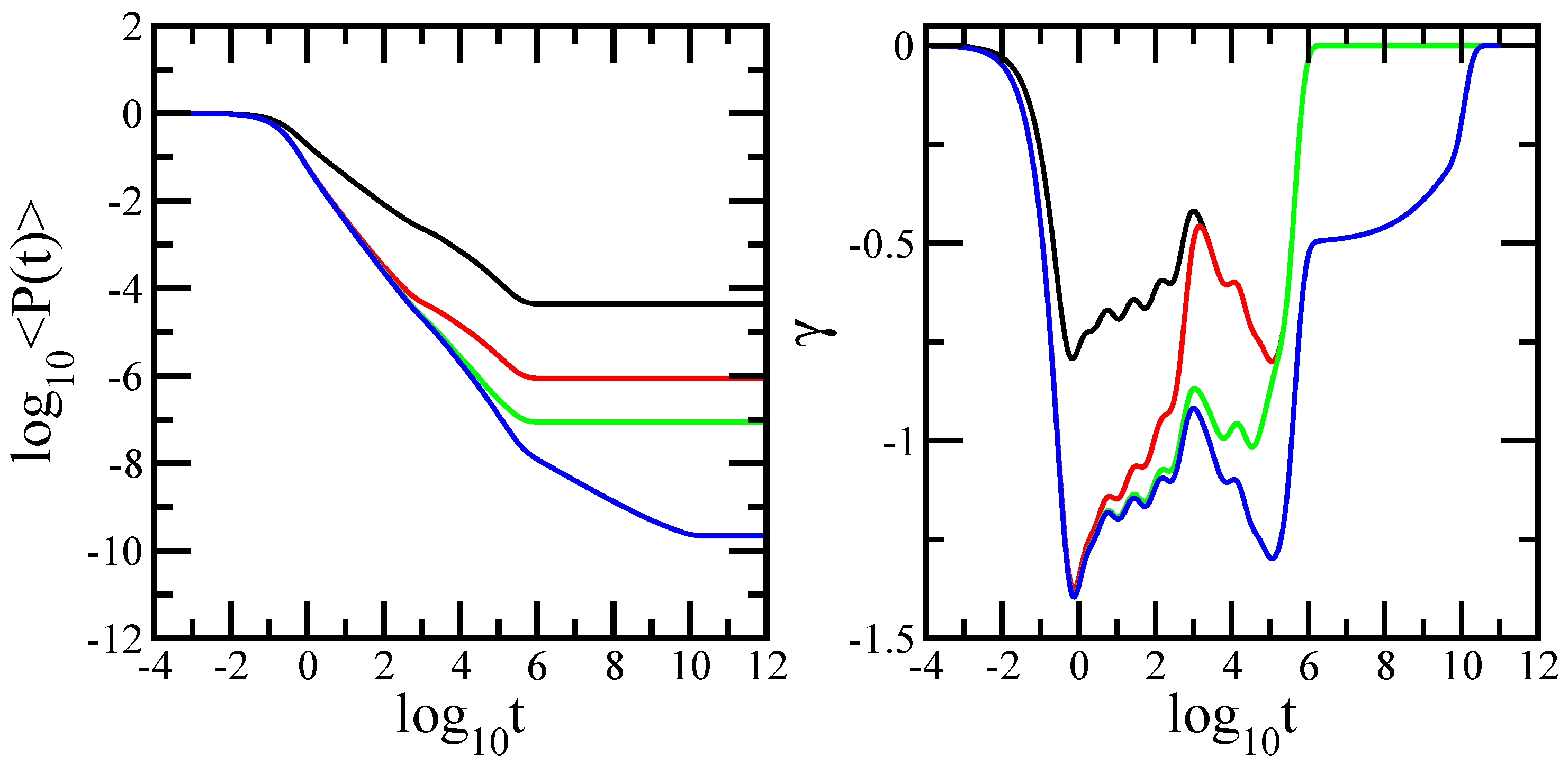
Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| Generation of dual Sierpinski gasket | |
| Generation of the dendrimer | |
| Number of layers of the multilayer network | |
| GGS | Generalized Gaussian structure |
Appendix A. Determination of the Eigenvalue Spectrum of the Dendrimer
Appendix B. Checking of the Total Number of Eigenvalues
References
- Rouse, P.E. A Theory of the Linear Viscoelastic Properties of Dilute Solutions of Coiling Polymers. J. Chem. Phys. 1953, 21, 1272–1280. [Google Scholar] [CrossRef]
- Zimm, B.H. Dynamics of Polymer Molecules in Dilute Solution: Viscoelasticity, Flow Birefringence and Dielectric Loss. J. Chem. Phys. 1956, 24, 269–278. [Google Scholar] [CrossRef]
- Ouchi, M.; Terashima, T.; Sawamoto, M. Transition metal-catalyzed living radical polymerization: Toward perfection in catalysis and precision polymer synthesis. Chem. Rev. 2009, 109, 4963–5050. [Google Scholar] [CrossRef] [PubMed]
- Matyjaszewski, K.; Xia, J. Atom transfer radical polymerization. Chem. Rev. 2001, 101, 2921–2990. [Google Scholar] [CrossRef] [PubMed]
- Hawker, C.J.; Bosman, A.W.; Harth, E. New polymer synthesis by nitroxide mediated living radical polymerizations. Chem. Rev. 2001, 101, 3661–3688. [Google Scholar] [CrossRef] [PubMed]
- Aida, T.; Meijer, E.W.; Stupp, S.I. Functional supramolecular polymers. Science 2012, 335, 813–817. [Google Scholar] [CrossRef] [PubMed]
- Yokozawa, T.; Yokoyama, A. Chain-growth polycondensation: The living polymerization process in polycondensation. Prog. Polym. Sci. 2007, 32, 147–172. [Google Scholar] [CrossRef]
- Fréchet, J.M.J.; Tomalia, D.A. Dendrimers and Other Dendritic Polymers; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Bosman, A.W.; Janssen, H.M.; Meijer, E.W. About dendrimers: Structure, physical properties, and applications. Chem. Rev. 1999, 99, 1665–1688. [Google Scholar] [CrossRef] [PubMed]
- Cai, C.; Chen, Z.Y. Rouse Dynamics of a Dendrimer Model in the θ Condition. Macromolecules 1997, 30, 5104–5117. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Cai, C. Dynamics of Starburst Dendrimers. Macromolecules 1999, 32, 5423–5434. [Google Scholar] [CrossRef]
- Burchard, W. Solution Properties of Branched Macromolecules. Adv. Polym. Sci. 1999, 143, 113–194. [Google Scholar]
- Ganazzoli, F.; La Ferla, R.; Raffaini, G. Intramolecular Dynamics of Dendrimers under Excluded-Volume Conditions. Macromolecules 2001, 34, 4222–4228. [Google Scholar] [CrossRef]
- Grimm, J.; Dolgushev, M. Dynamics of internally functionalized dendrimers. Phys. Chem. Chem. Phys. 2016, 18, 19050–19061. [Google Scholar] [CrossRef] [PubMed]
- Gurtovenko, A.A.; Blumen, A. Generalized Gaussian Structures: Models for Polymer Systems with Complex Topologies. Adv. Polym. Sci. 2005, 182, 171–282. [Google Scholar]
- Gurtovenko, A.A.; Markelov, D.A.; Gotlib, Y.Y.; Blumen, A. Dynamics of dendrimer-based polymer networks. J. Chem. Phys. 2003, 119, 7579–7590. [Google Scholar] [CrossRef]
- Dolgushev, M.; Blumen, A. Dynamics of chains and dendrimers with heterogeneous semiflexibility. J. Chem. Phys. 2010, 132, 124905. [Google Scholar] [CrossRef] [PubMed]
- Dolgushev, M.; Blumen, A. Dynamics of Semiflexible Chains, Stars, and Dendrimers. Macromolecules 2009, 42, 5378–5387. [Google Scholar] [CrossRef]
- Boris, D.; Rubinstein, M. A Self-Consistent Mean Field Model of a Starburst Dendrimer: Dense Core vs. Dense Shell. Macromolecules 1996, 29, 7251–7260. [Google Scholar] [CrossRef]
- Klos, J.S.; Sommer, J.-U. Simulations of Neutral and Charged Dendrimers in Solvents of Varying Quality. Macromolecules 2013, 46, 3107–3117. [Google Scholar] [CrossRef]
- Caminade, A.-M.; Majoral, J.-P. Dendrimers and nanotubes: A fruitful association. Chem. Soc. Rev. 2010, 39, 2034–2047. [Google Scholar] [CrossRef] [PubMed]
- Caminade, A.-M.; Ouali, A.; Keller, M.; Majoral, J.-P. Organocatalysis with dendrimers. Chem. Soc. Rev. 2012, 41, 4113–4125. [Google Scholar] [CrossRef] [PubMed]
- Boas, U.; Heegaard, P.M.H. Dendrimers in drug research. Chem. Soc. Rev. 2004, 33, 43–63. [Google Scholar] [CrossRef] [PubMed]
- Kazzouli, S.; Mignani, S.; Bousmina, M.; Majoral, J.-P. Dendrimer therapeutics: covalent and ionic attachments. New J. Chem. 2012, 36, 227–240. [Google Scholar] [CrossRef]
- Kobayashi, H.; Brechbiel, M.W. Nano-sized MRI contrast agents with dendrimer cores. Adv. Drug Deliv. Rev. 2005, 57, 2271–2286. [Google Scholar] [CrossRef] [PubMed]
- Rizzuto, R.; Pinton, P.; Carrington, W.; Fay, F.S.; Fogarty, K.E.; Lifshitz, L.M.; Tuft, R.A.; Pozzan, T. Close Contacts with the Endoplasmic Reticulum as Determinants of Mitochondrial Ca2+ Responses. Science 1998, 280, 1763–1766. [Google Scholar] [CrossRef] [PubMed]
- Borgese, N.; Francolini, M.; Snapp, E. Endoplasmic reticulum architecture: Structures in flux. Curr. Opin. Cell Biol. 2006, 18, 358–364. [Google Scholar] [CrossRef] [PubMed]
- Mannella, C.A. The relevance of mitochondrial membrane topology to mitochondrial function. Biochim. Biophys. Acta 2006, 1762, 140–147. [Google Scholar] [CrossRef] [PubMed]
- Chiti, F.; Webster, P.; Taddei, N.; Clark, A.; Stefani, M.; Ramponi, G.; Dobson, C.M. Designing conditions for in vitro formation of amyloid protofilaments and fibrils. Proc. Natl. Acad. Sci. USA 1999, 96, 3590–3594. [Google Scholar] [CrossRef] [PubMed]
- Woodcock, C.L.; Dmitov, S. Higher-order structure of chromatin and chromosomes. Curr. Opin. Genet. Dev. 2001, 11, 130–135. [Google Scholar] [CrossRef]
- Xie, N.; Shao, W.; Feng, L.; Lv, L.; Zhen, L. Fractal Analysis of Disordered Conductor-Insulator Composites with Different Conductor Backbone Structures near Percolation Threshold. J. Phys. Chem. C 2012, 116, 19517–19525. [Google Scholar] [CrossRef]
- Vicsek, T. Fractal Growth Phenomena; World Scientific: Singapore, 1989. [Google Scholar]
- Kouvaris, N.E.; Hata, S.; Diaz-Guilera, A. Pattern formation in multiplex networks. Sci. Rep. 2015, 5, 10840. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Friebe, C.; Hager, M.D.; Winter, A.; Schubert, U.S. Metal-Containing Polymers via Electropolymerization. Adv. Mater. 2012, 24, 332–345. [Google Scholar] [CrossRef] [PubMed]
- Winter, A.; Hoeppener, S.; Newkome, G.R.; Schubert, U.S. Terpyridine-Functionalized Surfaces: Redox-Active, Switchable, and Electroactive Nanoarchitecturesgland. Adv. Mater. 2011, 23, 3484–3498. [Google Scholar] [CrossRef] [PubMed]
- Winter, A.; Newkome, G.R.; Schubert, U.S. Catalytic Applications of Terpyridines and their Transition Metal Complexes. ChemCatChem 2011, 3, 1384–1406. [Google Scholar] [CrossRef]
- Newkome, G.R.; Wang, P.; Moorefield, C.N.; Cho, T.J.; Mohapatra, P.P.; Li, S.; Hwang, S.-H.; Lukoyanova, O.; Echegoyen, L.; Palagallo, J.A.; et al. Nanoassembly of a Fractal Polymer: A Molecular “Sierpinski Hexagonal Gasket”. Science 2006, 312, 1782–1785. [Google Scholar] [CrossRef] [PubMed]
- Shang, J.; Wang, Y.; Chen, M.; Dai, J.; Zhou, X.; Kuttner, J.; Hilt, G.; Shao, X.; Gottfried, J.M.; Wu, K. Assembling molecular Sierpinski triangle fractals. Nat. Chem. 2015, 7, 389–393. [Google Scholar] [CrossRef] [PubMed]
- Wu, B.; Lin, Y.; Zhang, Z.Z.; Chen, G.R. Trapping in dendrimers and regular hyperbranched polymers. J. Chem. Phys. 2012, 137, 044903. [Google Scholar] [CrossRef] [PubMed]
- Wu, B.; Zhang, Z.Z. Controlling the efficiency of trapping in treelike fractals. J. Chem. Phys. 2013, 139, 024106. [Google Scholar] [CrossRef] [PubMed]
- Blumen, A.; Volta, A.; Jurjiu, A.; Koslowski, T. Monitoring energy transfer in hyperbranched macromolecules through fluorescence depolarization. J. Lumin. 2005, 111, 327–334. [Google Scholar] [CrossRef]
- Blumen, A.; von Ferber, C.; Jurjiu, A.; Koslowski, T. Generalized Vicsek Fractals: Regular Hyperbranched Polymers. Macromolecules 2004, 37, 638–650. [Google Scholar] [CrossRef]
- Jurjiu, A.; Galiceanu, M.; Farcasanu, A.; Chiriac, L.; Turcu, F. Relaxation dynamics of Sierpinski hexagon fractal polymer: Exact analytical results in the Rouse-type approach and numerical results in the Zimm-type approach. J. Chem. Phys. 2016, 145, 214901. [Google Scholar] [CrossRef] [PubMed]
- Galiceanu, M.; Blumen, A. Target decay on irregular networks. J. Phys. Condens. Matter 2007, 19, 065122. [Google Scholar] [CrossRef]
- Jurjiu, A.; Koslowski, T.; Blumen, A. Dynamics of deterministic fractal polymer networks: Hydrodynamic interactions and the absence of scaling. J. Chem. Phys. 2003, 118, 2398–2404. [Google Scholar] [CrossRef]
- Jurjiu, A.; Biter, T.L.; Turcu, F. Relaxation dynamics of a multihierarchical polymer network. J. Chem. Phys. 2017, 146, 034902. [Google Scholar] [CrossRef] [PubMed]
- Volta, A.; Galiceanu, M.; Jurjiu, A. Relaxation dynamics of perturbed regular hyperbranched fractals. J. Phys. A Math. Theor. 2010, 43, 105205. [Google Scholar] [CrossRef]
- Jurjiu, A.; Dockhorn, R.; Mironova, O.; Sommer, J.-U. Two universality classes for random hyperbranched polymers. Soft Matter 2014, 10, 4935–4946. [Google Scholar] [CrossRef] [PubMed]
- Kurant, M.; Thiran, P. Layered complex networks. Phys. Rev. Lett. 2006, 96, 138701. [Google Scholar] [CrossRef] [PubMed]
- Buldyrev, S.V.; Parshani, R.; Paul, G.; Stanley, H.E.; Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 2010, 464, 1025–1028. [Google Scholar] [CrossRef] [PubMed]
- Parshani, R.; Buldyrev, S.V.; Havlin, S. Interdependent networks: Reducing the coupling strength leads to a change from a first to second order percolation transition. Phys. Rev. Lett. 2010, 105, 048701. [Google Scholar] [CrossRef] [PubMed]
- Galiceanu, M.; Strunz, W.T. Continuous-Time quantum walks on multilayer dendrimer networks. Phys. Rev. E 2016, 94, 022307. [Google Scholar] [CrossRef] [PubMed]
- Sommer, J.-U.; Blumen, A. On the statistics of generalized Gaussian structures: Collapse and random external fields. J. Phys. A 1995, 28, 6669–6674. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Clarendon Press: Oxford, UK, 1986. [Google Scholar]
- Bixon, M.; Zwanzig, R. Optimized Rouse-Zimm theory for stiff polymers. J. Chem. Phys. 1978, 68, 1896–1902. [Google Scholar] [CrossRef]
- Perico, A. Segmental relaxation in macromolecules. Acc. Chem. Res. 1989, 22, 336–342. [Google Scholar] [CrossRef]
- Toshchevikov, V.; Blumen, A.; Gotlib, Y.Y. Dynamics of Polymer Networks with Strong Differences in the Viscous Characteristics of their Crosslinks and Strands. Macromol. Theory Simul. 2007, 16, 359–377. [Google Scholar] [CrossRef]
- Schiessel, H. Unfold dynamics of generalized Gaussian structures. Phys. Rev. E 1998, 57, 5775–5781. [Google Scholar] [CrossRef]
- Ferla, R.L. Conformations and dynamics of dendrimers and cascade macromolecules. J. Chem. Phys. 1997, 106, 688–700. [Google Scholar] [CrossRef]
- Haggarty, S.J.; Clemons, P.A.; Schreiber, S.L. Chemical Genomic Profiling of Biological Networks Using Graph Theory and Combinations of Small Molecule Perturbations. J. Am. Chem. Soc. 2003, 125, 10543–10545. [Google Scholar] [CrossRef] [PubMed]
- Davis, M.J. Low-Dimensional Manifolds in Reaction-Diffusion Equations. 1. Fundamental Aspects. J. Phys. Chem. A 2006, 110, 5235–5256. [Google Scholar] [CrossRef] [PubMed]
- Markelov, D.; Dolgushev, M.; Lähderanta, E. NMR Relaxation in Dendrimers. In Graham; Webb, A., Ed.; Annual Reports on NMR Spectroscopy; Academic Press: Oxford, UK, 2017; Volume 91, pp. 1–66. [Google Scholar]
- Liu, H.; Dolgushev, M.; Qi, Y.; Zhang, Z. Laplacian spectra of a class of small-world networks and their applications. Sci. Rep. 2015, 5, 9024. [Google Scholar] [CrossRef] [PubMed]
- Jurjiu, A.; Biter, T.L.; Turcu, F. Dynamics of a Polymer Network Based on Dual Sierpinski Gasket and Dendrimer: A Theoretical Approach. Polymers 2017, 9, 245. [Google Scholar] [CrossRef]
- Percec, V. From Synthetic Macromolecules to Biological-Like Complex Systems. Adv. Polym. Sci. 2013, 216, 173–197. [Google Scholar]
- Sato, K.; Anzai, J. Dendrimers in layer-by-layer assemblies: Synthesis and applications. Molecules 2013, 18, 8440–8460. [Google Scholar] [CrossRef] [PubMed]
- Xiao, F.-X.; Pagliaro, M.; Xu, Y.-J.; Liu, B. Layer-by-layer assembly of versatile nanoarchitectures with diverse dimensionality: A new perspective for rational construction of multilayer assemblies. Chem. Soc. Rev. 2016, 45, 3088–3121. [Google Scholar] [CrossRef] [PubMed]
- Chang, J.; Zhao, Q.; Kang, L.; Li, H.; Xie, M.; Liao, X. Multiresponsive Supramolecular Gel Based on Pillararene-Containing Polymers. Macromolecules 2016, 49, 2814–2820. [Google Scholar] [CrossRef]
- Chen, H.; Hou, S.; Ma, H.; Li, X.; Tan, Y. Controlled gelation kinetics of cucurbit[7]uril-adamantane cross-linked supramolecular hydrogels with competing guest molecules. Sci. Rep. 2016, 6, 20722. [Google Scholar] [CrossRef] [PubMed]
- Shchipunov, Y.A.; Hoffmann, H. Indicative Evidence for Coexistence of Long and Short Polymer-like Micelles in Lecithin Organogel from Rheological Studies. Langmuir 1999, 15, 7108–7110. [Google Scholar] [CrossRef]
- Wang, X. Formation and elasticity of layer networks. J. Polym. Sci. Part B 1999, 37, 667–677. [Google Scholar] [CrossRef]
- Brunsveld, L.; Folmer, B.J.B.; Meijer, E.W.; Sijbesma, R.P. Supramolecular Polymers. Chem. Rev. 2001, 101, 4071–4098. [Google Scholar] [CrossRef] [PubMed]
- Hackelbusch, S.; Rossow, T.; van Assenberg, P.; Seiffert, S. Chain Dynamics in Supramolecular Polymer Networks. Macromolecules 2013, 46, 6273–6286. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Kellerer, H.; Blumen, A. Anisotropic excitation transfer to acceptors randomly distributed on surfaces. Biophys. J. 1984, 46, 1–8. [Google Scholar] [CrossRef]
- Bodunov, E.N.; Berberan-Santos, M.N.; Nunes Pereira, E.J.; Martinho, J.M.G. Eigenvalue spectrum of the survival probability of excitation in nonradiative energy transport. Chem. Phys. 2000, 259, 49–61. [Google Scholar] [CrossRef]
- Farinha, J.P.S.; Martinho, J.M.G. Resonance Energy Transfer in Polymer Nanodomains. J. Phys. Chem. C 2008, 112, 10591–10601. [Google Scholar] [CrossRef]
- Fruchey, K.; Lawler, C.M.; Fayer, M.D. Investigation of Nanostructure in Room Temperature Ionic Liquids using Electronic Excitation Transfer. J. Phys. Chem. B 2012, 116, 3054–3064. [Google Scholar] [CrossRef] [PubMed]
- Goodson, T.G. Optical Excitations in Organic Dendrimers Investigated by Time-Resolved and Nonlinear Optical Spectroscopy. Acc. Chem. Res. 2005, 38, 99–107. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Yoon, M.-C.; Yoo, H.; Kim, P.; Kim, D. Excitation energy transfer in multiporphyrin arrays with cyclic architectures: Towards artificial light-harvesting antenna complexes. Chem. Soc. Rev. 2012, 41, 4808–4826. [Google Scholar] [CrossRef] [PubMed]
- Webber, S.E. Polymer Micelles: An Example of Self-Assembling Polymers. J. Phys. Chem. B 1998, 102, 2618–2626. [Google Scholar] [CrossRef]
- Bunde, A.; Havlin, S. Fractals and Disordered Systems; Springer: Berlin, Germany, 1991. [Google Scholar]
- Vlassopoulos, D.; Pitsikalis, M.; Hadjichristidis, N. Linear Dynamics of End-Functionalized Polymer Melts: Linear Chains, Stars, and Blends. Macromolecules 2000, 33, 9740–9746. [Google Scholar] [CrossRef]
- Chen, S.; Döhler, D.; Binder, W.H. Rheology of hydrogen-bonded dendritic supramolecular polymer networks in the melt state. Polymer 2016, 107, 466–473. [Google Scholar] [CrossRef]
- Yan, T.; Schröter, K.; Herbst, F.; Binder, W.H.; Thurn-Albrecht, T. Nanostructure and Rheology of Hydrogen-Bonding Telechelic Polymers in the Melt: From Micellar Liquids and Solids to Supramolecular Gels. Macromolecules 2014, 47, 2122–2130. [Google Scholar] [CrossRef]
- Brassinne, J.; Stevens, A.M.; Van Ruymbeke, E.; Gohy, J.-F.; Fustin, C.-A. Hydrogels with Dual Relaxation and Two-Step Gel-Sol Transition from Heterotelechelic Polymers. Macromolecules 2013, 46, 9134–9143. [Google Scholar] [CrossRef]
- Goldansaz, H.; Fustin, C.-A.; Wübbenhorst, M.; van Ruymbeke, E. How Supramolecular Assemblies Control Dynamics of Associative Polymers: Toward a General Picture. Macromolecules 2016, 49, 1890–1902. [Google Scholar] [CrossRef]
- Watanabe, H.; Yao, M.-L.; Sato, T.; Osaki, K. Non-Newtonian Flow Behavior of Diblock Copolymer Micelles: Shear-Thinning in a Nonentangling Matrix. Macromolecules 1997, 30, 5905–5912. [Google Scholar] [CrossRef]
- Bian, Y.; Pejanovic, S.; Kenny, J.; Mijovic, J. Dynamics of Multifunctional Polyhedral Oligomeric Silsesquioxane/Poly(propylene oxide) Nanocomposites As Studied by Dielectric Relaxation Spectroscopy and Dynamic Mechanical Spectroscopy. Macromolecules 2007, 40, 6239–6248. [Google Scholar] [CrossRef]
- Squires, A.M.; Tajbakhsh, A.R.; Terentjev, E.M. Dynamic Shear Modulus of Isotropic Elastomers. Macromolecules 2004, 37, 1652–1659. [Google Scholar] [CrossRef]
- Bodunov, E.N. Theoretical Studies of Spectral Migration of Excitations in Three-Dimentional Media. Opt. Spectrosc. 1988, 84, 350–373. [Google Scholar]
- Kopelman, R.; Shortreed, M.; Shi, Z.-Y.; Tan, W.; Xu, Z.; Moore, J.S.; Bar-Haim, A.; Klafter, J. Spectroscopic Evidence for Excitonic Localization in Fractal Antenna Supermolecules. Phys. Rev. Lett. 1997, 78, 1239–1242. [Google Scholar] [CrossRef]
- Bar-Haim, A.; Klafter, J.; Kopelman, R. Dendrimers as Controlled Artificial Energy Antennae. J. Am. Chem. Soc. 1997, 119, 6197–6198. [Google Scholar] [CrossRef]
- Deng, J.C.; Jiang, X.; Zhang, X.; Hu, W.; Crawford, J.W. Continuous time random walk model better describes the tailing of atrazine transport in soil. Chemosphere 2008, 71, 2150–2157. [Google Scholar] [CrossRef] [PubMed]
- Bittelli, M.; Campbell, G.S.; Flury, M. Characterization of Particle Size Distribution in soils using a Fragmentation Model. Soil Sci. Soc. Am. J. 1999, 63, 782–788. [Google Scholar] [CrossRef]
- Bittelli, M.; Tomei, F.; Pistocchi, A.; Flury, M.; Boll, J.; Brooks, E.S.; Antolini, G. Development and testing of a physically based, three-dimensional model of surface and subsurface hydrology. Adv. Water Res. 2010, 33, 106–122. [Google Scholar] [CrossRef]
- Chen, S.G.; Ceulemans, R.; Impens, I. A fractal-based Populus canopy structure model for the calculation of light interception. For. Ecol. Manag. 1994, 69, 97–110. [Google Scholar] [CrossRef]
- Jurjiu, A.; Volta, A.; Beu, T. Relaxation dynamics of a polymer network modeled by a multihierarchical structure. Phys. Rev. E 2011, 84, 011801. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Wu, B.; Zhang, H.; Zhou, S.; Guan, J.; Wang, Z. Determining global mean-first-passage time of random walks on Vicsek fractals using eigenvalues of Laplacian matrices. Phys. Rev. E 2010, 81, 031118. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Julaiti, A.; Hou, B.; Zhang, H.; Chen, G. Mean first-passage time for random walks on undirected networks. Eur. Phys. J. B 2011, 84, 691–697. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jurjiu, A.; Turcu, F.; Galiceanu, M. Dynamics of a Complex Multilayer Polymer Network: Mechanical Relaxation and Energy Transfer. Polymers 2018, 10, 164. https://doi.org/10.3390/polym10020164
Jurjiu A, Turcu F, Galiceanu M. Dynamics of a Complex Multilayer Polymer Network: Mechanical Relaxation and Energy Transfer. Polymers. 2018; 10(2):164. https://doi.org/10.3390/polym10020164
Chicago/Turabian StyleJurjiu, Aurel, Flaviu Turcu, and Mircea Galiceanu. 2018. "Dynamics of a Complex Multilayer Polymer Network: Mechanical Relaxation and Energy Transfer" Polymers 10, no. 2: 164. https://doi.org/10.3390/polym10020164





