Modeling and Characterization of Grain Boundaries and Slip Transmission in Dislocation Density-Based Crystal Plasticity
Abstract
:1. Introduction
2. Dislocation Density-Based Crystal Plasticity
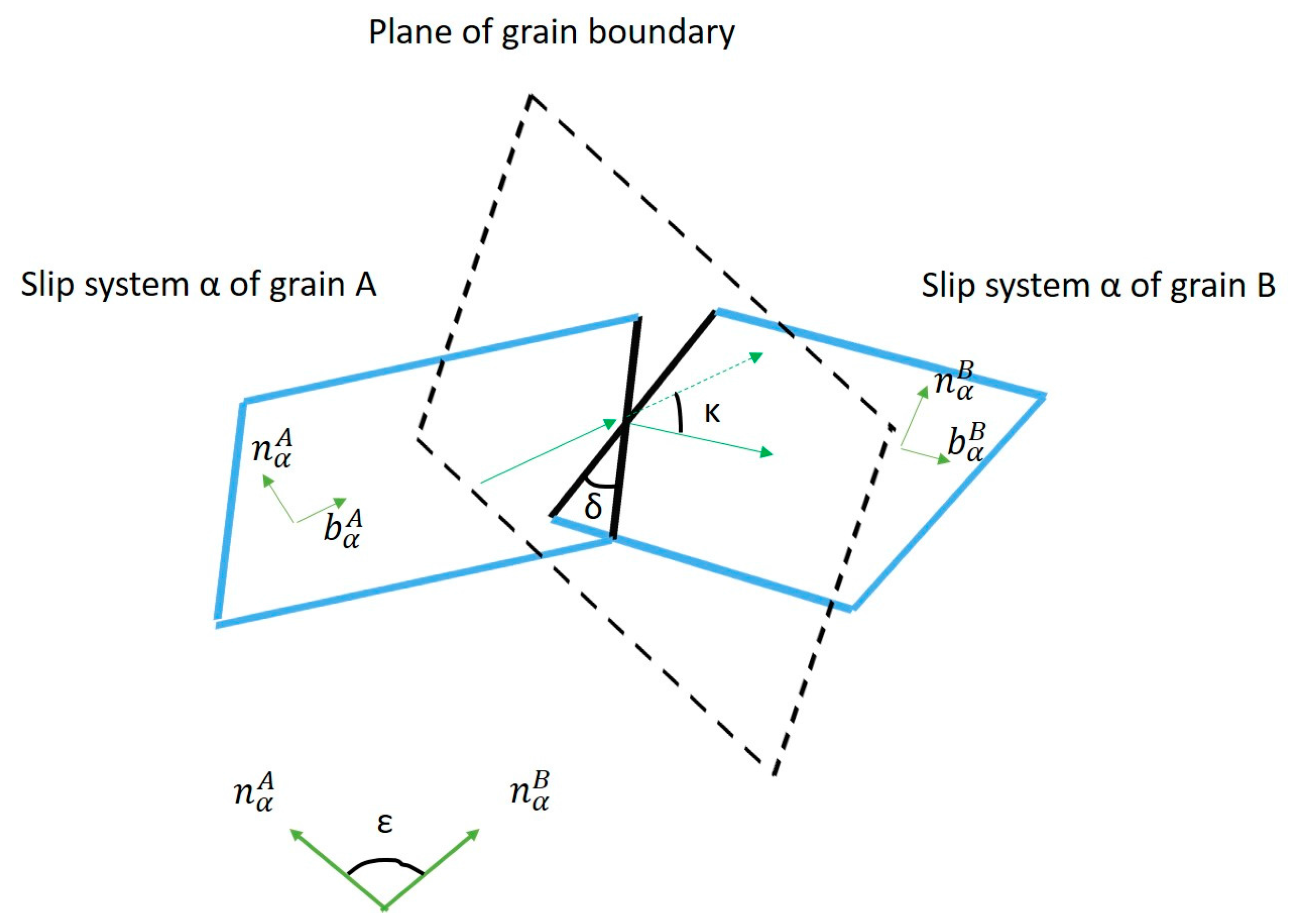
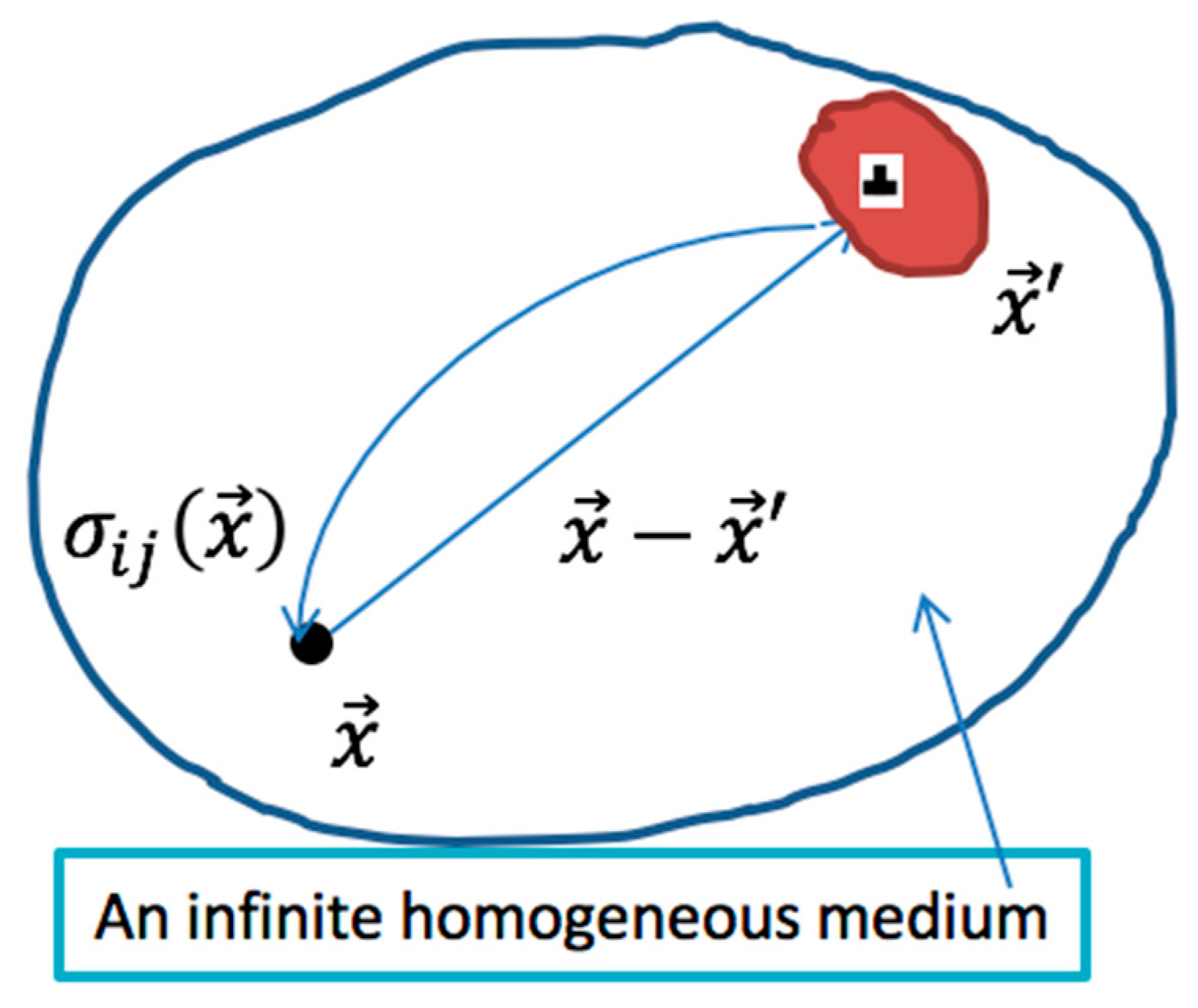
Grain Boundary Dislocation Flux Interaction Methodology
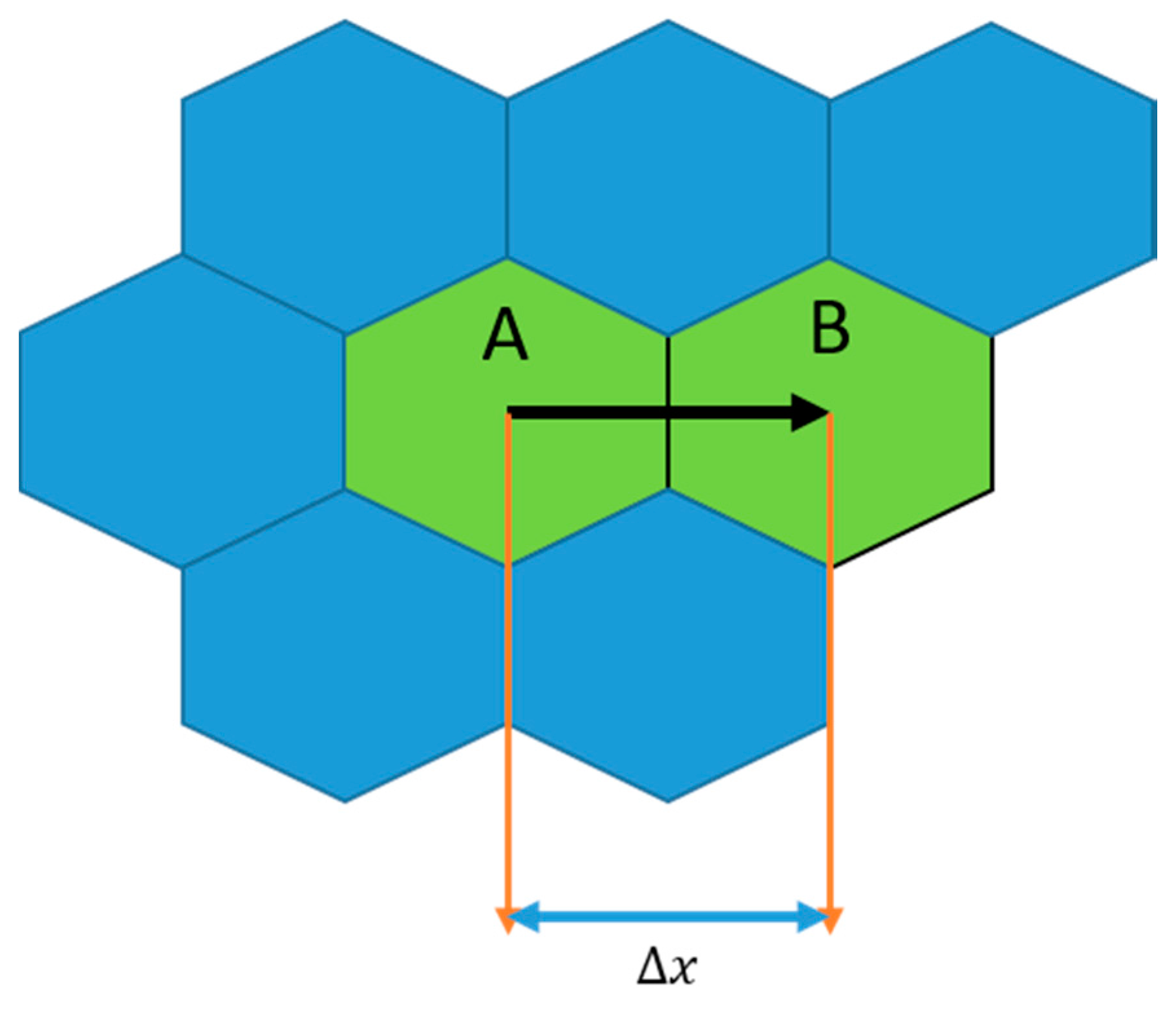
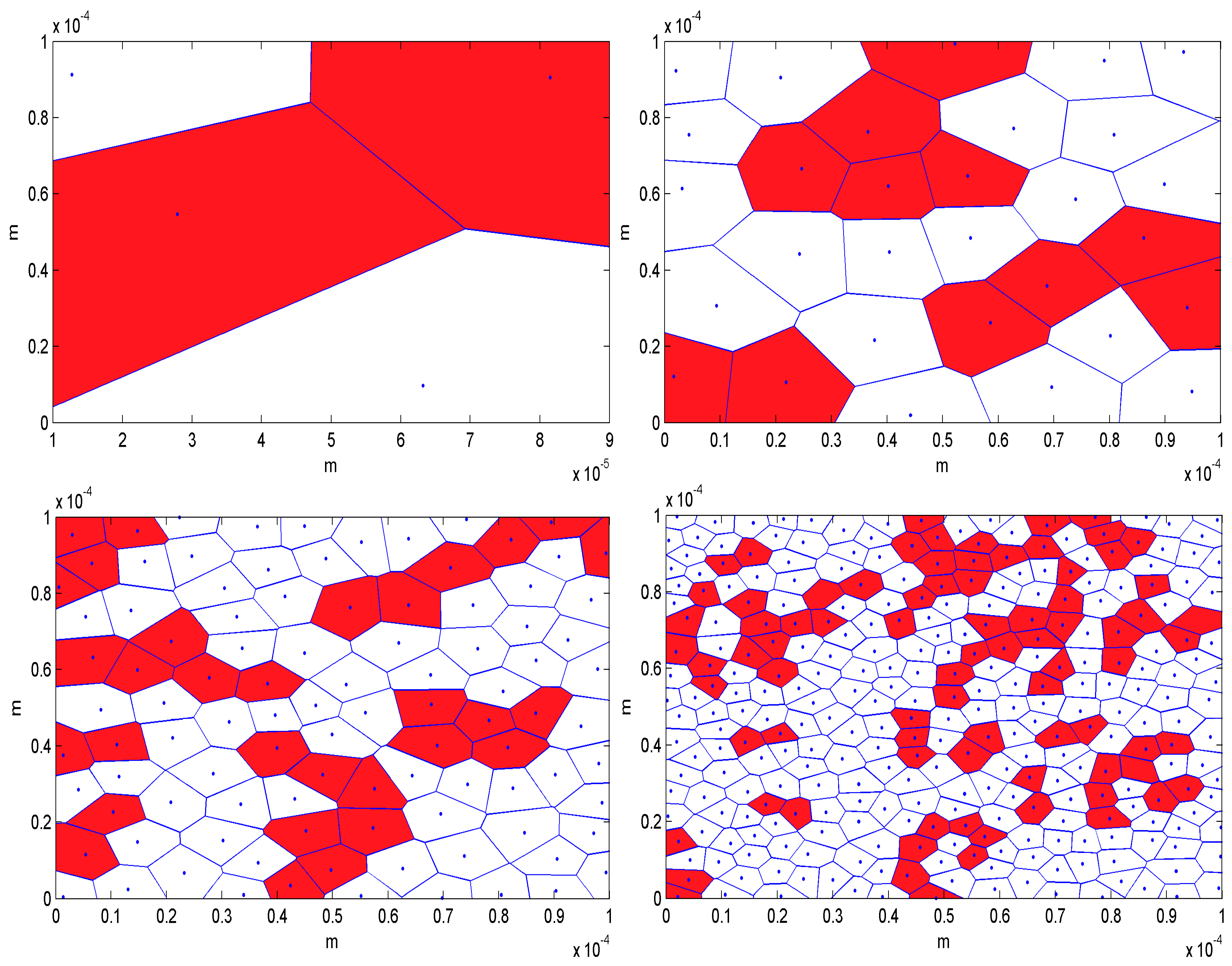
3. Implementation of 2D Controlled Poisson Voronoi Tessellation (CPVT) Model
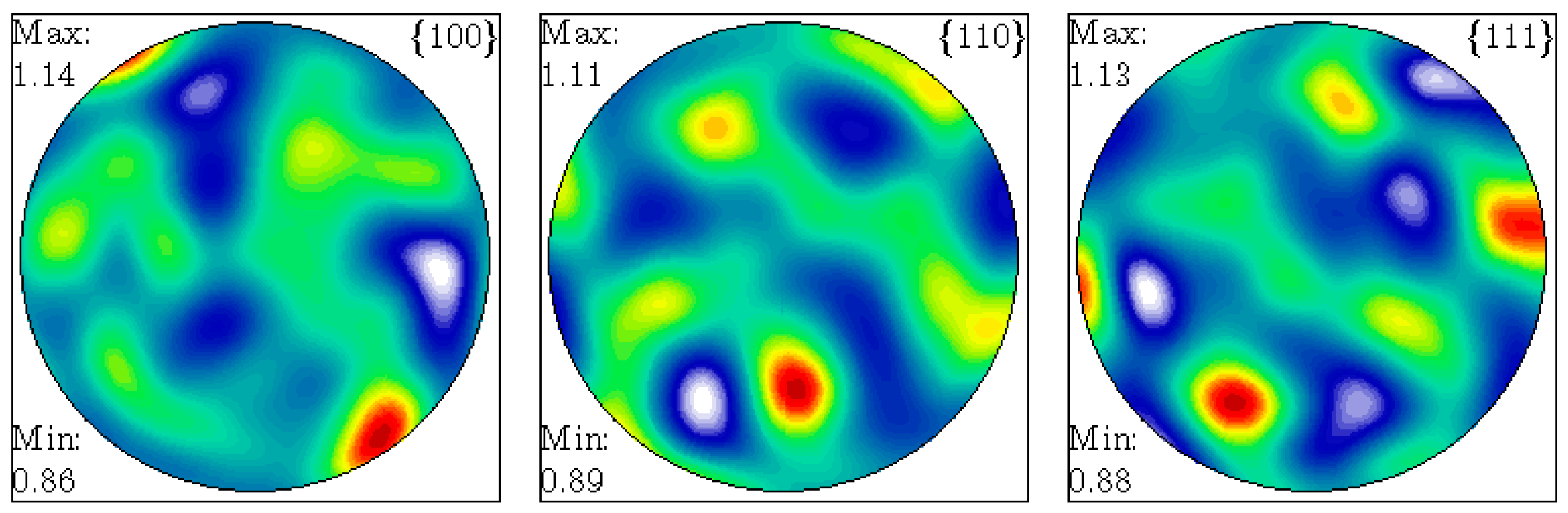
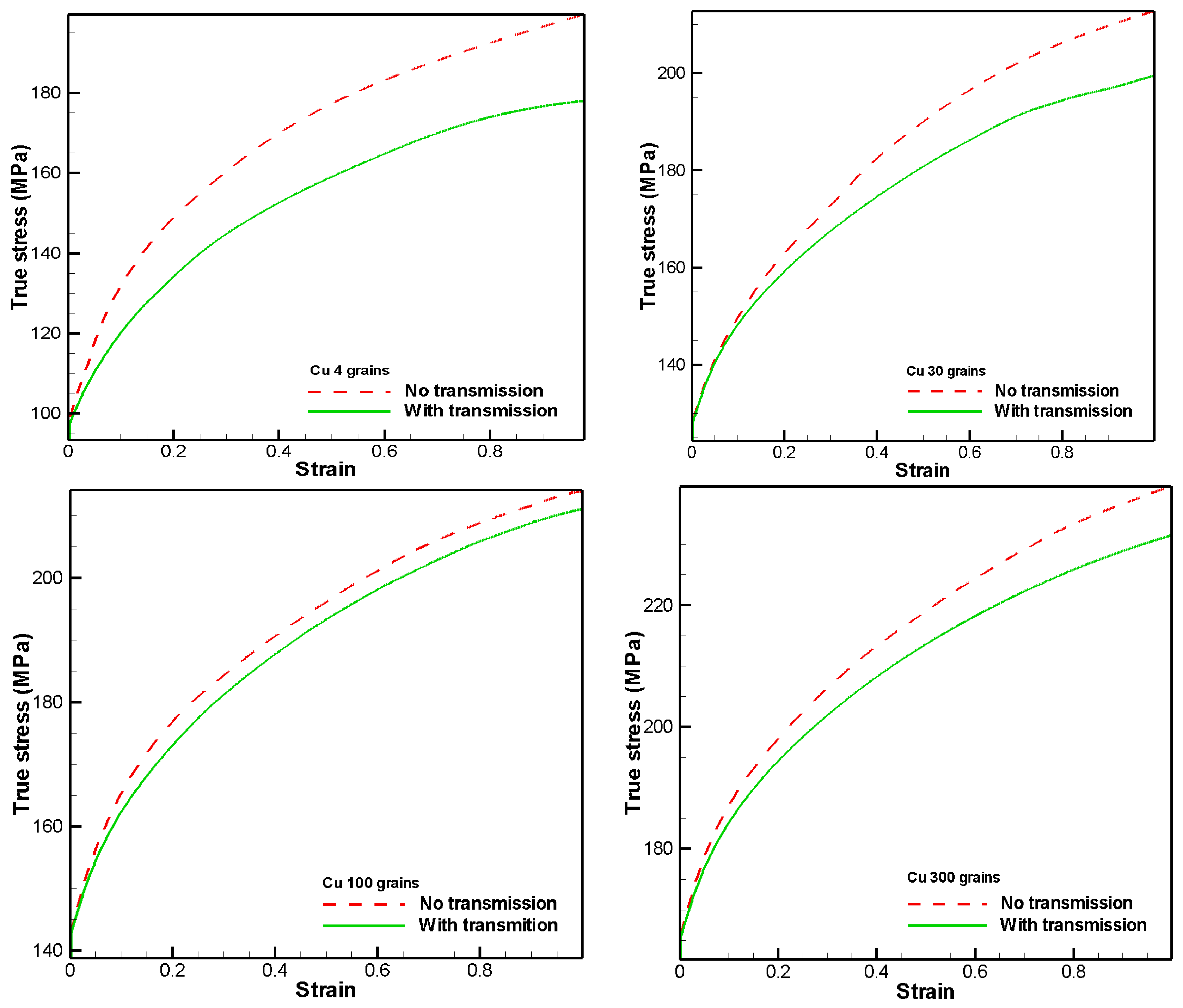
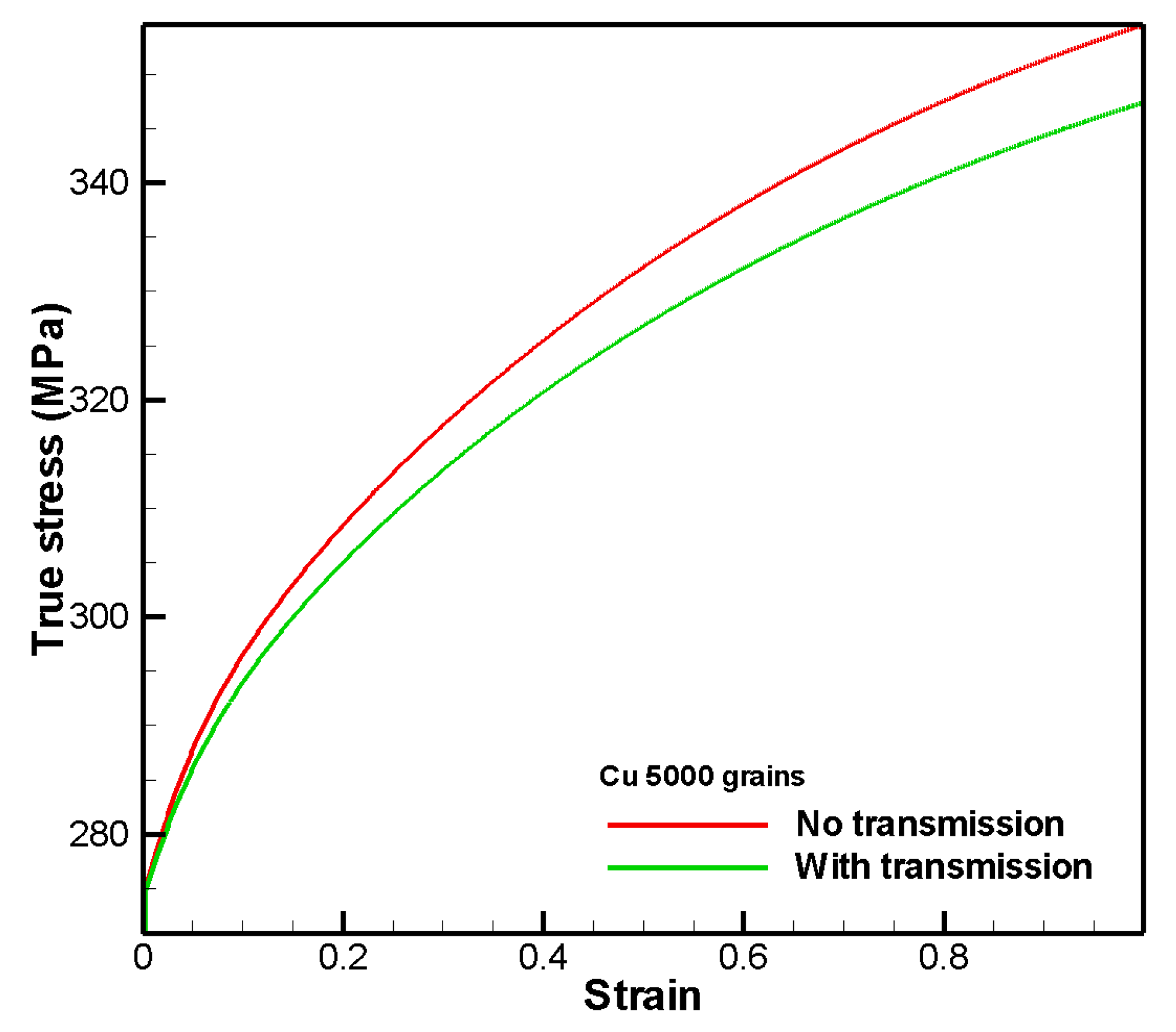
4. Numerical Results and Discussion
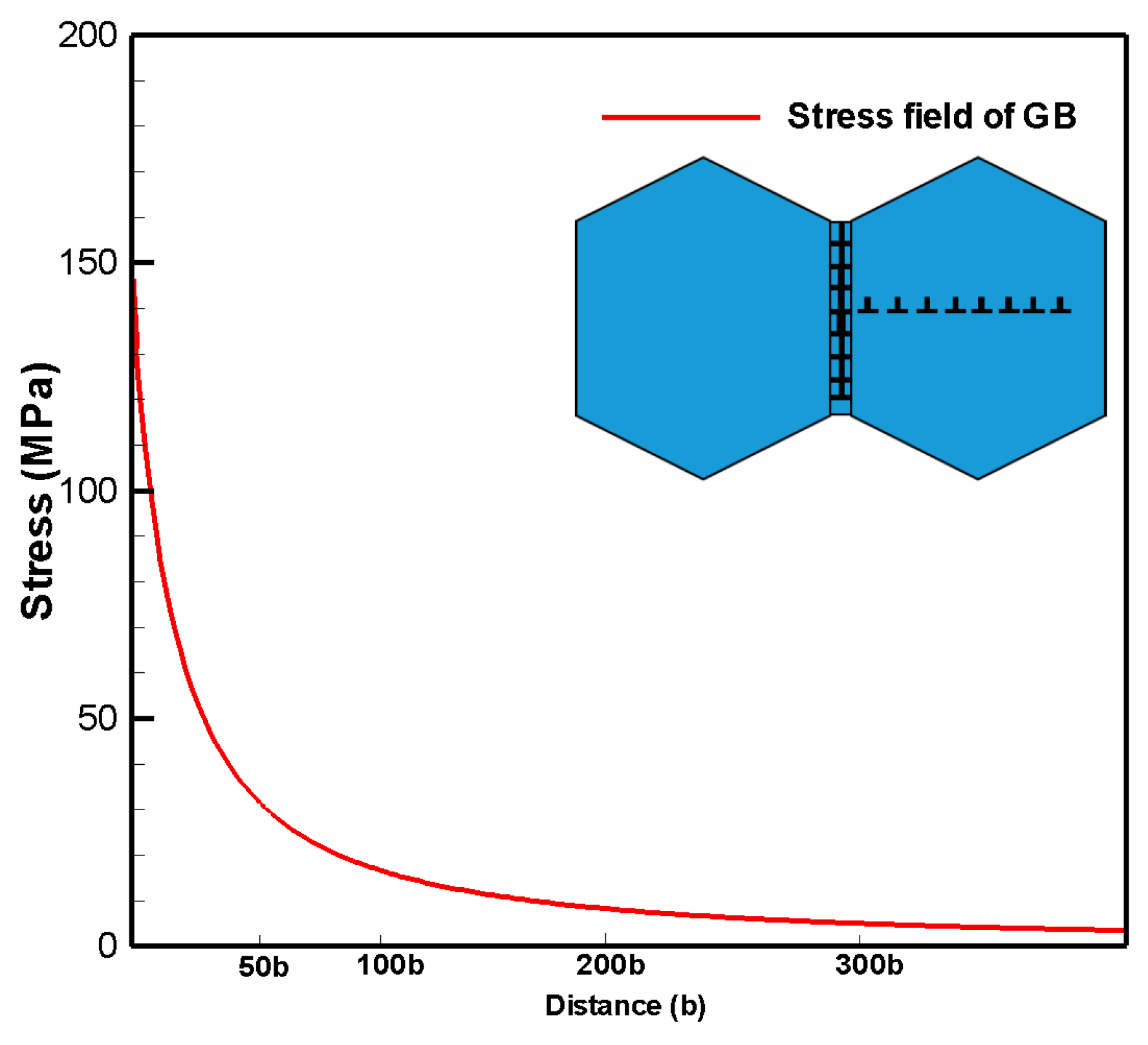
Effect of Extended Stress Field of Grain Boundary and Long-Range Interaction of Dislocations
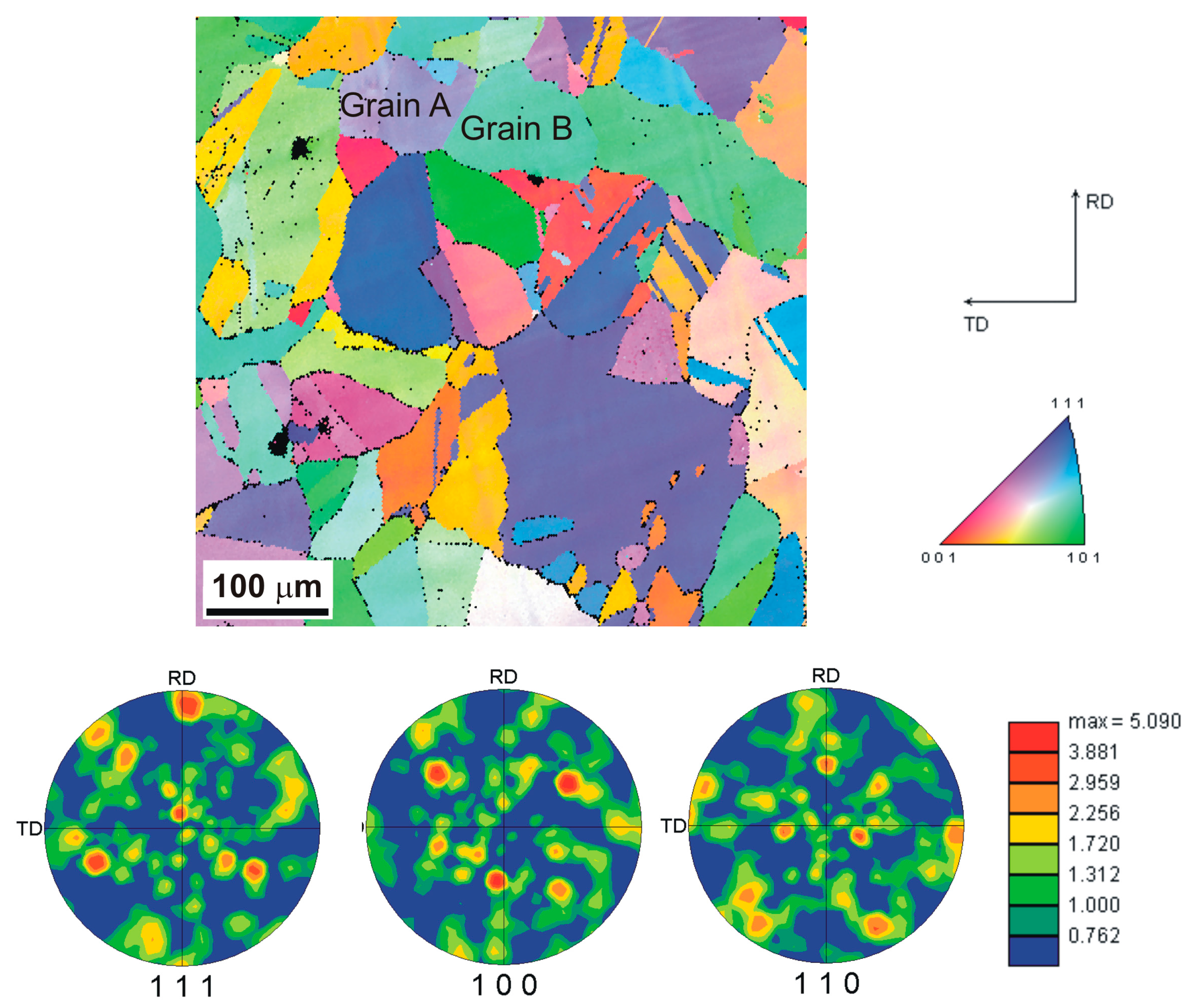
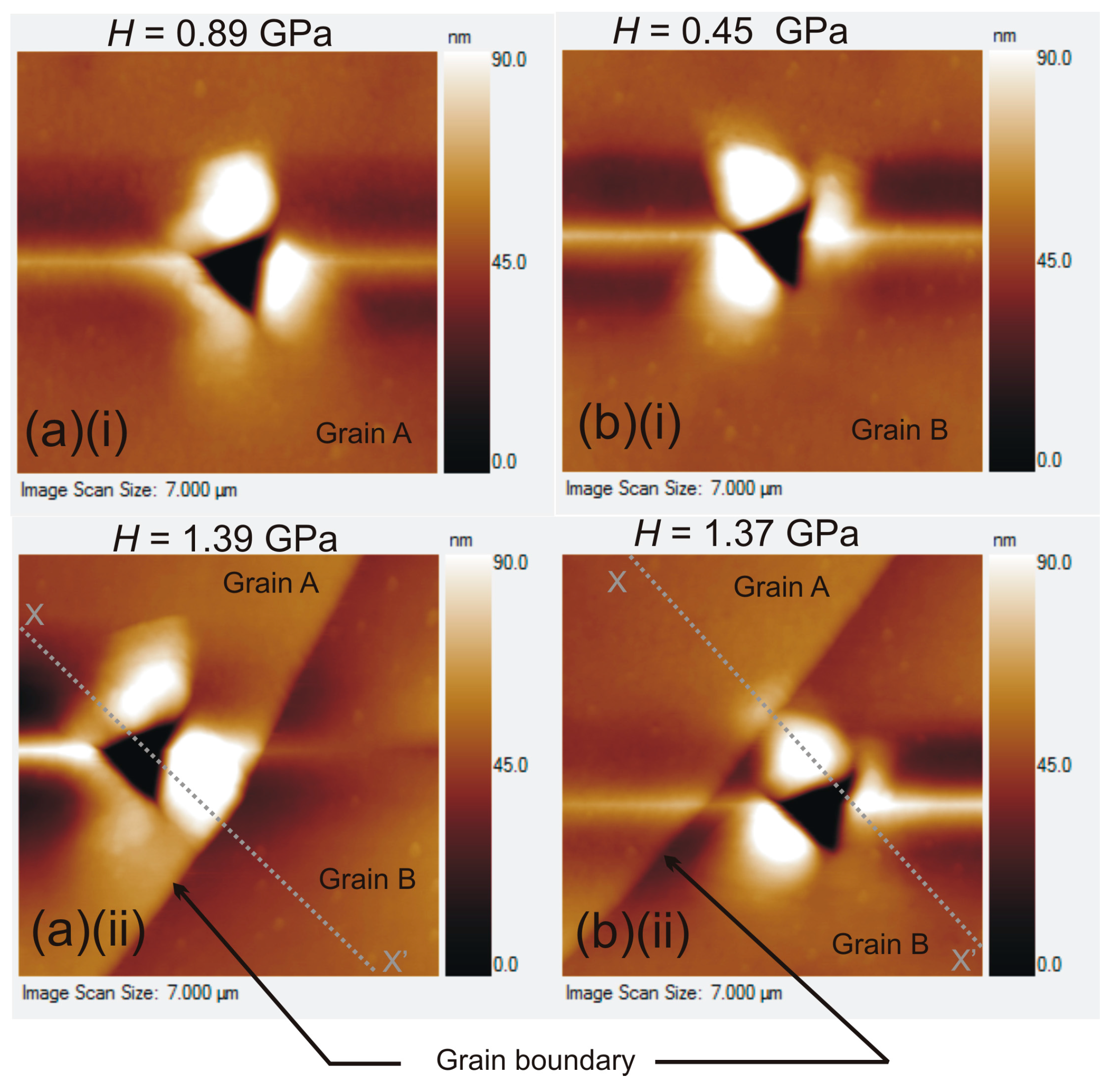
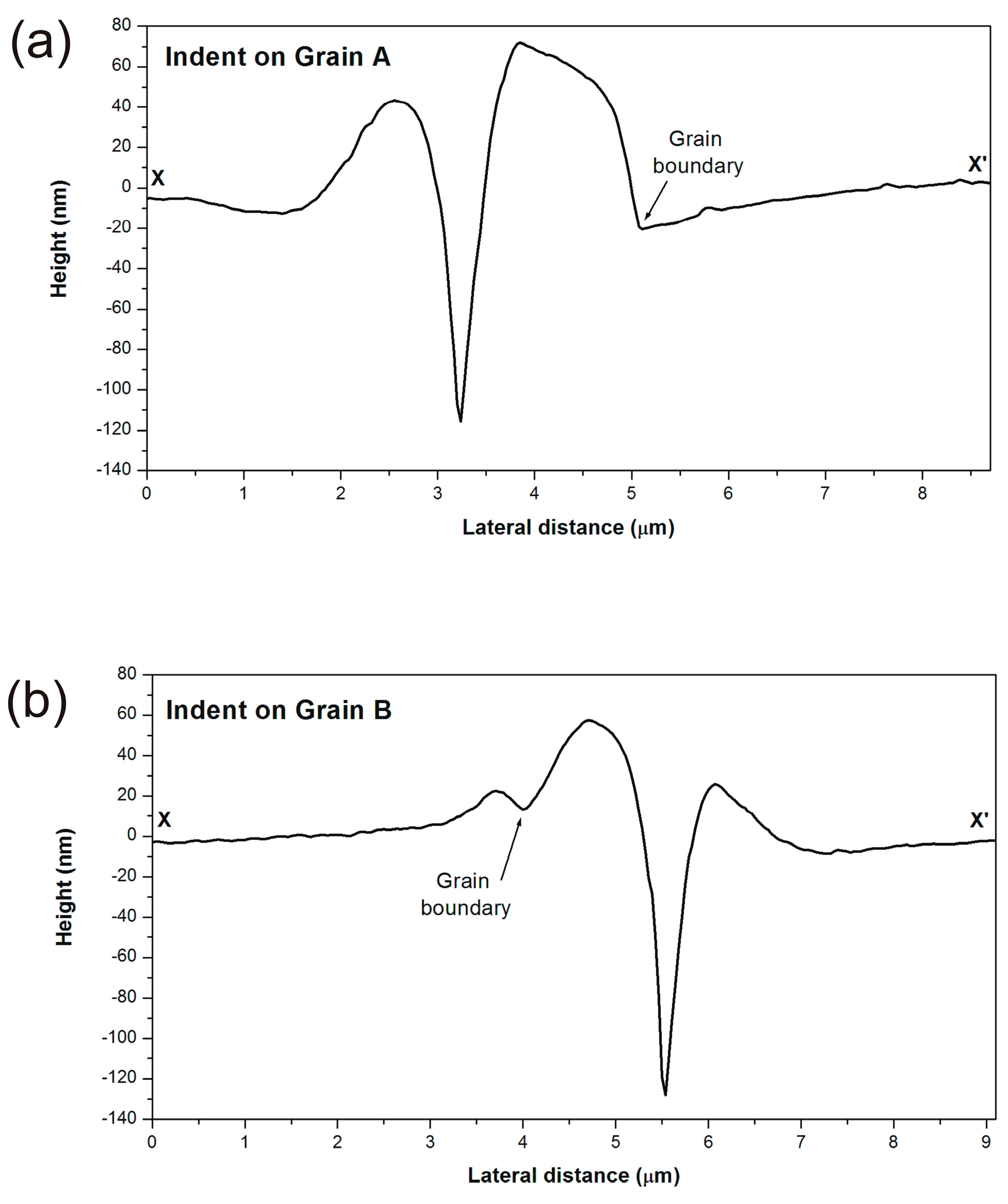
5. Experimental Study
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Stricker, M.; Gagel, J.; Schmitt, S.; Schulz, K.; Weygand, D.; Gumbsch, P. On slip transmission and grain boundary yielding. Comput. Micromech. Mater. 2016, 51, 271–278. [Google Scholar] [CrossRef]
- Shen, Z.; Wagoner, R.H.; Clsrk, W.A.T. Dislocation and grain boundary interactions in metals. Entomophaga 1994, 39, 107–119. [Google Scholar] [CrossRef]
- Hirth, J.P. The influence of grain boundaries on mechanical properties. Metall. Trans. 1972, 3, 3047–3067. [Google Scholar] [CrossRef]
- Petch, N.J. The cleavage strength of polycrystals. J. Iron Steel Inst. 1953, 174, 25–28. [Google Scholar]
- Hall, E.O. The deformation and ageing of mild steel. Proc. Phys. Soc. B 1951, 64, 747. [Google Scholar] [CrossRef]
- Leibfried, G. Verteilung von Versetzungen im statischen Gleichgewicht. Z. Phys. 1951, 130, 214–226. [Google Scholar] [CrossRef]
- Esheby, J.D.; Frank, F.; Nabarro, F.R. The equilibrium of linear arrays of dislocations. Philos. Mag. 1951, 42, 351–364. [Google Scholar] [CrossRef]
- Hirth, J.P.; Lothe, J. Theory of Dislocations; McGraw-Hill: New York, NY, USA, 1969. [Google Scholar]
- Shao, S.; Medyanik, S.N. Interaction of dislocations with incoherent interfaces in nanoscale FCC–BCC metallic bi-layers. Model. Simul. Mater. Sci. Eng. 2010, 18, 55010. [Google Scholar] [CrossRef]
- Askari, H.; Zbib, H.M.; Sun, X. Multiscale modeling of inclusions and precipitation hardening in metal matrix composites: Application to advanced high-strength steels. ASCE J. Nanomech. Micromech. 2013, 3, 24–33. [Google Scholar] [CrossRef]
- Lim, H.; Lee, M.G.; Kim, J.H.; Adams, B.L.; Wagoner, R.H. Simulation of polycrystal deformation with grain and grain boundary effects. Int. J. Plast. 2011, 27, 1328–1354. [Google Scholar] [CrossRef]
- Brentnall, W.D.; Rostoker, W. Some observations on microyielding. Acta Metall. 1965, 13, 187–198. [Google Scholar] [CrossRef]
- Hauser, J.J.; Chalmers, B. The plastic deformation of bicrystals of f.c.c. metals. Acta Metall. 1961, 9, 802–818. [Google Scholar] [CrossRef]
- Worthington, P.J.; Smith, E. The formation of slip bands in polycrystalline 3% silicon iron in the pre-yield microstrain region. Acta Metall. 1964, 12, 1277–1281. [Google Scholar] [CrossRef]
- Carrington, W.E.; McLean, D. Slip nuclei in silicon-iron. Acta Metall. 1965, 13, 493–499. [Google Scholar] [CrossRef]
- Bamford, T.A.; Hardiman, B.; Shen, Z.; Clark, W.A.T.; Wagoner, R.H. Micromechanism of slip propagation through a high angle boundary in alpha brass. Scr. Metall. 1986, 20, 253–258. [Google Scholar]
- Li, D.; Zbib, H.; Sun, X.; Khaleel, M. Predicting plastic flow and irradiation hardening of iron single crystal with mechanism-based continuum dislocation dynamics. Int. J. Plast. 2014, 52, 3–17. [Google Scholar] [CrossRef]
- Askari, H.; Young, J.; Field, D.; Kridli, G.; Li, D.; Zbib, H. A study of the hot and cold deformation of twin-roll cast magnesium alloy AZ31. Philos. Mag. 2014, 94, 381–403. [Google Scholar] [CrossRef]
- Lebensohn, R.A.; Tomé, C.N. A selfconsistent approach for the simulation of plastic deformation and texture development of polycrystals: Application to Zirconium alloys. Acta Metall. 1993, 41, 2611–2624. [Google Scholar] [CrossRef]
- Tomé, C.; Lebensohn, R.A. A self-consistant visco-plastic model: Calculation of rolling texture of anisotropic materials. Mater. Sci. Eng. A 1994, 175, 71–82. [Google Scholar]
- Orowan, E. Problems of plastic gliding. Proc. Phys. Soc. 1940, 52, 8–22. [Google Scholar] [CrossRef]
- Wei, Q.; Kecskes, L.; Jiao, T.; Hartwig, K.T.; Ramesh, K.T.; Ma, E. Adiabatic shear banding in ultrafine-grained Fe processed by severe plastic deformation. Acta Mater. 2004, 52, 1859–1869. [Google Scholar] [CrossRef]
- Bailey, J.E.; Hirsch, P.B. The dislocation distribution, flow stress, stored energy in cold worked polycrystalline silver. Philos. Mag. 1960, 5, 485–497. [Google Scholar] [CrossRef]
- Alankar, A. Development of a 3D Microstructure Sensetive Crystal Plasticity Model for Aluminum; Washington State University: Pullman, WA, USA, 2010. [Google Scholar]
- Ohashi, T.; K, M.; Zbib, H. A multiscale approach for modeling scale-dependent yield stress in polycrystalline metals. Int. J. Plast. 2007, 23, 897–914. [Google Scholar] [CrossRef]
- Taheri-Nassaj, N.; Zbib, H.M. A Mesoscale Model of Plasticity: Dislocation Dynamics and Patterning (1D). J. Eng. Mater. Technol. 2016, 138, 41015. [Google Scholar] [CrossRef]
- Hingwe, A.K.; Subramanian, K.N. Deformation of duplex crystals and two-phase bicrystals of alpha-beta brass. J. Mater. Sci. 1975, 10, 183–188. [Google Scholar] [CrossRef]
- Prantl, W.; Werner, E.; Stuwe, H.P. Statistical Treatment of Measured Orientation Relationships. Textures Microstruct. 1988, 8–9, 483. [Google Scholar] [CrossRef]
- Werner, E.; Prantel, W. Slip transfer across grain and phase boundaries. Acta Metall. Mater 1989, 38, 533–537. [Google Scholar] [CrossRef]
- Lange, F.F. Mathematical characterization of a general bicrystal. Acta Metllall. 1967, 15, 311–318. [Google Scholar] [CrossRef]
- Davis, K.G.; Teightsoonian, E.; Lu, A. Slip band continuity across grain boundaries in aluminum. Acta Metall. 1996, 14, 1677–1684. [Google Scholar] [CrossRef]
- Shen, Z.; Wagoner, R.H.; Clark, W.A. Dislocation pile-up and grain boundary interactions in 304 stainless stee. Scr. Metall. 1986, 20, 921–926. [Google Scholar] [CrossRef]
- Zhang, P.; Balint, D.; Lin, J. Controlled Poisson Voronoi tessellation for virtual grain structure generation: A statistical evaluation. Philos. Mag. 2011, 91, 4555–4573. [Google Scholar] [CrossRef]
- Zhang, P.; Karimpour, D.; Balint, D.; Lin, J.; Farrugia, D. A controlled Poisson Voronoi tessellation for grain and cohesive boundary generation applied to crystal plasticity analysis. Comput. Mater. Sci. 2012, 64, 84–89. [Google Scholar] [CrossRef]
- Cao, J.; Zhuang, W.; Wang, S.; Ho, K.; Zhang, N.; Lin, J.; Dean, T. An integrated crystal plasticity FE system for microforming simulation. J. Multiscale Model. 2009, 1, 107–124. [Google Scholar] [CrossRef]
- Akarapu, S. Dislocation Interactions with Interfaces; Washington State University: Pullman, WA, USA, 2009. [Google Scholar]
- Shizawa, K.; Zbib, H.M. A thermodynamical theory of gradient elastoplasticity with dislocation density tensor. I: Fundamentals. Int. J. Plast. 1999, 15, 899–938. [Google Scholar] [CrossRef]
- Nye, J. Some geometrical relations in dislcoated crystals. Acta Metall. 2015, 8, 159–168. [Google Scholar]
- Soer, W.A.; de Hosson, J.T.M. Detection of grain boundary resistance to slip transfer using nanoindentation. Mater. Lett. 2005, 59, 3192–3195. [Google Scholar] [CrossRef]
- Soifer, Y.M.; Verdyan, A.; Kazakevich, M.; Rabkin, E. Nanohardness of copper in the vicinity of grain boundary. Scr. Mater. 2002, 47, 799–804. [Google Scholar] [CrossRef]
- Oliver, W.; Pharr, G.M.J. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Boyer, H.E. Hardness Testing; Metals Park: Geauga, OH, USA, 1987. [Google Scholar]
- Tabor, D. Hardness of Metal; Calrendon Press: Wotton-under-Edge, UK, 1951. [Google Scholar]



| Terms | Definition |
|---|---|
| Multiplication and growth of resident dislocations as well as the production of new dislocations from Frank-Reed sources in the slip system α | |
| Mutual annihilation of two mobile edge or screw dislocations | |
| Mobile dislocations turns into immobile dislocations | |
| Immobile dislocations turns to mobilization | |
| cross-slip | |
| Annihilation between mobile and immobile dislocations |
| H (GPa) of Indent Made in Grain A | H (GPa) of Indent Made in Grain B | |
|---|---|---|
| Far from any grain boundaries (n = 50) * | 1.89, standard deviation = 0.09 | 1.70, standard deviation = 0.11 |
| Near the same grain boundary (n = 1) * | 94.72 (at ~2.0 µm from the grain boundary) | 113.34 (at ~1.5 µm from the grain boundary) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamid, M.; Lyu, H.; Schuessler, B.J.; Wo, P.C.; Zbib, H.M. Modeling and Characterization of Grain Boundaries and Slip Transmission in Dislocation Density-Based Crystal Plasticity. Crystals 2017, 7, 152. https://doi.org/10.3390/cryst7060152
Hamid M, Lyu H, Schuessler BJ, Wo PC, Zbib HM. Modeling and Characterization of Grain Boundaries and Slip Transmission in Dislocation Density-Based Crystal Plasticity. Crystals. 2017; 7(6):152. https://doi.org/10.3390/cryst7060152
Chicago/Turabian StyleHamid, Mehdi, Hao Lyu, Ben Jared Schuessler, Pui Ching Wo, and Hussein M Zbib. 2017. "Modeling and Characterization of Grain Boundaries and Slip Transmission in Dislocation Density-Based Crystal Plasticity" Crystals 7, no. 6: 152. https://doi.org/10.3390/cryst7060152





