Crystal Growth and Glass-Like Thermal Conductivity of Ca3RE2(BO3)4 (RE = Y, Gd, Nd) Single Crystals
Abstract
:1. Introduction
2. Experimental
3. Results and Discussion
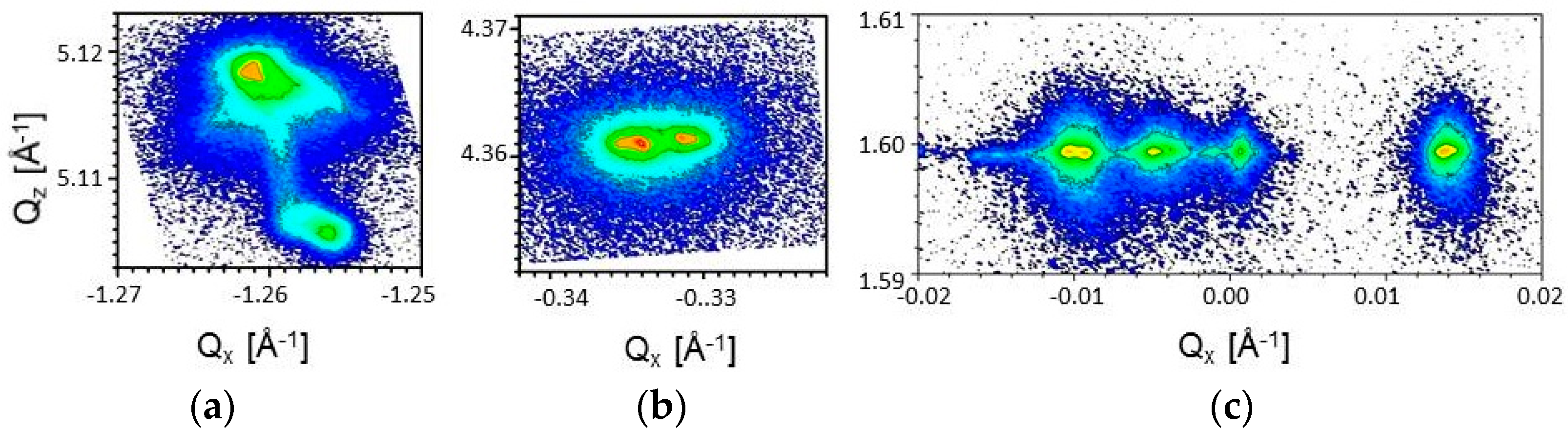
3.1. Crystal Structure
3.2. Chemical Composition
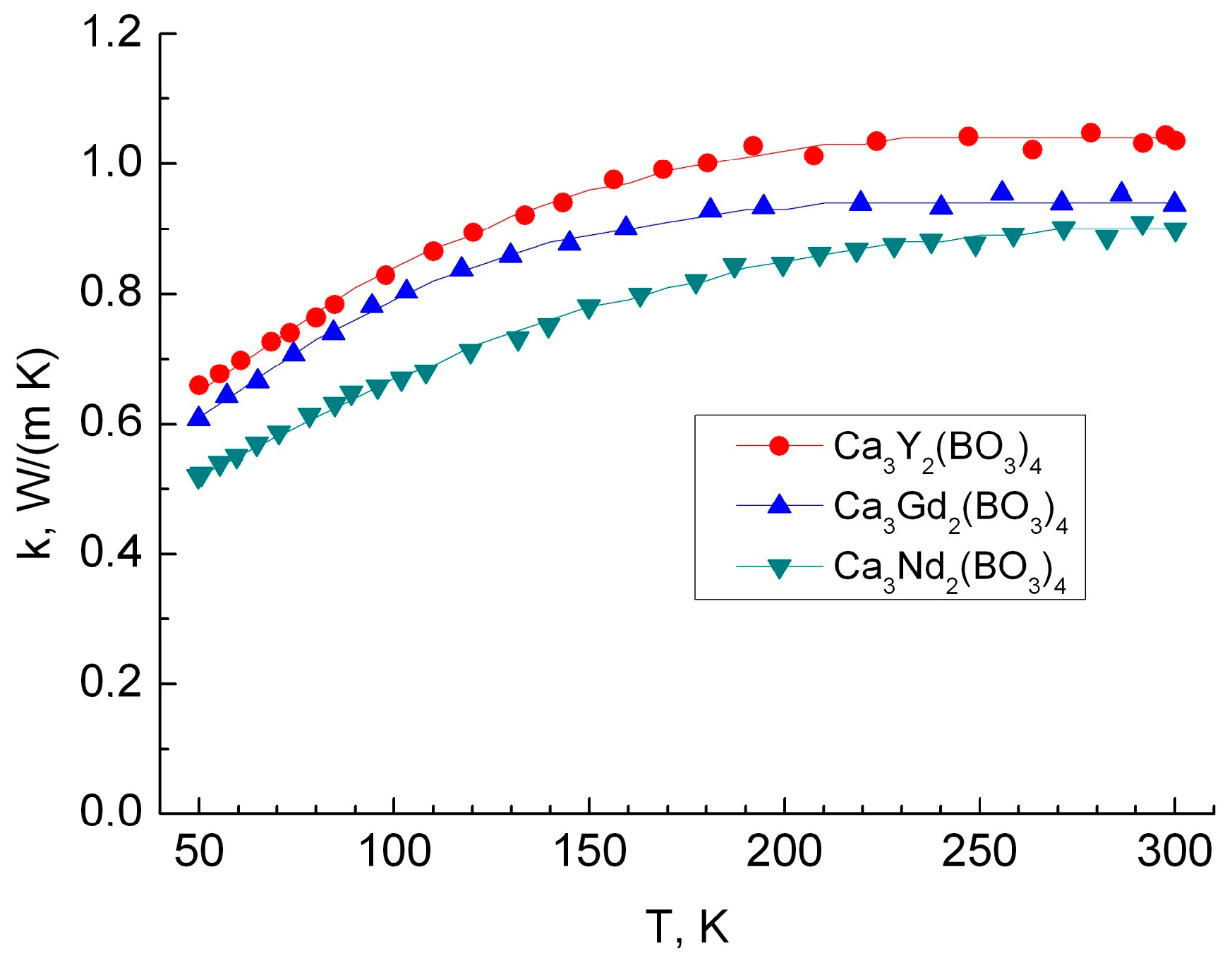
3.3. Thermal Conductivity
4. Conclusions
Author Contributions
Conflicts of Interest
References and Notes
- Loiko, P.A.; Yasukevich, A.S.; Gulevich, A.E.; Demesh, M.P.; Kosmyna, M.B.; Nazarenko, B.P.; Puzikov, V.M.; Shekhovtsov, A.N.; Kornienko, A.A.; Dunina, E.B.; et al. Growth, spectroscopic and thermal properties of Nd-doped disordered Ca9La(VO4)7 and Ca10(Li/K)(VO4)7 laser crystals. J. Lumin. 2013, 137, 252–258. [Google Scholar] [CrossRef]
- Pan, Z.; Ma, J.; Xu, H.; Tang, D.; Cai, H.; Yu, H.; Zhang, H.; Wange, J. 251 fs pulse generation with a Nd3+-doped Ca3Gd2(BO3)4 disordered crystal. RSC Adv. 2012, 5, 44137–44141. [Google Scholar] [CrossRef]
- Mill, B.V.; Tkachuk, A.M.; Belokoneva, E.L.; Ershova, G.I.; Mironov, D.I.; Razumova, I.K. Spectroscopic studies of Ln2Ca3B4O12-Nd (Ln-Y, La, Gd) crystals. J. Alloys Compd. 1998, 275–277, 291–294. [Google Scholar] [CrossRef]
- Haumesser, P.H.; Gaume, R.; Viana, B.; Vivien, D. Determination of laser parameters of ytterbium doped oxide crystalline materials. J. Opt. Soc. Am. B 2002, 19, 2365–2375. [Google Scholar] [CrossRef]
- Wei, B.; Hu, Z.; Lin, Z.; Zhang, L.; Wang, G. Growth and spectral properties of Er3+/Yb3+-codoped Ca3Y2(BO3)4 crystal. J. Cryst. Growth 2004, 273, 190–194. [Google Scholar] [CrossRef]
- Wang, Y.; Tu, C.; You, Z.; Li, J.; Zhu, Z.; Jia, G.; Lu, X.; Wu, B. Optical spectroscopy of Ca3Gd2(BO3)4:Nd3+ laser crystal. J. Mod. Opt. 2006, 53, 1141–1148. [Google Scholar] [CrossRef]
- Brenier, A.; Tu, C.; Wang, Y.; You, Z.; Zhu, Z.; Li, J. Diode-pumped laser operation of Yb3+-doped Y2Ca3B4O12 crystal. J. Appl. Phys. 2008, 104, 013102–013105. [Google Scholar] [CrossRef]
- Ji, Y.; Wang, Y.; Cao, J.; You, Z.; Wang, Y.; Tu, C. Spectroscopic analysis of Nd3+:Ca3Gd2(BO3)4 crystal and laser operating at 1.06 μm. J. Alloys Compd. 2011, 509, 9753–9757. [Google Scholar] [CrossRef]
- Kosmyna, M.B.; Nazarenko, B.P.; Radchenko, I.O.; Shekhovtsov, A.N. Characteristics of lasers based on binary vanadate and orthoborate single crystals with disordered structure. Funct. Mater. 2015, 22, 446–449. [Google Scholar] [CrossRef]
- Kosmyna, M.B.; Nazarenko, B.P.; Puzikov, V.M.; Shekhovtsov, A.N. Development of growth technologies for the photonic single crystals by the Czochralski method at Institute for Single Crystals, NAS of Ukraine. Acta Phys. Pol. A 2013, 123, 305–313. [Google Scholar] [CrossRef]
- Tu, C.; Wang, Y. The Recent Development of Rare Earth-Doped Borate Laser Crystals. In Solid State Laser; Al-Khursan, A., Ed.; INTECH Open Access Publisher: Rijeka, Croatia, 2012; pp. 63–118. [Google Scholar]
- Gudzenko, L.V.; Kosmyna, M.B.; Paszkowicz, W.; Shekhovtsov, A.N.; Behrooz, A.; Białogłowski, M. Growth and characterization of disordered double borate laser hosts. In Proceedings of the 5th International Workshop on Directionally Solidified Eutectic Ceramics, Warsaw, Poland, 3–7 April 2016.
- Berman, R. Thermal Conduction in Solids; Clarendon Press: Oxford, UK, 1976. [Google Scholar]
- Schwarzenbach, G.; Flaschka, H. Die Komplexometrische Titration; Ferdinand Enke Verlag: Stuttgart, Germany, 1965. (In German) [Google Scholar]
- Rodriguez-Carvajal, J. FULLPROF: A program for Rietveld refinement and pattern matching analysis. In Proceedings of the Satellite Meeting on Powder Diffraction of the XV Congress of the IUCr, Toulouse, France, 16–19 July 1990.
- Sirota, N.N.; Popov, P.A.; Ivanov, I.A. The Thermal Conductivity of Monocrystalline Gallium Garnets Doped with Rare-Earth Elements and Chromium in the Range 6–300 K. Cryst. Res. Technol. 1992, 27, 535–543. [Google Scholar] [CrossRef]
- Ivanov, S.; Zhurov, V.Y. ICDD Database. 2000; PDF480310. [Google Scholar]
- Ivanov, S.; Zhurov, V.Y. ICDD Database. 2000; PDF480293. [Google Scholar]
- Seo, H.J. Line broadening and crystallographic sites for Eu3+ in disordered double borate Ca3Gd2(BO3)4. J. Alloys Compd. 2014, 604, 100–105. [Google Scholar] [CrossRef]
- Dzhurinskiy, B.F.; Tanaev, N.V.; Aliev, O.A. Solubility and phase equilibria in systems Sm2O3-SrO-B2O3 and Eu2O3-SrO-B2O3. Inorg. Mater. 1968, 4, 1972–1975. (In Russian) [Google Scholar]
- Pan, Z.B.; Zhang, H.J.; Yu, H.H.; Xu, M.; Zhang, Y.Y.; Sun, S.Q.; Wang, J.Y.; Wang, Q.; Wei, Z.Y.; Zhang, Z.G. Growth and characterization of Nd-doped disordered Ca3Gd2(BO3)4 crystal. Appl. Phys. B Lasers Opt. 2012, 106, 197–209. [Google Scholar] [CrossRef]
- Haumesser, P.H.; Gaumé, R.; Benitez, J.M.; Viana, B.; Ferrand, B.; Aka, G.; Vivien, D. Czochralski growth of six Yb-doped double borate and silicate laser materials. J. Crystal Growth 2001, 233, 233–242. [Google Scholar] [CrossRef]
- Nemodruk, A.A.; Karalova, Z.K. Analytical Chemistry of Boron; Nauka: Moscow, Soviet Unoin, 1964. (In Russian) [Google Scholar]
- Debye, P. Vortrage uber die Kinetische Theorie der Materie and der Elektrizitat; B.G. Teubner: Berlin, Germany, 1914. [Google Scholar]
- Popov, P.A.; Skrobov, S.A.; Matovnikov, A.V.; Kosmyna, M.B.; Puzikov, V.M.; Nazarenko, B.P.; Shekhovtsov, A.N.; Behrooz, A.; Paszkowicz, W.; Khodasevich, I.A.; et al. Thermal conductivity investigation of Ca9RE(VO4)7 (RE = La, Nd, Gd) and Ca10M(VO4)7 (M = Li, Na, K) single crystals. Int. J. Thermophys. 2017, 38, 13. [Google Scholar]


| Crystal | a, Å | b, Å | c, Å | V, Å3 | Ref. |
|---|---|---|---|---|---|
| Ca3Y2(BO3)4 a | 7.1554 (2) | 15.4667 (3) | 8.5583 (3) | 947.15 (4) | [17] |
| Ca3Y2(BO3)4 a | 7.1690 (4) | 15.4758 (8) | 8.5587 (6) | 949.55 (17) | [20] |
| Ca3Y2(BO3)4 b | 7.1517 (2) | 15.4691 (4) | 8.5577 (2) | 946.74 (4) | this work |
| 7.152 ($) | 15.468 | 8.559 | 946.86 | this work HR (X) | |
| Ca3Gd2(BO3)4 a | 7.1953 (3) | 15.5348 (7) | 8.6197 (4) | 963.49(11) | [18] |
| Ca3Gd2(BO3)4 a | 7.1908 | 15.5359 | 8.6168 | 962.63 | [19] |
| Ca3Gd2(BO3)4:Nd b | 7.202 | 15.559 | 8.634 | 967.49 | [21] |
| Ca3Gd2(BO3)4:Yb b | 7:193 (1) | 15:543 (3) | 8:616 (1) | 963.2 (4) | [22] |
| Ca3Gd2(BO3)4 b | 7.1922 (2) | 15.5416 (4) | 8.6190 (2) | 963.41 (4) | this work |
| 7.195 | 15.530 | 8.619 | 963.67 | this work HR (Y) | |
| Ca3Nd2(BO3)4 b | 7.2384 (1) | 15.7121 (2) | 8.6666 (1) | 985.66 (2) | this work |
| 7.230 | 15.713 | 8.665 | 985.45 | this work HR (Z) |
| Crystal | Host Element Concentrations, wt % | |||
|---|---|---|---|---|
| RE | Ca | B | ||
| Ca3Y2(BO3)4 | Stoichiometrically calculated content | 33.3 | 22.5 | 8.1 |
| Grown in argon | 33.3 ± 0.1 | 22.3 ± 0.1 | 7.9 ± 0.1 | |
| Grown in air | 33.4 ± 0.1 | 22.2 ± 0.1 | 7.6 ± 0.1 | |
| Ca3Gd2(BO3)4 | Stoichiometrically calculated content | 46.9 | 17.9 | 6.5 |
| Grown in argon | 46.8 ± 0.1 | 18.0 ± 0.1 | 6.5 ± 0.1 | |
| Grown in air | 45.8 ± 0.1 | 18.2 ± 0.1 | 6.4 ± 0.1 | |
| Ca3Nd2(BO3)4 | Stoichiometrically calculated content | 44.8 | 18.7 | 6.7 |
| Grown in argon | 44.4 ± 0.1 | 19.5 ± 0.1 | 6.8 ± 0.1 | |
| A, 10−8 W/(m·К4) | B, 10−5 W/(m·К3) | C, 10−3 W/(m·К2) | D, W/(m·К) | |
|---|---|---|---|---|
| Ca3Y2(BO3)4 | 1.75 | −1.889 | 6.27 | 0.382 |
| Ca3Gd2(BO3)4 | 0.4031 | −0.8876 | 4.184 | 0.334 |
| Ca3Nd2(BO3)4 | 3.295 | 2.646 | 7.067 | 0.316 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gudzenko, L.V.; Kosmyna, M.B.; Shekhovtsov, A.N.; Paszkowicz, W.; Sulich, A.; Domagała, J.Z.; Popov, P.A.; Skrobov, S.A. Crystal Growth and Glass-Like Thermal Conductivity of Ca3RE2(BO3)4 (RE = Y, Gd, Nd) Single Crystals. Crystals 2017, 7, 88. https://doi.org/10.3390/cryst7030088
Gudzenko LV, Kosmyna MB, Shekhovtsov AN, Paszkowicz W, Sulich A, Domagała JZ, Popov PA, Skrobov SA. Crystal Growth and Glass-Like Thermal Conductivity of Ca3RE2(BO3)4 (RE = Y, Gd, Nd) Single Crystals. Crystals. 2017; 7(3):88. https://doi.org/10.3390/cryst7030088
Chicago/Turabian StyleGudzenko, L. V., M. B. Kosmyna, A. N. Shekhovtsov, W. Paszkowicz, A. Sulich, J. Z. Domagała, P. A. Popov, and S. A. Skrobov. 2017. "Crystal Growth and Glass-Like Thermal Conductivity of Ca3RE2(BO3)4 (RE = Y, Gd, Nd) Single Crystals" Crystals 7, no. 3: 88. https://doi.org/10.3390/cryst7030088






