Applicability of Effective Medium Approximations to Modelling of Mesocrystal Optical Properties
Abstract
:1. Introduction
2. Results
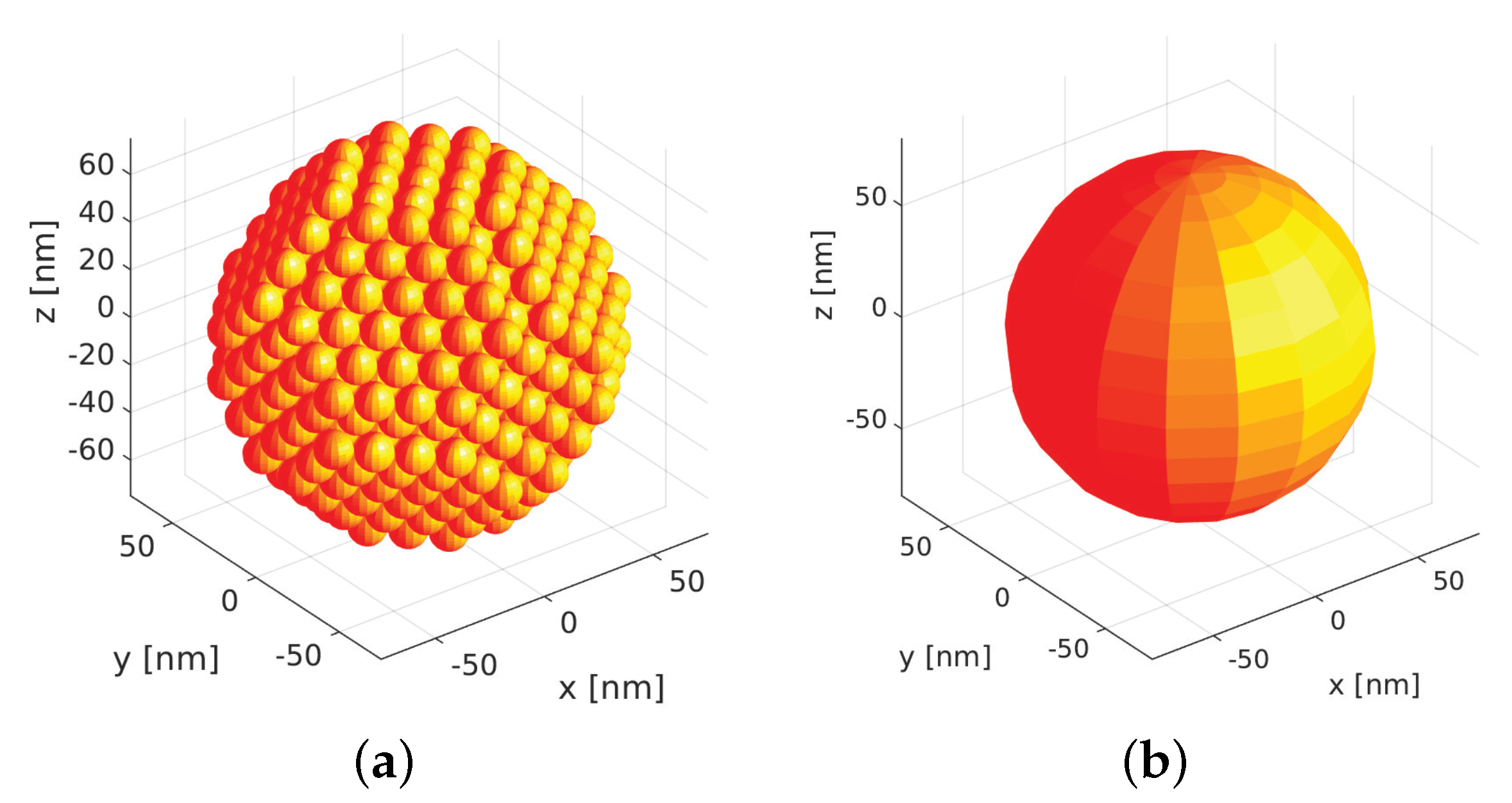
2.1. Light Scattering on Mesocrystalline Particles
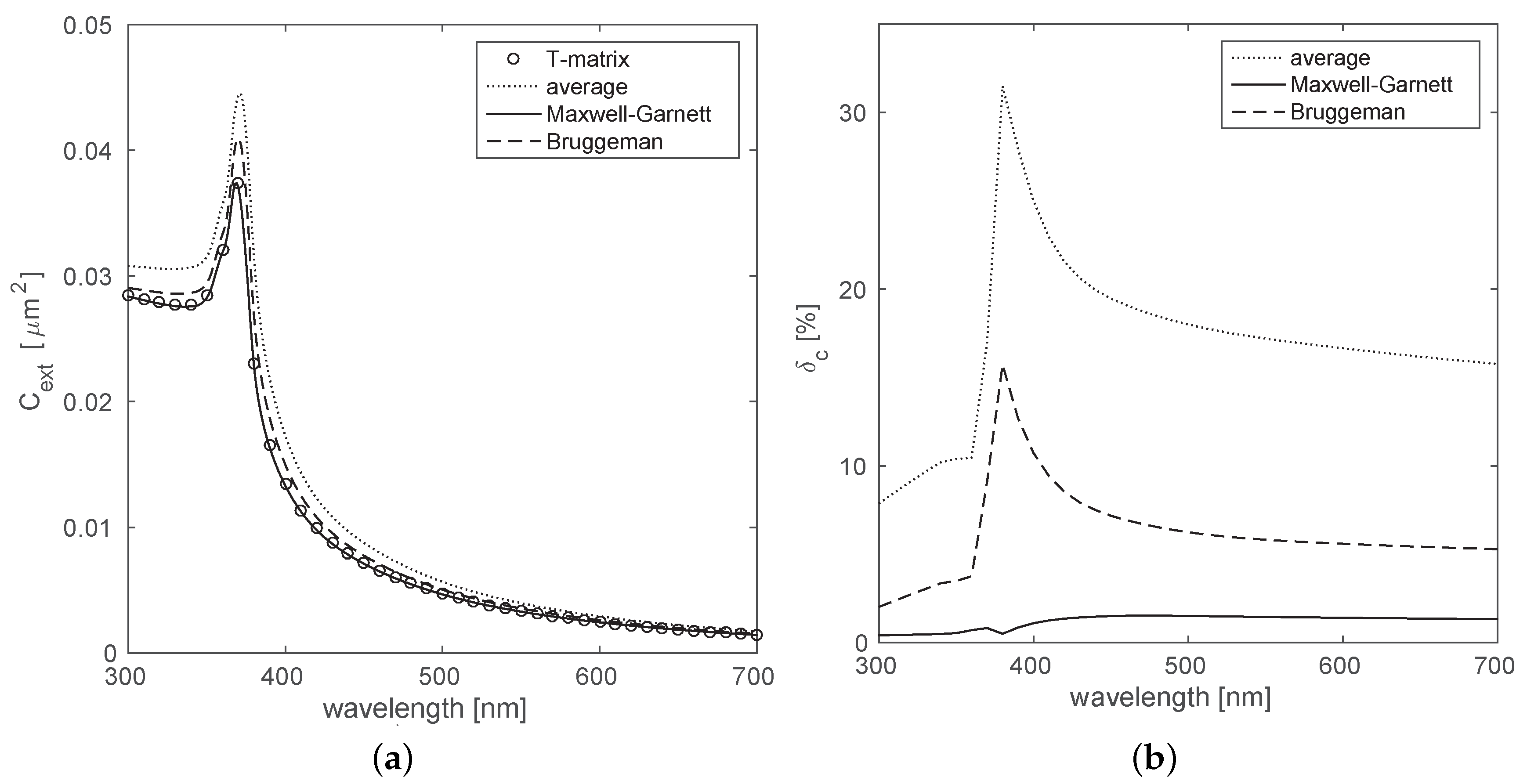
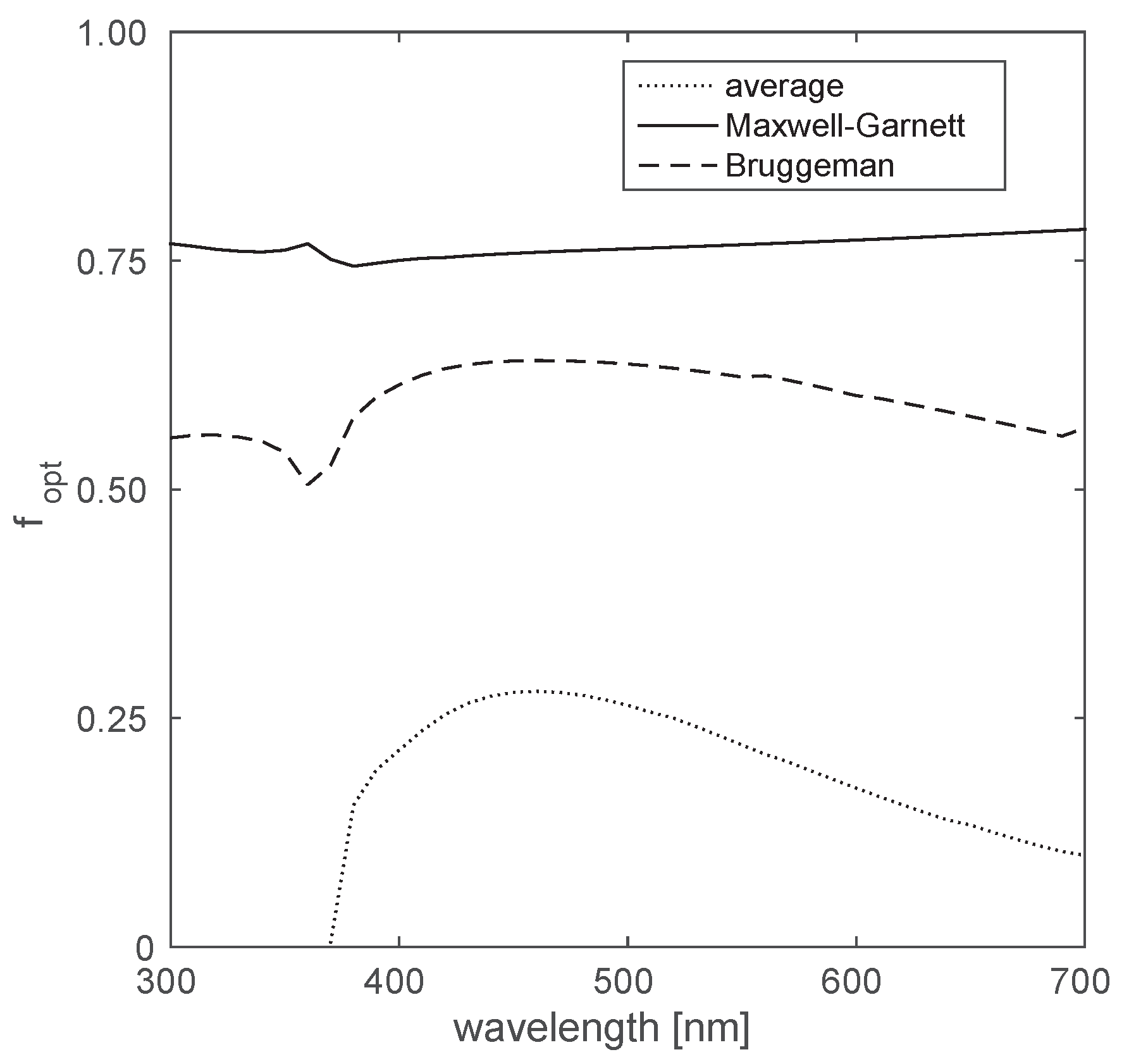
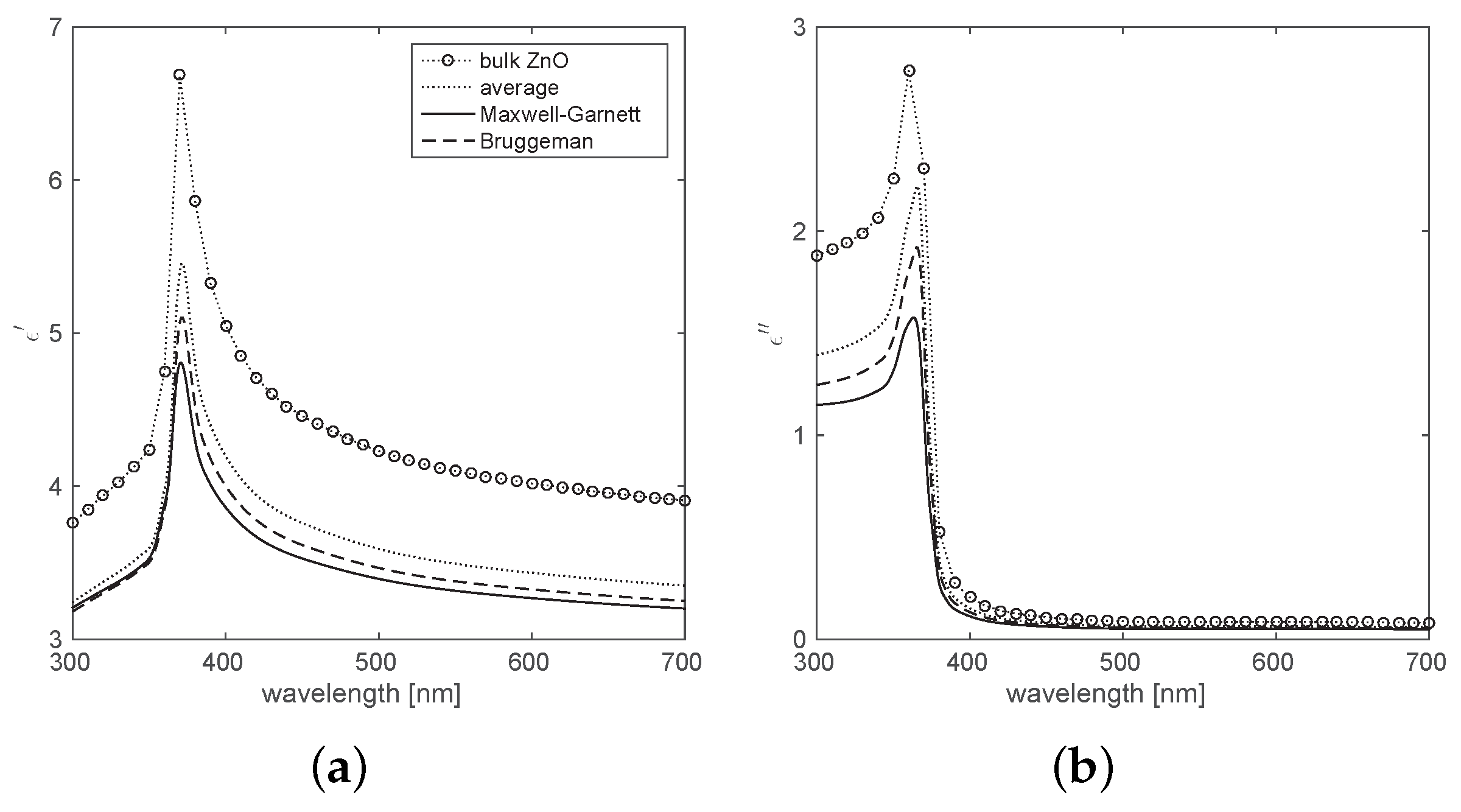
2.2. Fitting the T-Matrix Results with Effective Medium Theories
2.3. Size and Structure Variations
3. Discussion
4. Materials and Methods
4.1. Material Optical Properties
4.2. Effective Medium Approximations
4.3. Lorenz-Mie Scattering
4.4. T-Matrix Method
Acknowledgments
Conflicts of Interest
Abbreviations
| VSH | Vector Sperical Harmonics |
| FCC | face centered cubic |
| T-matrix | Transition Matrix |
References
- Song, R.Q.; Cölfen, H. Ordered Nanoparticle Superstructures. Adv. Mater. 2010, 22, 1301–1330. [Google Scholar] [CrossRef] [PubMed]
- Ma, M.G.; Cölfen, H. Mesocrystals—Applications and potential. Curr. Opin. Colloid Interface Sci. 2014, 19, 56–65. [Google Scholar] [CrossRef]
- Klupp Taylor, R.; Seifrt, F.; Zhuromskyy, O.; Peschel, U.; Leugering, G.; Peukert, W. Painting by Numbers: Nanoparticle-Based Colorants in the Post-Empirical Age. Adv. Mater. 2011, 23, 2554–2570. [Google Scholar] [CrossRef] [PubMed]
- Yablonovitch, E. Inhibited Spontaneous Emission in Solid-State Physics and Electronics. Phys. Rev. Lett. 1987, 58, 2059–2062. [Google Scholar] [CrossRef] [PubMed]
- Pendry, J. Photonics: Metamaterials in the sunshine. Nat. Mater. 2006, 5, 599–600. [Google Scholar] [CrossRef] [PubMed]
- Linden, S.; Enkrich, C.; Wegener, M.; Zhou, J.; Koschny, T.; Soukoulis, C.M. Magnetic Response of Metamaterials at 100 Terahertz. Science 2004, 306, 1351–1353. [Google Scholar] [CrossRef] [PubMed]
- Distaso, M.; Klupp Taylor, R.N.; Taccardi, N.; Wasserscheid, P.; Peukert, W. Influence of the Counterion on the Synthesis of ZnO Mesocrystals under Solvothermal Conditions. Chemistry 2011, 17, 2923–2930. [Google Scholar] [CrossRef] [PubMed]
- Distaso, M.; Wernet, R.; Segets, D.; Peukert, W. Tuning the size and the optical properties of ZnO mesocrystals synthesized under solvothermal conditions. Nanoscale 2012, 4, 864–873. [Google Scholar] [CrossRef] [PubMed]
- Garnett, J.C.M. Colours in Metal Glasses and in Metallic Films. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 1904, 203, 385–420. [Google Scholar] [CrossRef]
- Bruggeman, D.A.G. Berechnung verschiedener physikalischer Konstantern von heterogenen Substanzen. Ann. Phys. 1935, 5, 636–662. [Google Scholar] [CrossRef]
- Mishchenko, M.; Dlugach, J.; Liu, L. Applicability of the effective-medium approximation to heterogeneous aerosol particles. J. Quant. Spectrosc. Radiat. Transf. 2016, 178, 284–294. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Dlugach, Z.M.; Zakharova, N.T. Direct demonstration of the concept of unrestricted effective-medium approximation. Opt. Lett. 2014, 39, 3935–3938. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Panetta, R.L.; Yang, P. Inhomogeneity structure and the applicability of effective medium approximations in calculating light scattering by inhomogeneous particles. J. Quant. Spectrosc. Radiat. Transf. 2014, 146, 331–348. [Google Scholar] [CrossRef]
- Kahnert, M. Modelling radiometric properties of inhomogeneous mineral dust particles: Applicability and limitations of effective medium theories. J. Quant. Spectrosc. Radiat. Transf. 2015, 152, 16–27. [Google Scholar] [CrossRef]
- Mishchenko, M.; Dlugach, J.; Yurkin, M.; Bi, L.; Cairns, B.; Liu, L.; Panetta, R.; Travis, L.; Yang, P.; Zakharova, N. First-principles modeling of electromagnetic scattering by discrete and discretely heterogeneous random media. Phys. Rep. 2016, 632, 1–75. [Google Scholar] [CrossRef]
- Kahnert, F.M. Numerical methods in electromagnetic scattering theory. J. Quant. Spectrosc. Radiat. Transf. 2003, 79–80, 775–824. [Google Scholar] [CrossRef]
- Peterson, B.; Strom, S. T Matrix for Electromagnetic Scattering from an Arbitrary Number of Scatterers and Representations of E(3). Phys. Rev. D 1973, 8, 3661–3677. [Google Scholar] [CrossRef]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. Phys. 1908, 330, 377–445. [Google Scholar] [CrossRef]
- Wiersma, D.S. The smallest random laser. Nature 2000, 406, 132–133. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Schneider, J. Index of Refraction of ZnO. J. Appl. Phys. 1968, 39, 3049–3052. [Google Scholar] [CrossRef]
- Bergstrom, L.; Meurk, A.; Arwin, H.; Rowcliffe, D.J. Estimation of Hamaker Constants of Ceramic Materials from Optical Data Using Lifshitz Theory. J. Am. Ceram. Soc. 1996, 79, 339–348. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Mackowski, D.W.; Altenkirch, R.A.; Menguc, M.P. Internal absorption cross sections in a stratified sphere. Appl. Opt. 1990, 29, 1551–1559. [Google Scholar] [CrossRef] [PubMed]
- Kai, L.; Massoli, P. Scattering of electromagnetic-plane waves by radially inhomogeneous spheres: A finely stratified sphere model. Appl. Opt. 1994, 33, 501–511. [Google Scholar] [CrossRef] [PubMed]
- Waterman, P.C. Matrix Formulation of Electromagnetic Scattering. Proc. IEEE 1965, 53, 805–812. [Google Scholar] [CrossRef]
- Waterman, P.C. Symmetry, Unitarity, and Geometry in Electromagnetic Scattering. Phys. Rev. D 1971, 3, 825–839. [Google Scholar] [CrossRef]
- Tsang, L.; Kong, J.A.; Ding, K.H. Scattering of Electromagnetic Waves: Theories and Applications; Wiley-Interscience: Hoboken, NJ, USA, 2000. [Google Scholar]
- Mishchenko, M.; Hovenier, J.; Travis, L. Light Scattering by Nonspherical Particles. Theory, Measurement and Applications; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Agarwal, G.S. Relation between Waterman’s extended boundary condition and the generalized extinction theorem. Phys. Rev. D 1976, 14, 1168–1171. [Google Scholar] [CrossRef]
- Mishchenko, M.I. Light scattering by randomly oriented axially symmetric particles. J. Opt. Soc. Am. A 1991, 8, 871–882. [Google Scholar] [CrossRef]
- Wriedt, T. Using the T-Matrix Method for Light Scattering Computations by Non-axisymmetric Particles: Superellipsoids and Realistically Shaped Particles. Part. Part. Syst. Charact. 2002, 19, 256–268. [Google Scholar] [CrossRef]
- Mishchenko, M.; Travis, L.; Lacis, A. Scattering, Absorption and Emission of Light by Small Particles; Cambridge University Press: Cambridge, England, 2002. [Google Scholar]
- Mackowski, D.W. Calculation of total cross sections of multiple-sphere clusters. J. Opt. Soc. Am. A 1994, 11, 2851–2861. [Google Scholar] [CrossRef]
- Wriedt, T.; Doicu, A. Light scattering from a particle on or near a surface. Opt. Commun. 1998, 152, 376–384. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Videen, G.; Babenko, V.A.; Khlebtsov, N.G.; Wriedt, T. T-matrix theory of electromagnetic scattering by particles and its applications: A comprehensive reference database. J. Quant. Spectrosc. Radiat. Transf. 2004, 88, 357–406. [Google Scholar]
- Mishchenko, M.I.; Videen, G.; Babenko, V.A.; Khlebtsov, N.G.; Wriedt, T. Comprehensive T-matrix reference database: A 2004–06 update. J. Quant. Spectrosc. Radiat. Transf. 2007, 106, 304–324. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Videen, G.; Khlebtsov, N.G.; Wriedt, T.; Zakharova, N.T. Comprehensive T-matrix reference database: A 2006–07 update. J. Quant. Spectrosc. Radiat. Transf. 2008, 109, 1447–1460. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Zakharova, N.T.; Videen, G.; Khlebtsov, N.G.; Wriedt, T. Comprehensive T-matrix reference database: A 2007–2009 update. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 650–658. [Google Scholar] [CrossRef]
- Zakharova, N.T.; Videen, G.; Khlebtsov, N.G. Comprehensive T-matrix reference database: A 2009–2011 update. J. Quant. Spectrosc. Radiat. Transf. 2012, 113, 1844–1852. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Zakharova, N.T.; Khlebtsov, N.G.; Videen, G.; Wriedt, T. Comprehensive thematic T-matrix reference database: A 2014–2015 update. J. Quant. Spectrosc. Radiat. Transf. 2016, 178, 276–283. [Google Scholar] [CrossRef]
- Doicu, A.; Wriedt, T.; Eremin, Y. Light Scattering by Systems of Particles, Null-Field Method with Discrete Sources: Theory and Programs; Springer: Berlin, Germany; New York, NY, USA, 2006. [Google Scholar]
- Wriedt, T.; Hellmers, J. New Scattering Information Portal for the light-scattering community. J. Quant. Spectrosc. Radiat. Transf. 2008, 109, 1536–1542. [Google Scholar] [CrossRef]
- Mackowski, D.W.; Mishchenko, M.I. A Multiple sphere T-matrix Fortran code for use on parallel computer clusters. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 2182–2192. [Google Scholar] [CrossRef]
- Zhuromskyy, O.; Lomanets, V.; Peschel, U. Magnetic response from a composite of metal-dielectric particles in the visible range: T-matrix simulation. In Proceedings of the Electromagnetic and Light Scattering XIII, Taormina, Italy, 26–30 September 2011; Volume 89, p. C1V89S1P097.
- Zhuromskyy, O.; Pulbere, S.; Koban, W.; Peschel, U. Simulation of optical properties of particulate media by multi level superposition of T-matrices. In Nano Structures on Surfaces and Light Scattering; Wriedt, T., Eremin, Y., Hergert, W., Eds.; Institut für Werkstofftechnik: Bremen, Germany, 2011; pp. 45–48. [Google Scholar]
- Zhuromskyy, O.; Peschel, U. Lossless propagation of magnetic dipole excitations on chains of dielectric particles with high refractive index. Phys. Rev. B 2014, 90, 125117. [Google Scholar] [CrossRef]
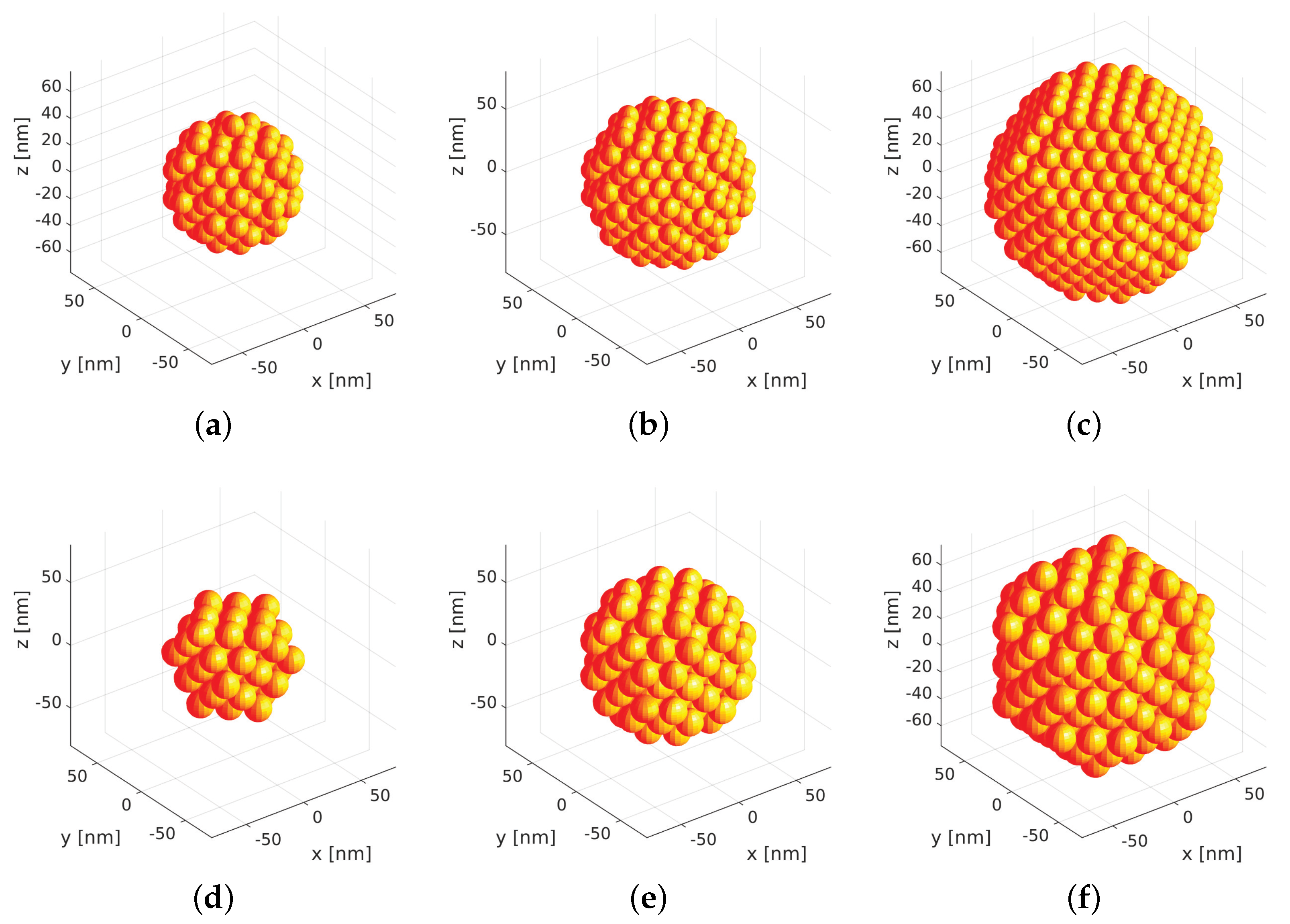

| Structure | d | D | |
|---|---|---|---|
| (a) | 15 nm | 141 | 86.3 nm |
| (b) | 15 nm | 321 | 113.5 nm |
| (c) | 15 nm | 675 | 145.5 nm |
| (d) | 20 nm | 55 | 84.1 nm |
| (e) | 20 nm | 135 | 113.4 nm |
| (f) | 20 nm | 249 | 139.1 nm |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuromskyy, O. Applicability of Effective Medium Approximations to Modelling of Mesocrystal Optical Properties. Crystals 2017, 7, 1. https://doi.org/10.3390/cryst7010001
Zhuromskyy O. Applicability of Effective Medium Approximations to Modelling of Mesocrystal Optical Properties. Crystals. 2017; 7(1):1. https://doi.org/10.3390/cryst7010001
Chicago/Turabian StyleZhuromskyy, Oleksandr. 2017. "Applicability of Effective Medium Approximations to Modelling of Mesocrystal Optical Properties" Crystals 7, no. 1: 1. https://doi.org/10.3390/cryst7010001





