Elastodynamic Analysis of a Hollow Cylinder with Decagonal Quasicrystal Properties: Meshless Implementation of Local Integral Equations

Abstract

A meshless approximation and local integral equation (LIE) formulation are proposed for elastodynamic analysis of a hollow cylinder made of quasicrystal materials with decagonal quasicrystal properties. The cylinder is assumed to be under shock loading. Therefore, the general transient elastodynamic problem is considered for coupled phonon and phason displacements and stresses. The equations of motion in the theory of compatible elastodynamics of wave type for phonons and wave-telegraph type for phasons are employed and can be easily modified to the elasto-hydro dynamic equations for quasicrystals (QCs). The angular dependence of the tensor of phonon–phason coupling coefficients handicaps utilization of polar coordinates, when the governing equations would be given by partial differential equations with variable coefficients. Despite the symmetry of the geometrical shape, the local weak formulation and meshless approximation are developed in the Cartesian coordinate system. The response of the cylinder in terms of both phonon and phason stress fields is obtained and studied in detail.

1. Introduction

The observation of five-fold rotational symmetry by the electron diffraction patterns with bright diffraction spots in a rapid cooled Al–Mn alloy in April 1982 by Shechtman [1] yields surprising discoveries on the structure of matter and its properties. Since the five-fold rotational symmetry was in contradiction with the basic laws of the symmetry of crystals and the pattern also did not exhibit translational periodicity, this discovery finally resulted in redefinition of the concept of crystals, and the order is now associated not only with periodicity but also with quasi-periodicity. Soon after that discovery, five-fold rotational symmetry and three-dimensional icosahedral quasicrystals were found. Now, we also know about pentagonal, octagonal, decagonal and twelve-fold decagonal quasicrystals, which are two-dimensional quasicrystals with quasi-periodic atomic arrangement along two directions and periodic along the third direction, which is just the direction of 5-, 8-, 10-, and 12-fold rotational symmetry axes, respectively. The planar quasicrystals are different from the two-dimensional ones, since the former belong to a two-dimensional structure (without the third dimension) with a quasiperiodic atomic arrangement. In one-dimensional quasicrystals, the atomic arrangement is quasiperiodic along one axis, and periodic along the plane perpendicular to the axis. The icosahedral and decagonal quasicrystals present the majority of observed quasicrystals. It should be stressed that the unusual structure of quasicrystals leads to a series of properties different from those of crystals. The thermal as well as electrical conductivity of quasicrystals is lower than that of the conventional metals. Due to the lack of periodicity, the Bloch theorem and Brillouin zone concept are inapplicable and the electronic structure as well as electronic energy spectra of quasicrystals exhibit different properties than crystals. Moreover, no conservative slip along crystallographic planes can be allowed in quasicrystals, which causes quasicrystals to be hard and brittle. Quasicrystals are deformable under applied external sources, and the physical basis of the elasticity of quasicrystals is substantially different from the classical elasticity [2,3]. The Landau theory is mostly used on elementary excitations and symmetry-breaking of condensed matter. The other approach is based on the unit cell description based on the Penrose tiling.

The numerical simulations play an important role in the investigation of phenomena in new materials as well as in design of structural elements. Some exact solutions have been presented for one-dimensional cases in beams and plates made of quasicrystals [4,5]. Yang et al. [5] proposed an exact solution for analysis of plates subjected to surface loading and made of one-dimensional orthorhombic quasicrystal. They obtained the displacement and stress fields in a sandwich plate with simply supported boundary conditions, which was assumed to be made of quasicrystals and crystals with two different stacking sequences.

One of the most important analyses in engineering applications is elastodynamic analysis of structures. The structures made of quasicrystals (QCs) may be under dynamic and transient loadings. Thus, the general dynamic theory for QCs should be used to obtain the realistic dynamic behaviors of QCs. There are some theories for the description of dynamic behaviors of QCs, which were presented in previously published papers. Recently, the importance of them are addressed in a research paper by Agiasofitou et al. [6], of which the most important of them are the elastodynamic properties of wave types for QCs presented by Fan et al. [2], Shi [7] and Fan [3]. A minimal model of the phonon–phason elastodynamic, which is a combination of models based on wave type and hydrodynamics of QCs, was proposed by Rochal et al. [8]. This model was adopted by many researchers as the elasto-hydrodynamics of QCs [9]. In another work, the icosahedral quasicrystals with inclusion of the pinning effect is dynamically analyzed using a minimal model of the phonon–phason dynamics considering resonant attenuation of low-frequency acoustic waves in the temperature range corresponding to thermal activation of phasons by Kozinkina et al. [10]. Recently, an elastodynamic model of the wave-telegraph type was proposed for the description of dynamic behaviors of QCs by Agiasofitou et al. [6].

There are some computational methods for solving the governing equations based on various elastodynamic models of QCs. For example, recently, the meshless local Petrov–Galerkin (MLPG) was successfully used by Sladek et al. [11] for bending analysis in 1D orthorhombic QCs under static and dynamic loadings. They used the Bak and elasto-hydrodynamic models for phason governing equation in the elastodynamic case of their problem. In addition, the MLPG method was employed for analysis of initial-boundary value crack problems in decagonal QCs by Sladek et al. [12]. There are some analytical techniques that can be applied to elastodynamic analysis of QCs, and were successfully used in other elastodynamic or thermoelasticity analyses. Hosseini et al. [13] proposed an analytical method based on series expansions for solutions of elastodynamic problems in functionally graded thick hollow cylinders under shock loading. In another work, they used the proposed analytical method for coupled thermoelasticity analysis based on Green–Naghdi theory (without energy dissipation) [14]. Wang et al. [15] presented analytical solutions for some defect problems in 1D hexagonal and 2D octagonal quasicrystals.

A fundamental solution was proposed for the time-dependent differential equations of anisotropic elasticity in 3D quasicrystals using the Fourier transform with respect to the space variables and matrix transformations by Cerdik Yaslan [16].

In this paper, we present an effective numerical method for dynamic analysis of cylinder made of 2D decagonal QCs while assuming translational symmetry along the axis of the cylinder. The conventional wave propagation equation is used for description of phonon waves while the dynamics of phasons is described by the wave–telegraph equation. Recall that the wave-telegraph equation can be easily modified to a diffusion type equation used in the elasto-hydrodynamic model of QCs. The governing equations of motions and constitutive equations for QCs cylinder are formulated and the utilization of the polar coordinate system is discussed. Then, the equations of motions in terms of momenta and stresses are considered in a local weak sense and the Local Integral Equations (LIE) are derived. The meshless approach is used for approximation of both the phonon and phason displacements, and the stress tensors are approximated by using the constitutive relationships and derivatives of approximated displacements. The dynamic response of the QC cylinder is studied in detail while presenting the comparison of results by using various formulations for QCs dynamics. Furthermore, the influence of the quasi periodicity (quasi periodic arrangement of atoms in plane orthogonal to the cylinder axis) on the angular dependence of the response of the QC hollow cylinder on the angularly symmetric loading is also studied.

2. Mathematical Formulations

Similar to other aperiodic crystals, quasi-periodicity induces new degrees of freedom. The Landau phenomenological theory on the symmetry-breaking of condensed matter [17] played the central role in the development of elasticity theory of quasicrystals and has been widely acknowledged. In many physical systems (classical or quantum), the motion presents the discrete spectrum (corresponding to an eigenvalue problem of a certain operator from the mathematical point of view), the lowest energy level state is called ground state, and that beyond the ground state is called the excited state. According to the Debye and Born theory of crystal lattices, the propagation of the lattice vibration under the long-wavelength approximation can be seen as continuum elastic waves. The quanta of lattice vibration (the smallest portion of energy of the elastic wave) is phonon (elastic waves belong to acoustic waves). Unlike the photon, the phonon is not an elementary particle, but, in the sense of quantization, the phonon exhibits natural similarity to elementary particles (phonons are quasi-particles emerging from the quantization of elastic waves in linearized elastic setting). It is known that standard liquid exhibits arbitrary translational as well as arbitrary rotational symmetry, and the periodicity of crystals breaks these symmetries of liquid. According to the Landau theory, the phonon is elementary excitation resulting from symmetry-breaking in the transition from liquid phase to crystal. In transition from crystals to quasicrystals, the break of periodic symmetry of crystals results in new elementary excitation called phasons. Thus, quasi-periodicity (similar to other aperiodic crystals) induces new degrees of freedom (phason displacements), but the phason modes in quasicrystals present different nature, i.e., the motion of atoms exhibits discontinuous jump rather than the long-wavelength propagation. The phason displacements describe relative atomic shifts, which assure quasi-periodicity of the atomic distribution. Hence, the phason field is insensitive to translations of coordinate frames in the physical space. Since we shall deal with quasicrystals within the phenomenological theory of continuum mechanics, the adjectives phonon and phason will be utilized just to distinguish between the displacements known in classical elasticity (phonon displacements) and new degrees of freedom induced by the quasi-periodicity in quasicrystalline materials (phason displacements).

Within linear elasticity, elastic free energy of quasicrystals consists of three types of quadratic terms: phonon–phonon, phason–phason and phonon–phason coupling terms [3]. Then, the constitutive laws are given as:

$${\mathsf{\sigma }}_{ij}=c_{ijkl}{\mathsf{\epsilon }}_{kl}+R_{ijkl}{\mathsf{\omega }}_{kl}\left(\mathsf{\sigma }=c:\mathsf{\epsilon }+R:\mathsf{\omega }\right),H_{ij}=R_{klij}{\mathsf{\epsilon }}_{kl}+K_{ijkl}{\mathsf{\omega }}_{kl}\left(H=\mathsf{\epsilon }:R+K:\mathsf{\omega }\right)$$

(1)

where ${\mathsf{\sigma }}_{ij}$ and $H_{ij}$ are the phonon and phason stresses, respectively, while the corresponding phonon strains ${\mathsf{\epsilon }}_{kl}$ and phason strains ${\mathsf{\omega }}_{kl}$ are defined in terms of gradients of the phonon displacements $u_i(x,t)$ and phason fields $w_i(x,t)$ as:

$${\mathsf{\epsilon }}_{ij}(x,t)=\frac{1}{2}\left[u_{i,j}(x,t)+u_{j,i}(x,t)\right]\mathsf{\epsilon }=\left(u\nabla +\nabla u\right)/2,{\mathsf{\omega }}_{ij}(x,t)=w_{i,j}(x,t)\mathsf{\omega }=w\nabla$$

(2)

Recall that ${\mathsf{\omega }}_{kl}$ is not symmetric, while ${\mathsf{\epsilon }}_{kl}$ is a symmetric tensor (the rigid body rotations have no contribution to deformation energy). The tensors of material coefficients and coupling coefficients are given as [3]:

$$\begin{gathered} c_{ijkl}=c_{12}{\mathsf{\delta }}_{ij}{\mathsf{\delta }}_{kl}+c_{66}({\mathsf{\delta }}_{ik}{\mathsf{\delta }}_{jl}+{\mathsf{\delta }}_{il}{\mathsf{\delta }}_{jk}),c_{66}=(c_{11}-c_{12})/2 \\ {K}_{ijkl}=K_1{\mathsf{\delta }}_{ik}{\mathsf{\delta }}_{jl}+K_2\left({\mathsf{\delta }}_{ij}{\mathsf{\delta }}_{kl}-{\mathsf{\delta }}_{il}{\mathsf{\delta }}_{jk}\right) \\ {R}_{ijkl}=R\left[\left({\mathsf{\delta }}_{i1}{\mathsf{\delta }}_{j2}+{\mathsf{\delta }}_{i2}{\mathsf{\delta }}_{j1}\right){\mathsf{\epsilon }}_{3lk}+\left({\mathsf{\delta }}_{i1}{\mathsf{\delta }}_{j1}-{\mathsf{\delta }}_{i2}{\mathsf{\delta }}_{j2}\right){\mathsf{\delta }}_{kl}\right] \end{gathered}$$

(3)

where $c_{11}$, $c_{12}$, $K_1$, $K_2$, and $R$ are five constants characterizing the material properties of quasi-crystals, and ${\mathsf{\epsilon }}_{3lk}$ is the permutation symbol with ${\mathsf{\epsilon }}_{123}=1$. Remember the following symmetry relationships, which are satisfied by the tensors of material coefficients:

$$c_{ijkl}=c_{klij}=c_{jikl}=c_{ijlk},K_{ijkl}=K_{klij},R_{ijkl}=R_{jikl}$$

(4)

In problems for a hollow cylinder with translational symmetry along the cylinder axis, the plane elasticity conditions are applicable and polar coordinates are appropriate for modelling of geometry. Performing the transformation from the Cartesian to polar components of tensors of material coefficients, we get the constitutive laws in polar coordinate system

$$\left(\begin{array}{c}{\mathsf{\sigma }}_{rr}\\ {\mathsf{\sigma }}_{\mathsf{\theta }\mathsf{\theta }}\\ {\mathsf{\sigma }}_{r\mathsf{\theta }}\\ {\mathsf{\sigma }}_{\mathsf{\theta }r}\end{array}\right)=\left(\begin{array}{ccc}{c}_{11}& c_{12}& 0\\ c_{12}& c_{11}& 0\\ 0& 0& c_{66}\\ 0& 0& c_{66}\end{array}\right)\left(\begin{array}{c}{\mathsf{\epsilon }}_{rr}\\ {\mathsf{\epsilon }}_{\mathsf{\theta }\mathsf{\theta }}\\ 2{\mathsf{\epsilon }}_{r\mathsf{\theta }}\end{array}\right)+R\left(\begin{array}{cccc}\cos 2\mathsf{\theta }& \cos 2\mathsf{\theta }& -\sin 2\mathsf{\theta }& \sin 2\mathsf{\theta }\\ -\cos 2\mathsf{\theta }& -\cos 2\mathsf{\theta }& \sin 2\mathsf{\theta }& -\sin 2\mathsf{\theta }\\ -\sin 2\mathsf{\theta }& -\sin 2\mathsf{\theta }& -\cos 2\mathsf{\theta }& \cos 2\mathsf{\theta }\\ -\sin 2\mathsf{\theta }& -\sin 2\mathsf{\theta }& -\cos 2\mathsf{\theta }& \cos 2\mathsf{\theta }\end{array}\right)\left(\begin{array}{c}{\mathsf{\omega }}_{rr}\\ {\mathsf{\omega }}_{\mathsf{\theta }\mathsf{\theta }}\\ {\mathsf{\omega }}_{r\mathsf{\theta }}\\ {\mathsf{\omega }}_{\mathsf{\theta }r}\end{array}\right)$$

(5)

$$\left(\begin{array}{c}{H}_{rr}\\ H_{\mathsf{\theta }\mathsf{\theta }}\\ H_{r\mathsf{\theta }}\\ H_{\mathsf{\theta }r}\end{array}\right)=R\left(\begin{array}{ccc}\cos 2\mathsf{\theta }& -\cos 2\mathsf{\theta }& -\sin 2\mathsf{\theta }\\ \cos 2\mathsf{\theta }& -\cos 2\mathsf{\theta }& -\sin 2\mathsf{\theta }\\ -\sin 2\mathsf{\theta }& \sin 2\mathsf{\theta }& -\cos 2\mathsf{\theta }\\ \sin 2\mathsf{\theta }& -\sin 2\mathsf{\theta }& \cos 2\mathsf{\theta }\end{array}\right)\left(\begin{array}{c}{\mathsf{\epsilon }}_{rr}\\ {\mathsf{\epsilon }}_{\mathsf{\theta }\mathsf{\theta }}\\ 2{\mathsf{\epsilon }}_{r\mathsf{\theta }}\end{array}\right)+\left(\begin{array}{cccc}{K}_1& K_2& 0& 0\\ K_2& K_1& 0& 0\\ 0& 0& K_1& -K_2\\ 0& 0& -K_2& K_1\end{array}\right)\left(\begin{array}{c}{\mathsf{\omega }}_{rr}\\ {\mathsf{\omega }}_{\mathsf{\theta }\mathsf{\theta }}\\ {\mathsf{\omega }}_{r\mathsf{\theta }}\\ {\mathsf{\omega }}_{\mathsf{\theta }r}\end{array}\right).$$

(6)

It is seen that the tensor of coupling coefficients is position dependent in a plane perpendicular to the periodic symmetrical axis of quasicrystals. Thus, the angular symmetry is inapplicable in such a quasicrystal cylinder even if the loading and boundary conditions were angularly symmetric. Moreover, the expressions for the phonon as well as phason strains and stresses are more harmful in the polar coordinate system than in the Cartesian coordinate system, and the governing equations in polar coordinates would be given by partial differential equations with variable coefficients. Therefore, the utilization of the polar coordinate system seems to be inappropriate in the considered problem despite the angular symmetry of the geometrical shape. Nevertheless, the constitutive laws are symmetric with respect to rotations on the angle equal to $\mathsf{\pi }$ as can be seen from the representations of the tensors of material coefficients in Equations (5) and (6) in the polar coordinate system.

The equations of motion in the theory of compatible elastodynamics of wave-telegraph type of quasicrystals in terms of the momenta and stresses take the form [4]:

$$\mathsf{\rho }{\ddot{u}}_i-{\mathsf{\sigma }}_{ij,j}=f_i\left(\mathsf{\rho }\ddot{u}-\mathsf{\sigma }\cdot \nabla =f\right)$$

(7)

$$\tilde{\mathsf{\rho }}{\ddot{w}}_i-H_{ij,j}-g_i^{fr}=g_i\left(\tilde{\mathsf{\rho }}\ddot{w}-H\cdot \nabla -g^{fr}=g\right)$$

(8)

where $f_i$, $g_i$ are the conventional (phonon) body force density and a generalized (phason) body force density, respectively, while $g_i^{fr}=-D_{ij}{\dot{w}}_j$ is the frictional force (dissipative force) vector. Recall the principal difference between $f_i$ and $g_i$. There are no bulk external fields acting on phason degrees of freedom, except we presume phason inertia [18,19,20]. However, it is proven that bulk phason self-action which has both the dissipative (frictional force) and conservative components with the latter being dependent on the phason field [20]. The phason self-action is inside the material elements in contrast to external actions. In the isotropic case, $D_{ij}=D{\mathsf{\delta }}_{ij}$ and $D>0$ is the phason friction coefficient. Introduction of the constitutive laws into Equations (7) and (8) yields the equations of motion for phonon and phason displacements. Both of these equations of motion are hyperbolic partial differential equation (PDE) with the phonon modes being described by a wave type equation while the phason modes by a telegraph type PDE. The latter equation leads to waves damped in time and finite propagation velocity. Since these two equations of motion are coupled, the phonon dynamics are affected by phason dynamics and vice versa. Recall that this model also includes two particular models developed before the Agiasofitou and Lazar models occur [6]: (i) the elastodynamic model of wave type ($\tilde{\mathsf{\rho }}=\mathsf{\rho }$, $D=0$) could describe phason waves with finite velocity but without attenuation; (ii) the hydrodynamic and/or the elasto-hydrodynamic model ($\tilde{\mathsf{\rho }}=0$, $D\ne 0$) support a diffusion type equation for the dynamics of the phason field. However, as is well known, the diffusion equation supports exclusively an infinite velocity of propagation. The physically inadmissible velocity of information propagation can be overcome by replacing the parabolic PDE by the hyperbolic one. In order to model waves damped exponentially in time and propagating with finite velocity as observed experimentally [21,22], Agiasofitou and Lazar [6] introduced a telegraph type equation for phason displacements. As shown above, utilization of the wave-telegraph equation enables us to step towards both the wave type and diffusion type description of phason dynamics by proper choice of the coefficients $\tilde{\mathsf{\rho }}$ and $D$.

Since initial-boundary value problems for the considered system of PDE are rather complicated for finding analytical solutions, we propose combining the Laplace transformation technique (with respect to the time variable) with a spatial discretization and approximation. Moreover, the application of the discretization to governing equations for displacements seems to be awkward, and we apply it directly to Equations (7) and (8) in a weak sense.

3. Weak Formulation of Local Integral Equations (LIEs)

Eliminating the time variable in governing Equations (7) and (8) by using the Laplace transformation, the governing equations for Laplace transforms become:

$$\mathsf{\rho }{s}^2\overline{u}(x,s)-\overline{\mathsf{\sigma }}\cdot \nabla (x,s)=\overline{f}(x,s)+\mathsf{\rho }\left(\dot{u}(x,0)+su(x,0)\right)$$

(9)

$$\left(\tilde{\mathsf{\rho }}{s}^2+Ds\right)\overline{w}(x,s)-\overline{H}\cdot \nabla (x,s)=\overline{g}(x,s)+\tilde{\mathsf{\rho }}\dot{w}(x,0)+\left(\tilde{\mathsf{\rho }}s+D\right)w(x,0)$$

(10)

If we assumed homogeneous initial conditions for both the phonon and phason displacement fields and vanishing body forces, the right-hand sides in Equations (9) and (10) would be equal to zero.

Let us consider the set of coupled governing Equations (9) and (10) in a weak sense on local subdomains considered around interior points $x^c\in {\mathsf{\Omega }}^c\subset \mathsf{\Omega }$. Taking the weight function as the Heaviside function supported on ${\mathsf{\Omega }}^c$, we obtain the system of local integral equations (LIE):

$${\displaystyle \underset{\partial {\mathsf{\Omega }}^c}{\int }\overline{n}(x,s)\cdot n(x)d\mathsf{\Gamma }}+{\displaystyle \underset{{\mathsf{\Omega }}^c}{\int }\left[-\mathsf{\rho }{s}^2\overline{u}(x,s)+\overline{f}(x,s)+\mathsf{\rho }\left(\dot{u}(x,0)+su(x,0)\right)\right]d\mathsf{\Omega }}=0$$

(11)

$${\displaystyle \underset{\partial {\mathsf{\Omega }}^c}{\int }\overline{H}(x,s)\cdot n(x)d\mathsf{\Gamma }}+{\displaystyle \underset{{\mathsf{\Omega }}^c}{\int }\left[-\left(\tilde{\mathsf{\rho }}{s}^2+Ds\right)\overline{w}(x,s)+\overline{g}(x,s)+\tilde{\mathsf{\rho }}\dot{w}(x,0)+\left(\tilde{\mathsf{\rho }}s+D\right)w(x,0)\right]d\mathsf{\Omega }}=0$$

(12)

in which we have utilized the Gauss divergence theorem and $\partial {\mathsf{\Omega }}^c$ is the boundary of ${\mathsf{\Omega }}^c$.

The derived local integral equations (LIEs) (11) and (12) are written in general vector form, and one can represent the vectors in an arbitrary coordinate system. The Cartesian coordinate system appears to be the most appropriate since the basis vectors are independent on the integration variables. Then, the component representation is obtained directly from Equations (11) and (12) as:

$${\displaystyle \underset{\partial {\mathsf{\Omega }}^c}{\int }{\overline{\mathsf{\sigma }}}_{ij}(x_1,x_2,s)n_j(x_1,x_2)d\mathsf{\Gamma }}+{\displaystyle \underset{{\mathsf{\Omega }}^c}{\int }\left[-\mathsf{\rho }{s}^2{\overline{u}}_i(x_1,x_2,s)+{\overline{f}}_i(x_1,x_2,s)+\mathsf{\rho }\left({\dot{u}}_i(x_1,x_2,0)+s{u}_i(x_1,x_2,0)\right)\right]d\mathsf{\Omega }}=0$$

(13)

$${\displaystyle \underset{\partial {\mathsf{\Omega }}^c}{\int }{\overline{H}}_{ij}(x_1,x_2,s)n_j(x_1,x_2)d\mathsf{\Gamma }}++{\displaystyle \underset{{\mathsf{\Omega }}^c}{\int }\left[-\left(\tilde{\mathsf{\rho }}{s}^2+Ds\right){\overline{w}}_i(x_1,x_2,s)+{\overline{g}}_i(x_1,x_2,s)+\tilde{\mathsf{\rho }}{\dot{w}}_i(x_1,x_2,0)+\left(\tilde{\mathsf{\rho }}s+D\right)w_i(x_1,x_2,0)\right]d\mathsf{\Omega }}=0$$

(14)

with $i,j\in \{1,2\}$.

In order to facilitate the integrations, it is appropriate to choose the local subdomain as a circle around the point $(x_1^c,x_2^c)$, i.e., ${\mathsf{\Omega }}^c=\{\forall (x_1,x_2);|x-x^c|\le r_0\}$. Then, the integration over $\partial {\mathsf{\Omega }}^c$ can be performed as the integration with respect to the angular variable. Now, in view of Equations (1)–(4), the LIE can be rewritten as:

$$\begin{array}{l}{\displaystyle \underset{\partial {\mathsf{\Omega }}^c}{\int }\left[c_{12}{n}_i{\partial }_k+c_{66}\left({\mathsf{\delta }}_{ik}{n}_j{\partial }_j+n_k{\partial }_i\right)\right]{\overline{u}}_k(x_1,x_2,s)d\mathsf{\Gamma }}+\\ +{\displaystyle \underset{\partial {\mathsf{\Omega }}^c}{\int }R\left[\left({\mathsf{\delta }}_{i1}{n}_2+{\mathsf{\delta }}_{i2}{n}_1\right){\mathsf{\epsilon }}_{3lk}{\partial }_l+\left({\mathsf{\delta }}_{i1}{n}_1-{\mathsf{\delta }}_{i2}{n}_2\right){\partial }_k\right]{\overline{w}}_k(x_1,x_2,s)d\mathsf{\Gamma }}+\\ +{\displaystyle \underset{{\mathsf{\Omega }}^c}{\int }\left[-\mathsf{\rho }{s}^2{\overline{u}}_i(x_1,x_2,s)+{\overline{f}}_i(x_1,x_2,s)+\mathsf{\rho }\left({\dot{u}}_i(x_1,x_2,0)+s{u}_i(x_1,x_2,0)\right)\right]d\mathsf{\Omega }}=0\end{array}$$

(15)

$$\begin{array}{l}{\displaystyle \underset{\partial {\mathsf{\Omega }}^c}{\int }R\left[\left({\overline{u}}_{1,2}(x_1,x_2,s)+{\overline{u}}_{2,1}(x_1,x_2,s)\right){\mathsf{\tau }}_i+\left({\overline{u}}_{1,1}(x_1,x_2,s)-{\overline{u}}_{2,2}(x_1,x_2,s)\right)n_i\right]d\mathsf{\Gamma }}+\\ +{\displaystyle \underset{\partial {\mathsf{\Omega }}^c}{\int }\left[K_1{\mathsf{\delta }}_{ik}{n}_j{\partial }_j+K_2\left(n_i{\partial }_k-n_k{\partial }_i\right)\right]{\overline{w}}_k(x_1,x_2,s)d\mathsf{\Gamma }}+\\ +{\displaystyle \underset{{\mathsf{\Omega }}^c}{\int }\left[-\left(\tilde{\mathsf{\rho }}{s}^2+Ds\right){\overline{w}}_i(x_1,x_2,s)+{\overline{g}}_i(x_1,x_2,s)+\tilde{\mathsf{\rho }}{\dot{w}}_i(x_1,x_2,0)+\left(\tilde{\mathsf{\rho }}s+D\right)w_i(x_1,x_2,0)\right]d\mathsf{\Omega }}=0\end{array}$$

(16)

with ${\mathsf{\tau }}_i$ being the unit tangent vector related to the unit outward normal vector as ${\mathsf{\tau }}_i={\mathsf{\epsilon }}_{3ji}{n}_j$.

Thus, what we need is to utilize certain approximation for the phonon as well as phason displacements and their gradients.

4. Meshless Approximation for Phonon and Phason Displacements

To the spatial variations of phonon and phason displacements ${\overline{u}}_k\left(x,s\right)$, ${\overline{w}}_k\left(x,s\right)$, the meshless approximation over a number of randomly located nodes $x^c$, $c=1,2,\mathrm{...},n$, is applied using the radial basis functions (RBF). Thus, the considered approximations take the form:

$${\overline{u}}_k\left(x,s\right)={\displaystyle \sum _{c=1}^n{U}_k^c\left(s\right)R^c(x)}$$

(17)

$${\overline{w}}_k\left(x,s\right)={\displaystyle \sum _{c=1}^n{W}_k^c\left(s\right)R^c(x)}$$

(18)

where $R^c(x)$ is the radial basis functions associated with the node $x^c$, and $U_k^c\left(s\right)$, $W_k^c\left(s\right)$ are expansion coefficients for phonon and phason displacements, respectively. The radial basis functions employed in this article are multiquadrics

$$R^c\left(x\right)={\left({\left|x-x^c\right|}^2+{\tilde{c}}^2\right)}^{\raisebox{1ex}{$m$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}.$$

(19)

The shape parameter $\tilde{c}$ is proportional to the minimum distance between nodes, while m is chosen to be $m=-2$. Taking the approximations as Equations (17) and (18) at nodal points, one obtains the following systems of equations:

$${\overline{u}}_k^b\left(s\right)={\displaystyle \sum _{c=1}^n{U}_k^c\left(s\right)R^c(x^b)},{\overline{u}}_k^b\left(s\right)={\overline{u}}_k\left(x^b,s\right)$$

(20)

$${\overline{w}}_k^b\left(s\right)={\displaystyle \sum _{c=1}^n{W}_k^c\left(s\right)R^c(x^b)},{\overline{w}}_k^b\left(s\right)={\overline{w}}_k\left(x^b,s\right)$$

(21)

which can be rewritten in the matrix notation as

$${\displaystyle \sum _{c=1}^n{R}^{bc}{U}_k^c}={\overline{u}}_k^b(s),{\displaystyle \sum _{c=1}^n{R}^{bc}{W}_k^c}={\overline{w}}_k^b(s)$$

(22)

Hence, the expansion coefficients can be expressed in terms of nodal unknowns as:

$$U_k^c={\displaystyle \sum _{b=1}^n{[R^{-1}]}^{cb}{\overline{u}}_k^b(s)},W_k^c={\displaystyle \sum _{b=1}^n{[R^{-1}]}^{cb}{\overline{w}}_k^b(s)}$$

(23)

Substituting Equation (23) into Equations (17) and (18), we receive

$${\overline{u}}_k\left(x,s\right)={\displaystyle \sum _{b=1}^n{U}_k^b\left(s\right)R^b(x)}={\displaystyle \sum _{b=1}^n{\displaystyle \sum _{c=1}^n{R}^b(x){[R^{-1}]}^{bc}{\overline{u}}_k^c\left(s\right)}}={\displaystyle \sum _{c=1}^n{\overline{u}}_k^c\left(s\right){\mathsf{\phi }}^c(x)}$$

(24)

$${\overline{w}}_k\left(x,s\right)={\displaystyle \sum _{b=1}^n{W}_k^b\left(s\right)R^b(x)}={\displaystyle \sum _{b=1}^n{\displaystyle \sum _{c=1}^n{R}^b(x){[R^{-1}]}^{bc}{\overline{w}}_k^c\left(s\right)}}={\displaystyle \sum _{a=1}^n{\overline{w}}_k^c\left(s\right){\mathsf{\phi }}^c(x)}$$

(25)

where

$${\mathsf{\phi }}^c(x)={\displaystyle \sum _{b=1}^n{R}^b(x){[R^{-1}]}^{bc}}$$

(26)

is the shape function associated with node $x^c$ and ${\overline{u}}_k^c\left(s\right)$, ${\overline{w}}_k^c\left(s\right)$ are the nodal values of the Laplace transforms of phonon and phason displacements, respectively.

Considering the problem without body forces (phonon body forces and conservative bulk phason self-action) and with homogeneous initial conditions, the discretized local integral equations (LIEs) (15) and (16) collocated at an interior node $x^c\in {\mathsf{\Omega }}^c\subset \mathsf{\Omega }$ can be written as:

$$\begin{gathered} {\displaystyle \sum _{a=1}^n{\overline{u}}_k^a(s){\displaystyle \underset{\partial {\mathsf{\Omega }}^c}{\int }\left[c_{12}{n}_i{\mathsf{\phi }}_{,k}^a+c_{66}\left({\mathsf{\delta }}_{ik}{n}_j{\mathsf{\phi }}_{,j}^a+n_k{\mathsf{\phi }}_{,i}^a\right)\right]d\mathsf{\Gamma }}}-\mathsf{\rho }{s}^2{\displaystyle \sum _{a=1}^n{\overline{u}}_i^a(s)}{\displaystyle \underset{{\mathsf{\Omega }}^c}{\int }{\mathsf{\phi }}^{a}d\mathsf{\Omega }}+ \\ +{\displaystyle \sum _{a=1}^n{\overline{w}}_k^a(s){\displaystyle \underset{\partial {\mathsf{\Omega }}^c}{\int }R\left[\left({\mathsf{\delta }}_{i1}{n}_2+{\mathsf{\delta }}_{i2}{n}_1\right){\mathsf{\epsilon }}_{3lk}{\mathsf{\phi }}_{,l}^a+\left({\mathsf{\delta }}_{i1}{n}_1-{\mathsf{\delta }}_{i2}{n}_2\right){\mathsf{\phi }}_{,k}^a\right]d\mathsf{\Gamma }}}=0 \end{gathered}$$

(27)

$$\begin{array}{l}{\displaystyle \sum _{a=1}^n{\overline{u}}_k^a(s)}{\displaystyle \underset{\partial {\mathsf{\Omega }}^c}{\int }R\left[\left({\mathsf{\delta }}_{k1}{\mathsf{\phi }}_{,2}^a+{\mathsf{\delta }}_{k2}{\mathsf{\phi }}_{,1}^a\right){\mathsf{\tau }}_i+\left({\mathsf{\delta }}_{k1}{\mathsf{\phi }}_{,1}^a-{\mathsf{\delta }}_{k2}{\mathsf{\phi }}_{,2}^a\right)n_i\right]d\mathsf{\Gamma }}+\\ +{\displaystyle \sum _{a=1}^n{\overline{w}}_k^a(s){\displaystyle \underset{\partial {\mathsf{\Omega }}^c}{\int }\left[K_1{\mathsf{\delta }}_{ik}{n}_j{\mathsf{\phi }}_{,j}^a+K_2\left(n_i{\mathsf{\phi }}_{,k}^a-n_k{\mathsf{\phi }}_{,i}^a\right)\right]d\mathsf{\Gamma }}}-\left(\tilde{\mathsf{\rho }}{s}^2+Ds\right){\displaystyle \sum _{a=1}^n{\overline{w}}_i^a(s){\displaystyle \underset{{\mathsf{\Omega }}^c}{\int }{\mathsf{\phi }}^{a}d\mathsf{\Omega }}}=0\end{array}$$

(28)

The global boundary of the analyzed domain is decomposed into two parts $\mathsf{\Gamma }={\mathsf{\Gamma }}_e\cup {\mathsf{\Gamma }}_n$, where ${\mathsf{\Gamma }}_e$ and ${\mathsf{\Gamma }}_n$ are parts on which essential and natural boundary conditions are prescribed, respectively.

For $x^b\in {\mathsf{\Gamma }}_e$, we collocate the meshless approximation of phonon and phason displacements, i.e.,

$${\displaystyle \sum _{c=1}^n{\overline{u}}_k^c\left(s\right){\mathsf{\phi }}^c(x^b)}={\overline{\tilde{u}}}_k\left(x^b,s\right)$$

(29)

$${\displaystyle \sum _{c=1}^n{\overline{w}}_k^c\left(s\right){\mathsf{\phi }}^c(x^b)}={\overline{\tilde{w}}}_k\left(x^b,s\right)$$

(30)

where the tilde denotes the prescribed values by boundary conditions. If the collocation point lies on the boundary, $x^b\in {\mathsf{\Gamma }}_n$, we define local subdomain as ${\mathsf{\Omega }}^b={\tilde{\mathsf{\Omega }}}^b\cap \mathsf{\Omega }$, where ${\tilde{\mathsf{\Omega }}}^b$ is the circular domain centered at $x^b$. Then, the boundary of local sub-domain consists of two parts $\partial {\mathsf{\Omega }}^b={\mathsf{\Gamma }}^b\cup {\mathrm{L}}^b$, where ${\mathrm{L}}^b=\partial {\tilde{\mathsf{\Omega }}}^b\cap \mathsf{\Omega }$, and ${\mathsf{\Gamma }}^b={\tilde{\mathsf{\Omega }}}^b\cap \mathsf{\Gamma }=\left({\tilde{\mathsf{\Omega }}}^b\cap {\mathsf{\Gamma }}_e\right)\cup \left({\tilde{\mathsf{\Omega }}}^b\cap {\mathsf{\Gamma }}_n\right)={\mathsf{\Gamma }}_e^b\cup {\mathsf{\Gamma }}_n^b$. For $x^b\in {\mathsf{\Gamma }}_n$, we consider the discretized LIEs (15) and (16) collocate at $x^b$:

$$\begin{gathered} {\displaystyle \sum _{a=1}^n{\overline{u}}_k^a(s){\displaystyle \underset{{\mathsf{\Gamma }}_e^b\cup L^b}{\int }\left[c_{12}{n}_i{\mathsf{\phi }}_{,k}^a+c_{66}\left({\mathsf{\delta }}_{ik}{n}_j{\mathsf{\phi }}_{,j}^a+n_k{\mathsf{\phi }}_{,i}^a\right)\right]d\mathsf{\Gamma }}}-\mathsf{\rho }{s}^2{\displaystyle \sum _{a=1}^n{\overline{u}}_i^a(s)}{\displaystyle \underset{{\mathsf{\Omega }}^b}{\int }{\mathsf{\phi }}^{a}d\mathsf{\Omega }}+ \\ +{\displaystyle \sum _{a=1}^n{\overline{w}}_k^a(s){\displaystyle \underset{{\mathsf{\Gamma }}_e^b\cup L^b}{\int }R\left[\left({\mathsf{\delta }}_{i1}{n}_2+{\mathsf{\delta }}_{i2}{n}_1\right){\mathsf{\epsilon }}_{3lk}{\mathsf{\phi }}_{,l}^a+\left({\mathsf{\delta }}_{i1}{n}_1-{\mathsf{\delta }}_{i2}{n}_2\right){\mathsf{\phi }}_{,k}^a\right]d\mathsf{\Gamma }}}=-{\displaystyle \underset{{\mathsf{\Gamma }}_n^b}{\int }{\overline{\tilde{t}}}_i(x,s)d\mathsf{\Gamma }} \end{gathered}$$

(31)

$$\begin{gathered} {\displaystyle \sum _{a=1}^n{\overline{w}}_k^a(s){\displaystyle \underset{{\mathsf{\Gamma }}_e^b\cup L^b}{\int }\left[K_1{\mathsf{\delta }}_{ik}{n}_j{\mathsf{\phi }}_{,j}^a+K_2\left(n_i{\mathsf{\phi }}_{,k}^a-n_k{\mathsf{\phi }}_{,i}^a\right)\right]d\mathsf{\Gamma }}}-\left(\tilde{\mathsf{\rho }}{s}^2+Ds\right){\displaystyle \sum _{a=1}^n{\overline{w}}_i^a(s){\displaystyle \underset{{\mathsf{\Omega }}^b}{\int }{\mathsf{\phi }}^{a}d\mathsf{\Omega }}}+ \\ +{\displaystyle \sum _{a=1}^n{\overline{u}}_k^a(s)}{\displaystyle \underset{{\mathsf{\Gamma }}_e^b\cup L^b}{\int }R\left[\left({\mathsf{\delta }}_{k1}{\mathsf{\phi }}_{,2}^a+{\mathsf{\delta }}_{k2}{\mathsf{\phi }}_{,1}^a\right){\mathsf{\tau }}_i+\left({\mathsf{\delta }}_{k1}{\mathsf{\phi }}_{,1}^a-{\mathsf{\delta }}_{k2}{\mathsf{\phi }}_{,2}^a\right)n_i\right]d\mathsf{\Gamma }}=-{\displaystyle \underset{{\mathsf{\Gamma }}_n^b}{\int }{\overline{\tilde{q}}}_i(x,s)d\mathsf{\Gamma }} \end{gathered}$$

(32)

where ${\overline{\tilde{t}}}_i(x,s)$ and ${\overline{\tilde{q}}}_i(x,s)$ are the Laplace transforms of prescribed values of phonon and phason tractions defined as $t_i(x,t)={\mathsf{\sigma }}_{ij}(x,t)n_j(x)$, $q_i(x,t)=H_{ij}(x,t)n_j(x)$, respectively. Equations (27)–(32) give us the complete set of algebraic equations for computation of unknown nodal values of the Laplace transforms of phonon and phason displacements. Having solved this system for unknowns, one can obtain the time-dependent solutions by applying the inverse Laplace-transformation to the transformed quantities such as the Talbot technique.

Recall that the proposed formulation and calculations are performed in the Cartesian representation of the phonon and phason stresses and displacements. The representation in the polar coordinate system can be obtained by using the Mohr’s circle technique.

5. Numerical Example and Discussions:

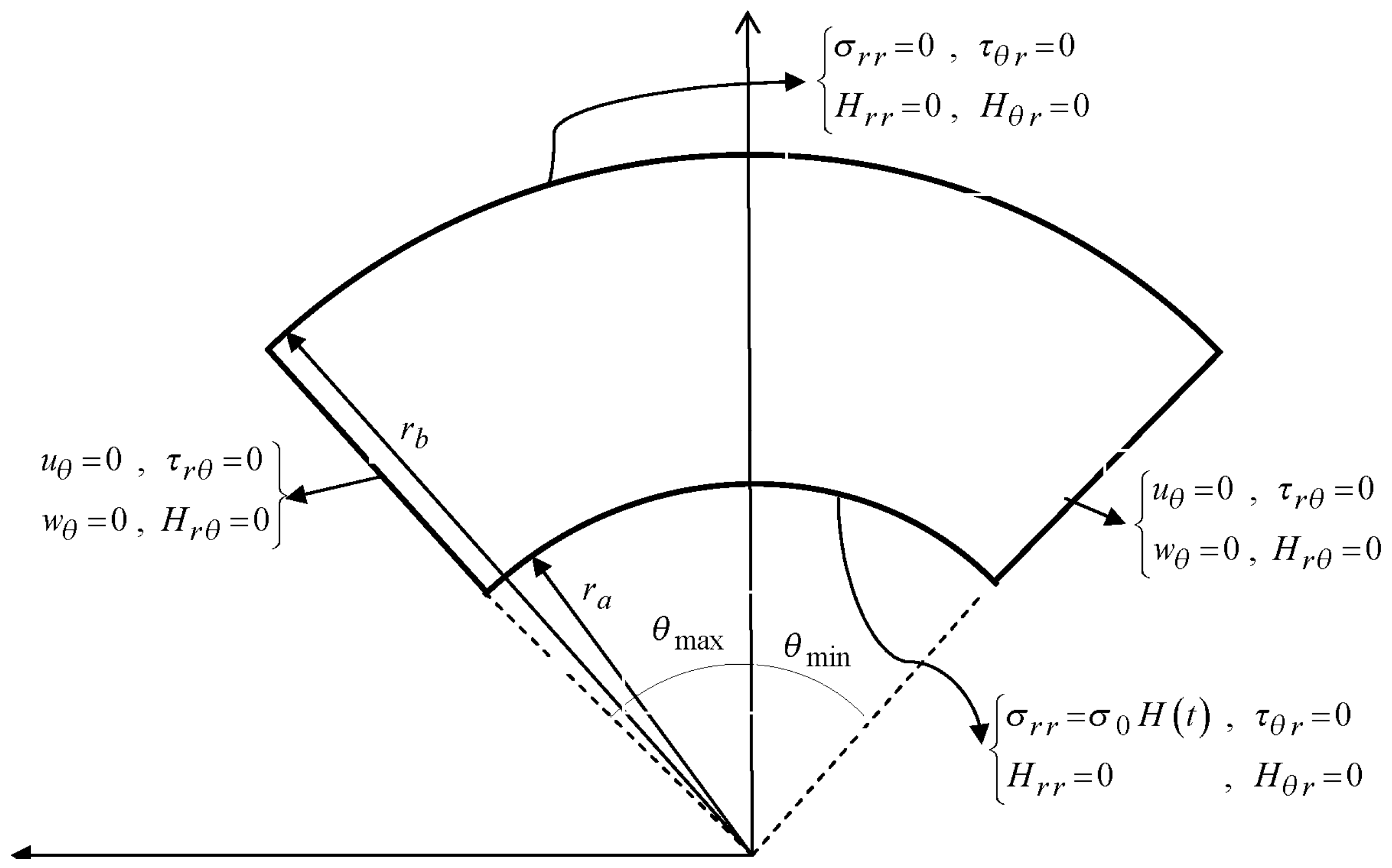
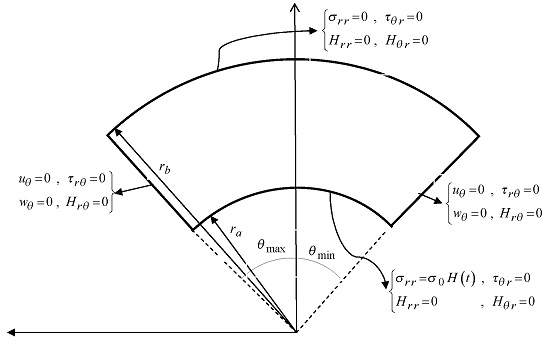
To show some numerical results of the problem, an infinite length sector of a hollow cylinder is assumed with the following mechanical properties and inner radius $r_a=1m$, outer radius $r_b=1m$ and ${\mathsf{\theta }}_{\text{min}}\le \mathsf{\theta }\le {\mathsf{\theta }}_{\text{max}}$, ${\mathsf{\theta }}_{\text{min}}=0$, ${\mathsf{\theta }}_{\text{max}}=\mathsf{\pi }$ for numerical analysis (see Figure 1).

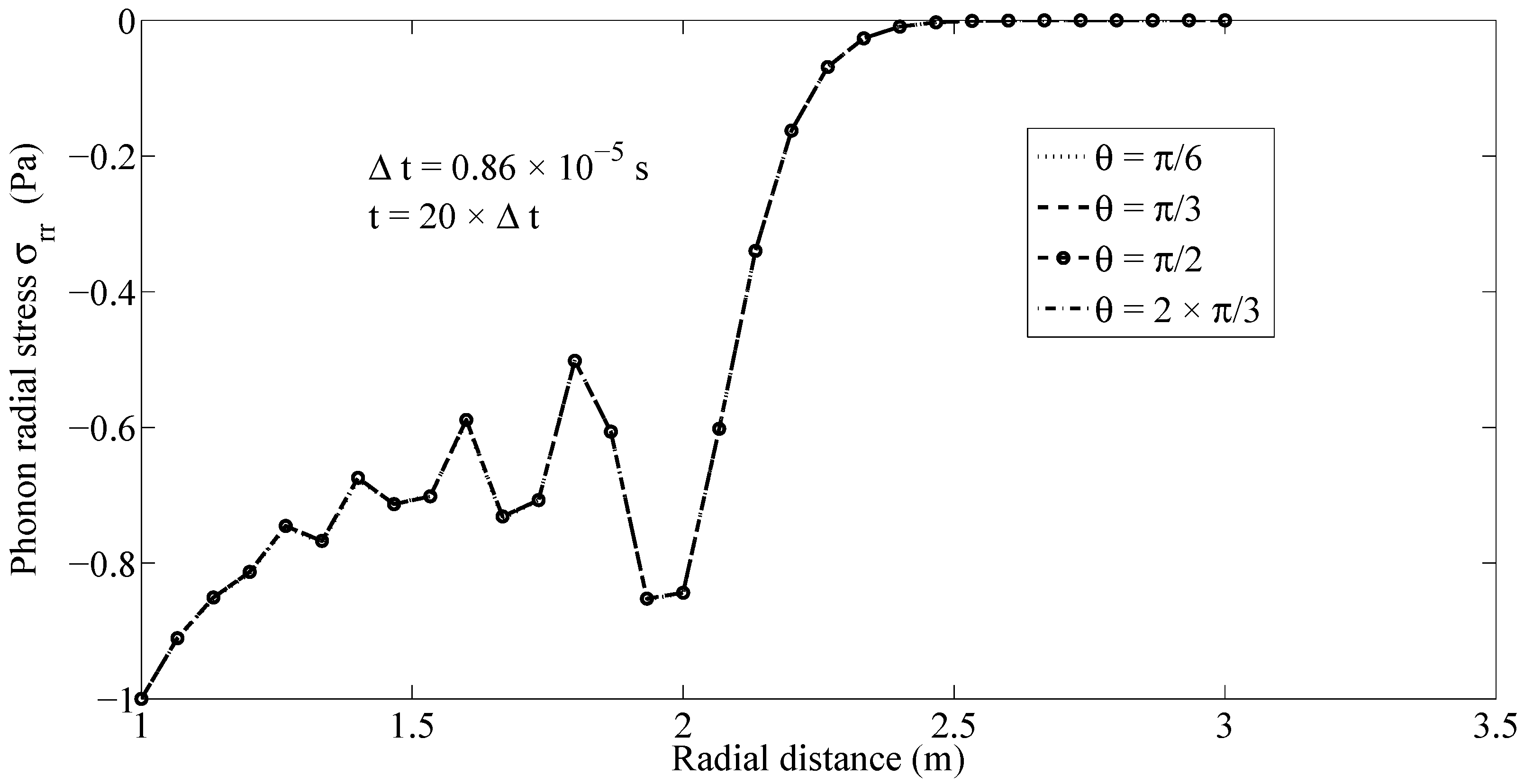
Firstly, to verify the presented method and data, the material of cylinder is assumed to be isotropic homogenous with the following mechanical properties:

$$c_{11}=234.3GPa,c_{22}=c_{11},c_{12}=57.4GPa,\mathsf{\rho }=4180kg/m^3{K}_2=0,K_1=0,R=0$$

(33)

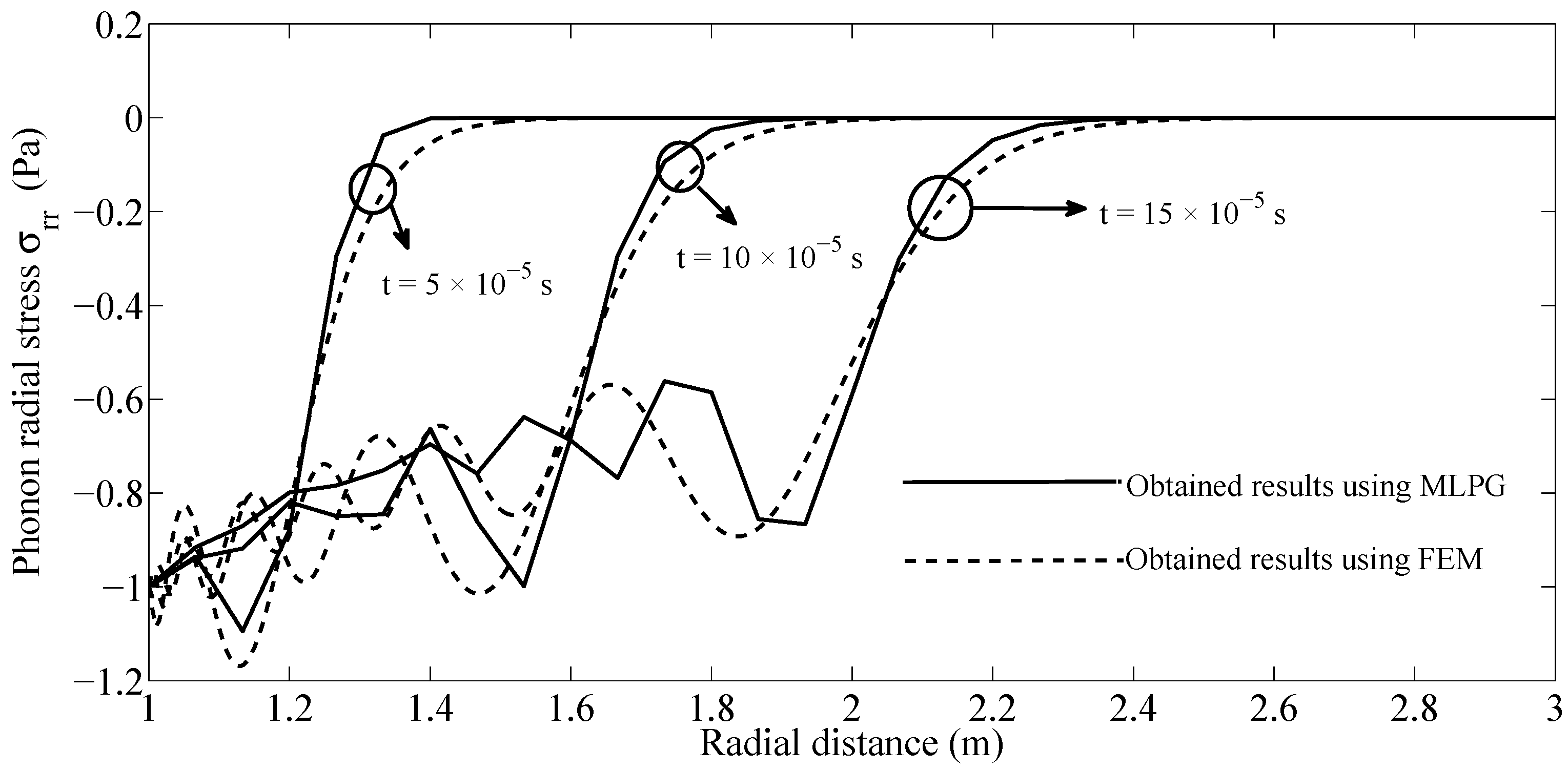
The considered boundary conditions for phonon modes are shown partially in Figure 1 and vanishing initial conditions are assumed. Since the phonon–phason coupling is absent, there is no phason response in the considered example and the dynamic behavior of cylinder is described as classical elastodynamic. The obtained results by the MLPG method for phonon radial stress along the radial direction, and $\mathsf{\theta }=\frac{\mathsf{\pi }}{2}$ at several time instants are compared with those obtained by finite element method (FEM), which are illustrated in Figure 2. The comparison shows a good agreement between the results.

The following mechanical properties correspond to Al–Ni–Co quasicrystals [11,12] and are considered for study on the transient response of QCs cylinder to Heaviside impact loading:

$$c_{11}=234.3GPa,c_{11}=c_{22},c_{12}=57.4GPa,K_1=122GPa{K}_2=24GPa,\mathsf{\rho }=4180kg/m^3,R=1.1GPa$$

(34)

Since the phason friction coefficient is assumed to be zero, the employed compatible elastodynamics of wave-telegraph type of quasicrystals degenerates to the elastodynamic model of wave type. The boundary of the analyzed domain is composed of four parts $\partial \mathsf{\Omega }=\partial {\mathsf{\Omega }}_a\cup \partial {\mathsf{\Omega }}_b\cup \partial {\mathsf{\Omega }}_m\cup \partial {\mathsf{\Omega }}_M$ as shown in Figure 1. In the shape of Cartesian components, the following boundary conditions are considered to study the dynamic behavior of both phonon and phason stress fields (see Figure 1):

$${t_i\left(x,t\right)|}_{\partial {\mathsf{\Omega }}_a}={\mathsf{\sigma }}_0{n}_i(x)H\left(t\right),{q_i\left(x,t\right)|}_{\partial {\mathsf{\Omega }}_a}=0$$

(35)

$${t_i\left(x,t\right)|}_{\partial {\mathsf{\Omega }}_b}=0,{q_i\left(x,t\right)|}_{\partial {\mathsf{\Omega }}_b}=0$$

(36)

$${u_i\left(x,t\right)n_i\left(x\right)|}_{\partial {\mathsf{\Omega }}_m}=0,{t_i\left(x,t\right){\mathsf{\tau }}_i\left(x\right)|}_{\partial {\mathsf{\Omega }}_m}=0,{w_i\left(x,t\right)n_i\left(x\right)|}_{\partial {\mathsf{\Omega }}_m}=0,{q_i\left(x,t\right){\mathsf{\tau }}_i\left(x\right)|}_{\partial {\mathsf{\Omega }}_m}=0$$

(37)

$${u_i\left(x,t\right)n_i\left(x\right)|}_{\partial {\mathsf{\Omega }}_M}=0,{t_i\left(x,t\right){\mathsf{\tau }}_i\left(x\right)|}_{\partial {\mathsf{\Omega }}_M}=0,{w_i\left(x,t\right)n_i\left(x\right)|}_{\partial {\mathsf{\Omega }}_M}=0,{q_i\left(x,t\right){\mathsf{\tau }}_i\left(x\right)|}_{\partial {\mathsf{\Omega }}_M}=0$$

(38)

where $H\left(t\right)$ is a Heaviside unit step function, $n_i(x)$ is the unit outward normal vector on the boundary, ${\mathsf{\tau }}_i\left(x\right)$ is the unit tangent vector on the boundary, and ${\mathsf{\sigma }}_0=-1\mathrm{Pa}$.

The response to the shock loading by normal stresses applied on the inner cylindrical surface of the considered sector of the hollow cylinder is illustrated via the spatial distributions at several time instants as well as via the time evolution of phonon and phason fields at certain points of the analyzed domain.

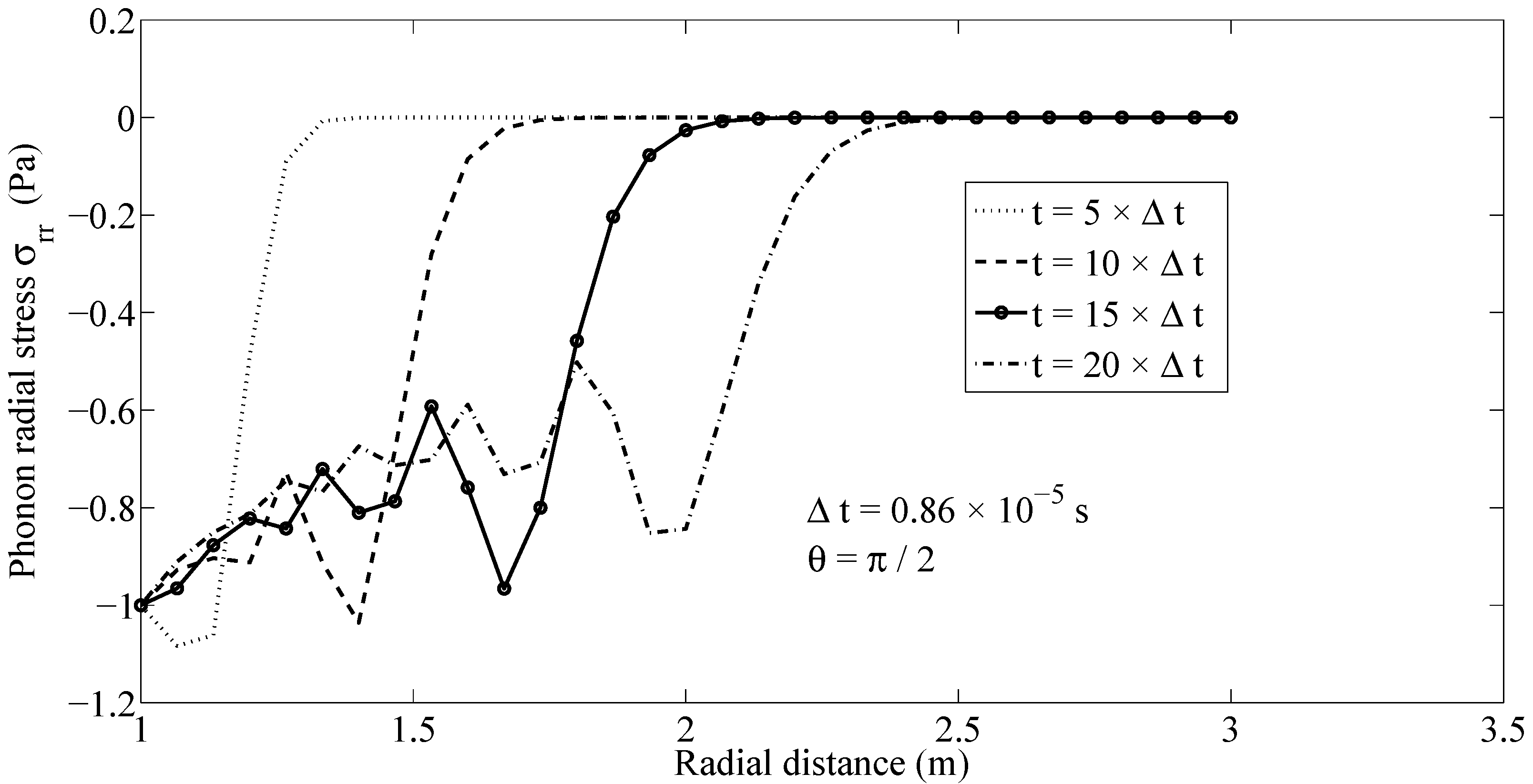
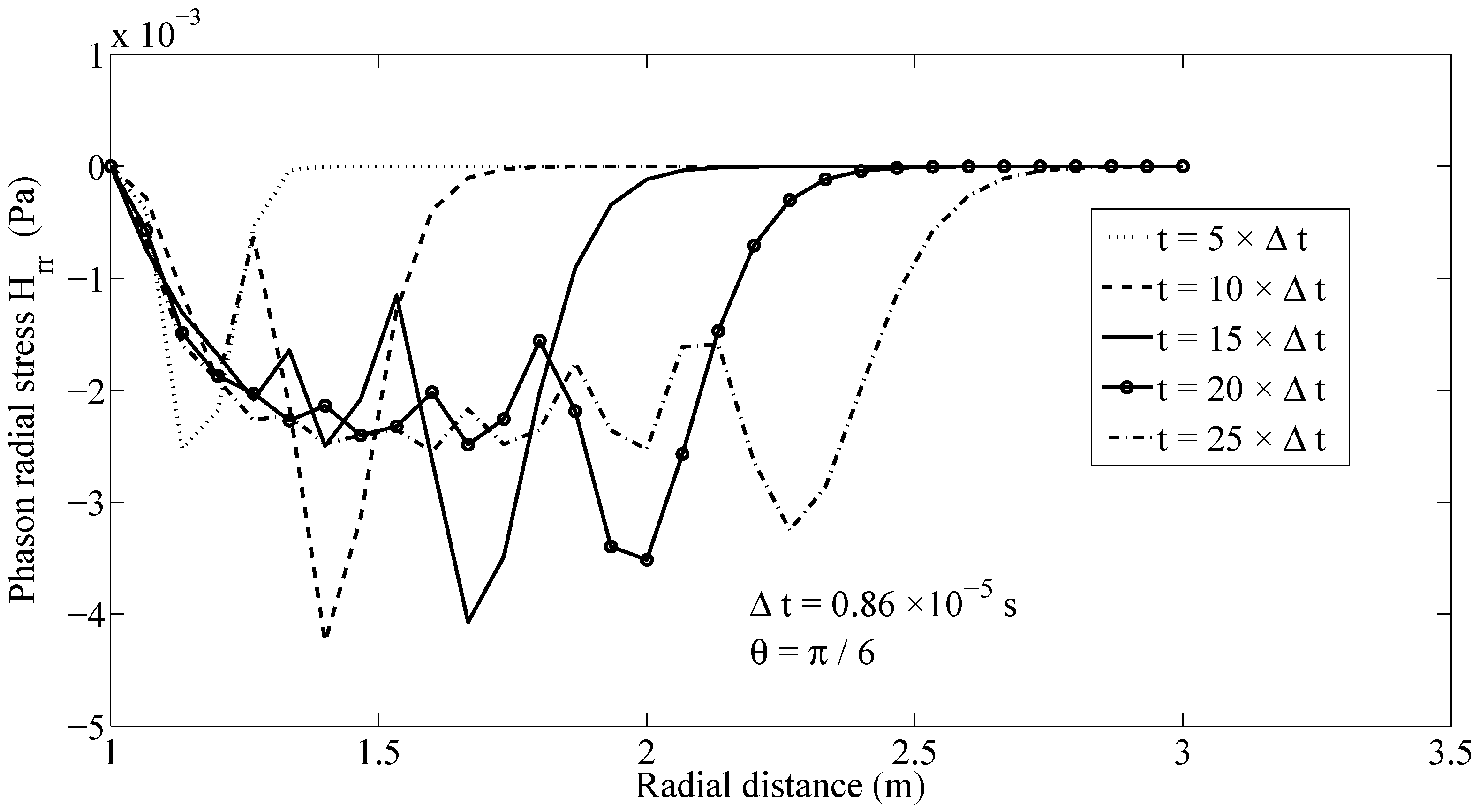
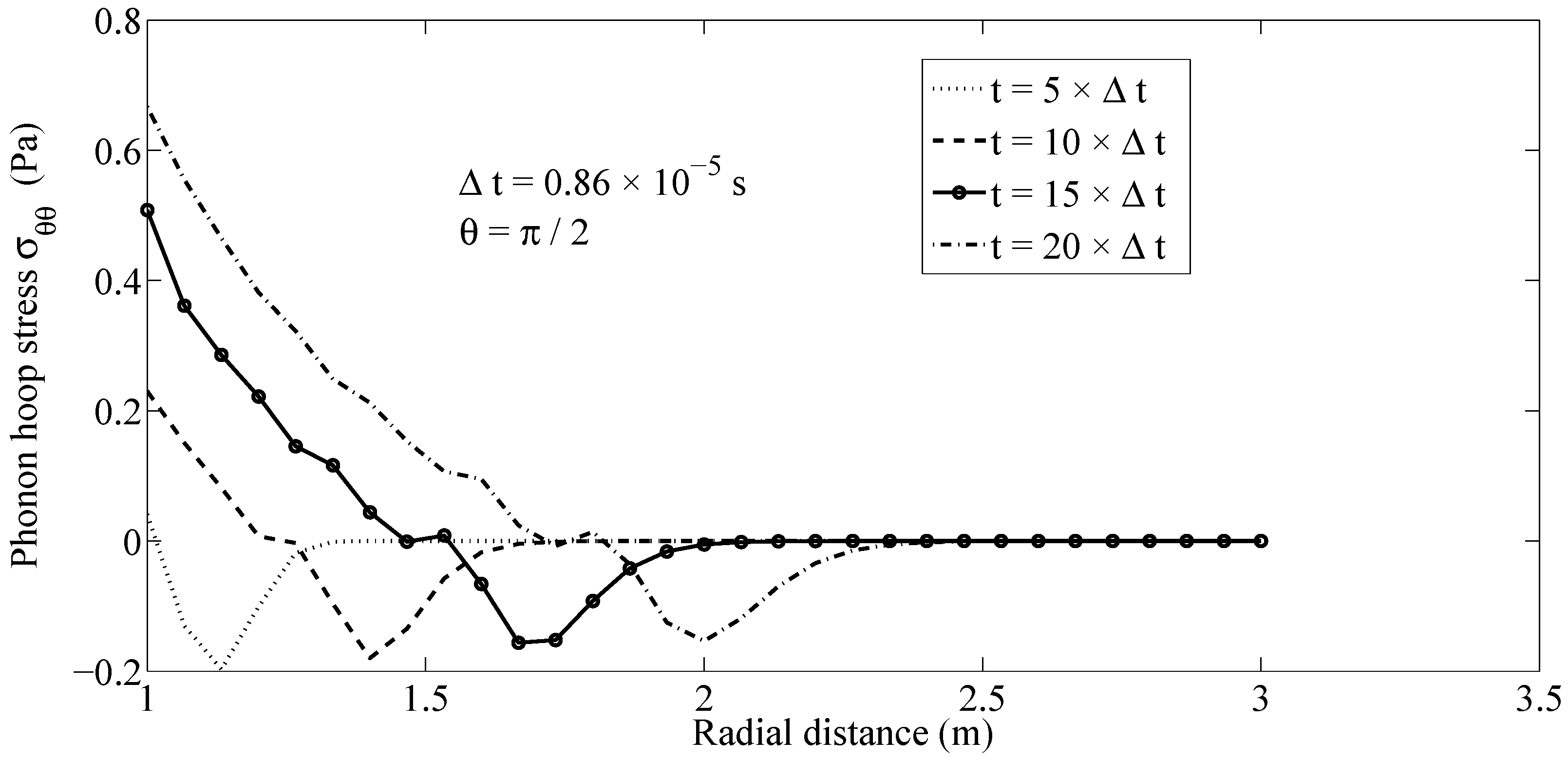
Figure 3 shows the distribution of phonon radial stresses ${\mathsf{\sigma }}_{rr}$ along the ray $(r,\mathsf{\theta }=\mathsf{\pi }/2)$ at several time instants, with the time step being assumed to be $\Delta t=0.86\times {10}^{-5}\mathrm{s}$. The propagation of phonon radial stress wave fronts can be tracked in Figure 3. Likewise, the wave front of phonon hoop stress ${\mathsf{\sigma }}_{\mathsf{\theta }\mathsf{\theta }}$ is propagated along the ray $(r,\mathsf{\theta }=\mathsf{\pi }/2)$ with a finite speed, as can be seen in Figure 4.

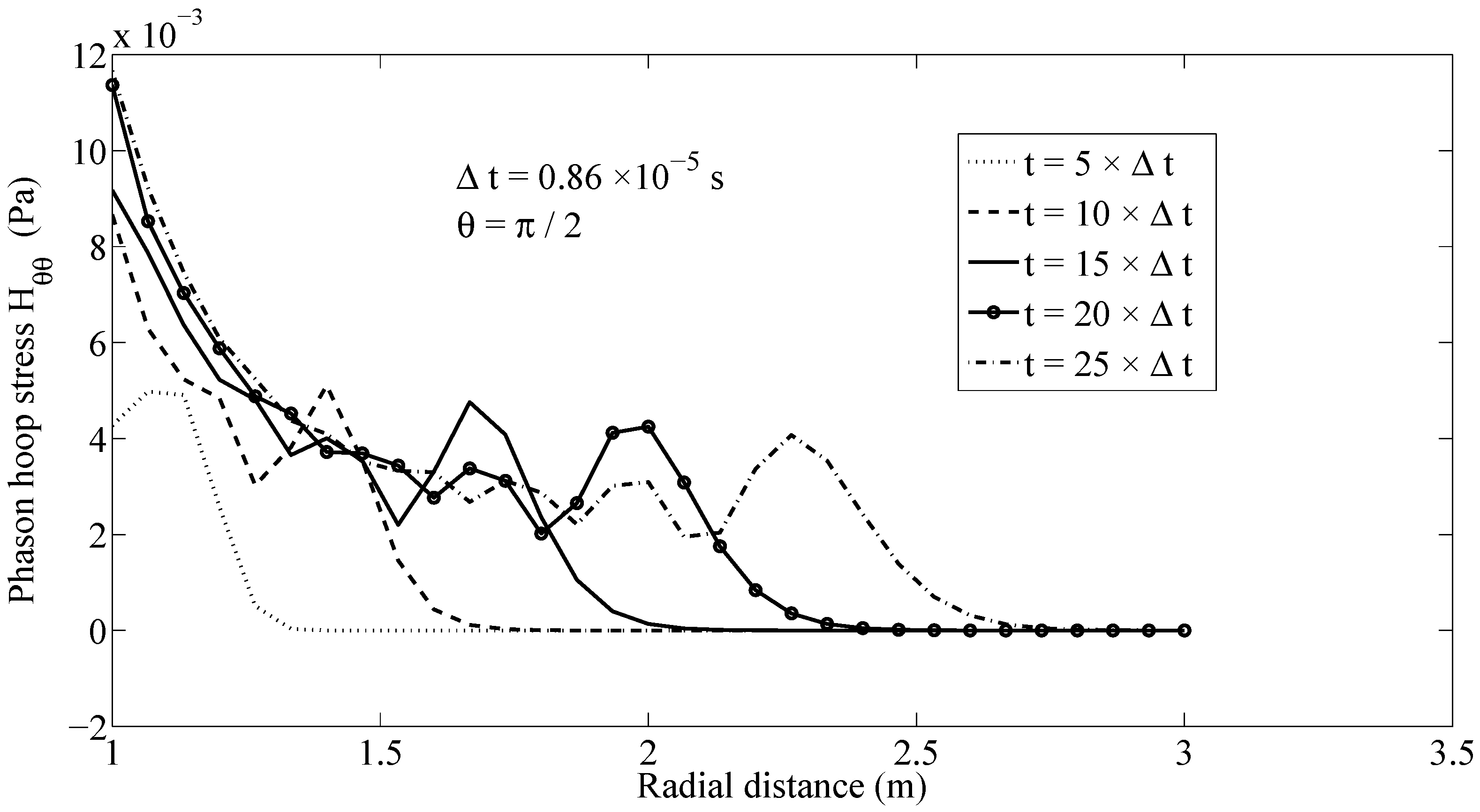
Owing to the coupling, the phason stress field is affected by the considered excitation in phonon stress field. Figure 5 depicts the wave propagation of the phason radial stress field $H_{rr}$ along ray $(r,\mathsf{\theta }=\mathsf{\pi }/6)$ with a finite speed. A similar behavior can be observed also for the phason hoop stress field $H_{\mathsf{\theta }\mathsf{\theta }}$, as shown in Figure 6. Figure 5 and Figure 6 demonstrate that the presented MLPG method has the capability to simulate the dynamic behavior of both phonon and phason fields and the interaction among them.

The problem is not angularly symmetric because of the phonon–phason coupling. Since the classical (phonon) stress loading is applied on the inner surface of a half of the infinite hollow cylinder, and the coupling coefficients are 100 times smaller than the classical elasticity coefficients, the response of phason fields is 100 times smaller than the response of phonon fields. Therefore the response of phonon fields is almost independent of the angular variable (see Figure 7), though such a dependence is evident in the response of the phason fields (see Figure 8).

The distributions of both phonon and phason radial displacements, $u_r$ and $w_r$, along the ray $(r,\mathsf{\theta }=\mathsf{\pi }/2)$ can be observed in Figure 9 and Figure 10. The wave fronts of both the phonon and phason radial displacements can be tracked at various time instants because of a finite speed of wave propagation. Again, the coupling between the phonon and phason fields is confirmed.

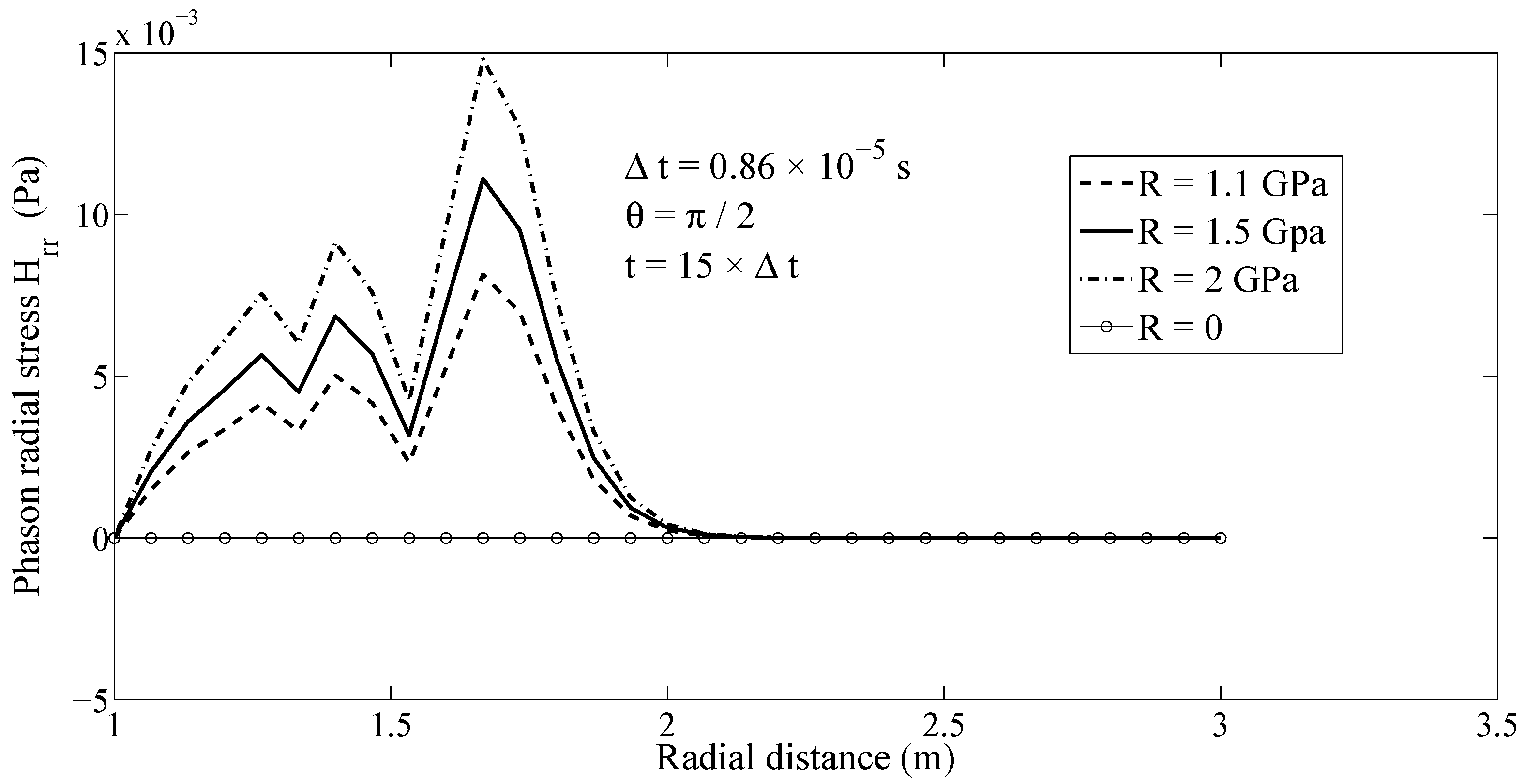
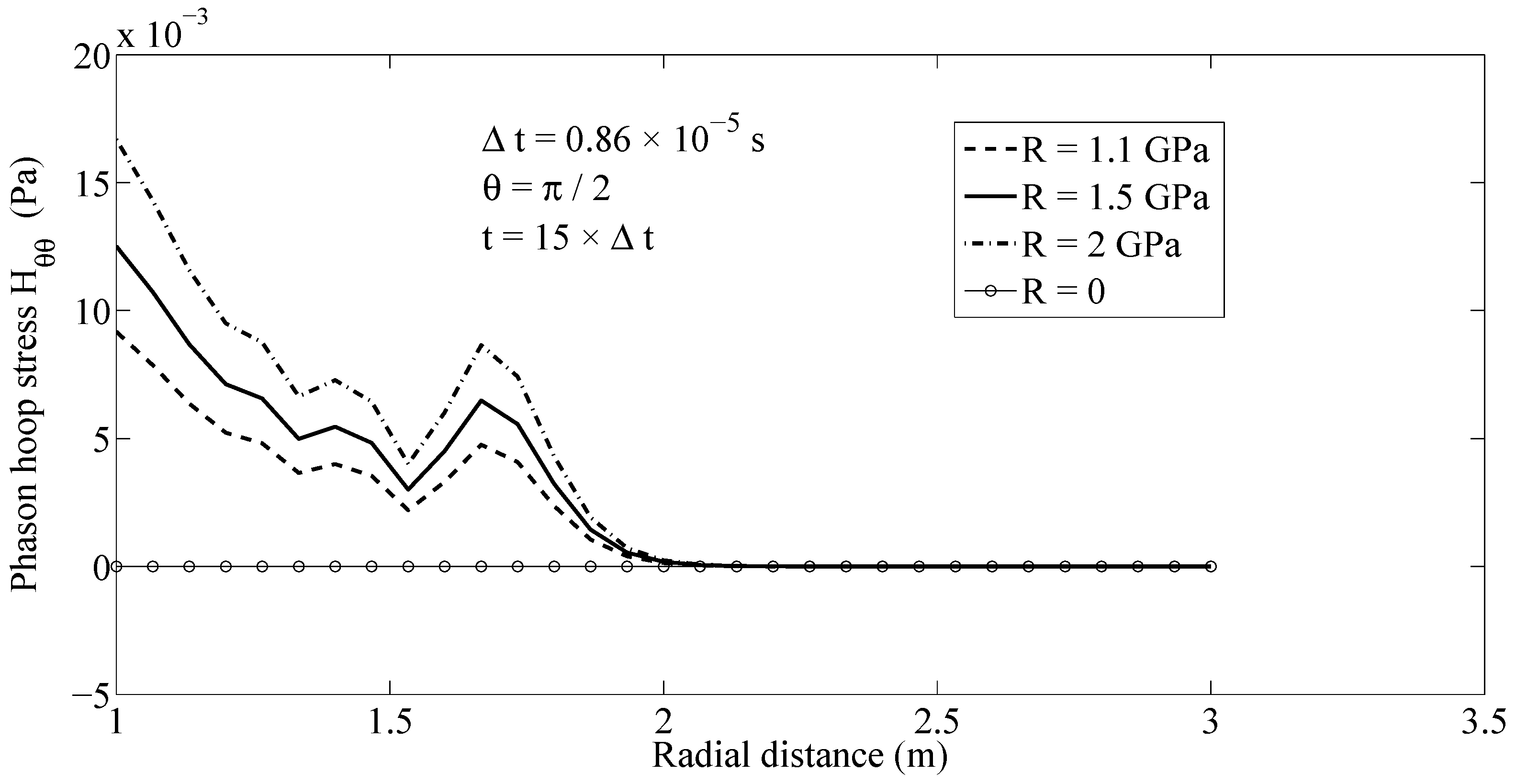
The effects of the value of $R$ on the results for the phason fields can be observed in Figure 11 and Figure 12 in which the distributions of phason radial and hoop stresses along the radial direction are drawn at $\mathsf{\theta }=\frac{\mathsf{\pi }}{2}$ in a half of the hollow cylinder for various values of $R$, respectively. As it can be seen in Figure 11 and Figure 12, the values of phason stress fields are increased by increasing the value of $R$.

6. Conclusions

The elastodynamic model of a wave–telegraph type is used to study the dynamic response of decagonal quasicrystals. It is shown that angular symmetry is inapplicable in the case of a hollow cylinder even if symmetric boundary conditions are assumed. The tensor of material coefficients obeying coupling between the phonon and phason fields is dependent on the angular coordinate in polar coordinate system. Since the governing equations in such a coordinate system would be given by the PDE with variable coefficients, the utilization of the polar coordinates appears to be inconvenient. Therefore, the formulation is presented in the Cartesian coordinate system. The local Petrov–Galerkin (MLPG) method together with the Laplace transform technique with respect to time variables are employed for numerical solutions of boundary value problems. For the spatial variation of field variables, we have used the meshless approximation based on the radial basis functions, and the Talbot technique is employed for numerical inversion of the Laplace transformation. In a numerical example, a finite sector of an infinitely long thick hollow cylinder is considered under a shock loading with holding angularly symmetric boundary conditions.

Attention is paid to a detailed explanation of coupling between the phonon and phason fields— wave propagation of both the phonon and phason stress and displacement waves with a finite speed. Since the phason response to force loading is approximately 1000 times smaller than the phonon response, the latter is affected negligibly by phason fields, despite the fact that phonon–phason coupling is considered. It has been shown that the proposed method is suitable for numerical simulations in rather complex problems. There are no restrictions on the geometry of the analyzed domain as well as on applied loads, and arbitrary material coefficients are allowed within the considered general elastodynamic model of the wave–telegraph type in decagonal quasicrystals. The presented methodology can be easily extended to other kinds of quasicrystals. Mariano and Planas [20] highlighted the role of the conservative bulk phason self-action in mechanical description of quasicrystals. In the presented analyses, the conservative bulk self-action is omitted. The next study will concern verification of such a role by numerical simulations.