Crystal-Structure Analysis with Moments of the Density-of-States: Application to Intermetallic Topologically Close-Packed Phases
Abstract
:1. Introduction
2. Methodology
2.1. Moments of the Density-of-States
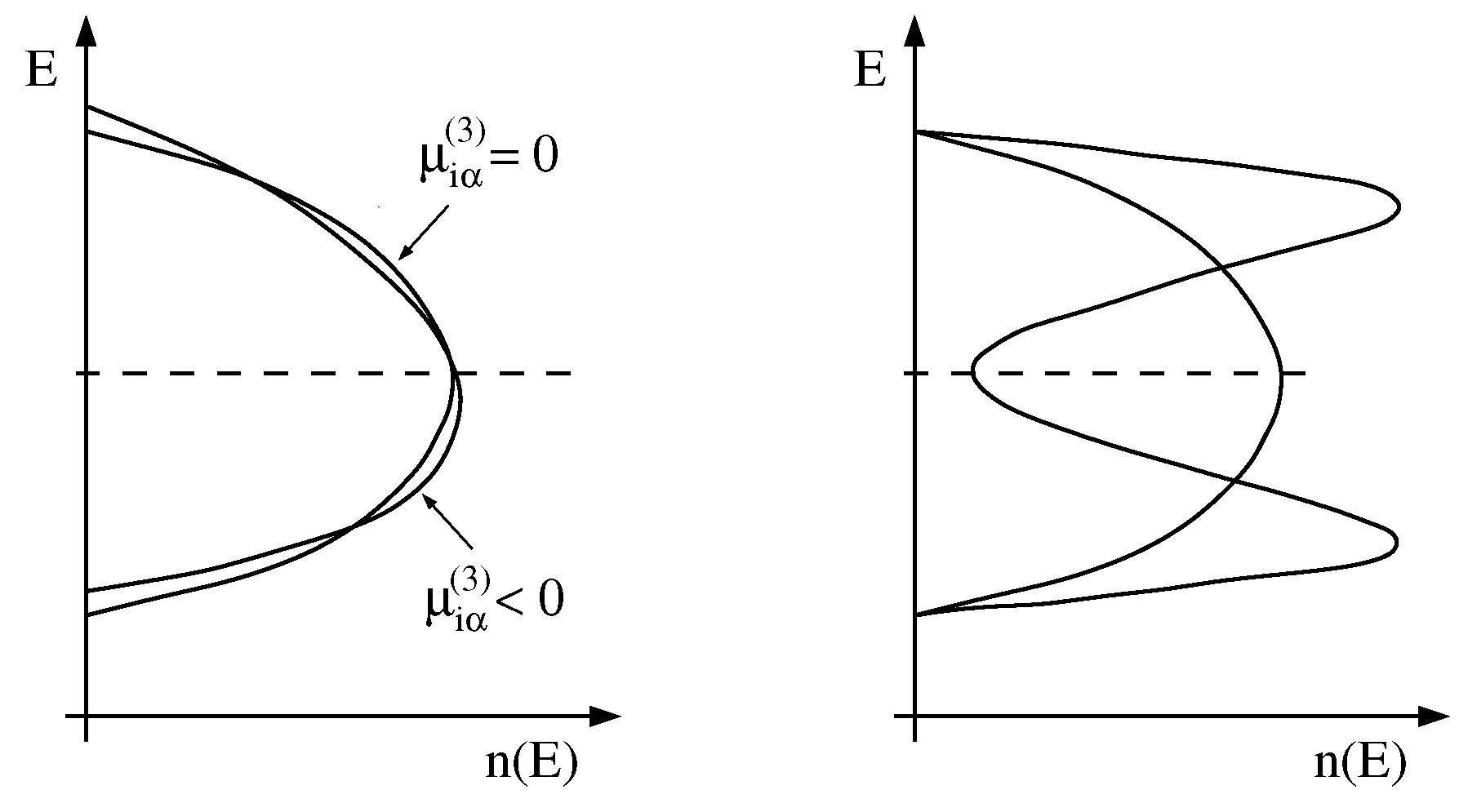
2.2. Computational Details
| Structure | fcc | χ | C14 | C15 | C36 | μ | A15 | σ | bcc |
|---|---|---|---|---|---|---|---|---|---|
| Z12 | (1) | 12 | 2, 6 | 4 | 4, 6, 6 | 1, 6 | 2 | 2, 8 | - |
| Z13 | - | (12) | - | - | - | - | - | - | - |
| Z14 | - | - | - | - | - | 2 | 6 | 8, 8 | (1) |
| Z15 | - | - | - | - | - | 2 | - | 4 | - |
| Z16 | - | 1, 4 | 4 | 2 | 4, 4 | 2 | - | - | - |
| 〈Z〉 | 12.00 | 13.10 | 13.33 | 13.33 | 13.33 | 13.39 | 13.50 | 13.57 | 14.00 |
2.3. Moments of TCP Phases
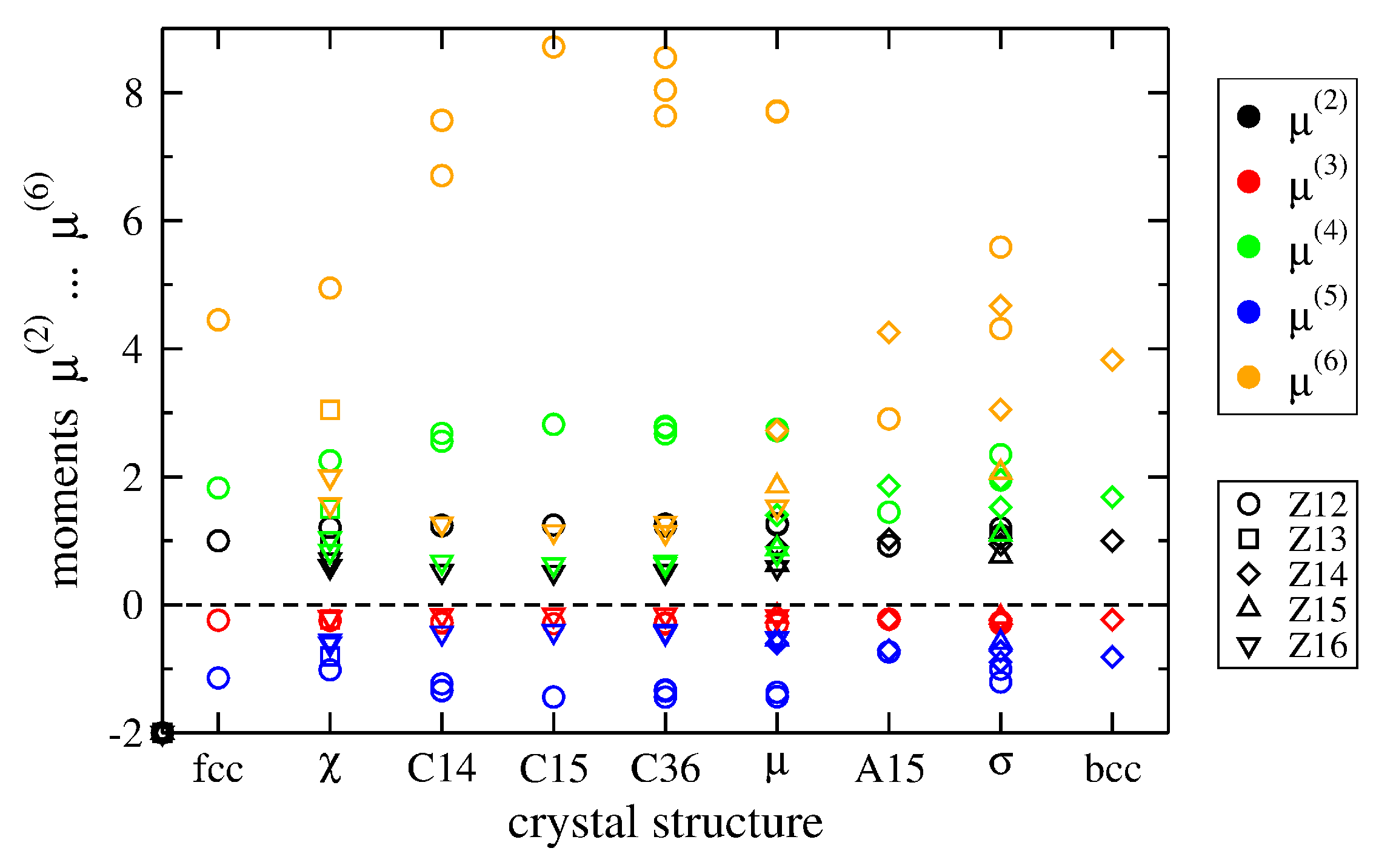
| bcc | χ | σ | A15 | fcc | μ | C14 | C36 | C15 | |
|---|---|---|---|---|---|---|---|---|---|
| bcc | 0.000 | 0.226 | 0.304 | 0.362 | 0.885 | 1.365 | 1.619 | 1.982 | 2.301 |
| χ | - | 0.000 | 0.220 | 0.315 | 0.808 | 1.301 | 1.550 | 1.922 | 2.247 |
| σ | - | - | 0.000 | 0.290 | 0.662 | 1.124 | 1.378 | 1.747 | 2.069 |
| A15 | - | - | - | 0.000 | 0.818 | 1.161 | 1.403 | 1.769 | 2.091 |
| fcc | - | - | - | - | 0.000 | 0.655 | 0.886 | 1.236 | 1.546 |
| μ | - | - | - | - | - | 0.000 | 0.257 | 0.623 | 0.947 |
| C14 | - | - | - | - | - | - | 0.000 | 0.375 | 0.702 |
| C36 | - | - | - | - | - | - | - | 0.000 | 0.327 |
| C15 | - | - | - | - | - | - | - | - | 0.000 |
3. Moments Analysis of Volume Changes and Internal Relaxations
3.1. Influence of Band Filling across TM Series
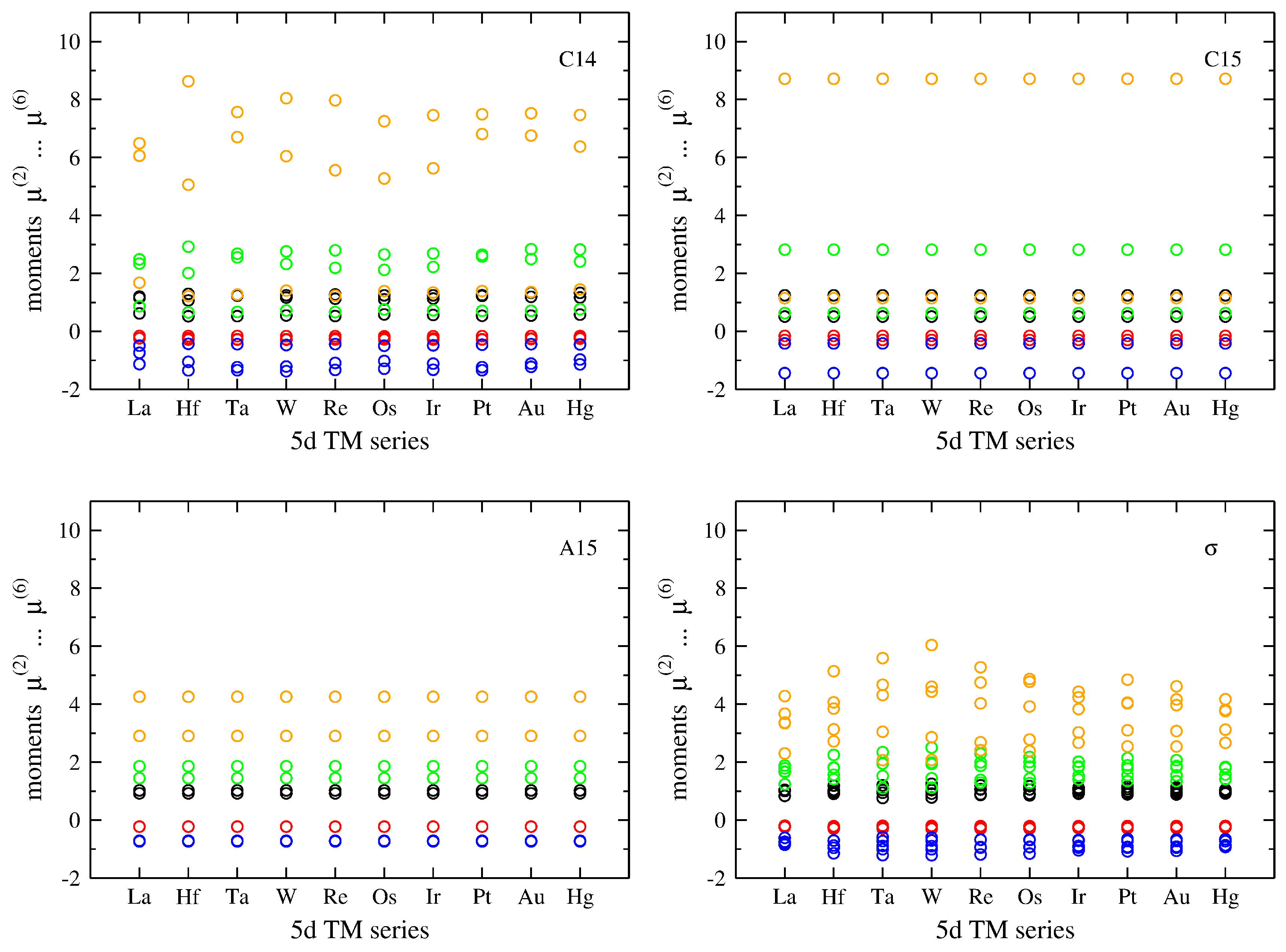

3.2. Atomic-Volume Differences in Compounds: V-Ta
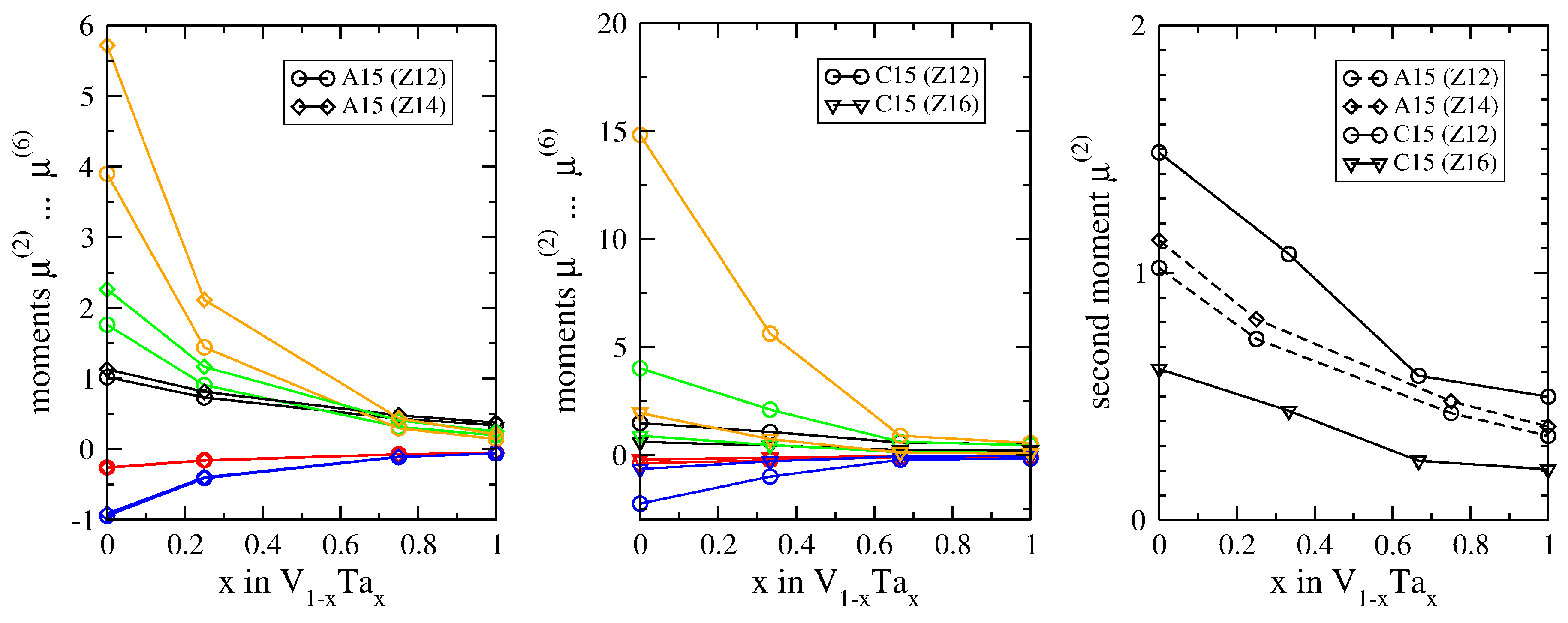
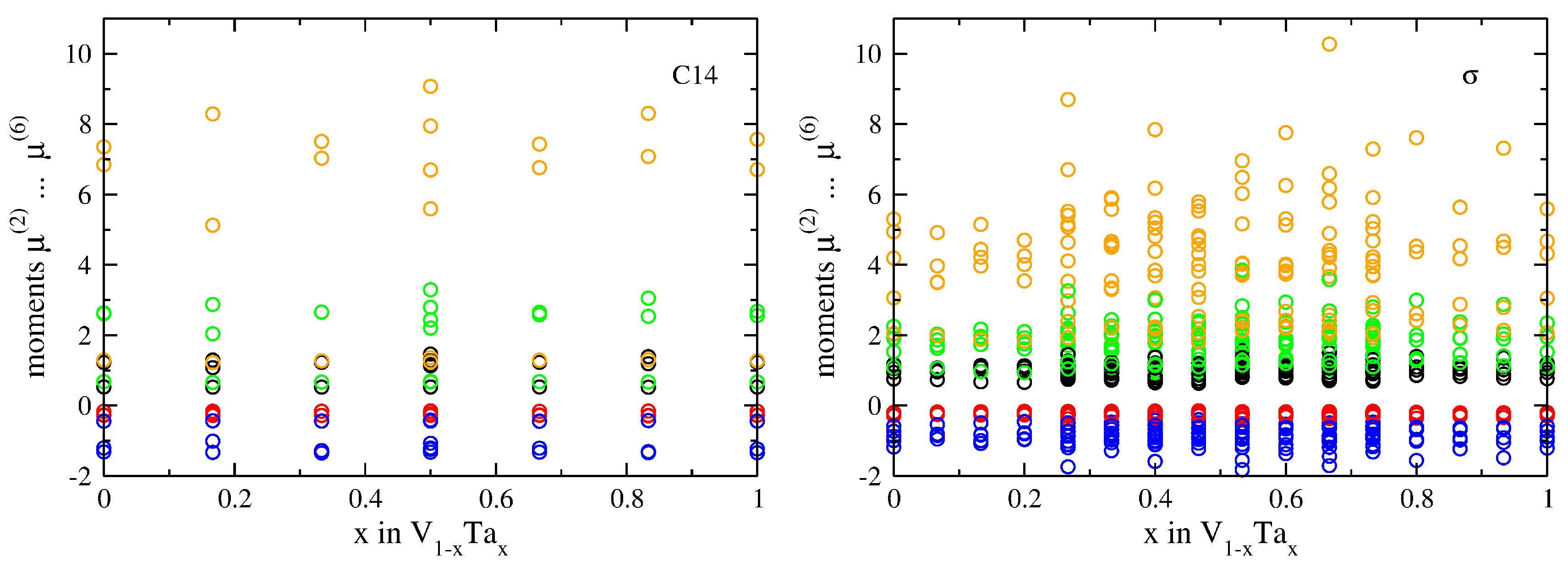
3.3. Influence of Magnetism: FeNb-C14
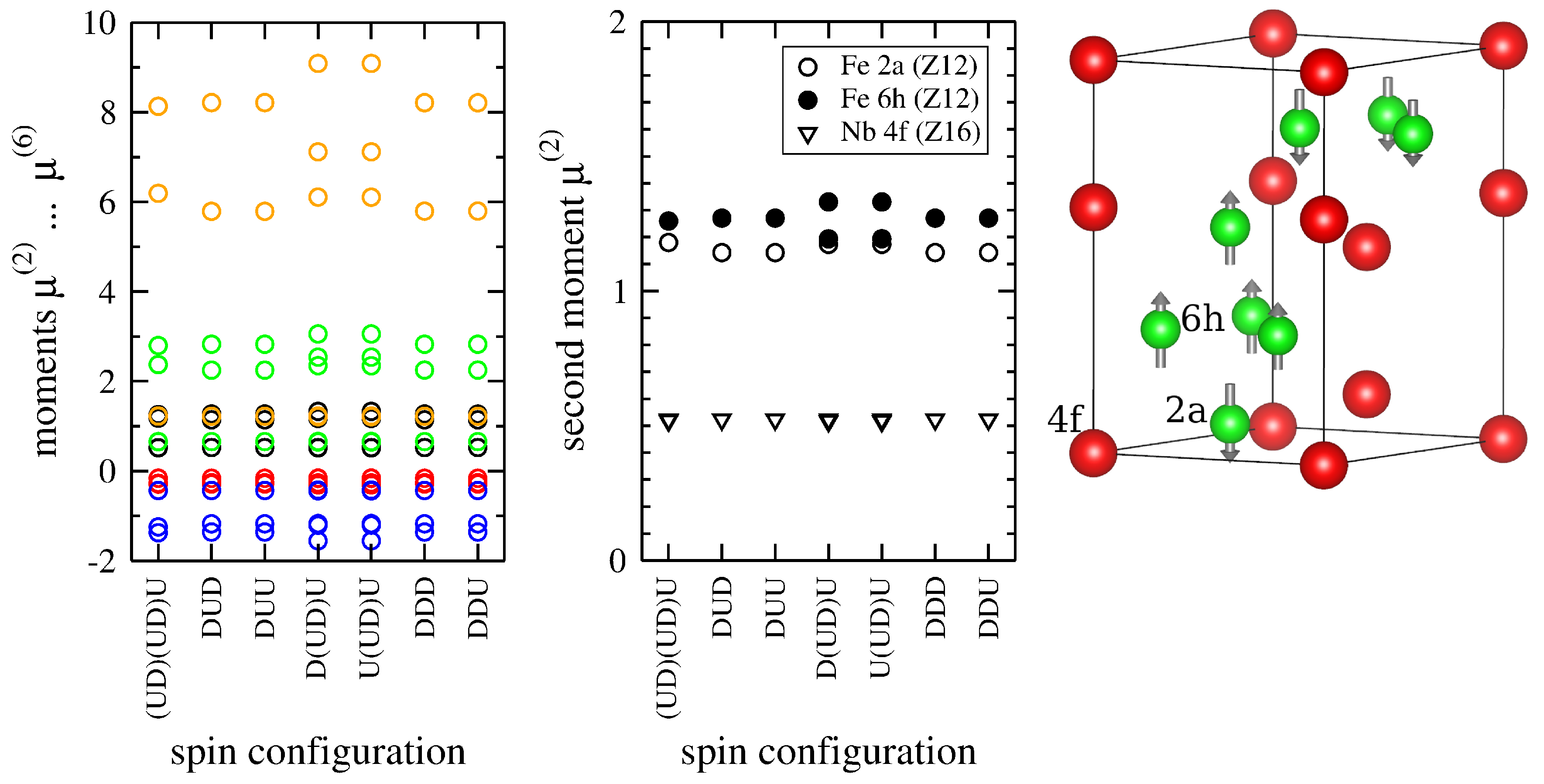
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rideout, S.P.; Manly, W.D.; Kamen, E.L.; Lement, B.S.; Beck, P.A. Intermediate phases in ternary alloy systems of transition elements. Trans. AIME 1951, 191, 872–876. [Google Scholar]
- Boesch, W.J.; Slaney, J.S. Preventing sigma phase embrittlement in Nickel base superalloys. Met. Prog. 1964, 86, 109–111. [Google Scholar]
- Morinaga, M.; Yukawa, M.; Adachi, H.; Ezaki, H. Superalloys 1984; Gell, M., Kortovich, C.S., Bricknell, R.H., Kent, W.B., Radavich, J.F., Eds.; The Metals, Minerals and Materials Society: Warrendale, PA, USA, 1984; p. 523. [Google Scholar]
- Watson, R.E.; Bennett, L.H. Transition-metal alloy formation. The occurence of topologically close packed phaeses—I. Acta Metall. 1984, 32, 477–489. [Google Scholar] [CrossRef]
- Laves, F.; Wallbaum, H.J. Über den Einfluß geometrischer Faktoren auf die stöchiometrische Formel metallischer Verbindungen, gezeigt an der Kristallstruktur des KNa2. Z. Anorg. Allg. Chem. 1942, 250, 110–120. [Google Scholar] [CrossRef]
- Seiser, B.; Drautz, R.; Pettifor, D.G. TCP phase predictions in Ni-based superalloys: Structure maps revisited. Acta Mater. 2011, 59, 749–763. [Google Scholar] [CrossRef]
- Joubert, J.M.; Phejar, M. Crystal chemistry and Calphad modeling of the χ phase. Prog. Mater. Sci. 2009, 54, 945–980. [Google Scholar] [CrossRef]
- Ohta, Y.; Pettifor, D.G. Size versus electronic factors in transition metal Laves phase stability. J. Phys. Condens. Matter 1990, 2. [Google Scholar] [CrossRef]
- Zhu, J.H.; Liu, C.T.; Pike, L.M.; Liaw, P.K. Enthalpies of formation of binary Laves phases. Intermetallics 2002, 10, 579–595. [Google Scholar] [CrossRef]
- Stein, F.; Palm, M.; Sauthoff, G. Structure and stability of Laves phases. Part I. Critical assessment of factors controlling Laves phase stability. Intermetallics 2004, 12, 713–720. [Google Scholar] [CrossRef]
- Hartsough, L.D. Stability of A15 type phases. J. Phys. Chem. Solids 1974, 35, 1691–1701. [Google Scholar] [CrossRef]
- Turchi, P.; Treglia, G.; Ducastelle, F. Electronic structure and phase stability of A15 transition metals and alloys. J. Phys. Met. Phys. 1983, 13. [Google Scholar] [CrossRef]
- Turchi, P.E.A.; Finel, A. Ordering phenomena in A15-based alloys. Phys. Rev. B 1992, 46. [Google Scholar] [CrossRef]
- Moriarty, J.A. Angular forces and melting in bcc transition metals: A case study of molybdenum. Phys. Rev. B 1994, 49. [Google Scholar] [CrossRef]
- Joubert, J.M. Crystal chemistry and Calphad modeling of the σ phase. Prog. Mater. Sci. 2008, 53, 528–583. [Google Scholar] [CrossRef]
- Berne, C.; Pasturel, A.; Sluiter, M.; Vinet, B. Ab Initio Study of Metastability in Refractory Metal Based Systems. Phys. Rev. Lett. 1999, 83, 1621–1623. [Google Scholar] [CrossRef]
- Berne, C.; Sluiter, M.; Kawazoe, Y.; Hansen, T.; Pasturel, A. Site occupancy in the Re-W sigma phase. Phys. Rev. B 2001, 64, 144103. [Google Scholar] [CrossRef]
- Berne, C.; Sluiter, M.; Pasturel, A. Theoretical approach of phase selection in refractory metals and alloys. J. Alloys Comp. 2002, 334, 27–33. [Google Scholar] [CrossRef]
- Sluiter, M.; Pasturel, A.; Kawazoe, Y. Site occupation in the Ni-Nb μ phase. Phys. Rev. B 2003, 67, 174203. [Google Scholar] [CrossRef]
- Sluiter, M.H.F.; Pasturel, A. Site occupation in the Cr-Ru and Cr-Os σ phase. Phys. Rev. B 2009, 80, 134122. [Google Scholar] [CrossRef]
- Crivello, J.C.; Joubert, J.M. First principles calculations of the σ and χ phases in the Mo-Re and W-Re systems. J. Phys. Condens. Matter 2010, 22, 035402. [Google Scholar] [CrossRef] [PubMed]
- Dubiel, S.M.; Cieslak, J.; Sturhahn, W.; Sternik, M.; Piekarz, P.; Stankov, S.; Parlinski, K. Vibrational properties of the α and σ Phase Fe-Cr Alloy. Phys. Rev. Lett. 2010, 104, 155503. [Google Scholar] [CrossRef] [PubMed]
- Pavlu, J.; Vrestal, J.; Sob, M. Ab initio study of formation energy and magnetism of sigma phase in Cr-Fe and Cr-Co system. Intermetallics 2010, 18, 212–220. [Google Scholar] [CrossRef]
- Hammerschmidt, T.; Bialon, A.; Pettifor, D.; Drautz, R. Topologically close-packed phases in binary transition-metal compounds: matching high-throughput ab initio calculations to an empirical structure map. New J. Phys. 2013, 15, 115016. [Google Scholar] [CrossRef]
- Palumbo, M.; Fries, S.; Hammerschmidt, T.; Abe, T.; Crivello, J.C.; Breidi, A.; Joubert, J.M.; Drautz, R. First-principles-based phase diagrams and thermodynamic properties of TCP phases in Re-X systems (X = Ta, V, W). Comput. Mater. Sci. 2014, 81, 433–445. [Google Scholar] [CrossRef]
- Ducastelle, F.; Cyrot-Lackmann, F. Moments developments and their application to the electronic charge distribution of d bands. J. Phys. Chem. Solids 1970, 31, 1295–1306. [Google Scholar] [CrossRef]
- Turchi, P.E.A. Interplay between local environment effect and electronic structure properties in close packed structures. Mater. Res. Soc. Symp. Proc. 1991, 206. [Google Scholar] [CrossRef]
- Hammerschmidt, T.; Seiser, B.; Drautz, R.; Pettifor, D.G. Modelling topologically close-packed phases in superalloys: Valence-dependent bond-order potentials based on ab-initio calculations. In Superalloys 2008; Reed, R.C., Green, K., Caron, P., Gabb, T., Fahrmann, M., Huron, E., Woodward, S., Eds.; The Metals, Minerals and Materials Society: Warrendale, PA, USA, 2008; p. 847. [Google Scholar]
- Seiser, B.; Hammerschmidt, T.; Kolmogorov, A.N.; Drautz, R.; Pettifor, D.G. Theory of structural trends within 4d and 5d transition metals topologically close-packed phases. Phys. Rev. B 2011, 83, 224116. [Google Scholar] [CrossRef]
- Németh, K.; Challacombe, M. Geometry optimization of crystals by the quasi-independent curvilinear coordinate approximation. J. Chem. Phys. 2005, 123, 194112. [Google Scholar] [CrossRef] [PubMed]
- Kuz’min, V.; Artemenko, A.; Muratov, E. Hierarchical QSAR technology based on the Simplex representation of molecular structure. J. Comput. Aided Mol. Des. 2008, 22, 403–421. [Google Scholar] [CrossRef] [PubMed]
- Isayev, O.; Fourches, D.; Muratov, E.; Oses, C.; Rasch, K.; Tropsha, A.; Curtarolo, S. Materials Cartography: Representing and Mining Materials Space Using Structural and Electronic Fingerprints. Chem. Mater. 2015, 27, 735–743. [Google Scholar] [CrossRef]
- Behler, J. Atom-centered symmetry functions for constructing high-dimensional neural network potentials. J. Chem. Phys. 2011, 134, 074106. [Google Scholar] [CrossRef]
- Rupp, M.; Tkatchenko, A.; Müller, K.R.; von Lilienfeld, O.A. Fast and accurate modeling of molecular atomization energies with machine learning. Phys. Rev. Lett. 2012, 108, 058301. [Google Scholar] [CrossRef] [PubMed]
- Bartók, A.; Kondor, R.; Csányi, G. On representing chemical environments. Phys. Rev. B 2013, 87, 184115. [Google Scholar] [CrossRef]
- Schablitzki, T.; Rogal, J.; Drautz, R. Topological fingerprints for intermetallic compounds for the automated classification of atomistic simulation data. Model. Simul. Mater. Sci. Eng. 2013, 21, 075008. [Google Scholar] [CrossRef]
- Von Lilienfeld, O.; Ramakrishnan, R.; Rupp, M.; Knoll, A. Fourier series of atomic radial distribution functions: A molecular fingerprint for machine learning models of quantum chemical properties. J. Quantum Chem. 2015, 115. [Google Scholar] [CrossRef]
- Cyrot-Lackmann, F. On the electronic structure of liquid transition metals. Adv. Phys. 1967, 16. [Google Scholar] [CrossRef]
- Haydock, R. Recursive solution of the Schrödinger equation. Comput. Phys. Commun. 1980, 20, 11–16. [Google Scholar] [CrossRef]
- Pettifor, D.G. Bonding and Structure of Molecules and Solids; Oxford Science Publications: New York, NY, USA, 1995. [Google Scholar]
- Horsfield, A.; Bratkovsky, A.M.; Fearn, M.; Pettifor, D.G.; Aoki, M. Bond-order potentials: Theory and implementation. Phys. Rev. B 1996, 53. [Google Scholar] [CrossRef]
- Drautz, R.; Pettifor, D.G. Valence-dependent analytic bond-order potential for transition metals. Phys. Rev. B 2006, 74, 174117. [Google Scholar] [CrossRef]
- Drautz, R.; Pettifor, D.G. Valence-dependent analytic bond-order potential for magnetic transition metals. Phys. Rev. B 2011, 84, 214114. [Google Scholar] [CrossRef]
- Drautz, R.; Hammerschmidt, T.; Cak, M.; Pettifor, D. Bond-Order Potentials: Derivation and parameterization for refractory elements. Model. Simul. Mater. Sci. Eng. 2015, 23, 074004. [Google Scholar] [CrossRef]
- Bieber, A.; Ducastelle, F.; Gautier, F.; Treglia, G.; Turchi, R. Electronic structure and relative stabilities of L12 and D022 ordered structures occuring in transition metal alloys. Solid State Commun. 1983, 45. [Google Scholar] [CrossRef]
- Bieber, A.; Gautier, F. Multiatom interactions, order and stability in binary transition metal alloys. Z. Phys. B Condens. Matter 1984, 57, 335–343. [Google Scholar] [CrossRef]
- Ducastelle, F.; Cyrot-Lackmann, F. Moments developments- II. Application to the crystalline structures and the stacking fault energies of transition metals. J. Phys. Chem. Solids 1971, 32, 285–301. [Google Scholar] [CrossRef]
- Chen, Y.; Kolmogorov, A.; Pettifor, D.; Shang, J.X.; Zhang, Y. Theoretical analysis of structural stability of TM5Si3 transition metal silicides. Phys. Rev. B 2010, 82, 184104. [Google Scholar] [CrossRef]
- Andersen, O.K.; Klose, W.; Nohl, H. Electronic structure of Chevrel-phase high-critical-field superconductors. Phys. Rev. B 1978, 17. [Google Scholar] [CrossRef]
- Pettifor, D.G.; Podloucky, R. The structures of binary compounds: II. Theory of the pd-bonded AB compounds. J. Phys. C Solid State Phys. 1986, 19. [Google Scholar] [CrossRef]
- Ladines, A.; Hammerschmidt, T.; Drautz, R. Structural stability of Fe-based topologically close-packed phases. Intermetallics 2015, 59, 59–67. [Google Scholar] [CrossRef]
- Sinha, A.K. Topologically close-packed structures of transition metal alloys. Prog. Mater. Sci. 1972, 15, 81–185. [Google Scholar] [CrossRef]
- Cak, M.; Hammerschmidt, T.; Drautz, R. Comparison of analytic and numerical bond-order potentials for W and Mo. J. Phys. Condens. Matter 2013, 26, 265002. [Google Scholar] [CrossRef] [PubMed]
- Ford, M.; Drautz, R.; Hammerschmidt, T.; Pettifor, D. Convergence of an analytic bond-order potential for collinear magnetism in Fe. Model. Simul. Mater. Sci. Eng. 2014, 22, 034005. [Google Scholar] [CrossRef]
- Hammerschmidt, T.; Seiser, B.; Ford, M.E.; Pettifor, D.G.; Drautz, R. BOPfox program for tight-binding and bond-order potential calculations. under preparation.
- Pettifor, D.G. The structures of binary compounds: I. Phenomenological structure maps. J. Phys. C 1986, 19. [Google Scholar] [CrossRef]
- Sutton, A.P.; Finnis, M.W.; Pettifor, D.G.; Ohta, Y. The tight-binding bond model. J. Phys. C 1988, 21. [Google Scholar] [CrossRef]
- Koßmann, J.; Zenk, C.; Lopez-Galilea, I.; Neumeier, S.; Kostka, A.; Huth, S.; Theisen, W.; Göken, M.; Drautz, R.; Hammerschmidt, T. Microsegregation and precipitates of an as-cast Co-based superalloy—microstructural characterization and phase stability modelling. J. Mater. Sci. 2015, 50, 6329–6638. [Google Scholar] [CrossRef]
- Lopez-Galilea, I.; Koßmann, J.; Kostka, A.; Drautz, R.; Roncery, L.M.; Hammerschmidt, T.; Huth, S.; Theisen, W. The thermal stability of topologically close-packed phases in the single-crystal Ni-base superalloy ERBO/1. J. Mater. Sci. 2016, 51, 2653–2664. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hammerschmidt, T.; Ladines, A.N.; Koßmann, J.; Drautz, R. Crystal-Structure Analysis with Moments of the Density-of-States: Application to Intermetallic Topologically Close-Packed Phases. Crystals 2016, 6, 18. https://doi.org/10.3390/cryst6020018
Hammerschmidt T, Ladines AN, Koßmann J, Drautz R. Crystal-Structure Analysis with Moments of the Density-of-States: Application to Intermetallic Topologically Close-Packed Phases. Crystals. 2016; 6(2):18. https://doi.org/10.3390/cryst6020018
Chicago/Turabian StyleHammerschmidt, Thomas, Alvin Noe Ladines, Jörg Koßmann, and Ralf Drautz. 2016. "Crystal-Structure Analysis with Moments of the Density-of-States: Application to Intermetallic Topologically Close-Packed Phases" Crystals 6, no. 2: 18. https://doi.org/10.3390/cryst6020018





