Hydrogen Desorption from Mg Hydride: An Ab Initio Study

Abstract

Hydrogen desorption from hydride matrix is still an open field of research. By means of accurate first-principle molecular dynamics (MD) simulations an Mg–MgH₂ interface is selected, studied and characterized. Electronic structure calculations are used to determine the equilibrium properties and the behavior of the surfaces in terms of structural deformations and total energy considerations. Furthermore, extensive ab-initio molecular dynamics simulations are performed at several temperatures to characterize the desorption process at the interface. The numerical model successfully reproduces the experimental desorption temperature for the hydride.

1. Introduction

The remarkable hydrogen capacity of magnesium has fostered intense research efforts in the last years in view of its future applications where light and safe hydrogen-storage media are needed. Magnesium can reversibly store about 7.6 wt% hydrogen, has light weight and is a low-cost material. However, further research is needed since Mg has a high operation temperature and slow absorption kinetics that prevent for the moment the use in practical applications. Two separate reasons could explain this problem: (a) hydrogen molecules do not readily dissociate on Mg surfaces; and (b) magnesium hydride is very stable up to high temperatures. Improvements on H₂ absorption and desorption kinetics can be obtained by mechanically milling MgH₂ and adding catalysts to magnesium and magnesium hydrides. The addition of small amounts of catalytic metals such as Pd or Ni to Mg hydride has been indicated as a promoting factor in the surface dissociation of the H₂ molecule (the clean Mg surface alone being unable to catalyse the dissociation). Moreover, other metallic additives, such as Al, Li, Mn, Ti etc., have been suggested to improve the hydriding properties of metallic Mg [1,2,3,4,5,6]. However a full understanding of the desorption mechanism at the interface Mg-MgH₂ is still lacking. From an experimental point of view there is not a clear evidence of which interfaces are involved in the hydrogen diffusion, and which is the atomic dynamics at the interfaces [7].

For these reasons a detailed study of the interface between Mg and MgH₂ is needed to characterize the dynamics of hydrogen at the interface. Further insights are gained by characterizing Mg–MgH₂ interfaces which are supposed to play a major role in the hydrogen diffusion during absorption and desorption cycles. By means of accurate ab initio molecular dynamics simulations based on the density-functional theory with norm-conserving pseudopotentials and plane-wave expansion (CPMD code [8,9]), an interface is selected, studied and characterized. Extensive electronic structure calculations are used to determine the equilibrium properties and the behaviour of the surfaces in terms of structural deformations and total energy considerations. Furthermore, the interface is studied at several values of the temperature, thereby characterizing the hydrogen atomic displacement and desorption.

In the next section the computational details are reported and the numerical model is verified on simple atomic system. In the third section free surfaces are both studied and characterized, while in the fourth section an interface is built and geometrically and energetically optimized. In the fifth section the influence of the temperature is studied on the hydrogen diffusion through the interface. In the last section we analyze the reconstitution of the interface after hydrogen diffusion.

2. Computational Details

We employed for all the calculations the CPMD (Car–Parrinello Molecular Dynamics) code based on Density Functional Theory and plane wave basis pseudopotential method [10,11]. Goedecker–Teter–Hutter pseudopotentials for magnesium and hydrogen together with Padé approximant LDA exchange-correlation potentials were used [12,13,14]. The LDA functional has well-known drawbacks as discussed in Ref. [15], especially for energy calculations, but it can reliably simulate structural properties (lattice size, equilibrium positions, elastic constants). Despite the high accuracy of Mg pseudopotentials which include semicore states, as required for example in studies like Ref. [16], the structural characterization of an interface requires large atomic systems to mimic bulk behavior on both sides. Thus in view of large-scale simulations, the pseudopotential with fewer valence electrons has been chosen, in order to save computational time and simulate the largest system. The electronic wave functions are expanded in a plane-wave basis set with a kinetic energy cut-off equal to 80 Ry. To check the agreement with experimental results, the latter value was optimized by preliminary calculations both on simple molecules (Mg₂, MgH and H₂) and on the crystalline structures of metallic Mg and magnesium hydride. All the calculations are performed in the supercell approximation, in view of the large-scale molecular dynamics simulation of the interface, with periodic boundary conditions meant to mimic an infinitely extended system.

The calculations for the diatomic molecules Mg₂, MgH and H₂ yield the following interatomic distances in good agreement with experimental values: D_Mg2 = 3.4056 Å (exp. D_Mg2 = 3.890 Å), D_MgH = 1.7362 Å (exp. D_MgH = 1.7297 Å) and D_H2 = 0.7681 Å (exp. D_H2 = 0.7414 Å).

The crystal structure of Mg is the hexagonal close-packed with experimental lattice parameter a_Mg = 3.2094 Å and c_Mg = 1.6327 × a_Mg with bonding energy of 1.53 eV/at. Geometry optimization of crystal structure gives a_Mg = 3.15 Å and c_Mg = 1.62 × a_Mg with a bonding energy of 1.59 eV/at.

Crystal MgH₂ is considered in the β-MgH₂ atomic structure, TiO₂-rutile type, that is observed at the atmospheric pressure and low temperatures [17]. The crystal structure is relaxed over a range of possible cell volumes, varying by hand the cell parameters and minimizing the total energy. The computed values for the cell parameters are in good agreement with experimental ones within 3%. In the case of MgH₂ we find a_MgH2 = b_MgH2 = 4.39 Å, c_MgH2 = 2.96 Å and u = 0.304 (experimental values: a_MgH2 = b_MgH2 = 4.501 Å , c_MgH2 = 3.02 Å) [18].

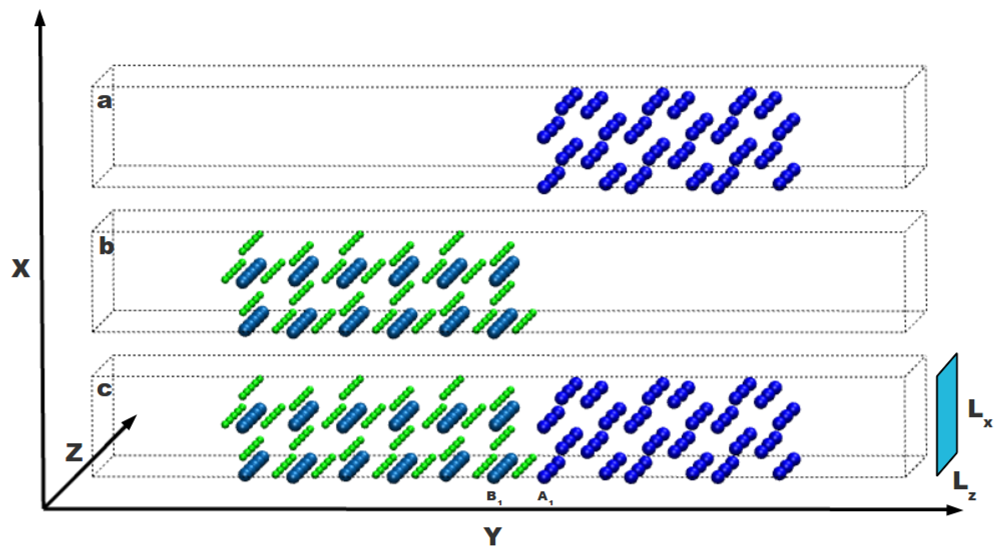
A supercell approach is used to simulate the atomic system with the interface. As shown in Figure 1, the Mg-MgH₂ interface is built by putting nearby two free surfaces obtained cutting both the Mg and MgH₂ crystals. The Mg part is sketched in Figure 1a and the MgH₂ one in Figure 1b: these systems can interact through their internal free surfaces forming an interface as shown in Figure 1c. Each internal free surface, selected according to periodic boundary conditions, is severally relaxed without taking into account any possible reconstruction upon changing the temperature (two layers of both external surfaces are kept fixed). Both sides of the whole system are long enough to take into account the structural modifications induced by the interface. Results reported in Ref. [19], on a similar system, confirm that the effects of relaxation propagate to the bulk atoms up to the third or fourth neighbor and that six neighbors are enough to attain bulk behavior on both sides.

Figure 1. Mg and MgH₂ crystalline systems with free surfaces on both sides in the y direction are reported in part (a) and (b) of the figure, respectively; In part (c) both systems are together to define an interface between them. External surfaces are separated by a void region and do not interact with each other. H atoms are in green, Mg atoms in the magnesium hydride side are in light blue and Mg atoms in the magnesium side are in dark blue.

Figure 1. Mg and MgH₂ crystalline systems with free surfaces on both sides in the y direction are reported in part (a) and (b) of the figure, respectively; In part (c) both systems are together to define an interface between them. External surfaces are separated by a void region and do not interact with each other. H atoms are in green, Mg atoms in the magnesium hydride side are in light blue and Mg atoms in the magnesium side are in dark blue.

The total length of the system is L_y = 50.3009 Å, while in the x and z direction the system has L_x= 6.2115 Å and L_z= 15.0939 Å, respectively. On both sides of the system, a void region of length 2 × L_x is considered to suppress the interaction, due to periodic boundary conditions, between the external surfaces of Mg and MgH₂.

Zero-temperature total energy calculations are used to evaluate interface stability. Subsequently, MD simulations at constant volume and constant temperature are performed by using Nose–Hoover thermostats [20,21]. One key quantity to predict the mechanical properties of the interface and to verify the reliability of our model is the work of adhesion. The latter quantity is defined as the bonding energy per unit area needed to reversibly separate an interface into two free surfaces, neglecting plastic and diffusional degrees of freedom. Through the paper all errors on the work of adhesion are taken as low as possible performing accurate fitting of energy data and a careful application of ab-initio methods for the computation of energies. This procedure ensures that errors are at the level of accuracy allowed by DFT-based calculations [15], i.e., <2% error for the work of adhesion and <10% error for the formation enthalpies.

3. Model Interface and Free Surfaces

In literature there are no references describing Mg-MgH₂ interfaces, neither experimentally nor theoretically. The main constraint in building the interface is in the selection of two commensurate surfaces (one for Mg and one for MgH₂) fulfilling a simulation cell with periodic boundary conditions (see Figure 1). Such a constraint narrows the possibilities of finding two suitable free surfaces for a proper interface. Among the low Miller index surfaces of both materials, it is found that the (110) of MgH₂ is nearly commensurate to either (010) or (100) of Mg, according to periodic boundary conditions in x and y directions, by minimizing the lattice mismatch. In both cases we have and . Keeping fixed the a_MgH2 lattice constant, a small distortion in the Mg and MgH₂ cell parameters is needed to obtain fully commensurable surfaces: the a_Mg and c_Mg parameters are thus scaled of about 1% and 2% respectively.

The interface considered in this work is facing the (010) of Mg and the (110) of MgH₂, which is more stable and thus more likely to appear in real situations.

3.1. Magnesium Free Surface

A bulk system composed of 72 Mg atoms is built to obtain two equal surfaces: one to be faced to the MgH₂ (on the left in Figure 1a) and the other (on the right in Figure 1a), on the opposite side, that will be frozen in presence of a void region. The 72 Mg atoms are in 6 layers exposing on both sides the (010) surface: the external surface (on the right) is the same of the internal one (on the left) but translated by a half lattice parameter (0.5×c_Mg) in the z direction. In Figure 2 the Mg system is depicted before and after geometry optimization (residual force on each atom less than 10^-2 eV/Å), performed by keeping fixed the first two layers on the right. The shadowed atoms represent initial positions of the magnesium before relaxation. The atomic optimization moves inward the atoms on the left in the y direction, reducing the thickness of the slab as it is generally expected for a metal. All the atoms belonging to the same row move together. Longer distance from the fixed atoms results in more displacement of the free layers. The outer layer moves about 0.9 Å, instead the inner layer moves less than 0.1 Å. All the displacements are shown in Table 1. This attenuation of layer displacement indicates that in the y direction the number of planes are enough to get a reliable Mg free surface on the left with bulk Mg atoms in the back. The atomic optimization lowers the total energy of the surface of about 0.03 eV/at. After the atomic optimization, molecular dynamics simulations at fixed temperature and volume are performed to study the thermal stability of the surface. The temperature is gradually raised (in steps of 100 K) till 900 K. At each temperature the system reaches the equilibrium and no reconstruction of the free surface is observed.

Figure 2. Magnesium free surface before and after geometry optimization. The shadowed atoms represent initial positions of the magnesium before relaxation. In parenthesis are shown distances in Å between initial and final positions of the Mg rows (see also Table 1).

Figure 2. Magnesium free surface before and after geometry optimization. The shadowed atoms represent initial positions of the magnesium before relaxation. In parenthesis are shown distances in Å between initial and final positions of the Mg rows (see also Table 1).

Table 1. Displacements in Å of Mg atoms after ionic relaxations with respect to initial positions, for magnesium free surface, magnesium hydride free surface and, Mg–MgH₂ interface. For the free surfaces all the atoms belonging to the same row move together, for the Mg–MgH₂ interface we indicated the range and the average of displacements.

Mg Row	Mg free surf.	MgH2 free surf.	Mg-MgH2 interface
			Mg side		MgH2 side
	displ. (Å)	displ. (Å)	range (Å)	average (Å)	range (Å)	average (Å)
1a	0.89	0.21	0.49–0.57	0.54	0.19–0.31	0.25
1b	0.55	–0.19	0.25–0.39	0.28	0.20–0.59	0.42
2a	0.66	–0.13	0.31–0.46	0.39	0.15–0.23	0.20
3b	0.35	0.07	0.17–0.20	0.18	0.22–0.36	0.27
3a	0.44	0.04	0.24–0.26	0.25	0.12–0.16	0.14
3b	0.19	–0.07	0.08–0.13	0.10	0.14–0.19	0.17
4a	0.26	–0.04	0.16–0.18	0.16	0.06–0.07	0.07
5b	0.09	0.01	0.06	0.06	0.07–0.09	0.08

Table 1. Displacements in Å of Mg atoms after ionic relaxations with respect to initial positions, for magnesium free surface, magnesium hydride free surface and, Mg–MgH₂ interface. For the free surfaces all the atoms belonging to the same row move together, for the Mg–MgH₂ interface we indicated the range and the average of displacements.

Mg Row	Mg free surf.	MgH2 free surf.	Mg-MgH2 interface
			Mg side		MgH2 side
	displ. (Å)	displ. (Å)	range (Å)	average (Å)	range (Å)	average (Å)
1a	0.89	0.21	0.49–0.57	0.54	0.19–0.31	0.25
1b	0.55	–0.19	0.25–0.39	0.28	0.20–0.59	0.42
2a	0.66	–0.13	0.31–0.46	0.39	0.15–0.23	0.20
3b	0.35	0.07	0.17–0.20	0.18	0.22–0.36	0.27
3a	0.44	0.04	0.24–0.26	0.25	0.12–0.16	0.14
3b	0.19	–0.07	0.08–0.13	0.10	0.14–0.19	0.17
4a	0.26	–0.04	0.16–0.18	0.16	0.06–0.07	0.07
5b	0.09	0.01	0.06	0.06	0.07–0.09	0.08

3.2. Magnesium Hydride Free Surface

We consider a MgH₂ crystalline system composed of 6 layers: 60 Mg atoms and 120 H atoms (see Figure 1b). The surface to be faced to the Mg surface is on the right. The external surface (on the left) is the same as the internal one (on the right) but translated by a half lattice parameter (0.5 × α_MgH2) in the x direction. As already done for the magnesium part, we performed an ionic relaxation to optimize the atomic geometry (residual force on each atom less than 10^-2 eV/Å): a void region is left on the left to suppress the interaction, due to the periodic boundary conditions, between the external surfaces of MgH₂. In Figure 3 the MgH₂ system is depicted before and after geometry optimization. The shadowed atoms represent initial positions of the magnesium and the hydrogen before relaxation. This optimization is performed by keeping fixed the first two layers of Mg atoms on the left to impose a bulk behaviour to the left part of the system. All the atoms belonging to the same row move together (in y direction only). Unlike magnesium system, the atom displacements are less pronounced (outer atoms move about 0.2 Å) and are not in only one direction. The upper layers move outward whereas the lower layers move inward. All the displacements are depicted in Table 1, where plus sign means outward movements and minus sign stands for inward movements. The displacements of the H atoms are negligible (less than 0.1 Å, except two rows that move 0.16 Å). Like before, the small displacements of the atoms near the fixed layers assure us that the size of the MgH₂ system is enough to simulate a reliable free surface. The atomic optimization reduce the total energy of the surface by about 0.01 eV/at. After the atomic optimization, molecular dynamics simulations at fixed temperature are performed to study the thermal stability of the surface. The temperature is gradually raised (in steps of 100 K) till 900 K. At each temperature the system reaches the equilibrium and no reconstruction of the free surface is observed.

Figure 3. Magnesium hydride free surface before and after geometry optimization. The shadowed atoms represent initial positions of atoms before relaxation. In parenthesis are shown distances in Å between initial and final positions of the Mg rows (see also Table 1). We indicated with Hr_a, Hr_b, Hr_c, and Hr_d, four groups of H atoms closer to the interface (see Section 5).

Figure 3. Magnesium hydride free surface before and after geometry optimization. The shadowed atoms represent initial positions of atoms before relaxation. In parenthesis are shown distances in Å between initial and final positions of the Mg rows (see also Table 1). We indicated with Hr_a, Hr_b, Hr_c, and Hr_d, four groups of H atoms closer to the interface (see Section 5).

4. Mg-MgH₂ Interface

We consider the supercell shown in Figure 1c in which the free surfaces of magnesium and magnesium hydride are facing each other at the distance 0.5×L_x. In this configuration the Mg atom (magnesium side) named A₁ is in front of the Mg atom (magnesium hydride side) named B₁. These Mg atoms have the same x and z coordinates and their y coordinates differs by 0.5×L_x. The B₁ atom has the coordinates (x_B, y_B, z_B), instead the A₁ atom has the coordinates (x_A, y_A, z_A) where x_A = x_B, y_A = y_B + 0.5×L_x and z_A = z_B. To find the interface configuration corresponding to the lowest total energy, we perform a geometry optimization moving rigidly by hand the Mg part and keeping fixed the MgH₂ one. The Mg part is moved in such a way that the coordinates x_A, y_A and z_A of the Mg atom, labelled A₁ in Figure 1c, are on a tridimensional grid x_A = x_B + dx, y_A = y_B + dy and z_A = z_B + dz, where the increments dx, dy and dz depend upon the integer index i, j, k:

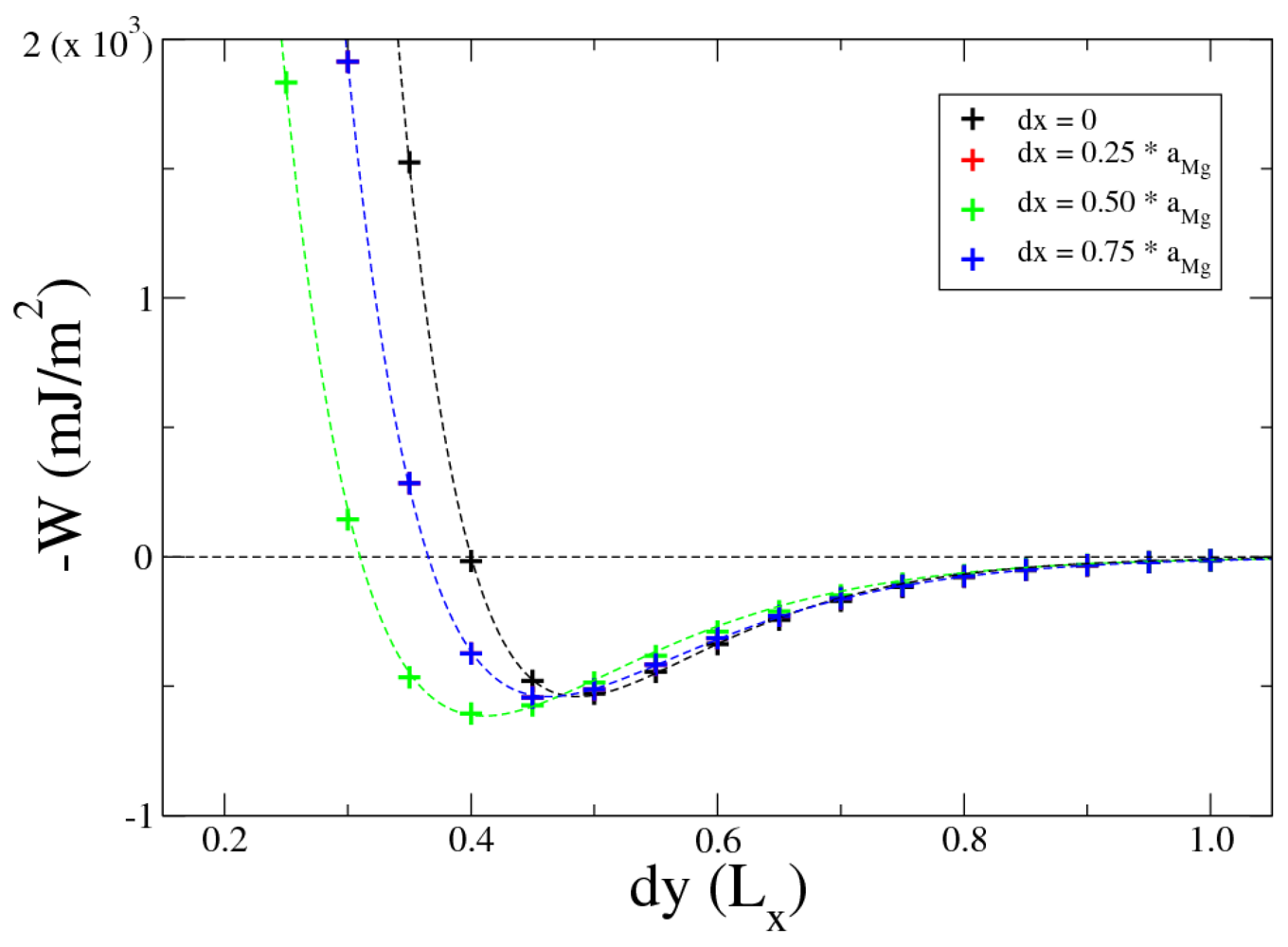
Total energy calculations are performed to minimize the energy of the whole system by varying the distance between the internal surfaces. The total energy of the system is minimized for k = 0, i = 2 and j = 8. The Mg atoms A₁ and B₁ are in the same plane xy (atoms of the Mg part are not shifted in z direction; dz_k=0 = 0), shifted from each other by dx_i=2 = 0.5 × a_Mg in x direction at the distance dy_j=8 = 0.4 × L_x in y direction. A good indicator of the reliability of this interface is the calculation of the work of adhesion W. W can be defined either in terms of the surface and interfacial energies (relative to the respective bulk materials), or by the difference in total energy between the interface and its isolated slabs:

Here σ_slabi is the surface energy of slab i, γ_inter is the interface energy, E_slabi is the total energy of the slab i, and E_inter is the total energy of the interface system. The total interface area is fixed by A = L_x ×L_z.

Figure 4 shows the opposite of work of adhesion (−W), for k = 0 (no shift in z direction between the Mg and MgH₂ slabs, dz = 0), varying i and j. These values of work of adhesion are calculated using Equation 1: the difference in total energy between the interfaces and the corresponding isolated slabs. Values for dx = 0.25 × a_Mg and dx = 0.75 × a_Mg are overlapped due to symmetry. The final configuration is characterized by a work of adhesion of W_ow = 605 mJ/m².

In Figure 4 calculated values of work of adhesion are fitted by the Rydberg function

where d^* = (dy − dy⁰)/l is the scaled separation, dy measures the separation between Mg and MgH₂ slabs, W₀ is the minimum at the equilibrium separation dy⁰ and l is a scaling length. Fitting with the function in Equation 2 the calculated values of work of adhesion by Equation 1, we found the values shown in Table 2. The very good agreement between calculated values of work of adhesion with the Rydberg function make us confident that the interfacial energy follows the universal binding energy relation (UBER) [22,23]. In the configuration with dz = 0 and dx = 0.50 × a_Mg, regression yields values for W₀ and dy⁰ (see third row in Table 2) that are very close to our values W_ow = 605 mJ/m² and dy = 0.4 × L_x.

Figure 4. Work of adhesion for Mg-MgH₂ interface with dz = 0 varying both dy and dx, dy is expressed in unit of L_x. Dotted lines are plots of the Rydberg function (2).

Figure 4. Work of adhesion for Mg-MgH₂ interface with dz = 0 varying both dy and dx, dy is expressed in unit of L_x. Dotted lines are plots of the Rydberg function (2).

Table 2. Values yielded by regression fitting with Rydberg function of calculated values of work of adhesion (see Figure 4); dy⁰ and l are expressed in unit of L_x.

	W0 (mJ/m2)	dy0 (Lx)	l (Lx)
dx = 0 × aMg	534	0.487	0.086
dx = 0.25 × aMg	540	0.463	0.098
dx = 0.50 × aMg	615	0.410	0.100
dx = 0.75 × aMg	540	0.463	0.098

Table 2. Values yielded by regression fitting with Rydberg function of calculated values of work of adhesion (see Figure 4); dy⁰ and l are expressed in unit of L_x.

	W0 (mJ/m2)	dy0 (Lx)	l (Lx)
dx = 0 × aMg	534	0.487	0.086
dx = 0.25 × aMg	540	0.463	0.098
dx = 0.50 × aMg	615	0.410	0.100
dx = 0.75 × aMg	540	0.463	0.098

Regarding the optimal interface stacking sequences, we find that the Mg atoms prefer sites which continue the hexagonal sequence of the magnesium hcp bulk across the interface. In fact the magnesium atoms on the interface that are on the plane z = 0, i.e., the atoms B₁ and its imagine in x direction on hydride side, and the atoms A₁ and its neighbor on magnesium side, take shape of half hexagon with A₁ and B₁ at distance of 0.94 × a_Mg.

Subsequently, we perform an ionic relaxation to further optimize the atomic geometry (residual force on each atom less than 10^-2 eV/Å), with reduction of the total energy of the system of 1.92 eV. This optimization has been performed by keeping fixed two layers of Mg atoms on both sides of the system to limit the influence of the external surfaces on the internal atoms near the interface. During the ionic relaxation, the internal surfaces are free to adapt to each other (see Figure 5). Analysing the displacements of the atoms, for the magnesium side, we observed the displacements of the Mg atoms inward to reduce the thickness of the Mg slab, as it is generally expected for a metal. In this case, the displacements are almost halved with respect to the Mg free surface case. Instead, for the magnesium hydride side, the Mg and H atoms move forward the interface with consequent widening of MgH₂ slab, and with respect to MgH₂ free surface, the displacements are increased. Atoms near the interface have a larger displacements with respect to bulk atoms. The displacements of the atoms in proximity of the interface are in the order of half angstrom. In particular we emphasize the tendency of the outer layer of Mg atoms on the hydride side to adapt to the saw-tooth shape of the magnesium free surface (see Figure 5b). This causes loss of z symmetry in the displacements of Mg and H atoms. Atoms belonging to the same row do not execute the same displacement (see Figure 5a). We resumed these results in Table 1. After geometry optimization the work of adhesion, computed by using Equation 1, is W_og = 395 mJ/m².

Figure 5. Two views of the Mg-MgH₂ interface after ionic relaxation. The shadowed atoms represent initial positions of atoms before relaxation. Displacements of the atoms are resumed in Table 1.

Figure 5. Two views of the Mg-MgH₂ interface after ionic relaxation. The shadowed atoms represent initial positions of atoms before relaxation. Displacements of the atoms are resumed in Table 1.

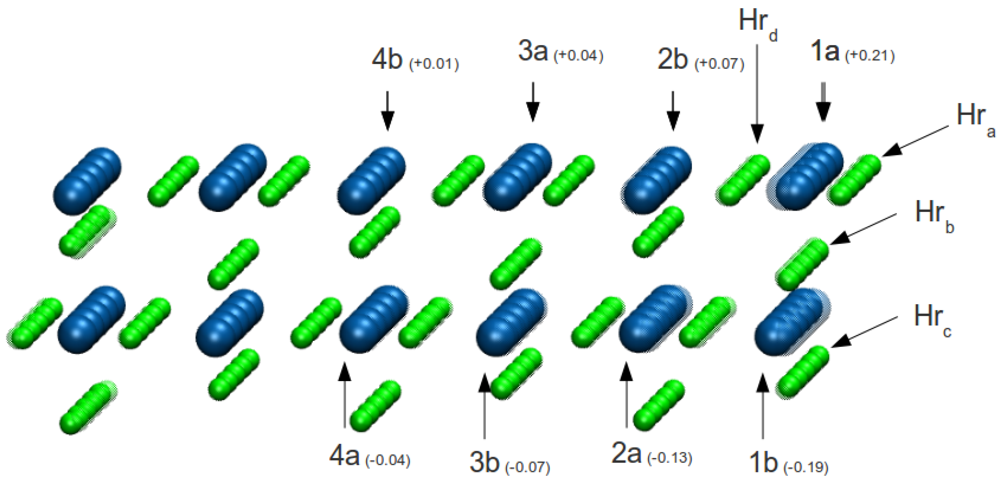
To determine which H atoms near the interface are more unstable, we removed in turn each of the five H atoms (h₁, h₂, h₃, h₄ and, h₅) on the outer row (Hr_a in Figure 3) and performed total energy calculations for the interfaces and corresponding hydride free surfaces. The values of the work of adhesion calculated by Equation 1 are lined up on second row of the Table 3.

Table 3. Work of adhesion and formation energy for the interfaces without one atom of hydrogen.

	h1	h2	h3	h4	h5
W (mJ/m2	1120	1160	1100	1160	1120
ΔH (eV)	0.71	0.53	0.88	0.53	0.71

Table 3. Work of adhesion and formation energy for the interfaces without one atom of hydrogen.

	h1	h2	h3	h4	h5
W (mJ/m2	1120	1160	1100	1160	1120
ΔH (eV)	0.71	0.53	0.88	0.53	0.71

Moreover, to establish the preferred desorption site of the H atoms, energy cost for the various positions were calculated from the total energies according to the following Equation:

where E_inter-H is total energy for the Mg-MgH₂ interface without one atom of hydrogen, is half total energy for the hydrogen molecule and E_inter is total energy for the Mg-MgH₂ interface after geometry optimization. The calculated values of ΔH are shown on third row of the Table 3. From these data we observe the inverse relation between the work of adhesion (W) and the formation energy (ΔH). The central position is the most energetically favourable for the desorption (the biggest ΔH and the lowest W) and moreover there is symmetry with respect to that central position.

5. Hydrogen Diffusion

To understand the atomic level dynamics of hydrogen displacement at the interface, MD simulations are performed at constant volume and constant temperature. Starting from a temperature of T= 300 K the system with interface is analyzed and characterized up to the temperature T = 900 K. Firstly the temperature is gradually raised (in steps of 100 K) till 600 K. Experimentally it is known that there is no hydrogen diffusion till 600 K. At each temperature the system reaches the equilibrium and no diffusion is observed. From this point on, the T = 600 K configuration is used as the starting configuration for higher temperature simulations at 700 K, 750 K, 800 K and 900 K. It is interesting to note that in this system, the hydrogen diffusion is clearly already started at the temperature T = 750 K, which is in very good agreement with experimental observations for unmilled MgH₂ without catalyst where hydrogen diffusion starts at T = 670 K [24]. This result makes us confident on the reliability of the numerical system. Hydrogen diffusion is complex phenomena that can be studied from analyzing the atomic dynamics in the temperature range T = 700–800 K.

Figure 6 depicts three atomic configurations, from which the influence of the temperature on the displacement of hydrogen atoms is clear. Diffusion of hydrogen atoms starts at T = 700 K (Figure 6a). At this temperature there is a tendency of hydrogen atoms to move towards the interface. This movement involves only the outer row of hydrogens. The internal hydrogen atoms move around their positions of equilibrium with a decreasing average width as the distance from the interface increases. At higher temperature, T = 750 K (Figure 6b), the tendency of hydrogens to move toward interface involves also internal rows of atoms. Moreover, the hydrogen atoms belonging to these rows diffuse by jumping from one lattice site to the nearest lattice site. At even higher temperature, T = 800 K (Figure 6c), the movement of the rows of hydrogens toward the interface is still present but the diffusion by jumping between lattice sites is replaced by hydrogen diffusion toward the interface. To quantify these observations, we report in Figure 7 the displacements d_i (t) =|r_i(t)- r_i(0)| of the hydrogen atoms from their initial positions during the molecular dynamics simulation, whereas r_i (0) and r_i (t) are the initial position of the i-th hydrogen atom and its position at time t, respectively.

Figure 6. Snapshots of Mg-MgH₂ interface during molecular dynamics for (a) T = 700 K; (b) T = 750 K; and (c) T = 800 K. H atoms are in green, Mg atoms in the magnesium hydride side are in light blue and Mg atoms in the magnesium side are in dark blue.

Figure 6. Snapshots of Mg-MgH₂ interface during molecular dynamics for (a) T = 700 K; (b) T = 750 K; and (c) T = 800 K. H atoms are in green, Mg atoms in the magnesium hydride side are in light blue and Mg atoms in the magnesium side are in dark blue.

Figure 7. Average displacements ⟨d(t)⟩ of the group of H atoms Hr_a (blue line), Hr_b (red line), Hr_c (green line), Hr_d (orange line) and, Hr_bulk (black line) for MD simulations at (a) T= 700 K; (b) T = 750 K; and (c) T = 800 K.

Figure 7. Average displacements ⟨d(t)⟩ of the group of H atoms Hr_a (blue line), Hr_b (red line), Hr_c (green line), Hr_d (orange line) and, Hr_bulk (black line) for MD simulations at (a) T= 700 K; (b) T = 750 K; and (c) T = 800 K.

To better characterize the hydrogen dynamics at the interface, as shown in Figure 3, five groups of atoms are considered: hydrogen atoms belonging to the outer row Hr_a, those that belong to the Hr_b Hr_c and Hr_d rows respectively, and all the others Hr_bulk. Averaging the displacements over these group of atoms, the quantities ⟨d(t)⟩_Hra, ⟨d(t)⟩_Hrb, ⟨d(t)⟩_Hrc, ⟨d(t)⟩_Hrd and ⟨d(t)⟩_Hrbulk are drawn in Figure 7 in blue line, red line, green line, orange line and black line, respectively. In panels (a), (b) and (c) of Figure 7 are reported these quantities for T= 700 K, T = 750 K and T = 800 K. For all temperatures the main contribution for hydrogen diffusion is due to the outer atoms (row Hr_a) and ⟨d(t)⟩_Hra increases with time. Instead, displacements of the "bulk" hydrogens ⟨d(t)⟩_Hrbulk are approximately constant (are about 0.5 Å). At T = 700 K displacements ⟨d(t)⟩_Hrb, ⟨d(t)⟩_Hrc and ⟨d(t)⟩_Hrd are oscillating but do not increase with time. They start to improve with time at higher temperature, and at T = 750 K the growth is faster and greater with respect to T = 800 K. We associate this behaviour to the pronounced feature of hydrogen atoms to jump from one lattice site to the nearest lattice site at T = 750 K. At these temperatures, diffusion of hydrogen atoms in the interface is clearly visible in the MD simulations. It is worth noting that no H atoms diffuse into the Mg lattice, which is in agreement with experimental evidence [6].

6. Evolution of the Desorption

To understand the behaviour of the system after the desorption of the outer hydrogen atoms, starting from the last configuration of MD simulation of the interface at T= 750 K, shown in Figure 8a, we removed by hand the hydrogens belonging to the rows Hr_a, Hr_b Hr_c and Hr_d (see Figure 3). These atoms are shadowed in panel (a) of Figure 8. Then, from this new system, a new ionic relaxation is performed as shown in Figure 8b. The ionic relaxation picks out how the magnesium atoms of the hydride deprived of hydrogens adapt to hcp magnesium bulk of the right side of the system. It is worth remarking that two Mg atoms are missing for a complete hcp magnesium free surface. To restore the good stoichiometry of the system, from the former configuration (Figure 8b) we added by hand two Mg atoms (Figure 8c) and performed a geometry optimization again, with the complete reconstruction of the hcp magnesium free surface and the creation of a "new" interface (Figure 8d).

Figure 8. Snapshots for the interface reconstitution. (a) Final configuration of MD simulation of the interface at T = 750 K. H atoms removed are shadowed; (b) configuration after geometry optimization without outer hydrogens; (c) configuration with two Mg atoms added (in red); (d) configuration after geometry optimization with two Mg atoms added and reconstruction of the "new" interface; (e) and (f) two snapshots of the MD simulation at T = 750 K.

Figure 8. Snapshots for the interface reconstitution. (a) Final configuration of MD simulation of the interface at T = 750 K. H atoms removed are shadowed; (b) configuration after geometry optimization without outer hydrogens; (c) configuration with two Mg atoms added (in red); (d) configuration after geometry optimization with two Mg atoms added and reconstruction of the "new" interface; (e) and (f) two snapshots of the MD simulation at T = 750 K.

Subsequently we performed MD simulation at T= 750 K. In panels (e) and (f) of Figure 8 are shown two snapshots of the MD simulation. These snapshots display the diffusion of hydrogen atoms in the "new" interface, with the "old" magnesium atoms of the hydride moving around the lattice position of hcp magnesium slab. Finally, to investigate the hydrogen dynamics at the new interface, in Figure 9 we presented similar graphs of those that are shown in Figure 7. Like previously, displacements of the "bulk" hydrogens (black line) are approximately constant and the main contribution for hydrogen diffusion is still due to the outer atoms (blue line, red line, green line and orange line). In conclusion, it is evident that the two interfaces produce the same results.

Figure 9. Average displacements ⟨d(t)⟩ of the group of H atoms Hr_a (blue line), Hr_b (red line), Hr_c (green line), Hr_d (orange line) and, Hr_bulk (black line) for MD simulations at T = 750 K, for the "new" interface.

Figure 9. Average displacements ⟨d(t)⟩ of the group of H atoms Hr_a (blue line), Hr_b (red line), Hr_c (green line), Hr_d (orange line) and, Hr_bulk (black line) for MD simulations at T = 750 K, for the "new" interface.

7. Conclusions

In conclusion, a reliable numerical model to understand the H desorption from MgH₂ is proposed. By ab-initio electronic structure calculations we studied and characterized the Mg–MgH₂ interface, composed of the (010) surface of magnesium and (110) surface of magnesium hydride. Furthermore, molecular dynamics simulations at several temperatures are performed to study the dynamics of hydrogen atoms at the interface. Desorption temperature is estimated, which is in agreement with experimental results. We have shown that ab-initio calculations are able to discover atomic level phenomena that are critical for the progress in a technologically relevant issue like the one related to the hydrogen storage.