Bifurcation Control of an Electrostatically-Actuated MEMS Actuator with Time-Delay Feedback
Abstract
:1. Introduction
2. Problem Formulation
3. Perturbation Analysis
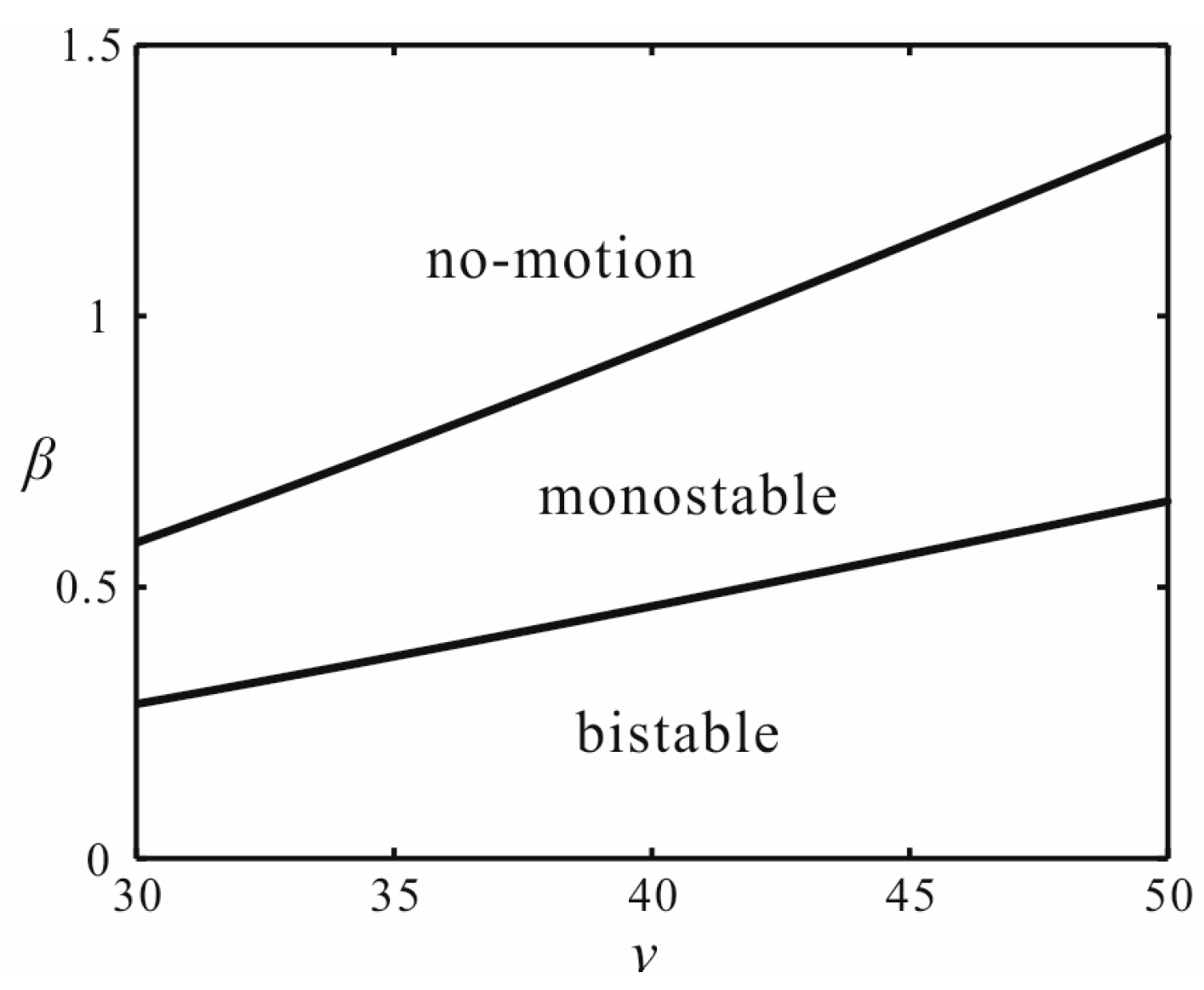
4. Bifurcation Control near the Origin
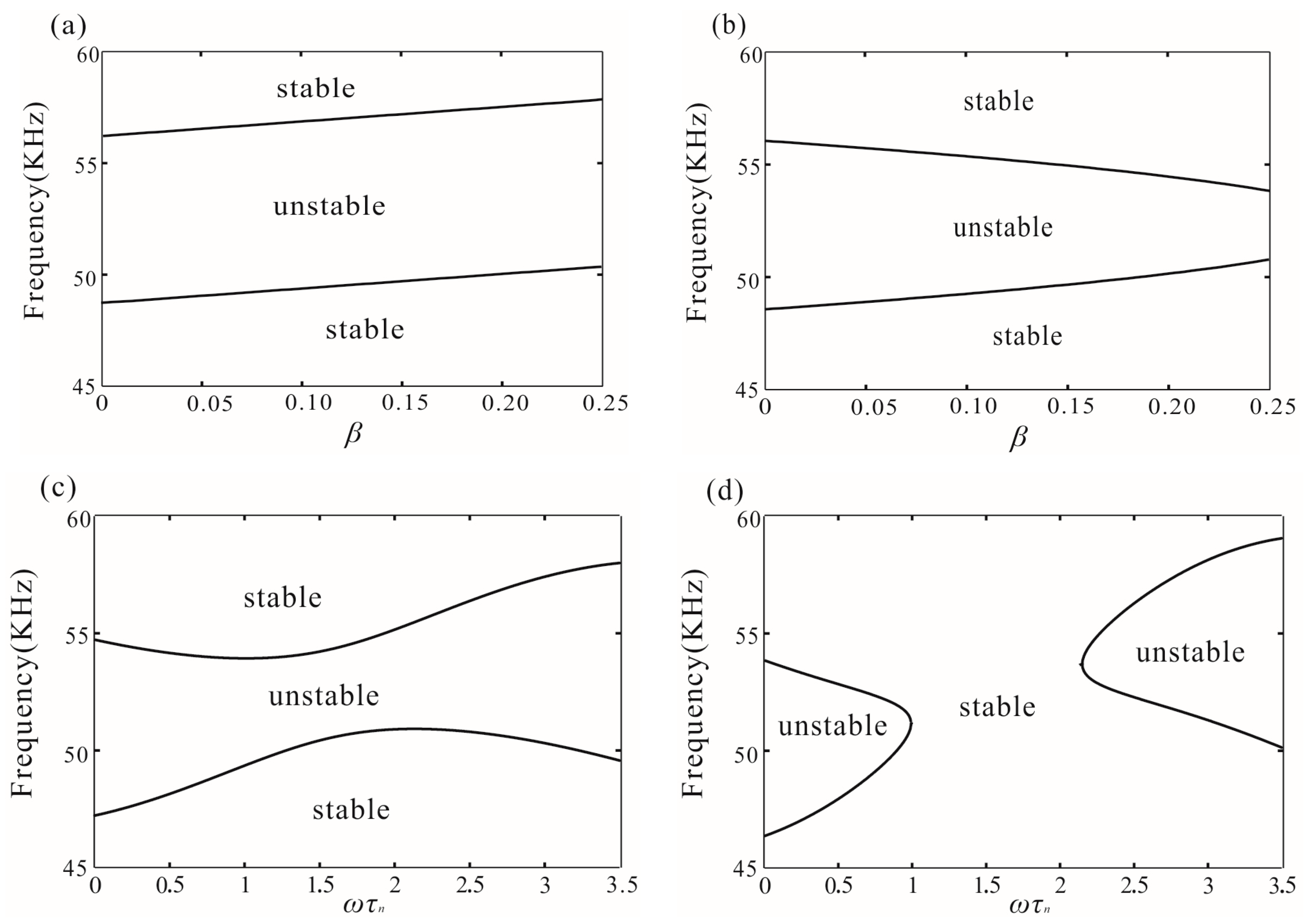
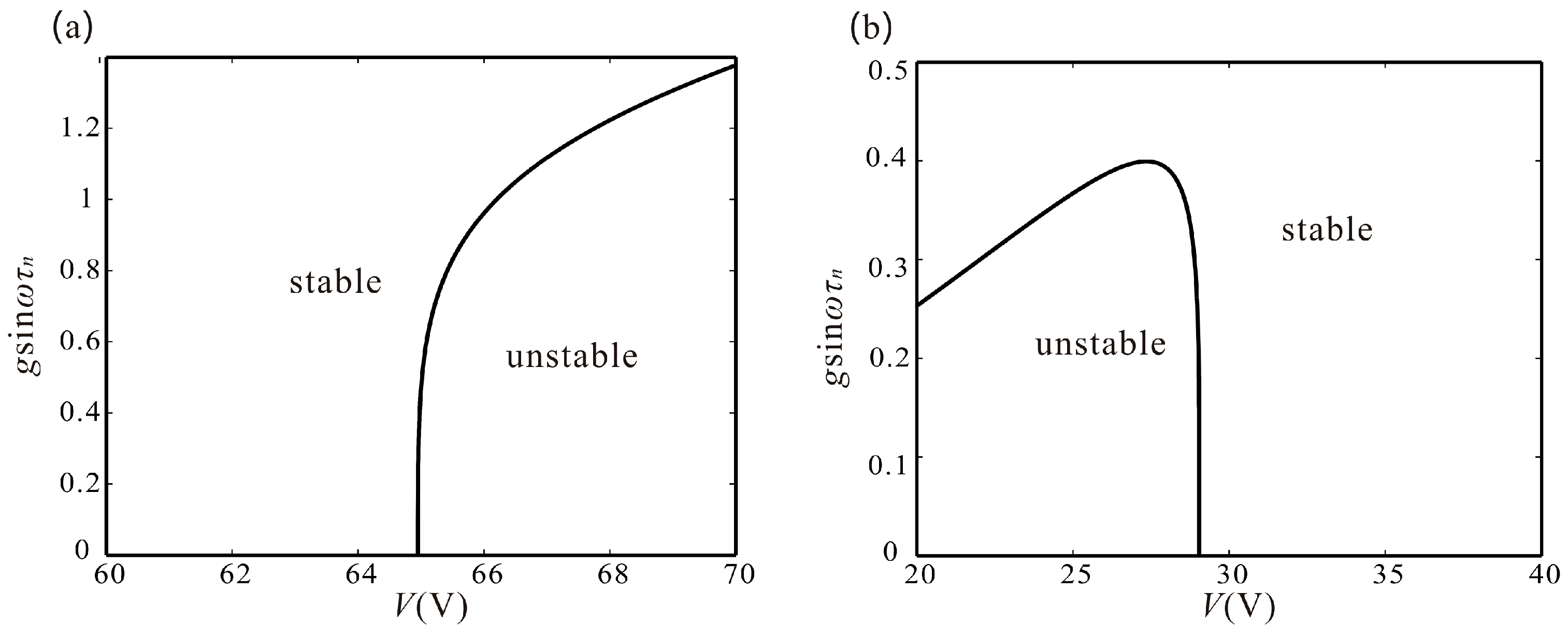
4.1. Stability of the Origin
4.2. Stability of the Untrivial Solution
5. Monostable Vibration
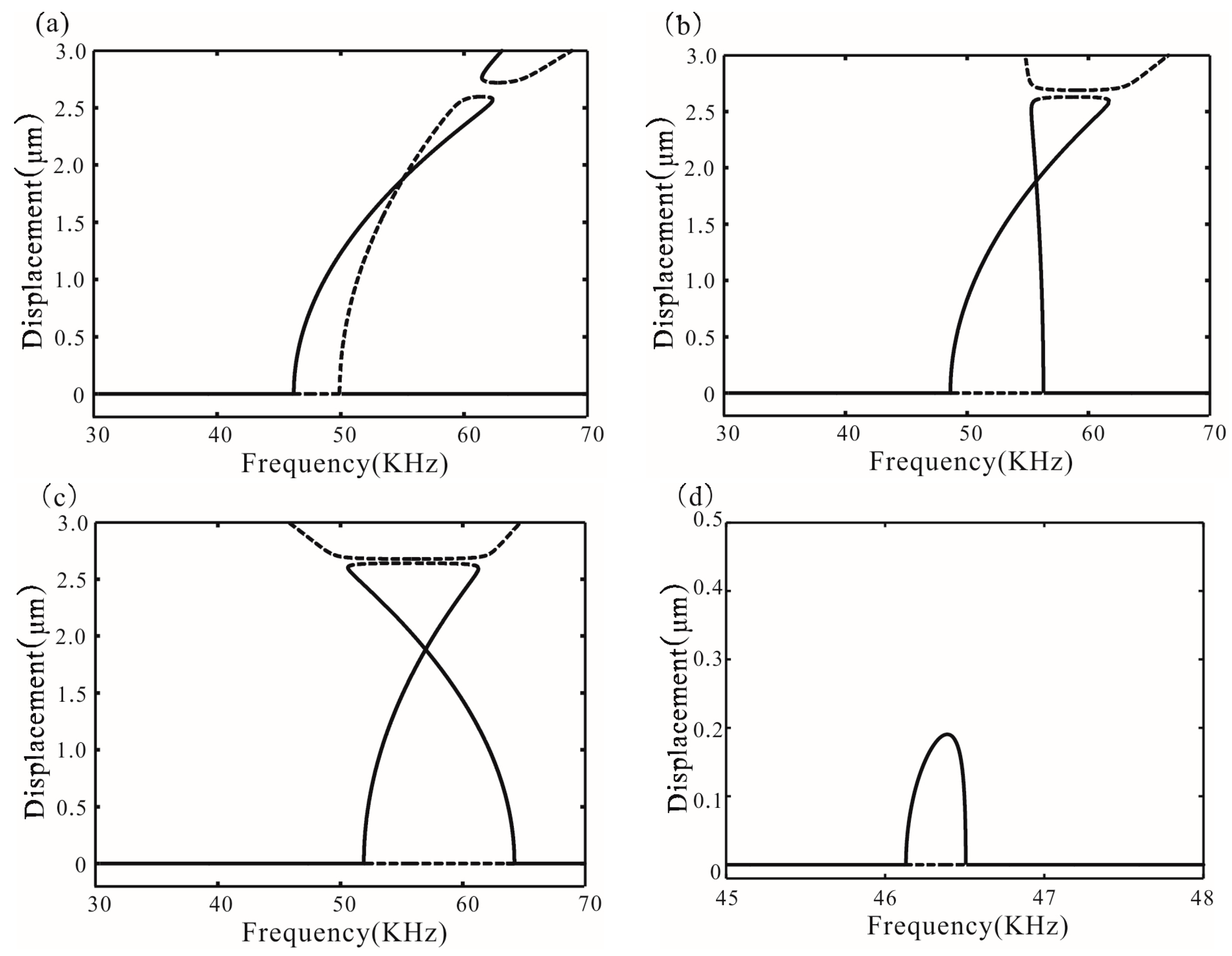
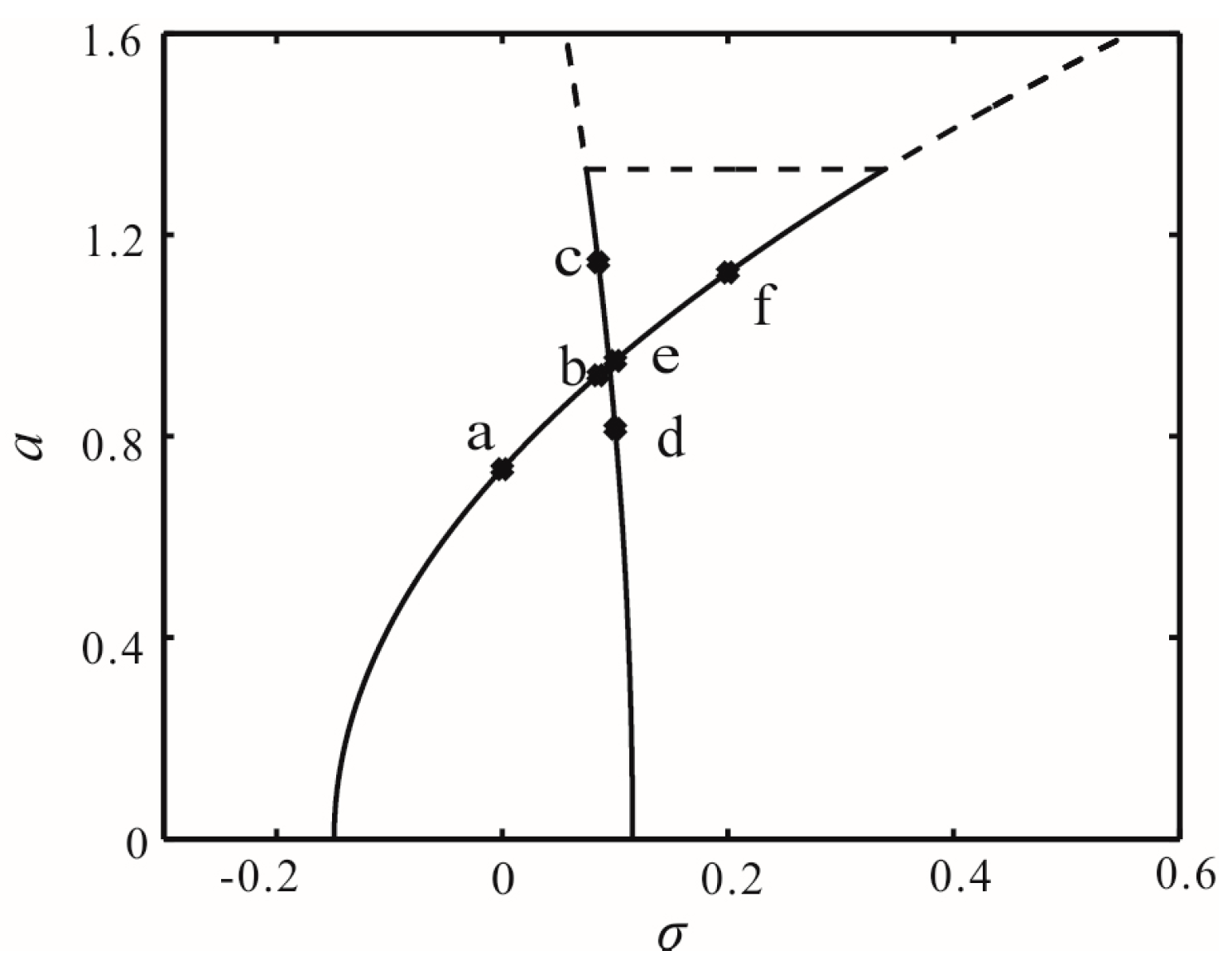
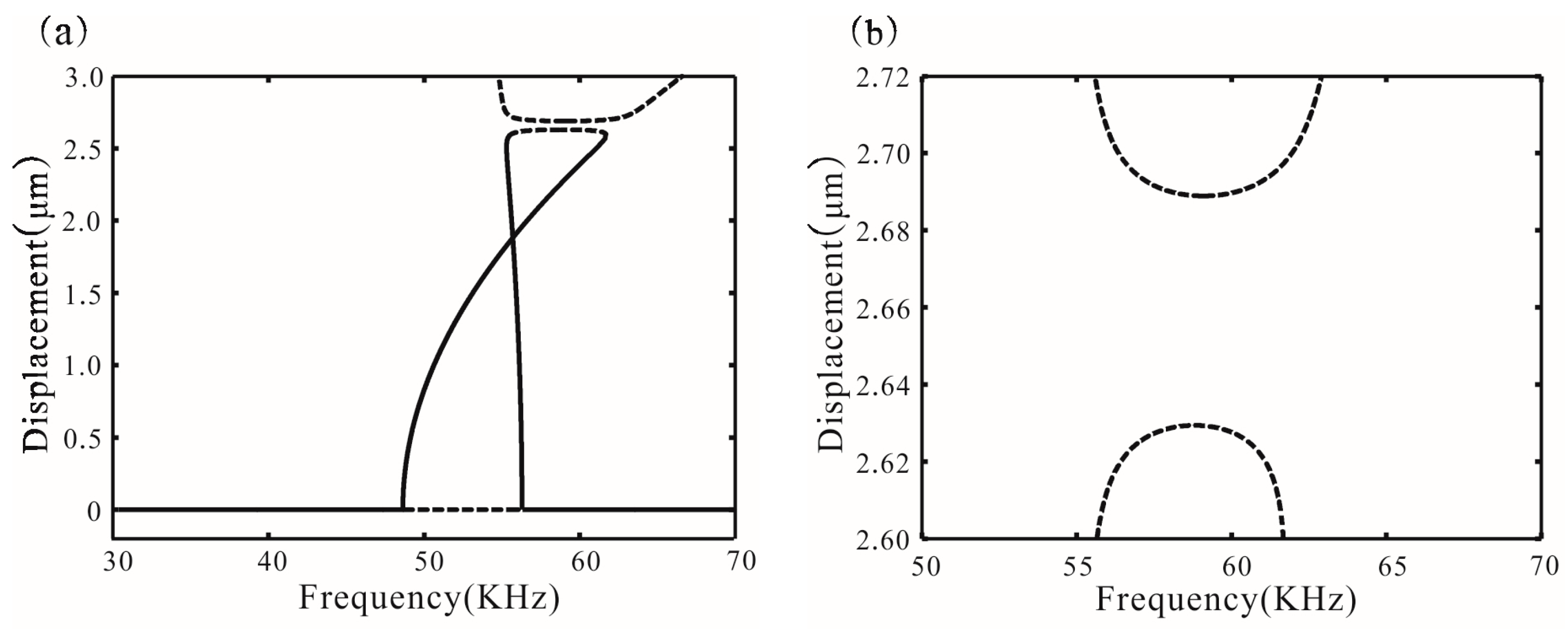
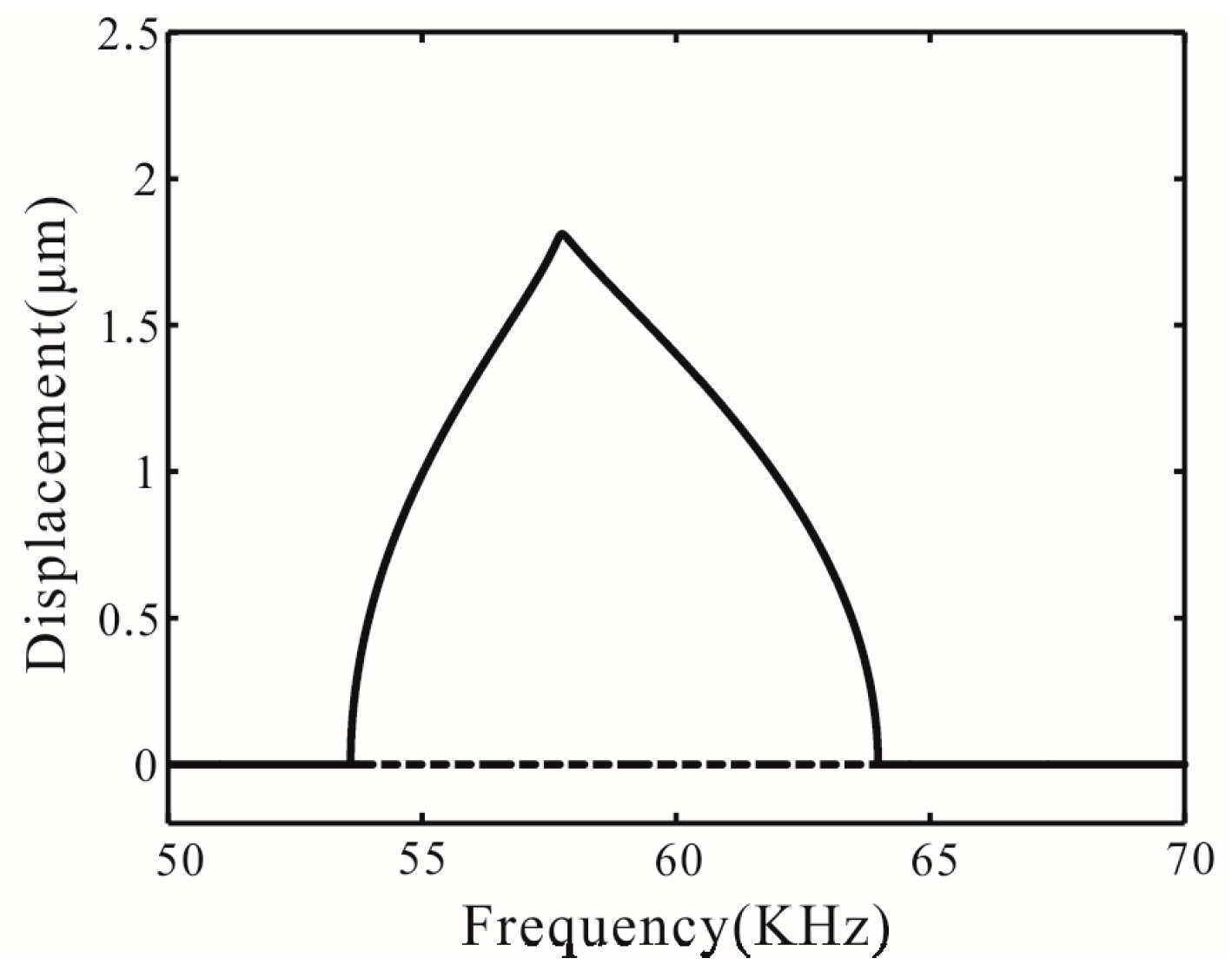
5.1. Global Bifurcation
5.2. Saddle Node Bifurcation
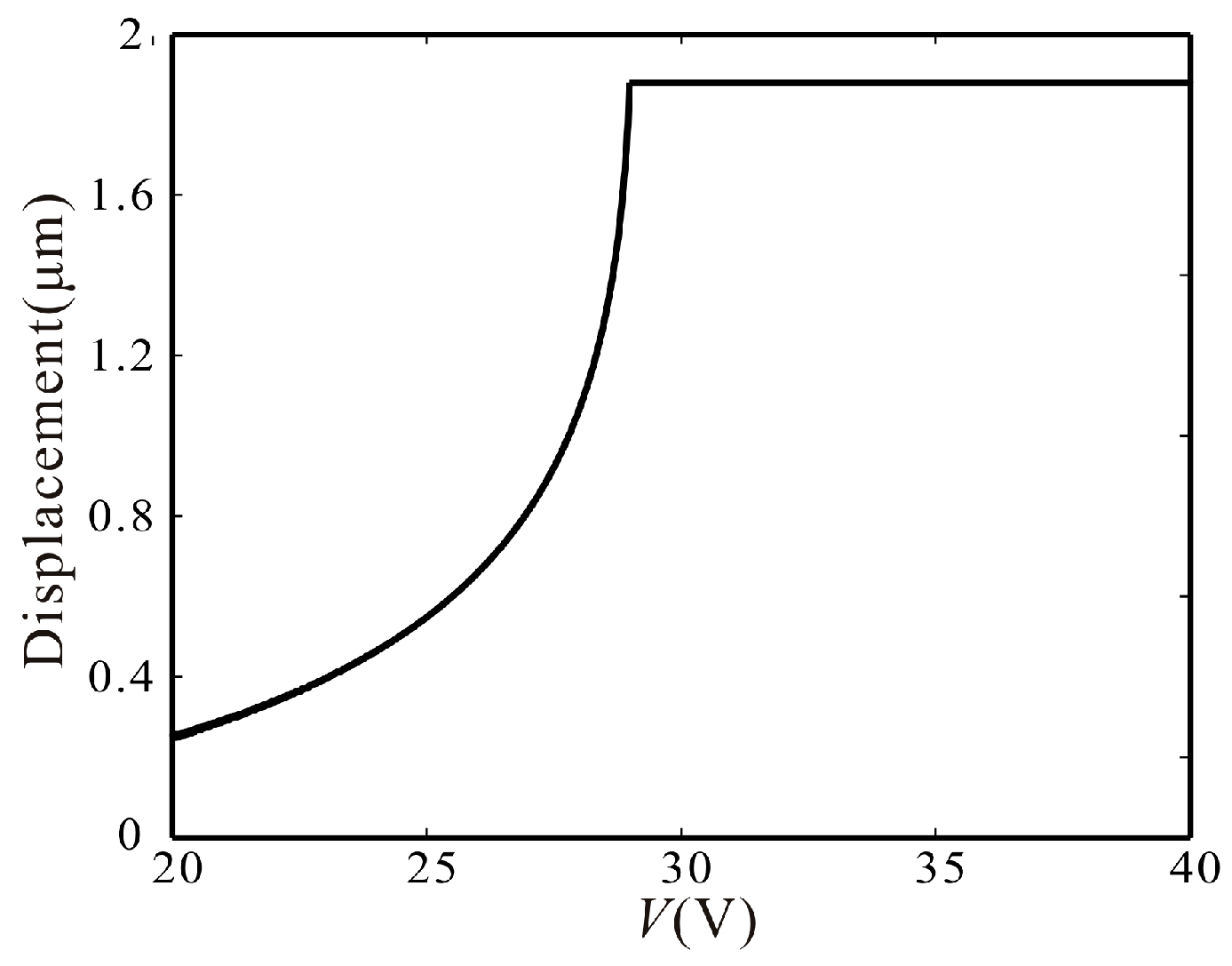
5.3. Monostable Parameter Vibration
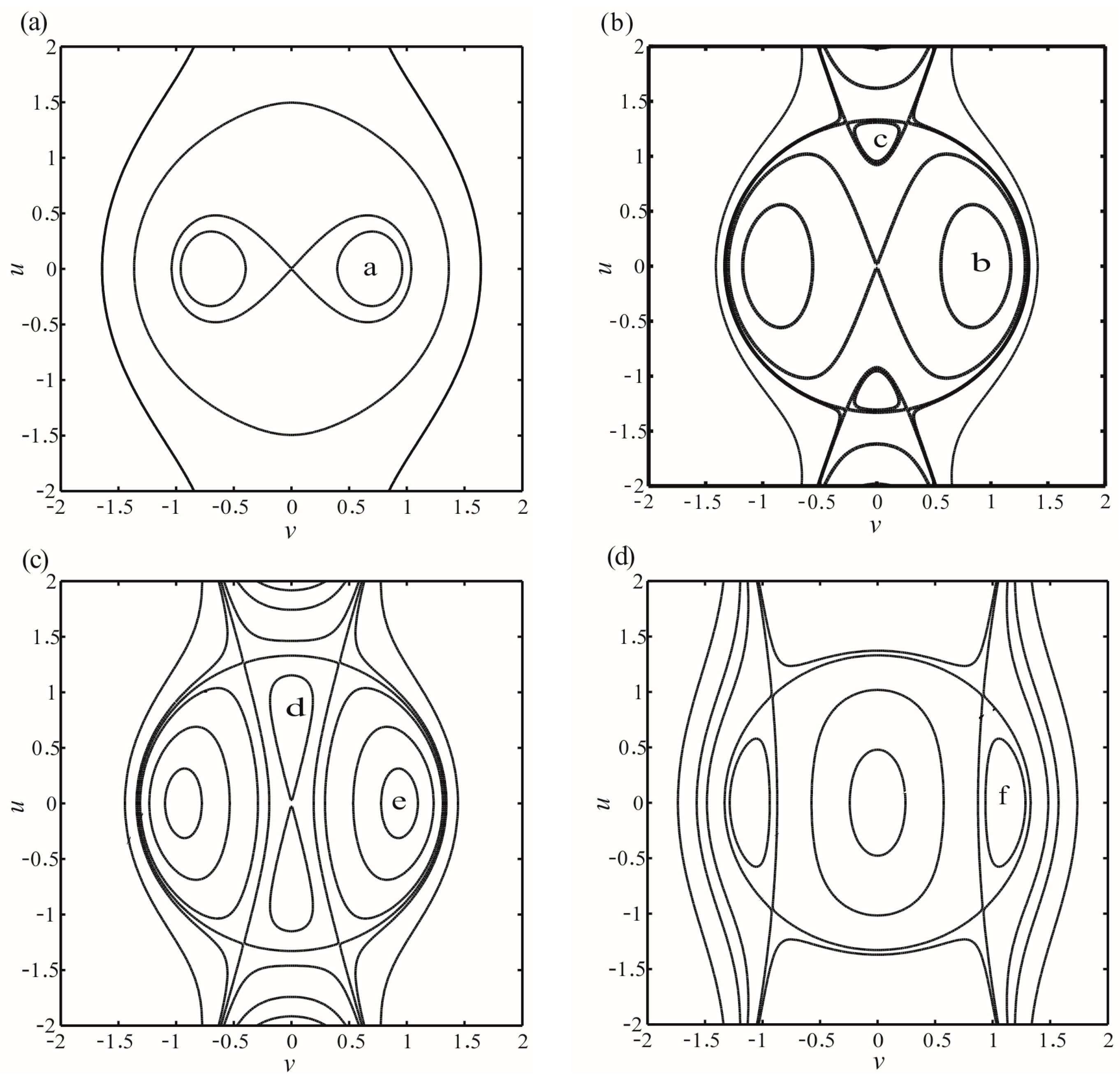
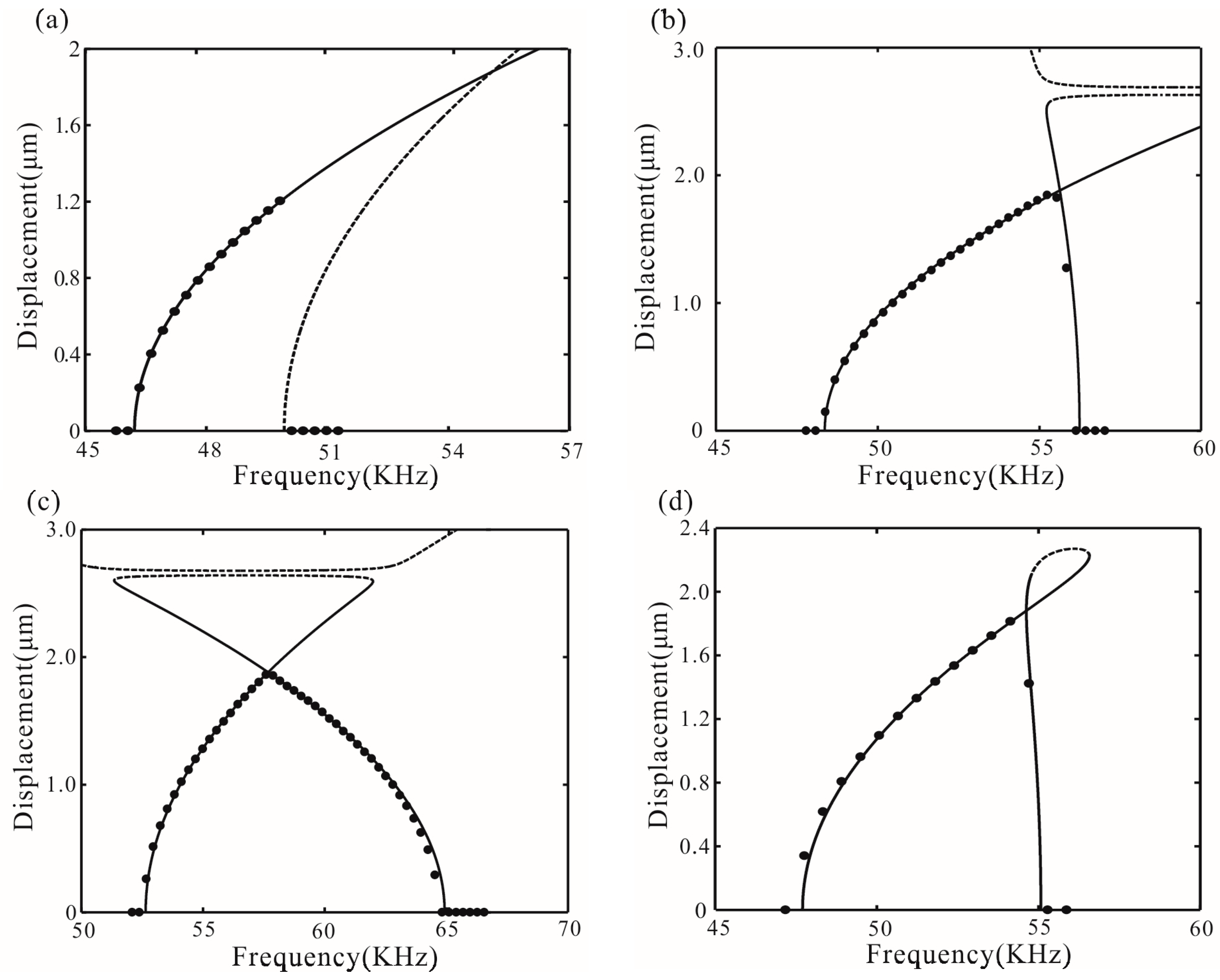
6. Numerical Simulation
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix B
References
- Alper, S.E.; Azgin, K.; Akin, T. A high-performance silicon-on-insulator MEMS gyroscope operating at atmospheric pressure. Sens. Actuators A Phys. 2007, 135, 34–42. [Google Scholar] [CrossRef]
- Rasekh, M.; Khadem, S.E. Design and performance analysis of a nanogyroscope based on electrostatic actuation and capacitive sensing. J. Sound Vib. 2013, 332, 6155–6168. [Google Scholar] [CrossRef]
- Xue, L.; Wang, L.X.; Xiong, T.; Jiang, C.Y.; Yuan, W.Z. Analysis of Dynamic Performance of a Kalman Filter for Combining Multiple MEMS Gyroscopes. Micromachines 2014, 5, 1034–1050. [Google Scholar] [CrossRef]
- Ouakad, H.M.; Younis, M.I. On using the dynamic snap-through motion of MEMS initially curved microbeams for filtering applications. J. Sound Vib. 2014, 333, 555–568. [Google Scholar] [CrossRef]
- Demartini, B.E.; Rhoads, J.F.; Turner, K.L.; Shaw, S.W.; Moehlis, J. Linear and Nonlinear Tuning of Parametrically Excited MEMS Oscillators. J. Microelectromech. Syst. 2007, 16, 310–318. [Google Scholar] [CrossRef]
- Rugar, D.; Grütter, P. Mechanical parametric amplification and thermomechanical noise squeezing. Phys. Rev. Lett. 1991, 67, 699–702. [Google Scholar] [CrossRef] [PubMed]
- Turner, K.L.; Miller, S.A.; Hartwell, P.G.; MacDonald, N.C.; Strogatz, S.H.; Adams, S.G. Five parametric resonances in a microelectromechanical system. Nature 1998, 396, 149–152. [Google Scholar] [CrossRef]
- Zhang, W.; Baskaran, R.; Turner, K.L. Effect of cubic nonlinearity on auto-parametrically amplified resonant MEMS mass sensor. Sens. Actuators A Phys. 2002, 102, 139–150. [Google Scholar] [CrossRef]
- Rhoads, J.F.; Shaw, S.W.; Turner, K.L.; Baskaran, R. Tunable Microelectromechanical Filters that Exploit Parametric Resonance. J. Vib. Acoust. 2005, 127, 423. [Google Scholar] [CrossRef]
- Zhang, W.; Baskaran, R.; Turner, K.L. Tuning the dynamic behavior of parametric resonance in a micromechanical oscillator. Appl. Phys. Lett. 2003, 82, 130–132. [Google Scholar] [CrossRef]
- Zhong, Z.; Zhang, W.; Meng, G.; Wu, J. Inclination Effects on the Frequency Tuning of Comb-Driven Resonators. J. Microelectromech. Syst. 2013, 22, 865–875. [Google Scholar] [CrossRef]
- Elshurafa, A.M.; Khirallah, K.; Tawfik, H.H.; Emira, A.; Abdel Aziz, A.K.S.; Sedky, S.M. Nonlinear Dynamics of Spring Softening and Hardening in Folded-MEMS Comb Drive Resonators. J. Microelectromech. Syst. 2011, 20, 943–958. [Google Scholar] [CrossRef]
- Siewe, M.S.; Hegazy, U.H. Homoclinic bifurcation and chaos control in MEMS resonators. Appl. Math. Model. 2011, 35, 5533–5552. [Google Scholar] [CrossRef]
- Rhoads, J.F.; Shaw, S.W.; Turner, K.L.; Moehlis, J.; DeMartini, B.E.; Zhang, W. Generalized parametric resonance in electrostatically actuated microelectromechanical oscillators. J. Sound. Vib. 2006, 296, 797–829. [Google Scholar] [CrossRef]
- Welte, J.; Kniffka, T.J.; Ecker, H. Parametric excitation in a two degree of freedom MEMS system. Shock Vib. 2013, 20, 1113–1124. [Google Scholar] [CrossRef]
- Han, J.; Zhang, Q.; Wang, W. Design considerations on large amplitude vibration of a doubly clamped microresonator with two symmetrically located electrodes. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 492–510. [Google Scholar] [CrossRef]
- Shao, S.; Masri, K.M.; Younis, M.I. The effect of time-delayed feedback controller on an electrically actuated resonator. Nonlinear Dyn. 2013, 74, 257–270. [Google Scholar] [CrossRef]
- Zhang, T.; Li, H. Adaptive pole placement control for vibration control of a smart cantilevered beam in thermal environment. J. Vib. Control 2013, 10, 1460–1470. [Google Scholar] [CrossRef]
- Yamasue, K.; Hikihara, T. Control of microcantilevers in dynamic force microscopy using time delayed feedback. Rev. Sci. Instrum. 2006, 77, 053703. [Google Scholar] [CrossRef] [Green Version]
- Nayfeh, A.H.; Nayfeh, N.A. Time-delay feedback control of lathe cutting tools. J. Vib. Control 2011, 18, 1106–1115. [Google Scholar] [CrossRef]
- Yamasue, K.; Hikihara, T. Persistence of chaos in a time-delayed-feedback controlled Duffing system. Phys. Rev. E 2006, 73, 036209. [Google Scholar] [CrossRef] [PubMed]
- Hikihara, T.; Kawagoshi, T. An experimental study on stabilization of unstable periodic motion in magneto-elastic chaos. Phys. Lett. A 1996, 211, 29–36. [Google Scholar] [CrossRef]
- Shehrin, S.; Clark, J.V. Active control of effective mass, damping and stiffness of MEMS. In Proceedings of the Design, Test, Integration and Packaging of MEMS/MOEMS, Barcelona, Spain, 16–18 April 2013.
- Mehta, A.; Cherian, S.; Hedden, D.; Thundat, T. Manipulation and controlled amplification of Brownian motion of microcantilever sensors. Appl. Phys. Lett. 2001, 78, 1637. [Google Scholar] [CrossRef]
- Morrison, T.M.; Rand, R.H. 2:1 Resonance in the delayed nonlinear Mathieu equation. Nonlinear Dyn. 2007, 50, 341–352. [Google Scholar] [CrossRef]
- Alsaleem, F.M.; Younis, M.I. Stabilization of electrostatic MEMS resonators using a delayed feedback controller. Smart Mater. Struct. 2010, 19, 035016. [Google Scholar] [CrossRef]
- Warminski, J. Frequency locking in a nonlinear MEMS oscillator driven by harmonic force and time delay. Int. J. Dyn. Control 2015, 3, 122–136. [Google Scholar] [CrossRef]
- Alsaleem, F.; Younis, M.I. Integrity Analysis of Electrically Actuated Resonators with Delayed Feedback Controller. J. Dyn. Syst. Meas. Control 2011, 133, 031011. [Google Scholar] [CrossRef]
- Kamiński, M.; Corigliano, A. Numerical solution of the Duffing equation with random coefficients. Meccanica 2015, 50, 1841–1853. [Google Scholar] [CrossRef]
- Kamiński, M.; Corigliano, A. Sensitivity, probabilistic and stochastic analysis of the thermo-piezoelectric phenomena in solids by the stochastic perturbation technique. Meccanica 2012, 47, 877–891. [Google Scholar] [CrossRef]
- Comi, C.; Corigliano, A.; Ghisi, A.; Zerbini, S. A resonant micro accelerometer based on electrostatic stiffness variation. Meccanica 2013, 48, 1893–1900. [Google Scholar] [CrossRef]
- Younis, M.I. MEMS Linear and Nonlinear Statics and Dynamics; Springer: New York, NY, USA, 2011. [Google Scholar]
- Najar, F.; Nayfeh, A.H.; Abdel-Rahman, E.M.; Choura, S.; El-Borgi, S. Dynamics and global stability of beam-based electrostatic microactuators. J. Vib. Control 2010, 16, 721–748. [Google Scholar] [CrossRef]
- Nizar, J.; Abdallah, R.; Carreno, A.A.A.; Younis, M.I. Higher order modes excitation of electrostatically actuated clamped–clamped microbeams: Experimental and analytical investigation. J. Micromech. Microeng. 2016, 26, 025008. [Google Scholar]
- Masri, K.M.; Younis, M.I. Investigation of the dynamics of a clamped–clamped microbeam near symmetric higher order modes using partial electrodes. Int. J. Dyn. Control 2015, 3, 173–182. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Introduction to Perturbation Techniques; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Khirallah, K. Parametric excitation, amplification, and tuning of MEMS folded-beam comb drive oscillator. J. Microelectromech. Syst. 2013, 22, 318–330. [Google Scholar] [CrossRef]
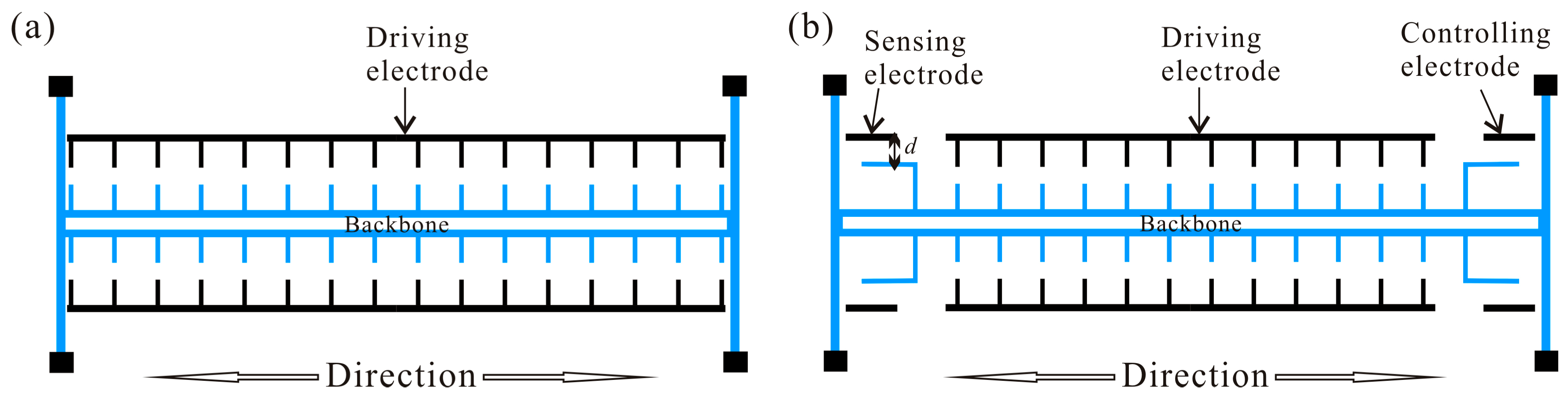
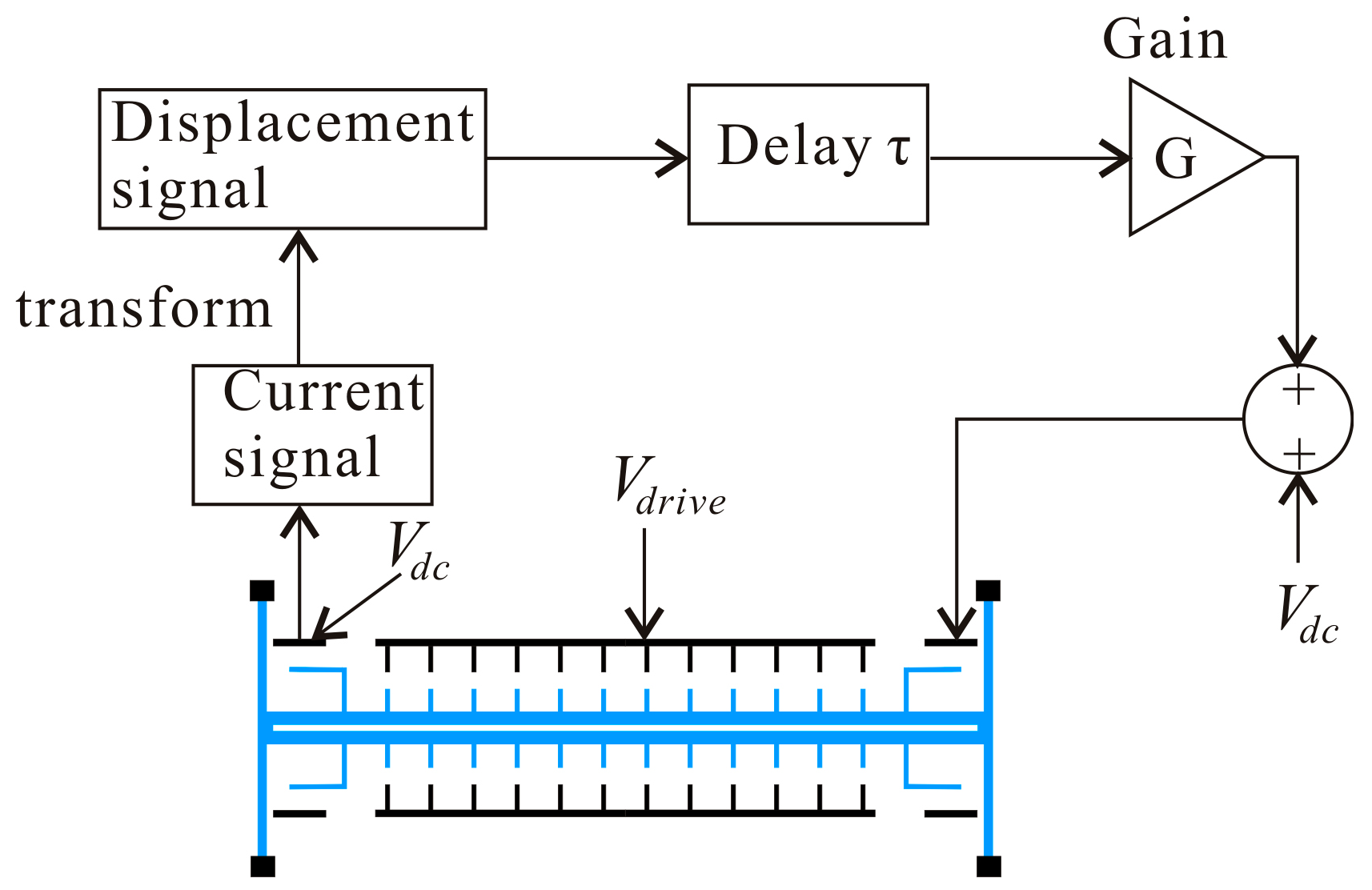
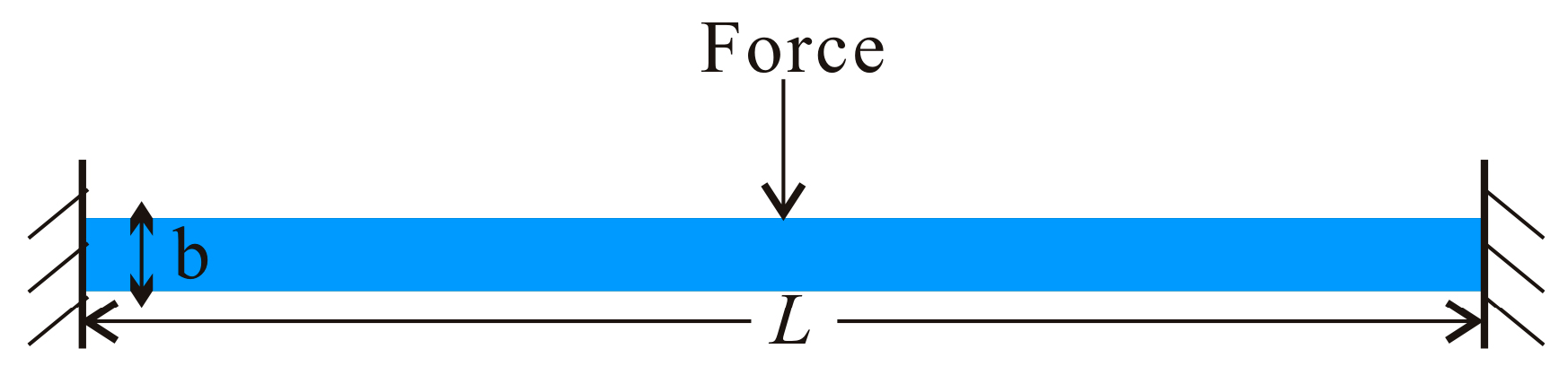
| Parameter | Value | Units |
|---|---|---|
| Mass density ρ | 2300 | Kg/m3 |
| Young’s modulus E | 150 | GPa |
| Beam length L | 320 | μm |
| Beam width b | 10 | μm |
| Beam thickness h | 2 | μm |
| Coefficients r1 | 5.3 × 10−3 | μN·μm−1·V−2 |
| Coefficients r3 | −1.5 × 10−3 | μN·μm−3·V−2 |
| Damping c | 5.42 × 10−3 | Ns·m−2 |
| Mass M | 5.95 × 10−10 | kg |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Zhang, Q.; Wang, W.; Han, J. Bifurcation Control of an Electrostatically-Actuated MEMS Actuator with Time-Delay Feedback. Micromachines 2016, 7, 177. https://doi.org/10.3390/mi7100177
Li L, Zhang Q, Wang W, Han J. Bifurcation Control of an Electrostatically-Actuated MEMS Actuator with Time-Delay Feedback. Micromachines. 2016; 7(10):177. https://doi.org/10.3390/mi7100177
Chicago/Turabian StyleLi, Lei, Qichang Zhang, Wei Wang, and Jianxin Han. 2016. "Bifurcation Control of an Electrostatically-Actuated MEMS Actuator with Time-Delay Feedback" Micromachines 7, no. 10: 177. https://doi.org/10.3390/mi7100177







