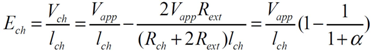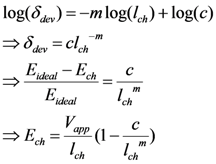1. Introduction
Generating high electric fields inside microchannels are needed for many microfluidic applications, such as lab-on-a-chip (LOC), micro-total-analysis-system (μTAS) and biomedical microelectromechanical systems (bioMEMS) [
1,
2]. Uniform or non-uniform distribution of the electric fields can be utilized to process biological elements, like cell lysis, electroporation, electrophoresis separation, deoxyribonucleic acid (DNA) detection and separation and electro-osmotic flow generation for electrokinetic (EK) microfluidic pumps [
3,
4,
5]. Electrical lysis on a portable microfluidic device is critical for point-of-care (POC) devices requiring access to internal contents of the cell. We are motivated to develop a POC device that performs DNA detection within few seconds. Such a development will be valuable for emergency responders, criminal investigators and forensic identification. In this work, electrical lysis of biological cells is investigated with a commonly used microchannel structure, where the electrode with excitation potential is positioned at one end of the microchannel, whereas the electrode at the other end of the microchannel is grounded [
5,
6,
7,
8,
9,
10]. The novelty of this work is the analysis of the estimation errors of electric fields of typical microfluidic devices used in such experiments and the models to reduce such estimation errors to achieve a high yield, which is critical for single-cell analysis.
The electric potential across the channel caused by the external electrical field can be evaluated with the Laplace equation,
![Micromachines 04 00243 i001]()
, where
![Micromachines 04 00243 i002]()
is the external electrical potential [
11]. The Poisson-Boltzmann equation is employed to govern the electric potential near the channel wall and in the bulk:
where
![Micromachines 04 00243 i004]()
is the electrical potential,
![Micromachines 04 00243 i005]()
is the free charge density,
![Micromachines 04 00243 i006]()
is the bulk concentration of the ions,
![Micromachines 04 00243 i007]()
is the ionic valence,
![Micromachines 04 00243 i008]()
is the elementary charge,
![Micromachines 04 00243 i009]()
is the dielectric constant of the medium,
![Micromachines 04 00243 i010]()
is the Boltzmann constant and
![Micromachines 04 00243 i011]()
is the temperature. The electric field distribution inside the microchannel can be estimated by the Poisson equation, which, for the case of uniform electric charge density in a linear, isotropic and homogeneous medium, becomes:
This is the most commonly used expression to estimate the electric field strengths inside the microchannels of microfluidic devices [
5,
6,
7,
8,
9], even though the assumptions involving dielectric constant, fringe field and parallel electrode surface are invalidated. Furthermore, solid-liquid interface develops an electrical double layer (EDL) with the characteristic thickness of the Debye length, which has significant influence on the behavior of ionic conductors. These factors lead to a significant estimation error when Expression (2) is used, which is increasingly critical as the dimensions of the microchannel become smaller––the general trend in microfluidics and nanofluidics.
To accurately determine the electric field distribution, the finite element method (FEM) is more acceptable, as results with higher confidence can be produced through incorporating proper simulation setup, such as boundary conditions and refining of mesh sizes at regions of non-uniformity [
8,
12]. Using this technique, the analytical expressions developed are design-specific [
12,
13,
14]. The microchannel structure under consideration has a uniform cross-section throughout its length, and the electrodes are placed at both terminals of the microchannel. There are a number of reports that share this topology [
5,
6,
7,
8,
9,
10,
15]. This work attempts to analyze the estimation error stemming from Expression (2) and proposes two analytical expressions to reduce the error. The findings are applicable for microchannels with uniform electric fields containing physiological solution—a practical scenario.
Single cell electrical lysis experiments were conducted using biological cells with applied electrical excitation. Electrical lysis is a phenomenon of complete cell membrane breakdown under a high electric field of a critical period [
8,
16,
17,
18]. Reports of various types of cell lysis using an electrical field are available, including yeast cells,
E. coli [
19], cancer cells [
20,
21,
22], mammalian cells [
23], leukocytes [
24], erythrocyte [
25], red blood cells [
8,
26] and Chinese hamster ovary cells [
6,
27]. In this work, non-invasively collected cell debris,
i.e., shredded cells, of epidermal tissue from human fingerprints are used as cell-samples.
Figure 1.
Finite element method (FEM) simulations (a) without and (b) with microchannel structures (microchannels of 100 μm-wide and 20 μm-deep) that depict high electric field distributions inside the microchannel structure, in the latter case away from the electrodes inside the reservoirs with normalized excitation (1 V). A 3D view of a reservoir is shown in the inset. Electric field distributions and electric potentials with the microchannel structure are plotted for five different electrode locations (1 to 5) inside the reservoirs. Note: Electric field distributions inside the fluidic subdomain are only shown in (b).
Figure 1.
Finite element method (FEM) simulations (a) without and (b) with microchannel structures (microchannels of 100 μm-wide and 20 μm-deep) that depict high electric field distributions inside the microchannel structure, in the latter case away from the electrodes inside the reservoirs with normalized excitation (1 V). A 3D view of a reservoir is shown in the inset. Electric field distributions and electric potentials with the microchannel structure are plotted for five different electrode locations (1 to 5) inside the reservoirs. Note: Electric field distributions inside the fluidic subdomain are only shown in (b).
2. Simulation of Electric Fields inside Microchannels
Before proceeding to a comprehensive analysis of electric fields inside microchannels, a qualitative comparison is depicted through electric field distribution without any microchannel structure (
Figure 1a) and with a microchannel structure (
Figure 1b). Maxwell3D simulator (Ansoft Corp. acquired by ANSYS Inc., Canonsburg, PA, USA) was used as the FEM tool. Isothermal boundary conditions were applied for the simulation box, whose size was determined iteratively by doubling each dimension until there was no significant change due to the box size in subsequent iterations. The mesh size was manually increased at the corners and inside small features to increase simulation accuracy at locations where a higher gradient is expected.
Figure 1a depicts that the electric field distribution without the microchannel was more pronounced around the electrodes, whereas for the case of a microchannel, as depicted in
Figure 1b, the higher electric field distribution was concentrated inside the microchannels. Evidently, an advantage of the microchannel structure is that the cell samples placed inside the microchannels away from the electrodes are exposed to high electric fields, thus reducing the possibility of the cell samples being effected by the electrolysis of water that occurs at the interface of the electrodes when a potential is applied. In addition, the use of microchannels lowers the current flow, power dissipation and energy consumption to produce a certain electric field inside the microchannel, due to the confinement of the electron flow-path.
2.1. Modeling of an Ideal Microchannel
To begin electric field analysis of the microfluidic device, an ideal model of a microchannel structure is considered, where the microchannel is a “rectangular box” with length, width and height of
lch,
wch and
hch, respectively. Both electrodes are in contact with the complete cross-sectional areas on both terminals of the microchannel. The microchannel contains physiological buffer fluid (e.g., D-PBS) with the relative permittivity (ε
r) and conductivity (σ
ch) used in the literature (80 and 1.6 S/m, respectively) [
28]. The microchannel structure along with the electrodes is enclosed within a large glass substrate. An electric field,
Ech, develops inside the microchannel as an excitation voltage,
Vapp, is applied across the electrode-pair. In this ideal case, the voltage across the microchannel,
Vch, is the same as
Vapp.
For this ideal model of the microchannel, electric flux generated inside the microchannel can be approximated as uniform. Thus,
Ech can be expressed using the electric field expression between two parallel electrodes [
11], given as:
Due to the current flow through the buffer fluid, the Columbic power dissipation,
Pd, inside the microchannel can be expressed as [
29]:
where
Rch is the electrical resistance of the microchannel. Using the resistivity law [
12],
Rch for the rectangular box can be expressed as:
where ρ
ch is the resistivity of the buffer fluid inside the microchannel and
Ach (
=wch × hch) is the cross-sectional area of the microchannel. Hence:
where
Λch (
=Ach × lch) is the volume of the microchannel. If ρ
ch is a constant, ignoring the effect of localized Joule heating, for a certain buffer fluid,
Pd is proportional to the volume of the microchannel for a specific electric field. For microchannel structures, small
Λch would lead to small power dissipation––another advantage of using microchannels for high electric field generation. The temperature increase inside a microchannel with a certain media depends on surface area, conductive heat transfer coefficient and thermal resistance.
The energy density,
uch, inside the microchannel due to the electric field can be expressed as [
11]:
Here, ε (
=ε
0ε
r) is the permittivity of the buffer fluid, where ε
0 is the permittivity of the free space and ε
r is the relative permittivity of the buffer fluid. The total energy stored,
Uch, can be obtained by integrating
uch over
Λch [
11]. For this ideal microchannel model,
Uch can be expressed by:
Hence, for a given electric field and buffer fluid, Uch is proportional to Λch. Furthermore, Uch is also proportional to Pd with a proportionality constant of ερch/2.
2.2. Modeling a Microchannel of the Microfluidic Device
The microfluidic device contains a microchannel that fluidically connects two access holes (reservoirs). To develop an electric field inside the microchannel, electrodes are inserted inside these access holes. Both the microchannel and the access holes contain the physiological buffer fluid (D-PBS) modeled by assigning proper conductivity and permittivity values, as mentioned above. The electrodes were excited with the applied voltage, Vapp. Notice that in this case, Vch is always smaller than Vapp. The microfluidic device was fabricated with two glass slides: top and bottom. The microchannel was created by an etching technique (wet etching with Hydrofluoric acid, HF) on the top surface of the bottom slide. This also created an etch pad at the bottom of the access hole. The two glass slides were thermally fused together, which produces great modification of microchannel height, as compared to other bonding techniques, such as adhesive.
2.3. Electric Field Simulations
Both models were simulated for a wide range of microchannel dimensions by using the FEM analysis tool. A script file was written that generated 175 different combinations of microchannel dimensions (lch, wch and hch). The ranges of lch, wch and hch were from 100 to 10,000 μm, from 1 to 1000 μm and from 10 to 1000 μm, respectively. The electrodes of 1 mm diameter were positioned at the middle of the access hole, 0.1 mm above the bottom plate in the practical model, and the dimensions of the access holes, electrodes and etch-holes were kept constant for all combinations. Each structure was simulated for a number of excitation voltages ranging from 1 V to 1000 V. The permittivity and conductivity of the buffer fluid were set to εr = 80 and σch = 1.6 S m−1, respectively, to match those of the physiological solution.
The resultant data shows that the mean values of the practical microchannel significantly deviate from those of the ideal model as
lch becomes smaller or
Ach becomes larger. These deviations, resulting in estimation errors if the expressions were derived in the last section for an ideal microchannel are applied for practical microchannels, should be taken under consideration for microfluidic devices involving generation of non-uniform electric fields. This is especially important for small lengths of microchannels, as reported in recent literature [
6,
8,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
30]. Thus, the deviation of the mean values between the ideal and the practical model are of particular interest. To quantify across a range of analysis domain, a metric denoting normalized error (
δdev) is introduced. Subtracting the mean values from the practical model from the ideal model and dividing it by the mean value of the ideal model, the
δdev is calculated. Mathematically:
From the simulation results, the values of
δdev are always positive, which indicates that the expressions of the ideal model are overestimated. This can be rationalized, due to the fact that
Vch is always smaller than
Vapp in practical microchannels, due to parasitics in the reservoir, and the electric field distribution is not uniform throughout the microchannel. As microchannel lengths become smaller, this non-uniformity increases, resulting in the higher value of
δdev.
Table 1 lists the range for 10% and 50% overestimations for various parameters and dimension of the practical microchannels. Estimation errors are critical to achieve high yields of lysate from minute cell samples. In practical applications with minute cell samples, low yield might lead to the inability to obtain DNA fragments required for downstream analysis, which is critical for single-cell analysis.
Table 1.
The overestimation error ranges for a practical microchannels when the expressions for an ideal microchannel are applied.
Table 1.
The overestimation error ranges for a practical microchannels when the expressions for an ideal microchannel are applied.
| Parameter | 10% overestimation range | 50% overestimation range |
|---|
| Ech | lch < 2300 μm | lch < 175 μm |
| Pd | Ach/lch < 0.7 μm2/μm | Ach/lch < 100 μm2/μm |
| uch | lch < 5000 μm | lch < 400 μm |
| Uch | Ach/lch < 0.7 μm2/μm | Ach/lch < 100 μm2/μm |
2.4. Expressions for Error Reduction in Practical Microchannels
An approach to reduce the estimation errors is to determine Vch for the practical microchannel. To calculate Vch, one has to determine the resistance introduced by the access holes that are in series with the microchannel resistance. In this section, two analytical expressions are derived to reduce estimation errors for the electric field. In this analysis, non-uniformity of the electric field distribution inside the microchannel and the capacitive component of the microchannel are neglected, assuming a DC excitation condition and steady state operation.
In this approach, the microchannel resistance (
Rch) is in series with the two resistances of the access holes external to the microchannel (
Rext). Ideal microchannel expressions can be applied for
Vch and
Ech; thus:
where α (
=Rch/2 Rext) is the ratio of channel resistance to total reservoir resistances. For large
lch,
Rch is much larger than
Rext. Hence, for α »1, the resulting Expression (10) will approach the expressions for an ideal microchannel. However, for very small
lch,
Rch is comparable or smaller than
Rext, thus the second term of the Expression (10) becomes significant. In the extreme cases where α « 1,
Ech diminishes to 0.
A second approach to reduce the estimation errors is to compensate for δ
dev. To apply this approach, the
δdev can be approximated as a linear relationship between log(
δdev) and log(
lch), which is motivated through careful observation of the data. Thus:
where
m is the slope of the
δdev curve,
c is a constant and
Eideal is the electric field in ideal model.
3. Experimental Results
As an experimental platform, a microfluidic device was developed to induce electric lysis of biological cells. The experiments were conducted at the Cardiovascular Devices Division, the University of Ottawa Heart Institute, Ottawa, Canada.
3.1. Device Design and Fabrication
The device was designed using the L-edit layout tool (Tanner EDA, CA) and fabricated using the Protolyne fabrication process from Micralyne Inc. (Edmonton, Alberta, Canada). Briefly, the fabricated device consisted of two fused glass slides, with dimensions of 95 mm × 16 mm × 1.1 mm each. Eight predefined access holes (reservoirs) of 2 mm diameter were through-drilled in the top slide. Eight etch-pads of 1.5 mm diameter were etched on the top surface of the bottom slide, such that they align with the access holes. Trenches were also etched on the top surface of the bottom slide, which formed microchannels when both glass slides were fused together. Seven trenches were designed of various lengths ranging from 8 to 17 mm. Here, the length of a microchannel was defined as the intersection of a trench and an access hole. The etch depth, which defined the height of a microchannel, is 20 μm based on fabrication process constraints. The widths of microchannels were 100 μm, a trade-off between free transport of cells and minimized power dissipation. Platinum (Pt) electrodes were inserted inside the access holes for electrical excitation.
3.2. Cell-Sample Preparation
Due to the lack of access to proper cell-lines, human fingerprint samples were used as the cell-sample source. Each fingerprint sample was collected from a finger of an individual on a sterile Petri dish. The fingerprint samples contain dead and damaged cells shredded from the epidermal tissue. To collect these cells from the surface of Petri dishes, 20 μL of physiological solution (Dulbecco’s Phosphate Buffered Saline, D-PBS) was applied. The D-PBS fluid maintains a pH of 7, required to preserve cell samples from osmotic pressure. The micropipette tip was rubbed on the surface of the Petri dish to detach the cell debris from the surface of the dish and to suspend them into the fluid, which was then collected by the micropipette. Average numbers of debris were calculated by overlapping the Petri dish on a 1 mm-square grid under an optical microscope to count the number of debris under each square, then calculating the average of 25 grids. The average number of debris on the surface for a wet fingerprint before the collection was 41.5 per mm2 and after the collection procedure was 21 per mm2, a collection efficiency of about 50%.
3.3. Experimental Procedure
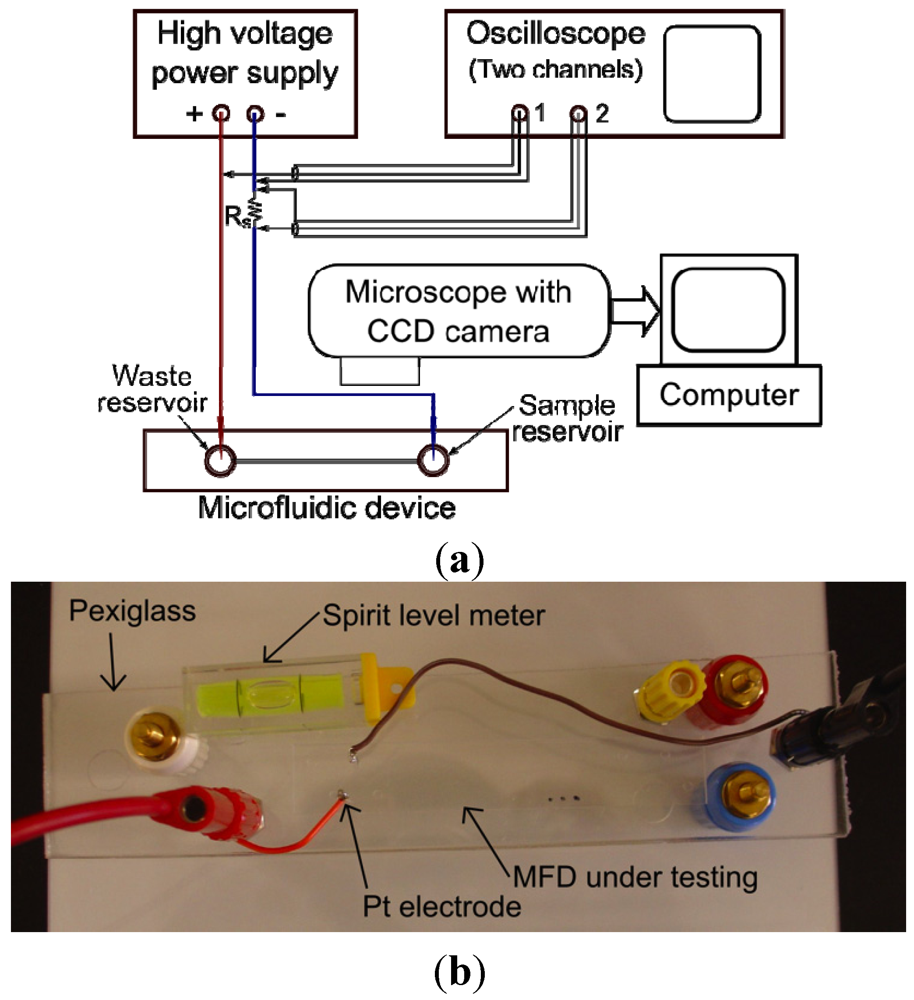
Before each experiment, the microfluidic device was washed with deionized water and dried by blowing warm air. Four microliters of the sample solution were introduced in one access hole, while 4 μL of D-PBS buffer fluid was introduced in an adjacent access hole. A pair of platinum electrodes were introduced in the access holes, and the device was positioned on the stage of an optical microscope (CKX41, Olympus Corp, Westmont, IL, USA) equipped with a CCD (charge-coupled device) camera (Infinity, Lumenera, Ottawa, Canada). The electrode-pair was then connected to a high voltage power supply (FB600, Fisher Scientific, Pittsburgh, PA, USA) and an oscilloscope (Tektronix 2430A, Beaverton, OR, USA) to the electrodes (Channel 1) and across a series resistance,
Rs, (Channel 2), as schematically shown
Figure 2a. Cells migrated through the microchannel when a constant low-electric field gradient was created by applying a voltage of below 200 V through the electrode-pair. When cells were positioned inside the microchannel, the flow was stopped, and a brief high-voltage DC pulse (700 V to 900 V) with a duration up to 9 s was applied through the electrode-pair to lyse the cells. Photographs and video clips (2 fps) were captured through the CCD camera of the optical microscope in phase contrast mode. A photograph of the microfluidic device with electrical connectivity is shown in
Figure 2b.
3.4. Fluorescence Imaging
Some cell-samples were stained to verify the structures of cells in the samples.
Figure 3 shows images of cell debris from a fingerprint sample under optical microscope in phase-contrast mode (a–b) and with staining in bright-field mode (c). The presence of haematoxylin stain indicates the existence of basophilic structures, such as histones, which are present in chromosomes inside the cell nucleus.
Figure 2.
(a) A schematic diagram of the experimental setup of the microfluidic device; (b) a photograph of the experimental setup showing the Pexiglass platform, microfluidic device (MFD), spirit level meter and the electrical connections of the platinum (Pt) electrodes inside the access holes.
Figure 2.
(a) A schematic diagram of the experimental setup of the microfluidic device; (b) a photograph of the experimental setup showing the Pexiglass platform, microfluidic device (MFD), spirit level meter and the electrical connections of the platinum (Pt) electrodes inside the access holes.
Figure 3.
Sample cells from a fingerprint observed under (a) 10X and (b) 40X lens with an optical microscope in phase-contrast mode; (c) stained cell-sample with haematoxylin dye clearly showing the cellular structures.
Figure 3.
Sample cells from a fingerprint observed under (a) 10X and (b) 40X lens with an optical microscope in phase-contrast mode; (c) stained cell-sample with haematoxylin dye clearly showing the cellular structures.
Cells were transported from the source reservoir (access hole) towards the waste reservoir through the microchannel by applying a low electric field created with the application of 100 to 200 V across the microchannel, generating a low electric field of a strength below 25 kV/m. As cells are negatively charged, they experience a force pulling them towards the positive electrodes, due to the combined effect of electrophoresis and electro-osmosis phenomena [
31,
32]. As cells moved inside the microchannel, the applied voltage was withdrawn to position cells inside the microchannel. Such positioning was verified with fluorescent cell marker (Alexa Flour 488 V) and observed under fluorescence microscope. The illuminated cell inside the microchannel, as seen in
Figure 4, verified that the cell was positioned inside the microchannel.
Figure 4.
Cell debris, labeled with Alexa Flour 488 V florescence dye, collected from a fingerprint sample, is positioned inside a microchannel and is observed under a fluorescence microscope. (a) Image of the cell with optical microscope with phase-contrast mode; (b) image of the cell with 488 nm laser in a fluorescence microscope.
Figure 4.
Cell debris, labeled with Alexa Flour 488 V florescence dye, collected from a fingerprint sample, is positioned inside a microchannel and is observed under a fluorescence microscope. (a) Image of the cell with optical microscope with phase-contrast mode; (b) image of the cell with 488 nm laser in a fluorescence microscope.
The electrophoretic movement of cells inside the microchannel was not uniform. It was observed that cells tend to adhere to the channel walls while migrating through the microchannel. Two factors might contribute to this type of behavior. Firstly, the surface of the microchannel contained irregularity at the micrometer scale. These irregularities of the channel surfaces were observed with scanning electron microscope (SEM) images, as shown in
Figure 5. The irregularities might stem from the chemical etching process of the fabrication technology and the orientation of the crystals. Surface irregularities of the channel walls were more pronounced compared to the channel bed. Secondly, the force developed due to the zeta potential, defined as the electrostatic potential generated by accumulation of surface charges along the silica-based channel surfaces [
2], might also contribute to the adherence tendency of the cells. This potential is due to the surface material of the microchannel (silica) and can be alleviated by surface treatment of the microchannel before experiments [
2].
Figure 5.
SEM photographs of (a) a microchannel and (b) an exposed trench (top glass slide removed) detailing the surface topography and roughness of the chemically etched microchannels.
Figure 5.
SEM photographs of (a) a microchannel and (b) an exposed trench (top glass slide removed) detailing the surface topography and roughness of the chemically etched microchannels.
3.5. Single Cell Electrical Lysis Experiments
A high voltage (700 V to 900 V) was applied to induce electrical lysis of biological cells. The developed electric field was higher than 100 kV/m, a typical electric field for electrical lysis of cells [
18,
19,
25].
Figure 6 shows a temporal sequence of microscopic images captured using the CCD camera of the microscope during an electrical lysis experiment. The sample cell inside the microchannel experienced a high electric field (>100 kV/m) and was lysed in about 6.5 s. The cell marked as “a” is completely lysed, whereas the cell marked as “b” is intact, due to the fact that the electric field developed inside the microchannel is high compared to that inside the reservoir. This experiment clearly demonstrates the difference of electric field inside and outside of the microchannel, which cannot be simply calculated using the electric field Expression (2).
Figure 6.
Temporal sequence of images of electrical lysis of a single sample cell under a high electric field inside a microchannel captured using an optical microscope. Here, (a) is a sample cell inside the microchannel, (b) is a cell inside the reservoir, (c) is the boundary of the reservoir on the top glass slide, (d) is the edge of the microchannel and (e) is the boundary of the etching on the bottom glass slide. Eight-hundred volts are applied to the microchannel of 9 mm length. The cell is observed to disappear between 6 and 6.5 s.
Figure 6.
Temporal sequence of images of electrical lysis of a single sample cell under a high electric field inside a microchannel captured using an optical microscope. Here, (a) is a sample cell inside the microchannel, (b) is a cell inside the reservoir, (c) is the boundary of the reservoir on the top glass slide, (d) is the edge of the microchannel and (e) is the boundary of the etching on the bottom glass slide. Eight-hundred volts are applied to the microchannel of 9 mm length. The cell is observed to disappear between 6 and 6.5 s.
Careful observation of the temporal sequence of photographs in
Figure 6 indicates that there was a gradual decrease of the contrast in the images of the sample cell “a” between 5 to 6 s. A logical deduction and explanation is that the electroporation phenomenon [
31,
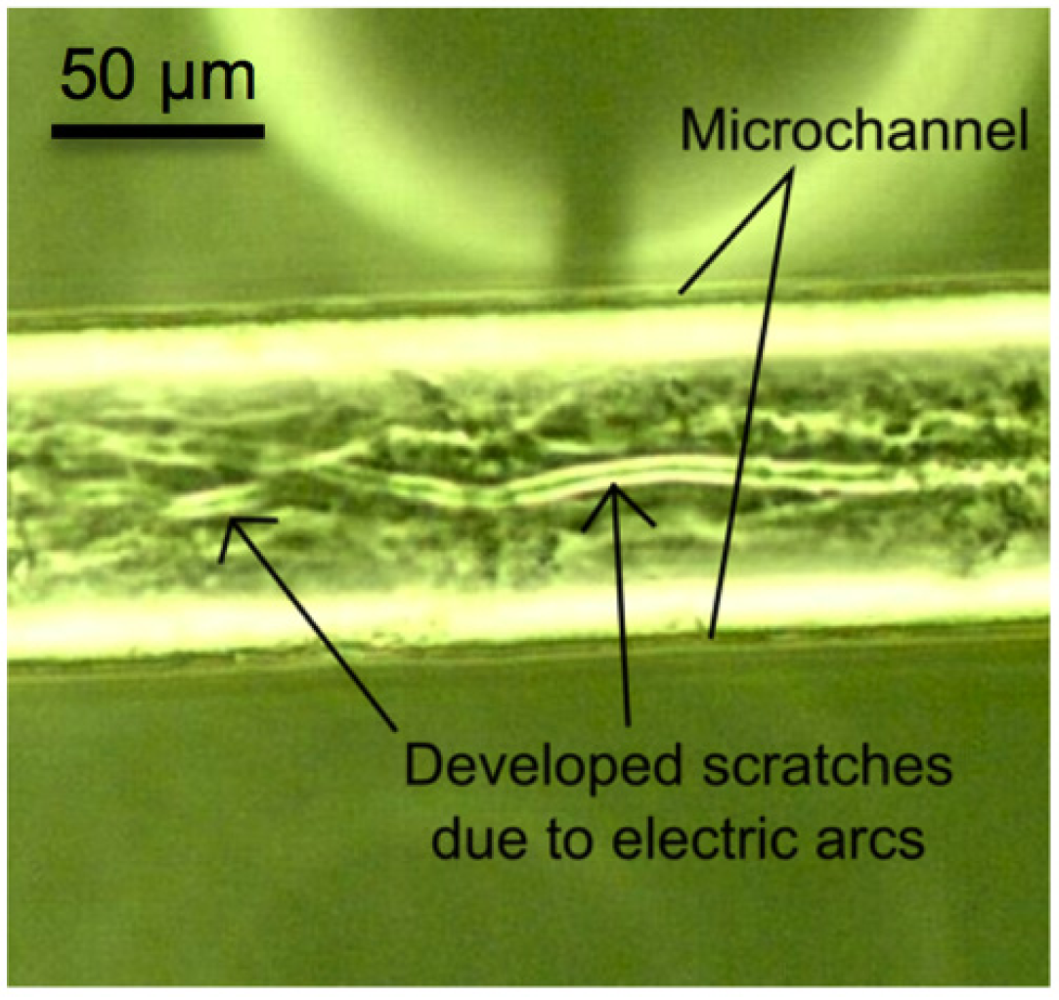
32], expected to occur just prior to cell lysis, had caused a reduction of the refractive index difference inside and outside of the cell. The duration of the electroporation was less than 1 s. A very high-applied voltage (>1500 V) resulted in bubble formation through breakdown of the water molecules and produced electric arcs that etched the inner surface of the microchannel, as can be observed in
Figure 7. The summaries of data obtained from the experiments of various related parameters are given in
Table 2,
Table 3.
Figure 7.
An optical microscope image of a microchannel showing damage of the microchannel surface from electric arcs generated with an applied voltage of 1800 V (electric field over 225 kV/m).
Figure 7.
An optical microscope image of a microchannel showing damage of the microchannel surface from electric arcs generated with an applied voltage of 1800 V (electric field over 225 kV/m).
Table 2.
Key observations with various electric field strengths.
Table 2.
Key observations with various electric field strengths.
| Electric field ranges | Observations |
|---|
| Below 100 kV/m | Cell movement observed |
| Between 100 to 200 kV/m | Electrical lysis observed |
| Above 200 kV/m | Bubble formation and electric arcs inside microchannels |
Table 3.
Results from electrical lysis experiments.
Table 3.
Results from electrical lysis experiments.
| Parameter | Value |
|---|
| Applied potential | Between 700 to 900 V |
| Pulse duration | 7 ± 2 s |
| Current flow | ~0.5 mA |
| Power dissipation | <300 mW |
4. Conclusions
Electric fields are commonly used in microfluidic devices and LOCs to stimulate, manipulate and analyze biological elements. The macro-scale approximation of electric field expression is still in use. Microscale electric field distribution, however, deviates from this estimation, due to the highly non-linear nature of the distribution pattern. In this work, we have conducted an analysis of electric fields inside the microchannels of an ideal and a practical model. Furthermore, analytical expressions were developed for the practical model to reduce the estimation error. FEM simulations, however, do not account for various factors, such as EDL, localized fluidic flow and vortex due to electrophoresis, thermal and electrical resistivity change due to Joule heating; these lead to new scopes of the refinement of this work.
The experiment shows a mechanism for single cell lysis with electric fields. A sample cell was lysed inside the microchannel of the microfluidic device by applying a high voltage (700 V to 900 V). The time required for lysis and corresponding power consumption were 7 ± 2 s and <300 mW, respectively. These results show promise for biological studies and experimentation of single cells with microfluidics and LOC technology that uses electrical lysis inside the microchannel environment to analyze single cell contents or sample preparation that combines with other on-chip biological processes downstream.
 , where
, where  is the external electrical potential [11]. The Poisson-Boltzmann equation is employed to govern the electric potential near the channel wall and in the bulk:
is the external electrical potential [11]. The Poisson-Boltzmann equation is employed to govern the electric potential near the channel wall and in the bulk:
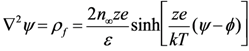
 is the electrical potential,
is the electrical potential,  is the free charge density,
is the free charge density,  is the bulk concentration of the ions,
is the bulk concentration of the ions,  is the ionic valence,
is the ionic valence,  is the elementary charge,
is the elementary charge,  is the dielectric constant of the medium,
is the dielectric constant of the medium,  is the Boltzmann constant and
is the Boltzmann constant and  is the temperature. The electric field distribution inside the microchannel can be estimated by the Poisson equation, which, for the case of uniform electric charge density in a linear, isotropic and homogeneous medium, becomes:
is the temperature. The electric field distribution inside the microchannel can be estimated by the Poisson equation, which, for the case of uniform electric charge density in a linear, isotropic and homogeneous medium, becomes: