1. Introduction
The dense-flowered cordgrass (
Spartina densiflora Brongn.) is a perennial grass native from salt marshes in the Atlantic coast of South America. It has been accidentally introduced in areas of North America (California and Washington), Europe (Gulf of Cadiz, southwestern Iberian Peninsula) and North Africa (Morocco) where it behaves as an aggressive invader [
1]. This cordgrass shows a strong adaptability to environmental conditions, being able to invade a variety of habitats from low unvegetated tidal flats [
2] to high topographic elevations in marshes [
1]. It grows in dense clumps and represents an extraordinary competitor for native marsh plant species. It can grow in almost mono-specific stands, which simplifies the ecosystem, reducing the richness and diversity of the marsh community [
3].
S. densiflora grows in the Gulf of Cadiz showing some of the highest net primary productivity values recorded for the species [
4,
5], as a proof of its ecological success here.
Currently,
S. densiflora has expanded along the southern Atlantic coast of the Iberian Peninsula from the Algarve in Portugal to Algeciras Bay (bay of Gibraltar) in Spain, perhaps accidentally introduced to Europe by the lumber trade between South America and Spain in the 16th century [
2]. In Doñana National Park, the species has a reduced distribution along the shores of the Guadalquivir River and the banks of some drainage channels. This is due to the “Montaña del Río” dike, an artificial 14-km silt levee that separates the marshes from the Guadalquivir River estuary limiting its expansion farther into the park. Salt-marsh restoration projects in Doñana surroundings have shown that the species can successfully invade if adequate ecological conditions exist [
6]. For this reason, it is important to be able to monitor
S. densiflora distribution so that adequate eradication measures can be taken before it is too late.
Initiating invasive species control at the beginning of an invasion may be critical for successful eradication of the invaders [
7,
8]. The evaluation of different techniques to control and eradicate
S. densiflora has revealed the difficulty of eliminating the species once established [
9], which gives priority toward early detection, as a management tool, in order to act promptly in case of invasion. The doctrine of early detection and rapid response to invasions has been adopted by land and water resource managers, and remote sensing could be the most cost-effective tool for detection [
10,
11,
12]. Therefore, it is essential to establish a system of early prevention, to control the spread of alien species and eradicate them. Remote sensing could facilitate this work, as it can cover large areas like marshes that are difficult to survey on the ground.
Compared to minerals, spectral separability of plants at the species level presents unique challenges. Reflectance spectra of plants in the visible wavelengths are mainly determined by the concentration of different pigments present in all species: chlorophylls a and b and carotenoids, while in the near infrared they are mainly influenced by the disposition of air spaces in the leaf structure [
13]. In addition, there is spectral variability within species and there is seasonal variation in aspects that influence reflectance spectra, like pigment concentration and leaf area index. This can be a limitation, or can be used for species identification by using the differences among species in temporal changes of spectral signatures [
14]. In spite of these shortcomings, remote sensing has proved to be a cost-effective tool for studies on vegetation distribution [
15,
16], and in particular, for the detection and mapping of invasive species [
10,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28]. Some studies have used low spatial resolution images such as Landsat TM [
14] or Hyperion [
25,
29]. However, in the initial stages vegetation patches of invasive species can be small and difficult to detect with medium resolution satellite sensors [
30]. So currently, high spatial resolution images from satellite or airborne sensors are needed for early detection [
23,
24].
Analysis of hyperspectral images taken from airborne sensors is complex and there are no easy well tested protocols for invasive species detections. There are a variety of hyperspectral sensors that have been tested with invasive species: like AVIRIS [
19,
20], CASI [
31,
32,
33,
34], Probe-1 [
21,
22], Hymap [
10,
26,
28,
35], SOC-700 [
23], and PHILLS II [
24]. Images need to be corrected for geometric and atmospheric effects [
23,
24,
35]. Numerous classification and detection algorithms have been used including supervised and unsupervised classification techniques [
27], spectral linear unmixing [
24], classification and regression trees [
22,
26], spectral angle mapper [
20,
36], neural networks [
33], and matched filters [
28]. It is common to perform data reduction techniques like Principal Component Analysis (PCA) or Minimum Noise Fraction (MNF) on the band raw data [
19,
24,
25], to work with band indexes, or with a certain selection of bands. Success is variable depending not only on the species but on the mixture of other species present [
26]. All this probably precludes a more extensive operational use of hyperspectral remote sensing for invasive species monitoring by environmental managers.
We wanted to test if it was possible to detect
S. densiflora with hyperspectral sensors in the marshes of Doñana National Park using relatively easy and fast processing techniques that could be used operationally for early detection and monitoring of the invasion progress. For that purpose, we planned to reduce data processing to the minimum and work with raw radiance images without data reduction techniques. Atmospheric correction is not essential for target discrimination if training spectra are taken from the image using ground-truth locations [
25]. We flew in tandem two airborne hyperspectral sensors: CASI-1500, which had already been used for invasive species detection [
31,
32,
33,
34,
37] and AHS, which has not been tested for that purpose, although it has proved successful for plant species discrimination [
38]. Being flown in tandem, atmospheric influence is similar on the spectra recorded by both sensors and atmospheric correction can be avoided if we want to compare target discrimination ability. We tested the comparative success of several spectral target detection techniques that are integrated in ENVI version 4.6.1. (Exelis Visual Information Solutions, Boulder, Colorado) Target Detection Wizard that guides step by step the user in the detection of the targets of interest [
39] and that can be easily applied by non-specialists in remote sensing.
5. Discussion
Our results show it is possible to accurately map the distribution of
S. densiflora in the Guadalquivir River marshes using airborne hyperspectral sensors. The results obtained were very promising using at-sensor radiance images and radiance spectra extracted from field delineated targets, without the need of an atmospheric correction or the use of data reduction techniques like the Minimum Noise Fraction transformation [
26,
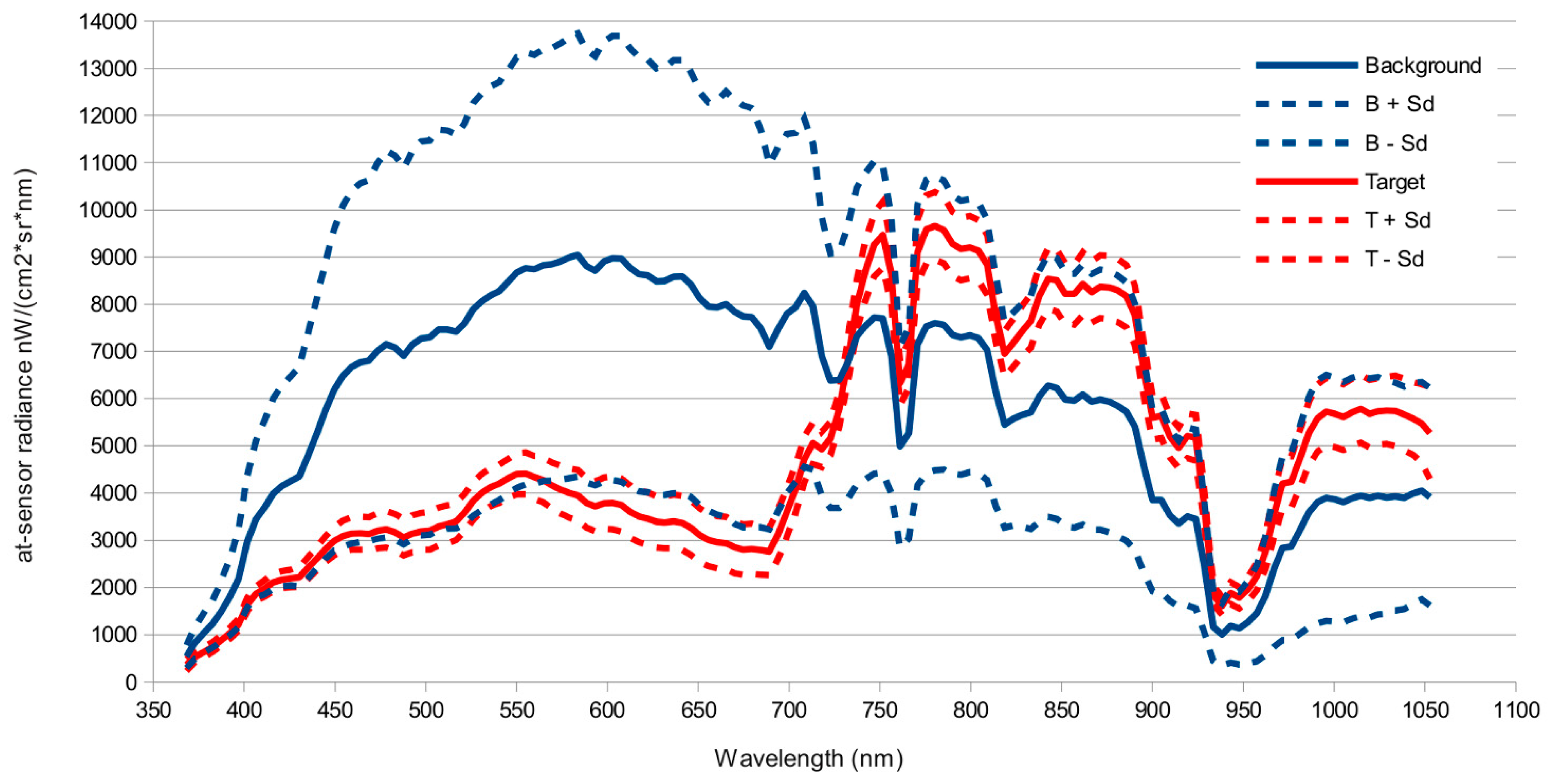
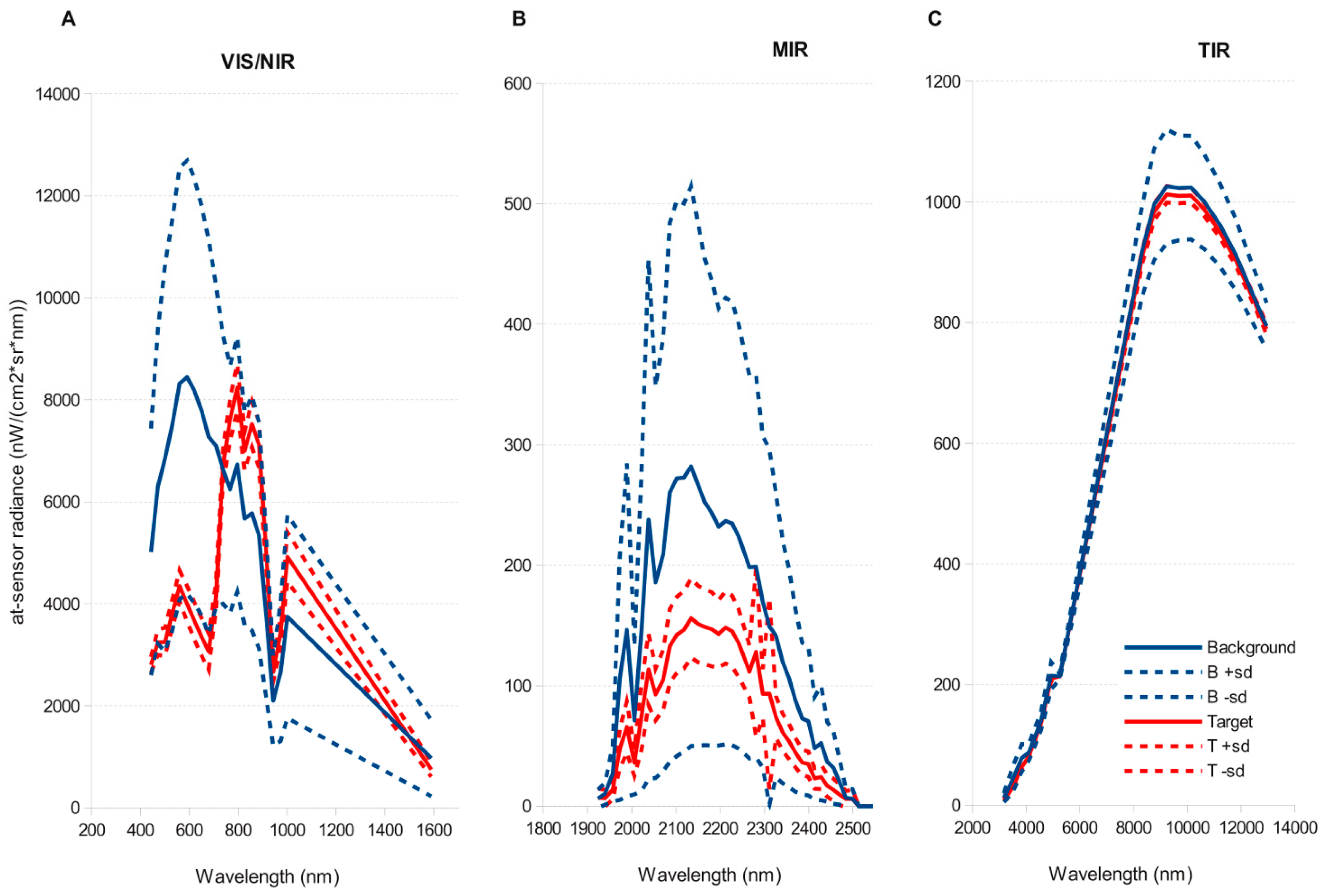
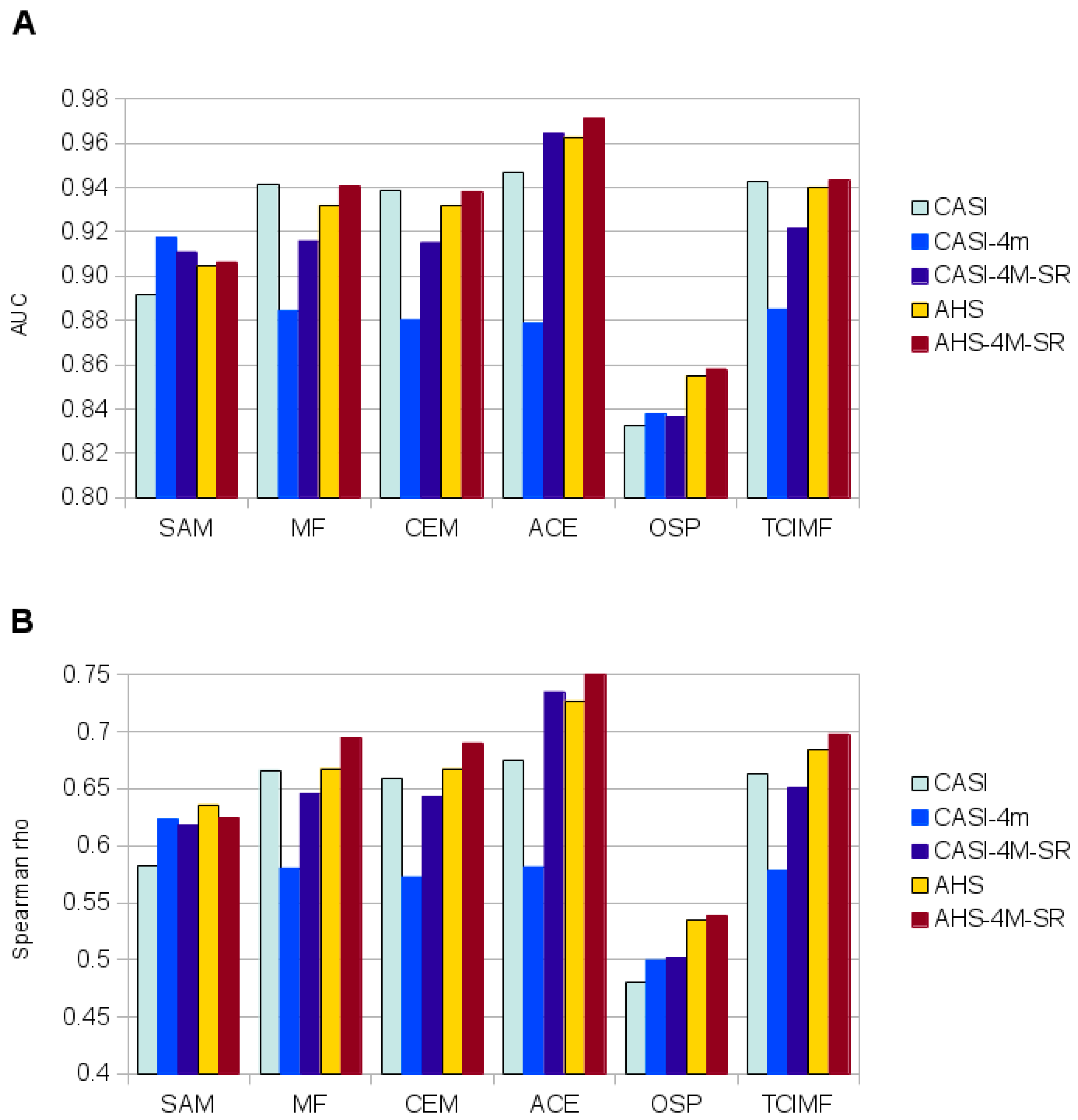
51]. This simplification halved computation time of detection models. Atmospheric correction and Minimum Noise Fraction Transformation only significantly improved detection for those algorithms that performed worse (SAM, OSP) on the original images, but did not improved predictions for the methods that performed best (ACE, TCIMF, MF or CEM). Both sensors tested, and most of the target detection models, gave reasonable to good results, although AHS sensor clearly outperformed CASI. The results indicated also significant effect of spatial resolution and spectral resolution. While higher spatial resolution seemed to be better, spectral resolution had the opposite effect and a reduced number of wider bands in the VNIR had a better performance than original images.
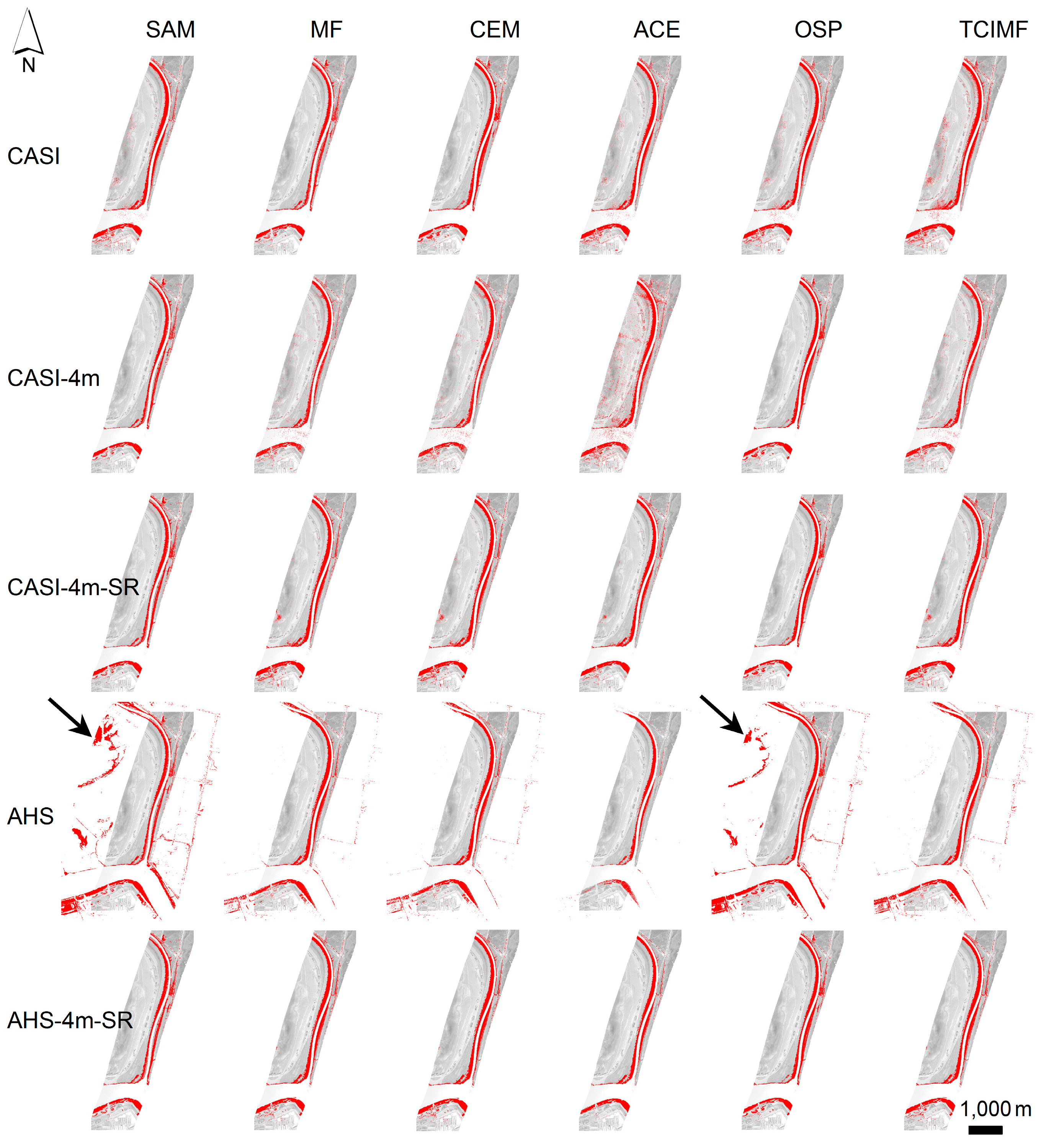
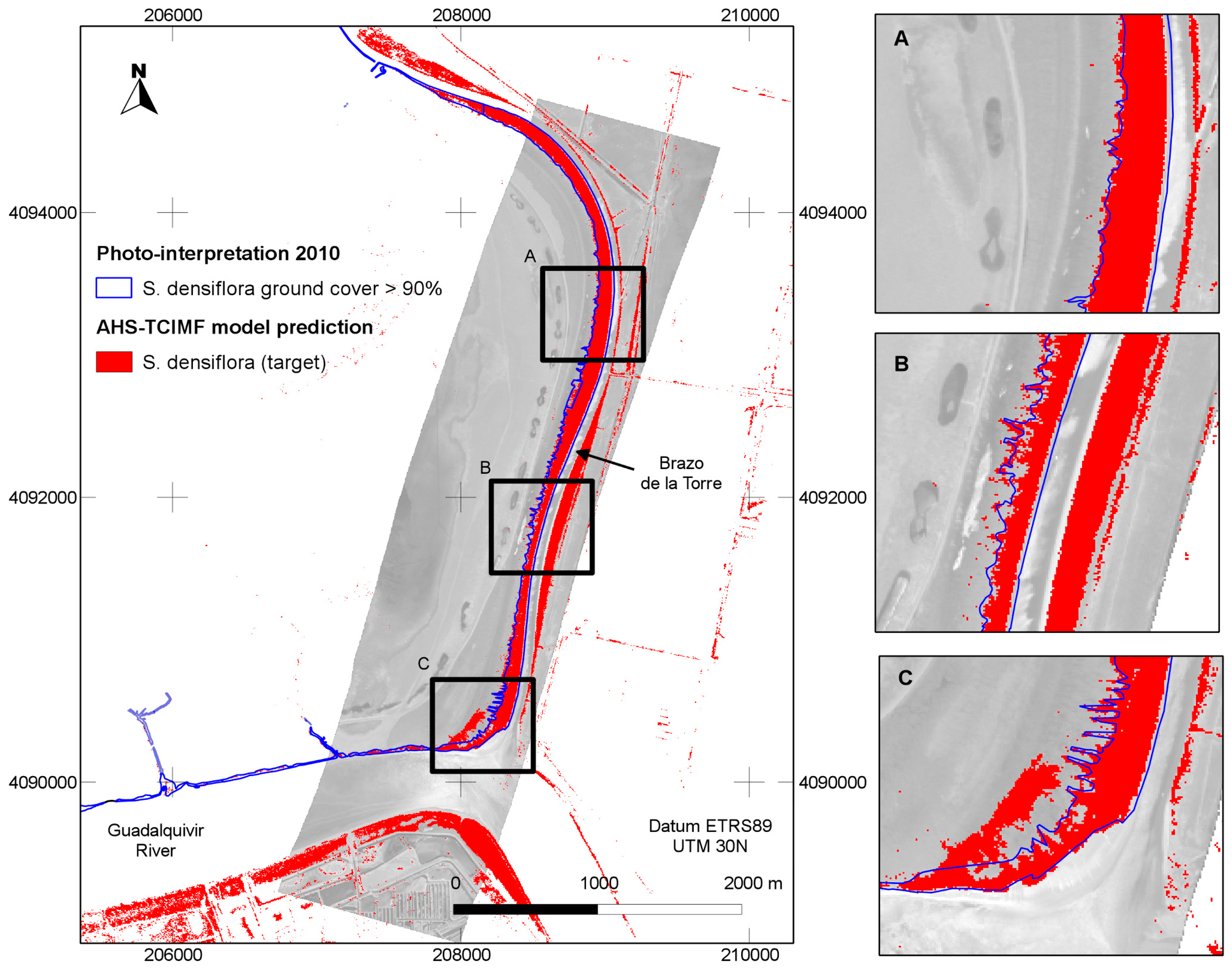
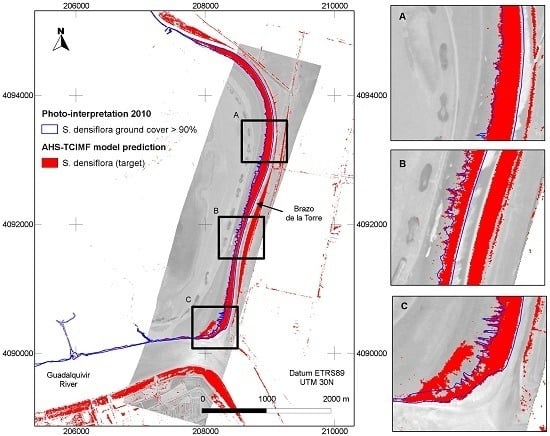
The general predictions of the spatial distribution of
S. densiflora in the study area (
Figure 5) tended to agree well with our previous knowledge of the species distribution, and was also in agreement with a previous photo interpretation of the study area (
Figure 6). The CASI image had a higher spatial and spectral resolution in the visible range, and a higher number of spectral bands, but this did not result in a clear discrimination advantage for the target of interest. The large dense monospecific stands of
S. densiflora that dominate the banks of the river result in less mixed pixels so the 4 m pixel of AHS could also help in classification accuracy [
66] but the decline in accuracy of CASI when resampled at 4 m suggest this is not the main factor. The AHS has a wider spectral range covering the VIS-NIR, SWIR, MIR and TIR parts of the spectrum that provides more dimensionality to discriminate target from background. This wider spectral range does not explain the better performance of AHS, because an image with the first 20 bands in the VNIR range performed slightly better than the original image with 79 bands. The better signal to noise ratio (SNR) in the AHS sensor is probably the explanation for the better performance of this sensor. The empirical mean SNR of the CASI sensor in our flight was 91.21 nW/(cm²·sr·nm), (range 4.36–184.46) versus a SNR of 246.76 (range 0.29–914.34) of the VIS-MIR channels of the AHS sensor. Detection errors caused by noise would also explain why CASI detection improves with spectral resampling. Belluco et al. [
51] indicate that in marshes spatial resolution is more important than spectral resolution, but against the expectation, the higher spatial resolution of the CASI sensor did not result in an advantage when compared with the AHS. At the same time, the higher spatial resolution of the CASI image is an advantage by itself as can be seen by the reduction in performance of CASI when resampled to the coarser resolution of AHS (
Table 5). This is also apparent in the GLM model (
Table 6) that indicates that a higher spatial resolution improves prediction.
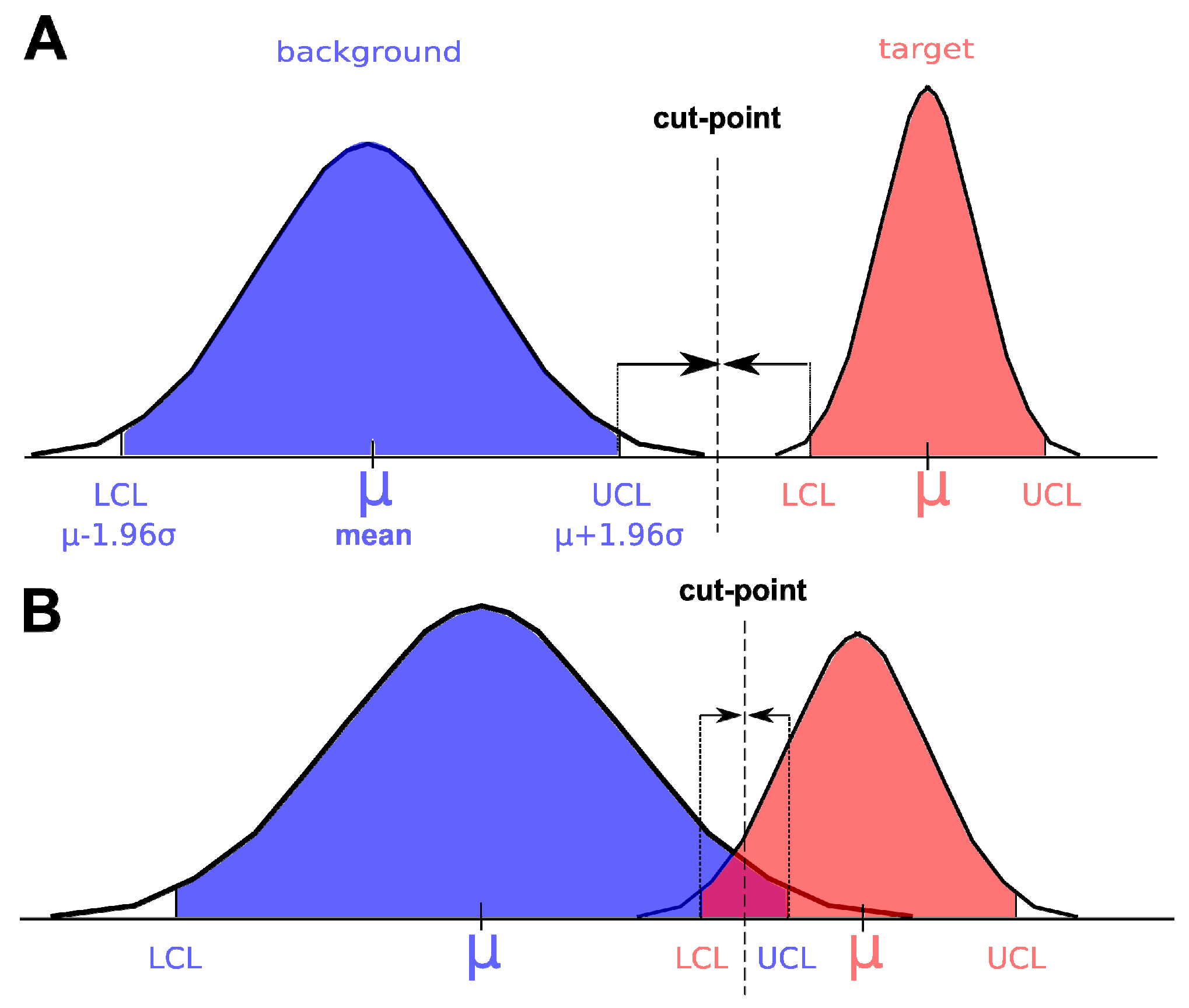
The different spectral target detection algorithms tested gave, in general, similar good results. In our case ACE outperformed the rest both with the CASI and the AHS images at the field evaluation site. This was a stronger test for the models because they were tested at a different area, target cover data were recorded in a semi-quantitative scale, evaluation points were sampled in areas where
S. densiflora could grow, and models tended to differ in prediction. With the test polygons (validation) four methods (ACE, TCIMF, MF and CEM) gave a perfect discrimination on the AHS image, and almost perfect (AUC = 0.9999) on the CASI image. Three methods (TCIMF, MF and CEM) gave almost identical results for each pixel (
Figure 7), suggesting that, in our setting, although algorithms differ their predictions cannot be distinguished. The OSP and the SAM algorithms were the ones that performed worse for both sensors, both with test polygons (validation) and at the new field evaluation site. They were also the ones that benefited from an atmospheric correction and MNF transformation. In addition, the classified images of OSP and SAM algorithms on the AHS image indicated the presence of
S. densiflora stands in areas where the species is not present like the shores of the “Lucio de los Ansares” (
Figure 5), suggesting that some models could perform poorly if extrapolated to other areas. However, on the other hand, the SAM algorithm showed a high correlation with
S. densiflora coverage at the field evaluation site (
Figure 8B) and a more gradual response in AUC values with the increase in
S. densiflora ground-cover (
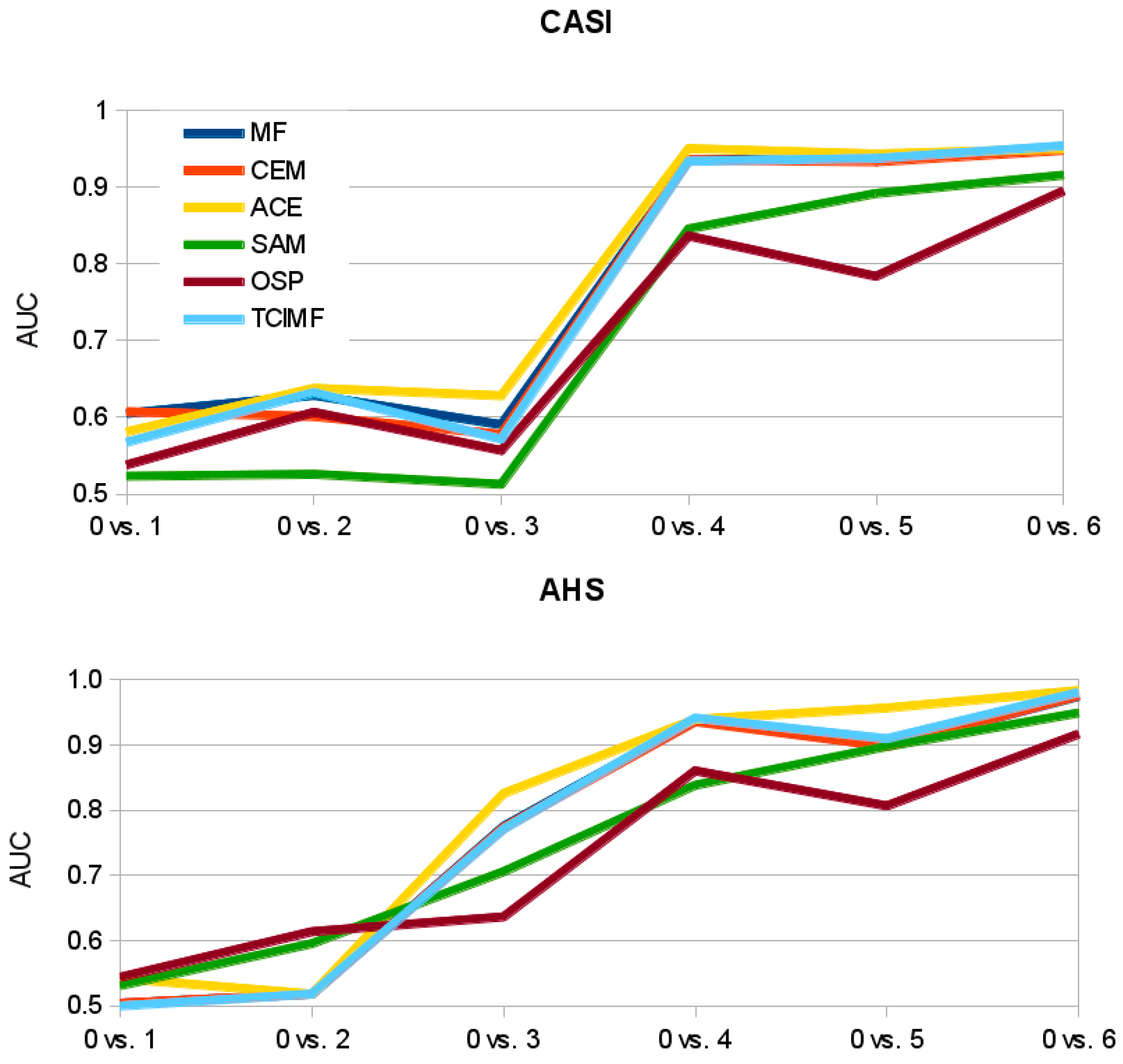
Figure 9). Other algorithms like ACE and TCIMF show a sharper step in the increase in AUC with increase in ground-cover (
Figure 9). This suggests that SAM might outperform the other algorithms when the aim is coverage estimation instead of target detection.
The high target detection accuracy showed by our results should be taken with caution, as it is based on a single date and a relatively small study site. The methods should be tested on a larger area and with a wider range of vegetation communities before using them operationally.
In this study, we have obtained a greater accuracy in the detection of
S. densiflora stands than in the single previous work we know in which hyperspectral sensors have been used for the identification of the species in salt-marshes. Judd et al. [
24] flew the PHILLS II hyperspectral sensor (421–966 nm, with 112 bands 4.5 nm wide) at a ground resolution of 4 m in Humboldt Bay, Northern California, obtaining a correct classification rate of 85.1% (Kappa = 0.762) for three dominant plant species (
Salicornia virginica,
Ditichlis spicata, and
S. densiflora). For
S. densiflora in this study they obtained reasonable omission errors (7.1%) but high commission errors (31.6%). Our best result with the TCIMF detection algorithm and AHS sensor has a 100% correct classification rate (Kappa = 1). If we consider our results using a hyperspectral sensor more similar to the PHILLS II, the CASI (360–1052 nm, 144 bands 2.5 nm wide), and at the same spatial resolution, 4 m, our results are still much better (omission error = 2.06%, commission error = 2.39%, Kappa = 0.965, correct classification rate = 98.38%). It is difficult to compare our results with previous work on species detection with hyperspectral sensors, because the aims of the studies, the species of interest, the habitats, the sensors used, the modeling methods, and even the way of reporting results vary greatly among studies. Previous plant classification studies with hyperspectral sensors in wetlands give correct classification rates ranging from 65% for vegetation communities in the Everglades, Florida [
20], 93% for
Egeria densa detection at local sites in the Sacramento-San Joaquin Delta [
35] up to 99.2% for salt-marsh communities at San Felice marsh at the Lagoon of Venice, Italy [
67].But at the same time, a single invasive species
Colubrina asiatica gave 100% correct classification rates in the same study in the Everglades [
20], and
Egeria densa was poorly detected when models were extrapolated to the coarse scale of the whole Sacramento-San Joaquin Delta (29% correct classification rate) [
35]. It has been shown that many factors influence plant species detection with hyperspectral sensors that are due not only to the plant species spectral characteristics and the study design but also the environmental context like species, structural and landscape diversity of the site [
26]. For this reason, although our results were very good in detecting
S. densiflora it still needs to be tested if our models can be extrapolated to the whole Doñana marshes with similar success.
One of the aims of our study was to test if species detection with hyperspectral sensors could be employed operationally, using methods that can be readily available for non-experts in remote sensing data analysis. Our results are encouraging because we were able to get almost 100% discrimination of
S. densiflora without the need of an atmospheric correction or data reduction techniques, just working with raw band data. The models cannot be directly extrapolated to other hyperspectral sensors, other dates, or other areas flown with different atmospheric conditions. However, some of the methods are easy to employ operationally as they only require the identification of a few
S. densiflora populations present in the image, information usually available to park managers, to extract a few training spectra. These methods could be tested in hyperspectral satellite images (Chris PROBA, Hyperion) as this would facilitate and reduce costs of regular monitoring of
S. densiflora distribution. All the spectral detection methods employed are implemented in the “Target Detection Wizard” in ENVI [
39], so they can be used with little training by a technician. Our results also indicate that AHS is a hyperspectral sensor that, although has a limited spectral resolution in the visible and near infrared and has received limited attention for vegetation mapping [
38,
57], can be successfully used for plant species discrimination. Our results also indicate that spectral detection techniques deriving from statistical signal processing like CEM, ACE, OSP and TCIMF [
53] that have received limited attention in the literature of vegetation classification with remote sensing are methods that can give similar or better results to those currently employed like SAM.