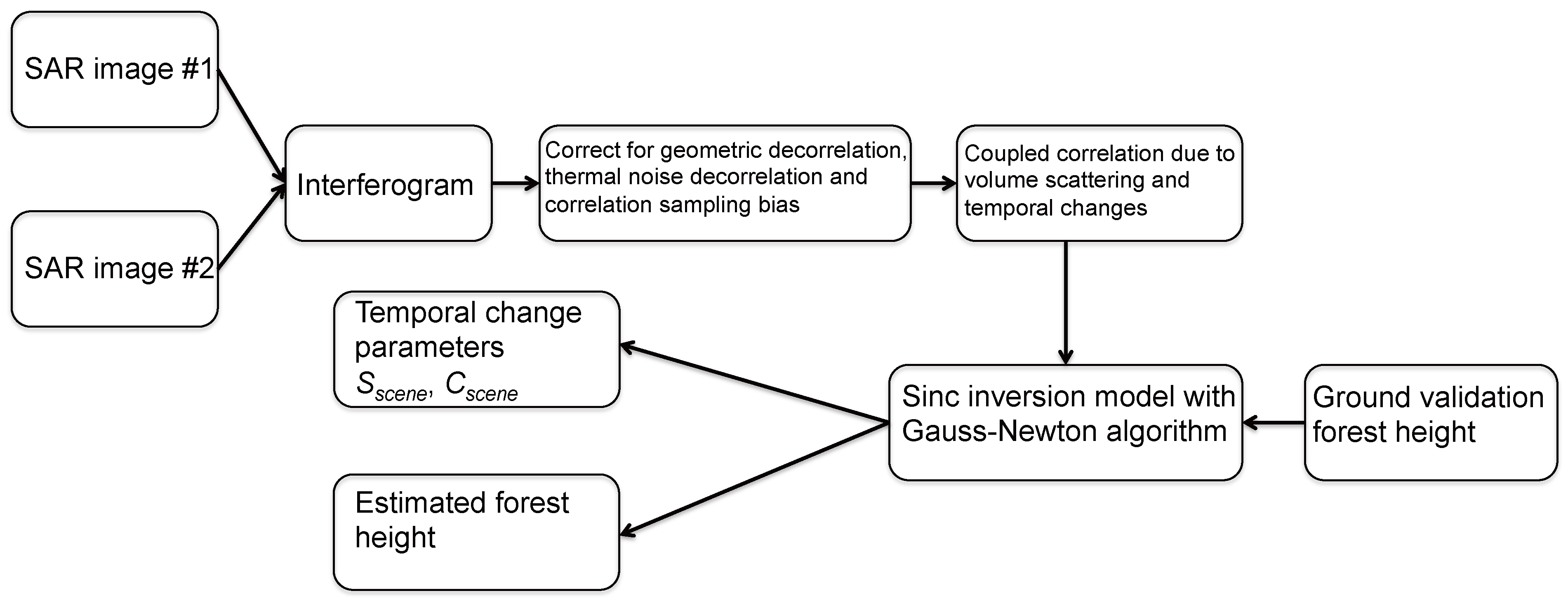
Appendix A. The Assumption of Constant Temporal Change Parameters and Forest Backscatter Profile/Extinction Coefficient
In
Section 2 of this work, a distinction is made between the modified RVoG (
i.e., Equation (1)) and those of previous works (e.g., [
6,
8,
9,
13]). Here, in Equation (1), although the parameters of temporal change effects (
i.e.,
γdv,
γdg and
σr) tend to be spatially varying (
i.e., target-dependent), it is assumed that they follow some scene-wide mean behavior (and thus are constant) for all of the targets in an interferogram (
i.e., InSAR “scene”), which implies that both the dielectric change and the wind-induced motion level are uniform. This is different from the target-dependent effect of temporal decorrelation in [
4,
5,
6,
13], where the height-dependent term in
γv&m was not introduced, and the wind-induced motion was included in the variable,
γdv. The effect of this difference is that the temporal correlation coefficient becomes biased, and is a target (e.g., height) -dependent estimator.
Noting the above difference, in this work, both the height-dependent and -independent terms are considered with the target-varying parameters set to be constant values, which will have the effect of increasing estimation error with the benefit of employing a simplified model that can be applied scene-wide as shown in
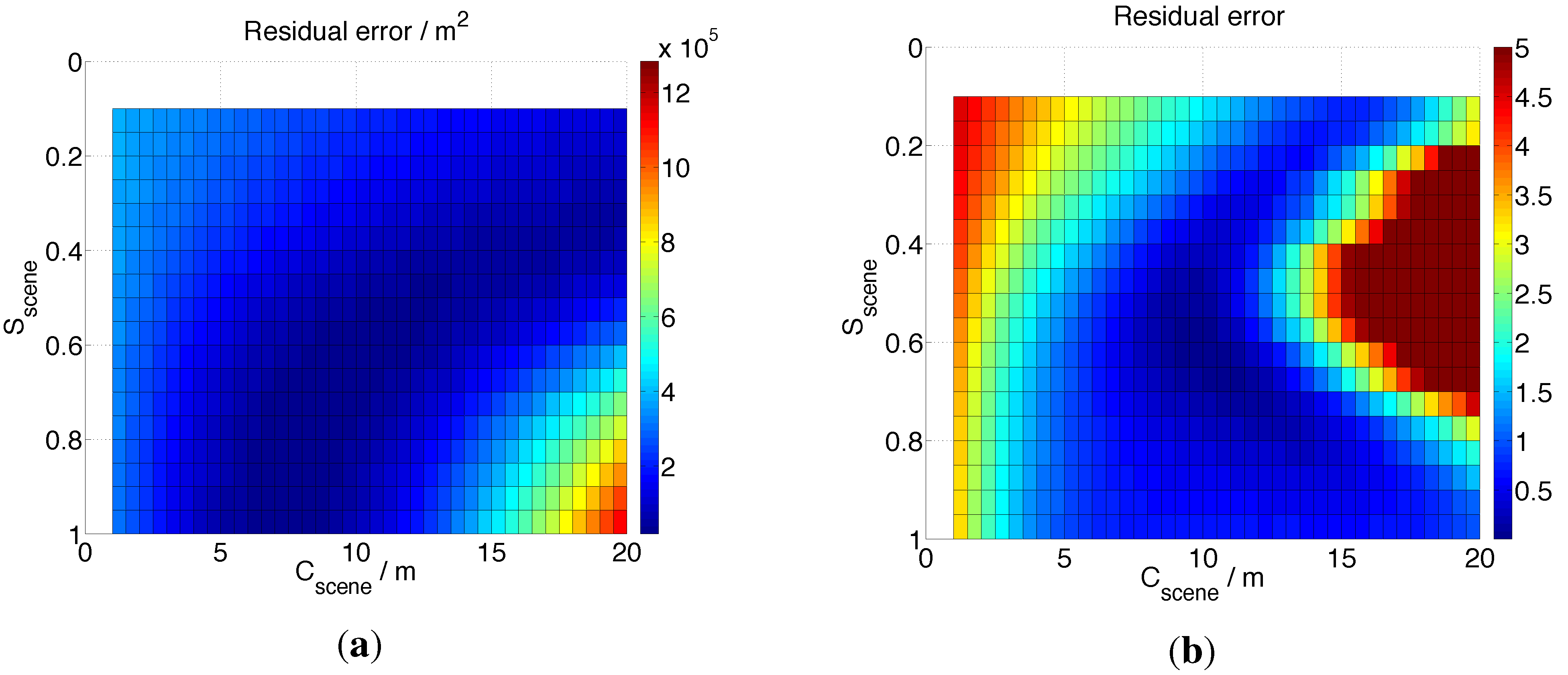
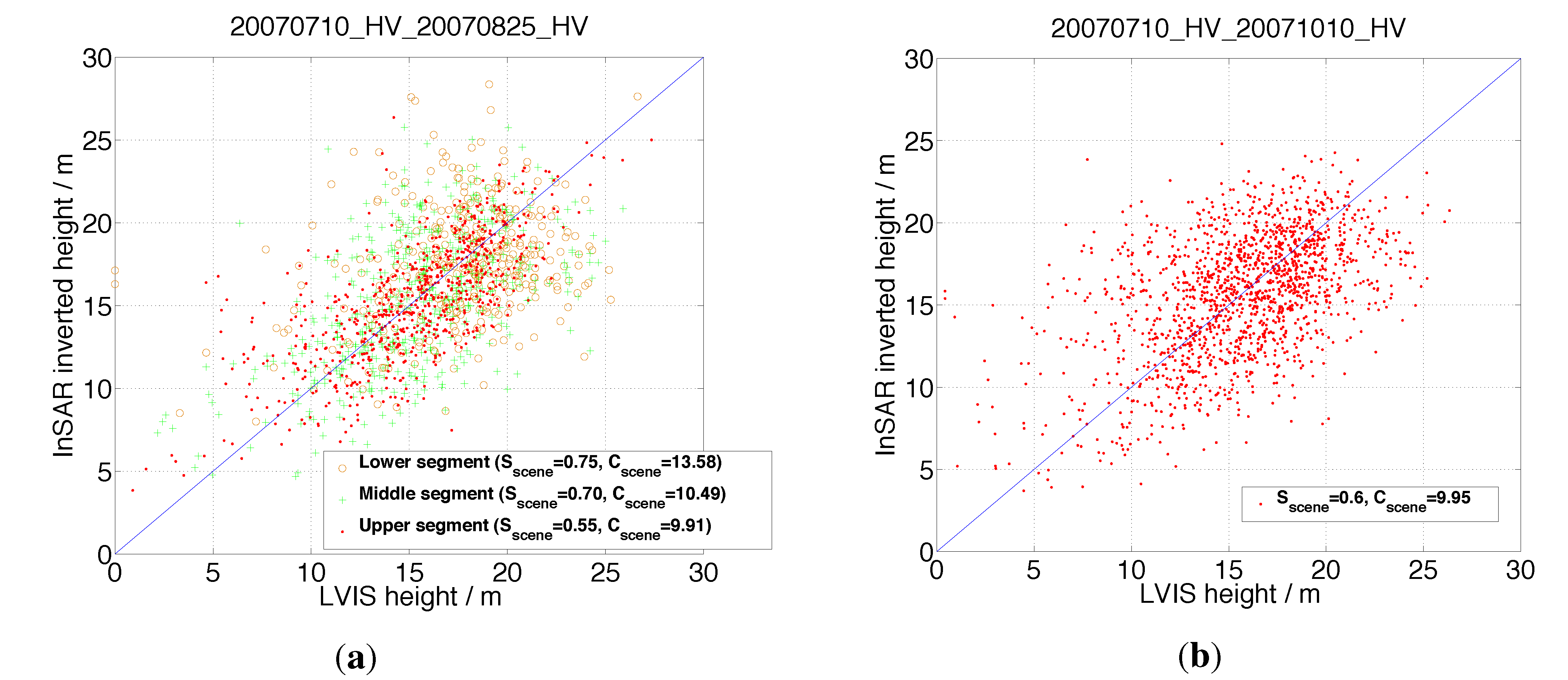
Section 5. The target-dependence of these parameters across a scene leads to RMSE < 4 m in the forest height estimation. Note importantly, this assumption only works under the conditions that the temporal decorrelation does not exhibit a spatially-varying gradient across the scene. When the temporal decorrelation has a strong gradient across the scene (e.g., see
Figure 8a; primarily caused by nonuniform precipitation), the scene can be broken into smaller component parts, and in so much as ancillary measures of forest heights are available, these variations can be accounted for. In the case that the spatial variation of the model parameters is not desired, different time periods for the observations (with no precipitation occurring) can be chosen (as in
Figure 8b).
To provide more insight into the temporal decorrelation gradient observed in
Figure 8a, a comparison can be made with ancillary observations of precipitation data that were collected from NOAA’s National Climate Data Center (NCDC; [
20]) during the time period of the satellite passes. For the inversion shown in
Figure 8a, it can be seen that the “upper” (
i.e., northern) segment has smaller values of
Sscene and
Cscene than the “lower” (
i.e., southern) portion. This implies that the weather conditions over the northern region were changing more compared to the southern region during the repeat period 07/10/2007–08/25/2007. These results were compared to the inversion shown in
Figure 8b which used observations from 07/10/2007–10/10/2007, and can be characterized by a single set of temporal change parameters, implying that the weather conditions were uniform over the region.
In
Figure 5, the locations of two climate observing stations (marked as “North Station” and “South Station”) in central Maine are shown. The precipitation data associated with these two stations in July, August and October 2007 are given in
Figure 14. The collection dates of the interferograms are indicated by vertical dashed lines. For interferogram 07/10/2007–08/25/2007, it can be seen that the precipitation for both north and south stations are similar on 07/10/2007, while the north station recorded a heavier rainfall on 08/25/2007 than the south station. In contrast, for interferogram 07/10/2007–10/10/2007, both north and south stations experienced similar level of precipitation on 07/10/2007 and 10/10/2007, hence providing evidence for the source of the temporal decorrelation gradient observed in
Figure 8a, and not observed in
Figure 8b.
An alternative way to look at this homogeneity issue while performing the mosaicking task is through the overlapping regions from adjacent interferometric estimates of forest height. When there is a spatially-varying feature of the temporal change effects across the region, large errors are occurring and scenes should be replaced with alternate or new observations.
Another assumption that is made in enforcing a constant value for the parameter
Cscene in deriving Equation (10) is that, all of the forests with different height values across the given scene have the scaled versions of extinction-weighted backscattering profile and height-dependent motion profile. To examine this assumption in more detail, the reader is referred to
Figure 15 where a short forest stand of height
h1 and a taller forest stand with height
h2 (
h2 =
c · h1, where
c is a scaling constant) are shown. Denoting the Gaussian motion profile in Equation (8) as,
ρr(
z), the mean-value theorem can be applied to Equation (8) for
h1 and
h2 such that
Mathematically, the choice of the mean value ξ depends on the functional forms of both σV(z) and ρr(z). By using a change of variables, it can be shown that if and then ξ2 = c · ξ1 or equivalently . That is, when the extinction-weighted backscattering profile and the height-dependent motion profile of different forest stands are scaled versions of each other, the proportionality of the mean value with respect to the forest height is the same for all of the forest stands.
Figure 14.
Precipitation data from NOAA’s National Climate Data Center in July, August and October 2007. The data was recorded at both north and south stations in central Maine. The collection dates of the corresponding interferograms are indicated by dashed lines.
Figure 14.
Precipitation data from NOAA’s National Climate Data Center in July, August and October 2007. The data was recorded at both north and south stations in central Maine. The collection dates of the corresponding interferograms are indicated by dashed lines.
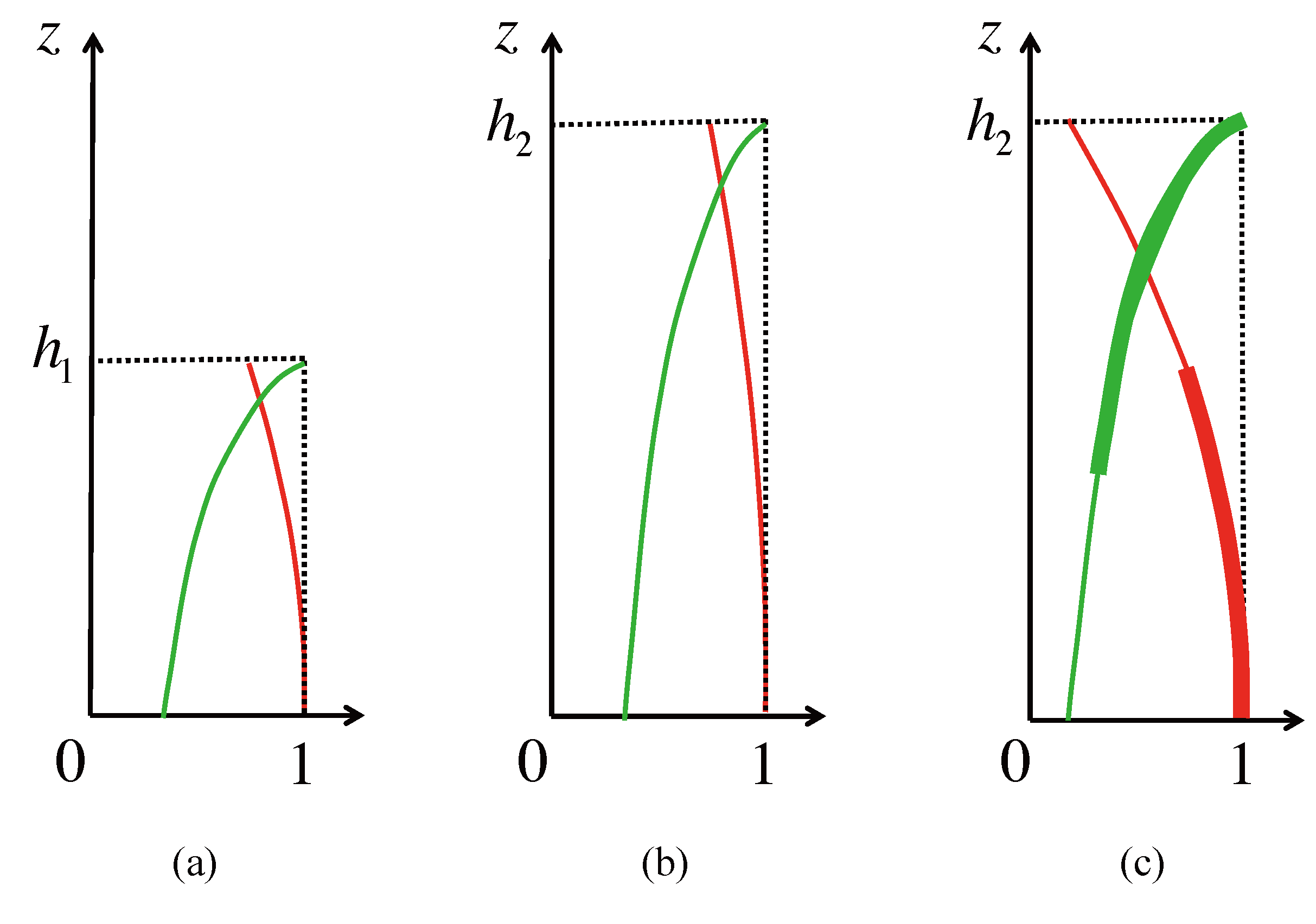
In most cases, however, this requirement is not strictly satisfied, as illustrated in
Figure 15. Here, for forests with constant extinction coefficient and constant wind-induced motion level as assumed in
Section 3.3 (e.g.,
Figure 4a), the profiles of
σV(
z) and
ρr(
z) are illustrated in
Figure 15a,c for heights
h1 and
h2, respectively. However, in order to guarantee the same proportionality of the mean value, we would desire the profiles at height
h2 are nothing more than scaled versions of the ones at height
h1,
i.e.,
Figure 15b. Therefore, the proportionality (denoted by
α in
Section 3.1) will have a perturbation for various forest heights in
Figure 4a. For example, the standard deviation of
α is calculated as 0.07, which in turn results in a standard deviation of 1.11 for
Cscene through using Equation (11). In spite of this small perturbation of
α (and thus
Cscene), the overall fit as shown in
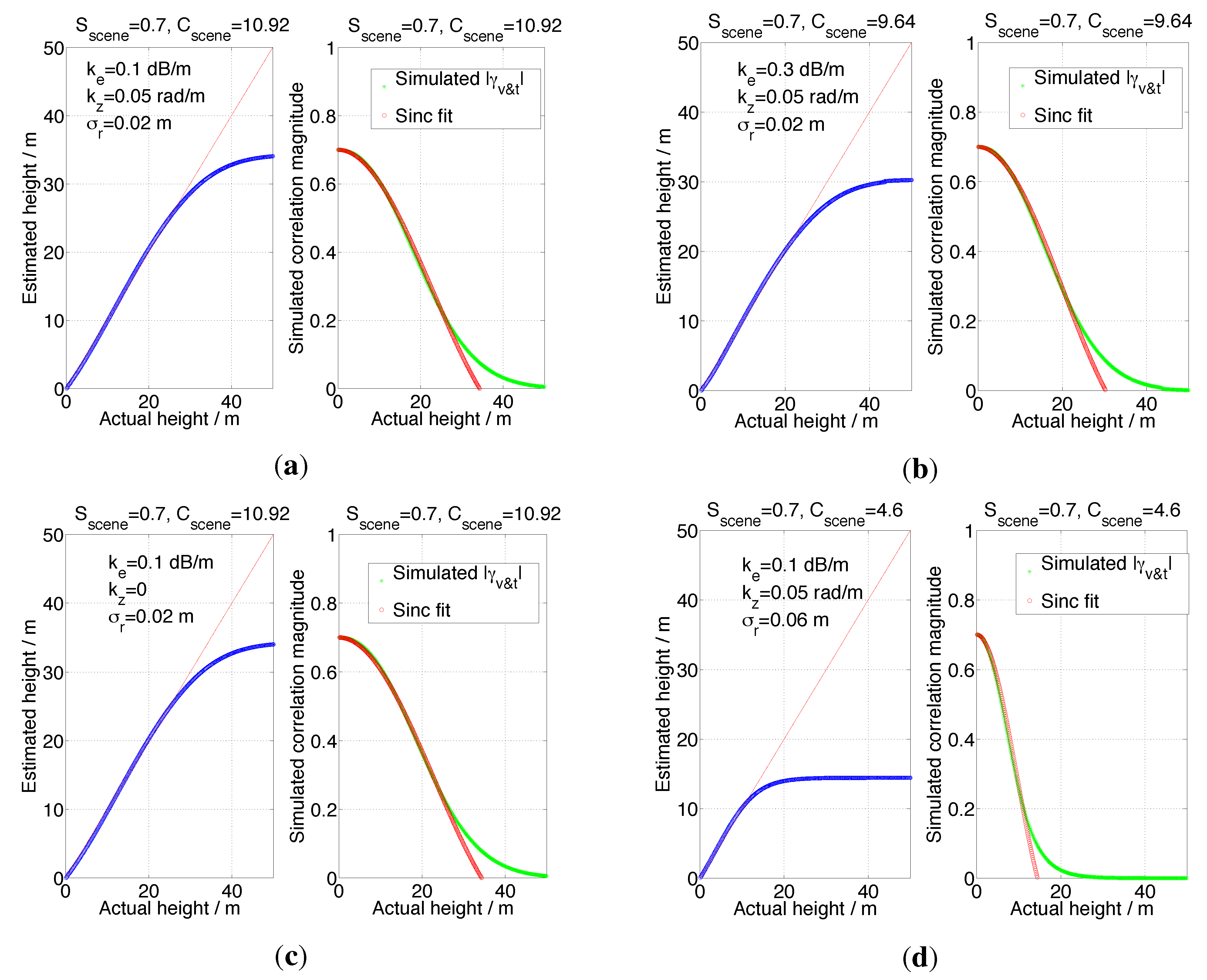
Figure 4a is still quite good (RMSE = 0.25 m and R = 99.97% for heights under the saturation point). So far, we have seen that the requirement of the scaled versions of profiles for different heights could be weakly satisfied with small perturbation occurring but the overall quality of the fitting is still good.
Since we already considered constant wind-induced motion level in the mean sense, for the constant extinction coefficient as mentioned above and utilized in
Section 3.3, we can still apply the same idea by considering its mean value across the whole scene. As seen from
Figure 4b, the fitting parameter
Cscene has a weak dependence on the extinction coefficient
ke compared to the wind-induced motion level
σr (
Figure 4d). Therefore, if we can consider constant motion level in terms of its mean behavior, we can also safely treat the extinction coefficient in the same way, since the target-dependence of
ke is expected to have a smaller effect on the fitting parameter
Cscene than that due to
σr.
Figure 15.
Illustration of different functional forms of the extinction-weighted backscattering profile (normalized; “green” curve) and the height-dependent motion profile (“red” curve). (a) shows the profiles for a short forest stand at height h1, (b) shows the profiles that are scaled versions of (a) for a taller forest stand at height h2, while (c) shows the profiles for the taller forest stand at height h2 using the same functional forms of σV(z) (i.e., constant extinction coefficient) and ρr (z) (i.e., constant wind-induced motion level) as (a). Note the highlighted curve segments in (c) exactly correspond to the profiles in (a).
Figure 15.
Illustration of different functional forms of the extinction-weighted backscattering profile (normalized; “green” curve) and the height-dependent motion profile (“red” curve). (a) shows the profiles for a short forest stand at height h1, (b) shows the profiles that are scaled versions of (a) for a taller forest stand at height h2, while (c) shows the profiles for the taller forest stand at height h2 using the same functional forms of σV(z) (i.e., constant extinction coefficient) and ρr (z) (i.e., constant wind-induced motion level) as (a). Note the highlighted curve segments in (c) exactly correspond to the profiles in (a).
Appendix B. Polarization-Dependence of the Forest Height Inversion Procedure
The forest height inversion procedure used in
Figure 12 is based on Equation (7) which is a version of the correlation model (4), simplified by assuming that
m = 0 for HV-pol data. For the more general case, where both
µ, the ground-to-volume temporal decorrelation ratio due to dielectric change, and
m, the ground-to-volume power ratio, are not trivial values (e.g., for the case of co-polarized transmit and receive channels), the contribution of ground scattering can be further investigated.
To understand these effects of undoing these assumptions, the general correlation model, Equation (4), is rewritten as
with
where
µ and m will bias
γ′v&m from
γv&m.
To obtain the inverted forest height, Equation (10) is used to determine
hv , while we maintain the same
Sscene and
Cscene as in the simplified model (see
Figure 4a) but
γv&
t is replaced by Equation (19) while calculating the simulated correlation magnitude. When
m = 0, this reduces to the simplified model.
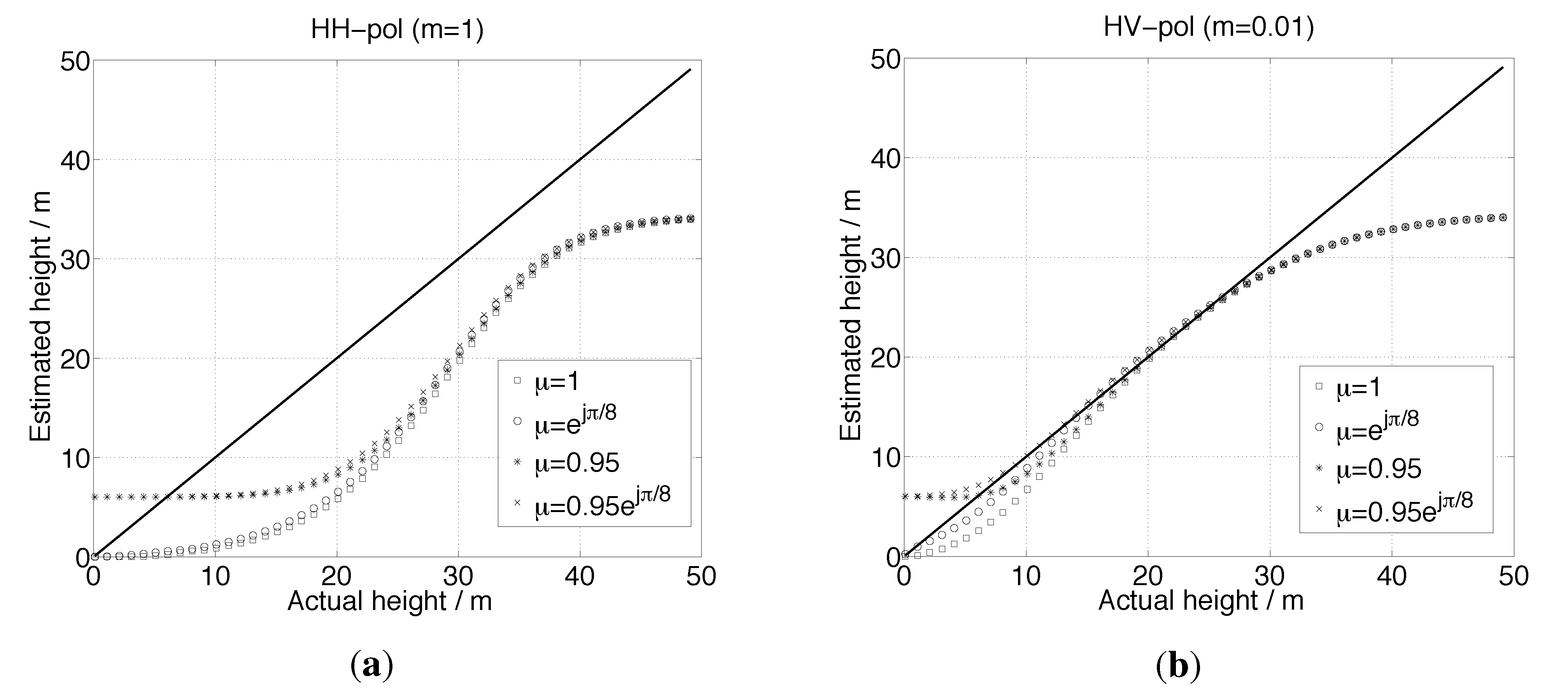
Figure 16 demonstrates the simulated inversion results when
m = 1 (large m, or HH-pol data;
Figure 4a) and
m = 0.01 (
Figure 4b for HV-pol), where the value of
m is referenced to a 30 m tall canopy as in [
3]. Both subplots demonstrate the inversion model performance with
allowing
µ to have magnitude and/or phase bias in comparison with
µ = 1.
From the plots shown in
Figure 16 it can be seen that significant contributions from ground scattering (from the HH-polarized case in (a)) create a non-linear relationship between actual and estimated heights, whereas for the HV-pol data (small
m), the model works well under almost all values of heights. For the small
m case, differences between the simulated and estimated heights only exist at the short and very tall extremes of the inversion. It is for this reason that a preference is given for the use of cross-polarized data in the inversion, a fact that has been borne out in observational data as well.
Figure 16.
Simulated forest height inversion results using (
a)
m = 1 (HH-pol) and (
b)
m = 0.01 (HV-pol). The instrumental and forest parameters are the same as in
Figure 4a, so are the fitting parameters (
Sscene and
Cscene). Results are shown with
.
Figure 16.
Simulated forest height inversion results using (
a)
m = 1 (HH-pol) and (
b)
m = 0.01 (HV-pol). The instrumental and forest parameters are the same as in
Figure 4a, so are the fitting parameters (
Sscene and
Cscene). Results are shown with
.
Although it would be better to make a rigorous mathematical proof in order to validate this assumption, we note the above simulation method (e.g.,
Figure 16) is sufficient at this stage. The purpose of this assumption is to show when
m ≠ 0, bias exists in the inverted forest height. However, as long as
m is small, this only affects the lower end of the height range (e.g., short vegetation and ground), which can be tolerated if
m is small enough, or alternatively can be masked out through the use of a forest/non-forest map since there is usually extra temporal decorrelation causing overestimation of the low heights. The fact of HV-polarized data with
m being small enough in the present work has been validated both by the simulation results (
Figure 16) and the experimental results ( and ).
In the above simulation, an extinction coefficient of
ke = 0.1 dB/m (less than the values used in [
3,
9]) is used to characterize a sparse forest at L-band. If a dense forest is studied with a greater
ke = 0.3 dB/m (as in [
9]), the bias in the lower end of the height range will become much less pronounced,
i.e., the model performs much better. However, if a very spare forest is examined, the extinction effect will be so small that the ground-to-volume ratio will be huge even for a 30 m tall canopy. The inversion result for the HV-polarized data in this case will look very much like the HH-polarized data in the above simulation (
Figure 16a). The forest heights will thus be severely underestimated, however, since the forest is very sparse, the mean ground truth height will also be very small (close to the ground). As this paper deals with the forest height through averaging a large area (not the maximum height), the biased difference between the estimated and ground truth heights can be tolerated for very sparse forests.
In the presence of temporal decorrelation, it is important to note that
Sscene,
m and
µ will be polarization-dependent. Therefore, the PolInSAR version [
6,
15] of this problem will have additional unknowns when temporal decorrelation is expected to play a role in the observations, and thus the inversion becomes an underdetermined problem [
13]. While sophisticated techniques (e.g., adapting PolInSAR methods to accommodate Equation (4)) might lead to more accurate inversion, the simplified inversion model shown here (based on HV-pol data only) has been shown to generate meaningful results from repeat-pass InSAR correlation measurements with long repeat periods. Such algorithms thus are important tools for making use of accumulated data from the JERS-1, ALOS-1 & -2 data sets, as well as the planned DESDynI-R (now called NISAR) mission.
Appendix C. Effective Range of kz for this Work and the Small-kz Assumption
Generally speaking, an InSAR correlation magnitude varies with the
kz value as indicated in
Figure 6 and in [
11] (under unfrozen conditions). In this appendix, the range of
kz values that can be used for this inversion model are explored. In order to do this it is useful to differentiate the decorrelation effects from the variety of sources, as they change with respect to
kz. Although these decorrelation components are demonstrated here as simulation results, as mentioned in
Section 3.3, these simulation parameters are intentionally chosen to be such in order to mimic the experimental results in
Section 5. To create an example, a 20 m tall canopy is used and the
kz-dependence of various correlation components is illustrated in
Figure 17 with the same forest parameters as in
Figure 4a, and using a viewing geometry consistent with ALOS/PALSAR.
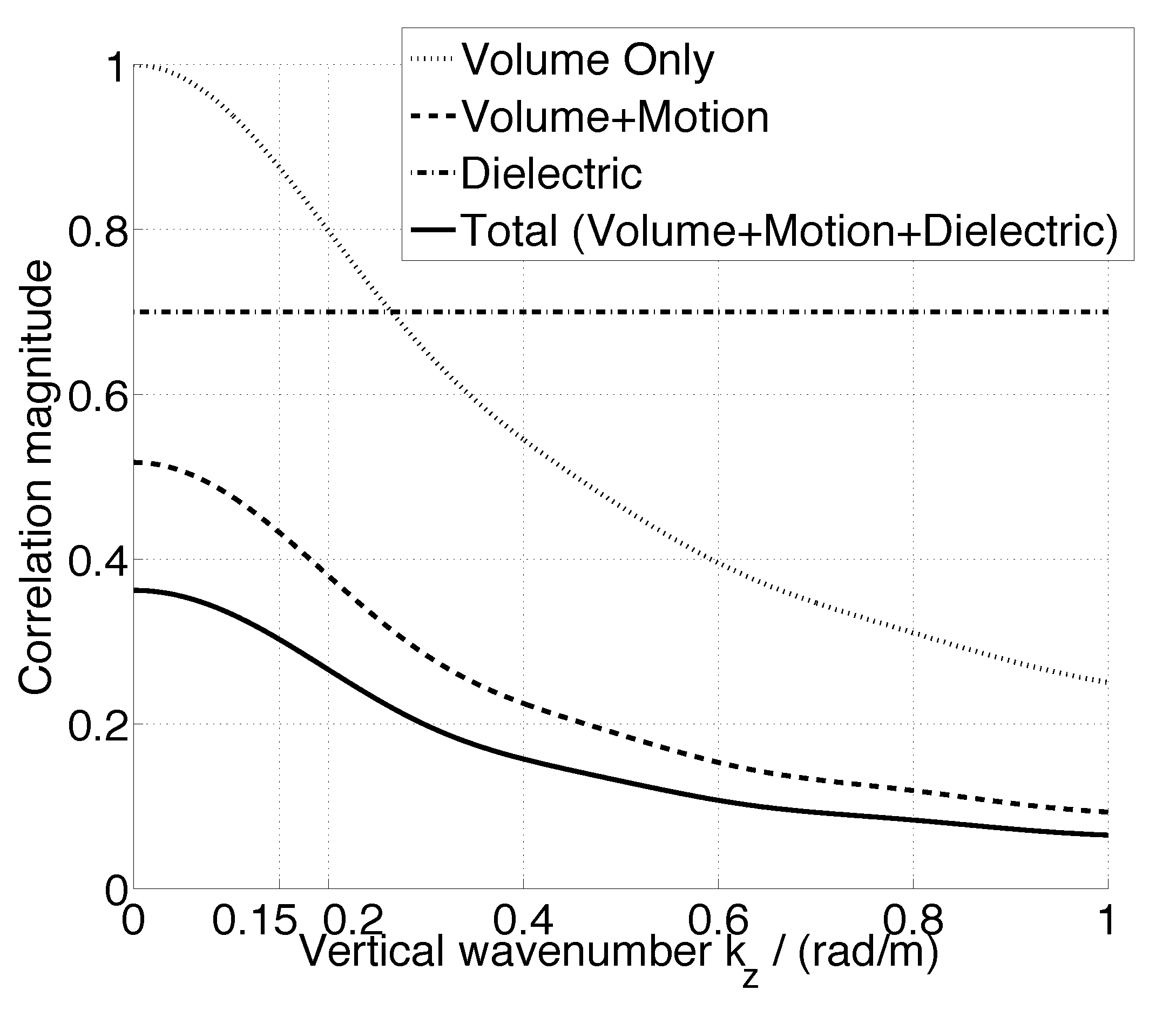
In
Figure 17, the “Volume Only” contribution is from volume scattering and no motion, “Dielectric” is the model for the loss of correlation magnitude due to dielectric changes in the volume (a constant factor that manifests itself in the model constant,
Sscene), “Volume+Motion” is the magnitude of the coupled correlation component due to volume scattering and random motion (|
γv&m|, as in Equation (5)), and “Total (Volume+Motion+Dielectric)” is the combined correlation magnitude from all volume scattering and temporal changes, |
γv&t|. In this example, it is assumed that the geometric decorrelation has been compensated for and that the thermal noise correlation is negligible for 20 m tall canopy.
From
Figure 17, it can be seen that as the vertical wavenumber increases, the total observed correlation decreases, as expected (which agrees with the observations in
Figure 6), and that the combined effect of all correlations can make this total correlation quite low (below a value of 0.3). This has the effect of making the correlation magnitude difficult to measure [
16], and also is an indication of a loss of information in the observation itself. For these reasons, for any model and subsequent inversion used, it is important to use those correlations that have the highest values, such as those shown in
Figure 6. Because of the variety of sources of decorrelation when a 46 day repeat-period is introduced (
i.e., both dielectric and motion changes occur in the target), those observations with the shortest baselines will have the largest correlations, and hence information content. So long as there is a height-dependent sensitivity of the decorrelation on these changes (e.g., [
8,
9]), a signature will exist that can be exploited to estimate forest height.
Figure 17.
Illustration of the
kz-dependence for all of the correlation components involved in the current work by utilizing ALOS’s viewing geometry over a 20 m tall canopy. The forest and temporal change parameters are chosen as in
Figure 4a. The effective range of
kz for this study is
kz < 0.15 rad/m.
Figure 17.
Illustration of the
kz-dependence for all of the correlation components involved in the current work by utilizing ALOS’s viewing geometry over a 20 m tall canopy. The forest and temporal change parameters are chosen as in
Figure 4a. The effective range of
kz for this study is
kz < 0.15 rad/m.
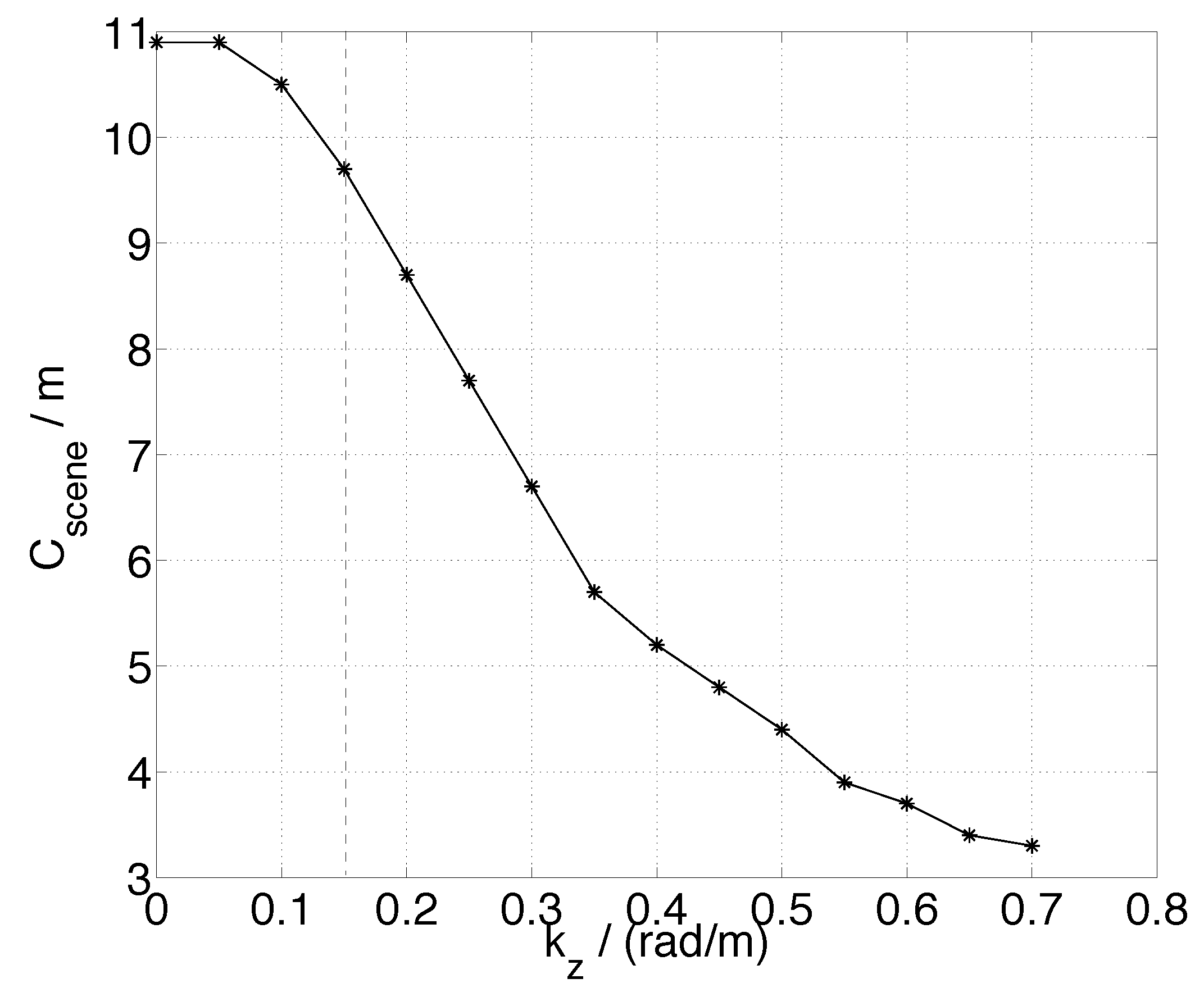
The effect of changing the vertical wavenumber,
kz, from zero to some other value, under these circumstances will lead to a graceful degradation in the model’s performance, because the effect of this larger wavenumber will only be to decrease the correlation. Note that when
kz ≠ 0, a non-zero value of
kz will be included in the model via the scene-wide parameter,
Cscene, derived in Equation (7) through Equation (11). While in that derivation, the vertical wavenumber was assumed to be zero, a non-zero but small value of that parameter will have the effect of scaling the argument of the exponential function given in Equation (9), or equivalently, scaling the argument of the sinc function used in Equation (10). In other words, the fitting parameter
Cscene will be
kz -dependent in order to compensate the model degradation. This effect can be better illustrated by
Figure 18, which shows the fitted parameter
Cscene as a function of
kz with other simulation parameters fixed as in
Figure 4a. As mentioned in
Section 3.1, the value
πCscene represents the invertible range of forest height through using the simplified inversion model (“sinc” relationship) with fitting parameters
Sscene and
Cscene. If
Cscene becomes very small (e.g., <5 m as seen in
Figure 18), this simplified inversion approach will be insufficient to characterize the height variation of natural forests under the presence of correlation measurement uncertainty. Note for the small
kz values (
i.e.,
kz < 0.15 rad/m and preferably < 0.05 rad/m as stated above), the value of
Cscene is only slightly changed, which is in agreement with
Figure 4a, where
kz = 0.05 rad/m and
Figure 4c, where
kz = 0 rad/m. The reason for this can be seen in the effect of
kz on the total decorrelation curve shown in
Figure 17, where the behavior of the curve for small values of
kz is at its peak, and relatively unchanged for values of
kz < 0.15 rad/m (as indicated by the vertical dotted line included in
Figure 17), which serves as the effective range of
kz for this study. Therefore, we have demonstrated that for any non-zero small
kz , this simplified inversion model (
i.e., the sinc relationship as in Equation (10)) can always work well with
Cscene being weakly dependent on
kz (in comparison to Equation (11) where
kz was neglected), which is referred to as the “small-
kz assumption” in this study.
Figure 18.
The
kz-dependence of the inversion model degradation. Particularly, the fitted parameter
Cscene is shown as a function of
kz with
πCscene related to the invertible range of forest height characterizing the model performance. The smaller
Cscene, the worse model performance. The forest and temporal change parameters in this simulation are set to be the same as
Figure 4a. The case where
kz = 0.15 rad/m (
i.e., boundary of the effective range for small
kz in this study) is indicated by a vertical dashed line.
Figure 18.
The
kz-dependence of the inversion model degradation. Particularly, the fitted parameter
Cscene is shown as a function of
kz with
πCscene related to the invertible range of forest height characterizing the model performance. The smaller
Cscene, the worse model performance. The forest and temporal change parameters in this simulation are set to be the same as
Figure 4a. The case where
kz = 0.15 rad/m (
i.e., boundary of the effective range for small
kz in this study) is indicated by a vertical dashed line.