1. Introduction
Prior to satellite observations, our understanding of changes in global phytoplankton was relatively poor. Since the advent of satellite remote sensing of surface chlorophyll-
a (Chl
-a) concentrations in the late 1970s, it has been possible to estimate surface phytoplankton biomass at near global scales. Remote sensing tools have proven to overcome the greatest limitations that classical observational methods suffer by providing global coverage and a continuous temporal sampling rate. Sensors such as the recently terminated SeaWiFS and the on-going MODIS-
Aqua are passive ocean color instruments that measure surface water radiance that can be converted into near-surface Chl
-a concentrations. Due to the presence of this pigment in all phytoplankton organisms, Chl
-a is commonly used as a phytoplankton biomass indicator throughout the water column though the relationship between surface Chl
-a and the biomass is indirect and non-linear [
1]. The one to two day revisit cycle of the ocean color sensors on board these polar orbiting satellite platforms is ideal for large-scale quantitative studies of the spatial and temporal ocean productivity rates, and its relationship with climate modes of variability.
At the interannual scale, El Niño—Southern Oscillation (ENSO) is not only the dominant global mode of climate variability, but also the determining mode in global ocean productivity [
2,
3]. As a natural mode of the climate system, ENSO represents the quasi-periodic oscillation that exists due to the “internal” coupling of the atmosphere and ocean on year-to-year time scales. However, recent ENSO discussions have focused on the differences between two El Niño types, the classic canonical (eastern Pacific) El Niño and the central Pacific (CP) El Niño (also known as El Niño “Modoki”) that has been observed more frequently over the past few decades (e.g., [
4]). The eastern Pacific (EP) ENSO mode is commonly described in terms of a basin-wide coupling of the ocean and atmosphere across the tropical Pacific that manifests itself as a quasi-periodic variability of the climate system on a time scale of 2–8 years [
5]. In the neutral “phase” of ENSO (
i.e., neither El Niño nor La Niña conditions), the climatic conditions are characterized by high sea level pressure (SLP) over the central-eastern subtropical Pacific, with strong trade winds pushing the surface waters westward into the Western Pacific Warm Pool (WPWP) [
6]. This statistically averaged state of the tropical Pacific climate provides deeper cooler waters to upwell along the eastern and equatorial boundaries creating a cold tongue that extends from the east to central Tropical Pacific. One effect of this cold tongue is to enrich the phytoplankton response around the equator as the upwelling brings nutrient rich waters into the euphotic zone where it is consumed by these organisms [
7]. For the composite EP El Niño phase, SLP in the central-eastern subtropical Pacific tends to be reduced, the trade winds are weaker, and the central-eastern equatorial Pacific is anomalously warm and nutrient-depleted due to the reduction in upwelling. EP El Niño events tend to concomitantly show an anomalous decrease of phytoplankton in the Tropical Pacific [
8], except in the WPWP region, where the deep nutrient rich waters have a greater chance to surface due to a shoaling thermocline [
9]. Conversely the La Niña phase of EP ENSO, which is associated with an enhancement of the trade winds, leads to an anomalous increase of phytoplankton in the central-eastern equatorial Pacific.
The CP El Niño [
10]—otherwise known as El Niño “Modoki”—differs from the canonical El Niño in that it is characterized by a SST anomaly at the eastern edge of the WPWP, flanked zonally by two opposite signed anomalies [
11]. It is thought that CP El Niño events are excited by anomalous westerly winds in the western Pacific, which push the warm surface layer waters from the off-equatorial western Pacific towards the equator, driving a downwelling equatorial Kelvin wave, which induces a deepening of the thermocline from the central to the eastern Pacific [
11]. This is followed by easterly wind anomalies in the eastern Pacific creating convergence in the central Pacific, further deepening the central Pacific thermocline. Thus the SST warming in the central Pacific is further strengthened by downwelling equatorial Kelvin waves from the west, and Rossby waves from the east [
11]. CP El Niño displays a strong decadal periodicity [
11,
12], and has increased in intensity in recent decades, unlike EP El Niño [
13]. Recent works reveal that CP El Niño events induce low values of remotely sensed phytoplankton indicators in the eastern part of the WPWP [
14–
16] while the examination of the strongest CP and EP El Niños to date (
i.e., 1997–1998 EP El Niño and 2009–2010 CP El Niño) suggests that horizontal processes (e.g., intrusion of nutrient-deficient warm pool waters) dominate during a CP event while vertical processes (e.g., nutricline suppression) and mixing play a larger role in an EP event [
17].
These two ENSO mechanisms have been identified as the leading global Chl
-a drivers at interannual time-scales in the past decade using the Empirical Orthogonal Functions (EOF) technique [
3,
14]. EOF analysis is a commonly used technique in climate and earth sciences, often used to isolate the leading modes of variability in the geo-data that typically relate to forcing climatic mechanisms and processes [
18]. However, EOFs do not take into account propagating features [
18]. This limitation has the potential to underestimate the importance of the driving mechanisms being examined. Here, we use a variant of this technique, the extended EOF (EEOF) that provides a dynamical expression of the traditional EOF.
In this paper, we aim to describe and interpret the Tropical and South Pacific Chl
-a patterns in the context of the dominant and dynamical interannual modes of Pacific and near-global climate variability—specifically the EP and CP ENSO modes. We characterize the variability associated with ENSO changes throughout the South Pacific and the Tropics. Further, we describe and illustrate how an ENSO transition affects Chl
-a. Finally, we discuss decadal-scale changes in Chl
-a concentrations in the context of recent increases in CP El Niño frequency—a mode with a clear and strong decadal peak. We demonstrate that at least since the late 1990s, the Chl
-a signal has been more connected with the CP El Niño structure than with the classical EP ENSO mode—consistent with the increased frequency and intensity of the CP mode over the past 30 years [
4,
13,
16].
2. Data
The primary data investigated in this study are satellite remote sensed Chl
-a estimates. These data were retrieved from the Oregon State University Ocean Productivity website [
19] originally collected by NASA [
20] and are a combination of r2009.1 SeaWiFS and MODIS-
Aqua satellite Chl-
a products. The dataset comprises of monthly-averaged matrices (maps) of 1080 × 2160 pixels, resolved at 1/6° per pixel, increasing polewards in km resolution at a rate of cosine (latitude). Ocean color data here are only available to 45° latitude, as the lack of sunlight during wintertime limits the remotely sensed observations further poleward. The Chl
-a observations were derived from SeaWiFS for the period October 1997–December 2007 after which there were significant gaps in the SeaWiFS dataset. Consequently MODIS-
Aqua data were used from January 2008–October 2010. Chl
-a observations from the two missions compare very well with correlations of r
2 > 0.8 while the bias and root-mean-square deviation (RMSD) are within acceptable values (e.g., [
21]) allowing for such a merger with minimal artifacts. Additionally, we have compared the SeaWiFS and MODIS-
Aqua Chl
-a data between July 2002 and December 2007, when there is overlap between the two missions and full coverage for the spatial domain of this study (
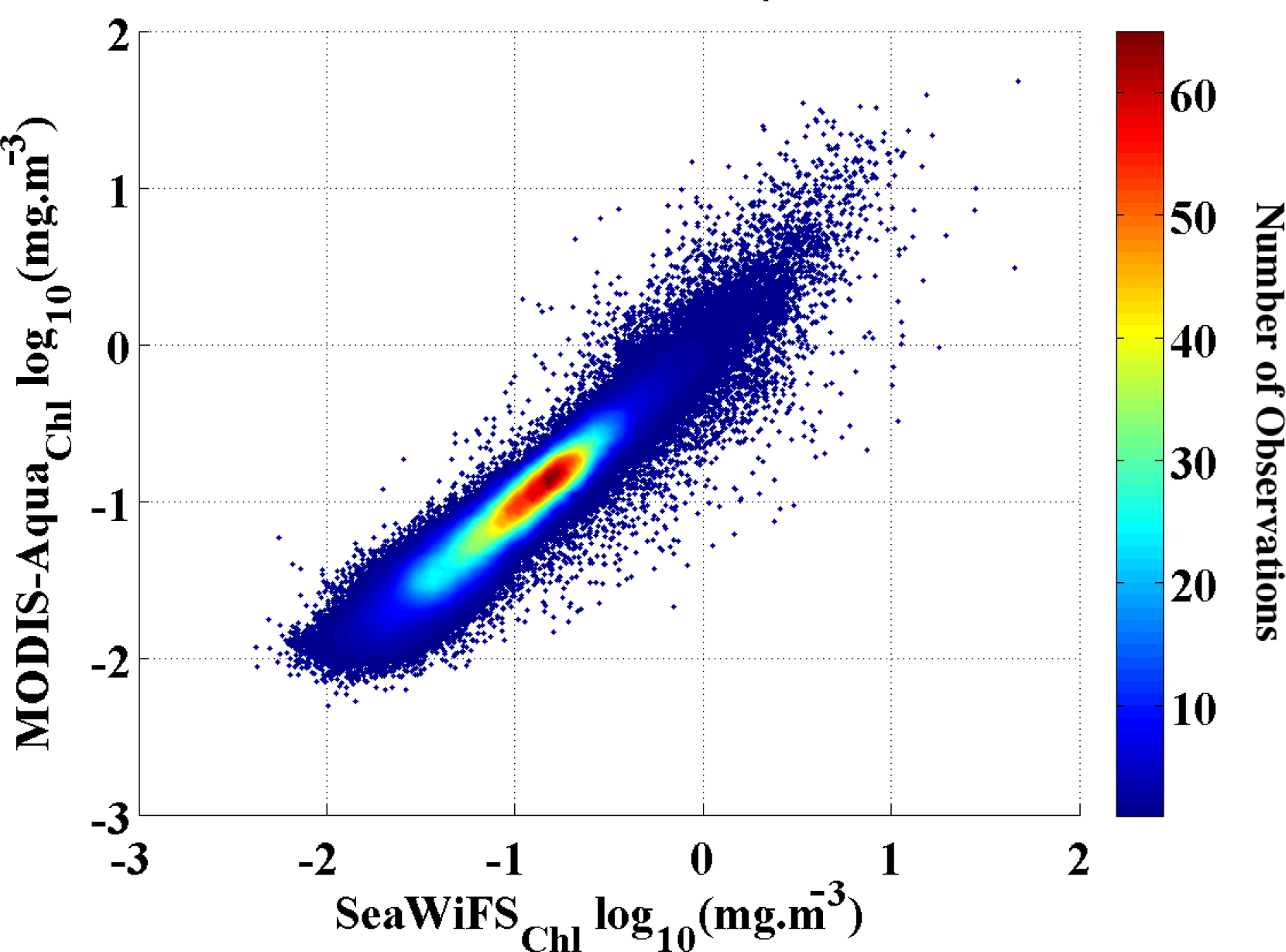
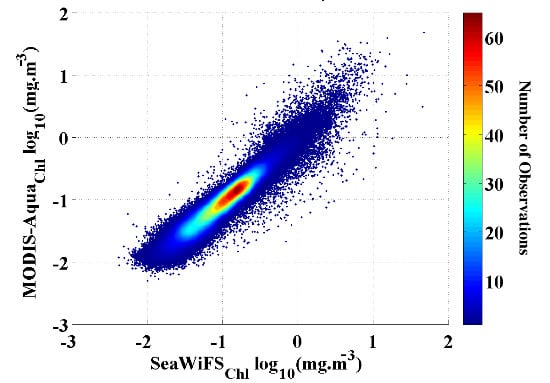
Figure 1). We found a strong (r
2 = 0.93) and significant (p << 0.01) correlation between the two datasets with a low RMSD = 0.10 and standard deviation (STD) < 0.001. Hence, we are confident that our merged Chl
-a data set is free of any significant artifacts and that the results of the analysis are not affected by the data transition.
The phases of the EP ENSO are characterized by several available indices derived from several geophysical variables. For the present study, we selected the Multivariate ENSO Index (MEI) since it is the most comprehensive index for basin-scale climate investigations of ENSO. It takes into account six observed atmosphere and ocean physical variables across the tropical Pacific: sea level pressure, zonal and meridional surface wind components, sea surface temperature, surface air temperature and total cloudiness fraction of the sky [
22–
24]. MEI data were obtained from the US National Oceanic and Atmospheric Administration [
25].
The CP (or Modoki) El Niño has only recently been identified as a distinct climatic phenomenon [
10,
11]. Consequently, there are fewer simple metrics available to diagnose and/or monitor CP ENSO changes. Here we have adopted the Improved El Niño Modoki Index (IEMI) developed by [
26], which we calculated using the UK Met Office Hadley Centre SST (HadISST) dataset [
27]. We also use the same dataset for the additional SST analysis outlined in the following section.
3. Methods
Before delving into the methodology, we first provide here a justification for the extent of the study domain and choice of analysis by providing some general statistical comparisons of the MEI and Chl
-a data (first described in [
28]).
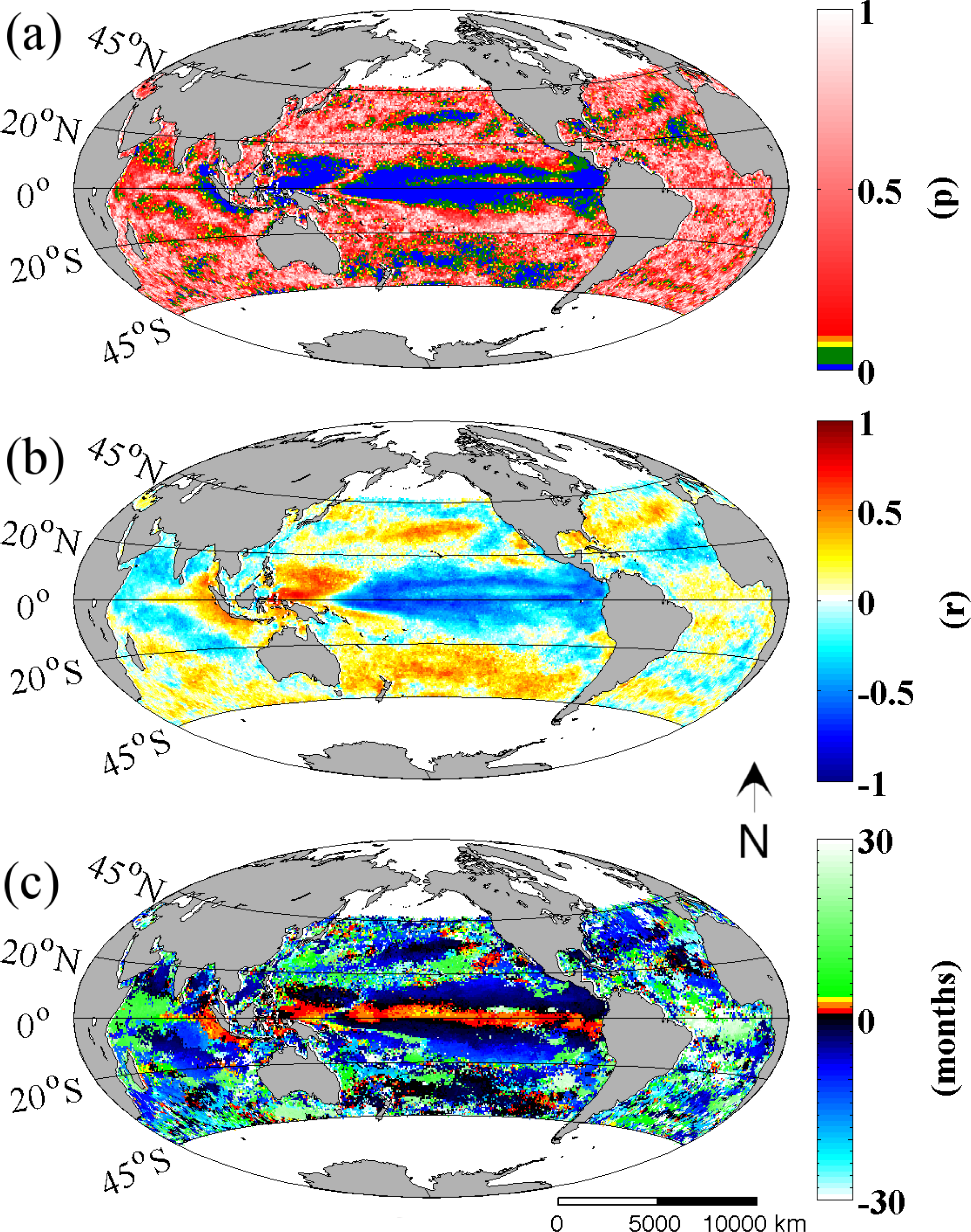
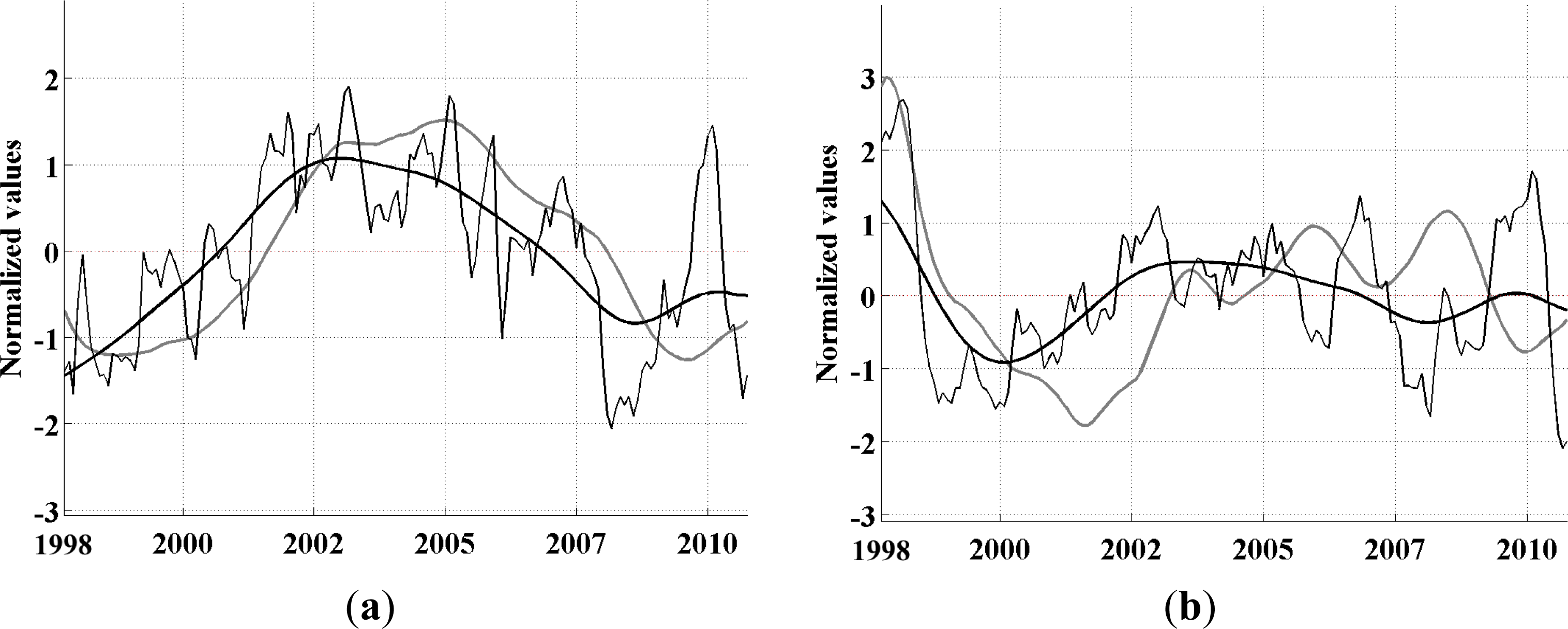
Figure 2 shows the spatial distribution of statistical significance, correlation coefficient and the time lag of the best correlation coefficient, between the MEI and Chl
-a time series from 45°N to 45°S. It can be readily seen here that ENSO (represented by the MEI) has a more significant influence on Chl
-a concentrations over the Pacific than in other ocean basins (
Figure 2a). Furthermore, significant relationships are found to exist not only in the tropical region of the Pacific but further poleward to 35°N and 45°S. These extra-tropical regions also display high correlation coefficients, albeit with an inverse relationship to that observed throughout the Tropical Pacific, with the exception of the Western Pacific where a positive correlation coefficient is observed (
Figure 2b). Direct and highly significant relationships are also found in the subtropical regions while the mid-latitudes of the South Pacific also stand out with a consistently positive relationship. This is in stark contrast to the northern hemisphere equivalent latitudes where correlation coefficients change sign. Most interesting of these results is that while all observed Chl
-a regions track well with the MEI, they display different timing with respect to a best fit with the ENSO signal (
Figure 2c). The results indicate that the ENSO index is significantly coupled and synchronous with Chl
-a patterns that occur off the equatorial belt (shaded in black in
Figure 2c) but lagged with the patterns at the equator (shaded in red in same figure). It is also noteworthy that Chl
-a variability over the Equatorial Pacific and also at the west coast of Java and Sumatra in the Indian basin (with either a direct or inverse relationship to the MEI) has a positive (leading) best fit to the MEI, and in some regions at three or more months earlier. This best fit is delayed towards the poles.
Based on our focus on ENSO signals, and the above results, we selected the tropical and South Pacific basin-wide area extending meridionally from 20°N to 45°S, zonally from 140°E to 70°W, and coarsened to a 1° grid-scale. The aim of this paper is to study the ENSO related Chl
-a propagating patterns in the South Pacific. Hence, we have included both the South Pacific and the Tropical Pacific regions within the study area. The North Pacific to 20° N is included in our analysis in order to ensure that tropical processes are captured including near-equatorial wave dynamics; however our primary focus is the Chl
-a variability in the South Pacific. Slow moving mid-latitude Rossby waves are known to play an important role in ENSO dynamics and setting the timing of lagged relationships [
29]. We therefore included much of the mid-latitude South Pacific in our domain as we hypothesize that ENSO related Chl
-a variability will be found well outside of the tropical region. Also excluding the mid-latitudes of the North Pacific provides the advantage of faster computation without compromising the study domain of interest. Chl
-a anomalies (Chl
-aA) were calculated by removing the log-normal monthly average at each pixel. That is, we calculate the monthly mean using log values, convert back to normal distribution, and then remove this value from the original monthly data. All data were also de-trended in time, using linear regression. The power spectra for both climate indices (MEI and IEMI) were calculated for the same period as the Chl
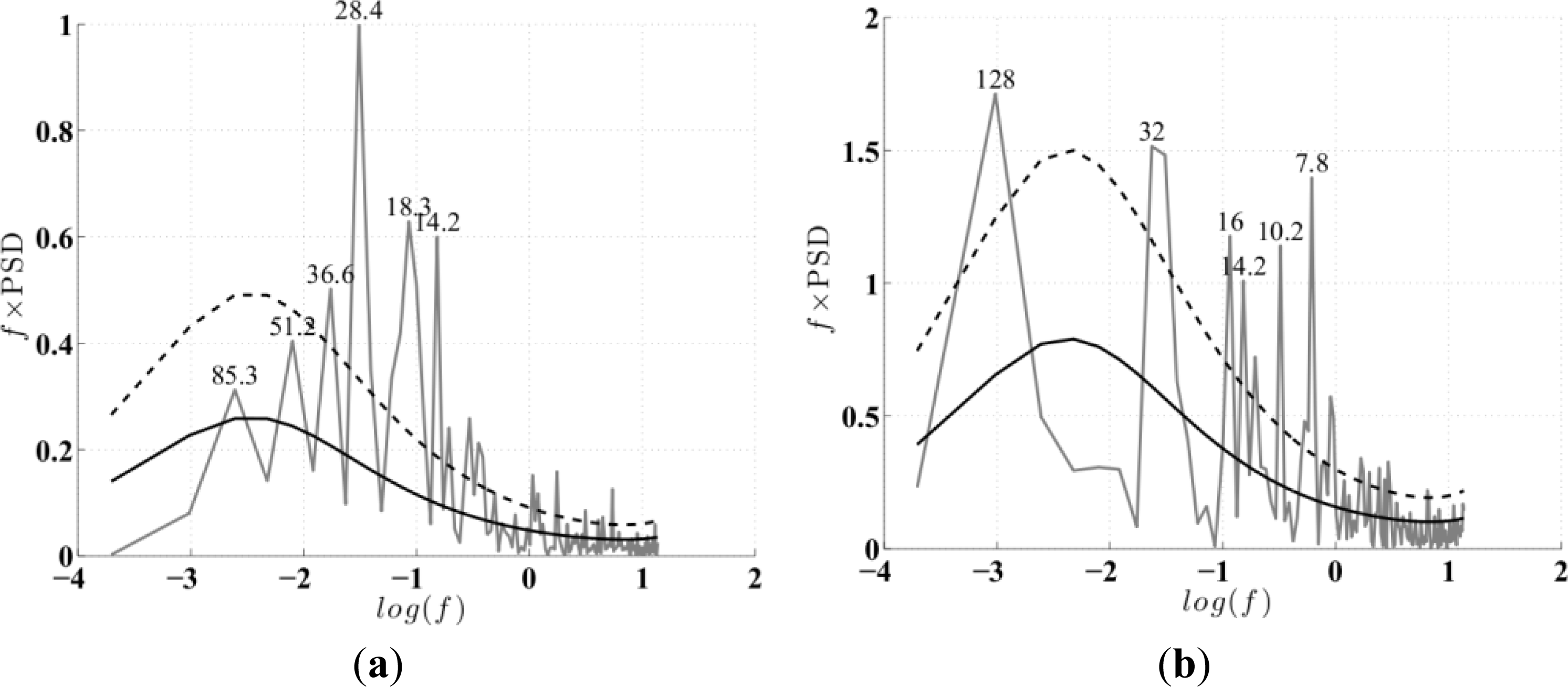
-a record to determine the periodicity of the ENSO signals. Peaks with maximum power above the mean red noise spectrum, and at the 95% confidence levels [
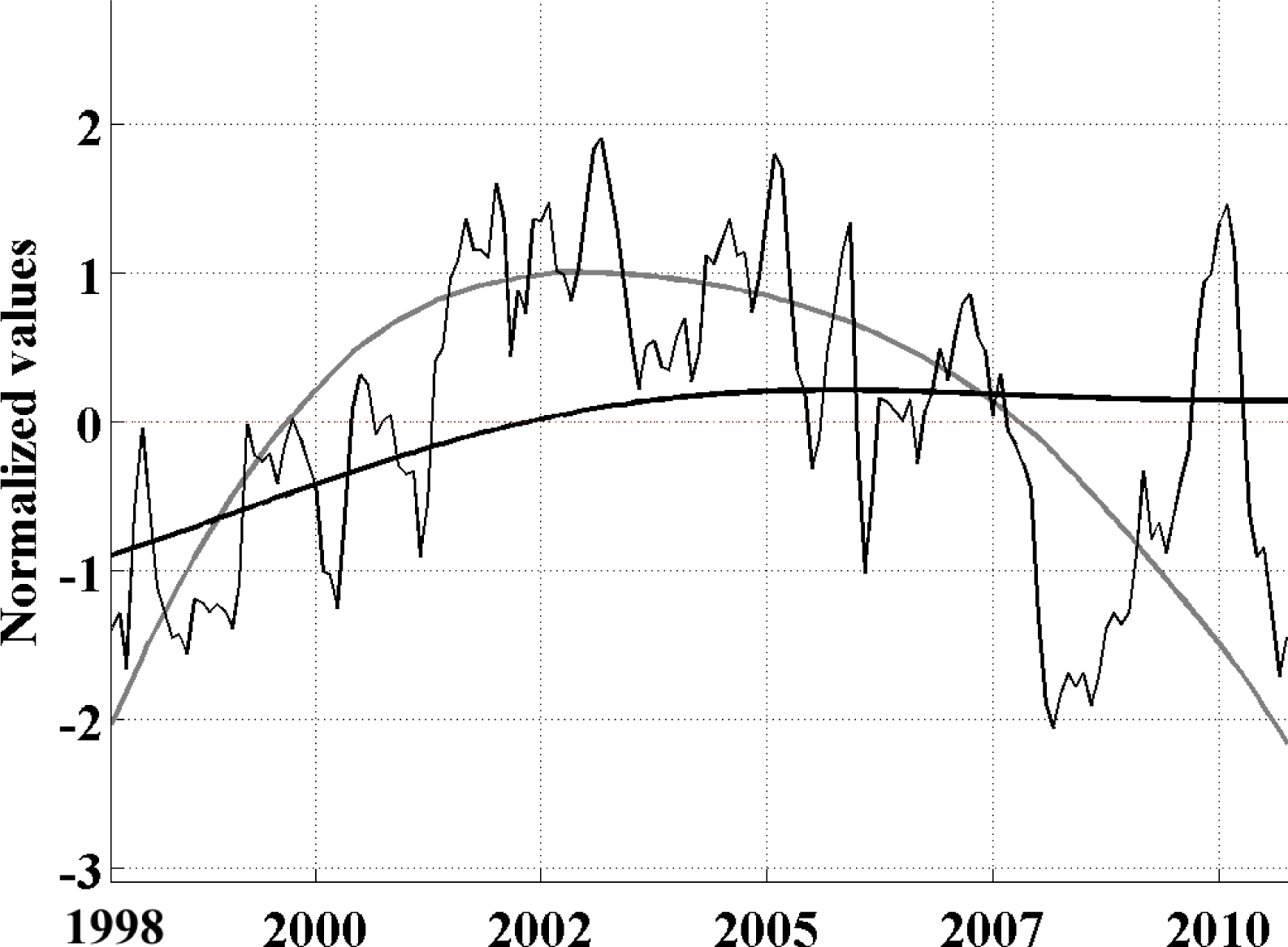
4], corresponded to 28- and 128-month periodicities for the MEI and IEMI respectively (
Figure 3a,b). These power spectra maxima indicate the dominant propagating frequencies in the ENSO signal which were taken as the relevant lag (L) periods for an EEOF analysis of Chl
-aA to explore whether its propagating variability is well explained by these periodicities. This analysis is described below.
The standard EOF analysis is a commonly used technique in geophysical research since it can summarize large datasets in space and time into only a few distinct modes that may be linked to important mechanisms [
30]. A limitation of EOF analysis is that it is unable to account for leads and lags in propagating features, which may be incorrectly identified as two (or more) modes in quadrature, when in fact they are simply part of a single dynamically propagating process [
30]. Because the technique yields a standing wave-like pattern, propagating signals are often isolated into different modes with a similar temporal series.
Figure 2 and further analysis by [
28] demonstrate that propagations and lags exist between ENSO and Chl
-a variability and provides the motivation for utilizing a methodology which accounts for this.
The
extended EOF technique takes account of lag sequences in the time series, and hence propagation within individual modes—by truncating the data into several subsets of predefined time lengths (also known as “lag-sequence lengths”) and concatenating these prior to applying the EOF analysis. Prior to calculating the anomaly values and reshaping the data into space × time, a time lag (L) is predefined. L represents the cycle of the period of events that the analysis will focus on. Then the matrix is rearranged and concatenated into the following form:
Data matrix
F, which consists of a time series of geographical locations, has dimensions [M × (L + 1)] × (N − L) where M represents locations, and N time increments. The EOF is then computed as per usual. For a comprehensive explanation of the EOF or EEOF technique, the reader is referred to [
18]. Example applications of the technique are also provided by [
31–
33]. We use the monthly data directly as our time increment for the analysis. The EEOF analysis was then applied using two predefined lag-sequence lengths. These are: lag-sequence length L = 28 months, based on the frequency of maximum power (above red noise) in the MEI that characterizes the EP ENSO (
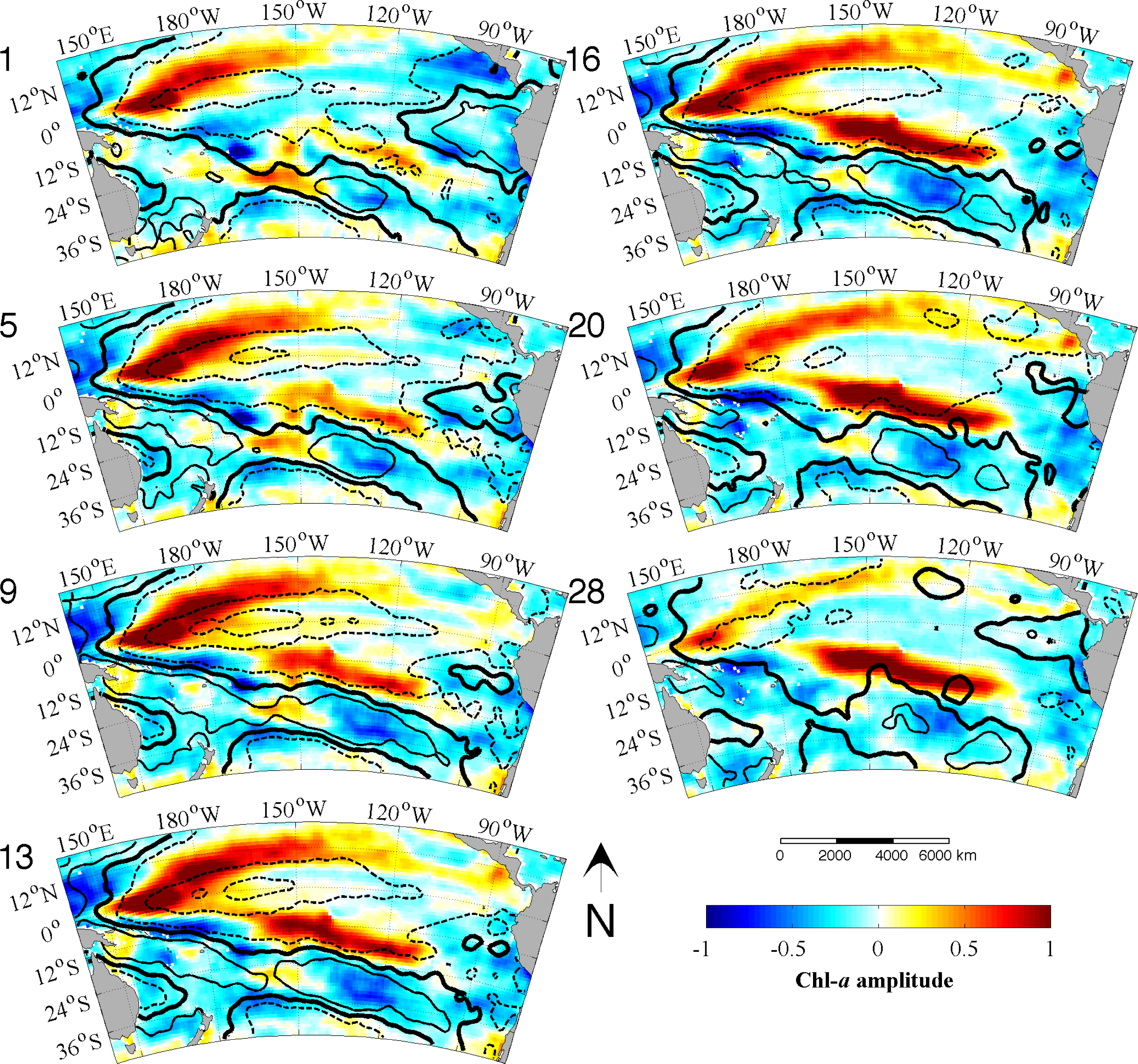
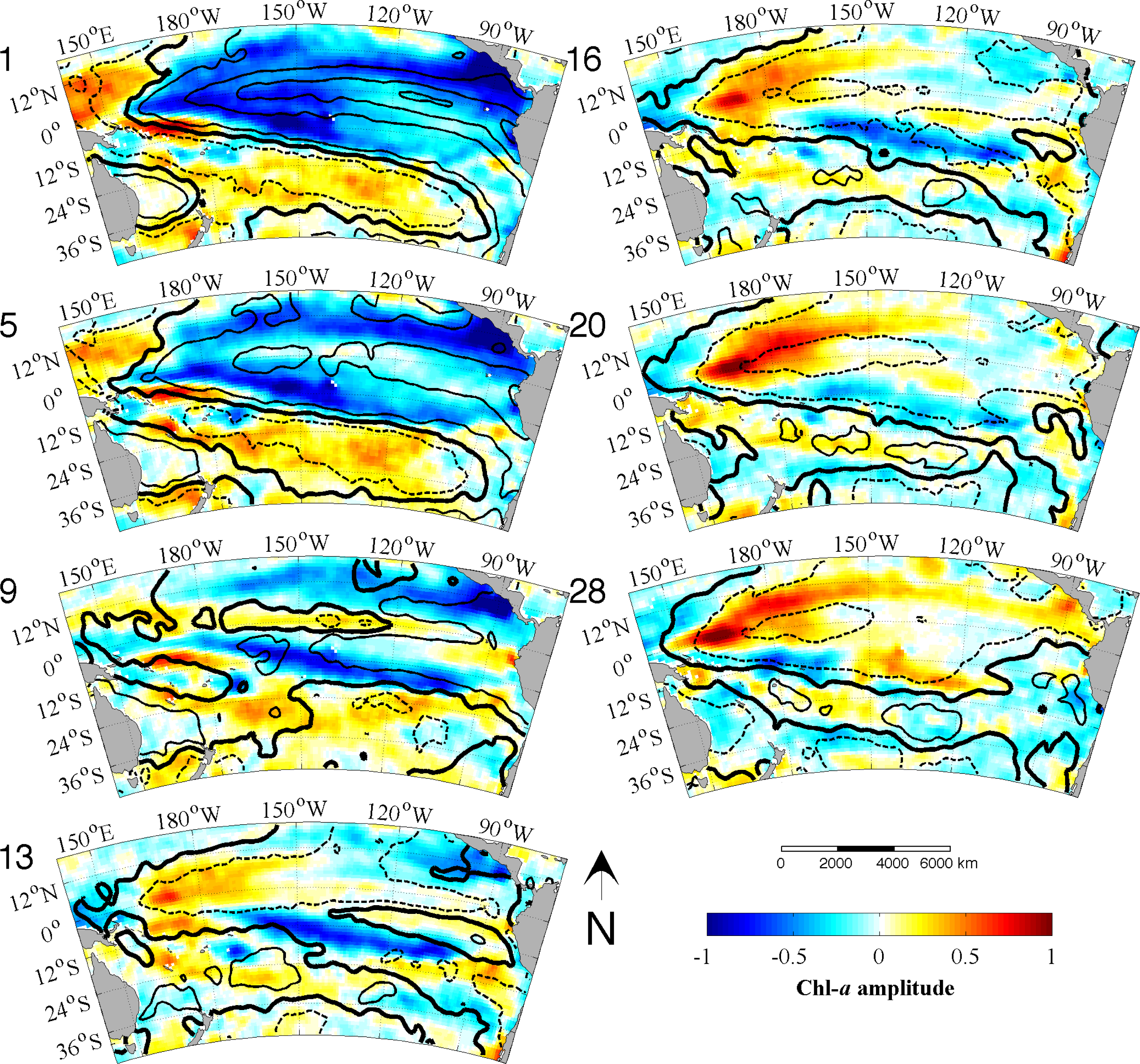
Figure 3a); and L = 128 months, corresponding to the maximum power in the IEMI (
Figure 3b). Each EEOF analysis is independent of the other,
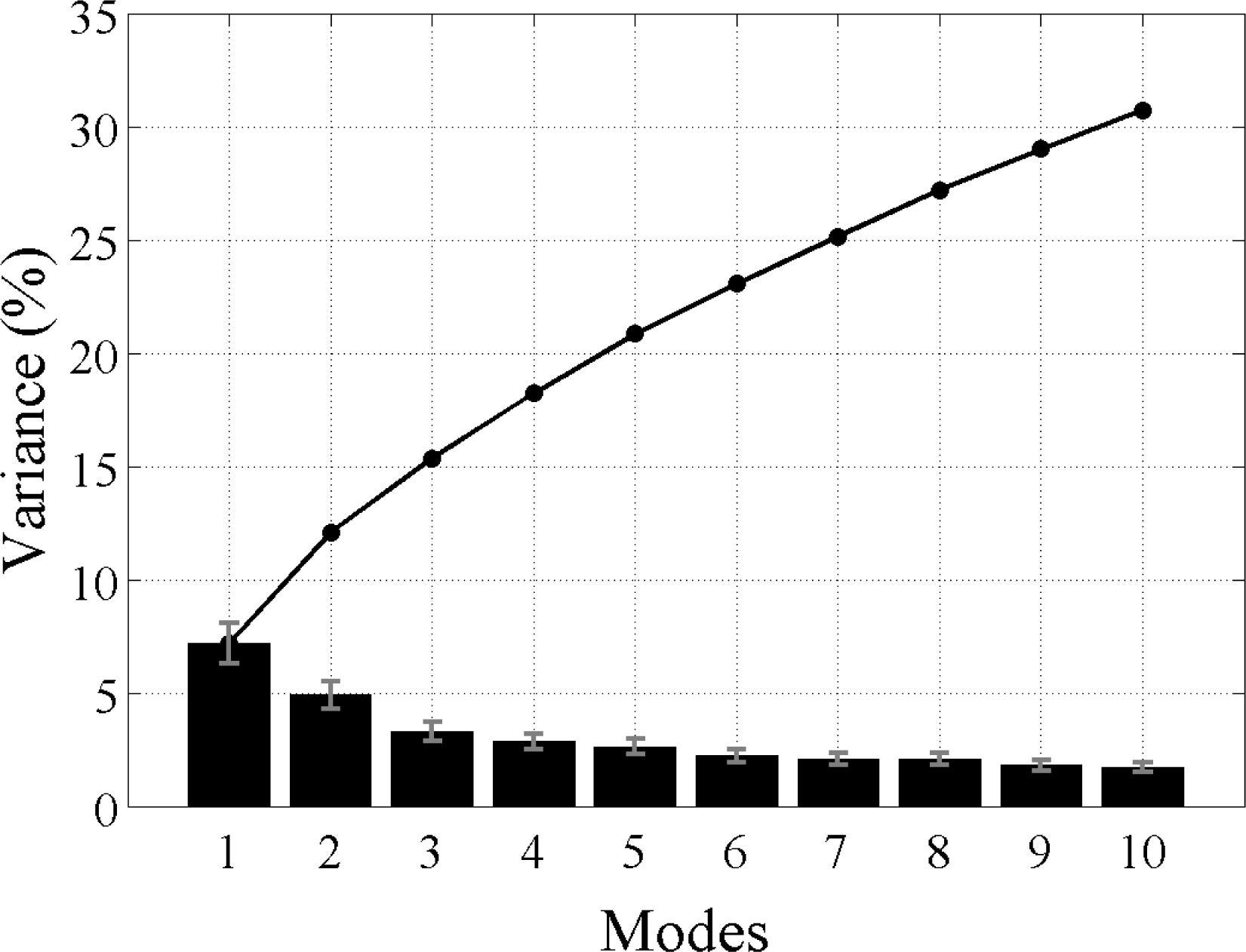
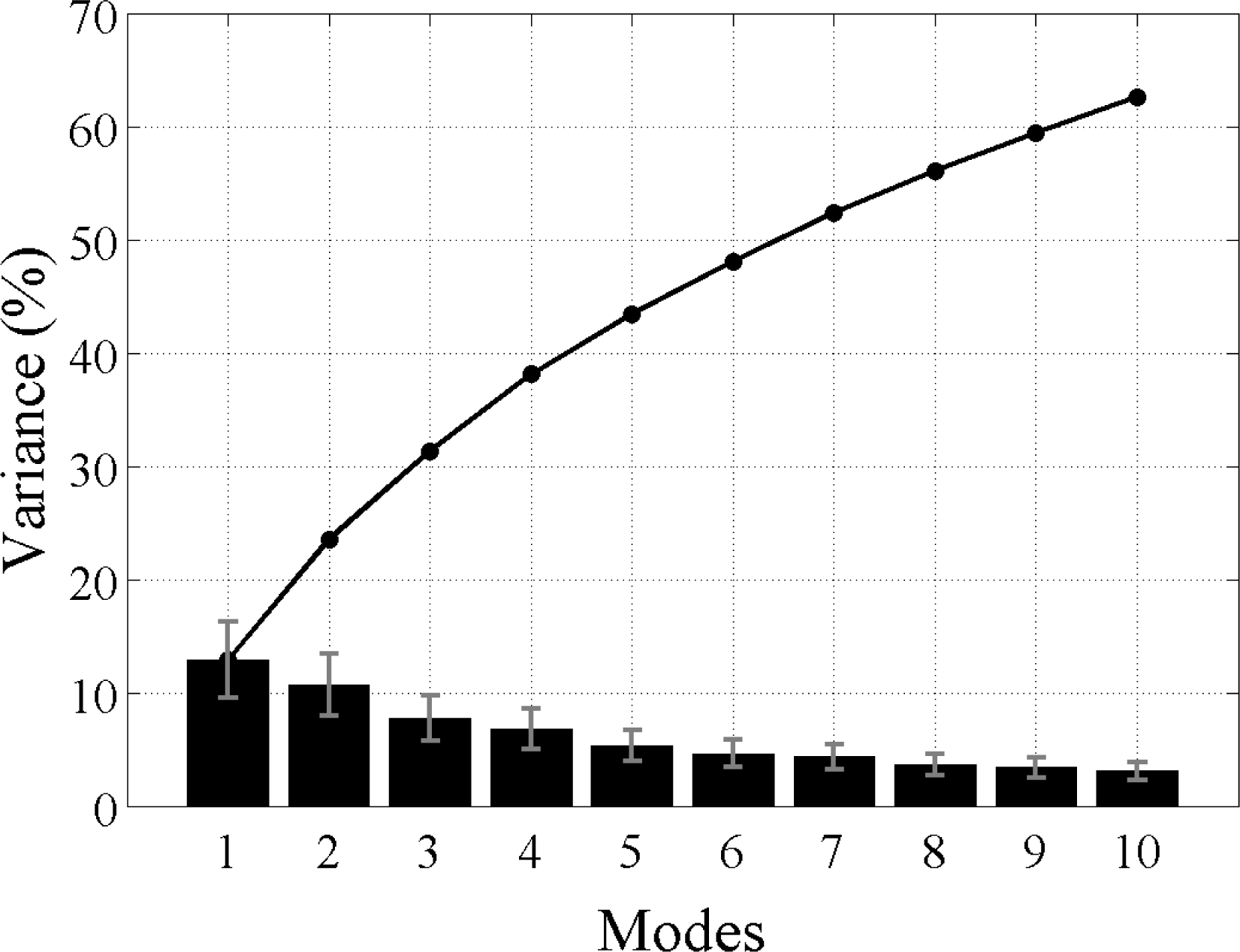
i.e., the modes yielded by the L28 analysis explain all of the variability in the data, as do the modes produced by the L128 analysis. The sum of all the modes in each analysis adds up to 100% with the first mode explaining the most variance and then less for each subsequent mode thereafter. However, not all modes describe large, coherent structures and generally most of the secondary modes will contain random, stochastic variability explaining a very small percentage (e.g., 1%–2%) of the variance. The aim of an EOF analysis is to utilize only a small (physically meaningful) number of modes, which should explain most of the variance and discard the rest. Because Chl
-a variability is strongly dominated by the seasonal cycle and higher frequencies, the individual modes here, even the leading ones, are not expected to explain a large amount of variability (≪20%). In other words, the variance at these timescales makes a much smaller contribution to the total Chl
-a variability in the region. The large study area is also likely to contribute to the lower variance in each mode, as smaller scale variability cannot account for the variance in the greater spatial domain.
The EEOF component time series or Principal Components (PCs) and the two ENSO-type climate indices were then comparatively tested for any statistical relationships. Significances of the correlations were determined against the
effective number of degrees of freedom according to [
34], taking into account the autocorrelation in the time series which provides a more conservative but also more robust result. Finally, the Chl
-aA PCs were projected onto SST anomaly (SSTA) fields for the same spatial and temporal domain as the Chl
-a, with the aim of characterizing the climate that couples these variables. SSTA is also computed by removing the monthly climatology. The SST data are then concatenated in the same manner as the Chl
-a data prior to the EOF analysis, as dictated by the assigned lag. Projecting the PCs onto the concatenated SSTA data yields SST spatial variability maps that complement the Chl
-aA modes for each respective EEOF analysis. Since no information regarding ENSO is directly added to this analysis, where the SSTA patterns derived from the Chl
-aA PCs resemble ENSO phases provides strong evidence for a connection between Chl
-a variability and ENSO. Furthermore, we also compare the correlation with the climate indices and examine the total percentage of variance explained by the first 10 modes in each analysis to determine which ENSO type each analysis relates to, if any.
6. Conclusions
In the present study, using an Extended Empirical Orthogonal Function (EEOF) analysis approach applied to the most recent 13-yr satellite record of Chl-a, in combination with sea surface temperature (SST) records and El Niño—Southern Oscillation (ENSO) indices based on various climatic parameters, we have shown that ENSO driven propagation can explain interannual Chl-a variability in the South Pacific. This paper demonstrates the usefulness of the EEOF, an underutilized method in the literature, in examining propagating signals. We identified the power spectra maximum periodicity in the Multivariate ENSO Index (MEI) and Improved ENSO Modoki Index from October 1997–October 2010 as being 28 months (L28) and 128 months (L128), respectively. For the recent record that comprised of four central Pacific (CP) El Niño events, the classical eastern Pacific (EP) ENSO, whose influence on phytoplankton is far more widely reported in the literature, explained less Chl-a variability and less significantly (L28 Principal Components (PC) 2 at r2 = 0.26, p = 0.94; negligible for L28 and L128 PC1) than the CP mode (L28 PC1 at r2 = 0.40, p < 0.01; L128 PC1 at r2 = 0.36, p < 0.01).We found that the MEI power spectral maximum of 28 months relates to ENSO high frequency processes, which might represent a transition between phases, and is observed in the EEOF Mode 2 Chl-aA pattern.
The existence and independence of CP ENSO is a highly topical contemporary issue within the ENSO community. Our results add further evidence to the debate and outline some important outcomes: namely that (i) whether the CP mode is independent or not, it also manifests in the South Pacific Chl-a data with real consequences for ocean biology and is not merely a methodological artifact in the SST or sea level pressure (SLP) data, and (ii) there is indeed a low frequency (decadal) signal in the South Pacific Chl-a with CP characteristics, but a longer time series is required to sufficiently test the independence of this signal from EP ENSO. The implications of the differing roles of EP ENSO and CP ENSO on phytoplankton variability is that the prevalence of one flavor of ENSO over another can potentially lead to varied impacts on ocean ecology and ocean carbon fluxes, making this a key issue warranting further investigation as longer datasets and subsurface data become available.