Harmonization of Fraction of Absorbed Photosynthetically Active Radiation (FAPAR) from Sea-ViewingWide Field-of-View Sensor (SeaWiFS) and Medium Resolution Imaging Spectrometer Instrument (MERIS)
Abstract
:1. Introduction
2. JRC-FAPAR Product
3. Harmonization Method
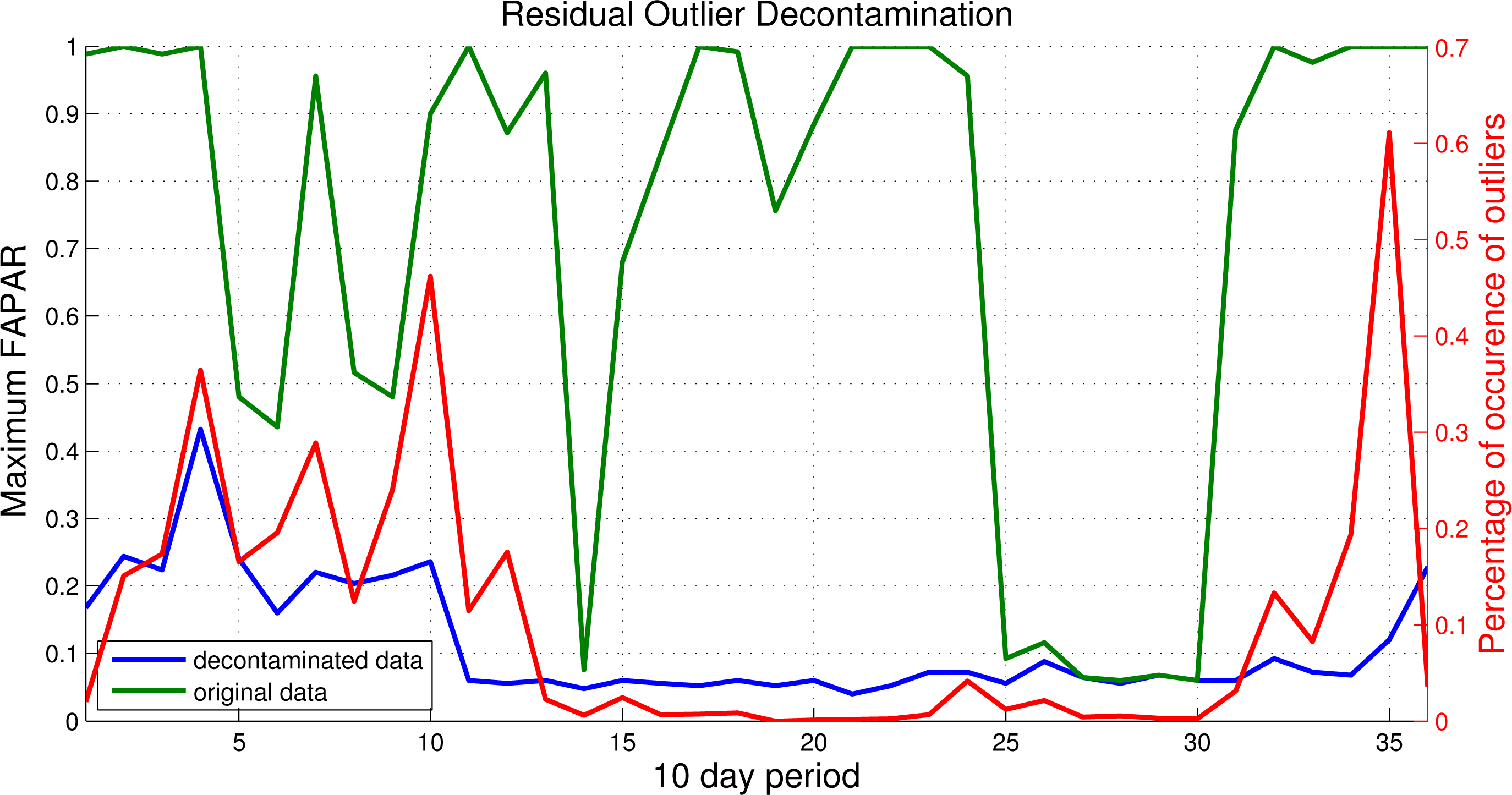
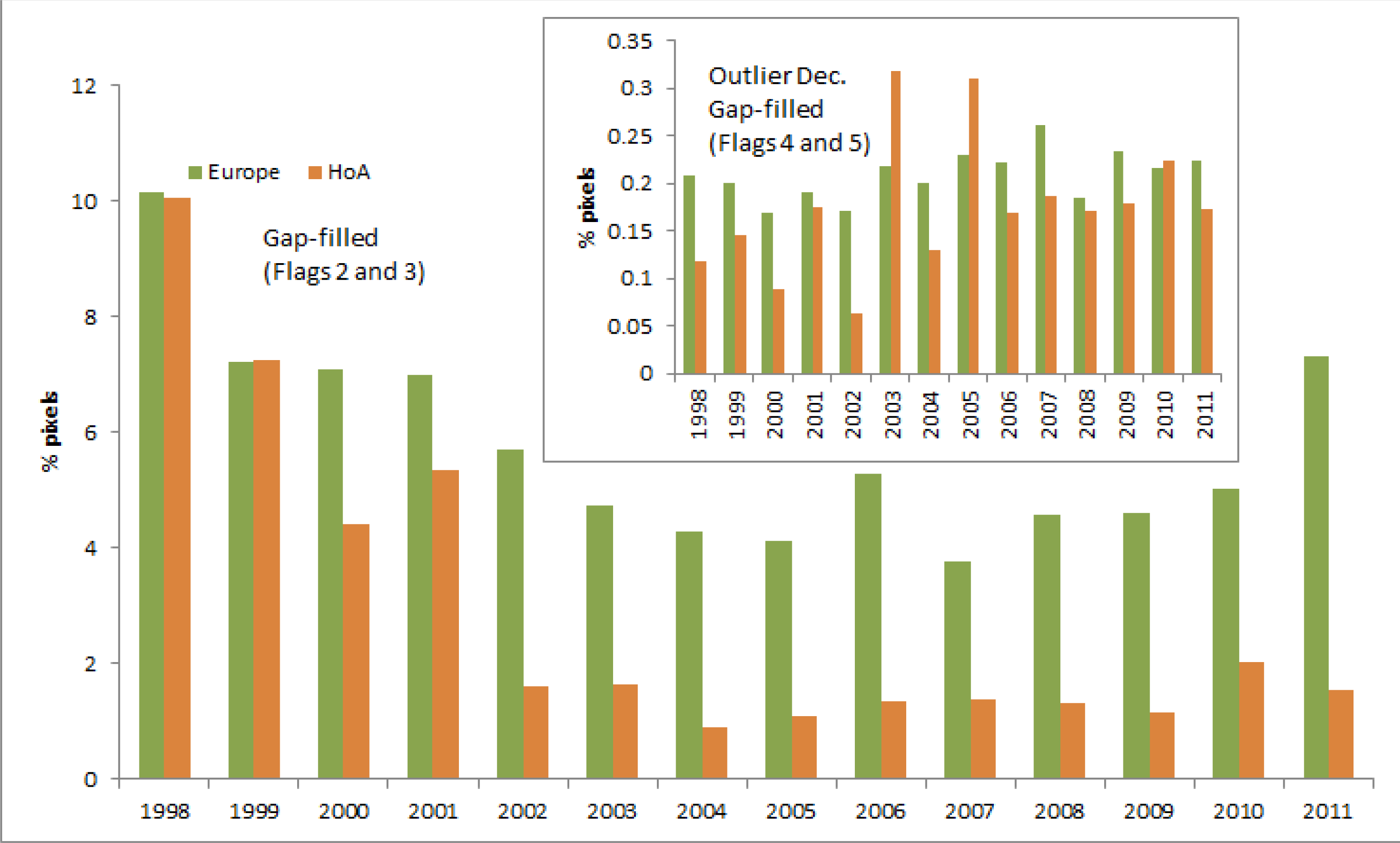
3.1. Residual Outlier Decontamination
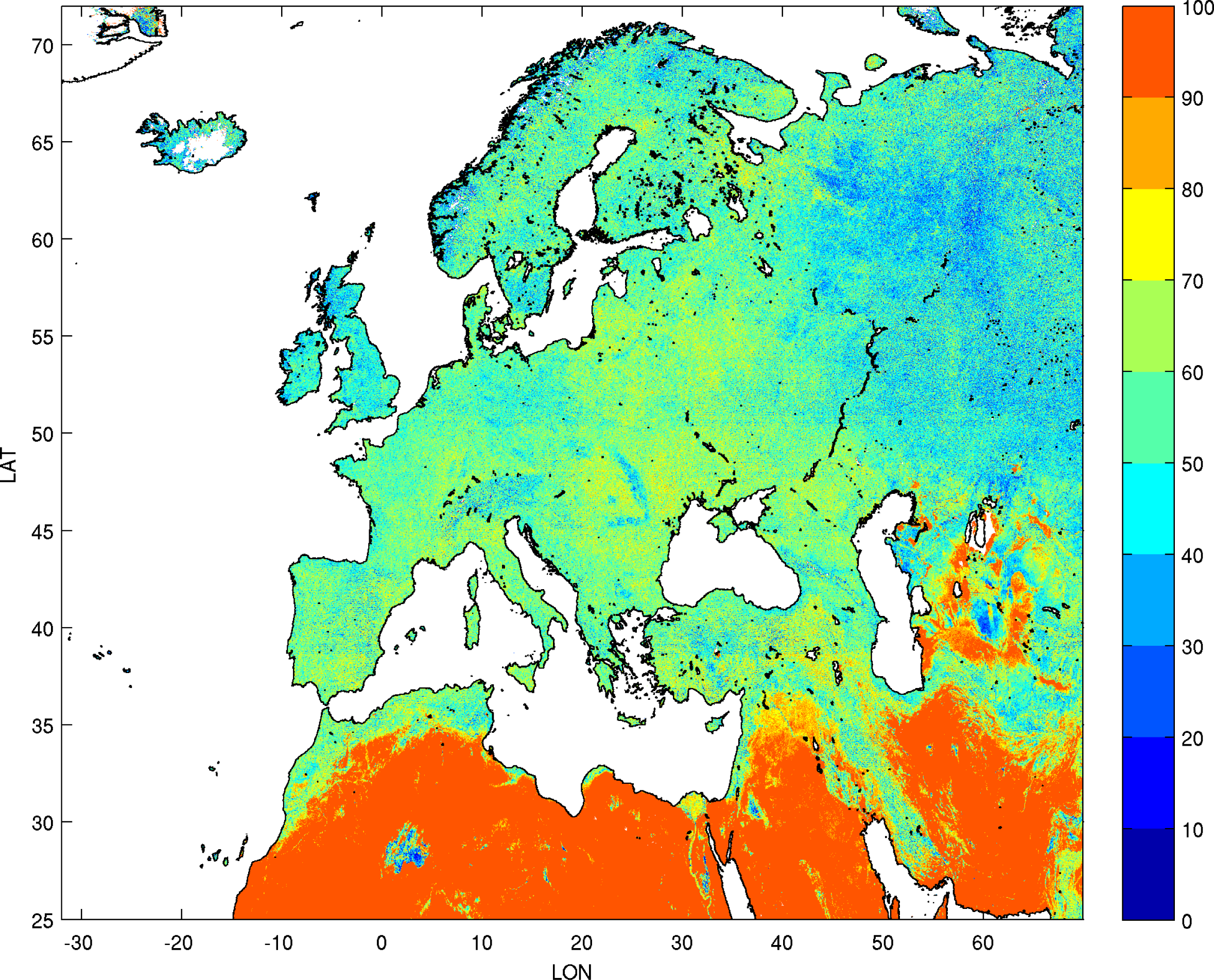
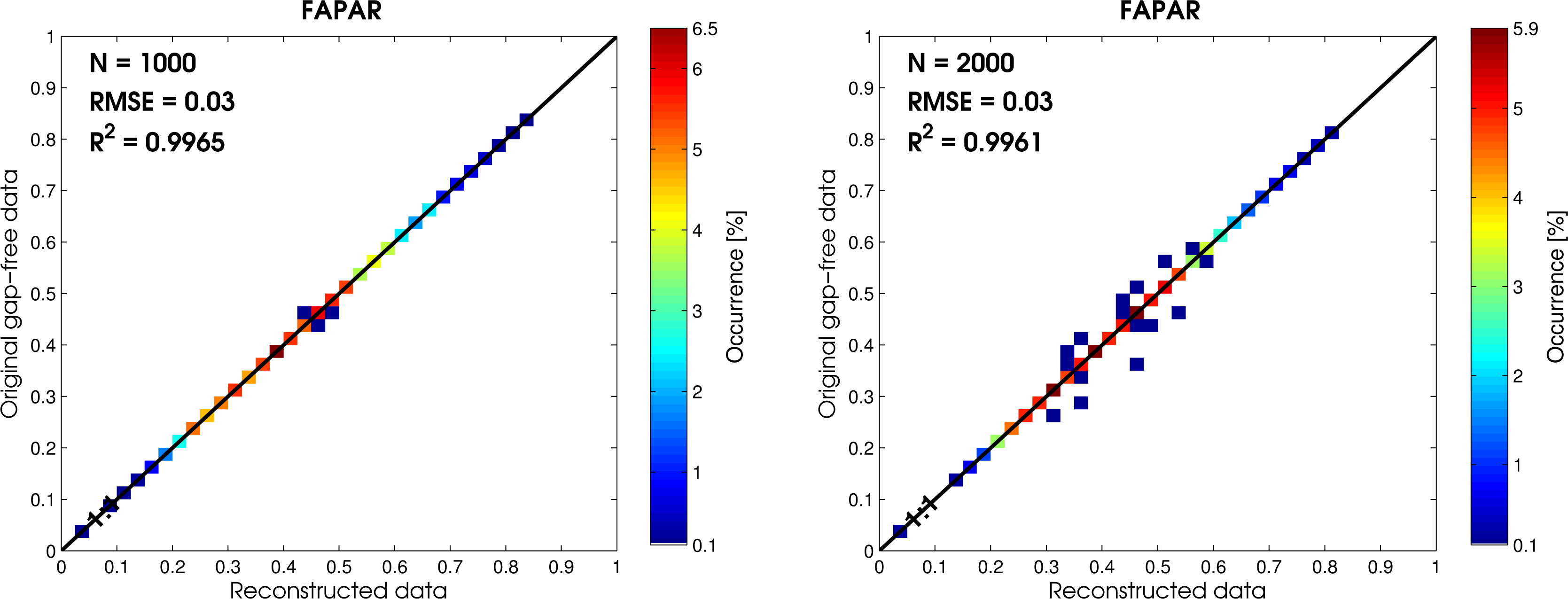
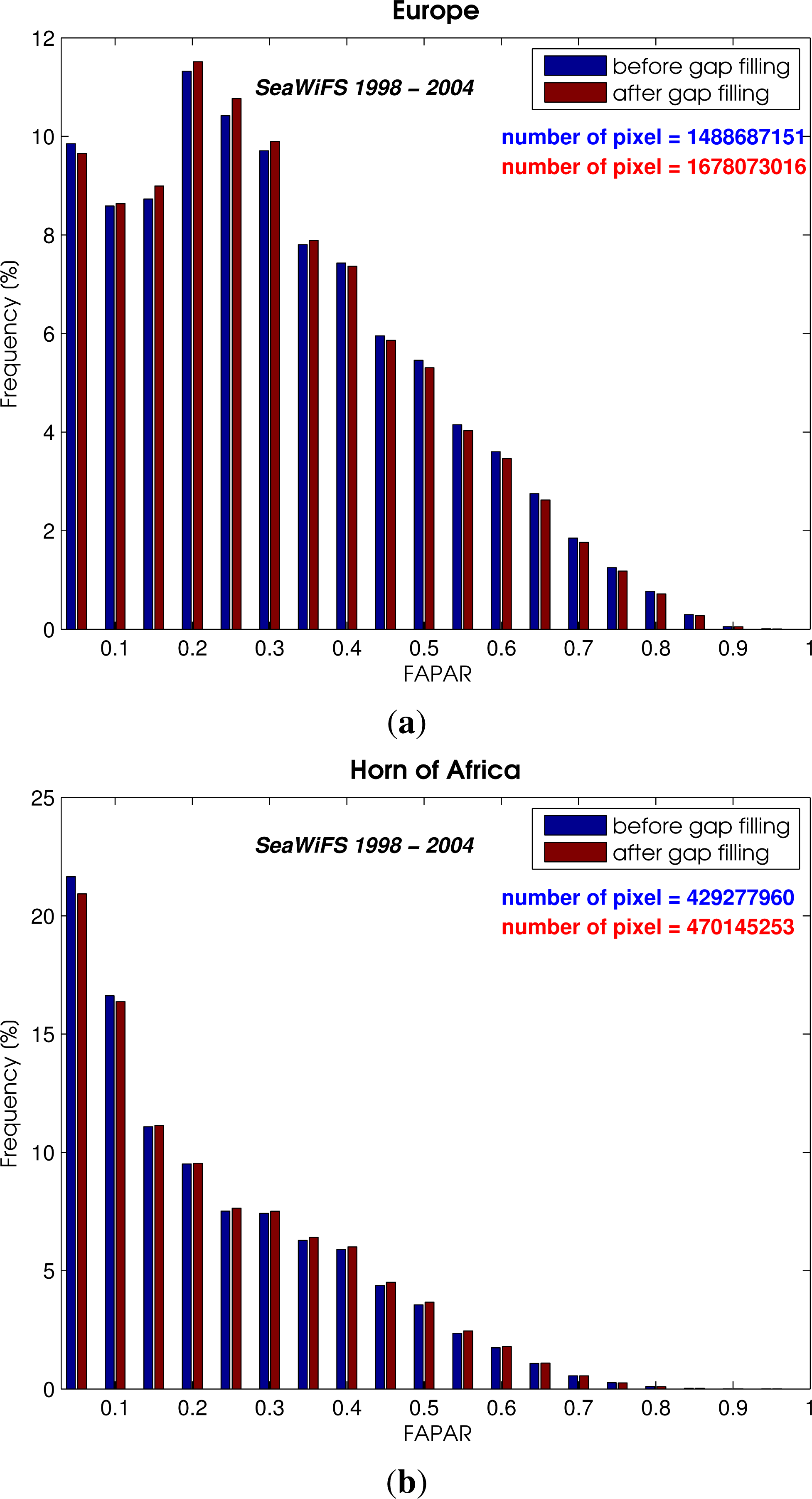
3.1.1. Gap Filling
3.1.2. Correction of SeaWiFS Data
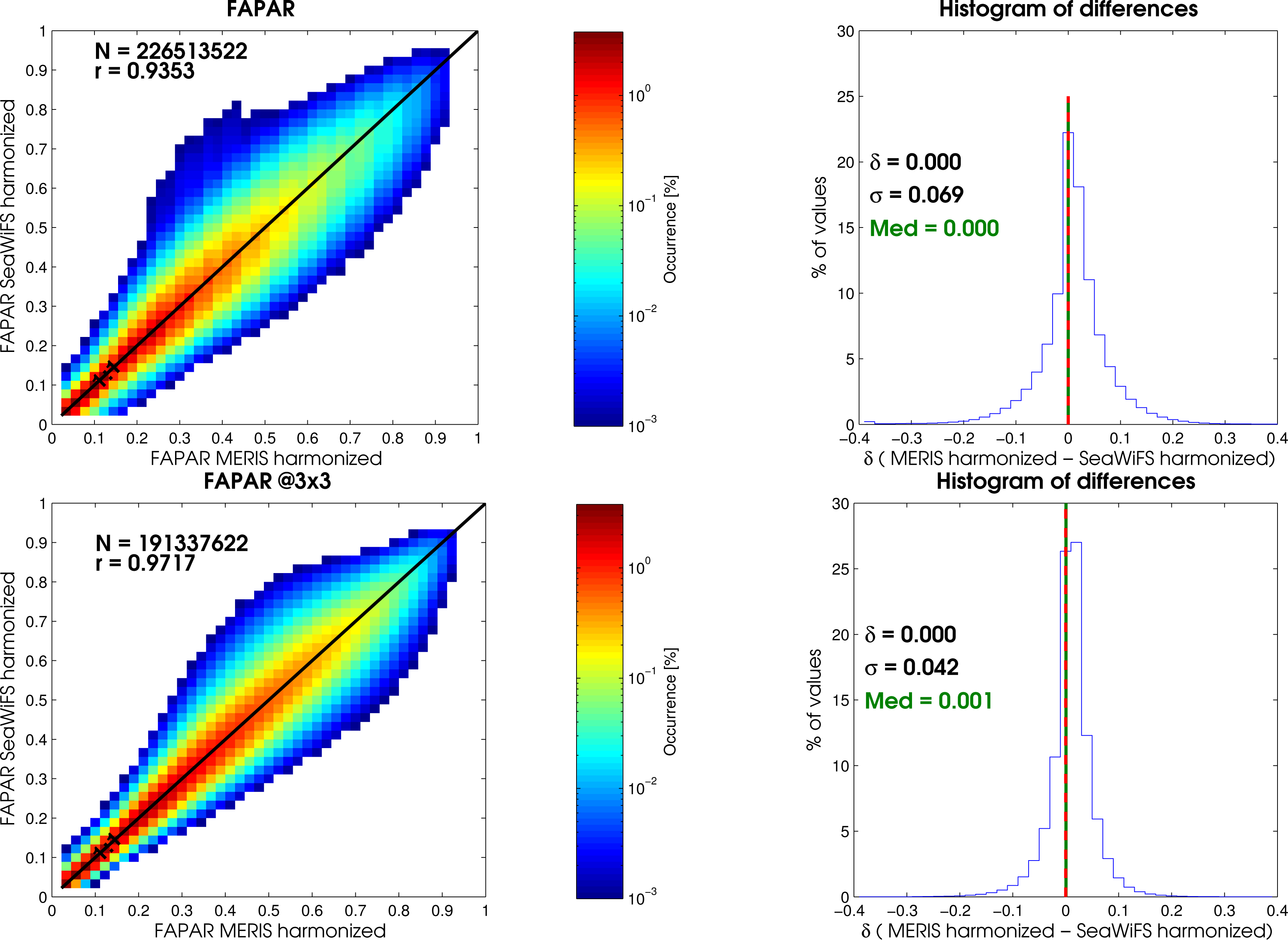
4. Results
5. Impact of Harmonization on Data Series Analysis
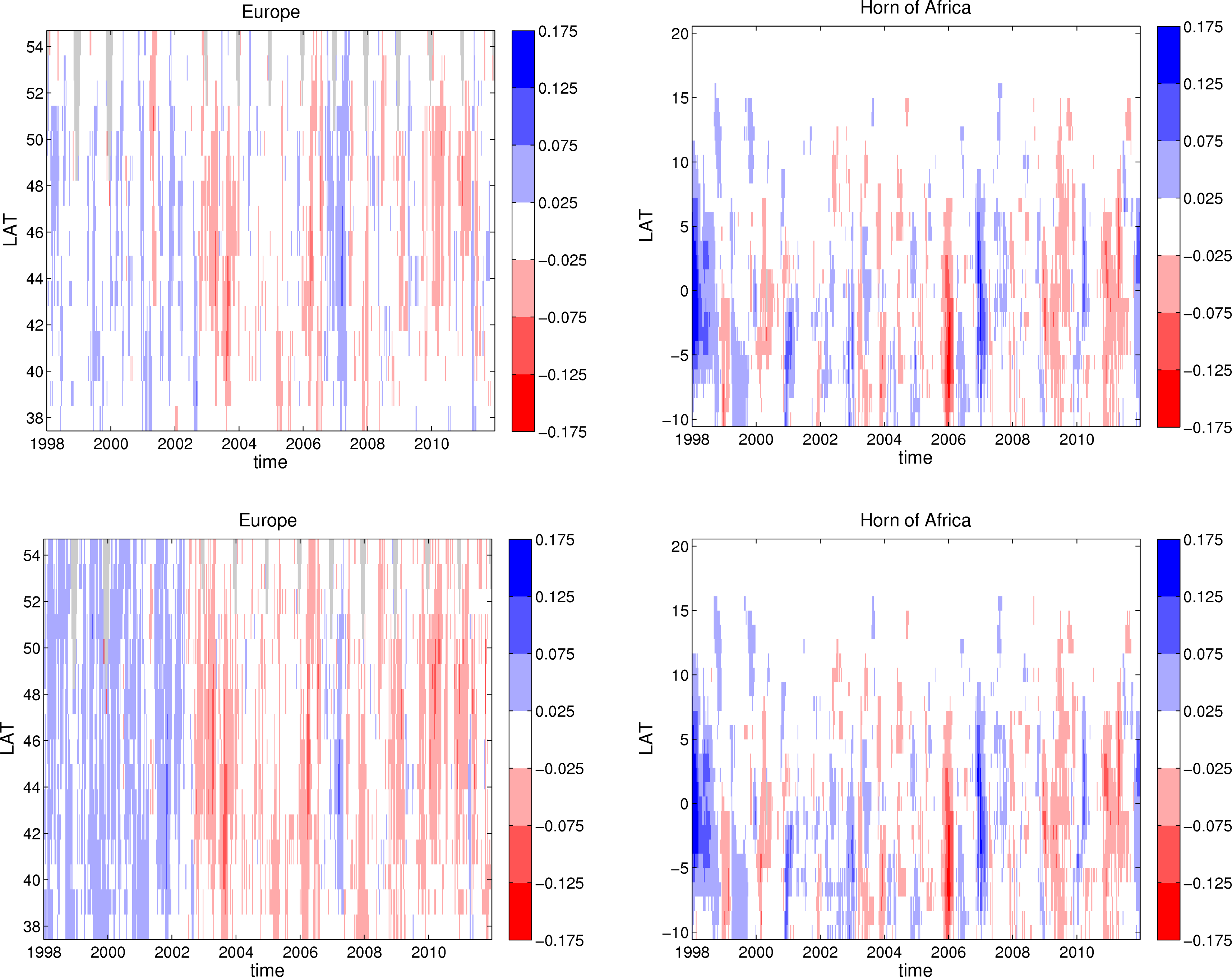
5.1. Spatial Anomalies
5.2. Temporal Anomalies
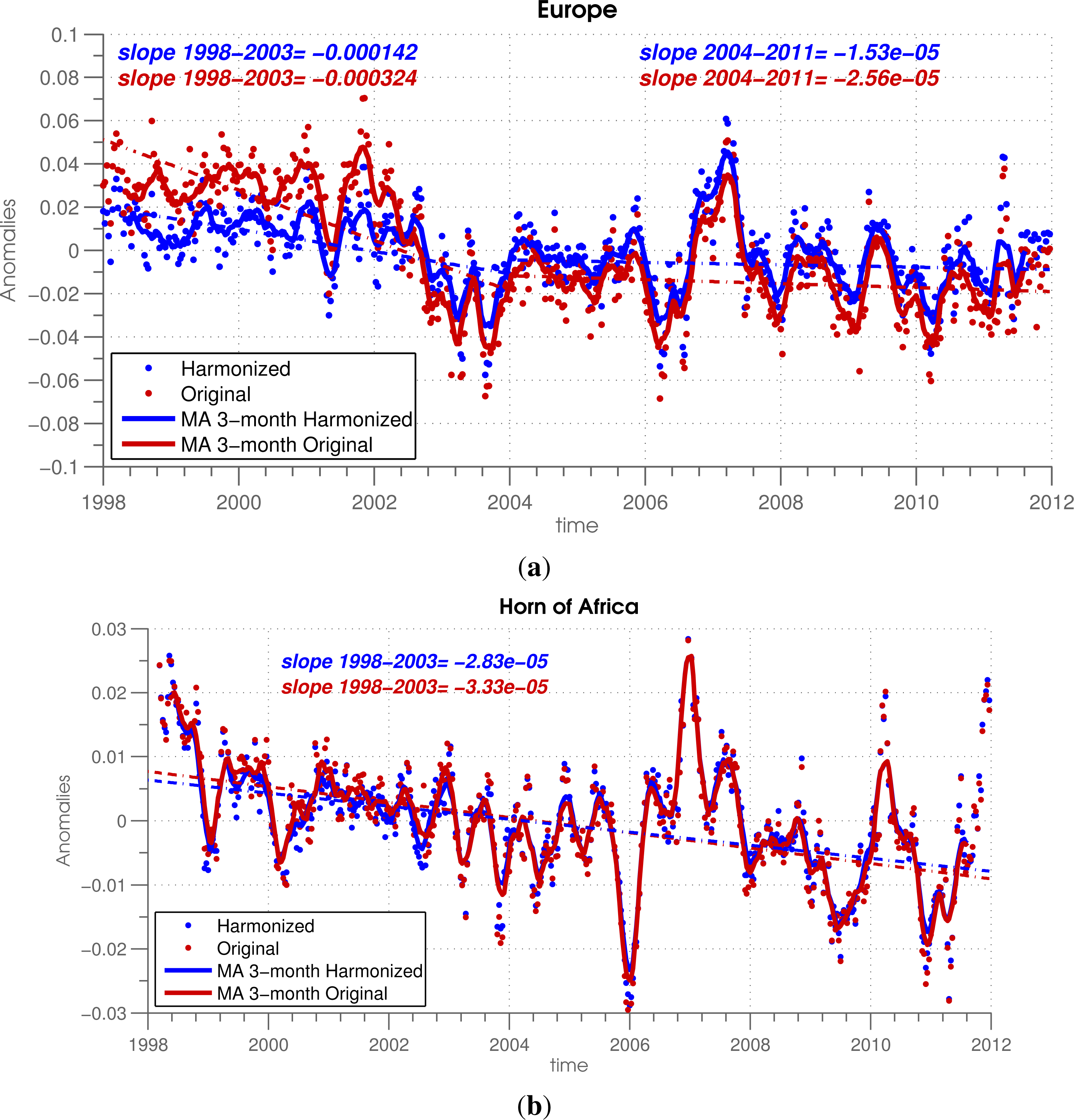
5.3. Trends in Temporal Anomalies
6. Conclusions
Acknowledgments
Conflict of Interest
References
- GTOS, Terrestrial Essential Climate Variables for Assessment, Mitigation and Adaptation; GTOS 52; Food and Agriculture Organization, UN: Rome, Italy, 2008.
- Moriondo, M.; Giannakopoulos, C.; Bindi, M. Climate change impact assessment: The role of climate extremes in crop yield simulation. Clim. Chang 2011, 104, 679–701. [Google Scholar]
- Fischer, E.; Schär, C. Consistent geographical patterns of changes in high-impact European heatwaves. Nat. Geosci 2010, 3, 398–403. [Google Scholar]
- Mahecha, M.D.; Fürst, L.M.; Gobron, N.; Lange, H. Identifying multiple spatiotemporal patterns: A refined view on terrestrial photosynthetic activity. Pattern Recognit. Lett 2010, 31, 2309–2317. [Google Scholar]
- Wang, K.; Mao, J.; Dickinson, R.E.; Shi, X.; Post, W.M.; Zhu, Z.; Myneni, R.B. Evaluation of CLM4 solar radiation partitioning scheme using remote sensing and site level FPAR datasets. Remote Sens 2013, 5, 2857–2882. [Google Scholar]
- Mills, E. Insurance in a climate of change. Science 2005, 309, 1040–1044. [Google Scholar]
- Knorr, W.; Gobron, N.; Scholze, M.; Kaminski, T.; Schnur, R.; Pinty, B. Impact of terrestrial biosphere carbon exchanges on the anomalous CO2 increase in 2002–2003. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Böttcher, H.; Eisbrenner, K.; Fritz, S.; Kindermann, G.; Kraxner, F.; McCallum, I.; Obersteiner, M. An assessment of monitoring requirements and costs of ‘Reduced Emissions from Deforestation and Degradation’. Carbon Balanc. Manag 2009, 4, 7. [Google Scholar] [CrossRef]
- Corbera, E.; Schroeder, H. Governing and implementing REDD+. Environ. Sci. Policy 2011, 14, 89–99. [Google Scholar]
- Peskett, L.; Schreckenberg, K.; Brown, J. Institutional approaches for carbon financing in the forest sector: Learning lessons for REDD+ from forest carbon projects in Uganda. Environ. Sci. Policy 2011, 14, 216–229. [Google Scholar]
- GCOS, Summary Report of the Eleventh Session of the WMO-IOC-UNEP-ICSU; WMO/TD 1189; Rep. GCOS-87; WMO: Melbourne, Australia, 2003.
- Running, S.W. Global primary production from terrestrial vegetation: Estimates integrating satellite remote sensing and computer simulation technology. Sci. Total Environ 1986, 56, 233–242. [Google Scholar]
- Sellers, P.J.; Dickinson, R.E.; Randall, D.A.; Betts, A.K.; Hall, F.G.; Berry, J.A.; Collatz, G.J.; Denning, A.S.; Mooney, H.A.; Nobre, C.A.; et al. Modeling the exchanges of energy, water, and carbon between continents and the atmosphere. Science 1997, 275, 502–509. [Google Scholar]
- Meroni, M.; Marinho, E.; Sghaier, N.; Verstrate, M.M.; Leo, O. Remote sensing based yield estimation in a stochastic framework—Case study of durum wheat in Tunisia. Remote Sens 2013, 5, 539–557. [Google Scholar]
- Pinty, B.; Lavergne, T.; Widlowski, J.L.; Gobron, N.; Verstraete, M.M. On the need to observe vegetation canopies in the near-infrared to estimate visible light absorption. Remote Sens. Environ 2008, 113, 10–23. [Google Scholar]
- Gobron, N.; Pinty, B.; Verstraete, M.M.; Widlowski, J.L. Advanced spectral algorithm and new vegetation indices optimized for up coming sensors: Development, accuracy and applications. IEEE Trans. Geosci. Remote Sens 2000, 38, 2489–2505. [Google Scholar]
- Gobron, N.; Pinty, B.; Aussédat, O.; Chen, J.; Cohen, W.; Fensholt, R.; Gond, V.; Huemmrich, K.; Lavergne, T.; Mélin, F.; et al. Evaluation of fraction of absorbed photosynthetically active radiation products for different canopy radiation transfer regimes: Methodology and results using Joint Research Center products derived from SeaWiFS against ground-based estimations. J. Geophys. Res.-Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Gobron, N.; Pinty, B.; Aussédat, O.; Taberner, M.; Faber, O.; Mélin, F.; Lavergne, T.; Robustelli, M.; Snoeij, P. Uncertainty estimates for the FAPAR operational products derived from MERIS-Impact of top-of-atmosphere radiance uncertainties and validation with field data. Remote Sens. Environ 2008, 112, 1871–1883. [Google Scholar]
- Donlon, C.; Berruti, B.; Buongiorno, A.; Ferreira, M.H.; Féménias, P.; Frerick, J.; Goryl, P.; Klein, U.; Laur, H.; Mavrocordatos, C.; et al. The Global Monitoring for Environment and Security (GMES) sentinel-3 mission. Remote Sens. Environ 2012, 120, 37–57. [Google Scholar]
- Gobron, N.; Pinty, B.; Verstraete, M.M.; Govaerts, Y. The MERIS Global Vegetation Index (MGVI): Description and preliminary application. Int. J. Remote Sens 1999, 20, 1917–1927. [Google Scholar]
- Mélin, F.; Steinich, C.; Gobron, N.; Pinty, B.; Verstraete, M. Optimal merging of LAC and GAC data from SeaWiFS. Int. J. Remote Sens 2002, 23, 801–807. [Google Scholar]
- Gobron, N.; Ceccherini, G. Multi-Sensor Intercomparison of JRC-FAPAR Products: JRC and VITO Implementation; EUR Report 25668 EN; Publications Office of the European Union: Luxembourg, 2012. [Google Scholar]
- Pinty, B.; Gobron, N.; Mélin, F.; Verstraete, M.M. Time Composite Algorithm Theoretical Basis Document; EUR Report 20150 EN; Institute for Environment and Sustainability, European Commission Joint Research Centre: Ispra, Italy, 2002. [Google Scholar]
- Aussédat, O.; Gobron, N.; Pinty, B.; Taberner, M. MERIS Level 3 Land Surface Time Composite-Product File Description; EUR Report 22165 EN; Institute for Environment and Sustainability, European Commission Joint Research Centre: Ispra, Italy, 2006. [Google Scholar]
- Gobron, N.; Belward, A.; Pinty, B.; Knorr, W. Monitoring biosphere vegetation 1998–2009. Geophys. Res. Lett 2010, 37, L15402. [Google Scholar] [CrossRef]
- Gobron, N.; Pinty, B.; Aussédat, O.; Taberner, M.; Faber, O.; Mélin, F.; Lavergne, T.; Robustelli, M.; Snoeij, P. Uncertainty estimates for the FAPAR operational products derived from MERIS-impact of top-of-atmosphere radiance uncertainties and validation with field data. Remote Sens. Environ 2008, 112, 1871–1883. [Google Scholar]
- Musial, J.; Verstraete, M.M.; Gobron, N. Comparing the effectiveness of recent algorithms to fill and smooth incomplete and noisy time series. Atmos. Chem. Phys. Discuss 2011, 11, 14259–14308. [Google Scholar]
- Ibanez, F.; Conversi, A. Prediction of missing values and detection of ‘exceptional events’ in a chronological planktonic series: A single algorithm. Ecol. Model 2002, 154, 9–23. [Google Scholar]
- Wang, G.; Garcia, D.; Liu, Y.; de Jeu, R.; Johannes Dolman, A. A three-dimensional gap filling method for large geophysical datasets: Application to global satellite soil moisture observations. Environ. Model. Softw 2012, 30, 139–142. [Google Scholar]
- Schär, C.; Jendritzky, G. Hot news from summer 2003. Nature 2004, 432, 559–560. [Google Scholar]
- Gobron, N.; Pinty, B.; Mélin, F.; Taberner, M.; Verstraete, M.M.; Belward, A.S.; Lavergne, T.; Widlowski, J.L. The state of vegetation in europe following the 2003 drought. Int. J. Remote Sens 2005, 26, 2013–2020. [Google Scholar]
- Dutra, E.; Magnusson, L.; Wetterhall, F.; Cloke, H.; Balsamo, G.; Boussetta, S.; Pappenberger, F. The 2010–2011 drought in the Horn of Africa in ECMWF reanalysis and seasonal forecast products. Int. J. Climatol. 2012, 33. [Google Scholar] [CrossRef]
- Peterson, T.; Stott, P.; Herring, S. Explaining extreme events of 2011 from a climate perspective. Bull. Am. Meteorol. Soc 2012, 93, 1041–1067. [Google Scholar]
- Jung, M.; Verstraete, M.; Gobron, N.; Reichstein, M.; Papale, D.; Bondeau, A.; Robustelli, M.; Pinty, B. Diagnostic assessment of European gross primary production. Glob. Chang. Biol 2008, 14, 2349–2364. [Google Scholar]
- Institute for Environment and Sustainability, European Commission Joint Research Centre. Earth Land Information System (ELIS). Available online: http://fapar.jrc.ec.europa.eu (accessed on 6 May 2013).



| Outlier Decontamination | Gap-Filling | Bias Correction | Flag |
|---|---|---|---|
| No | No | No | 0 |
| No | No | Yes | 1 |
| No | Yes | No | 2 |
| No | Yes | Yes | 3 |
| Yes | Yes | No | 4 |
| Yes | Yes | Yes | 5 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ceccherini, G.; Gobron, N.; Robustelli, M. Harmonization of Fraction of Absorbed Photosynthetically Active Radiation (FAPAR) from Sea-ViewingWide Field-of-View Sensor (SeaWiFS) and Medium Resolution Imaging Spectrometer Instrument (MERIS). Remote Sens. 2013, 5, 3357-3376. https://doi.org/10.3390/rs5073357
Ceccherini G, Gobron N, Robustelli M. Harmonization of Fraction of Absorbed Photosynthetically Active Radiation (FAPAR) from Sea-ViewingWide Field-of-View Sensor (SeaWiFS) and Medium Resolution Imaging Spectrometer Instrument (MERIS). Remote Sensing. 2013; 5(7):3357-3376. https://doi.org/10.3390/rs5073357
Chicago/Turabian StyleCeccherini, Guido, Nadine Gobron, and Monica Robustelli. 2013. "Harmonization of Fraction of Absorbed Photosynthetically Active Radiation (FAPAR) from Sea-ViewingWide Field-of-View Sensor (SeaWiFS) and Medium Resolution Imaging Spectrometer Instrument (MERIS)" Remote Sensing 5, no. 7: 3357-3376. https://doi.org/10.3390/rs5073357




