Evaluation of CLM4 Solar Radiation Partitioning Scheme Using Remote Sensing and Site Level FPAR Datasets
Abstract
:1. Introduction
2. Methodology
2.1. Model Description
2.2. Model Simulation
2.3. Observation Data Description
2.3.1. Moderate Resolution Imaging Spectroradiometer (MODIS) Fraction of Absorbed Photosynthetically Active Radiation (FPAR)
2.3.2. Fraction of Photosynthetically Active Radiation (FPAR) 3g/Leaf Area Index (LAI) 3g Derived from Global Inventory Modeling and Mapping Studies (GIMMS)
2.3.3. Joint Research Center (JRC) FPAR
2.3.4. Site-Level FPAR
2.4. Assessment of Consistency between Model and Observation Data Sets
2.4.1. Diurnal Cycle
2.4.2. Seasonal Cycle
2.4.3. Long-Term Trends
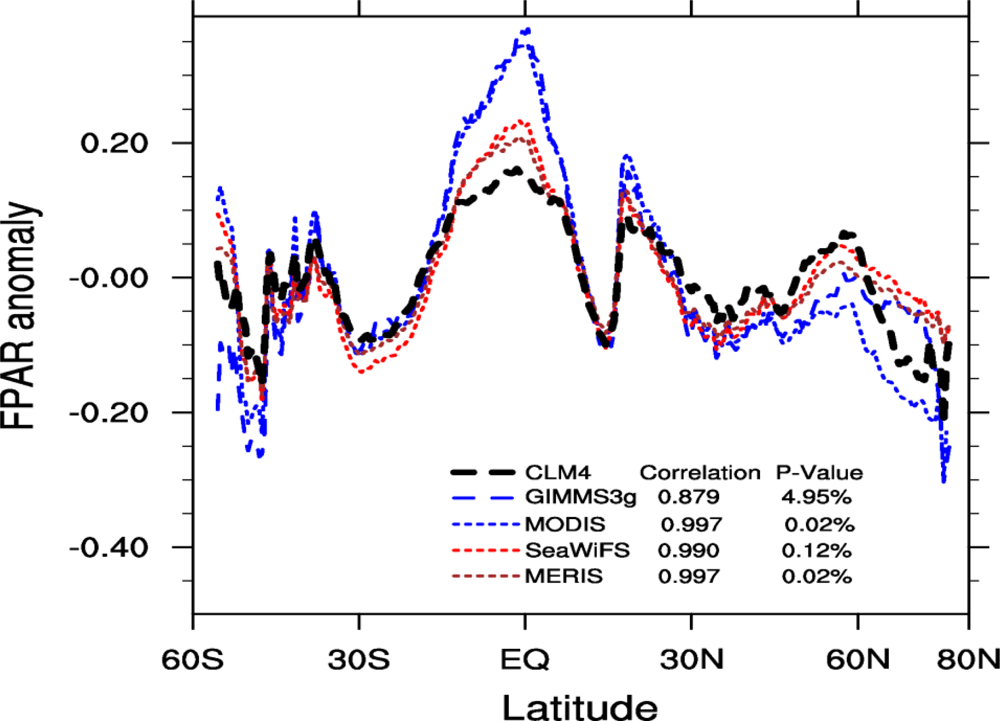
2.4.4. Zonal Patterns
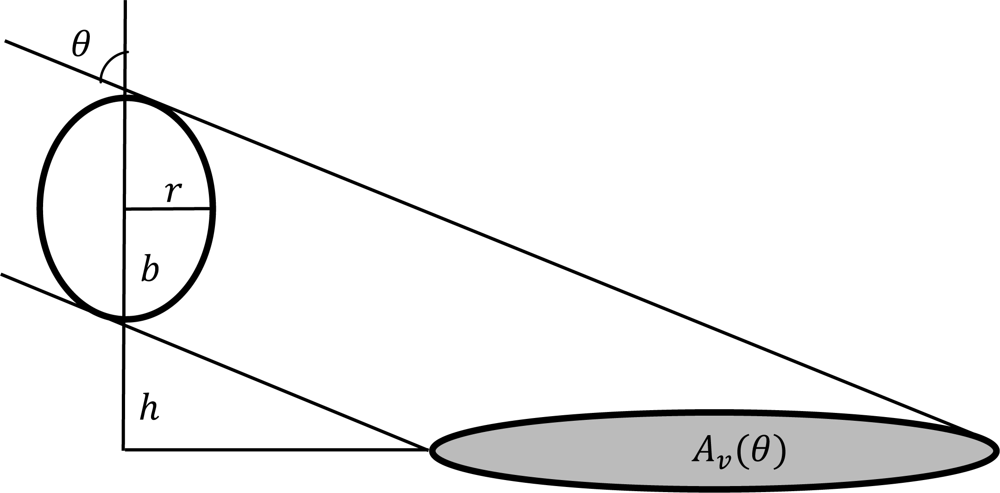
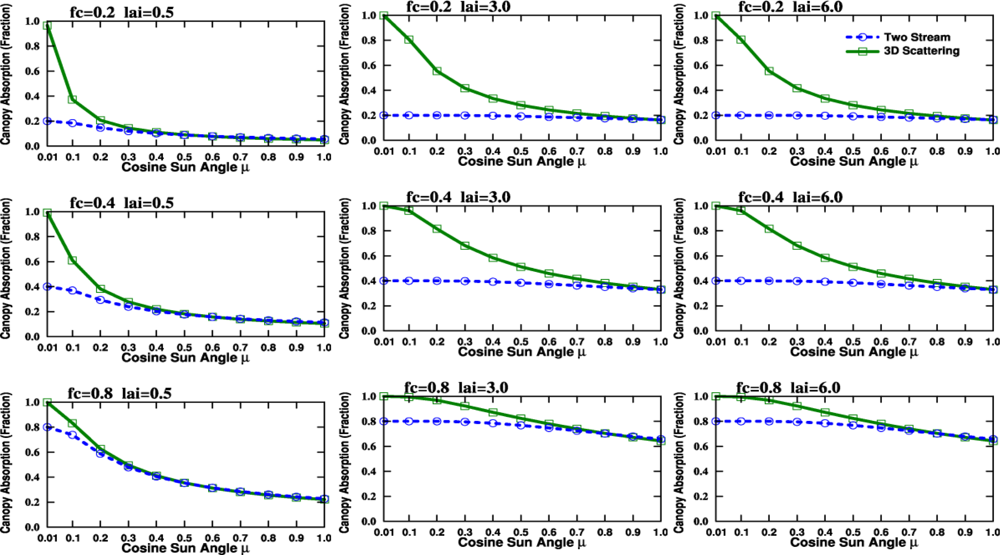
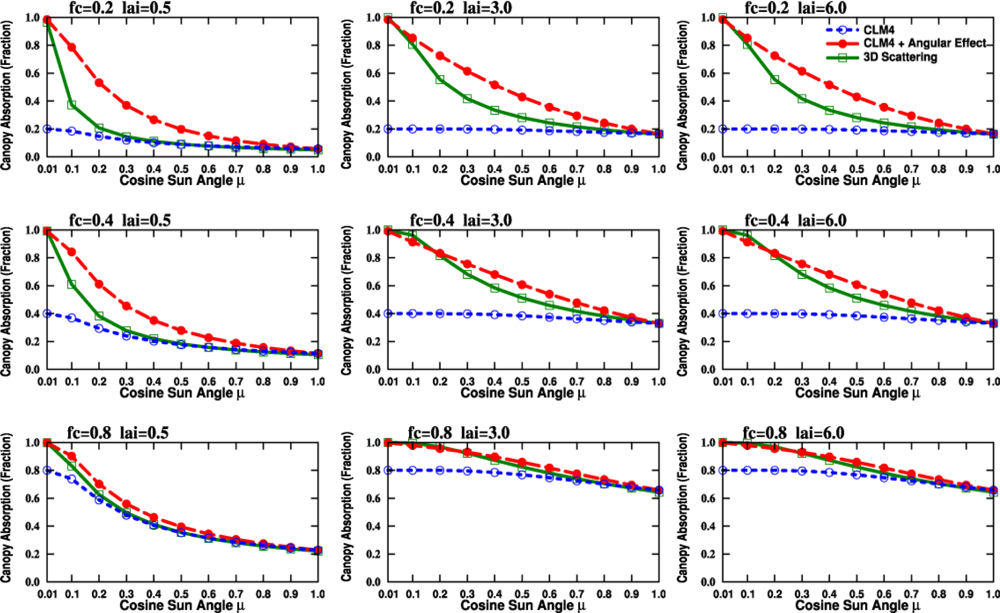
2.5. The Angular Effect in Fraction of Absorbed Photosynthetically Active Radiation (FPAR) under Direct Solar Radiation
3. Results
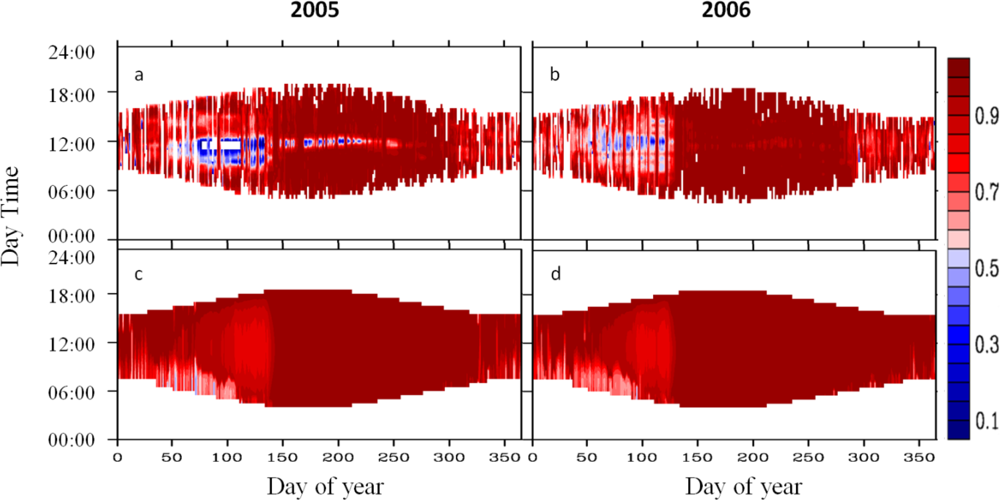
3.1. Diurnal Cycle
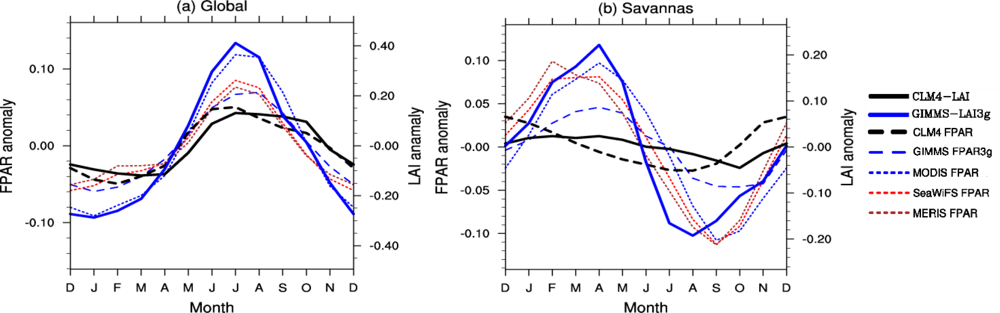
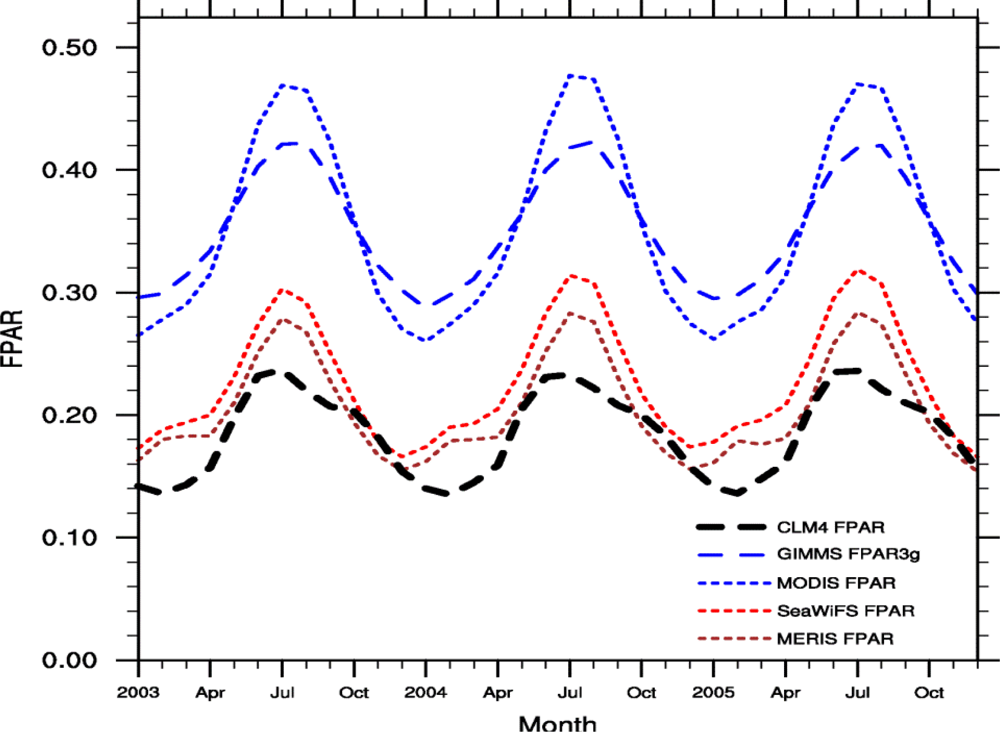
3.2. Seasonal Cycle
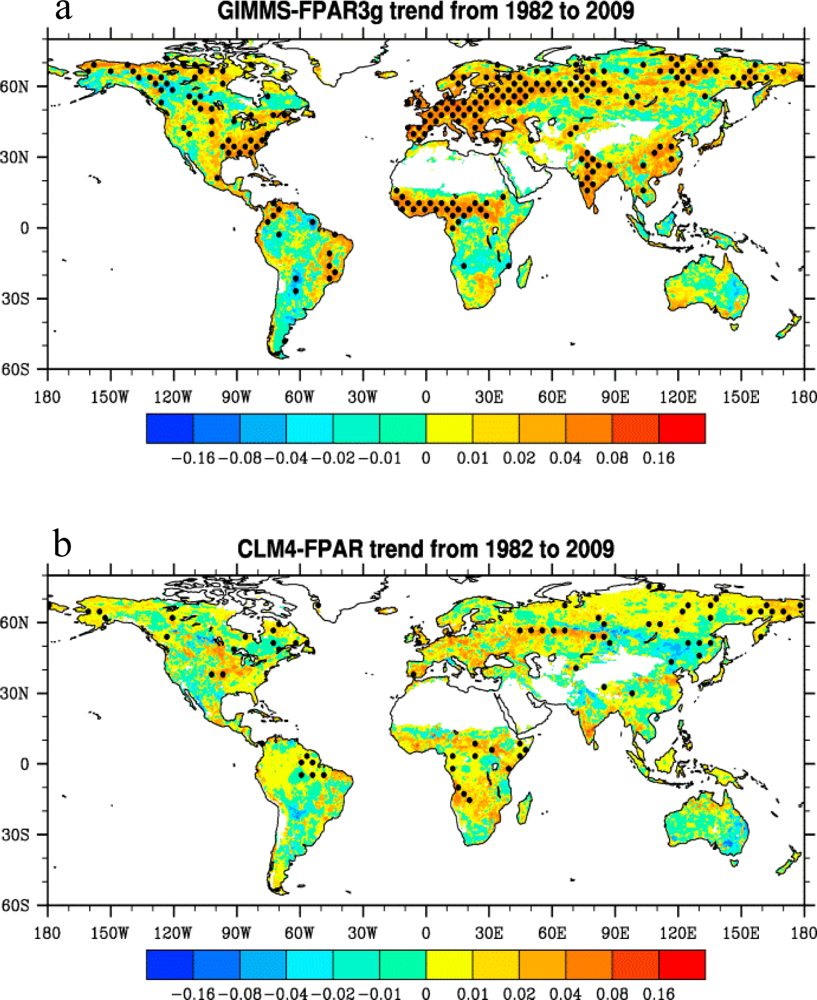
3.3. Long-Term Trends
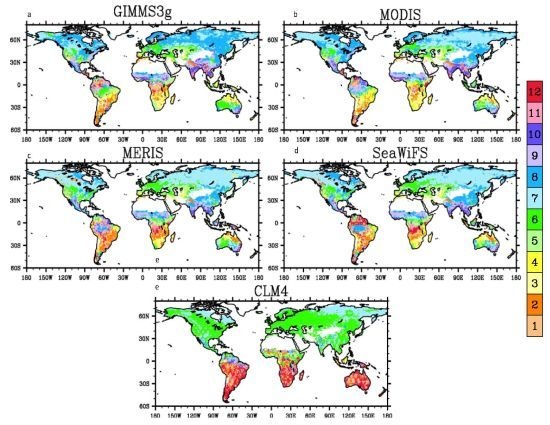
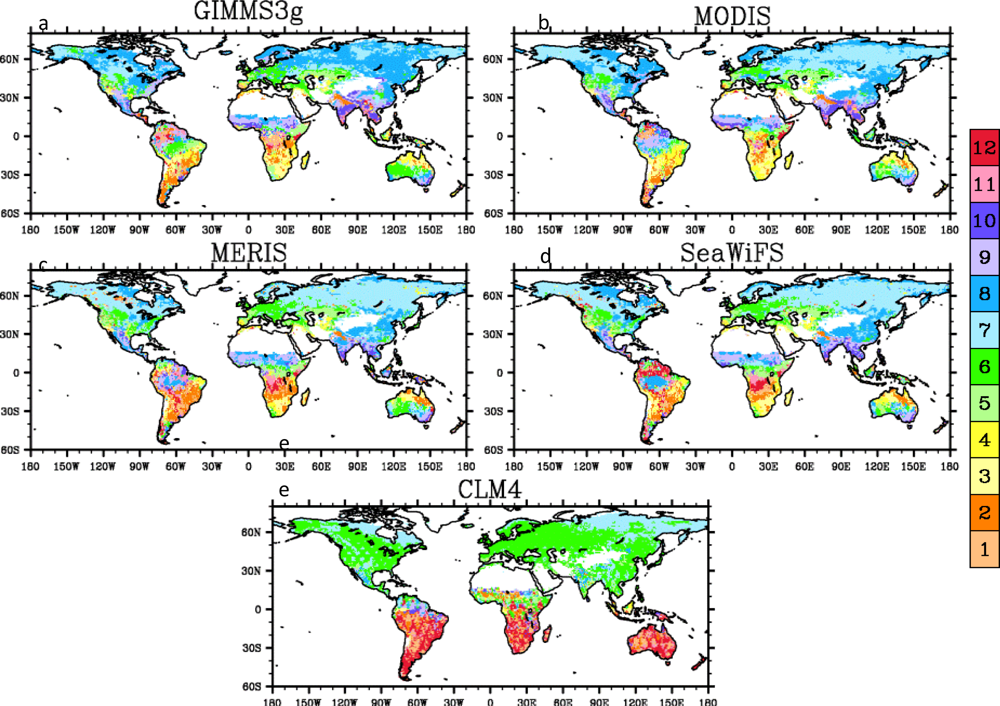
3.4. Spatial Patterns
4. Discussion
4.1. Problems with the Diurnal Cycle in the CLM4
4.2. Spatial Patterns of Month with Maximum Fraction of Absorbed Photosynthetically Active Radiation (FPAR) in the Amazon
4.3. Absolute Value
4.4. Comparison with Previous Study
5. Conclusions
Acknowledgments
- Conflict of InterestThe authors declare no conflict of interest.
References
- Dickinson, R.E. Land surface processes and climate—Surface albedos and energy balance. Adv. Geophys. 1983, 25, 305–353. [Google Scholar]
- Avissar, R.; Verstraete, M.M. The representation of continental surface processes in atmospheric models. Rev. Geophys. 1990, 28, 35–52. [Google Scholar]
- Sellers, P.J.; Dickinson, R.E.; Randall, D.A.; Betts, A.K.; Hall, F.G.; Berry, J.A.; Collatz, G.J.; Denning, A.S.; Mooney, H.A.; Nobre, C.A.; et al. Modeling the exchanges of energy, water, and carbon between continents and the atmosphere. Science 1997, 275, 502–509. [Google Scholar]
- Viterbo, P.; Betts, A.K. Impact on ECMWF forecasts of changes to the albedo of the boreal forests in the presence of snow. J. Geophys. Res. 1999, 104, 27803–27810. [Google Scholar]
- Ma, Y.; Su, Z.; Koike, T.; Yao, T.; Ishikawa, H.; Ueno, K.; Menenti, M. On measuring and remote sensing surface energy partitioning over the Tibetan Plateau—from GAME/Tibet to CAMP/Tibet. Phys. Chem. Earth 2003, 28, 63–74. [Google Scholar]
- Gu, L.; Meyers, T.; Pallardy, S.G.; Hanson, P.J.; Yang, B.; Heuer, M.; Hosman, K.P.; Riggs, J.S.; Sluss, D.; Wullschleger, S.D. Direct and indirect effects of atmospheric conditions and soil moisture on surface energy partitioning revealed by a prolonged drought at a temperate forest site. J. Geophys. Res. 2006, 111, 1–13. [Google Scholar]
- Li, S.-G.; Eugster, W.; Asanuma, J.; Kotani, A.; Davaa, G.; Oyunbaatar, D.; Sugita, M. Energy partitioning and its biophysical controls above a grazing steppe in central Mongolia. Agric. For. Meteorol. 2006, 137, 89–106. [Google Scholar]
- Peng, Y.; Gitelson, A.A.; Keydan, G.; Rundquist, D.C.; Moses, W. Remote estimation of gross primary production in maize and support for a new paradigm based on total crop chlorophyll content. Remote Sens. Environ. 2011, 115, 978–989. [Google Scholar]
- Zhang, Q.; Middleton, E.M.; Gao, B.-C.; Cheng, Y.-B. Using EO-1 hyperion to simulate HyspIRI products for a coniferous forest: The fraction of PAR absorbed by chlorophyll (fAPARchl) and leaf water content (LWC). IEEE Trans. Geosci. Remote Sens. 2012, 50, 1844–1852. [Google Scholar]
- Houborg, R.; Cescatti, A.; Migliavacca, M.; Kustas, W.P. Satellite retrievals of leaf chlorophyll and photosynthetic capacity for improved modeling of GPP. Agric. For. Meteorol. 2013, 177, 10–23. [Google Scholar]
- Betts, A.K.; Ball, J.H.; Beljaars, A.C.M.; Miller, M.J.; Viterbo, P.A. The land surface-atmosphere interaction: A review based on observational and global modeling perspectives. J. Geophys. Res. 1996, 101, 7209–7225. [Google Scholar]
- Baldocchi, D.D.; Law, B.E.; Anthoni, P.M. On measuring and modeling energy fluxes above the floor of a homogeneous and heterogeneous conifer forest. Agric. For. Meteorol. 2000, 102, 187–206. [Google Scholar]
- Dickinson, R.E.; Zhou, L.; Tian, Y.; Liu, Q.; Lavergne, T.; Pinty, B.; Schaaf, C.B.; Knyazikhin, Y. A three-dimensional analytic model for the scattering of a spherical bush. J. Geophys. Res. 2008, 113, D20113. [Google Scholar]
- Pinty, B.; Lavergne, T.; Kaminski, T.; Aussedat, O.; Giering, R.; Gobron, N.; Taberner, M.; Verstraete, M.M.; Voβbeck, M.; Widlowski, J.-L. Partitioning the solar radiant fluxes in forest canopies in the presence of snow. J. Geophys. Res. 2008, 113, D04104. [Google Scholar]
- Guan, H.; Wilson, J.L. A hybrid dual-source model for potential evaporation and transpiration partitioning. J. Hydrol. 2009, 377, 405–416. [Google Scholar]
- Pinty, B.; Lavergne, T.; Dickinson, R.E.; Widlowski, J.L.; Gobron, N.; Verstraete, M.M. Simplifying the interaction of land surfaces with radiation for relating remote sensing products to climate models. J. Geophys. Res. 2006, 111, D02116. [Google Scholar]
- Bonan, G.B.; Lawrence, P.J.; Oleson, K.W.; Levis, S.; Jung, M.; Reichstein, M.; Lawrence, D.M.; Swenson, S.C. Improving canopy processes in the Community Land Model version 4 (CLM4) using global flux fields empirically inferred from FLUXNET data. J. Geophys. Res. 2011, 116, 1–22. [Google Scholar]
- Oleson, K.W.; Lawrence, D.M.; Gordon, B.; Flanner, M.G.; Kluzek, E.; Peter, J.; Levis, S.; Swenson, S.C.; Thornton, E.; Feddema, J. Technical Description of Version 4.0 of the Community Land Model (CLM); NCAR Technical Note NCAR/TN 478+STR; The National Center for Atmospheric Research (NCAR): Boulder, CO, USA, 2010. [Google Scholar]
- Niu, G.-Y.; Yang, Z.-L. Effects of vegetation canopy processes on snow surface energy and mass balances. J. Geophys. Res. 2004, 109, D23111. [Google Scholar]
- Bonan, G.B.; Levis, S.; Kergoat, L.; Oleson, K.W. Landscapes as patches of plant functional types: An integrating concept for climate and ecosystem models. Glob. Biogeochem. Cy. 2002, 16, 1021. [Google Scholar]
- Myneni, R.; Hoffman, S.; Knyazikhin, Y.; Privette, J.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.; et al. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ. 2002, 83, 214–231. [Google Scholar]
- Senna, M.C.A.; Costa, M.H.; Shimabukuro, Y.E. Fraction of photosynthetically active radiation absorbed by Amazon tropical forest: A comparison of field measurements, modeling, and remote sensing. J. Geophys. Res. 2005, 110, G01008. [Google Scholar]
- Gobron, N.; Pinty, B.; Aussedat, O.; Chen, J.M.; Cohen, W.B.; Fensholt, R.; Gond, V.; Huemmrich, K.F.; Lavergne, T.; Mélin, F.; et al. Evaluation of fraction of absorbed photosynthetically active radiation products for different canopy radiation transfer regimes: Methodology and results using Joint Research Center products derived from SeaWiFS against ground-based estimations. J. Geophys. Res. 2006, 111. [Google Scholar]
- Gobron, N.; Pinty, B.; Aussedat, O.; Taberner, M.; Faber, O.; Melin, F.; Lavergne, T.; Robustelli, M.; Snoeij, P. Uncertainty estimates for the FAPAR operational products derived from MERIS—Impact of top-of-atmosphere radiance uncertainties and validation with field data. Remote Sens. Environ. 2008, 112, 1871–1883. [Google Scholar]
- Steinberg, D.C.; Goetz, S.J.; Hyer, E.J. Validation of MODIS FPAR products in boreal forests of Alaska. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1818–1828. [Google Scholar]
- Huemmrich, K.F.; Privette, J.L.; Mukelabai, M.; Myneni, R.B.; Knyazikhin, Y. Time-series validation of MODIS land biophysical products in a Kalahari woodland, Africa. Int. J. Remote Sen. 2005, 26, 4381–4398. [Google Scholar]
- Levis, S.; Bonan, G.; Vertenstein, M.; Oleson, K. The Community Land Model’s Dynamic Global Vegetation Model (CLM-DGVM): Technical Description and User’s Guide; NCAR Technical Note NCAR/TN-459+IA; University Corporation for Atmospheric Research (NCAR): Boulder, CO, USA, 2004. [Google Scholar]
- McCallum, I.; Wagner, W.; Schmullius, C.; Shvidenko, A.; Obersteiner, M.; Fritz, S.; Nilsson, S. Comparison of four global FAPAR datasets over Northern Eurasia for the year 2000. Remote Sens. Environ. 2010, 114, 941–949. [Google Scholar]
- Knyazikhin, Y.; Martonchik, J.V; Myneni, R.B.; Diner, D.J.; Running, S.W. Synergistic algorithm for estimating vegetation canopy leaf area index and fraction of absorbed photosynthetically active radiation from MODIS and MISR data. J. Geophys. Res. 1998, 103, 32257–32275. [Google Scholar]
- Gobron, N.; Pinty, B.; Mélin, F.; Taberner, M.; Verstraete, M.M.; Robustelli, M.; Widlowski, J.L. Evaluation of the MERIS/ENVISAT FAPAR product. Adv. Space Res. 2007, 39, 105–115. [Google Scholar]
- Weiss, M.; Baret, F.; Garrigues, S.; Lacaze, R. LAI and fAPAR CYCLOPES global products derived from VEGETATION. Part 2: Validation and comparison with MODIS collection 4 products. Remote Sens. Environ. 2007, 110, 317–331. [Google Scholar]
- Zhang, Q.; Xiao, X.; Braswell, B. Characterization of seasonal variation of forest canopy in a temperate deciduous broadleaf forest, using daily MODIS data. Remote Sens. Environ. 2006, 105, 189–203. [Google Scholar]
- Ollinger, S.; Smith, M.-L. Net primary production and canopy nitrogen in a temperate forest landscape: An analysis using imaging spectroscopy, modeling and field data. Ecosystems 2005, 8, 760–778. [Google Scholar]
- CRUNCEP Data. Available online: http://dods.extra.cea.fr/data/p529viov/cruncep/ (accessed on 6 April 2013).
- Tian, Y.; Dickinson, R.E.; Zhou, L.; Zeng, X.; Dai, Y.; Myneni, R.B.; Knyazikhin, Y.; Zhang, X.; Friedl, M.; Yu, H.; Wu, W.; Shaikh, M. Comparison of seasonal and spatial variations of leaf area index and fraction of absorbed photosynthetically active radiation from Moderate Resolution Imaging Spectroradiometer (MODIS) and common land model. J. Geophys. Res. 2004, 109, D01103. [Google Scholar]
- Thornton, P.E.; Zimmermann, N.E. An improved canopy integration scheme for a land surface model with prognostic canopy structure. J. Clim. 2007, 20, 3902–3923. [Google Scholar]
- Thornton, P.E.; Law, B.E.; Gholz, H.L.; Clark, K.L.; Falge, E.; Ellsworth, D.S.; Goldstein, A.H.; Monson, R.K.; Hollinger, D.; Falk, M. Modeling and measuring the effects of disturbance history and climate on carbon and water budgets in evergreen needleleaf forests. Agric. For. Meteorol. 2002, 113, 185–222. [Google Scholar]
- Thornton, P.E.; Rosenbloom, N.A. Ecosystem model spin-up: Estimating steady state conditions in a coupled terrestrial carbon and nitrogen cycle model. Ecol. Model. 2005, 189, 25–48. [Google Scholar]
- Shi, X.; Mao, J.; Thornton, P.E.; Hoffman, F.M.; Post, W.M. The impact of climate, CO2, nitrogen deposition and land use change on simulated contemporary global river flow. Geophys. Res. Lett. 2011, 38, L08704. [Google Scholar]
- Mao, J.; Shi, X.; Thornton, P.E.; Hoffman, F.M.; Zhu, Z.; Myneni, R.B. Global latitudinal-asymmetric vegetation growth trends and their driving mechanisms: 1982–2009. Remote Sens. 2013, 5, 1484–1497. [Google Scholar]
- Zhao, M.; Heinsch, F.A.; Nemani, R.R.; Running, S.W. Improvements of the MODIS terrestrial gross and net primary production global data set. Remote Sens. Environ. 2005, 95, 164–176. [Google Scholar]
- Samanta, A.; Costa, M.H.; Nunes, E.L.; Vieira, S.A.; Xu, L.; Myneni, R.B. Comment on “Drought-induced reduction in global terrestrial net primary production from 2000 through 2009”. Science 2011, 333, 1093–1093. [Google Scholar]
- Yuan, H.; Dai, Y.; Xiao, Z.; Ji, D.; Shangguan, W. Reprocessing the MODIS leaf area index products for land surface and climate modelling. Remote Sens. Environ. 2011, 115, 1171–1187. [Google Scholar]
- Zhu, Z.; Bi, J.; Pan, Y.; Ganguly, S.; Samanta, A.; Xu, L.; Anav, A.; Nemani, R.R.; Myneni, R.B. global data sets of vegetation LAI3g and FPAR3g derived from GIMMS NDVI3g for the period 1981 to 2011. Remote Sens. 2013, 5, 927–948. [Google Scholar]
- Myneni, R.B.; Ramakrishna, R.; Nemani, R.; Running, S.W. Estimation of global leaf area index and absorbed par using radiative transfer models. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1380–1393. [Google Scholar]
- Gobron, N.; Mélin, F.; Pinty, B.; Verstraete, M.M.; Widlowski, J.-L.; Bucini, G. A Global Vegetation Index for SeaWiFS: Design and Applications. In Remote Sensing and Climate Modeling: Synergies and Limitations SE-1; Beniston, M., Verstraete, M.M., Eds.; Springer: New York, NY, USA, 2001; Volume 7, pp. 5–21. [Google Scholar]
- Gobron, N.; Belward, a.; Pinty, B.; Knorr, W. Monitoring biosphere vegetation 1998–2009. Geophys. Res. Lett. 2010, 37, 1–6. [Google Scholar]
- Pinty, B.; Gobron, N.; Melin, F.; Verstraete, M. A Time Composite Algorithm for FAPAR Products: Theoretical Basis Document; EUR Rep. 20150 EN; Institute for Environment and Sustainability-Joint Research Centre: Ispra, Italy, 2002; pp. 1–8. [Google Scholar]
- AmeriFlux Web Page. Available online: http://public.ornl.gov/ameriflux/ (accessed on 6 April 2013).
- Wang, K.; Dickinson, R.; Liang, S. Observational evidence on the effects of clouds and aerosols on net ecosystem exchange and evapotranspiration. Geophys. Res. Lett. 2008, 35, 1–5. [Google Scholar]
- Loveland, T.R.; Belward, A.S. The IGBP-DIS global 1 km land cover data set, DISCover: First results. Int. J. Remote Sens. 1997, 18, 3289–3295. [Google Scholar]
- Lawrence, P.J.; Chase, T.N. Representing a new MODIS consistent land surface in the Community Land Model (CLM 3.0). J. Geophys. Res. 2007. [Google Scholar] [CrossRef]
- Mao, J.; Thornton, P.; Shi, X. Remote sensing evaluation of CLM4 GPP for the period 2000–2009. J. Clim. 2012, 5327–5342. [Google Scholar]
- Strahler, A.; Jupp, D. Modeling bidirectional reflectance of forests and woodlands using Boolean models and geometric optics. Remote Sens. Environ. 1990, 166, 153–166. [Google Scholar]
- Schaefer, K.; Schwalm, C.R.; Williams, C.; Arain, M.A.; Barr, A.; Chen, J.M.; Davis, K.J.; Dimitrov, D.; Hilton, T.W.; Hollinger, D.Y. A model-data comparison of gross primary productivity: Results from the North American Carbon Program site synthesis. J. Geophys. Res. 2012, 117, G03010. [Google Scholar]
- Heil, G. W.; Muys, B.; Hansen, K. Environmental Effects of Afforestation in North-Western Europe: From Field Observations to Decision Support; Springer: New York, NY, USA, 2007; Volume 1. [Google Scholar]
- Huber, S.; Fensholt, R. Analysis of teleconnections between AVHRR-based sea surface temperature and vegetation productivity in the semi-arid Sahel. Remote Sens. Environ. 2011, 115, 3276–3285. [Google Scholar]
- Epstein, H.E.; Raynolds, M.K.; Walker, D.A.; Bhatt, U.S.; Tucker, C.J.; Pinzon, J.E. Dynamics of aboveground phytomass of the circumpolar Arctic tundra during the past three decades. Environ. Res. Lett. 2012, 7, 15506. [Google Scholar]
- Tape, K.; Sturm, M.; Racine, C. The evidence for shrub expansion in Northern Alaska and the Pan-Arctic. Glob. Change Biol. 2006, 12, 686–702. [Google Scholar]
- Zeng, H.; Jia, G.; Epstein, H. Recent changes in phenology over the northern high latitudes detected from multi-satellite data. Environ. Res. Lett. 2011, 6, 045508. [Google Scholar]
- Walker, D.A.; Epstein, H.E.; Raynolds, M.K.; Kuss, P.; Kopecky, M.A.; Frost, G.V.; Daniëls, F.J.A.; Leibman, M.O.; Moskalenko, N.G.; Matyshak, G.V.; et al. Environment, vegetation and greenness (NDVI) along the North America and Eurasia Arctic transects. Environ. Res. Lett. 2012, 7, 015504. [Google Scholar]
- Dickinson, R.E. Determination of the multi-scattered solar radiation from a leaf canopy for use in climate models. J. Comput. Phys. 2008, 227, 3667–3677. [Google Scholar]
- Saleska, S.R.; Miller, S.D.; Matross, D.M.; Goulden, M.L.; Wofsy, S.C.; Da Rocha, H.R.; De Camargo, P.B.; Crill, P.; Daube, B.C.; De Freitas, H.C.; et al. Carbon in Amazon forests: Unexpected seasonal fluxes and disturbance-induced losses. Science 2003, 302, 1554–1557. [Google Scholar]
- Huete, A.R.; Didan, K.; Shimabukuro, Y.E.; Ratana, P.; Saleska, S.R.; Hutyra, L.R.; Yang, W.; Nemani, R.R.; Myneni, R. Amazon rainforests green-up with sunlight in dry season. Geophys. Res. Lett. 2006, 33, 2–5. [Google Scholar]
- Oleson, K.W.; Niu, G.-Y.; Yang, Z.-L.; Lawrence, D.M.; Thornton, P.E.; Lawrence, P.J.; Stöckli, R.; Dickinson, R.E.; Bonan, G.B.; Levis, S.; Dai, A.; Qian, T. Improvements to the Community Land Model and their impact on the hydrological cycle. J. Geophys. Res.-Biogeosci. 2008, 113, G01021. [Google Scholar]
- Lawrence, D.M.; Oleson, K.W.; Flanner, M.G.; Thornton, P.E.; Swenson, S.C.; Lawrence, P.J.; Zeng, X.; Yang, Z.-L.; Levis, S.; Sakaguchi, K.; et al. Parameterization improvements and functional and structural advances in Version 4 of the community land model. J. Adv. Model. Earth Syst. 2011, 3, M03001. [Google Scholar]
- Peng, D.; Zhang, B.; Liu, L.; Fang, H.; Chen, D. Characteristics and drivers of global NDVI-based FPAR from 1982 to 2006. Glob. Biogeochem. Cy. 2012, 26, 1–15. [Google Scholar]




| GIMMS3g | MODIS | SeaWiFS | MERIS | |||||
|---|---|---|---|---|---|---|---|---|
| γ | p-value | γ | p-value | γ | p-value | γ | p-value | |
| Global | 0.953 | 3.36E-04 | 0.942 | 3.34E-04 | 0.894 | 8.65E-06 | 0.873 | 9.25E-05 |
| Evergreen Needle Leaf Forest | 0.86 | 0.66 | 0.86 | 3.28E-04 | 0.934 | 0.96 | 0.893 | 0.44 |
| Evergreen Broad Leaf Forest | 0.14 | 2.35E-05 | −0.860 | 4.10E-06 | −0.016 | 4.11E-07 | 0.246 | 5.25E-06 |
| Deciduous Needle Leaf Forest | 0.919 | 1.90E-05 | 0.944 | 1.91E-04 | 0.965 | 1.57E-05 | 0.941 | 6.61E-06 |
| Deciduous Broad Leaf Forest | 0.923 | 1.78E-05 | 0.875 | 2.92E-05 | 0.926 | 2.09E-05 | 0.938 | 4.34E-05 |
| Mixed Forest | 0.924 | 1.92E-07 | 0.916 | 4.78E-07 | 0.921 | 1.35E-08 | 0.908 | 1.01E-08 |
| Open Shrublands | 0.97 | 1.96E-02 | 0.964 | 2.56E-05 | 0.982 | 1.22E-04 | 0.983 | 2.55E-04 |
| Woody Savannas | 0.66 | 0.94 | 0.918 | 0.90 | 0.887 | 0.28 | 0.868 | 0.11 |
| Savannas | 0.024 | 1.80E-06 | 0.042 | 1.51E-06 | 0.341 | 1.35E-05 | 0.487 | 1.58E-05 |
| Grassland | 0.952 | 2.07E-06 | 0.954 | 1.13E-05 | 0.928 | 8.99E-05 | 0.926 | 2.43E-04 |
| Croplands | 0.95 | 3 1.70E-06 | 0.942 | 4.59E-06 | 0.894 | 8.83E-05 | 0.873 | 2.12E-04 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wang, K.; Mao, J.; Dickinson, R.E.; Shi, X.; Post, W.M.; Zhu, Z.; Myneni, R.B. Evaluation of CLM4 Solar Radiation Partitioning Scheme Using Remote Sensing and Site Level FPAR Datasets. Remote Sens. 2013, 5, 2857-2882. https://doi.org/10.3390/rs5062857
Wang K, Mao J, Dickinson RE, Shi X, Post WM, Zhu Z, Myneni RB. Evaluation of CLM4 Solar Radiation Partitioning Scheme Using Remote Sensing and Site Level FPAR Datasets. Remote Sensing. 2013; 5(6):2857-2882. https://doi.org/10.3390/rs5062857
Chicago/Turabian StyleWang, Kai, Jiafu Mao, Robert E. Dickinson, Xiaoying Shi, Wilfred M. Post, Zaichun Zhu, and Ranga B. Myneni. 2013. "Evaluation of CLM4 Solar Radiation Partitioning Scheme Using Remote Sensing and Site Level FPAR Datasets" Remote Sensing 5, no. 6: 2857-2882. https://doi.org/10.3390/rs5062857