Estimating Crop Coefficients Using Remote Sensing-Based Vegetation Index
Abstract
:1. Introduction
2. Material and Methodology
2.1. Study Area and Crop Evapotranspiration Dataset
2.2. NDVI and Kc Model Development and Validation
3. Result and Discussion
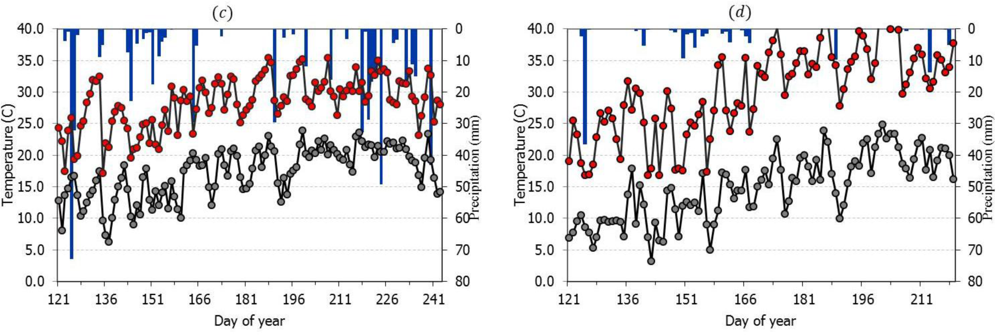
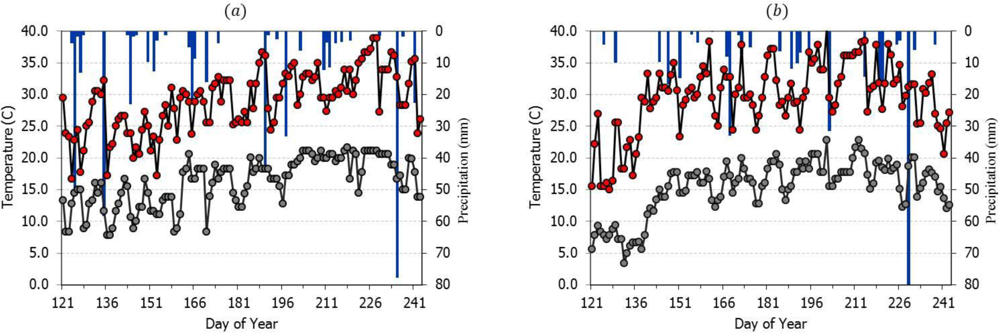
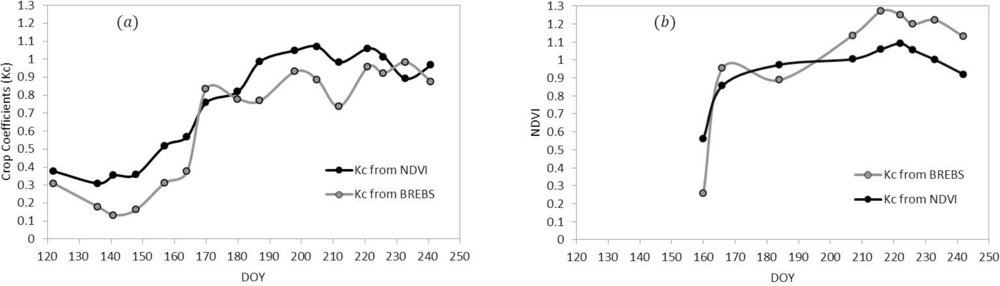
3.1. Seasonal NDVI and Crop Coefficient Patterns for Selected Agricultural Land Use
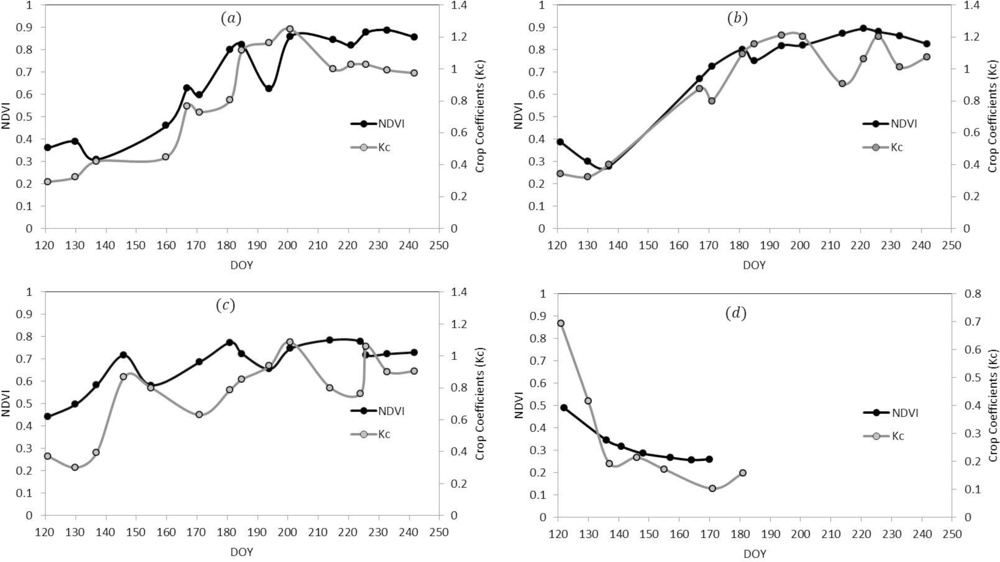
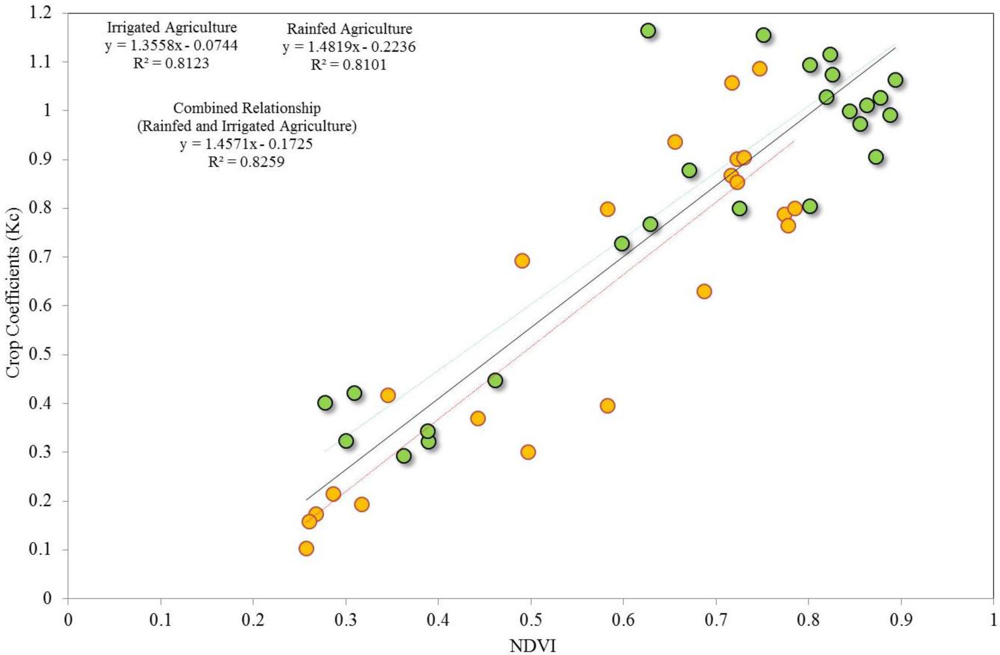
3.2. Development of NDVI and Crop Coefficient Relationship
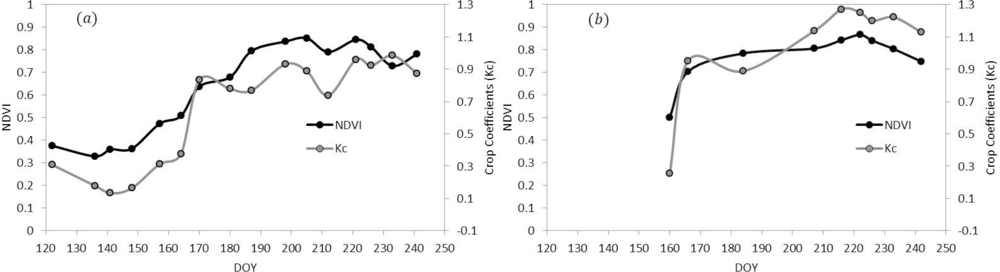
3.3. Validation of NDVI and Crop Coefficient Relationship
3.4. Uncertainties, Errors and Accuracies for NDVI and Crop Coefficient Relationship
4. Conclusion
References
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Smith, M.; Raes, D.; Wright, J.L. The FAO-56 dual crop coefficient method for predicting evaporation from soil and application extensions. J. Irrig. Drain. Eng 2005, 131, 2–13. [Google Scholar]
- Allen, R.G.; Walter, I.A.; Elliot, R.L.; Howell, T.A.; Itenfisu, D.; Jensen, M.E.; Snyder, R.L. The ASCE Standardized Reference Evaportranspiration Equation; American Society of Civil Engineers: Danvers, MA, USA, 2005; p. 59. [Google Scholar]
- Justice, C.O.; Townshend, J.R.G. Special issue on the Moderate Resolution Imaging Spectroradiometer (MODIS): A new generation of land surface monitoring. Remote Sens. Environ 2002, 83, 1–2. [Google Scholar]
- Doorenbos, J.; Pruitt, W.O. Guidelines for Predicting Crop Water Requirements; Irrigation and Drainge Paper 24; FAO: Rome, Italy, 1975. [Google Scholar]
- Kamble, B.; Chemin, Y.H. GIPE in GRASS Raster Addons. Available online: https://svn.osgeo.org/grass/grass-addons/grass6/imagery/gipe/i.vi.grid/description.html (accessed on 1 October 2012).
- Kamble, B.; Irmak, A. Assimilating Remote Sensing-Based ET into SWAP Model for Improved Estimation of Hydrological Predictions. Proceeding of the 2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; 3. [CrossRef]
- Sellers, P.J. Canopy reflectance, photosynthesis and transpiration. Int. J. Remote Sens 1985, 6, 1335–1372. [Google Scholar]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ 1979, 8, 127–150. [Google Scholar]
- Boegh, E.; Soegaard, H.; Hanan, N.; Kabat, O.; Lesch, L. A remote sensing study of the NDVI-Ts relationship and the transpiration from sparse vegetation in the Sahel based on high resolution data. Remote Sens. Environ 1998, 69, 224–240. [Google Scholar]
- Hunsaker, D.J.; Pinter, P.J., Jr.; Kimball, B.A. Wheat basal crop coefficients determined by normalized difference vegetation index. Irrig. Sci 2005, 24, 1–14. [Google Scholar]
- Bastiaanssen, W.G.M. SEBAL-based sensible and latent heat fluxes in the irrigated Gediz Basin, Turkey. J. Hydrol 2000, 229, 87–100. [Google Scholar]
- Irmak, S. Nebraska water and energy flux measurement, modeling, and research network (NEBFLUX). Trans. ASABE 2010, 53, 1097–1115. [Google Scholar]
- Jensen, M.E.; Burman, R.D.; Allen, R.G. (Eds.) Evapotranspiration and Irrigation Water Requirements; ASCE: Reston, VA, USA, 1990.
- Bausch, W.C.; Neale, C.M.U. Spectral inputs improve Maize crop coefficients and irrigation scheduling. Trans. ASAE 1989, 32, 1901–1908. [Google Scholar]
- Jayanthi, H.; Neale, C.M.U.; Wright, J.L. Seasonal Evapotranspiration Estimation Using Canopy Reflectance: A Case Study Involving Pink Beans. Proceedings of Remote Sensing and Hydrology 2000, Santa Fe, NM, USA, 2–7 April 2000; pp. 302–305.
- Irmak, A.; Ratcliffe, I.; Ranade, P.; Hubbard, K.; Singh, R.K.; Kamble, B.; Kjaersgaard, J. Estimation of land surface evapotranspiration with a satellite remote sensing procedure. Great Plains Res 2011, 21, 73–88. [Google Scholar]
- Benedetti, R.; Rossinni, P. On the use of NDVI profiles as a tool for agricultural statistics: The case study of wheat yield estimate and forecast in Emilia Romagna. Remote Sens. Environ 1993, 45, 311–326. [Google Scholar]
- Choudhury, B.J.; Ahmed, N.U.; Idso, S.B.; Reginato, R.J.; Daughtry, C.S.T. Relations between evaporation coefficients and vegetation indices studies by model simulations. Remote Sens. Environ 1994, 50, 1–17. [Google Scholar]
- Irmak, A.; Kamble, B. Evapotranspiration data assimilation with genetic algorithms and SWAP model for on-demand irrigation. Irrig. Sci 2009, 28, 101–112. [Google Scholar]
- Hubbard, K.G.; Sivakumar, M.V.K. (Eds.) Automated Weather Stations for Applications in Agriculture and Water Resources Management: Current Use and Future Perspectives. Proceedings of an International Workshop, Lincoln, NE, USA, 6–10 March 2000.
- Allen, R.G.; Clemmens, A.J.; Burt, C.M.; Solomon, K.; O’Halloran, T. Prediction accuracy for projectwide evapotranspiration using crop coefficients and reference evapotranspiration. J. Irrig. Drain. Eng 2005, 131, 24–36. [Google Scholar]
- Gamon, J.A.; Field, C.B.; Goulden, M.; Griffn, K.; Hartley, A.; Joel, G.; Penuelas, J.; Valentini, R. Relationships between NDVI, canopy structure and photosynthesis in three Californian vegetation types. Ecol. Appl 1995, 5, 28–41. [Google Scholar]
- Tasumi, M.; Allen, R.; Trezza, R.; Wright, J. Satellite-Based energy balance to assess within-population variance of crop coefficient curves. J. Irrig. Drain. Eng 2005, 131, 94–109. [Google Scholar]
- Hubbard, K.G. Climatic factors that limit daily evapotranspiration in sorghum. Clim. Res 1992, 2, 73–80. [Google Scholar]
- Baldocchi, D.; Falge, E.; Gu, L.H.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc 2001, 82, 2415–2434. [Google Scholar]
- Verma, S.B.; Dobermann, A.; Cassman, K.G.; Walters, D.T.; Knops, J.M.H.; Arkebauer, T.J.; Suyker, A.E.; Burba, G.G.; Amos, B.; Yang, H.S. Annual carbon dioxide exchange in irrigated and rainfed maize based agro-ecosystems. Agric. For. Meteorol 2005, 131, 77–96. [Google Scholar]
- Singh, R.; Irmak, A. Estimation of crop coefficients using satellite remote sensing. J. Irrig. Drain. Eng 2009, 135, 597–608. [Google Scholar]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric 1985, 1, 96–99. [Google Scholar]
- Hargreaves, G.H.; Allen, R.G. History and evaluation of Hargreaves evapotranspiration equation. J. Irrig. Drain. Eng 2003, 129, 53–63. [Google Scholar]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with ERTS, Proceedings of Third ERTS Symposium, Washington, DC, USA, 10–14 December 1973; 1, pp. 309–317.
- Gitelson, A.; Vina, A.; Masek, J.; Verma, S.; Suyker, A. Synoptic monitoring of gross primary productivity of maize using Landsat data. IEEE Geosci. Remote Sens. Lett 2008, 5, 133–137. [Google Scholar]


| Year | Name | Latitude | Longitude | Elevation (m) | Canopy Height | Vegetation Type | Crop |
|---|---|---|---|---|---|---|---|
| 2007 | Mead Irrigated Rotation | 41.1649 | −96.4701 | 362 | 1.83 m | Agriculture (maize-soybean rotation) | Maize |
| 2007 | Mead Rainfed | 41.1797 | −96.4396 | 363 | 1.71 m | Agriculture (maize) | Maize |
| 2007 | Mead Irrigated Continuous | 41.1651 | −96.4766 | 361 | 2.90 m | Agriculture (continuous maize) | Maize |
| 2007 | Cottonwood | 43.95 | −101.8466 | 744 | 20–40 cm | Grassland/range | Grass |
| 2007 | South-Central Agricultural Laboratory, Clay Center | 40.56667 | −98.1333 | 552 | N/A | Agriculture Soybean/maize | Maize |
| 2006 | South-Central Agricultural Laboratory, Clay Center | 40.56667 | −98.133333 | 552 | N/A | Agriculture (Soybean/maize) | Soybean |
| Sites | Mean | Max | Min | Standard Deviation | ||||
|---|---|---|---|---|---|---|---|---|
| NDVI | Kc | NDVI | Kc | NDVI | Kc | NDVI | Kc | |
| Cottonwood, SD, USA | 0.318 | 0.279 | 0.490 | 0.693 | 0.257 | 0.103 | 0.083 | 0.208 |
| Mead Irrigated Rotation, NE, USA | 0.676 | 0.822 | 0.822 | 5.302 | 0.309 | 0.293 | 0.209 | 0.316 |
| Mead Irrigated, NE, USA | 0.706 | 0.905 | 0.894 | 1.212 | 0.277 | 0.323 | 0.218 | 0.323 |
| Mead Rainfed, NE, USA | 0.676 | 0.763 | 0.785 | 1.086 | 0.442 | 0.300 | 0.104 | 0.240 |
| SCAL-2007 | 0.767 | 1.034 | 0.866 | 1.271 | 0.502 | 0.257 | 0.111 | 0.320 |
| SCAL-2006 | 0.636 | 0.635 | 0.852 | 0.984 | 0.330 | 0.133 | 0.200 | 0.323 |
| Statistical Index | 2006 | 2007 |
|---|---|---|
| Mean error | 0.12 | −0.09 |
| Mean absolute error | 0.14 | 0.17 |
| Mean square error | 0.02 | 0.03 |
| Root mean square error | 0.16 | 0.19 |
| Ratio of standard deviations | 0.9 | 0.51 |
| Nash-Sutcliffe efficiency | 0.75 | 0.62 |
| Willmott index of agreement | 0.93 | 0.84 |
| Coefficient of persistence | −0.01 | 0.62 |
| Pearson product-moment correlation coefficient | 0.95 | 0.95 |
| Coefficient of determination | 0.91 | 0.90 |
Share and Cite
Kamble, B.; Kilic, A.; Hubbard, K. Estimating Crop Coefficients Using Remote Sensing-Based Vegetation Index. Remote Sens. 2013, 5, 1588-1602. https://doi.org/10.3390/rs5041588
Kamble B, Kilic A, Hubbard K. Estimating Crop Coefficients Using Remote Sensing-Based Vegetation Index. Remote Sensing. 2013; 5(4):1588-1602. https://doi.org/10.3390/rs5041588
Chicago/Turabian StyleKamble, Baburao, Ayse Kilic, and Kenneth Hubbard. 2013. "Estimating Crop Coefficients Using Remote Sensing-Based Vegetation Index" Remote Sensing 5, no. 4: 1588-1602. https://doi.org/10.3390/rs5041588




